Как влияет диэлектрик на емкость конденсаторов?… -reshimne.ru
Новые вопросы
Ответы
С увеличением диэлектрической проницаемости диэлектрика емкость конденсатора увеличивается. Конденсаторы, равные по своим геометрическим размерам, но содержащие в себе различные диэлектрики, имеют различную емкость.
Похожие вопросы
1) Сумма проекций всех сил, приложенных к телу на данную ось, равна
нулю. Как направлена равнодействующая такой системы сил?
2)Чему равны проекции ускорения точки на естественные оси?…
Кубановедение 6 класс кто сможет, помогите пж!!!))1 Почему черноземные почвы считают богатством Кубани ? мне нужно сообщение…
Почему князя Романа называли богобоязненным и благочестливым человеком. ..
..
Придумать не большой философский рассказ)) Заранин спасибо…
Наблюдая Луну с использованием созданного им телескопа, Галилей смог показать, что тезис Аристотеля о совершенстве небес неверен. На основании чего он сделал этот вывод?…
Больная отметила , что после подкожной инъекции в области правого плеча на третьи сутки появились боль , краснота , припухлость .На седьмые сутки припухлость и болезненность увеличились .Какое осложнение после подкожных инъекций развилось у больной?Какую помощь необходимо оказать?…
Математика
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Немецкий язык
МХК
ОБЖ
Психология
Электричество и магнетизм
Еще М.
На рис. 3.2 показан опыт, в котором демонстрируется зависимость емкости конденсатора от свойств среды между его обкладками. Между пластинами заряженного плоского конденсатора, присоединенного к электрометру, помещают диэлектрик — пластину из оргстекла. При этом показания электрометра уменьшаются, что говорит об увеличении емкости конденсатора. После удаления диэлектрика разность потенциалов увеличивается, возвращаясь к прежнему значению.
Рис. 3.2. Исследование зависимости емкости плоского конденсатора от диэлектрических свойств среды
Когда изолятор заполняет все пространство между обкладками, емкость конденсатора возрастает в раз, где безразмерная величина принимает разные значения для различных материалов. Эта величина называется диэлектрической проницаемостью данного вещества.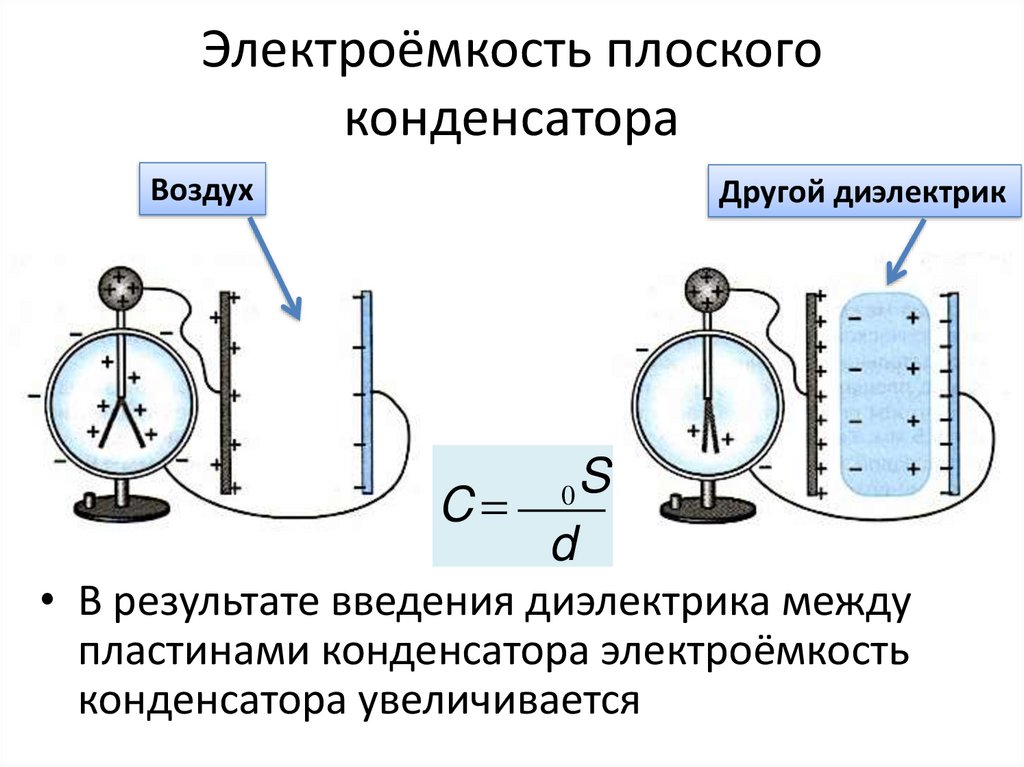
Рассмотрим снова плоский конденсатор. Зарядим его и вставим внутрь диэлектрическую пластину (рис. 3.3).
Рис. 3.3. Плоский конденсатор с диэлектрической пластиной между обкладками
Величины, относящиеся к конденсатору без диэлектрика, будем снабжать индексом 0. Так как заряд конденсатора не меняется при помещении в него диэлектрика, записываем соотношения
|
(3.1) |
Здесь мы использовали экспериментальный факт увеличения емкости конденсатора с диэлектриком в раз. Из соотношений (3.1) следует, что при том же заряде на обкладках разность их потенциалов U уменьшается в раз по сравнению с «пустым» конденсатором
Поскольку поле в плоском конденсаторе однородно, получаем следующую связь между напряженностью Е0 поля в вакууме и в диэлектрике Е
Иными словами, присутствие диэлектрика между пластинами может приводить к уменьшению напряженности электрического поля в конденсаторе.
Необходимо отметить, что простое уменьшение поля в раз внутри диэлектрика имеет место тогда и только тогда, когда поверхность диэлектрика представляет собой эквипотенциальную поверхность того поля, которое было бы в отсутствие диэлектрика. Именно этот случай и имеет место при помещении в плоский конденсатор плоскопараллельной диэлектрической пластины, внешние плоские поверхности которой параллельны плоским обкладкам конденсатора и, соответственно, совпадают с двумя эквипотенциальными поверхностями поля конденсатора без диэлектрика. То же самое имеет место, например, в случае помещения в сферический конденсатор сферического слоя диэлектрика с поверхностями концентрическими обкладкам этого конденсатора.
Если, к примеру, в однородное электрическое поле (как в идеальном плоском конденсаторе) поместить плоскопараллельную диэлектрическую пластину так, что её поверхности составят некоторый угол с направлением поля и, тем самым, они не будут совпадать с его эквипотенциальными поверхностями, то величина поля внутри этой пластины будет довольно сложным образом зависеть от угла  Не следует также думать, что внесение в поле диэлектрика всегда приводит к уменьшению напряженности поля, она может и возрасти: всё зависит от «геометрии» задачи. Ниже на рисунке 3.4 показано, что при помещении в электрическое поле тонкого длинного диэлектрического стержня параллельно силовым линиям внешнего поля, напряженность поля вне стержня у его концов увеличивается в результате появления на концах стержня «поляризационных» зарядов.
Не следует также думать, что внесение в поле диэлектрика всегда приводит к уменьшению напряженности поля, она может и возрасти: всё зависит от «геометрии» задачи. Ниже на рисунке 3.4 показано, что при помещении в электрическое поле тонкого длинного диэлектрического стержня параллельно силовым линиям внешнего поля, напряженность поля вне стержня у его концов увеличивается в результате появления на концах стержня «поляризационных» зарядов.
Рис. 3.4. Напряженность поля на оси тонкого диэлектрического стержня
Уменьшение разности потенциалов между обкладками и увеличение емкости конденсатора мы наблюдали в решенной выше задаче о сферическом конденсаторе с металлической оболочкой между обкладками. Там причина уменьшения разности потенциалов была ясна: на оболочке наводились индуцированные заряды, которые компенсировали внешнее поле от обкладок. Соответственно, электрическое поле существовало только в пространстве, не занятом оболочкой. Если бы оболочка заняла весь объем конденсатора, разность потенциалов между обкладками и поле внутри него стали бы равными нулю.
Если бы оболочка заняла весь объем конденсатора, разность потенциалов между обкладками и поле внутри него стали бы равными нулю.
В диэлектрике нет зарядов, способных перемещаться по всему его объёму, но идея возникновения на его поверхности каких-то дополнительных зарядов (их называют в этом случае поляризационными или связанными) кажется привлекательной из-за возможности объяснить экспериментальные факты. Поэтому мы принимаем макроскопическую модель, которая, разумеется, должна быть обоснована впоследствии на микроскопическом уровне и проверена на практике вместе со всеми ее следствиями. Мы предположим, что при помещении диэлектрика в электрическое поле на его поверхности возникают поляризационные заряды с плотностью (рис. 3.5).
Рис. 3.5. Сферическая частица в однородном электрическом поле напряжённостью Е.
Знаками «+» и «–» показаны связанные заряды, возникшие на поверхности частицы при её поляризации.
Электрические силы, действующие на положительные (F+) и отрицательные (F–) связанные заряды, одинаковы
Поляризационные заряды создают дополнительное электрическое поле , направленное противоположно полю от зарядов на обкладках (см. рис. 3.3). Это и объясняет меньшую величину результирующего поля Е по сравнению с полем E0. Действительно, для простейшей геометрии плоского конденсатора (см. выше замечание о форме поверхности диэлектрика) изменение поля в диэлектрике сводится только к изменению величины его напряженности в раз
|
(3.2) |
Отсюда мы находим, какая часть результирующего поля создается поляризационными зарядами, а какая — зарядами на обкладках
|
(3. |
Отрицательный знак указывает на противоположное направление поля поляризационных зарядов. Зная связь поверхностной плотности зарядов с напряженностью создаваемого ими поля
Находим плотность поляризационных зарядов
|
|
(3.4) |
Заметим, что случаю проводника соответствует предел
Действительно, тогда , а поле внутри материала полностью компенсируется, получаем
откуда
Значения e для некоторых диэлектриков приведены в таблице (для газов — при нормальных условиях).
Таблица
Значения диэлектрической проницаемости для некоторых веществ
|
Диэлектрик |
|
Диэлектрик |
|
|
Гелий |
1,00007 |
Жидкий гелий |
1,047 |
|
Водород |
1,00027 |
Жидкий водород |
1,23 |
|
Азот |
1,00058 |
Жидкий азот |
1,43 |
|
Бумага |
3,5 |
Трансформаторное масло |
4,5 |
|
Фарфор |
6,5 |
Лёд |
16 |
|
Этиловый спирт |
25,1 |
Глицерин |
56,2 |
|
Вода |
81,1 |
Титанат стронция |
310 |
|
|
|
|
|
Обратите внимание: одни и те же вещества при разных условиях имеют различные диэлектрические свойства. Значит, для их объяснения необходимо построить теорию на микроскопическом уровне, исходящую из свойств атомов и молекул и учитывающую состояние вещества.
Значит, для их объяснения необходимо построить теорию на микроскопическом уровне, исходящую из свойств атомов и молекул и учитывающую состояние вещества.
Дополнительная информация
http://chemister.da.ru/Chemie/Tables/dielectric.htm — диэлектрические проницаемости некоторых веществ;
http://www.radioland.net.ua/contentid-381-page1.html — основные типы диэлектриков, применяемые в конденсаторах;
http://ufn.ru/ufn67/ufn67_11/Russian/r6711n.pdf — статья «Вещества с высокой и сверхвысокой диэлектрической проницаемостью»;
http://www.chipdip.ru/video.aspx?vid=ID000292886&tag=dielectric — видео «Пироэлектрики»;
http://gos-rz.narod.ru/2/20.htm — сегнетоэлектрики, их применение;
http://www.rci.rutgers.edu/~ecerg/projects/ferroelectric.html — керамические сегнетоэлектрики;
http://www.chipdip.ru/video.aspx?vid=ID000292814&tag=dielectric — видео «Сегнетокерамика».
Емкость конденсатора на что влияет
Регистрация Вход. Ответы Mail. Вопросы — лидеры Задача по физике 1 ставка. Провод КСПВ, вопрос к электрикам 1 ставка.
Ответы Mail. Вопросы — лидеры Задача по физике 1 ставка. Провод КСПВ, вопрос к электрикам 1 ставка.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Подскажите, на что влияют мощность трансформатора и емкость конденсатора?
- Емкость конденсатора
- Как влияет диэлектрик на емкость конденсаторов?
- Конденсатор – для новичков в радиоделе. Что влияет на емкость конденсатора
- Влияние конденсатора на качество баса
- Конденсатор
- Электрический конденсатор
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: изменение емкости конденсатора
youtube.com/embed/637w-dV4nJ4″ frameborder=»0″ allowfullscreen=»»/>Подскажите, на что влияют мощность трансформатора и емкость конденсатора?
Электрические конденсаторы являются средством накопления электроэнергии в электрическом поле. Типичными областями применения электрических конденсаторов являются сглаживающие фильтры в источниках электропитания, цепи межкаскадной связи в усилителях переменных сигналов, фильтрация помех, возникающих на шинах электропитания электронной аппаратуры и т д.
Электрические характеристики конденсатора определяются его конструкцией и свойствами используемых материалов. При выборе конденсатора для конкретного устройства нужно учитывать следующие обстоятельства:.
Может быть указано сопротивление диэлектрика конденсатора. В табл. Таблица 1. Характеристики керамических, электролитических конденсаторов и конденсаторов на основе металлизированной пленки.
Таблица 2. Характеристики слюдяных конденсаторов и конденсаторов на основе полиэстера и полипропилена. Таблица 3. Характеристики слюдяных конденсаторов на основе поликарбоната, полистирена и тантала. Керамические конденсаторы применяются в разделительных цепях, электролитические конденсаторы используются также в разделительных цепях и сглаживающих фильтрах, а конденсаторы на основе металлизированной пленки применяются в высоковольтных источниках электропитания.
Таблица 3. Характеристики слюдяных конденсаторов на основе поликарбоната, полистирена и тантала. Керамические конденсаторы применяются в разделительных цепях, электролитические конденсаторы используются также в разделительных цепях и сглаживающих фильтрах, а конденсаторы на основе металлизированной пленки применяются в высоковольтных источниках электропитания.
Слюдяные конденсаторы используются в звуковоспроизводящих устройствах, фильтрах и осцилляторах. Конденсаторы на основе полиэстера — это конденсаторы общего назначения, а конденсаторы на основе полипропилена применяются в высоковольтных цепях постоянного тока. Конденсаторы на основе поликарбоната используются в фильтрах, осцилляторах и времязадающих цепях. Конденсаторы на основе полистирена и тантала используются также во времязадающих и разделительных цепях. Они считаются конденсаторами общего назначения.
Небольшие замечания и советы по работе с конденсаторами. Всегда нужно помнить, что рабочие напряжения конденсаторов следует уменьшать при возрастании температуры окружающей среды, а для обеспечения высокой надежности необходимо создавать большой запас по напряжению. Если задано максимальное постоянное рабочее напряжение конденсатора, то это относится к максимальной температуре при отсутствии дополнительных оговорок.
Если задано максимальное постоянное рабочее напряжение конденсатора, то это относится к максимальной температуре при отсутствии дополнительных оговорок.
Поэтому конденсаторы всегда работают с определенным запасом надежности. Тем не менее нужно обеспечивать их реальное рабочее напряжение на уровне 0,5—0,6 разрешенного значения.
Если для конденсатора оговорено предельное значение переменного напряжения, то это относится к частоте Гц. Для более высоких частот или в случае импульсных сигналов следует дополнительно снижать рабочие напряжения во избежание перегрева приборов из-за потерь в диэлектрике.
Конденсаторы большой емкости с малыми токами утечки способны довольно долго сохранять накопленный заряд после выключения аппаратуры. Для обеспечения большей безопасности следует в цепь разряда подключить параллельно конденсатору резистор сопротивлением 1 МОм 0,5 Вт. В высоковольтных цепях часто используется последовательное включение конденсаторов. Для выравнивания напряжений на них нужно параллельно каждому конденсатору подключить резистор сопротивлением от к0м до 1 МОм.
Керамические проходные конденсаторы могут работать на очень высоких частотах свыше 30 МГц. Их устанавливают непосредственно на корпусе прибора или на металлическом экране. Неполярные электролитические конденсаторы имеют емкость от 1 до мкФ и рассчитаны на действующее значение напряжения 50 В. Кроме того, они дороже обычных полярных электролитических конденсаторов. При выборе конденсатора фильтра источника электропитания следует обращать внимание на амплитуду импульса зарядного тока, который может значительно превосходить допустимое значение.
Например, для конденсатора емкостью 10 мкФ эта амплитуда не превышает 5 А. При использовании электролитического конденсатора в качестве разделительного необходимо правильно определить полярность его включения.
Ток утечки этого конденсатора может влиять на режим усилительного каскада. В большинстве случаев применения электролитические конденсаторы взаимозаменяемы. Следует лишь обращать внимание на значение их рабочего напряжения.
Вывод от внешнего слоя фольги полистиреновых конденсаторов часто помечается цветным штрихом. Его нужно присоединять к общей точке схемы. На высоких частотах сопротивление паразитных индуктивностей конденсатора возрастает, что ухудшает его рабочие характеристики.
Его нужно присоединять к общей точке схемы. На высоких частотах сопротивление паразитных индуктивностей конденсатора возрастает, что ухудшает его рабочие характеристики.
На рисунке 2 приведена упрошенная эквивалентная схема конденсатора с учетом инцуктивносги вводов. Цветовая маркировка конденсаторов.
На корпусе большинства конденсаторов написаны их номинальная емкость и рабочее напряжение. Однако встречается и цветовая маркировка.
Некоторые конденсаторы маркируют надписью в две строки. На второй строке приведены допустимое постоянное напряжение и код материала диэлектрика. Монолитные керамические конденсаторы маркируются кодом, состоящим из трех цифр.
Третья цифра показывает, сколько нулей нужно подписать к первым двум, чтобы получить емкость в пикофарадах.
Цветовой код для обозначения номинала конденсатора кб. Что означает код на конденсаторе? Код означает, что нужно приписать три нуля к числу 10, тогда получится емкость конденсатора — 10 пФ. Искать в Школе для электрика:. Электрические конденсаторы Электрические конденсаторы являются средством накопления электроэнергии в электрическом поле.
Электрические конденсаторы Электрические конденсаторы являются средством накопления электроэнергии в электрическом поле.
При выборе конденсатора для конкретного устройства нужно учитывать следующие обстоятельства: а требуемое значение емкости конденсатора мкФ, нФ, пФ , б рабочее напряжение конденсатора то максимальное значение напряжения, при котором конденсатор может работать длительно без изменения своих параметров , в требуемую точность возможный разброс значений емкости конденсатора , г температурный коэффициент емкости зависимость емкости конденсатора от температуры окружающей среды , д стабильность конденсатора, е ток утечки диэлектрика конденсатора при номинальном напряжении и данной температуре.
Характеристики керамических, электролитических конденсаторов и конденсаторов на основе металлизированной пленки Параметр конденсатора. Тип конденсатора. На основе металлизированной пленки. От 2,2 пФ до 10 нФ. От нФ до 68 мкФ. Диапазон изменения температуры окружающей среды, о С. Параметр конденсатора. На основе поликарбоната. На основе полистирена.
Параметр конденсатора. На основе поликарбоната. На основе полистирена.
На основе тантала. От 10 нФ до 10 мкФ. От нФ до мкФ.
Емкость конденсатора
Конденсатор является одной из самых важных частей любой мало-мальски сложной схемы. Наибольшую ценность для нас представляет его емкость. Что это такое? Как она измеряется? Какие есть нюансы? Эти, а также и другие вопросы будут рассмотрены в рамках статьи. Это название характеристики проводника, которая обозначает возможность накопления электрического заряда.
Конденсатор — элемент обладающий электрической емкостью. Емкость Поэтому важно знать, как влияют на емкость расположенные вблизи данного.
Как влияет диэлектрик на емкость конденсаторов?
Ru — форумы для гитаристов У нас самая большая гитарная тусовка. Добро пожаловать, Гость. Пожалуйста, войдите или зарегистрируйтесь. Не получили письмо с кодом активации? В теме В разделе По форуму Google Яндекс. Автор Тема: На что влияет емкость конденсатора в потенциометре тона? Прочитано раз.
Конденсатор – для новичков в радиоделе. Что влияет на емкость конденсатора
Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Войти Регистрация. Изменение ёмкости керамических конденсаторов от температуры и напряжения, или как ваш конденсатор на 4,7мкФ превращается в 0,33мкФ Автор оригинала: Mark Fortunato.
Atoll AM SE — два массивных тороидальных трансформатора общей мощностью в ВА, суммарный показатель емкости буферных конденсаторов — мкФ. Сравнение в конкретном случае не совсем корректное, конструктивно модели разные.
Влияние конденсатора на качество баса
Файлы Галереи Справка Календарь Все разделы прочитаны. Посетителям Новеньким Патриотам. Регистрируясь на данном ресурсе Вы соглашаетесь с действующими Правилами форума и обязуетесь их соблюдать. Незнание правил не освобождает Вас от наказания за их нарушение! На форуме действует ряд ограничений для новых пользователей: запрещено заниматься торговлей, устанавливать автар и подпись, принимать участие в опросах, личный ящик ограничен ю сообщениями. Для снятия ограничений Вам надо оставить на форуме более 10 сообщений, а также с момента вашей регистрации должно пройти не менее 30 дней.
Для снятия ограничений Вам надо оставить на форуме более 10 сообщений, а также с момента вашей регистрации должно пройти не менее 30 дней.
Конденсатор
Алюминиевые электролитические конденсаторы широко используются в различных электро- и радиотехнических приборах теле-, радио-, аудиоустройствах, стиральных машинах, кондиционерах воздуха и т. Применение на постоянном напряжении с наложенной переменной составляющей пульсирующее напряжение :. Алюминиевый электролитический конденсатор имеет простую конструкцию. Две ленты из конденсаторной бумаги проложены между двумя лентами из специальным образом обработанной алюминиевой фольги и эта комбинация из четырех лент свернута в рулон. Бумага, служащая сепаратором для алюминиевых электродов, пропитана электропроводящим раствором. К электродам присоединены выводы, образуя активный элемент конденсатора.
Увеличение емкости конденсатора на выходе источника питания выше некоторого значения не приводит к заметному улучшению качества выходного.
Электрический конденсатор
Заряд и разряд конденсатора. Конденсатор представляет собой устройство, способное накапливать электрические заряды. Простейшим конденсатором являются две металлические пластины электроды , разделенные каким-либо диэлектриком.
Увеличение емкости конденсатора С увеличивает коэффициент усиления усилителя и уменьшает величину фазового сдвига. Увеличение емкости конденсатора на выходе источника питания выше некоторого значения не приводит к заметному улучшению качества выходного напряжения. Увеличение емкости конденсаторов С12, С14 вызывает снижение чувствительности, а уменьшение — увеличение. Увеличение емкости конденсатора увеличивает длительность.
Конденсатор — элемент обладающий электрической емкостью. Емкость проводников, удаленных от других предметов уединенных проводников , зависит от размеров и формы самих проводников.
Это зависит от геометрических параметров проводника. Коэффициент пропорциональности С называют электроемкостью — физическая величина, численно равная заряду, который необходимо сообщить проводнику для того, чтобы изменить его потенциал на единицу. Единица измерения емкости в СИ — фарада. По этой формуле можно рассчитать емкость Земли. Необходимость в устройствах, накапливающих заряд, есть, а уединенные проводники обладают малой емкостью. Опытным путем было обнаружено, что электроемкость проводника увеличивается, если к нему поднести другой проводник — за счет явления электростатической индукции.
Единица измерения емкости в СИ — фарада. По этой формуле можно рассчитать емкость Земли. Необходимость в устройствах, накапливающих заряд, есть, а уединенные проводники обладают малой емкостью. Опытным путем было обнаружено, что электроемкость проводника увеличивается, если к нему поднести другой проводник — за счет явления электростатической индукции.
Конденсатор является пассивным электронным компонентом. Ёмкость конденсатора измеряется в фарадах. Первые конденсаторы, состоящие из двух проводников, разделенных непроводником диэлектриком , упоминаемые обычно как конденсатор Эпинуса или электрический лист, были созданы ещё раньше [3]. Конденсатор является пассивным электронным компонентом [4].
Отношение — емкость — конденсатор
Cтраница 2
Одной из важнейших характеристик изоляции является диэлектрическая проницаемость е, представляющая собой отношение емкости конденсатора с принятой для него изоляцией к емкости конденсатора тех же размеров, изоляцией которого является вакуум. [16]
[16]
Из формулы ( 5) видно, что диэлектрическую проницаемость вещества е можно определить как отношение емкости конденсатора с диэлектриком из данного вещества к емкости конденсатора тех же размеров, диэлектриком которого является вакуум. [17]
Из формулы ( 1 — 4) следует, что диэлектрическую проницаемость вещества ег можно определить как отношение емкости конденсатора с данным диэлектриком к емкости конденсатора тех же размеров, диэлектриком которого является вакуум. [18]
Из формулы ( 1 — 4) видно, что диэлектрическую проницаемость вещества е можно определить как отношение емкости конденсатора с диэлектриком из данного вещества к емкости конденсатора тех же размеров, диэлектриком которого является вакуум. [19]
| Диэлектрик сложного состава с различными механизмами поляризации в электрическом поле ( а и его эквивалентная схема ( б. [20] |
Из формулы ( 1 — 4) следует, что диэлектрическую проницаемость вещества ег можно определить как отношение емкости конденсатора с данным диэлектриком к емкости конденсатора тех же размеров, диэлектриком которого является вакуум. [21]
[21]
Удельными характеристиками называются отношение одной из электрических характеристик конденсатора к его объему или массе; так, например, удельная емкость представляет собой отношение емкости конденсатора к его объему; удельная реактивная мощность — отношение реактивной мощности конденсатора к его объему или массе. [22]
Удельными характеристиками называются отношение одной из электрических характеристик конденсатора к его объему или весу; так, некоторые из них: удельная емкость представляет собой отношение емкости конденсатора к его объему, мкф / см3; удельная реактивная мощность — отношение реактивной мощности конденсатора к его объему или — весу, квар / дм3 или квар. [23]
Причина использования такой системы записи состоит в том, что е является важной характеристикой свойств диэлектрика, имеющей, помимо связи с а, и большое самостоятельное значение: диэлектрическая проницаемость е может быть определена как отношение емкости конденсатора, заполненного данным диэлектриком, к емкости конденсатора в отсутствие диэлектрика. [24]
[24]
Диэлектрическая проницаемость горных пород — величина, показывающая, во сколько раз напряженность электрического поля в горной породе меньше напряженности внешнего электрического поля, в которое помещена порода. Численно равна отношению емкости конденсатора, заполненного породой, к емкости пустого конденсатора. Влажность также значительно влияет на проницаемость. [25]
Электроотрицательность элемента есть мера его способности притягивать электроны. Эта величина представляет собой отношение емкости конденсатора, между обкладками которого находится вакуум, к емкости конденсатора, заполненного измеряемым веществом. По своей относительной проницаемости растворители делятся на две категории. Полярные растворители ( вода, спирты, ацетон, пиридин) характеризуются большими еотн, а неполярные ( пентан, бензол, тетра-хлорометан) — малыми. [26]
Величины, приведенные в табл. 71, выражают следующие понятия. Диэлектрическая проницаемость численно равна отношению емкости конденсатора при наличии между его обкладками испытуемого диэлектрика к емкости того же конденсатора при вакууме. Тангенс угла диэлектрических потерь tg 8 характеризует потери мощности, поглощаемой электроизоляционными материалами — в переменном электрическом поле. Электрическая прочность электроизоляционных материалов численно равна величине пробивного напряжения, отнесенного к толщине материала в точке пробоя.
[27]
Диэлектрическая проницаемость численно равна отношению емкости конденсатора при наличии между его обкладками испытуемого диэлектрика к емкости того же конденсатора при вакууме. Тангенс угла диэлектрических потерь tg 8 характеризует потери мощности, поглощаемой электроизоляционными материалами — в переменном электрическом поле. Электрическая прочность электроизоляционных материалов численно равна величине пробивного напряжения, отнесенного к толщине материала в точке пробоя.
[27]
Скорость распространения электромагнитных колебаний в кабелях связи зависит от применяемого в нем диэлектрика. В большинстве практических случаев цотн 1; еотн можно определить по отношению емкости конденсатора с данным диэлектриком к емкости того же конденсатора в вакуумном исполнении. [28]
Диэлектрическая постоянная является безразмерной величиной, характеризующей изолирующие свойства среды. Если эта среда заполняет пространство между пластинами конденсатора, то ее диэлектрическая постоянная равна отношению емкости конденсатора в этом состоянии к емкости того же конденсатора, когда между его пластинами находится вакуум. [29]
[29]
Диэлектрометрия, как метод исследования электронной структуры, динамики молекул и межмолекулярных взаимодействий в растворах и чистых жидкостях, основан на изучении процессов поляризации веществ под воздействием внешнего электрического поля. Своми корнями ди-электрометрия уходит в конец прошлого столетия к работам Фарадея, который обнаружил, что отношение емкостей заполненного и пустого конденсатора является постоянной характеристикой заполняющего конденсатор вещества, которая получила название диэлектрической проницаемости ( е), а само вещество — название диэлектрика. Примерно в то же время, изменяя диэлектрическую проницаемость в переменном электрическом поле, Друдэ обнаружил, что для ряда веществ в определенной области частот / переменного поля наблюдается зависимость е от /, получившая название аномальной дисперсии диэлектрической проницаемости. Непосредственно измеряемыми в диэлектрометрии являются макроскопические характеристики е и е исследуемых жидкостей, которые отражают их способность поляризоваться или индуцировать в себе заряды под воздействием внешнего электрического поля. [30]
[30]
Страницы: 1 2 3
Влияние — диэлектрик — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
| Сгущение линий электрической индукции однородным диэлектрическим шаром, помещенным в однородном. [1] |
Влияние диэлектрика на электрическое поле заключается прежде всего в том, что диэлектрик ослабляет напряженность электрического поля. По обобщенному закону Кулона в однородной диэлектрической среде, имеющей диэлектрическую постоянную г, электрические заряды взаимодействуют с силой, в е раз меньшей, чем в вакууме. [2]
Влияние диэлектрика на энергию W e сказывается в том, что при неизменном распределении свободных зарядов значения ф в разных диэлектриках различны. [3]
Рассматриваются влияние диэлектрика на электрическое поле и различные механизмы поляризации.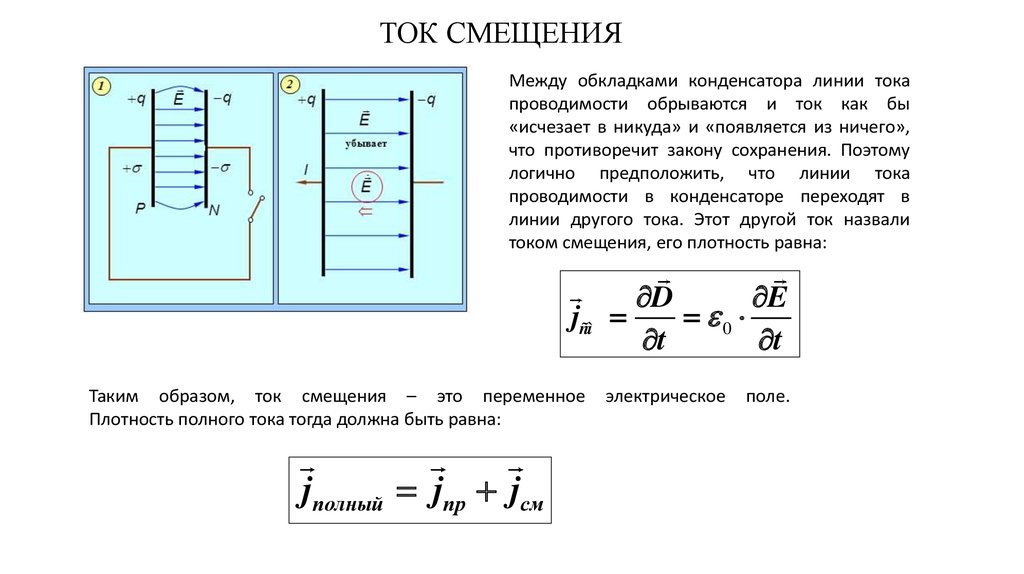 Выводится соотношение между плотностями объемных и поверхностных связанных зарядов и поляризованностъю. Обсуждаются явления на границе между диэлектриками.
[4]
Выводится соотношение между плотностями объемных и поверхностных связанных зарядов и поляризованностъю. Обсуждаются явления на границе между диэлектриками.
[4]
Первое объяснение причины — влияния диэлектрика на емкость заключалось в следующем. Кавендиш полагал, что электричество из металла проникает в глубь диэлектрика на некоторую конечную глубину и это приводит к уменьшению толщины слоя диэлектрика, а следовательно, к увеличению емкости. [5]
Например, было рассмотрено [120] влияние диэлектрика в случае спиральной опоры для коаксиальной линии, однако большинство работ [181, 220, 227, 275, 286, 311 ] посвящено определению влияния непрерывной оболочки на характеристики металлической спирали. В обстоятельном исследовании Тьена [300] показано, что фазовая скорость и импеданс связи уменьшаются за счет коэффициента диэлектрической нагрузки. Этот коэффициент обычно имеет значения от 0 2 до 0 8 и может быть увеличен, если спираль закрепляется посредством трубок или уголков так, что основная масса диэлектрика удаляется от поверхности спирали. [6]
[6]
При эквивалентной замене (V.42) предполагается, что влияние диэлектрика на замедление волны пропорционально произведению напряженности поля на площадь, занимаемую диэлектриком. При этом предполагается также, что напряженность электрического поля до и после введения диэлектрика мало изменяется и в первом приближении остается неизменной. При замене по формуле (V.42) диэлектрическая постоянная реального образца и эквивалентной системы одинаковы. Искомым является размер эквивалентной трубки. Так как поле меняется по частоте, то размеры эквивалентного диэлектрика также зависят от частоты. [7]
Формулы (17.17) и (17.21) позволяют полностью учесть влияние диэлектрика на электрическое поле. Создаваемая связанными зарядами напряженность поля вычисляется по тем же формулам, по которым определяется напряженность в вакууме, порождаемая свободными зарядами. [8]
Ослаблением поля в диэлектрике, обусловленным поляризацией последнего, объясняют влияние диэлектрика на силу взаимодействия между наэлектризованными телами. Теперь становится понятным, почему сила взаимодействия между зарядами имеет наибольшую величину в вакууме и почему в формулу закона Кулона входит диэлектрическая проницаемость среды ес.
[9]
Теперь становится понятным, почему сила взаимодействия между зарядами имеет наибольшую величину в вакууме и почему в формулу закона Кулона входит диэлектрическая проницаемость среды ес.
[9]
Из сопоставления равенств ( а) и ( б) получается, что влияние диэлектрика на поле, возбуждаемое свободными зарядами, сводится к некоторому дополнительному полю в вакууме, обусловленному связанными зарядами. [10]
Силовые трубки, заполненные движущейся несжимаемой жидкостью, легко объясняли опыт Фарадея, обнаружившего влияние диэлектрика, промежуточной непроводящей среды, на процесс зарядки конденсатора. В рамки теории Максвелла легко и просто укладывались понятия о сопротивлении, испытываемом струями жидкости. [11]
При выполнении работ лаборатории студенты знакомятся с электростатическими полями различной конфигурации, движением заряженных частиц в электростатическом поле, силовым взаимодействием заряженных тел, изучением полей методом электростатической ванны, влиянием диэлектрика на электростатическое поле, выполняют опыт Милликена по определению величины элементарного заряда, изучают гальванометр магнитоэлектрической системы и метод компенсационных измерений. [12]
[12]
Заметим, что формула (41.06) и все следующие из нее выводы остаются справедливыми, если весь отрезок 0zL запол — нен диэлектриком; в этом случае нужно лишь считать — kL f и учесть влияние диэлектрика на волновые сопротивления WQ и W. Боковую стенку поршня необязательно считать бесконечно тонкой: она может иметь любую толщину. [13]
В опытах Фарадея пламя можно рассматривать как проводник, связанный с землей. Влияние диэлектрика выражается в появлении кажущейся электризации на его поверхности. Эта кажущаяся электризация, воздействуя на проводящее пламя, притягивает к себе электричество противоположного знака, распределяющееся по поверхности диэлектрика, тогда как электричество того же знака отталкивается через пламя на землю. Таким образом, на поверхности диэлектрика появляется действительная электризация, компенсирующая влияние кажущейся электризации. При устранении индуцирующей силы кажущаяся электризация исчезает, а действительная электризация остается и уже не компенсируется кажущейся. [14]
[14]
| Схематическое устройство конденсаторов основных типов. [15] |
Страницы: 1 2
определение, основные понятия и примеры решений
Содержание:
- Плоские конденсаторы
- Конденсатор сферического типа
- Конденсатор цилиндрического типа
- Расчёт емкостных батарей, соединений конденсаторов
Определение 1
Конденсатором называют любые два проводника, разделённые диэлектрическим слоем. Такие проводники должны обладать зарядами одинаковыми по величине, но противоположными по знаку.
Возникающее электрическое поле будет полностью расположено внутри, между проводниками. По этой причине на электрическую ёмкость конденсатора не влияет его внешнее окружение. А на разность потенциалов между пластинами не влияет величина заряда.
Выражение для электроёмкости выглядит так:
$ C=\frac{q}{\phi_1-\phi_2} = \frac{q}{U} $
Величины $ {\phi_1-\phi_2=U}$ определяют разность потенциалов, которая также носит название «напряжение» и обозначается «U». Как следует из определения, ёмкость — положительная величина. Её размер определяется габаритами пластин конденсатора, их взаимным расположением, типом диэлектрика. Форма пластин, конструкция конденсатора создаются таким образом, чтобы максимально снизить влияние на внутреннее поле со стороны любых внешних сил или полей. Электрическое поле конденсатора начинается на обкладке с зарядом «+» и заканчивается на обкладке со знаком «-». Ёмкость конденсаторов измеряют так же, как и ёмкость проводников, в международной системе СИ для этого используют Фарады (Ф). Один Фарад — ёмкость конденсатора, где при заряде 1 Кельвин, разность потенциалов 1 Вольт.
Как следует из определения, ёмкость — положительная величина. Её размер определяется габаритами пластин конденсатора, их взаимным расположением, типом диэлектрика. Форма пластин, конструкция конденсатора создаются таким образом, чтобы максимально снизить влияние на внутреннее поле со стороны любых внешних сил или полей. Электрическое поле конденсатора начинается на обкладке с зарядом «+» и заканчивается на обкладке со знаком «-». Ёмкость конденсаторов измеряют так же, как и ёмкость проводников, в международной системе СИ для этого используют Фарады (Ф). Один Фарад — ёмкость конденсатора, где при заряде 1 Кельвин, разность потенциалов 1 Вольт.
Существуют три основных типа конденсаторов: плоские, сферические, цилиндрические. Вычислить ёмкость можно, если найти напряжение на обкладках и определить величину заряда.
Плоские конденсаторы
Определение 2
Плоский конденсатор — элемент состоящий из двух или нескольких плоских пластин, расположенных друг напротив друга, имеющих одинаковый по величине, но разный по знаку заряд. Чтобы не возникало воздушного разряда, пластины разделяют слоем диэлектрика.
Чтобы не возникало воздушного разряда, пластины разделяют слоем диэлектрика.
Для вычисления ёмкости плоского конденсатора используется выражение:
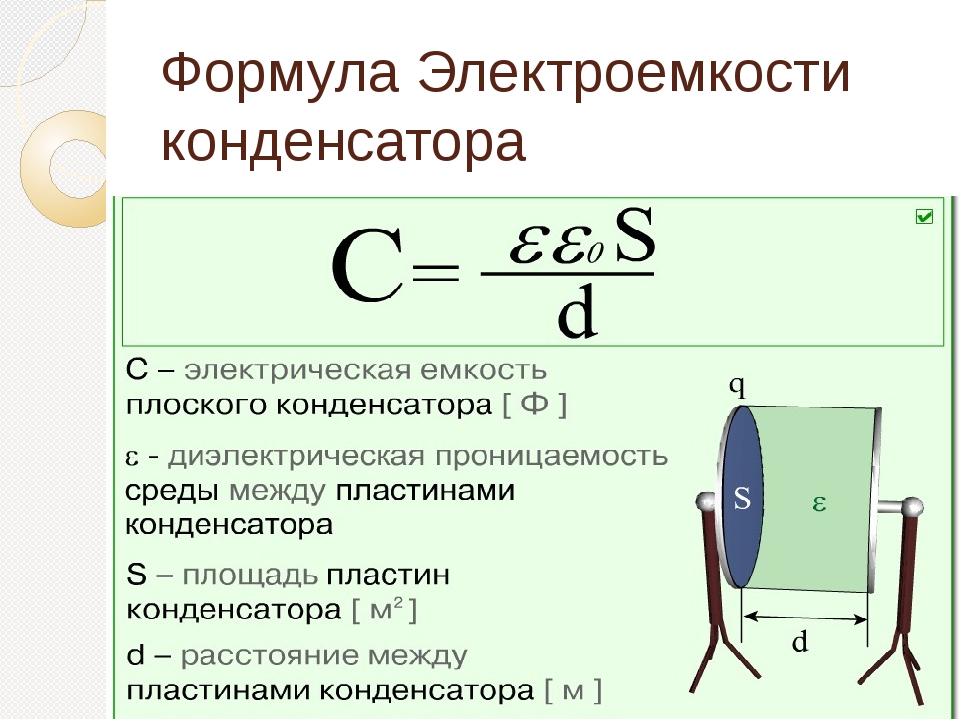
$C=\frac{\epsilon\epsilon_0 S}{d}$.
Здесь S — площадь пластин, чем она больше, тем выше ёмкость. Величина зазора между пластинами — d. Чем меньше d, тем больше ёмкость. Диэлектрическая проницаемость — ε. Она также оказывает значительное влияние на величину ёмкости.
Пример 1
Возьмём конденсатор состоящий из двух пластин, между которыми воздух, и определим его ёмкость. Затем поместим между пластинами диэлектрик, параметр ε которого выше, чем у воздуха. Измерения показывают, что ёмкость конденсатора увеличивается существенно, прямо пропорционально повышению диэлектрической проницаемости.
Чаще всего, при создании плоских конденсаторов делают не две пластины, а «пакет» обкладок в несколько слоёв. Электрическая ёмкость такого элемента, имеющего n слоёв, вычисляется с учётом толщины каждого i-го слоя $d_i$, а также диэлектрической проницаемости каждого слоя $ε_i$.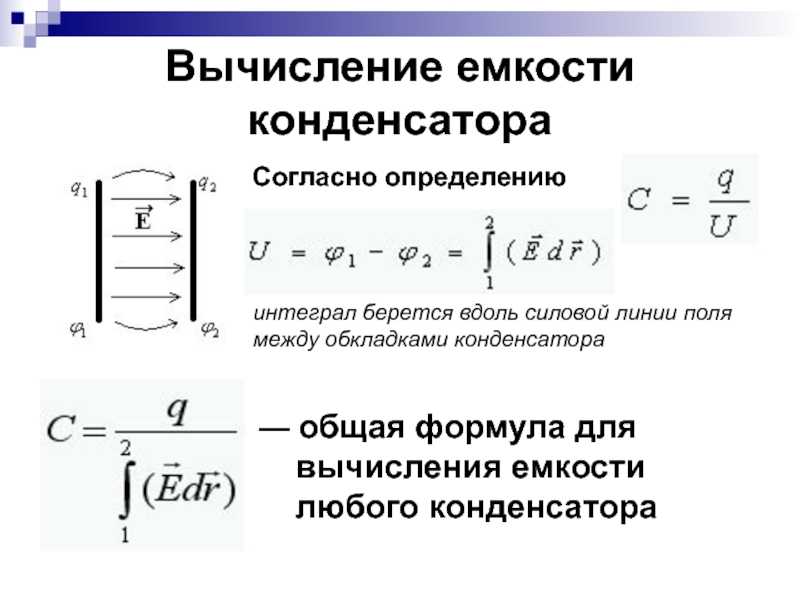
Конденсатор сферического типа
Определение 3
Сферический конденсатор отличается формой обкладок, у него они представляют собой сферы. И внешняя, и внутренняя — обе оболочки выполнены в виде сфер.
В отличии от плоского конденсатора, в сферическом площадь поверхности разнозаряженных пластин отличается. И формула для вычисления ёмкости элемента изменится:
$ C = 4\pi\epsilon\epsilon_0\frac{R_1 R_2}{R_2-R_1} $,
где $ R_1 $ и $ R_2 $ являются радиусами обкладок.
Конденсатор цилиндрического типа
Отдельная формула используется для вычисления параметров конденсатора цилиндрической формы:
$ C = 2\pi\epsilon\epsilon_0 \frac{l}{ln{\frac{R_2}{R_1}}} $.
В уравнении использованы следующие параметры: l — высота, $R_1 и R_2$ – радиусы пластин. Конденсатор цилиндрического вида выполнен в виде вложенных друг в друга соосных цилиндрических пластин. Они выполнены из проводящего материала, а между ними находится диэлектрик.
Определение 4
Параметр, характеризующий конденсаторы — пробивное напряжение. 4 \frac{В}{м}$
4 \frac{В}{м}$
8.5: Конденсатор с диэлектриком
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4396
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Описывать влияние диэлектрика в конденсаторе на емкость и другие свойства
- Рассчитайте емкость конденсатора, содержащего диэлектрик
Как мы обсуждали ранее, изоляционный материал, помещенный между пластинами конденсатора, называется диэлектриком. Вставка диэлектрика между пластинами конденсатора влияет на его емкость. Чтобы понять почему, давайте рассмотрим эксперимент, описанный на рисунке \(\PageIndex{1}\). Первоначально конденсатор емкостью \(C_0\) при наличии воздуха между его пластинами заряжается от батареи до напряжения \(V_0\). Когда конденсатор полностью заряжен, батарея отключается. Заряд \(Q_0\) остается на пластинах, и измеряется разность потенциалов между пластинами, равная \(V_0\). Теперь предположим, что мы вставляем диэлектрик, который полностью заполняет зазор между пластинами. Если мы проследим за напряжением, мы обнаружим, что показания вольтметра упали до меньшего значения \(В\). Мы записываем это новое значение напряжения как часть исходного напряжения \(V_0\) с положительным числом \(\каппа, \, \каппа > 1\).
Первоначально конденсатор емкостью \(C_0\) при наличии воздуха между его пластинами заряжается от батареи до напряжения \(V_0\). Когда конденсатор полностью заряжен, батарея отключается. Заряд \(Q_0\) остается на пластинах, и измеряется разность потенциалов между пластинами, равная \(V_0\). Теперь предположим, что мы вставляем диэлектрик, который полностью заполняет зазор между пластинами. Если мы проследим за напряжением, мы обнаружим, что показания вольтметра упали до меньшего значения \(В\). Мы записываем это новое значение напряжения как часть исходного напряжения \(V_0\) с положительным числом \(\каппа, \, \каппа > 1\).
\[V = \frac{1}{\kappa}V_0.\]
Постоянная \(\каппа\) в этом уравнении называется диэлектрической проницаемостью материала между пластинами, и ее значение является характеристикой материала. Подробное объяснение того, почему диэлектрик снижает напряжение, дано в следующем разделе. Различные материалы имеют разные диэлектрические постоянные (таблица значений для типичных материалов представлена в следующем разделе). Как только батарея отключается, заряд не может течь к батарее от пластин конденсатора. Следовательно, введение диэлектрика не влияет на заряд пластины, который остается равным \(Q_0\). Следовательно, находим, что емкость конденсатора с диэлектриком равна
Как только батарея отключается, заряд не может течь к батарее от пластин конденсатора. Следовательно, введение диэлектрика не влияет на заряд пластины, который остается равным \(Q_0\). Следовательно, находим, что емкость конденсатора с диэлектриком равна
\[C = \frac{Q_0}{V} = \frac{Q_0}{V_0/\каппа} = \каппа \frac{Q_0}{V_0} = \каппа C_0. \метка{eq1}\]
Это уравнение говорит нам, что емкость \(C_0\) пустого (вакуумного) конденсатора может быть увеличена в \(\каппа\) раз, когда мы полностью вставляем диэлектрический материал. заполнить пространство между его пластинами . Обратите внимание, что уравнение \ref{eq1} также можно использовать для пустого конденсатора, установив \(\kappa = 1\). Другими словами, мы можем сказать, что диэлектрическая проницаемость вакуума равна 1, что является эталонным значением.
Рисунок \(\PageIndex{1}\): (a) Полностью заряженный вакуумный конденсатор имеет напряжение \(V_0\) и заряд \(Q_0\) (заряды остаются на внутренних поверхностях пластины; на схеме указан знак платы за каждую тарелку). (b) На шаге 1 батарея отключена. Затем, на шаге 2, в заряженный конденсатор вставляется диэлектрик (то есть электрически нейтральный). Когда теперь измеряется напряжение на конденсаторе, обнаруживается, что значение напряжения уменьшилось до \(V = V_0/\kappa\). На схеме указан знак индуцированного заряда, который теперь присутствует на поверхностях диэлектрического материала между пластинами.
(b) На шаге 1 батарея отключена. Затем, на шаге 2, в заряженный конденсатор вставляется диэлектрик (то есть электрически нейтральный). Когда теперь измеряется напряжение на конденсаторе, обнаруживается, что значение напряжения уменьшилось до \(V = V_0/\kappa\). На схеме указан знак индуцированного заряда, который теперь присутствует на поверхностях диэлектрического материала между пластинами. Принцип, выраженный уравнением \ref{eq1}, широко используется в строительной отрасли (рис. \(\PageIndex{2}\)). Металлические пластины в электронном искателе шипов эффективно действуют как конденсатор. Вы кладете искатель гвоздей плоской стороной на стену и непрерывно перемещаете его в горизонтальном направлении. Когда искатель перемещается по деревянной стойке, емкость ее пластин изменяется, потому что древесина имеет другую диэлектрическую проницаемость, чем гипсовая стена. Это изменение запускает сигнал в цепи, и, таким образом, шпилька обнаруживается. 92}{\каппа C_0} = \фракция{1}{\каппа} U_0. \метка{8.12}\]
\метка{8.12}\]
Когда образец диэлектрического материала подносится к пустому заряженному конденсатору, образец реагирует на электрическое поле зарядов на обкладках конденсатора. Как мы узнали из раздела «Электрические заряды и поля по электростатике», на поверхности образца будут индуцированные заряды; однако они не являются свободными зарядами, как в проводнике, потому что в идеальном изоляторе нет свободно движущихся зарядов. Эти индуцированные заряды на поверхности диэлектрика имеют противоположный знак по отношению к свободным зарядам на пластинах конденсатора, поэтому они притягиваются свободными зарядами на пластинах. Следовательно, диэлектрик «втягивается» в зазор, а работа по поляризации диэлектрического материала между пластинами совершается за счет запасенной электрической энергии, которая уменьшается в соответствии с уравнением \ref{8.12}.
Пример \(\PageIndex{1}\): вставка диэлектрика в изолированный конденсатор с диэлектрической проницаемостью 2,1 полностью заполняет пространство между обкладками конденсатора (см.
 рисунок \(\PageIndex{1}\)). Какие значения:
рисунок \(\PageIndex{1}\)). Какие значения:- емкость,
- заряд плиты,
- разность потенциалов между пластинами, а
- энергия, запасенная в конденсаторе с диэлектриком и без него?
Стратегия
Отождествим исходную емкость \(C_0 = 20,0 \, пФ\) и исходную разность потенциалов \(V_0 = 40,0 \, В\) между пластинами. Мы комбинируем уравнение \ref{eq1} с другими соотношениями, включающими емкость и замену.
Раствор
а. Емкость увеличивается до \[С = \каппа С_0 = 2,1(20,0 мкФ) = 42,0 мкФ. \номер\]
б. Без диэлектрика заряд на обкладках равен \[Q_0 = C_0V_0 = (20,0 \, пФ)(40,0 \, В) = 0,8 \, нКл. \номер\] Поскольку батарея отключается до того, как вставлен диэлектрик, заряд пластины не зависит от диэлектрика и остается равным 0,8 нКл.
г. С диэлектриком разность потенциалов становится \[V = \frac{1}{\kappa}V_0 = \frac{1}{2.1}40,0 \, V = 19,0 \, V. 2 = 16,0 \, нДж . \nonumber\] Со вставленным диэлектриком мы используем уравнение \ref{8.12}, чтобы найти, что накопленная энергия уменьшается до \[U = \frac{1}{\kappa}U_0 = \frac{1}{2.1} 16,0 \ , нДж = 7,6 \, нДж. \номер\]
2 = 16,0 \, нДж . \nonumber\] Со вставленным диэлектриком мы используем уравнение \ref{8.12}, чтобы найти, что накопленная энергия уменьшается до \[U = \frac{1}{\kappa}U_0 = \frac{1}{2.1} 16,0 \ , нДж = 7,6 \, нДж. \номер\]
Значение
Обратите внимание, что влияние диэлектрика на емкость конденсатора заключается в резком увеличении его емкости. Этот эффект намного глубже, чем простое изменение геометрии конденсатора.
Упражнение \(\PageIndex{1}\)
Когда диэлектрик вставлен в изолированный и заряженный конденсатор, накопленная энергия уменьшается до 33% от первоначального значения.
- Что такое диэлектрическая проницаемость?
- Как меняется емкость?
- Ответить
а. 3,0; б. \(С = 3,0 \, С_0\)
Эта страница под названием 8.5: Конденсатор с диэлектриком распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- Емкость
- диэлектрик
- диэлектрическая проницаемость
- источник@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
18.5 Конденсаторы и диэлектрики – физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Вычислять энергию, запасенную в заряженном конденсаторе, и емкость конденсатора
- Объяснить свойства конденсаторов и диэлектриков
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
- (Ф) спроектировать и рассчитать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.
Кроме того, руководство по физике для средней школы рассматривает содержание этого раздела в лабораторной работе под названием «Электрический заряд», а также следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире.
 Ожидается, что студент:
Ожидается, что студент:- (Ф) спроектировать и рассчитать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.
Основные термины раздела
| конденсатор | диэлектрик |
Поддержка учителей
Поддержка учителей
Чтобы представить конденсаторы, в этом разделе подчеркивается их способность накапливать энергию. Диэлектрики введены как способ увеличить количество энергии, которое может храниться в конденсаторе. Чтобы представить идею хранения энергии, обсудите с учащимися другие механизмы хранения энергии, такие как плотины или батареи. Спросите, у кого больше мощность.
Конденсаторы
Поддержка учителей
Поддержка учителей
Объясните, что электрические конденсаторы являются жизненно важными частями всех электрических цепей. На самом деле, все электрические устройства имеют емкость, даже если конденсатор явно не встроен в устройство.
На самом деле, все электрические устройства имеют емкость, даже если конденсатор явно не встроен в устройство.
[BL]Попросите учащихся определить, как слово емкость используется в повседневной жизни. Предложите им найти определение в словаре. Сравните и сопоставьте обыденное значение со значением термина в физике.
[OL]Спросите учащихся, слышали ли они слово конденсатор , используемый вместе с электричеством, например, на электростанциях или в электрических цепях. Попросите их описать, как используется это слово.
[AL]Обсудите, как пружина способна накапливать механическую энергию. Обсудите, какие свойства пружины увеличивают ее способность накапливать энергию. Укажите, что эти свойства присущи пружине.
Снова рассмотрим рентгеновскую трубку, рассмотренную в предыдущем примере задачи. Как создать однородное электрическое поле? Один положительный заряд создает электрическое поле, направленное от него, как показано на рис. 18.17. Это поле неоднородно, так как расстояние между линиями увеличивается по мере удаления от заряда. Однако, если мы объединим положительный и отрицательный заряды, мы получим электрическое поле, показанное на рис. 18.19.(а). Обратите внимание, что между зарядами силовые линии электрического поля расположены более равномерно.
18.17. Это поле неоднородно, так как расстояние между линиями увеличивается по мере удаления от заряда. Однако, если мы объединим положительный и отрицательный заряды, мы получим электрическое поле, показанное на рис. 18.19.(а). Обратите внимание, что между зарядами силовые линии электрического поля расположены более равномерно.
Что произойдет, если мы поместим, скажем, пять положительных зарядов в линию напротив пяти отрицательных зарядов, как показано на рис. 18.27? Теперь область между линиями заряда содержит довольно однородное электрическое поле.
Рисунок 18.27 Красные точки — положительные заряды, синие — отрицательные. Направление электрического поля показано красными стрелками. Обратите внимание, что электрическое поле между положительными и отрицательными точками довольно однородно.
Мы можем распространить эту идею еще дальше и на два измерения, поместив две металлические пластины лицом к лицу и зарядив одну положительным зарядом, а другую равной по величине отрицательной зарядкой. Это можно сделать, подключив одну пластину к положительной клемме батареи, а другую пластину к отрицательной клемме, как показано на рис. 18.28. Электрическое поле между этими заряженными пластинами будет чрезвычайно однородным.
Это можно сделать, подключив одну пластину к положительной клемме батареи, а другую пластину к отрицательной клемме, как показано на рис. 18.28. Электрическое поле между этими заряженными пластинами будет чрезвычайно однородным.
Рисунок 18.28 Две параллельные металлические пластины заряжаются противоположным зарядом, соединяя пластины с противоположными клеммами батареи. Величина заряда на каждой пластине одинакова.
Давайте подумаем о работе, необходимой для зарядки этих пластин. До того, как пластины подключены к батарее, они нейтральны, то есть имеют нулевой суммарный заряд. Размещение первого положительного заряда на левой пластине и первого отрицательного заряда на правой пластине требует очень мало работы, потому что пластины нейтральны, поэтому противоположные заряды отсутствуют. Теперь рассмотрите возможность размещения второго положительного заряда на левой пластине и второго отрицательного заряда на правой пластине. Поскольку первые два заряда отталкивают вновь прибывших, к двум новым зарядам нужно приложить силу на расстоянии, чтобы они оказались на пластинах. Это определение работы, которое означает, что по сравнению с первой парой требуется больше работы, чтобы положить вторую пару зарядов на пластины. Чтобы разместить третий положительный и отрицательный заряды на пластинах, требуется еще больше работы, и так далее. Откуда эта работа? Батарея! Его химическая потенциальная энергия преобразуется в работу, необходимую для разделения положительных и отрицательных зарядов.
Это определение работы, которое означает, что по сравнению с первой парой требуется больше работы, чтобы положить вторую пару зарядов на пластины. Чтобы разместить третий положительный и отрицательный заряды на пластинах, требуется еще больше работы, и так далее. Откуда эта работа? Батарея! Его химическая потенциальная энергия преобразуется в работу, необходимую для разделения положительных и отрицательных зарядов.
Несмотря на то, что батарея работает, эта работа остается в рамках системы аккумуляторной пластины. Следовательно, закон сохранения энергии говорит нам, что если потенциальная энергия батареи уменьшится до отдельных зарядов, энергия другой части системы должна увеличиться на ту же величину. По сути, энергия батареи запасается в электрическом поле между пластинами. Эта идея аналогична рассмотрению того, что потенциальная энергия поднятого молота хранится в гравитационном поле Земли. Если бы гравитационное поле исчезло, у молота не было бы потенциальной энергии. Точно так же, если бы между пластинами не существовало электрического поля, между ними не накапливалась бы энергия.
Если мы сейчас отсоединим пластины от батареи, они будут удерживать энергию. Мы могли бы, например, подключить пластины к лампочке, и лампочка будет гореть до тех пор, пока эта энергия не будет израсходована. Таким образом, эти пластины обладают способностью накапливать энергию. По этой причине устройство, подобное этому, называется конденсатором. Конденсатор — это совокупность объектов, которые в силу своей геометрии могут накапливать энергию электрического поля.
Различные реальные конденсаторы показаны на рис. 18.29.. Обычно они изготавливаются из проводящих пластин или листов, разделенных изоляционным материалом. Они могут быть плоскими или свернутыми или иметь другую геометрию.
Рисунок 18.29 Некоторые типовые конденсаторы. (кредит: Уинделл Оскей)
Емкость конденсатора определяется его емкостью C , которая определяется как
С=QV,C=QV,
18,35
, где Q — величина заряда на каждой пластине конденсатора, а В — это разность потенциалов при переходе от отрицательной пластины к положительной.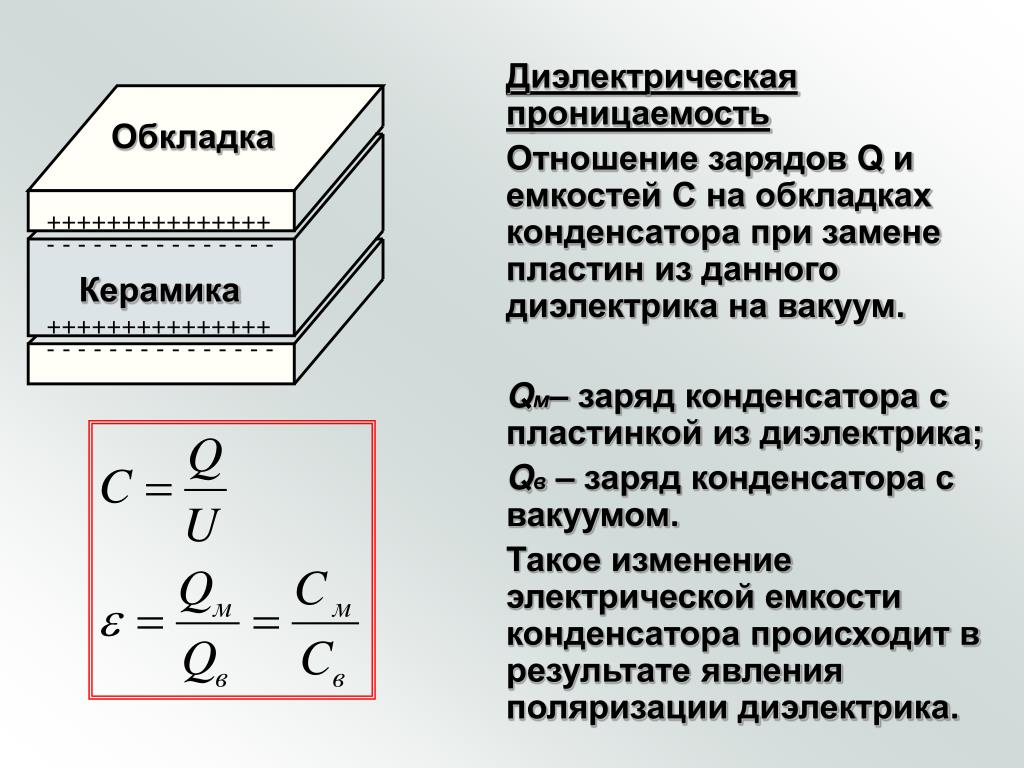 Это означает, что и Q , и V всегда положительны, поэтому емкость всегда положительна. Из уравнения для емкости видно, что единицами измерения емкости являются C/V, которые называются фарадами (F) в честь английского физика девятнадцатого века Майкла Фарадея.
Это означает, что и Q , и V всегда положительны, поэтому емкость всегда положительна. Из уравнения для емкости видно, что единицами измерения емкости являются C/V, которые называются фарадами (F) в честь английского физика девятнадцатого века Майкла Фарадея.
Уравнение C=Q/VC=Q/V имеет смысл: конденсатор с плоскими пластинами (подобный показанному на рис. 18.28) размером с футбольное поле может удерживать большой заряд, не требуя слишком большой работы на единицу заряда для втолкнуть заряд в конденсатор. Таким образом, Q будет большим, а V будет маленьким, поэтому емкость C будет очень большой. Вдавливание того же заряда в конденсатор размером с ноготь потребовало бы гораздо больше работы, поэтому V было бы очень большим, а емкость была бы намного меньше.
Хотя из уравнения C=Q/VC=Q/V кажется, что емкость зависит от напряжения, на самом деле это не так. Для данного конденсатора отношение запасенного в конденсаторе заряда к разности напряжений между обкладками конденсатора всегда остается одним и тем же. Емкость определяется геометрией конденсатора и материалами, из которых он изготовлен. Для плоского конденсатора, между пластинами которого ничего нет, емкость равна
Для данного конденсатора отношение запасенного в конденсаторе заряда к разности напряжений между обкладками конденсатора всегда остается одним и тем же. Емкость определяется геометрией конденсатора и материалами, из которых он изготовлен. Для плоского конденсатора, между пластинами которого ничего нет, емкость равна
C0=ε0Ad,C0=ε0Ad,
18,36
где А площадь пластин конденсатора и d их расстояние между собой. Мы используем C0C0 вместо C , потому что между пластинами конденсатора ничего нет (в следующем разделе мы увидим, что происходит, когда это не так). Константа ε0,ε0, равная эпсилон ноль , называется диэлектрической проницаемостью свободного пространства, и ее значение равно
.ε0=8,85×10−12 Ф/мε0=8,85×10−12 Ф/м
18.37
Возвращаясь к энергии, запасенной в конденсаторе, мы можем спросить, сколько именно энергии запасает конденсатор. Если конденсатор зарядить, подав на него напряжение 90 274 В 90 275, например, подключив его к батарее с напряжением 90 274 В 90 275, то электрическая потенциальная энергия, запасенная в конденсаторе, равна 90 034.
Если конденсатор зарядить, подав на него напряжение 90 274 В 90 275, например, подключив его к батарее с напряжением 90 274 В 90 275, то электрическая потенциальная энергия, запасенная в конденсаторе, равна 90 034.
UE=12CV2.UE=12CV2.
18,38
Обратите внимание, что форма этого уравнения аналогична форме для кинетической энергии, K=12mv2K=12mv2 .
Смотреть физику
Откуда взялась емкость?
В этом видео показано, как определяется емкость и почему она зависит только от геометрических свойств конденсатора, а не от напряжения или накопленного заряда. При этом он дает хороший обзор понятий работы и электрического потенциала.
Проверка захвата
Если увеличить расстояние между пластинами конденсатора, как изменится его емкость?
- Удвоение расстояния между пластинами конденсатора уменьшит емкость в четыре раза.
- Удвоение расстояния между пластинами конденсатора уменьшит емкость в два раза.

- Удвоение расстояния между пластинами конденсатора увеличивает емкость в два раза.
- Удвоение расстояния между пластинами конденсатора увеличит емкость в четыре раза.
Виртуальная физика
Зарядите конденсатор
В этой симуляции вам представлен конденсатор с плоскими пластинами, подключенный к батарее переменного напряжения. Аккумулятор изначально находится при нулевом напряжении, поэтому конденсатор не заряжен. Сдвиньте ползунок батареи вверх и вниз, чтобы изменить напряжение батареи, и наблюдайте за зарядами, которые накапливаются на пластинах. Отображение емкости, заряда верхней пластины и накопленной энергии при изменении напряжения батареи. Вы также можете отобразить линии электрического поля в конденсаторе. Наконец, проверьте напряжение между различными точками этой цепи с помощью вольтметра.
Проверка захвата
Верно или неверно — в конденсаторе накопленная энергия всегда положительна, независимо от того, заряжена ли верхняя пластина отрицательным или положительным зарядом.
- ложный
- правда
Рабочий пример
Емкость и заряд, хранящиеся в конденсаторе с параллельными пластинами
(a) Какова емкость плоского конденсатора с металлическими пластинами площадью 1,00 м 2 каждая, разделенными расстоянием 0,0010 м? б) Какой заряд сохраняется в этом конденсаторе, если напряжение 3,00·10 3 В на него подается?
Стратегия ЗА (А)
Используйте уравнение C0=ε0AdC0=ε0Ad .
Решение для (a)
Ввод данных значений в это уравнение для емкости плоского конденсатора дает 9 F=8,9 нФ.C=ε0Ad=(8,85×10-12 Ф/м)1,00 м20,0010 м=8,9×10-9 Ф=8,9 нФ.
18,39
Обсуждение для (a)
Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу, или использование диэлектрика (будет обсуждаться ниже).
Стратегия ЗА (Б)
Зная C , найдите накопленный заряд, решив уравнение C=Q/VC=Q/V для заряда Q .
Решение для (b)
Заряд Q на конденсаторе равен
Q=CV=(8,9×10-9F)(3,00×103В)=2,7×10-5C.Q=CV=(8,9×10 -9F)(3,00×103В)=2,7×10-5C.
18,40
Обсуждение для (b)
Этот заряд лишь немного превышает типичный заряд статического электричества. Больше заряда можно сохранить, используя диэлектрик между обкладками конденсатора.
Рабочий пример
Какая батарея нужна для зарядки конденсатора?
Ваш друг дает вам конденсатор емкостью 10 мкФ10 мкФ. Чтобы хранить 120 мкКл120 мкКл на этом конденсаторе, аккумулятор какого напряжения нужно купить?
Стратегия
Используйте уравнение C=Q/VC=Q/V, чтобы найти напряжение, необходимое для зарядки конденсатора.
Решение
Решение C=Q/VC=Q/V для напряжения дает V=Q/CV=Q/C . Вставка C=10 мкФ=10×10-6FC=10 мкФ=10×10-6F и Q=120 мкC=120×10-6CQ=120 мкC=120×10-6C дает
V=QC=120×10−6C10×10−6F=12VV=QC=120×10−6C10×10−6F=12V
18.41
Обсуждение
Такую батарею должно быть легко достать. Остается вопрос, содержит ли аккумулятор достаточно энергии для обеспечения нужного заряда. Уравнение UE=12CV2UE=12CV2 позволяет рассчитать требуемую энергию.
UE=12CV2=12(10×10-6F)(12В)2=72мJUE=12CV2=12(10×10-6F)(12В)2=72мДж
18,42
Обычный коммерческий аккумулятор может легко обеспечить это много энергии.
Практические задачи
23.
Какое напряжение на 35 мкФ при заряде 25 нКл?
- 8,75 × 10 −13 В
- 0,71 × 10 −3 В
- 1,4 × 10 −3 В
- 1,4 × 10 3 В
24.
Какое напряжение находится на конденсаторе емкостью 100 мкФ, хранящем 10 Дж энергии?
- −4,5 × 10 2 В
- 4,5 × 10 2 В
- ±4,5 × 10 2 В
- ±9 × 10 2 В
Диэлектрики
Поддержка учителей
Поддержка учителей
Объясните, что диэлектрик является сокращением от диэлектрический материал , который имеет особые электрические свойства, которые будут обсуждаться в этом разделе. Слово диэлектрик используется для обозначения способности материала накапливать энергию. Напомните учащимся, что изолятор используется для обозначения способности материала препятствовать прохождению электрического заряда.
[BL][OL]Обратите внимание, что префикс к означает два или два. В сочетании со словом электрический это означает, что диэлектрик может иметь два электрических заряда.
В сочетании со словом электрический это означает, что диэлектрик может иметь два электрических заряда.
[AL]Спросите учащихся, знают ли они другие слова, которые используют префикс di в науке (двухатомный, двуокись углерода, диполь, …).
Прежде чем приступить к решению некоторых примеров задач, давайте посмотрим, что произойдет, если мы поместим изоляционный материал между пластинами заряженного конденсатора, а затем отсоединим его от заряжаемой батареи, как показано на рис. 18.30. Поскольку материал является изолирующим, заряд не может перемещаться через него с одной пластины на другую, поэтому заряд Q на конденсатор не меняется. Между пластинами заряженного конденсатора существует электрическое поле, поэтому изолирующий материал поляризуется, как показано в нижней части рисунка. Электроизоляционный материал, который поляризуется в электрическом поле, называется диэлектриком.
На рис. 18.30 показано, что отрицательный заряд молекул материала смещается влево, в сторону положительного заряда конденсатора. Этот сдвиг происходит из-за электрического поля, которое действует слева на электроны в молекулах диэлектрика. Правые стороны молекул теперь лишены небольшого количества отрицательного заряда, поэтому их суммарный заряд положительный.
Рисунок 18.30 Верхний и нижний конденсаторы несут одинаковый заряд Q . Верхний конденсатор не имеет диэлектрика между пластинами. Нижний конденсатор имеет диэлектрик между пластинами. Молекулы в диэлектрике поляризуются электрическим полем конденсатора.
Поддержка учителей
Поддержка учителей
Укажите положительный и отрицательный поверхностный заряд на каждой стороне диэлектрика. Обсудите со студентами, что линии электрического поля нарисованы так, что они касаются поверхностных зарядов, потому что линии электрического поля всегда начинаются или заканчиваются на заряде. Таким образом, через диэлектрик проходит меньше линий электрического поля, а это означает, что электрическое поле внутри диэлектрика слабее.
Таким образом, через диэлектрик проходит меньше линий электрического поля, а это означает, что электрическое поле внутри диэлектрика слабее.
Все электроизоляционные материалы являются диэлектриками, но некоторые из них являются лучшими диэлектриками, чем другие. Хорошим диэлектриком является тот, молекулы которого позволяют своим электронам сильно смещаться в электрическом поле. Другими словами, электрическое поле немного оттягивает их электроны от их атома, но они не убегают полностью от своего атома (именно поэтому они являются изоляторами).
На рис. 18.31 показано макроскопическое изображение диэлектрика в заряженном конденсаторе. Обратите внимание, что линии электрического поля в конденсаторе с диэлектриком разнесены дальше, чем линии электрического поля в конденсаторе без диэлектрика. Это означает, что электрическое поле в диэлектрике слабее, поэтому оно хранит меньше электрической потенциальной энергии, чем электрическое поле в конденсаторе без диэлектрика.
Куда делась эта энергия? На самом деле молекулы в диэлектрике действуют как крошечные пружинки, и энергия электрического поля идет на то, чтобы растянуть эти пружинки. При таком ослаблении электрического поля разница напряжений между двумя сторонами конденсатора меньше, поэтому становится легче зарядить конденсатор. Таким образом, помещение диэлектрика в конденсатор перед его зарядкой позволяет накопить в конденсаторе больше заряда и потенциальной энергии. Параллельная пластина с диэлектриком имеет емкость
C=κε0Ad=κC0,C=κε0Ad=κC0,
18,43
где κκ ( каппа ) — безразмерная постоянная, называемая диэлектрической проницаемостью . Поскольку κκ больше 1 для диэлектриков, емкость увеличивается, когда диэлектрик помещается между пластинами конденсатора. Диэлектрическая проницаемость некоторых материалов показана в таблице 18.1.
| Материал | Диэлектрическая проницаемость (κκ) |
|---|---|
| Вакуум | 1.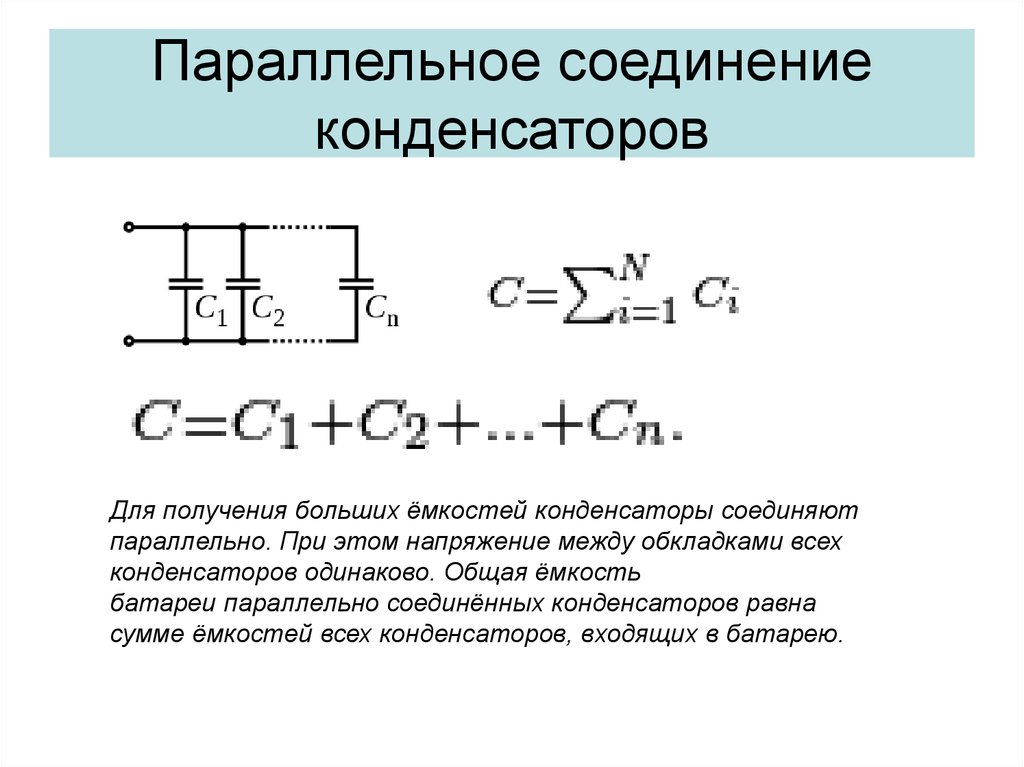 00000 00000 |
| Воздух | 1.00059 |
| Плавленый кварц | 3,78 |
| Неопреновый каучук | 6,7 |
| Нейлон | 3,4 |
| Бумага | 3,7 |
| Полистирол | 2,56 |
| Стекло пирекс | 5,6 |
| Силиконовое масло | 2,5 |
| Титанат стронция | 233 |
| Тефлон | 2.1 |
| Вода | 80 |
Стол 18.1 Диэлектрические постоянные для различных материалов при 20 °C
Рисунок
18.31
Верхний и нижний конденсаторы несут одинаковый заряд Q. Между пластинами верхнего конденсатора нет диэлектрика. Нижний конденсатор имеет диэлектрик между пластинами. Поскольку некоторые линии электрического поля заканчиваются и начинаются на поляризационных зарядах в диэлектрике, электрическое поле в конденсаторе менее сильное.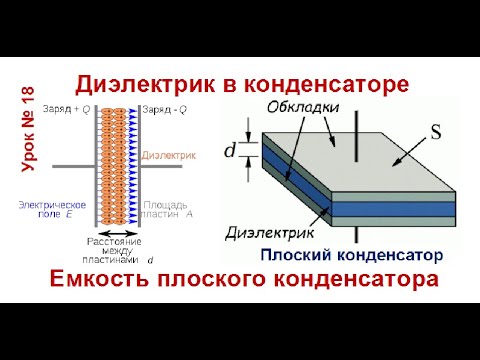 Таким образом, при том же заряде конденсатор запасает меньше энергии, если он содержит диэлектрик.
Таким образом, при том же заряде конденсатор запасает меньше энергии, если он содержит диэлектрик.
Поддержка учителей
Поддержка учителей
Подчеркнем, что линии электрического поля в диэлектрике менее плотные, чем в конденсаторе без диэлектрика, что показывает, что электрическое поле в диэлектрике слабее.
Рабочий пример
Конденсатор для вспышки камеры
Типичная вспышка для компактной камеры использует конденсатор емкостью около 200 мкФ200 мкФ. (а) Если разность потенциалов между обкладками конденсатора составляет 100 В, то есть 100 В подается «через конденсатор», сколько энергии хранится в конденсаторе? б) Если бы диэлектриком, используемым в конденсаторе, был лист нейлона толщиной 0,010 мм, какова была бы площадь поверхности пластин конденсатора?
Стратегия ЗА (А)
Учитывая, что V=100VV=100V и C=200×10-6FC=200×10-6F, мы можем использовать уравнение UE=12CV2UE=12CV2, чтобы найти электрическую потенциальную энергию, запасенную в конденсаторе.
Решение для (a)
Вставка заданных величин в UE=12CV2UE=12CV2 дает
UE=12CV2=12(200×10−6F)(100В)2=1,0 Дж.UE=12CV2=12(200×10 −6F)(100 В)2=1,0 Дж.
18,44
Обсуждение для (a)
Этой энергии достаточно, чтобы поднять 1-килограммовый мяч примерно на 1 м над землей. Вспышка длится примерно 0,001 с, поэтому мощность, отдаваемая конденсатором за это короткое время, равна P=UEt=1,0J0,001с=1kWP=UEt=1,0J0,001с=1кВт. Учитывая, что автомобильный двигатель выдает около 100 кВт мощности, для маленького конденсатора это неплохо!
Стратегия ЗА (Б)
Поскольку пластины конденсатора находятся в контакте с диэлектриком, мы знаем, что расстояние между пластинами конденсатора составляет d = 0,010 мм = 1,0 × 10–5 м d = 0,010 мм = 1,0 × 10–5 м. Из предыдущей таблицы диэлектрическая проницаемость нейлона составляет κ=3,4 κ=3,4. Теперь мы можем использовать уравнение C=κε0AdC=κε0Ad, чтобы найти площадь A конденсатора.
Решение (b)
Решение уравнения площади A и подстановка известных величин дает
C=κε0AdA=Cdκε0=(200×10-6F)(1,0×10-5м)(3,4)(8,85×10-12F/м)=66м2.C=κε0AdA=Cdκε0=(200×10-6F )(1,0×10-5м)(3,4)(8,85×10-12 Ф/м)=66м2.
18,45
Обсуждение для (b)
Это слишком большая площадь, чтобы свернуть ее в конденсатор, достаточно маленький, чтобы поместиться в портативную камеру. Вот почему в этих конденсаторах используются не простые диэлектрики, а более продвинутая технология для получения высокой емкости.
Практические задачи
25.
При напряжении 12 В на конденсаторе он принимает заряд 10 мКл. Какова его емкость?
- 0,83 мк F
- 83 мкм F
- 120 мкм F
- 830 μ F
26.
Конденсатор с плоскими пластинами имеет площадь 10 см 2 и расстояние между пластинами 100 мк м . Какова его емкость, если между пластинами конденсатора находится бумага?
- 3,3 × 10 −10 F
- 3,3 × 10 −8 F
- 3,3 × 10 −6 Ф
- 3,3 × 10 −4 F
Проверьте свое понимание
27.
Если площадь плоского конденсатора удвоится, как изменится его емкость?
Емкость останется прежней.
Емкость удвоится.
Емкость увеличится в четыре раза.

Емкость увеличится в восемь раз.
28.
Если удвоить площадь пластинчатого конденсатора и уменьшить расстояние между пластинами в четыре раза, как изменится емкость?
Увеличится в два раза.
Увеличится в четыре раза.
Увеличится в шесть раз.
Увеличится в восемь раз.

Диэлектрики
ДиэлектрикиДалее: Конденсаторы в серии и Вверх: Емкость Предыдущий: Емкость Строго говоря, выражение (108) для емкости параллельного пластинчатый конденсатор действителен только в том случае, если область между тарелки — это вакуум. Однако это выражение оказывается довольно хорошим приближением, если область заполнена воздухом. Но, что произойдет, если пространство между пластинами заполнено изолирующим материал, например, стекло или пластик?
Мы могли бы исследовать этот вопрос экспериментально.
Предположим, что мы начали с заряженного плоского конденсатора, пластины которого
были разделены вакуумным зазором, и который был отсоединен от любой батареи
или другой источник заряда. Мы могли бы измерить разницу напряжений между пластинами.
с помощью вольтметра. Предположим, что мы
вставил кусок изоляционного материала ( напр. , стекло) в зазор между пластинами, а затем повторно измерил
разница напряжений между пластинами.
Мы обнаружим, что новая разность напряжений
был на меньше чем на , несмотря на то, что заряд на пластинах
был неизменным. Обозначим отношение напряжений как .
Так как , то
емкость конденсатора должна увеличиться на
фактор, когда теплоизоляционная плита была вставлена между пластинами.
, стекло) в зазор между пластинами, а затем повторно измерил
разница напряжений между пластинами.
Мы обнаружим, что новая разность напряжений
был на меньше чем на , несмотря на то, что заряд на пластинах
был неизменным. Обозначим отношение напряжений как .
Так как , то
емкость конденсатора должна увеличиться на
фактор, когда теплоизоляционная плита была вставлена между пластинами.
Изолирующий
материал, который имеет эффект увеличения емкости вакуумного параллельного
пластинчатый конденсатор, когда он вставлен между своими пластинами, называется диэлектрический материал и коэффициент, на который емкость называется диэлектрической проницаемостью этого материала. Конечно, варьируется от материала к материалу. Немного
примерные значения приведены в таблице 1. Обратите внимание, однако, что всегда больше
чем единица, поэтому заполнение зазора между пластинами параллельной пластины
конденсатор с диэлектрическим материалом всегда увеличивает емкость
устройство в той или иной степени. С другой стороны, воздух лишь на процент больше
чем для вакуума ( т. е. , ), поэтому конденсатор с воздушным наполнением практически
неотличим от вакуумного конденсатора.
С другой стороны, воздух лишь на процент больше
чем для вакуума ( т. е. , ), поэтому конденсатор с воздушным наполнением практически
неотличим от вакуумного конденсатора.
|
Формула для емкости плоского конденсатора с диэлектрическим наполнением
является
| (109) |
куда
| (110) |
называется диэлектрической проницаемостью диэлектрического материала между пластинами.
 Обратите внимание, что диэлектрическая проницаемость диэлектрика
материала всегда больше, чем
диэлектрическая проницаемость вакуума
Обратите внимание, что диэлектрическая проницаемость диэлектрика
материала всегда больше, чем
диэлектрическая проницаемость вакуума Как мы можем объяснить снижение напряжения, которое происходит, когда мы вставляем
диэлектрик между пластинами вакуумного плоского конденсатора?
Ну, а если разность напряжений между пластинами уменьшить, то
во столько же раз должно уменьшиться электрическое поле между пластинами.
Другими словами, электрическое поле, создаваемое зарядом
хранящиеся на пластинах конденсатора, должны быть частично компенсированы
противодействующим электрическим полем, создаваемым самим диэлектриком
при помещении во внешнее электрическое поле. Что это
причиной этого противодействующего поля? Получается, что встречное поле
произведено поляризация составляющих молекул
диэлектрическими, когда они помещены в электрическое поле (см. раздел 3.4).
Если достаточно мала, то степень
поляризация каждой молекулы пропорциональна сила поляризующего поля
. Отсюда следует, что сила противодействующего поля также пропорциональна
к . На самом деле константа пропорциональности равна , поэтому . Суммарное электрическое поле между пластинами равно . Следовательно, и поле, и
напряжение между пластинами уменьшается в несколько раз
по отношению к вакуумному корпусу.
В принципе, диэлектрическая проницаемость диэлектрика
материал можно рассчитать по
свойства молекул, из которых состоит
материал. На практике этот расчет слишком сложен для выполнения, за исключением
для очень простых молекул. Обратите внимание, что результат, что степень поляризации
поляризуемая молекула пропорциональна внешнему электрическому полю — сила разрушается, если становится слишком большой (точно так же, как у Гука).
закон нарушается, если мы слишком сильно натягиваем пружину).
Однако, к счастью, напряженность поля, встречающаяся в обычных
лабораторные эксперименты, как правило, недостаточно масштабны, чтобы опровергнуть это
результат.
908:25
Отсюда следует, что сила противодействующего поля также пропорциональна
к . На самом деле константа пропорциональности равна , поэтому . Суммарное электрическое поле между пластинами равно . Следовательно, и поле, и
напряжение между пластинами уменьшается в несколько раз
по отношению к вакуумному корпусу.
В принципе, диэлектрическая проницаемость диэлектрика
материал можно рассчитать по
свойства молекул, из которых состоит
материал. На практике этот расчет слишком сложен для выполнения, за исключением
для очень простых молекул. Обратите внимание, что результат, что степень поляризации
поляризуемая молекула пропорциональна внешнему электрическому полю — сила разрушается, если становится слишком большой (точно так же, как у Гука).
закон нарушается, если мы слишком сильно натягиваем пружину).
Однако, к счастью, напряженность поля, встречающаяся в обычных
лабораторные эксперименты, как правило, недостаточно масштабны, чтобы опровергнуть это
результат.
908:25
Мы видели, что когда диэлектрический материал из диэлектрика
константа помещается в униформу
электрическое поле, создаваемое между пластинами плоского конденсатора, затем
материал поляризуется, что приводит к уменьшению напряженности поля
между пластинами с некоторым коэффициентом. Так как особо ничего нет
особенно об электрическом поле между пластинами конденсатора,
мы предполагаем, что этот результат является довольно общим. Таким образом, если пространство заполнено
с диэлектрической средой, то закон Кулона переписывается как
908:25
Так как особо ничего нет
особенно об электрическом поле между пластинами конденсатора,
мы предполагаем, что этот результат является довольно общим. Таким образом, если пространство заполнено
с диэлектрической средой, то закон Кулона переписывается как
908:25
| (111) |
и формула для электрического поля, создаваемого точечным зарядом, принимает вид
| (112) |
и т.д. Ясно, что в диэлектрической среде законы электростатики принимают точно такой же вид, как и в вакууме, за исключением того, что диэлектрическая проницаемость свободное пространство заменяется диэлектрической проницаемостью среды. Диэлектрические материалы имеют общий эффект уменьшение электрических полей и разностей потенциалов, создаваемых электрическими обвинения.
 Такие материалы чрезвычайно
полезны, потому что они препятствуют распаду.
Например, если мы заполним конденсатор с плоскими пластинами диэлектриком.
материал, то мы эффективно увеличиваем количество заряда, которое мы можем хранить
на устройстве до того, как произойдет поломка.
908:25
Такие материалы чрезвычайно
полезны, потому что они препятствуют распаду.
Например, если мы заполним конденсатор с плоскими пластинами диэлектриком.
материал, то мы эффективно увеличиваем количество заряда, которое мы можем хранить
на устройстве до того, как произойдет поломка.
908:25Далее: Конденсаторы в серии и Вверх: Емкость Предыдущий: Емкость Ричард Фицпатрик 2007-07-14
Понимание диэлектрика конденсатора
Диэлектрик конденсаторов находится в изоляционном материале, используемом для разграничения пластин от контакта друг с другом. Сегодня вы узнаете о различных типах диэлектрических материалов, используемых в конденсаторе, и о том, как они влияют на емкость. Вы также узнаете уравнение, формулу и расчет электрического материала конденсатора.
Подробнее: Конденсатор
Помимо общего размера проводящих пластин и их расстояния друг от друга, тип диэлектрического материала, используемого в конденсаторе, является еще одним фактором, который может повлиять на общую емкость.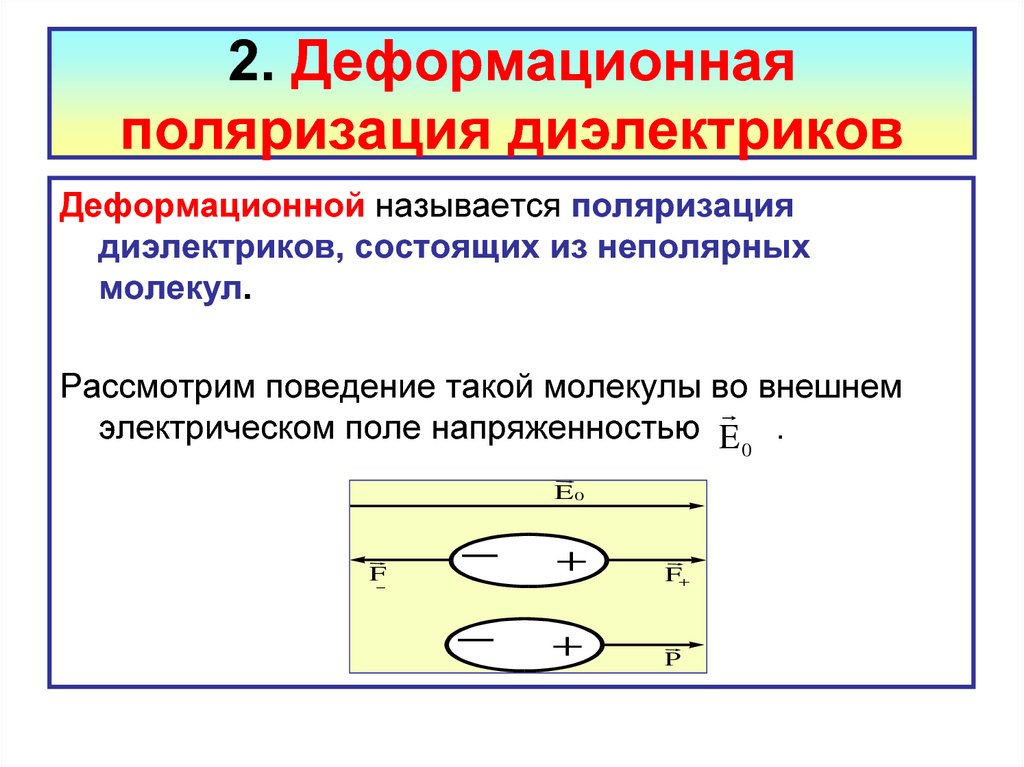 Это также известно как диэлектрическая проницаемость (ε) диэлектрика. Проводящие пластины конденсатора обычно изготавливаются из металлической фольги или металлической пленки, обеспечивающей поток электронов и заряд, но в качестве диэлектрика всегда используется изоляционный материал. В качестве диэлектрика в конденсаторе могут использоваться различные типы изоляционных материалов. Они отличаются своей способностью блокировать или пропускать электрический заряд.
Это также известно как диэлектрическая проницаемость (ε) диэлектрика. Проводящие пластины конденсатора обычно изготавливаются из металлической фольги или металлической пленки, обеспечивающей поток электронов и заряд, но в качестве диэлектрика всегда используется изоляционный материал. В качестве диэлектрика в конденсаторе могут использоваться различные типы изоляционных материалов. Они отличаются своей способностью блокировать или пропускать электрический заряд.
Как упоминалось во введении к этой статье, диэлектрический материал может быть изготовлен из ряда изоляционных материалов или комбинаций этих материалов. Наиболее распространенными типами являются воздух, бумага, полиэстер, полипропилен, майлар, керамика, стекло, масло или множество других материалов.
Процесс, при котором диэлектрический материал или изолятор увеличивает емкость конденсатора по сравнению с воздухом, известен как диэлектрическая проницаемость, K. Диэлектрик с высокой диэлектрической проницаемостью является намного лучшим изолятором, чем диэлектрический материал с более низкой диэлектрической проницаемостью. . Диэлектрическая проницаемость является безразмерной величиной, поскольку она относится к свободному пространству.
. Диэлектрическая проницаемость является безразмерной величиной, поскольку она относится к свободному пространству.
Подробнее: Понимание заряда в конденсаторе
Фактическая диэлектрическая проницаемость или «комплексная диэлектрическая проницаемость» диэлектрического материала между пластинами является произведением диэлектрической проницаемости свободного пространства (ε o ) и относительной диэлектрической проницаемости (ε р ) материала, используемого в качестве диэлектрика. Он задается как:
Комплексная диэлектрическая проницаемость
Другими словами, если взять диэлектрическую проницаемость свободного пространства, ε o в качестве нашего базового уровня и сделать его равным единице, когда вакуум свободного пространства заменяется на какой-либо другой тип изоляционного материала, их диэлектрическая проницаемость относится к основному диэлектрику свободного пространства, что дает коэффициент умножения, называемый «относительной диэлектрической проницаемостью», ε р .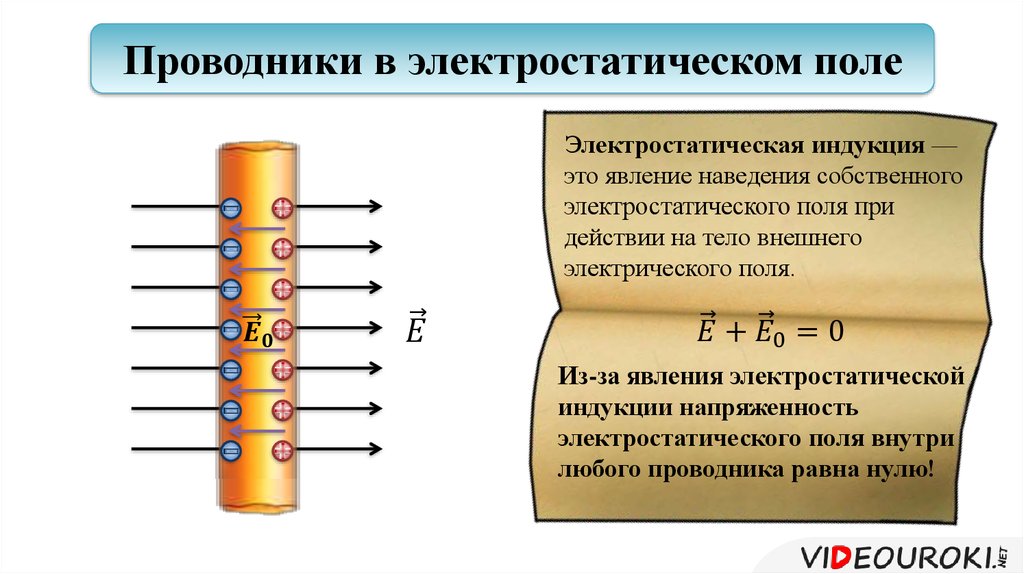 таким образом, значение комплексной диэлектрической проницаемости ε всегда будет равно относительной диэлектрической проницаемости, умноженной на единицу.
таким образом, значение комплексной диэлектрической проницаемости ε всегда будет равно относительной диэлектрической проницаемости, умноженной на единицу.
Типичная единица диэлектрической проницаемости, ε или диэлектрическая проницаемость для обычных материалов: чистый вакуум = 1,0000, воздух = 1,0006, бумага = от 2,5 до 3,5, стекло = от 3 до 10, слюда = от 5 до 7, дерево = от 3 до 8 , порошки оксидов металлов = от 6 до 20 и т. д. окончательное уравнение для всех этих материалов обозначается как:
Подробнее: Понимание конденсаторного делителя напряжения
Обычный метод, используемый для увеличения общей емкости конденсатора малого размера, заключается в соединении нескольких пластин в одном корпусе конденсатора. Например, вместо одного набора параллельных пластин конденсатор может иметь множество отдельных пластин, соединенных вместе, что увеличивает площадь поверхности A пластин.
Стандартный конденсатор с параллельными пластинами имеет две пластины, обозначенные A и B. Мы можем сказать, что n = 2, так как количество пластин конденсатора равно двум, где «n» обозначает количество пластин. Тогда приведенное выше уравнение для конденсатора с одной плоской пластиной имеет вид:
Мы можем сказать, что n = 2, так как количество пластин конденсатора равно двум, где «n» обозначает количество пластин. Тогда приведенное выше уравнение для конденсатора с одной плоской пластиной имеет вид:
Конденсатор может иметь две параллельные пластины, но только одна сторона каждой пластины контактирует с диэлектриком посередине, поскольку другая сторона каждой пластины образует внешнюю часть конденсатора. Если две половинки пластин свести и соединить их вместе, то будет эффективная целая пластина, контактирующая с диэлектриком. Для однопластинчатого конденсатора n – 1 = 2 – 1, что равно 1, как C = (ε o * ε r x 1 x A)/d, что также может быть записано как C = (ε o *ε r *A)/d, что является приведенным выше стандартным уравнением.
Теперь предположим, что у нас есть конденсатор, состоящий из 9 чередующихся пластин, тогда n = 9, как показано на рисунке. Тогда мы обсуждаем многопластинчатый конденсатор.
Допустим, у нас есть пять пластин, подключенных к одному выводу (A), и четыре пластины к другому выводу (B). тогда обе стороны четырех пластин, соединенных с выводом B, находятся в контакте с диэлектриком, тогда как только одна сторона каждой из внешних пластин, соединенных с выводом A, находится в контакте с диэлектриком. С приведенным выше объяснением полезная площадь поверхности каждого набора пластин составляет всего восемь, а его емкость определяется как:
тогда обе стороны четырех пластин, соединенных с выводом B, находятся в контакте с диэлектриком, тогда как только одна сторона каждой из внешних пластин, соединенных с выводом A, находится в контакте с диэлектриком. С приведенным выше объяснением полезная площадь поверхности каждого набора пластин составляет всего восемь, а его емкость определяется как:
Подробнее: Понимание емкости в цепях переменного тока
Современные конденсаторы можно классифицировать в соответствии с характеристиками и свойствами их изолирующего диэлектрика:
Присоединяйтесь к нашему информационному бюллетеню
Низкие потери, высокая стабильность , такие как слюда, низкокалиевая керамика , Полистирол.
Средняя потеря, средняя стабильность, например бумага, пластиковая пленка, керамика с высоким содержанием калия.
Поляризованные конденсаторы, такие как электролитические, танталовые.
Это все, что касается этой статьи, в которой обсуждались различные типы диэлектрических материалов, используемых в конденсаторе, а также расчеты, уравнения и формулы.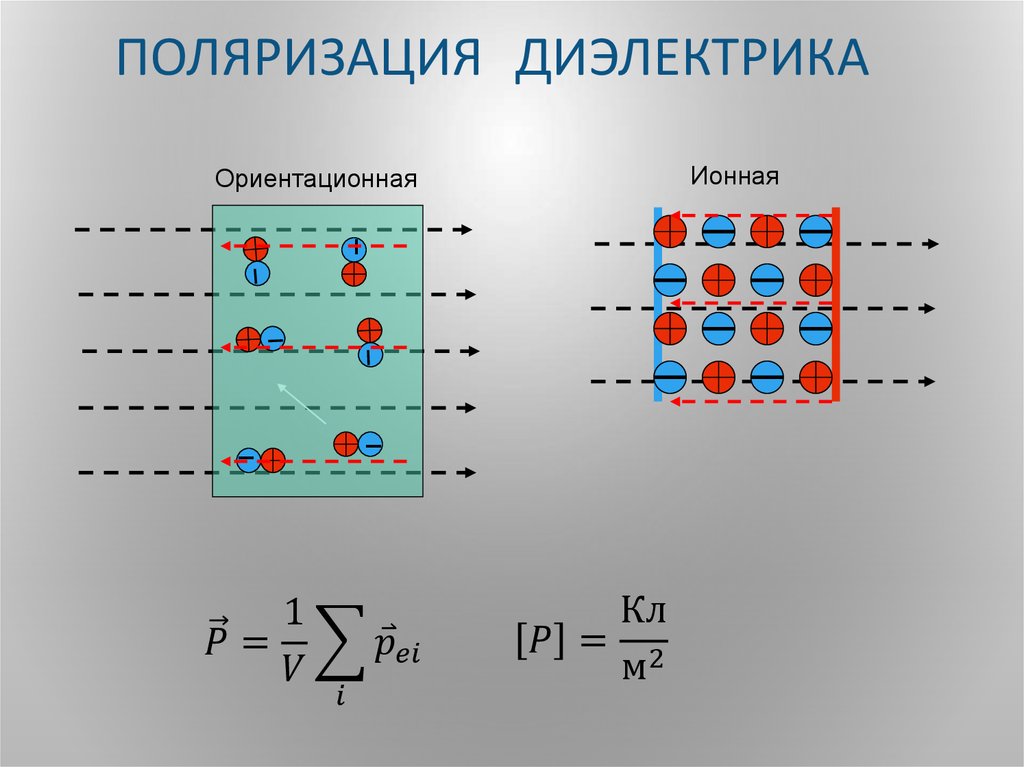 Я надеюсь, что вы получили много от чтения, если это так, пожалуйста, поделитесь с другими студентами. Спасибо за чтение, увидимся!
Я надеюсь, что вы получили много от чтения, если это так, пожалуйста, поделитесь с другими студентами. Спасибо за чтение, увидимся!
Эффект диэлектрической емкости – определение и применение
Диэлектрик – это электрический изолятор, который поляризуется приложенным электрическим полем. Когда диэлектрический материал находится в электрическом поле, электрические заряды не протекают через материал, как они протекают в электрическом проводнике. Они лишь незначительно смещаются от своего среднего положения равновесия и вызывают диэлектрическую поляризацию. Из-за диэлектрической поляризации положительные заряды смещаются в направлении поля, а отрицательные — в направлении, противоположном полю. Это дополнительно создает внутреннее электрическое поле, которое уменьшает общее поле внутри самого диэлектрика. Если диэлектрик состоит из слабо связанных молекул, эти молекулы поляризуются, а затем переориентируются.
Что такое конденсаторы?
Конденсаторы также могут называться электрическими конденсаторами. Конденсатор — это электронный компонент с двумя выводами, способный накапливать энергию в виде электрического заряда. Обычно они предназначены для усиления и увеличения эффекта емкости. Таким образом, они учитывают такие свойства, как размер и форма. Накопительная емкость емкости варьируется от малой до высокой.
Конденсатор — это электронный компонент с двумя выводами, способный накапливать энергию в виде электрического заряда. Обычно они предназначены для усиления и увеличения эффекта емкости. Таким образом, они учитывают такие свойства, как размер и форма. Накопительная емкость емкости варьируется от малой до высокой.
Использование диэлектрика в конденсаторах
В промышленных конденсаторах в качестве промежуточной среды между накопленными положительными и отрицательными зарядами используется твердый диэлектрический материал. Преимущество использования такого диэлектрического материала состоит в том, что он предотвращает прямой электрический контакт проводящей пластины. Однако высокая диэлектрическая проницаемость может обеспечить больший накопленный заряд при заданном напряжении. В этом можно убедиться, рассмотрев случай линейного диэлектрика с диэлектрической проницаемостью ε и толщиной d между двумя проводящими пластинами с однородной плотностью заряда σε. Здесь плотность заряда равна
Здесь плотность заряда равна
\[\sigma \epsilon = \frac{\epsilon V}{d}\]
И емкость на единицу площади на
\[c = \frac{\sigma \epsilon}{V} = \frac {\epsilon}{d}\]
Из этого видно, что большее ε приводит к большему накопленному заряду и, следовательно, к большей емкости.
Диэлектрические материалы, используемые в конденсаторах, также выбираются в соответствии с их устойчивостью к ионизации. Это помогает конденсатору работать при более высоких напряжениях до того, как изолирующий диэлектрик ионизируется и начинает пропускать нежелательный ток.
Влияние диэлектрика на емкость
Когда диэлектрик помещается между пластинами плоского конденсатора, занимающего область, диэлектрик поляризуется электрическим полем. Поверхностные плотности заряда называются σp и — σp.
Диэлектрическая проницаемость вещества — это явление, при котором емкость увеличивается по сравнению с вакуумным значением, когда диэлектрик полностью вставлен между пластинами конденсатора
(изображение будет загружено в ближайшее время)
Емкость плоскопараллельного конденсатора с диэлектрической пластиной
(изображение будет загружено в ближайшее время)
На двух пластинах микроскопический дипольный момент материала защитит заряды. Таким образом, это изменит эффект диэлектрического материала, вставленного между двумя пластинами. Материалы имеют проницаемость, которая определяется относительной проницаемостью K
Таким образом, это изменит эффект диэлектрического материала, вставленного между двумя пластинами. Материалы имеют проницаемость, которая определяется относительной проницаемостью K
Таким образом, емкость определяется по формуле:
\[C = \frac{\epsilon A}{d} = k\frac{\epsilon_{0}A}{ г}\]
Поместив диэлектрик между пластинами, можно увеличить емкость конденсатора с параллельными пластинами, поскольку диэлектрик имеет относительную диэлектрическую проницаемость k больше 1. k также иногда называют диэлектрической проницаемостью.
Некоторые практические диэлектрики
Диэлектрические материалы могут быть твердыми, жидкими или газообразными. Твердые диэлектрики чаще всего используются в электротехнике, и они являются очень хорошими изоляторами. Примеры включают фарфор, стекло и пластмассу. Воздух, азот и гексафторид серы являются тремя широко используемыми газообразными диэлектриками.
Знаете ли вы?
Значение статической диэлектрической проницаемости всех материалов больше единицы, ее значение для вакуума.

Значение диэлектрической проницаемости при комнатной температуре (25 °C или 77 °F) составляет 1,00059 для воздуха, 2,25 для парафина, 78,2 для воды и около 2000 для титаната бария (BaTiO3), когда электрическое поле перпендикулярно главной оси кристалла.
Поскольку значение диэлектрической проницаемости воздуха почти такое же, как у вакуума, воздух не увеличивает емкость конденсатора для всех практических целей.
Диэлектрическая проницаемость жидкостей и твердых тел определяется путем сравнения значения емкости, когда диэлектрик находится на месте, с ее значением, когда конденсатор заполнен воздухом.
Наличие диэлектрического материала влияет на все другие электрические явления.
Емкость конденсатора, заполненного диэлектриком, больше, чем в вакууме.

Как диэлектрик увеличивает емкость конденсатора? – Советы мудреца
Содержание
- 1 Как диэлектрик увеличивает емкость конденсатора?
- 2 Как увеличивается емкость конденсатора, если между пластинами конденсатора находится диэлектрик?
- 3 Что происходит, когда диэлектрическое вещество помещается между параллельными пластинами конденсатора?
- 4 Каков результат замены диэлектрика в конденсаторе диэлектриком с большей диэлектрической проницаемостью?
- 5 Когда диэлектрик помещен между пластинами заряженного конденсатора Электрическое поле между пластинами?
- 6 Когда между пластинами конденсатора вставлен диэлектрик, какой из них правильный?
- 7 Как диэлектрик конденсатора влияет на емкость?
- 8 Как увеличивается емкость параллельной пластины?
Как диэлектрик увеличивает емкость конденсатора?
Введение диэлектрика в конденсатор уменьшает электрическое поле, что снижает напряжение и увеличивает емкость. Конденсатор с диэлектриком сохраняет тот же заряд, что и без диэлектрика, но при более низком напряжении. Поэтому конденсатор с диэлектриком более эффективен.
Конденсатор с диэлектриком сохраняет тот же заряд, что и без диэлектрика, но при более низком напряжении. Поэтому конденсатор с диэлектриком более эффективен.
Как увеличивается емкость конденсатора, если между пластинами конденсатора находится диэлектрик?
Электрическое поле между пластинами плоского конденсатора прямо пропорционально емкости C конденсатора. Если общий заряд на обкладках остается постоянным, то разность потенциалов на обкладках конденсатора уменьшается. Таким образом, диэлектрик увеличивает емкость конденсатора.
Когда диэлектрический материал вставлен между пластинами конденсатора, он увеличивает его?
Если между пластинами конденсатора, оставленного подключенным к батарее, вставлена диэлектрическая пластина, т.е. заряд на ней увеличивается, то емкость (С) увеличивается, разность потенциалов (В) между пластинами остается неизменной и энергия, запасенная в конденсаторе, увеличивается.
Почему емкость плоского конденсатора увеличивается при вставке диэлектрического материала между его пластинами?
Когда диэлектрическая среда вводится между пластинами плоского конденсатора, диэлектрик поляризуется электрическим полем между пластинами.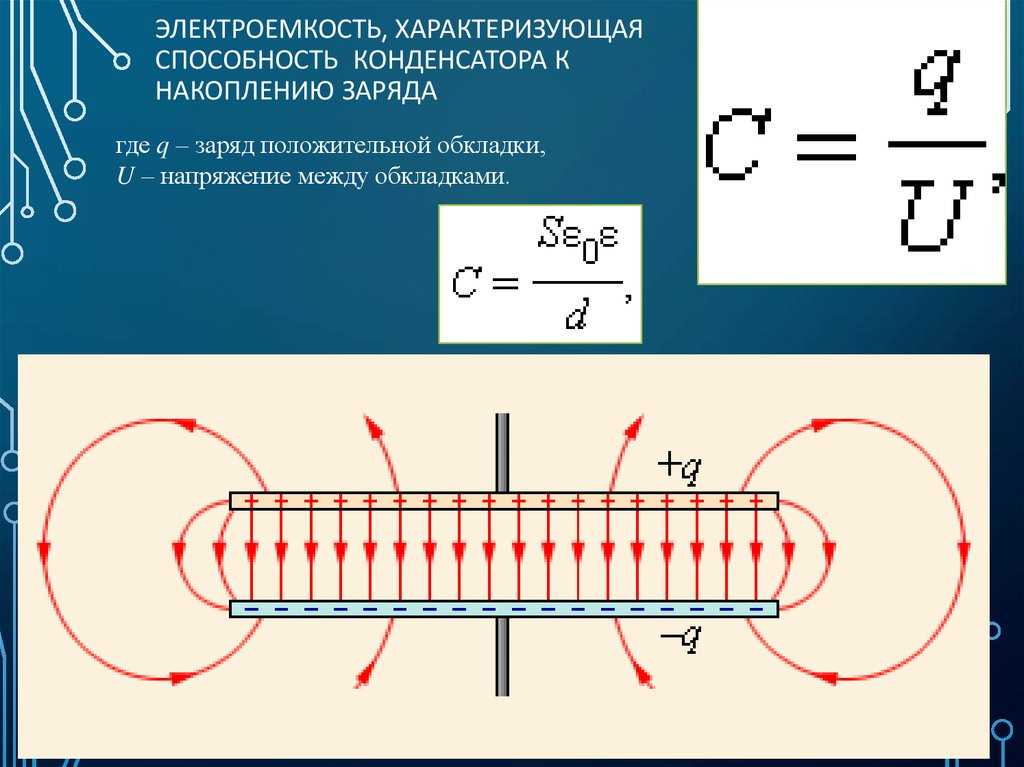 Следовательно, емкость конденсатора увеличивается.
Следовательно, емкость конденсатора увеличивается.
Что происходит, когда диэлектрическое вещество помещается между параллельными пластинами конденсатора?
Параллельная пластина с диэлектриком Когда диэлектрик помещается между заряженными пластинами, поляризация среды создает электрическое поле, противоположное полю зарядов на пластине. Диэлектрическая проницаемость k определяется как отражение степени уменьшения эффективного электрического поля, как показано ниже.
Каков результат замены диэлектрика в конденсаторе диэлектриком с большей диэлектрической проницаемостью?
Каков результат замены диэлектрика в конденсаторе диэлектриком с большей диэлектрической проницаемостью? Конденсатор будет иметь более высокую разность потенциалов при данной потенциальной энергии. Конденсатор может хранить меньше потенциальной энергии при заданной разности потенциалов.
Когда диэлектрик помещен в электрическое поле, электрическое поле внутри диэлектрика?
Диэлектрик поляризуется, когда его помещают в электрическое поле. Поле, создаваемое за счет поляризации, минимизирует влияние внешнего поля. Следовательно, электрическое поле внутри диэлектрика уменьшается при помещении его во внешнее электрическое поле.
Поле, создаваемое за счет поляризации, минимизирует влияние внешнего поля. Следовательно, электрическое поле внутри диэлектрика уменьшается при помещении его во внешнее электрическое поле.
Если между пластинами заряженного конденсатора поместить диэлектрический материал, емкость конденсатора изменится?
Добавление диэлектрика к конденсатору увеличивает емкость в К раз. Заряд на конденсаторе будет увеличиваться при постоянном напряжении и. Если конденсатор отключен, то есть заряд поддерживается постоянным, потенциал на конденсаторе уменьшится.
Когда диэлектрик помещен между пластинами заряженного конденсатора Электрическое поле между пластинами?
При введении диэлектрического материала между пластинами заряженного конденсатора возникает электрическое поле между пластинами. Когда электрическое поле между пластинами уменьшается, а емкость двух пластин увеличивается.
Когда между пластинами конденсатора вставлен диэлектрик, какое из них верно?
Когда диэлектрик полностью помещен между двумя пластинами конденсатора, его диэлектрическая проницаемость увеличивается по сравнению с вакуумным значением.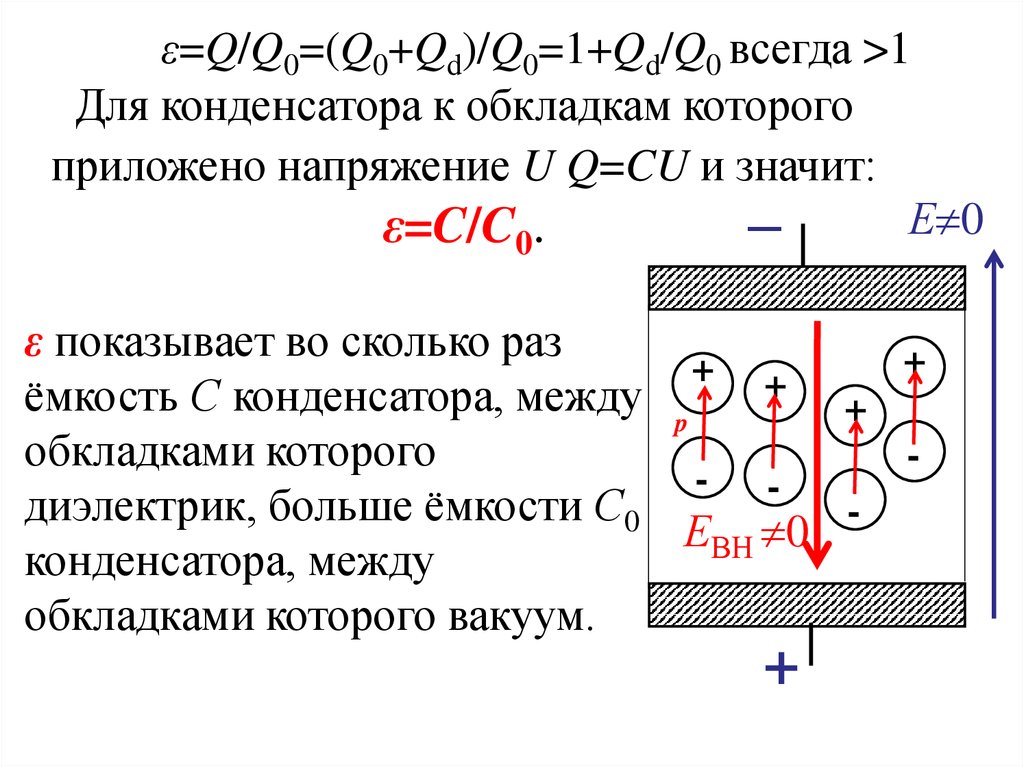
Как на емкость плоского конденсатора влияет расстояние между пластинами?
Следовательно, с увеличением площади пластин увеличивается емкость. Емкость прямо пропорциональна электростатическому силовому полю между пластинами. Это поле сильнее, когда пластины расположены ближе друг к другу. Следовательно, при уменьшении расстояния между пластинами емкость увеличивается.
Каков эффект от введения диэлектрика между пластинами воздушного конденсатора с параллельными пластинами?
Когда диэлектрический материал вводится между пластинами И когда диэлектрический материал помещается между пластинами плоского конденсатора, то из-за поляризации зарядов по обе стороны диэлектрика создается собственное электрическое поле, которое действует в направление, противоположное направлению поля из-за …
Как диэлектрик конденсатора влияет на емкость?
Полное заполнение пространства между обкладками конденсатора диэлектриком увеличивает емкость на коэффициент диэлектрической проницаемости: C = KC o, где C o – емкость при отсутствии диэлектрика между обкладками.


 3)
3)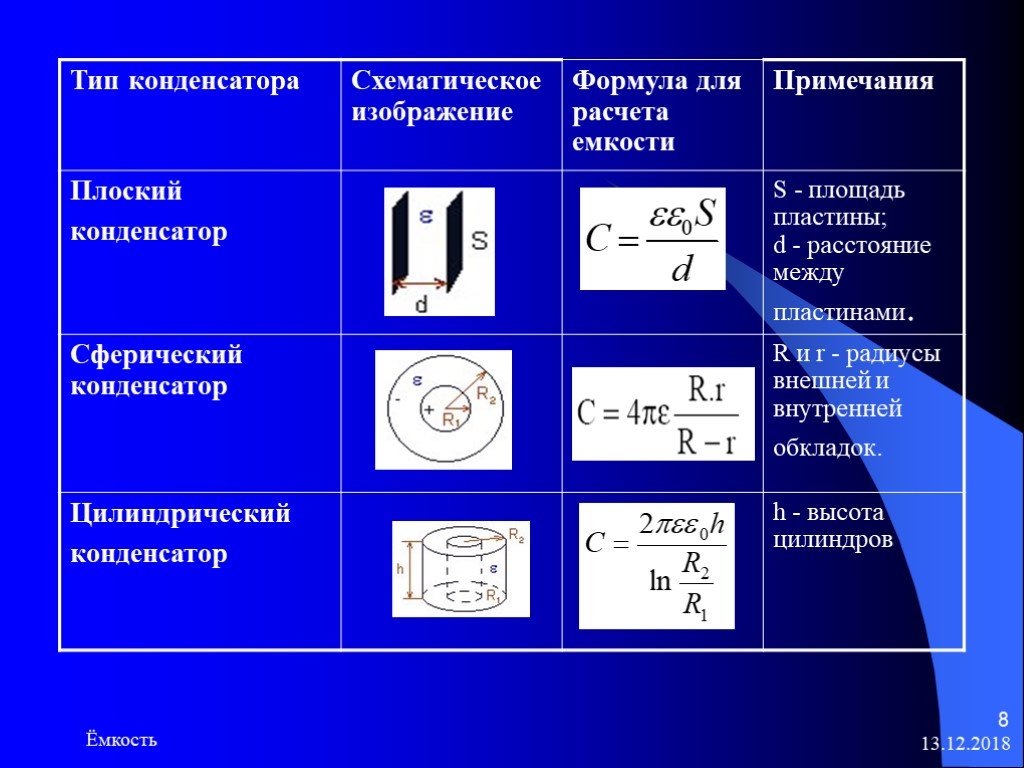 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2 Ожидается, что студент:
Ожидается, что студент: