Электричество и магнетизм
Еще М. Фарадей обнаружил, что если между обкладками конденсатора поместить диэлектрическую пластину, то емкость конденсатора возрастает.
На рис. 3.2 показан опыт, в котором демонстрируется зависимость емкости конденсатора от свойств среды между его обкладками. Между пластинами заряженного плоского конденсатора, присоединенного к электрометру, помещают диэлектрик — пластину из оргстекла. При этом показания электрометра уменьшаются, что говорит об увеличении емкости конденсатора. После удаления диэлектрика разность потенциалов увеличивается, возвращаясь к прежнему значению.
Рис. 3.2. Исследование зависимости емкости плоского конденсатора от диэлектрических свойств среды
Когда изолятор заполняет все пространство между обкладками, емкость конденсатора возрастает в раз, где безразмерная величина принимает разные значения для различных материалов. Эта величина называется диэлектрической проницаемостью
Рассмотрим снова плоский конденсатор. Зарядим его и вставим внутрь диэлектрическую пластину (рис. 3.3).
Рис. 3.3. Плоский конденсатор с диэлектрической пластиной между обкладками
Величины, относящиеся к конденсатору без диэлектрика, будем снабжать индексом 0. Так как заряд конденсатора не меняется при помещении в него диэлектрика, записываем соотношения
|
(3.1) |
Здесь мы использовали экспериментальный факт увеличения емкости конденсатора с диэлектриком в
Поскольку поле в плоском конденсаторе однородно, получаем следующую связь между напряженностью Е0 поля в вакууме и в диэлектрике Е
Иными словами, присутствие диэлектрика между пластинами может приводить к уменьшению напряженности электрического поля в конденсаторе.
Необходимо отметить, что простое уменьшение поля в
Если, к примеру, в однородное электрическое поле (как в идеальном плоском конденсаторе) поместить плоскопараллельную диэлектрическую пластину так, что её поверхности составят некоторый угол с направлением поля и, тем самым, они не будут совпадать с его эквипотенциальными поверхностями, то величина поля внутри этой пластины будет довольно сложным образом зависеть от угла , и будет равна только при .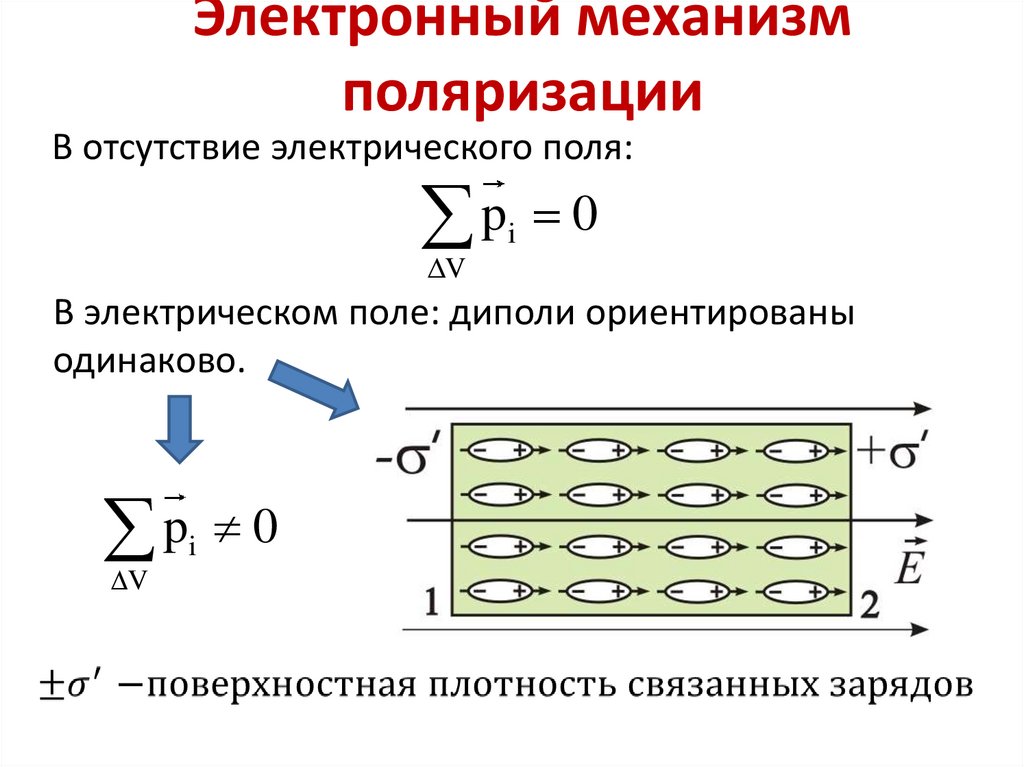
Не следует также думать, что внесение в поле диэлектрика всегда приводит к уменьшению напряженности поля, она может и возрасти: всё зависит от «геометрии» задачи. Ниже на рисунке 3.4 показано, что при помещении в электрическое поле тонкого длинного диэлектрического стержня параллельно силовым линиям внешнего поля, напряженность поля вне стержня у его концов увеличивается в результате появления на концах стержня «поляризационных» зарядов.
Рис. 3.4. Напряженность поля на оси тонкого диэлектрического стержня
Уменьшение разности потенциалов между обкладками и увеличение емкости конденсатора мы наблюдали в решенной выше задаче о сферическом конденсаторе с металлической оболочкой между обкладками. Там причина уменьшения разности потенциалов была ясна: на оболочке наводились индуцированные заряды, которые компенсировали внешнее поле от обкладок. Соответственно, электрическое поле существовало только в пространстве, не занятом оболочкой.
В диэлектрике нет зарядов, способных перемещаться по всему его объёму, но идея возникновения на его поверхности каких-то дополнительных зарядов (их называют в этом случае поляризационными или связанными) кажется привлекательной из-за возможности объяснить экспериментальные факты. Поэтому мы принимаем макроскопическую модель, которая, разумеется, должна быть обоснована впоследствии на микроскопическом уровне и проверена на практике вместе со всеми ее следствиями. Мы предположим, что при помещении диэлектрика в электрическое поле на его поверхности возникают поляризационные заряды с плотностью (рис. 3.5).
Рис. 3.5. Сферическая частица в однородном электрическом поле напряжённостью Е.
Знаками «+» и «–» показаны связанные заряды, возникшие на поверхности частицы при её поляризации.
Электрические силы, действующие на положительные (F+) и отрицательные (
Поляризационные заряды создают дополнительное электрическое поле , направленное противоположно полю от зарядов на обкладках (см. рис. 3.3). Это и объясняет меньшую величину результирующего поля Е по сравнению с полем E0. Действительно, для простейшей геометрии плоского конденсатора (см. выше замечание о форме поверхности диэлектрика) изменение поля в диэлектрике сводится только к изменению величины его напряженности в раз
|
|
Отсюда мы находим, какая часть результирующего поля создается поляризационными зарядами, а какая — зарядами на обкладках
|
(3. |
3)Отрицательный знак указывает на противоположное направление поля поляризационных зарядов. Зная связь поверхностной плотности зарядов с напряженностью создаваемого ими поля
Находим плотность поляризационных зарядов
|
|
(3.4) |
Заметим, что случаю проводника соответствует предел
Действительно, тогда , а поле внутри материала полностью компенсируется, получаем
откуда
Значения e для некоторых диэлектриков приведены в таблице (для газов — при нормальных условиях).
Таблица
Значения диэлектрической проницаемости для некоторых веществ
|
Диэлектрик |
|
Диэлектрик |
|
|
Гелий |
1,00007 |
Жидкий гелий |
1,047 |
|
Водород |
1,00027 |
|
1,23 |
|
Азот |
1,00058 |
Жидкий азот |
1,43 |
|
Бумага |
3,5 |
Трансформаторное масло |
4,5 |
|
Фарфор |
6,5 |
Лёд |
16 |
|
Этиловый спирт |
25,1 |
Глицерин |
56,2 |
|
Вода |
81,1 |
Титанат стронция |
310 |
|
|
|
|
|
Обратите внимание: одни и те же вещества при разных условиях имеют различные диэлектрические свойства.
Значит, для их объяснения необходимо построить теорию на микроскопическом уровне, исходящую из свойств атомов и молекул и учитывающую состояние вещества.
Дополнительная информация
http://chemister.da.ru/Chemie/Tables/dielectric.htm — диэлектрические проницаемости некоторых веществ;
http://www.radioland.net.ua/contentid-381-page1.html — основные типы диэлектриков, применяемые в конденсаторах;
http://ufn.ru/ufn67/ufn67_11/Russian/r6711n.pdf — статья «Вещества с высокой и сверхвысокой диэлектрической проницаемостью»;
http://www.chipdip.ru/video.aspx?vid=ID000292886&tag=dielectric — видео «Пироэлектрики»;
http://gos-rz.narod.ru/2/20.htm — сегнетоэлектрики, их применение;
http://www.rci.rutgers.edu/~ecerg/projects/ferroelectric.html — керамические сегнетоэлектрики;
http://www.chipdip.ru/video.aspx?vid=ID000292814&tag=dielectric — видео «Сегнетокерамика».
Элементарный учебник физики Т2
Элементарный учебник физики Т2
ОглавлениеИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮГлава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4.  Положительные и отрицательные заряды§ 5. Что происходит при электризации? § 6. Электронная теория. § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 15. Сложение полей. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле. § 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 27.  Соединение с Землей.§ 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 36. Диэлектрическая проницаемость. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила. § 40. Признаки электрического тока. § 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 48. Зависимость сопротивления от температуры.  § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? § 55. Шунтирование измерительных приборов. Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64. Электрическая проводка. Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 68. Движение ионов в электролитах. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе.  § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 82. Соединение источников тока. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов. § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII.  ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ§ 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 93. Искровой разряд. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108. Природа электрического тока в полупроводниках. § 109. Движение электронов в полупроводниках. § 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. 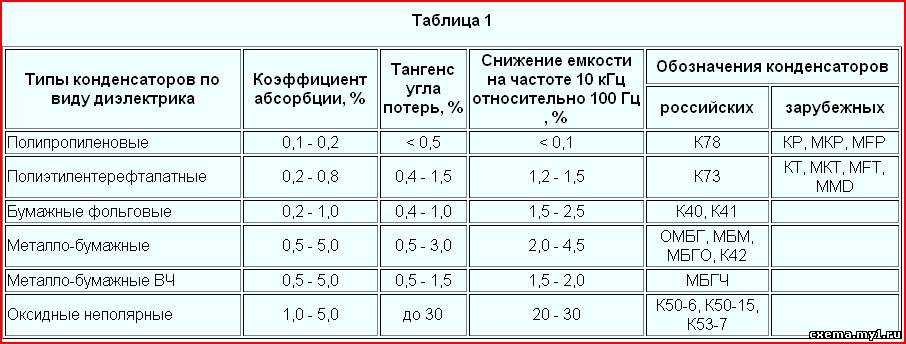 Полюсы магнита и его нейтральная зона.§ 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 121. Сложение магнитных полей. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током. § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128.  Магнитное поле Земли.§ 129. Элементы земного магнетизма. § 130. Магнитные аномалии и магнитная разведка полезных ископаемых. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока. Правило Ленца. § 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144.  Магнитная проницаемость железа.§ 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. Глава XVII. ПЕРЕМЕННЫЙ ТОК § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. Индуктивность катушки. § 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока.  § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением. § 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов.  § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы |
С. Элементарный учебник физики. Т.2. Электричество и магнетизм. — М.: Наука, 1985. — 479 c.
Диэлектрики
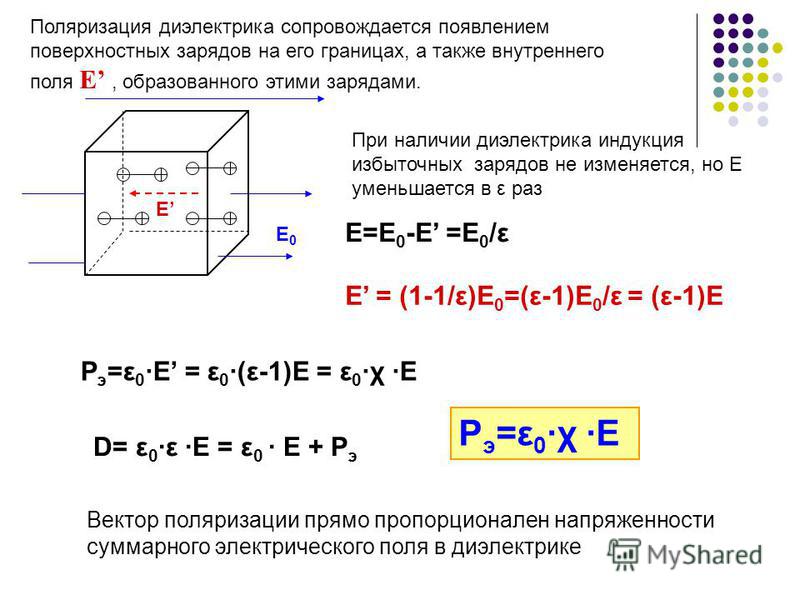
Диэлектрики Если материал содержит полярные молекулы, они обычно будут иметь случайную ориентацию, когда не будет приложено электрическое поле. Приложенное электрическое поле поляризует материал, ориентируя дипольные моменты полярных молекул.
Наличие диэлектрика уменьшает электрическое поле, создаваемое данной плотностью заряда. Коэффициент k, на который эффективное поле уменьшается из-за поляризации диэлектрика, называется диэлектрической проницаемостью материала.
| Индекс Концепции конденсаторов Концепции диполей | |||
| Назад |
Емкость набора заряженных параллельных пластин увеличена за счет вставки диэлектрического материала. Емкость обратно пропорциональна электрическому полю между пластинами, а наличие диэлектрика снижает эффективное электрическое поле. Диэлектрик характеризуется диэлектрической проницаемостью k, и емкость умножается на этот коэффициент.
| Индекс Концепции конденсаторов | |||||||||||
|
Диэлектрическая проницаемость k определяется как отражение степени уменьшения эффективного электрического поля, как показано ниже. Диэлектрическая проницаемость — это характеристика пространства, а относительная диэлектрическая проницаемость или «диэлектрическая постоянная» — это способ охарактеризовать уменьшение эффективного поля из-за поляризации диэлектрика. Емкость параллельного расположения пластин увеличивается в k раз.
Вставка диэлектрика между пластинами конденсатора влияет на его емкость. Чтобы понять почему, давайте рассмотрим эксперимент, описанный на рисунке \(\PageIndex{1}\). Первоначально конденсатор емкостью \(C_0\) при наличии воздуха между его пластинами заряжается от батареи до напряжения \(V_0\). Когда конденсатор полностью заряжен, батарея отключается. Заряд \(Q_0\) остается на пластинах, и измеряется разность потенциалов между пластинами, равная \(V_0\). Теперь предположим, что мы вставляем диэлектрик, который полностью заполняет зазор между пластинами. Если мы проследим за напряжением, мы обнаружим, что показание вольтметра упало до меньшего значения \(В\). Мы записываем это новое значение напряжения как часть исходного напряжения \(V_0\) с положительным числом \(\каппа, \, \каппа > 1\).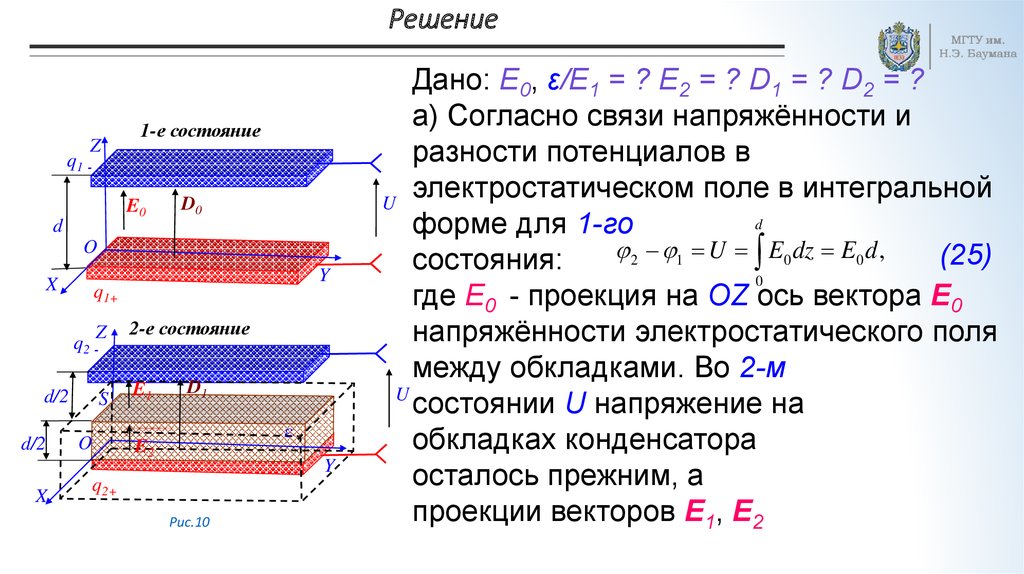
Подробное объяснение того, почему диэлектрик снижает напряжение, дано в следующем разделе. Различные материалы имеют разные диэлектрические постоянные (таблица значений для типичных материалов представлена в следующем разделе). Как только батарея отключается, заряд не может течь к батарее от пластин конденсатора. Следовательно, введение диэлектрика не влияет на заряд пластины, который остается равным \(Q_0\). Следовательно, находим, что емкость конденсатора с диэлектриком равна
Другими словами, мы можем сказать, что диэлектрическая проницаемость вакуума равна 1, что является эталонным значением.
Когда искатель перемещается по деревянной стойке, емкость ее пластин изменяется, потому что древесина имеет другую диэлектрическую проницаемость, чем гипсовая стена. Это изменение запускает сигнал в цепи, и, таким образом, шпилька обнаруживается. 92}{\каппа C_0} = \фракция{1}{\каппа} U_0. \метка{8.12}\]
12}.
2 = 16,0 \, нДж . \nonumber\] Со вставленным диэлектриком мы используем уравнение \ref{8.12}, чтобы найти, что накопленная энергия уменьшается до \[U = \frac{1}{\kappa}U_0 = \frac{1}{2.1} 16,0 \ , нДж = 7,6 \, нДж. \номер\]
