Ток равен мощность поделить

Как рассчитать мощность электрического тока?

Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.

Как рассчитать силу тока, рассчитать мощность, ампераж — Постройка

Наверное, каждый кто делал или делает ремонт электрики сталкивался с проблемой определения той или иной электрической величины.

Для кого-то это становится настоящим камнем преткновения, а для кого-то все предельно ясно и каких-либо сложностей при определении той или иной величины нет.

Данная статья посвящена именно первой категории – то есть для тех, кто не очень силен в теории электрических цепей и тех показателей, которые для них характерны.

Итак, для начала вернемся немного в прошлое и постараемся вспомнить школьный курс физики, касательно электрики. Как мы помним, основные электрические величины определяются на основании всего одного закона – закона Ома. Именно этот закон является базой проведения абсолютно для любых расчетов и имеет вид:

Отметим, что в данном случае речь идет о расчете самой простейшей электрической цепи, которая выглядит следующим образом:

Подчеркнем, что абсолютно любой расчет ведется именно посредством этой формулы. То есть путем не сложных математических вычислений можно определить ту или иную величину зная при этом два иных электрических параметра.

Как бы там ни было, наш ресурс призван упростить жизнь тому кто делает ремонт, а поэтому мы упростим решение задачи определения электрических параметров, вывив основные формулы и предоставив возможность произвести расчет электрических цепей онлайн.

Как узнать ток зная мощность и напряжение?

В данном случае формула вычисления выглядит следующим образом:

Расчет силы тока онлайн:

(Не целые числа вводим через точку. Например: 0.5)

Как узнать напряжение зная силу тока?

Для того, чтобы узнать напряжение, зная при этом сопротивление потребителя тока можно воспользоваться формулой:

Расчет напряжения онлайн:

Если же сопротивление неизвестно, но зато известна мощность потребителя, то напряжение вычисляется по формуле:

Определение величины онлайн:

Как рассчитать мощность зная силу тока и напряжения?

Здесь необходимо знать величины действующего напряжения и действующей силы тока в электрической цепи. Согласно формуле предоставленной выше, мощность определяется путем умножения силы тока на действующее напряжение.

Расчет цепи онлайн:

Как определить потребляемую мощность цепи имея тестер, который меряет сопротивление?

Этот вопрос был задан в комментарие в одном из материалов нашего сайта. Поспешим дать ответ на этот вопрос. Итак, для начала измеряем тестером сопротивление электроприбора (для этого достаточно подсоединить щупы тестера к вилке шнура питания). Узнав сопротивление мы можем определить и мощность, для чего необходимо напряжение в квадрате разделить на сопротивление.

Онлайн расчет:

Формула расчета сечения провода и как определяется сечение провода

Довольно много вопросов связано с определением сечения провода при построении электропроводки. Если углубиться в электротехническую теорию, то формула расчета сечения имеет такой вид:

Конечно же, на практике, такой формулой пользуются довольно редко, прибегая к более простой схеме вычислений. Эта схема довольно проста: определяют силу тока, которая будет действовать в цепи, после чего согласно специальной таблице определяют сечение. Более детально по этому поводу можно почитать в материале – «Сечение провода для электропроводки»

Приведем пример. Есть бойлер мощностью 2000 Вт, какое сечение провода должно быть, чтобы подключить его к бытовой электропрводке? Для начала определим силу тока, которая будет действовать в цепи:

Понятие электрической мощности и способы ее расчета

С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.

В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.

Через напряжение и ток

Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I

• P – активная мощность;
• U – напряжение приложенное к участку цепи;
• I — сила тока, протекающего через соответствующий участок.

Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.

Через напряжение и сопротивление

Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:

I = U/R

Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:

P = U*(U/R)=U 2 /R

• P – величина нагрузки;
• U – приложенная разность потенциалов;
• R – сопротивление нагрузки.

Через ток и сопротивление

Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.

Какие процессы протекают в проводниках при прохождении через них тока?

Если некое тело, обладающее способностью проводить электрический ток, поместить таким образом, что с одной стороны будет находиться положительный полюс, а с другой отрицательный, то по нему начинает проходить электрический ток. Ток представляет собой в очень упрощенном виде движение отрицательных электронов, имеющее направленность. При этом частицы, имеющие отрицательный заряд, притягиваются к положительному полюсу. Именно за счет этого принято различать полярность электрической цепи, что легко заметить при подключении элементов питания, которые устанавливаются с учетом плюса и минуса.

При движении электроны встречают на своем пути атомы вещества, которым передается часть энергии в результате столкновения, что приводит к нагреву тела, пропускающее ток. При этом при столкновении происходит подтормаживание электронов. Появляющееся электрическое поле имеет способность заново ускорять замедленные электроны, которые снова начинают свое движение к положительному полюсу. Весь этот процесс будет бесконечным, пока тело подключено к источнику электрического поля. Именно движущиеся электроны испытывают на себе сопротивление поля, при этом существует прямая связь между количеством препятствий на пути заряженных частиц и значением данной величины. Сопротивление тока в цепи увеличивается при увеличении количества столкновении электронов.

Пример расчета полной мощности для электродвигателя

Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.

Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:

В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:

Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.

Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.

Рис. 2. Шильд электродвигателя

Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:

• полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
• коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
• тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
• напряжение, при соединении обмоток треугольником составит 220 В;
• сила тока при том же способе соединения – 13,3 А.

Расчет электрического тока по мощности: формулы, онлайн расчет, выбор автомата

Проектируя электропроводку в помещении, начинать надо с расчета силы тока в цепях. Ошибка в этом расчете может потом дорого обойтись. Электрическая розетка может расплавиться под действием слишком сильного для нее тока. Если ток в кабеле больше расчетного для данного материала и сечения жилы, проводка будет перегреваться, что может привести к расплавлению провода, обрыва или короткого замыкания в сети с неприятными последствиями, среди которых необходимость полной замены электропроводки – еще не самое плохое.

Знать силу тока в цепи надо и для подбора автоматических выключателей, которые должны обеспечивать адекватную защиту от перегрузки сети. Если автомат стоит с большим запасом по номиналу, к моменту его срабатывания оборудование может уже выйти из строя. Но если номинальный ток автоматического выключателя меньше тока, возникающего в сети при пиковых нагрузках, автомат будет доводить до бешенства, постоянно обесточивая помещение при включении утюга или чайника.

Формула расчета мощности электрического тока

Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.

В реальных условиях в формулу добавляется еще одна составляющая и формула для однофазной сети приобретает вид:

I = P/(U*cos φ),

а для трехфазной сети: I = P/(1,73*U*cos φ),

где U для трехфазной сети принимается 380 В, cos φ – это коэффициент мощности, отражающий соотношение активной и реактивной составляющих сопротивления нагрузки.

Для современных блоков питания реактивная компонента незначительна, величину cos φ можно принимать равной 0,95. Исключение составляют мощные трансформаторы (например, сварочные аппараты) и электродвигатели, они имеют большое индуктивное сопротивление. В сетях, где планируется подключение подобных устройств, максимальную силу тока следует рассчитывать с использованием коэффициента cos φ, равного 0,8 или рассчитать силу тока по стандартной методике, а потом применить повышающий коэффициент 0,95/0,8 = 1,19.

Подставив действующие значения напряжения 220 В/380 В и коэффициента мощности 0,95, получаем I = P/209 для однофазной сети и I = P/624 для трехфазной сети, то есть в трехфазной сети при одинаковой нагрузке ток втрое меньше. Никакого парадокса тут нет, так как трехфазная проводка предусматривает три фазных провода, и при равномерной нагрузке на каждую из фаз она делится натрое. Поскольку напряжение между каждым фазным и рабочим нулевым проводами равно 220 В, можно и формулу переписать в другом виде, так она нагляднее: I = P/(3*220*cos φ).

Подбираем номинал автоматического выключателя

Применив формулу I = P/209, получим, что при нагрузке с мощностью 1 кВт ток в однофазной сети будет 4,78 А. Напряжение в наших сетях не всегда равно в точности 220 В, поэтому не будет большой ошибкой силу тока считать с небольшим запасом как 5 А на каждый киловатт нагрузки. Сразу же видно, что в удлинитель, промаркированный «5 А», утюг мощностью 1,5 кВт включать не рекомендуется, так как ток будет в полтора раза превышать паспортную величину. А еще сразу можно «проградуировать» стандартные номиналы автоматов и определить, на какую нагрузку они рассчитаны:

• 6 А – 1,2 кВт;
• 8 А – 1,6 кВт;
• 10 А – 2 кВт;
• 16 А – 3,2 кВт;
• 20 А – 4 кВт;
• 25 А – 5 кВт;
• 32 А – 6,4 кВт;
• 40 А – 8 кВт;
• 50 А – 10 кВт;
• 63 А – 12,6 кВт;
• 80 А – 16 кВт;
• 100 А – 20 кВт.

С помощью методики «5 ампер на киловатт» можно оценить силу тока, возникающую в сети при подключении бытовых устройств. Интересуют пиковые нагрузки на сеть, поэтому для расчета следует использовать максимальную потребляемую мощность, а не среднюю. Эта информация содержится в документации на изделия. Вряд ли стоит самому рассчитывать этот показатель, суммируя паспортные мощности компрессоров, электродвигателей и нагревательных элементов, входящих в устройство, так как есть еще такой показатель, как коэффициент полезного действия, который придется оценивать умозрительно с риском сильно ошибиться.

При проектировании электропроводки в квартире или загородном доме не всегда доподлинно известны состав и паспортные данные электрооборудования, которое будет подключаться, но можно воспользоваться ориентировочными данными обычных для нашего быта электроприборов:

• электросауна (12 кВт) — 60 А;
• электроплита (10 кВт) — 50 А;
• варочная панель (8 кВт) — 40 А;
• электроводонагреватель проточный (6 кВт) — 30 А;
• посудомоечная машина (2,5 кВт) — 12,5 А;
• стиральная машина (2,5 кВт) — 12,5 А;
• джакузи (2,5 кВт) — 12,5 А;
• кондиционер (2,4 кВт) — 12 А;
• СВЧ-печь (2,2 кВт) — 11 А;
• электроводонагреватель накопительный (2 кВт) — 10 А;
• электрочайник (1,8 кВт) — 9 А;
• утюг (1,6 кВт) — 8 А;
• солярий (1,5 кВт) — 7,5 А;
• пылесос (1,4 кВт) — 7 А;
• мясорубка (1,1 кВт) — 5,5 А;
• тостер (1 кВт) — 5 А;
• кофеварка (1 кВт) — 5 А;
• фен (1 кВт) — 5 А;
• настольный компьютер (0,5 кВт) — 2,5 А;
• холодильник (0,4 кВт) — 2 А.

Примеры задач

Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.

Рис. 3. Последовательная расчетная цепь

Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:

P = U 2 /R = 81 / (10+20+30) = 1.35 Вт

Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:

Рис. 4. Параллельная схема подключения

Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:

Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:

P = I 2 *R = 25*6 = 150 Вт

Ток равен мощность поделить

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.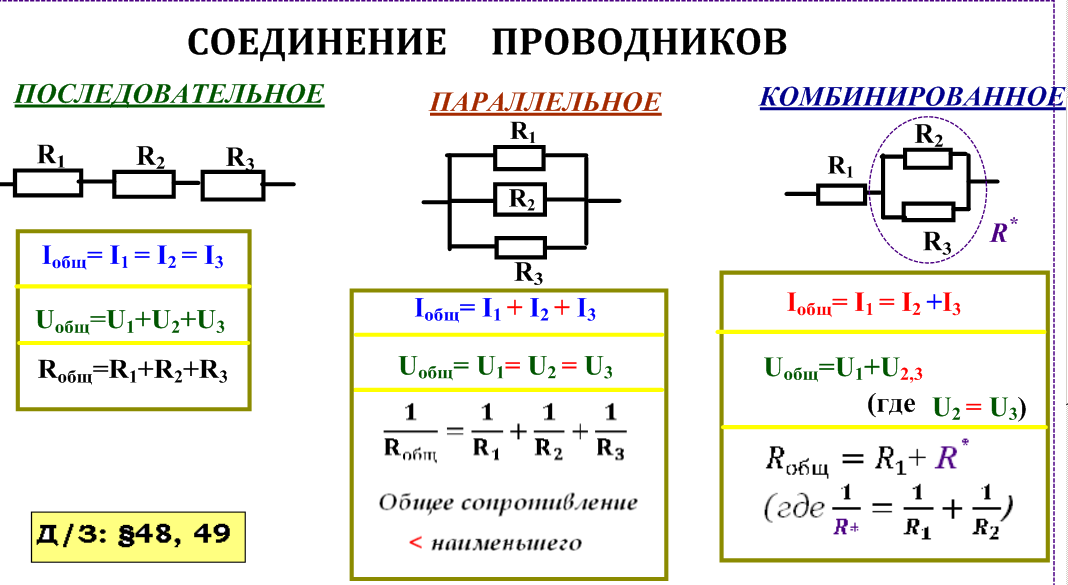

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Лампочка и постоянное напряжение

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт

Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I – сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.

Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

Подаем напряжение с блока питания на лампу и вуаля!

Замеряем напряжение на клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.

К этим же клеммах цепляем и наш осциллограф

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

Лампочка и переменное напряжение

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Расчеты напряжения, тока и сопротивления в последовательно-параллельных и параллельно-последовательных цепях – Школы схемотехники

Электрические цепи используются во всех электрических устройствах, используемых всеми людьми каждый день. Многие из этих схем очень сложны и имеют большое разнообразие элементов и компонентов, которые вместе управляют устройством, таким как бытовая техника или другие устройства.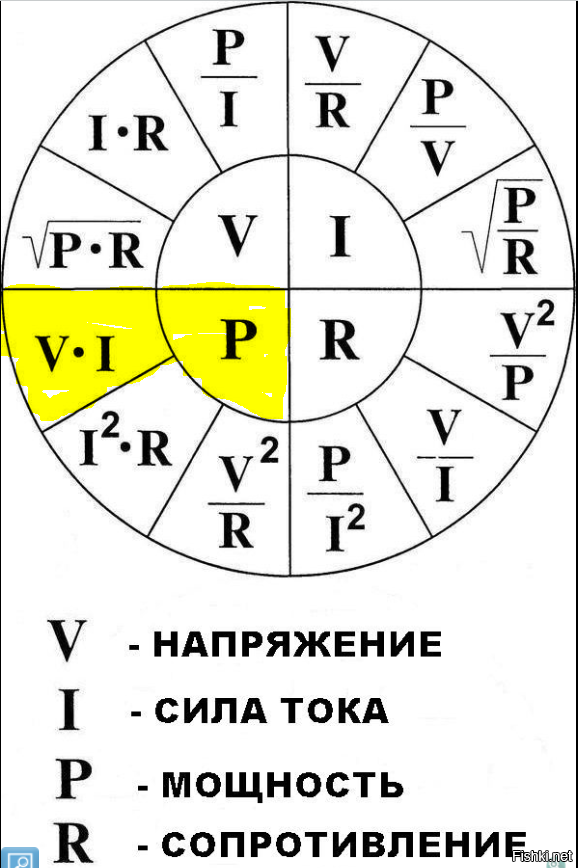

Прежде чем приступить к работе над сложными схемотехническими проектами, вы должны начать с основ, которые включают понимание основ напряжения, электрического тока, электрического сопротивления и т. д. Важно уметь различать последовательные, параллельные и параллельно-последовательные соединения.

Эта практика служит для проверки теоретических знаний, изученных в классе, о законе Ома, различных типах соединений и т. д. В каждом процессе, который мы выполняли, проводилось сравнение между теоретическими данными, полученными из расчетов, выполненных на бумаге, и экспериментальными данными. , которые были получены в лабораторной практике, можно наблюдать.

Эти процессы объясняются шаг за шагом, отвечая на вопросы в рабочем руководстве, так что все, что было сделано на практике, было проанализировано, и представлены теоретическая основа и математический анализ каждого расчета. Следует заметить, что теоретические и экспериментальные данные тесно связаны и что как теория, так и практика имеют большое значение в изучении этого предмета.

Содержание

1. ЗАДАЧИ

1.1. ОБЩАЯ ЦЕЛЬ

«Научиться теоретически и экспериментально определять значения напряжения, электрического тока и сопротивления в элементах, соединенных последовательно, параллельно и параллельно-последовательно».

1.2. КОНКРЕТНЫЕ ЗАДАЧИ

• Попрактикуйтесь в использовании мультиметра.
• Попрактикуйтесь в использовании макетной платы.
• Примените закон Ома и делитель напряжения, чтобы получить значения напряжения, сопротивления и тока.
• Научитесь экспериментально измерять напряжения, значения сопротивления и электрические токи.
• Уметь собирать последовательно-параллельные и параллельно-последовательные цепи, определяя свойства тока и напряжения, возникающие при каждом типе соединения.

2. ОБОСНОВАНИЕ

Понимание последовательно-параллельных и параллельно-последовательных соединений является базовым и основополагающим для каждого студента-электрика.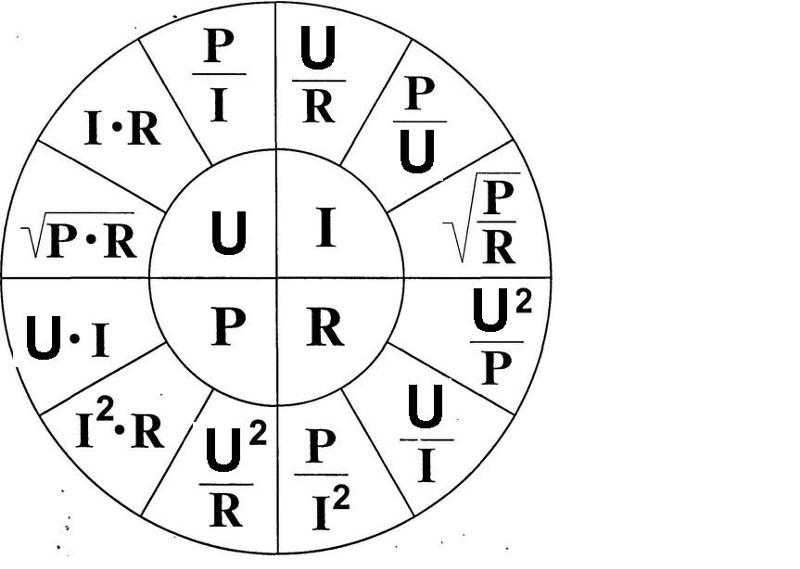 Вы не можете приступать к электрическим проектам, если плохо знаете эти понятия и не можете определить значения напряжения, сопротивления и тока, а также соотношения между этими значениями при любом типе соединения.

Эта практика и настоящий отчет оправданы ввиду необходимости изучения тем, упомянутых в предыдущем абзаце . В конце будет хорошо понято, насколько то, что было изучено теоретически, верно при применении на практике.

3. ТЕОРЕТИЧЕСКАЯ ОСНОВА

3.1. ОСНОВНЫЕ ПОНЯТИЯ

3.1.1. ЧТО ТАКОЕ НАПРЯЖЕНИЕ

Разность потенциалов между двумя точками (1 и 2) электрического поля называется напряжением и равна работе, которую совершает указанная единица положительного заряда для переноса ее из точки 1 в точку 2.

Не зависит от пути, пройденного грузом (консервативное поле), и зависит исключительно от потенциала точек 1 и 2 поля; выражается формулой:

V1-V2 = E x r

V1-V2 = E x r

где В1 – В2  – разность потенциалов, Е – напряженность поля в ньютонах/кулонах, r – расстояние в метрах между точками 1 и 2, то же, что и потенциал, в Международной системе единиц разность потенциалов измеряется в вольтах.

Если две точки, имеющие разность потенциалов, соединить проводником, то будет протекать электрический ток. Часть заряда с высоким потенциалом переместится по проводнику в точку с низким потенциалом и при отсутствии внешнего источника (генератора) этот ток перестанет течь, когда в обеих точках будет одинаковое электрическое напряжение (закон Генри). Этот перенос зарядов и есть то, что известно как электрический ток.

Разность потенциалов между двумя точками цепи также часто называют падением напряжения. Когда через эти точки может циркулировать электрический ток, полярность падения напряжения определяется его условным направлением, то есть от точки наибольшего потенциала к точке наименьшего потенциала. Поэтому, если ток I течет с сопротивления R на рис. 1, из точки А в точку В, то в ней произойдет падение напряжения с указанной полярностью и говорят, что точка А более положительна, чем В.

Тот факт, что две точки имеют одинаковый электрический потенциал, не означает, что они имеют одинаковый заряд.

 

3.1.2. ЧТО ТАКОЕ ЭЛЕКТРИЧЕСКИЙ ТОК

Это электрический заряд, который проходит через сечение или проводник в единицу времени . В Международной системе единиц это выражается в кулонов в секунду, единица

называется ампер.

Если интенсивность постоянна во времени, говорят, что ток непрерывен; в противном случае она называется переменной. Если в какой-либо точке проводника не происходит накопления или распределения нагрузки, ток является стационарным. По закону Ома сила тока равна напряжению, деленному на сопротивление, которому сопротивляются тела:

3.1.3. ЧТО ТАКОЕ ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ

Электрическое сопротивление R вещества определяется как сопротивление, с которым сталкивается электрический ток, проходя через него. Его величина измеряется в омах и обозначается греческой заглавной буквой омега (Ω). Материя имеет четыре состояния по отношению к потоку электронов. Это проводники, полупроводники, резисторы и диэлектрики.

Все они определяются степенью противодействия электрическому току (потоку электронов).

Это определение действительно для постоянного тока и для переменного тока в случае чистых резистивных элементов, то есть без индуктивной или емкостной составляющей. Если эти реактивные компоненты существуют, противодействие текущей циркуляции называется импедансом.

В зависимости от величины этого противодействия вещества классифицируются как проводящие, изолирующие и полупроводниковые. Есть также определенные материалы, в которых при определенных температурных условиях возникает явление, называемое сверхпроводимостью, при котором значение сопротивления практически равно нулю.

Группа реальных резисторов

Электрическое сопротивление измеряется с помощью омметра, устройства, предназначенного для измерения электрического сопротивления в омах. Поскольку сопротивление — это существующая в проводнике разность потенциалов, деленная на силу тока, проходящего через него, омметр должен измерять два параметра, а для этого он должен иметь собственный генератор для выработки электрического тока.

3.1.4. ЗАКОН ОМА

Поскольку электрическое сопротивление в цепи очень важно для определения интенсивности потока электронов, ясно, что оно также очень важно для количественных аспектов электричества. Со временем было обнаружено, что при равенстве прочих обстоятельств увеличение сопротивления цепи сопровождается уменьшением силы тока. Точное определение этой взаимосвязи должно было быть отложено до разработки достаточно безопасных измерительных инструментов. В 1820 году Георг Симон Ом, школьный учитель из Германии, обнаружил, что ток в цепи прямо пропорционален разности потенциалов, создаваемой током, и обратно пропорционален токоограничивающему сопротивлению. Математически выражено:

где I — ток, V — разность потенциалов и R — сопротивление.

Это основное соотношение названо в честь физика, который больше всего вмешался в его формулировку: оно называется Закон Ома.

Если знак пропорциональности закона Ома заменить знаком равенства, то получим:

Закон Ома для определения электрического тока (А)

Закон Ома для определения значений сопротивления (Ом)

V=I R

V=I R

Закон Ома для определения напряжения (Вольты)

Таким образом, Закон Ома определяет единицу электрического сопротивления, а также напряжения и тока, делая простые зазоры представленных уравнений, пока есть два известных значения и одно неизвестное.

3.2. ТИПЫ СОЕДИНЕНИЙ

3.2.1. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ

Два или более резистора соединены последовательно, когда при приложении к набору разности потенциалов все они проходят через один и тот же ток. Схема последовательного соединения резисторов показана на рисунке ниже:

Резисторы, соединенные последовательно

3.2.2. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

Два или более резистора соединены параллельно, если они имеют два общих вывода, так что при приложении разности потенциалов UAB все резисторы имеют одинаковое падение напряжения UAB. Параллельное соединение показано следующим образом:

резисторы, соединенные параллельно

3.2.3. ПАРАЛЛЕЛЬНОЕ ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ

При параллельном последовательном соединении вы можете найти наборы резисторов, соединенные последовательно с наборами резисторов, соединенными параллельно, как показано ниже: резисторов параллельно, а затем соединяя их с набором резисторов последовательно.

3.3. ПОСЛЕДОВАТЕЛЬНЫЕ РЕЗИСТОРЫ И ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ

Делитель напряжения является основным инструментом, используемым, когда вы хотите узнать конкретные напряжения резисторов, когда вы знаете общее напряжение на двух резисторах. Необходимо учитывать, что делитель напряжения работает для анализа двух сопротивлений, и что если вы хотите определить с помощью делителя напряжения напряжения более чем двух сопротивлений, то это следует делать путем сложения сопротивлений, применяя делитель напряжения два на два, шаг за шагом. шаг, пока не получите общее количество сопротивлений. Это очень полезно, потому что во многих случаях невозможно применить закон Ома, потому что у вас есть только значение сопротивления, но неизвестно напряжение. Именно тогда применяется делитель напряжения, по следующим формулам и по схеме, показанной ниже:

Другим важным инструментом является делитель тока, который работает с параллельными резисторами.