2\), откуда получаем требуемое равенство.

 

Утверждение

Если в прямоугольной системе координат точка \(M\) – середина отрезка \(PQ\), где \(P(x_1;y_1), \ Q(x_2;y_2)\), то

\[M\left(\dfrac{x_1 + x_2}{2}; \dfrac{y_1 + y_2}{2}\right)\]

Доказательство

Пусть \(M(a;b)\).

 

1) Пусть \(PQ\parallel Oy \Rightarrow x_1=x_2=a\). Значит, \(a=\dfrac{x_1+x_2}2=\dfrac{a+a}2\) – верно.

 

Т.к. \(PM=MQ\), следовательно, \(|y_2-b|=|y_1-b| \Rightarrow y_2-b=y_1-b\) или \(y_2-b=b-y_1\), что равносильно \(y_2=y_1\) или \(b=\dfrac{y_1+y_2}2\). Первое равенство невозможно (т.к. тогда точки \(P\) и \(Q\) совпадают).

 

2) Случай \(PQ\parallel Ox \Rightarrow y_1=y_2=b\) доказывается аналогично.

 

3) \(x_1\ne x_2, y_1\ne y_2\).

 

Тогда \(Ma=b\) – средняя линия трапеции \(x_1PQx_2\), следовательно, равна полусумме оснований, то есть \(b=\dfrac{y_1+y_2}2\).

 

Аналогично \(a=\dfrac{x_1+x_2}2\).

 

\[{\Large{\text{Векторы на координатной плоскости}}}\]

Лемма

Если векторы \(\overrightarrow a\) и \(\overrightarrow b\) коллинеарны, то существует такое число \(\lambda\ne 0\), что \(\overrightarrow a=\lambda\overrightarrow b\).

 

Доказательство

1) Если \(\overrightarrow a\uparrow \uparrow \overrightarrow b\).

 

Рассмотрим вектор \(\dfrac1{|\overrightarrow a|}\overrightarrow a\). Данный вектор сонавправлен с \(\overrightarrow a\), а его длина равна \(1\). Тогда вектор \(\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\) также сонаправлен с \(\overrightarrow a\), но его длина равна \(|\overrightarrow b|\). То есть равен вектору \(\overrightarrow b\).

 

2) Если \(\overrightarrow a\uparrow \downarrow \overrightarrow b\).

 

Аналогично доказывается, что \(\overrightarrow b=-\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\).

 

Определение

Если вектор \(\overrightarrow p\) представлен как линейная комбинация двух векторов: \(\overrightarrow p=\alpha\overrightarrow a+\beta \overrightarrow b\), то говорят, что вектор \(\overrightarrow p\) разложен по векторам \(\overrightarrow a\) и \(\overrightarrow b\).

 

\(\alpha, \beta\) – коэффициенты разложения.  

Пусть векторы \(\overrightarrow i\), \(\overrightarrow j\) – векторы, длины которых равны \(1\), а направление совпадает с направлением осей \(Ox\) и \(Oy\) соответственно. Такие векторы называются единичными векторами.

 

Тогда если \(\overrightarrow p=a\overrightarrow i+b\overrightarrow j\), то \(\{a;b\}\) – координаты вектора \(\overrightarrow p\).

 

Свойства координат вектора

1. Равные векторы имеют равные координаты.

 

2. Координаты суммы векторов равны сумме координат каждого вектора: если \(\overrightarrow a\{x_1;y_1\}, \ \overrightarrow b\{x_2;y_2\}\), то \(\overrightarrow a+\overrightarrow b=\{x_1+x_2;y_1+y_2\}\).

 

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: \(\overrightarrow a\{x;y\}, \ \lambda \) – число, то \(\lambda\overrightarrow a\{\lambda x;\lambda y\}\). 2}\).  

\[{\Large{\text{Скалярное произведение векторов}}}\]

Определение

Пусть от одной точки отложены два вектора \(\overrightarrow {AB}\) и \(\overrightarrow {AC}\). Тогда угол между этими векторами – это угол \(\angle BAC\), не превышающий развернутого угла.

 

Скалярное произведение векторов \(\overrightarrow a\) и \(\overrightarrow b\) – это число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: \(\overrightarrow a\cdot \overrightarrow b\) или \((\overrightarrow a, \overrightarrow b)\). \[(\overrightarrow a, \overrightarrow b)=|\overrightarrow a|\cdot |\overrightarrow b|\cdot \cos\widehat{(\overrightarrow a, \overrightarrow b)}\]

Следствия

1. Если ненулевые векторы взаимно перпендикулярны, то косинус угла между ними равен нулю, следовательно, и их скалярное произведение равно нулю.

 

2. Если угол между ненулевыми векторами острый, то скалярное произведение положительно.

2=0 \Leftrightarrow |\overrightarrow a|=0\).

 

2. Переместительный закон: \(\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow a\).

 

3. Распределительный закон: \(\overrightarrow a \cdot (\overrightarrow b+\overrightarrow c)=\overrightarrow a\cdot \overrightarrow b+\overrightarrow a\cdot \overrightarrow c\).

 

4. Сочетательный закон: \((\lambda\overrightarrow a)\cdot \overrightarrow b=\lambda (\overrightarrow a\cdot \overrightarrow b)\).

Как найти координаты вектора зная его длину

Координаты вектора. Направляющие косинусы

Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.

Координаты вектора

Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $\overline$, начало которого совпадает с началом системы координат (рис. 1).

Сумма двух векторов, заданных координатами

Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.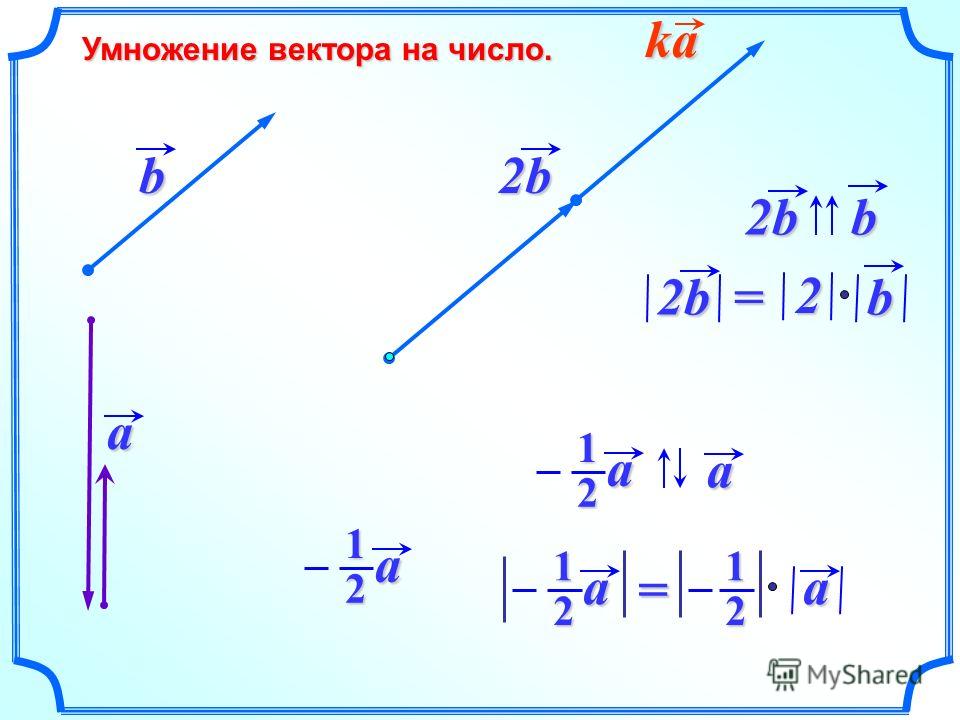

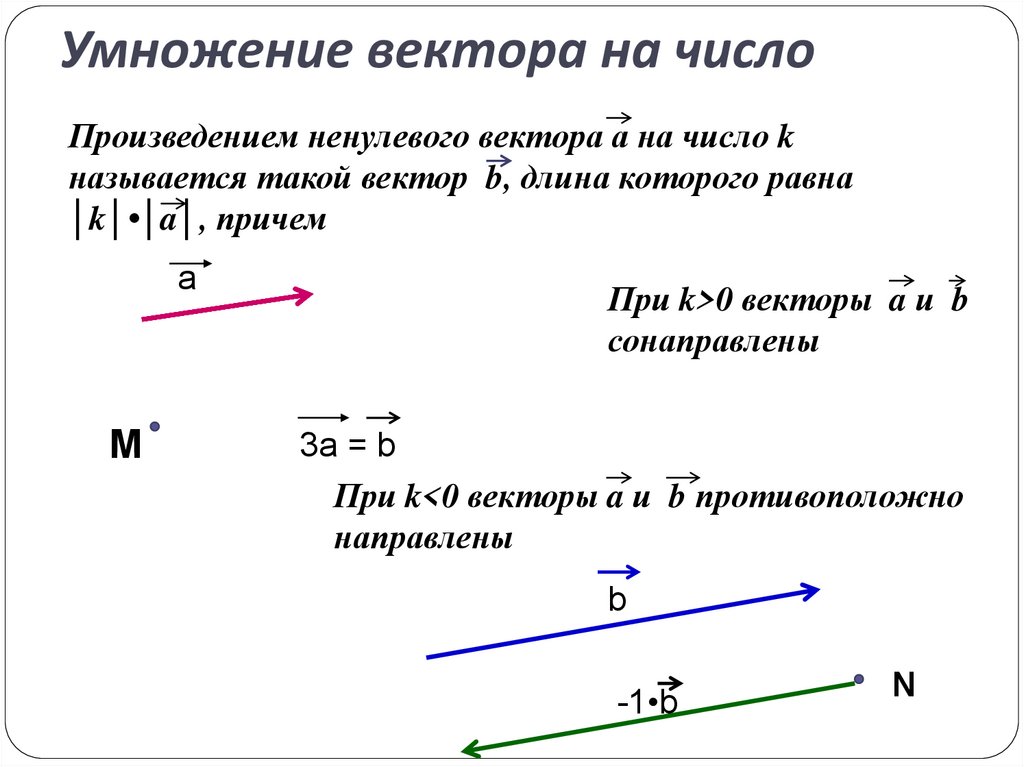
Умножение вектора на число

Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.

Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $A\left(a_ ; a_\right)$ и $B\left(b_ ; b_\right)$. Тогда координаты вектора $\overline=\left(x_ ; y_\right)$ находятся по формулам (рис. 4):

Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.

Задание. Найти координаты вектора $\overline$, если $A(-4 ; 2), B(1 ;-3)$

Решение. $\overline=(1-(-4) ;-3-2)=(5 ;-5)$

Направляющие косинусы

Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.

Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.

Здесь $\alpha$, $\beta$ и $\gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.

Как найти координаты вектора

Чтобы найти координаты вектора \(\ \overline \) , если заданы координаты его начала и конца, необходимо вычесть соответствующие координаты начала из координат конца. Если точки установлены на плоскости и имеют соответственно координаты \(\ A\left(x_ ; y_\right) \quad\quad B\left(x_ ; y_\right) \), то координаты вектора \(\ \overline \) рассчитываются по формуле:

ПРИМЕРЫ РАСПОЛОЖЕНИЯ ВЕКТОРНЫХ КООРДИНАТ

Подставляя координаты заданных точек, получаем:

Чтобы найти вектор \(\ \overline \) , оригинальная формула принимает вид:

Характеристики вектора: длина, направление, координаты

У любого вектора есть 2 главные характеристики:

• длина (математики говорят «модуль вектора»)
• направление (в какую сторону вектор на рисунке направлен)

Третья характеристика вектора – это его координаты.

Примечание:

Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.

Что такое координаты вектора

Координаты вектора – это длины его теней на осях координат (его проекции на оси).

Координаты вектора указывают так:

\( a_ \) – это «x» координата вектора, проекция вектора \( \vec \) на ось Ox;

\( a_ \) — это «y» координата вектора, проекция вектора \( \vec \) на ось Oy;

Координаты вектора можно получить из координат его начальной и конечной точек:

«координата вектора» = «конец» — «начало»

Пример:

\( A \left( 1;1 \right) \) — начальная точка,

\( B \left( 4;3 \right) \) — конечная точка,

\[ \overrightarrow = \left\; AB_ \right\> \]

\[ \begin AB_ = 4 – 1; AB_ = 3 \\ AB_ = 3 – 1; AB_ = 2 \end \]

Длина вектора (в чем измеряется, как посчитать)

Длину вектора (его модуль) обозначают так:

Как вычислить длину вектора по его координатам

Когда известны координаты вектора, его длину считают так:

\( a_ \) и \( a_ \) — это числа, координаты вектора \( \vec \)

Для двухмерного вектора:

Для трехмерного вектора:

Как вычислить длину вектора с помощью рисунка

Если вектор нарисован на клетчатой бумаге, длину считаем так:

1). Если вектор лежит на линиях клеточек тетради:

— считаем количество клеточек.

Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.

2). Если вектор не лежит вдоль линий:

— проводим вертикаль и горизонталь пунктиром.

\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;

— затем применяем формулу:

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

• угол \( \alpha \) между вектором и горизонталью (осью Ox),
• или угол \( \beta \) вежду вектором и вертикалью (осью Oy).

Словами указать направление вектора можно так:

• вектор длиной 5 единиц направлен под углом 30 градусов к горизонтали;
• Или же: вектор длиной 5 единиц направлен под углом 60 градусов к вертикали.

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

• угол между вектором и осью Oz;
• и один из углов: между вектором и осью Oy, или между вектором и осью Ox;

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Нахождение длины вектора через координаты начала и. Вектор. Координаты вектора

На оси абсцисс и ординат называются координатами вектора .

Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).

Формула определения координат вектора для двухмерных задач.

В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:

= (x 2 — x 1 ; y 2 — y 1).

Формула определения координат вектора для пространственных задач.

В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:

= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).

Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).

Свойства координат вектора.

1. Любые равные векторы в единой системе координат имеют равные координаты .

2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.

3. Квадрат длины любого вектора равен сумме квадратов его координат .

4.При операции умножения вектора на действительное число каждая его координата умножается на это число.

5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .

6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.

Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.

Как обычно, немного самой необходимой теории.

Вектор — это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:

Здесь точка А — начало вектора, а точка В — его конец.

У вектора есть два параметра: его длина и направление.

Длина вектора — это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается

Два вектора называются равными , если они имеют одинаковую длину и сонаправлены.

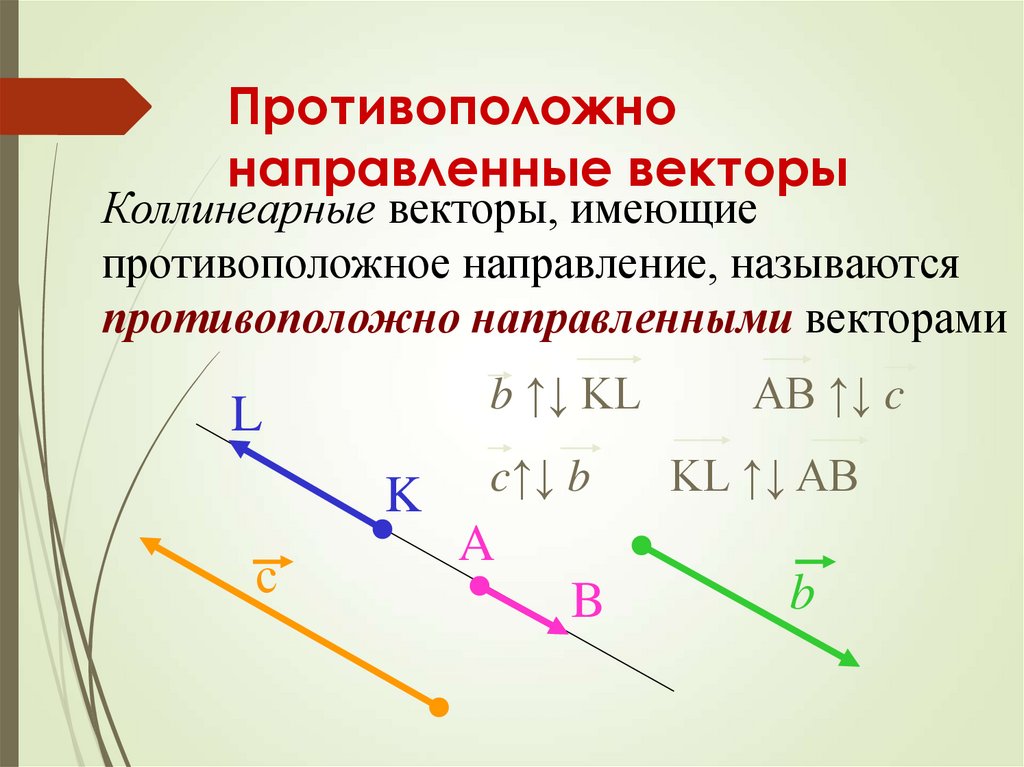
Два вектора называются сонаправленными , если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:

Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:

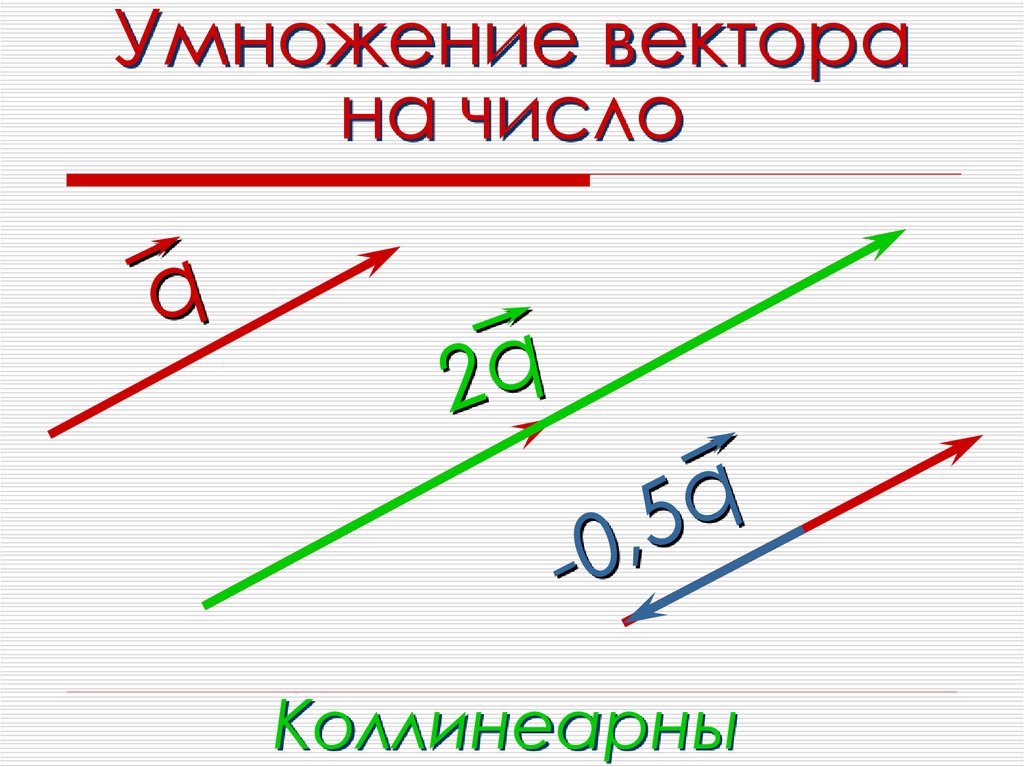
Вектора, лежащие на параллельных прямых называются коллинеарными : вектора , и — коллинеарны.

Произведением вектора на число называется вектор, сонаправленный вектору , если title=»k>0″>, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :

Чтобы сложить два вектора и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :

Это правило сложения векторов называется правилом треугольника .

Чтобы сложить два вектора по правилу параллелограмма , нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:

Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :

Отсюда вытекает правило нахождения разности двух векторов : чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора (то есть конец вычитаемого с концом уменьшаемого):

Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами:

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

Предлагаю вам решить задачи из Открытого банка заданий для , а затем сверить све решение с ВИДЕОУРОКАМИ:

1 . Задание 4 (№ 27709)

Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .

2 . Задание 4 (№ 27710)

Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).

3 . Задание 4 (№ 27711)

Две стороны прямоугольника ABCD O . Найдите длину суммы векторов и .

4 . Задание 4 (№ 27712)

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O . Найдите длину разности векторов и . (чертеж из предыдущей задачи).

5 . Задание 4 (№ 27713)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .

6 . Задание 4 (№ 27714)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .

7 .Задание 4 (№ 27715)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).

8 .Задание 4 (№ 27716)

Диагонали ромба ABCD равны 12 и 16.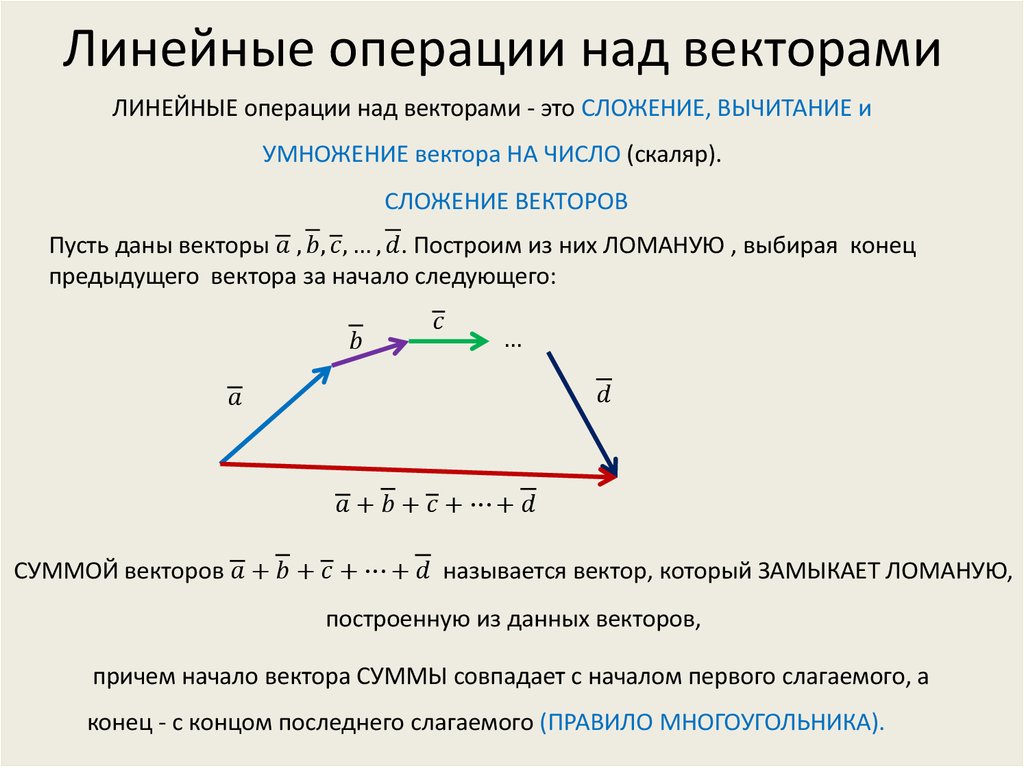 Найдите длину вектора — .

9 . Задание 4 (№ 27717)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .

10 . Задание 4 (№ 27718)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).

11 .Задание 4 (№ 27719)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).

12 . Задание 4 (№ 27720)

ABC равны Найдите длину вектора +.

13 . Задание 4 (№ 27721)

Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).

14 . Задание 4 (№ 27722)

Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).

Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox

Oxy

О А ОА .

, откуда ОА .

Таким образом, .

Рассмотрим пример.

Пример.

Решение.

:

Ответ:

Oxyz в пространстве.

А ОА будет диагональю.

В этом случае (так как ОА ОА .

Таким образом, длина вектора .

Пример.

Вычислите длину вектора

Решение.

, следовательно,

Ответ:

Прямая на плоскости

Общее уравнение

Ax + By + C ( > 0).

Вектор = (А; В) — нормальный вектор прямой.

В векторном виде: + С = 0 , где — радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 — прямая параллельна оси Ox ;

2) Ax + C = 0 — прямая параллельна оси Oy ;

3) Ax + By = 0 — прямая проходит через начало координат;

4) y = 0 — ось Ox ;

5) x = 0 — ось Oy .

Уравнение прямой в отрезках

где a, b — величины отрезков, отсекаемых прямой на осях координат.

Нормальное уравнение прямой (рис. 4.11)

где — угол, образуемый нормально к прямой и осью Ox ; p — расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

Здесь — нормируемый множитель прямой; знак выбирается противоположным знаку C , если и произвольно, если C = 0 .

Нахождение длины вектора по координатам.

Длину вектора будем обозначать . Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy . Пусть в ней задан вектор и он имеет координаты . Получим формулу, позволяющую находить длину вектора через координаты и .

Отложим от начала координат (от точки О ) вектор . Обозначим проекции точки А на координатные оси как и соответственно и рассмотрим прямоугольник с диагональю ОА .

В силу теоремы Пифагора справедливо равенство , откуда . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что и , а по построению длина ОА равна длине вектора , следовательно, .

Таким образом, формула для нахождения длины вектора по его координатам на плоскости имеет вид .

Если вектор представлен в виде разложения по координатным векторам , то его длина вычисляется по этой же формуле , так как в этом случае коэффициенты и являются координатами вектора в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам :

Ответ:

Теперь получим формулу для нахождения длины вектора по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор и обозначим проекции точки А на координатные оси как и . Тогда мы можем построить на сторонах и прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае (так как ОА – диагональ прямоугольного параллелепипеда), откуда . Определение координат вектора позволяет нам записать равенства , а длина ОА равна искомой длине вектора, следовательно, .

Таким образом, длина вектора в пространстве равна корню квадратному из суммы квадратов его координат , то есть, находится по формуле .

Пример.

Вычислите длину вектора , где — орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора по координатным векторам вида , следовательно, . Тогда по формуле нахождения длины вектора по координатам имеем .

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. 2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.

Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:

Понятие вектора

Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!

То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким образом, равных векторов может быть бесчисленное множество.

Обозначение векторов

Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.

Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Суммой двух векторов АВ и ВС будет являться вектор АС .

Записывается как АВ +ВС =АС .

Это правило называется – правилом треугольника .

То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).

Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b , или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

* * *

Правило параллелограмма

Это правило является следствием изложенного выше.

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a , и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.

Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма в изменнёном виде.

Пусть даны два вектора, найдём их разность:

Мы построили вектор противоположный вектору b, и нашли разность.

Координаты вектора

Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть, координаты вектора представляют собой пару чисел.

Если

И координаты векторов имеют вид:

То c 1 = a 1 + b 1 c 2 = a 2 + b 2

Если

То c 1 = a 1 – b 1 c 2 = a 2 – b 2

Модуль вектора

Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Рассмотрим задачи:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО .

Найдём вектор, который будет являться результатом АО –ВО:

АО –ВО =АО +(–ВО )=АВ

То есть разность векторов АО и ВО будет являться вектор АВ. А его длина равна восьми.

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ +AD .

Найдём вектор, который будет являться суммой векторов AD и AB BC равен вектору AD . Значит AB +AD =AB +BC =AC

AC это длина диагонали ромба АС , она равна 16.

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО +ВО .

Найдём вектор, который будет являться суммой векторов АО и ВО ВО равен вектору OD, з начит

AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

По теореме Пифагора:

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16.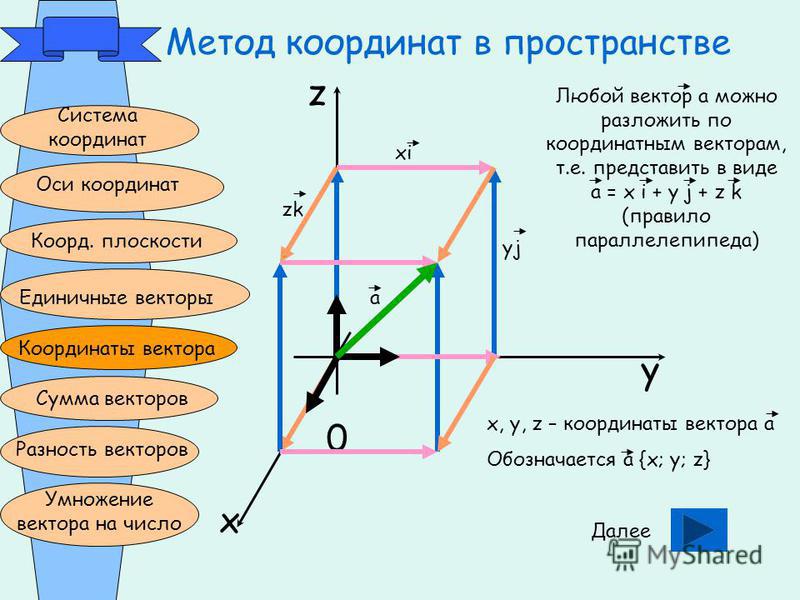 Найдите длину вектора АО –ВО .

Найдём вектор, который будет являться результатом АО –ВО :

АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном треугольнике AOB. вычислим катеты:

По теореме Пифагора:

Стороны правильного треугольника ABC равны 3.

Найдите длину вектора АВ –АС .

Найдём результат разности векторов:

СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.

27663. Найдите длину вектора а (6;8).

27664. Найдите квадрат длины вектора АВ .

Изменение базиса — Учебники по исчислению

Изменение базиса — Учебник по исчислению HMC

Пусть $V$ — векторное пространство, а $S = \{{\bf v_1,v_2, \ldots, v_n}\}$ — множество векторы в $V$. Напомним, что $S$ образует базис для $V$, если выполняются следующие два условия: пусть $V$ — векторное пространство и пусть $S = \{{\bf v_1,v_2, \ldots, v_n}\} $ — набор векторов в $V$. Напомним, что $S$ образует базис для $V$, если выполняются следующие два условия:

Если $S = \{{\bf v_1,v_2, \ldots, v_n}\}$ является базисом для $V $, то каждый вектор ${\bf v} \in V$ может быть выражен однозначно как линейная комбинация ${\bf v_1,v_2, \ldots, v_n}$: $$ {\bf v} = c_1{\bf v_1} + c_2{\bf v_2} + \cdots + c_n{ \bf v_n}. $$ Думайте о $\left[\begin{array}{c} c_1\\ c_2\\ \vdots \\ c_n \end{array}\right]$ как о координатах относительного ${\bf v}$ к базе $S$. Если $V$ имеет размерность , это количество векторов, необходимых для формирования основы. $n$, то каждый набор из $n$ линейно независимых векторов в $V$ образует базис для $V$. В каждом приложении у нас есть выбор, какую основу мы используем. В этом уроке мы опишем преобразование координат векторов при смене базиса. 92$. Для вектора ${\bf v} \in V$ по заданным его координатам $[{\bf v}]_B$ в базисе $B$ мы хотели бы иметь возможность выразить ${\bf v}$ в его координат $[{\bf v}]_{B’}$ в базисе $B’$, и наоборот.

Предположим, что базисные векторы ${\bf u’}$ и ${\bf w’}$ для $B’$ имеют следующие координаты относительно базиса $B$:

\begin{выравнивание*} ~[{\bf u’}]_B & = & \left[\begin{array}{c} a \\ b \end{массив}\right] \qquad \\ ~[{\bf w’}]_B & = & \left[\begin{array}{c} c \\ d \end{массив}\right]. \qquad \end{выравнивание*}

Это означает, что \begin{выравнивание*} {\bf u’} & = & a{\bf u} + b{\bf w} \\ {\bf ш’} & = & c{\bf u} + d{\bf ш} \end{выравнивание*}

изменение матрицы координат с $B’$ на $B$ $$ P = \left[\begin{array}{cc} a & c \\ b & d \\ \end{array} \right ] $$ определяет изменение координат ${\bf v} \in V$ при замене базиса с $B’$ на $B$. $$ [{\bf v}]_B = P[{\bf v}]_{B’} = \left[\begin{array}{cc} a & c \\ b & d \\ \end{array } \right][{\bf v}]_{B’}. $$ То есть, если мы знаем координаты ${\bf v}$ относительно базиса $B’$, умножение этого вектора на матрицу замены координат дает нам координаты ${\bf v}$ относительно базиса базис $B$. 9{-1}[{\bf v}]_B $$

Пример

Пусть $B = \left\{\left[{1 \top 0} \right],\left[{0 \top 1}\right]\right\}$ и $B’ = \left\{\left[{3 \top 1} \right],\left[{-2 \top 1}\право]\право\}$. {-1} = \left[\begin{массив}{cc} \frac{1}{5} & \frac{2}{5} \\ -\frac{1}{5} и \frac{3}{5} \конец{массив}\справа], $$ мы можем убедиться, что $$ [{\bf v}]_{B’} = \left[\begin{массив}{cc} \frac{1}{5} & \frac{2}{5} \\ -\frac{1}{5} и \frac{3}{5} \end{массив}\right]\left[\begin{массив}{c} 4\3 \end{массив}\right] = \left[\begin{массив}{c} 2\1 \конец{массив}\справа] $$ с чего мы начали.

В следующем примере мы вводим третий базис, чтобы посмотреть на связь между двумя нестандартными базами .

Пример

Пусть $B” = \left\{ \left[ {2 \top 1} \right],\left[ {1 \top 4} \right]\right\}$. Чтобы найти изменение матрицы координат из базиса $B’$ из предыдущего примера в $B”$, сначала выразим базисные векторы $\left[ {3 \atop 1} \right]$ и $\left[ { -2 \поверх 1} \справа]$ $B’$ как линейные комбинации базисных векторов $\left[ {2 \поверх 1} \справа]$ и $\left[ {1 \поверх 4} \справа] $ of $B”$: \begin{eqnarray*} \mbox{Set }\left[ \begin{array}{c} 3 \\ 1 \end{array}\right] & = & a\left[\begin {array}{c} 2 \\ 1 \end{массив}\right] + b\left[\begin{array}{c} 1 \\ 4 \end{массив}\right] \\ \left[\begin {array}{c} -2 \\ 1 \end{массив}\right] & = & c \left[\begin{array}{c} 2 \\ 1 \end{массив}\right] + d\left [\begin{array}{c} 1 \\ 4 \end{array}\right] \end{eqnarray*} и решить полученные системы r $a,b,c,$ и $d$: \begin{ eqnarray*} \left[ \begin{array}{c} 3 \\ 1 \end{массив}\right] & = & \frac{11}{7} \left[\begin{array}{c} 2 \ \ 1 \end{массив}\right] – \frac{1}{7}\left[\begin{array}{c} 1 \\ 4 \end{массив}\right] \\ \left[\begin{ array}{c} -2 \\ 1 \end{array}\right] & = & \frac{- 9}{7}\left[\begin{array}{c} 2 \\ 1 \end{массив}\right] + \frac{4}{7}\left[\begin{array}{c} 1 \\ 4 \end{array}\right] \end{eqnarray*} Таким образом, матричная форма перехода $B’$ в $B”$ равна $$ \left[\begin{array}{cc} \frac{11}{ 7} & \frac{-9}{7} \\ \frac{-1}{7} & \frac{4}{7} \end{массив}\right]. $$ Вектор ${\bf v}$ с координатами $\left[ {2 \atop 1} \right]$ относительно базиса $B’$ имеет координаты $$ \left[\begin{array}{cc} \frac{11}{7} & \frac{-9}{7} \\ \frac{-1}{9} & \frac{4}{7} \end{массив}\right]\left[\ begin{array}{c} 2 \\ 1 \end{array}\right] = \left[\begin{array}{c} \frac{13}{7} \\ \frac{2}{7} \ end{array}\right] $$ относительно базиса $B”$. Вернемся к стандартному базису: $$ [ {\bf v} ]_B = \frac{13}{7}\left[\begin{array}{c} 2 \\ 1 \end{array}\right ] + \frac{2}{7}\left[\begin{array}{c} 1 \\ 4 \end{array}\right] = \left[\begin{array}{c} 4 \\ 3 \ end{array}\right], $$, что согласуется с результатами предыдущего примера.

Вращение осей координат

Предположим, мы получаем новую систему координат из стандартной прямоугольной системе координат, вращая оси против часовой стрелки на угол $\theta$. Новый базис $B’ = \left\{{\bf u’, v’}\right\}$ единичных векторов вдоль осей $x’$ и $y’$ соответственно, имеет координаты \begin{выравнивание*} ~[{\bf u’}]_B & = & \left[\begin{массив}{c} \cos\тета \\ \sin\тета \конец{массив}\справа] \\ ~[{\bf v’}]_B & = & \left[\begin{массив}{c} -\sin\theta \\ \cos\theta \end{массив} \right] \end{выравнивание*} в исходной системе координат. 9{-1} = \left[ \begin{массив}{cc} \cos\тета и \sin\тета\\ -\sin\тета и \cos\тета \end{массив}\right]$. Вектор $\left[ {x \поверх y} \right]_B$ в исходная система координат имеет координаты $\left[ {x’ \ над y’} \right]_{B’}$ задано $$ \left[\begin{массив}{с} х’ \\ у’ \end{массив}\right]_{B’} = \left[\begin{массив}{cc} \cos\тета и \sin\тета\\ -\sin\тета и \cos\тета \end{массив}\right]\left[\begin{массив}{c} х\у \end{массив}\right]_{B} $$ в повернутой системе координат. 9{-1}[{\bf v}]_{B}. \end{выравнивание*}

---

[Я готов пройти тест.] [Мне нужно просмотреть больше.]

Задачи, Матрица, Угол и Компоненты

Когда вы смотрите на простой лист бумаги, вы обращаете внимание только на его 2 измерения, то есть смотрите только на длину и ширину, возможно, потому что он такой плоский. Однако что произойдет, если перед вами окажется коробка? Ваше зрение, кажется, улучшилось до трех измерений, потому что вы рассматриваете не только длину и ширину, но и высоту или, возможно, толщину коробки.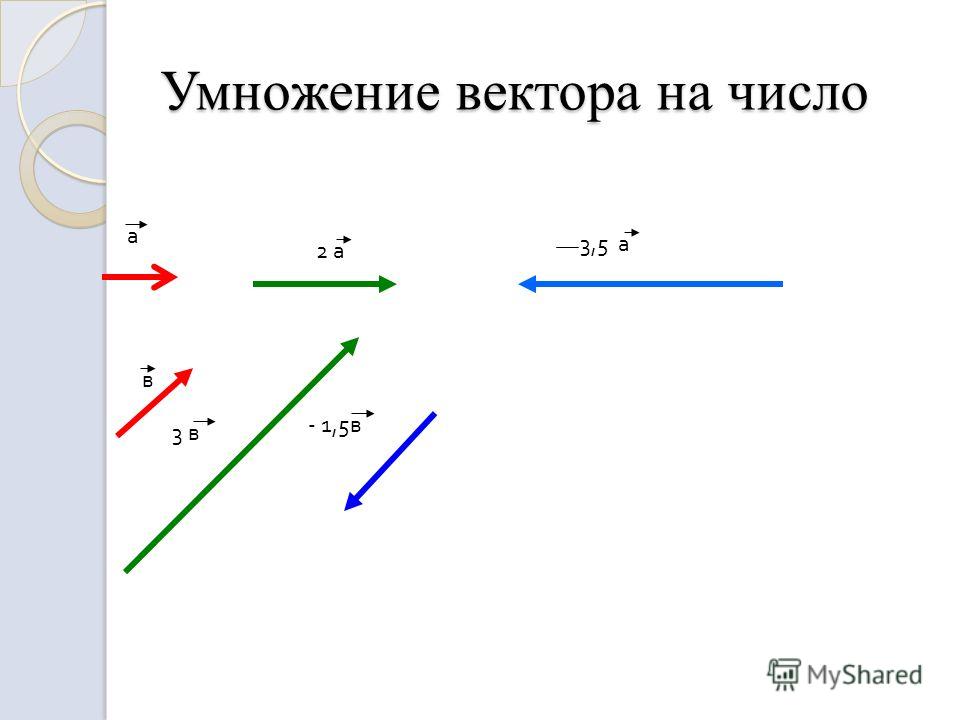 В этой статье будут рассмотрены Трехмерные векторы .

Что такое трехмерные векторы?

Трехмерные или трехмерные векторы — это векторы, представленные на трехмерной плоскости или в пространстве с тремя координатами, такими как x, y и z.

Если мы представим трехмерную плоскость с осью i, j и k (которая представляет оси x, y и z соответственно), мы можем записать трехмерный вектор как сумму его компонентов i, j и k.

Представьте себе вектор, который проходит от начала координат (0,0,0) до координат (3,2,5). Мы могли бы записать этот вектор как

Для этого вектора компонент i будет равен 3, компонент j будет равен 2, а компонент k будет равен 5.

Каковы координаты трехмерного вектора?

Трехмерный вектор имеет три координаты, представленные по осям x, y и z. Вспомните, что в двумерной плоскости у вас есть координаты только по осям x и y. Таким образом, в двумерном векторе координаты задаются в виде (x, y). Однако координаты трехмерных векторов задаются в виде (x, y, z)

Как построить трехмерный вектор?

Начните с рисования набора осей. Во-первых, нарисуйте вертикальную ось Z. Перпендикулярно этому нарисуйте ось Y. Между осями z и y нарисуйте ось x. Обратите внимание, что все 3 оси перпендикулярны друг другу.

Трехмерная ось (math.brown.edu)

После этого поместите шкалу на каждую ось и отметьте точку, в которую входит начало вектора. Затем нарисуйте стрелку между началом координат и началом вектора. Наконец, отметьте координаты головы стрелки.

3D-вектор

3D-вектор Матрица

Вектор также может быть записан в матричной форме. В этой форме мы можем записать вектор в виде трех строк матрицы с одним столбцом. Первая строка — компонент i, вторая строка — компонент j, а третья строка — компонент k.

Мы не записываем члены x, y и z в матричной форме.

Если мы используем приведенный выше вектор в качестве примера, мы получим:

Мы можем объединить два вектора, чтобы найти скалярное произведение этих векторов.

Предположим, что у нас есть вектор и вектор , скалярное произведение можно найти, следуя приведенному ниже методу:

Шаг 1: транспонировать вектор , то есть преобразовать его из 3 строк по 1 вектору-столбцу в 1 строку по 3 вектора-столбца .

Для вектора , вектор

Шаг 2: Запишите скалярное произведение обоих векторов как произведение обеих матриц.

Шаг 3: Выполните умножение матриц:

Шаг 4: Упростите матрицу. Вы должны получить матрицу 1 на 1.

Пусть вектор и вектор . Найдите скалярное произведение векторов и .

Решение:

Написание оба вектора в форме матрицы, мы получаем:

и

Шаг 1:

Шаг 2:

Шаг 3:

Шаг 4:

.

Что такое трехмерные векторные уравнения?

По сути, есть два основных трехмерных уравнения. Однако третье уравнение, которое представляет собой угол между трехмерными векторами, выводится из этих двух основных уравнений. Двумя основными уравнениями являются скалярное произведение и величина трехмерного векторного уравнения.

Dot Product 3D векторов

для двух определенных 3D -векторов A (x ₁ , Y ₁ , Z ₁ ) и B (x ₂ , Y ₂ , Z ₂ , Y ₂ , Z ₂ , Y ₂ , Z ₂ , Y ₂ , Z ₂ , Y ₂ , Z ₂ , Y представлены в векторной форме

и

Скалярное произведение

Найдите произведение векторов G и K, расположенных (-1, 2, 3) и (0, 5, 1) самолет.

Решение:

Применяя формулу скалярного произведения

Затем,

Величина трехмерного вектора

Величина трехмерного вектора выводится с использованием расширенной теоремы Пифагора. Напомним, что теорема Пифагора применяется, зная, что оси x и y перпендикулярны, обратите внимание, что дополнительная ось z в 3D перпендикулярна обеим осям x и y. Следовательно, чтобы вычислить величину некоторого трехмерного вектора A (x ₁ , y ₁ , z ₁ ), который представлен в векторной форме.

Применить

Найдите величину вектора C, заданную

Решение:

, поскольку величина вектора рассчитывается как

. Затем величина вектора C равен

HOW. рассчитывается ли угол между 3D-векторами?

Чтобы найти угол между двумя соответствующими 3D-векторами, используйте приведенную ниже формулу:

Иллюстрация угла между двумя векторами в 3D, StudySmarter Originals

Где — угол между векторами a и b, — скалярное произведение векторов a и b, а где и — величины векторов a и b соответственно.

Найдите модуль вектора, идущего от начала координат к координатам (2,1,2).

Решение:

Вектор можно записать как

Используя приведенное выше уравнение:

9002 Следовательно:

Теперь мы можем объединить все, что мы узнали, чтобы найти угол между двумя векторами!

Найдите угол между векторами и вектором .

Решение:

Написание матричной формы этих векторов:

и

Вектор письма в транскрипте:

Следовательно:

Величина вектора:

Начиная с:

Следовательно:

3-мерные векторы — ключевые выводы

• 3D-векторы имеют значения i, j и k для осей x, y и соответственно.
• Трехмерные векторы могут быть записаны в матричной форме.
• В этой форме мы можем найти скалярное произведение двух векторов, выполнив матричное умножение.
• Также найдя величину этих векторов с помощью расширенной версии теоремы Пифагора, мы можем найти угол между этими векторами.
• Графики векторов состоят из рисования осей, координат, где заканчивается и начинается вектор, и рисования линии, соединяющей обе точки.

Линейные преобразования и умножение матриц

Что такое линейные преобразования?
Что такое векторное пространство?
Как выполнить умножение матриц?

Этот пост является продолжением предыдущего поста, что является обязательным условием для прочтения этого. В последнем посте я рассмотрел базисные векторы, интервалы и линейные комбинации.

---

Концептуализация линейных преобразований

A Линейное преобразование — это просто функция, функция $f(x)$. Он принимает ввод, число x, и дает нам вывод для этого числа. Однако в линейной алгебре мы используем букву T для преобразования.

$$T(input_x) = output_x$$

Или с векторными координатами на входе и соответствующими векторными координатами на выходе

$$ \begin{bматрица} х_{ввод}\\ у_ {ввод} \end{bmatrix} = \begin{bmatrix} х_{выход}\\ у_ {выход} \end{bmatrix} $$

Мы могли бы думать о преобразовании в терминах преобразования вектора, когда мы существенно преобразуем координаты вектора или даже базисные векторы для некоторого вектора. Идея состоит в том, что мы даем некоторые векторные координаты в качестве входных данных, а затем получаем выходные данные из этих векторных координат.

Каждый раз, когда мы это делаем, мы можем визуализировать трансформацию, представляя вектор, перемещающийся из одной позиции в другую — каждый вектор в пространстве перемещается с трансформацией.

Преимущество трансформаций в том, что нам нужно всего

1. Координаты любого вектора в нашем пространстве и
2. Базисные векторы

Затем, если мы сделаем преобразование, мы преобразуем все векторы в нашем пространстве вместе с базисными векторами. Это означает, что нам просто нужно найти преобразованные базисные векторы, чтобы вычислить любой преобразованный вектор в нашем пространстве.

Как выполнить линейное преобразование?

Мы можем написать подобное общее уравнение для вектора $\vec{v}$ с векторными координатами $\begin{bmatrix}x\\y\end{bmatrix}$ и базисными векторами $\hat{i} = \ begin{bmatrix}i_1\\i_2\end{bmatrix}$ и $\hat{j} = \begin{bmatrix}j_1\\j_2\end{bmatrix}$

$$ T\left(\begin{bmatrix}x\\y\end{bmatrix}\right)= х \ начало {bmatrix} я_1\\ i_2 \end{bmatrix} + у \ начало {bmatrix} j_1\\ j_2 \end{bmatrix} $$

Таким образом, это означает, что нам просто нужно заменить $\hat{i}$ и $\hat{j}$ после преобразования, и мы можем просто выполнить умножение, как описано в Основах линейной алгебры 1.

An Альтернативный способ представления вышеизложенного и, возможно, более интуитивный способ численного понимания преобразования будет примерно таким:

$$ преобразовано _ {\ vec {v}} = x (преобразовано _ {\ hat {i}}) + y (преобразовано _ {\ hat {j}}) $$

Чтобы получить преобразованный вектор (выходной), мы берем координаты входного вектора x и y и масштабируем с преобразованными базисными векторами $\hat{i}$ и $\hat{j}$. Тогда то, что x и y заканчиваются, является преобразованными векторными координатами для вектора $\vec{v}$.

Что происходит численно

— т.е. что происходит между вводом и выводом?

Все, что происходит численно, заключается в том, что мы определяем правило, которое диктует, как мы преобразовываем любой вектор — именно так вы выполняете численное преобразование. Такое правило может быть неправильным, но держись за меня; Так что же может быть за правило? Часто бывает так, что мы определяем, в какое измерение должно преобразоваться наше текущее векторное пространство. 9{2}$ означает все действительные числа в двумерном пространстве.

---

Прежде чем двигаться дальше, мы не коснулись умножения векторов. Так как же нам перемножать матрицы? Позвольте мне расширить то, что вы узнали в Основах линейной алгебры 2 — масштабирование вектора по числу.

Допустим, у нас есть матрица A , определенная как таковая, где a, b, c и d — действительные числа

$$ А = \begin{bmatrix} а и б\\ CD \end{bmatrix} $$

И вектор $\vec{v}$, определенный как

$$ \vec{v} = \begin{bmatrix} Икс\\ у \end{bmatrix} $$

Затем мы могли бы перемножить их вместе, точно так же, используя векторное умножение:

$$ \begin{bматрица} а и б\\ CD \end{bmatrix} \begin{bматрица} Икс\\ у \end{bmatrix} = х \begin{bmatrix} а\\ с \end{bmatrix} + у \begin{bmatrix} б\\ г \end{bmatrix} = \begin{bmatrix} топор + по\\ сх + ду \end{bmatrix} $$

Обратите внимание, что мы можем определить вектор как матрицу, поэтому мы также можем назвать это умножением матриц.

Умножение матриц: Умножаем строки на столбцы . Это означает, что вы берете первое число в первой строке второй матрицы и масштабируете (умножаете) его на первый столбец в первой матрице. Вы делаете это с каждым числом в строке и столбце, затем переходите к следующей строке и столбцу и делаете то же самое.

Теперь мы можем определить линейное преобразование. Мы можем начать с задания матрицы A чисел, а затем пусть вектор $\vec{v}$ будет любым возможным вектором в нашем векторном пространстве

$$ А = \begin{bmatrix} -2 и 6\\ 3 и 1 \end{bmatrix} \begin{bматрица} Икс\\ у \end{bmatrix} $$

Тогда мы можем выбрать и сказать, что определяем наше линейное преобразование как $T(\vec{v}) = A \vec{v}$. Это означает, что для каждой векторной координаты в нашем векторе $\vec{v}$ мы должны умножить ее на матрицу A .

$$ Т(\vec{v}) = А \vec{v} \rightarrow \begin{bmatrix} -2 и 6\\ 3 и 1 \end{bmatrix} \begin{bматрица} Икс\\ у \end{bmatrix} $$

Как я только что показал вам выше, где мы определили матрицу A с помощью a, b, c и d, мы можем выполнить умножение следующим образом

$$ Т(\vec{v}) = А \vec{v} \rightarrow \begin{bmatrix} -2 и 6\\ 3 и 1 \end{bmatrix} \begin{bматрица} Икс\\ у \end{bmatrix} = х \begin{bmatrix} -2\\ 3 \end{bmatrix} + у \begin{bmatrix} 6\\ 1 \end{bmatrix} = \begin{bmatrix} -2х + 6у\\ 3x + 1г \end{bmatrix} $$

Вычисление преобразованного вектора?

Чтобы вычислить любой вектор после преобразования, все, что нам нужно сделать, как описано выше в этом посте, — это записать базисные векторы. Если мы знаем, где находятся базисные векторы после преобразования, вычисление любого преобразованного вектора становится до бешенства простым.

Я подчеркивал эту матрицу A на протяжении всего поста по очень конкретной причине. Представьте, что первый столбец матрицы равен $\hat{i}$, а второй столбец равен $\hat{j}$ 9.0007

$$ А = \begin{bmatrix} \шляпа{i}_x и \шляпа{j}_x\\ \шляпа{i}_y и \шляпа{j}_y \end{bmatrix} $$

Теперь становится очевидным, что мы можем по любому вектору вычислить любой вектор в преобразованном векторном пространстве. Итак, если у нас есть преобразованные $\hat{i}$ и $\hat{j}$, мы можем просто передать любой вектор в эту формулу вместе с преобразованными базисными векторами, и это даст нам преобразованный вектор (где T означает для преобразованных):

$$ \begin{bматрица} T _ {\ шляпа {i} _x} и T _ {\ шляпа {j} _x} \\ T _ {\ шляпа {i} _y} и T _ {\ шляпа {j} _y} \end{bmatrix} \begin{bматрица} \vec{v}_x \\ \vec{v}_y \end{bmatrix} $$

Как насчет умножения матриц 2×2?

Этот случай тоже несложный. Предположим, у нас есть матрицы A (слева) и B (справа). Мы просто умножаем строки первой матрицы на столбцы второй матрицы:

$$ \begin{bматрица} а и б\\ CD \end{bmatrix} \begin{bматрица} е & ж \\ г и ч \end{bmatrix} = \begin{bmatrix} ае + бг и аф + бч \\ ce + dg и cf + dh \end{bmatrix} $$

НО! Это нелегко запомнить, поэтому здесь есть интуитивный способ, как я показал ранее. Разделим процесс на 2:

1. Умножим матрицу A на первый столбец в матрице B
2. Умножим матрицу A на второй столбец в матрице B
9036 Этот сценарий известен, I показывал вам это ранее:

$$ \begin{bматрица} а и б\\ CD \end{bmatrix} \begin{bматрица} е \\ грамм \end{bmatrix} = е \begin{bmatrix} а \\ с \end{bmatrix} + г \begin{bmatrix} б\ г \end{bmatrix} = \begin{bmatrix} ае+бг\ се + дг \end{bmatrix} $$

$$ \begin{bматрица} а и б\\ CD \end{bmatrix} \begin{bматрица} ф\ час \end{bmatrix} = f \begin{bmatrix} а \\ с \end{bmatrix} + ч \begin{bmatrix} б\ г \end{bmatrix} = \begin{bmatrix} аф+бч\ ср + дч \end{bmatrix} $$

Сложив два результата вместе, мы получим уравнение выше:

$$ \begin{bматрица} а и б\\ CD \end{bmatrix} \begin{bматрица} е & ж \\ г и ч \end{bmatrix} = \begin{bmatrix} ае + бг и аф + бч \\ ce + dg и cf + dh \end{bmatrix} $$

---

Очевидно, этому нужно было многому научиться. Но мы могли бы также пойти дальше и задать надвигающийся вопрос, что может быть неправильным линейным преобразованием? Потому что мы только что определили некоторое линейное преобразование и предположили, что оно правильное. Пока я не буду углубляться в тему, но, как предлагает WolframAlpha, нам нужно, чтобы 2 условия были истинными, прежде чем мы сможем назвать это линейным преобразованием.

---

Резюме (из вопросов вверху):

1. Что такое линейные преобразования?
   Линейные преобразования — это функция $T(x)$, в которой мы получаем входные данные и преобразуем их по определенному правилу. Примером является $T(\vec{v})=A \vec{v}$, где для каждой векторной координаты в нашем векторе $\vec{v}$ мы должны умножить ее на матрицу A.
2. Что такое векторное пространство?
   Векторное пространство — это набор всех векторов в нашем пространстве, которые мы определяем в измерениях. Мы можем выполнять операции над этими векторами, например.