Изменяется ли частота света в зависимости от среды: и почему нет?
Частота света связана с количеством световых волн, проходящих из фиксированной точки в единицу секунды. Так что свет любой длины волны обладает определенной частотой, которая ему соответствует.
Свет обладает способностью изменять свои физические свойства при прохождении через разные среды и подвергается определенному процессу, вызывающему изменение их свойств. Частота также является свойством световой волны.. Изменяется ли частота света в зависимости от среды? Это один из знакомых вопросов, которые мы собираемся обсудить в этом посте.
Говоря об изменении среды, легкие процессы, такие как преломление и дифракция удобнее говорить об изменении со средой распространения. В обоих случаях свет распространяется из одной среды в другую с разными индексами.
Изменяется ли частота света в зависимости от среды?Мы знали, что частота обратно пропорциональна длине волны. Когда белый свет падает на стекло или призму, происходит изменение среды, так как свет распространяется из воздушной среды к призме, индексы которой отличаются друг от друга.
Когда белый свет падает на стекло или призму, происходит изменение среды, так как свет распространяется из воздушной среды к призме, индексы которой отличаются друг от друга.
Призма способна преломлять падающую белую световую волну, которая может рассеиваться на заметные цвета с другой длиной волны. Так мы можем наблюдать изменение длины волны падающего белого света, когда он попадает на другую среду, и скорость падающего света тоже меняется, но частота не меняется. Частота падающего света остается прежним.
Изображение с описанием Изменяется ли частота светаКогда свету приходится переходить из одной среды в другую, он должен отклоняться либо из-за преломления, либо из-за дифракции или интерференции. Рассмотрим пример преломления белого света на призме. Показатель преломления призмы немного больше, чем у воздуха; таким образом, происходит искривление света, вызывающее преломление. Преломляющее изображение, которое мы получаем, представляет собой полосу цветов с разными длинами волн, называемую дисперсией.
Положение рассеянных цветов в спектре обусловлено изменением скорости и длины волны. Цвет в полосе, скорость которой меньше, будет накапливать наименьшее количество позиций, следовательно, длина волны также меньше, поэтому выглядит тусклее. Таким образом скорость также менялась со средой. Группа цветов вместе дает визуальный спектр; частота всего спектра остается неизменной, потому что это объект, определяемый источником коллективно.
Таким образом, хотя скорость и длина волны меняются, частота не меняется вместе со средой; он остается постоянным.
Другими словами, длина волны уменьшается по мере пропорционального уменьшения скорости при перемещении между двумя разными средами. Если взять отношение длины волны к скорости, то оно будет постоянным. Отношение длины волны и скорости света есть не что иное, как частота. Видно, что частота не меняется со средой.
Почему частота света остается постоянной?Свет имеет способность отклоняться, когда он проходит через среду с разными показателями преломления. В соответствии с их показателями преломления, чем плотнее, либо реже, скорость света либо замедляется, либо становится быстрой.
В соответствии с их показателями преломления, чем плотнее, либо реже, скорость света либо замедляется, либо становится быстрой.
Игровой автомат свет соответствует пакету энергии в виде фотонов; таким образом, каждое свойство света также связано с энергией. Энергия света постоянна в каждой среде, потому что величина силы, вызывающей колебания фотона, остается постоянной. Это колебание связано с амплитудой света, которая является одной из частотных сущностей. Следовательно, частота света также остается постоянной.
Кредиты изображения: Изображение предоставлено Герд Альтманн из PixabayПостоянную частоту света можно математически описать с помощью выражения
Е = hν
Где E — энергия света, h — постоянная Планка, а ν — частота света.
Поскольку энергия света называется постоянной и существует еще один постоянный фактор; таким образом, частота также постоянна.
Свет квантуется; это означает, что он не может потерять или получить энергию, которая дает постоянную частоту в каждой среде.
Частота — это термин, который никогда не меняется ни в какой среде, поскольку он соответствует энергии.
Когда звуковая волна переходит из более плотной среды в более разреженную, мы можем наблюдать уменьшение длины волны; таким образом, слышимость может меняться, но частота зависит только от источника звука, а не от среды; таким образом, он остается постоянным.
Частота не зависит от среды распространения?Да, конечно, частота всегда не зависит от среды распространения; это означает, что на частоту не влияют свойства среды.
Частота полностью зависит от источника. Если изменится сам источник, изменится и частота. Он всегда остается независимым от среды распространения.
Связь между скоростью и длиной волны можно выразить, рассматривая скорость света в вакууме.
Приведенное выше утверждение означает, что чем больше длина волны света, тем меньше его частота. Математически уравнение зависимости частоты и длины волны можно записать как
Математически уравнение зависимости частоты и длины волны можно записать как
ню=с/λ; где ν — частота, λ — длина волны, c — скорость света.
На какие факторы света влияет изменение среды?На изменение среды при распространении влияют два фактора; они есть
- Длина волны – длина волны падающего света может увеличиваться или уменьшаться в зависимости от показателей среды.
- Скорость – скорость замедления света при распространении из более плотной среды в более разреженную.
Скорость обратно пропорциональна показателю преломления среды, а длина волны пропорциональна скорости.
Если показатель преломления среды увеличивается, скорость света уменьшается; это приводит к уменьшению длины волны света. Увеличение показателя преломления относится к более плотной среде; таким образом, в более плотной среде скорость меньше и пропорционально длине волны.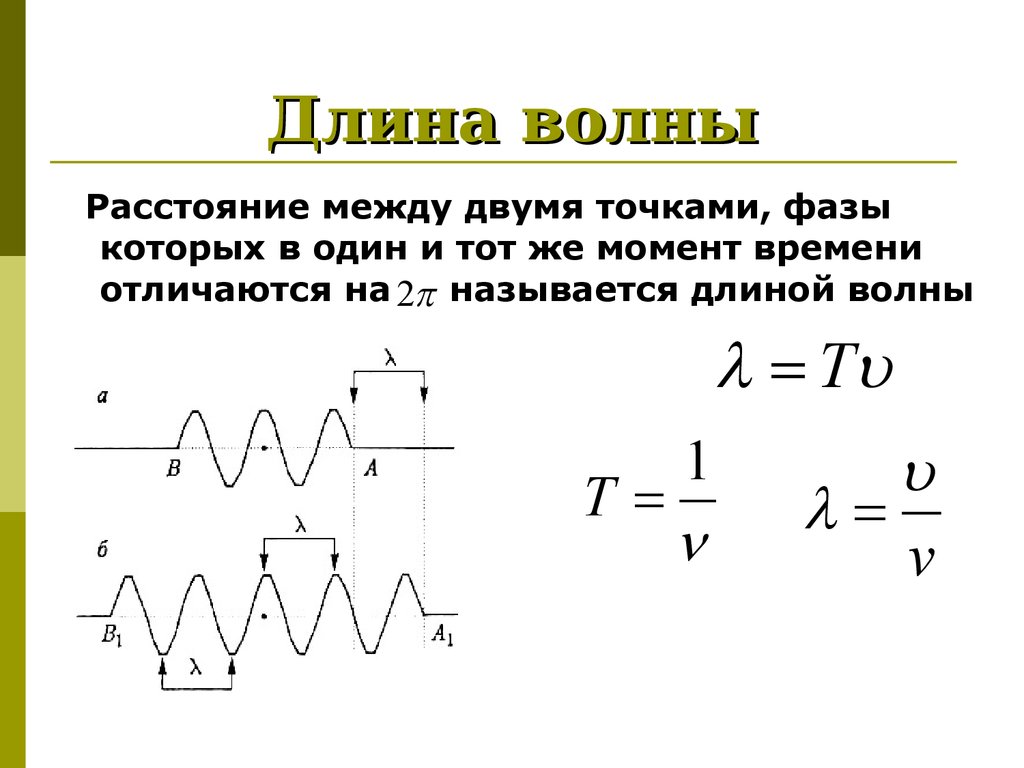 Однако скорость света больше в более разреженной среде и, следовательно, больше длина волны.
Однако скорость света больше в более разреженной среде и, следовательно, больше длина волны.
В квантовой механике кванты относятся к энергетическим пакетам или фотонам.
Квантованный свет означает, что свет переносит пакеты энергии в зависимости от частоты источника, и его характеризуют четыре набора квантовых чисел. Он существует и в дискретном состоянии, оставаясь, таким образом, везде постоянным.
физический смысл, размерность, формулы, примеры расчета
Вы хотите знать, в чем разница между волновым числом и угловым волновым числом и как их рассчитать? Тогда эта статья как раз для вас. Мы подробно объясним эту тему и покажем на примере, как можно рассчитать эти величины.
Если вы рассматриваете электромагнитную волну с определенной длиной волны, то волновое число является обратным этой длине волны – оно ведет себя противоположным образом. Например, если длина волны увеличивается, волновое число уменьшается. Если, с другой стороны, длина волны уменьшается, то волновое число увеличивается.
Если, с другой стороны, длина волны уменьшается, то волновое число увеличивается.
Волновое число в спектроскопии
Волновое число k определяется в спектроскопии как обратная величина длины волны λ, то есть ξ = 1 / λ (называется еще пространственной частотой). Однако его также можно выразить через частоту f и скорость света в вакууме c, тогда ξ = f / c или также через число n длин волн, укладывающихся в определенную длину l, то есть ξ = n / l .
В целом, для волнового числа применимо следующее соотношение: ξ = 1 / λ = f / c = n / l .
Важно: Волновое число ξ не следует путать с частотой f. Частота имеет единицу измерения Гц = 1 / с = с-1 и определяется через обратную величину периода T: f = 1 / T . Она показывает, как часто электромагнитная волна колеблется в секунду.
Единица измерения волнового числа
Обычно волновое число выражается в в следующих единицах измерения (в СИ): 1 / м = м-1 , что соответствует числу колебаний на метр. Однако единица может быть также преобразована, например, в единицы 1 / см = см-1 или 1 / мм = мм-1 .
Однако единица может быть также преобразована, например, в единицы 1 / см = см-1 или 1 / мм = мм-1 .
Между этими единицами измерения существует следующая взаимосвязь: 1 м-1 = 0,01 см-1 = 0,001 мм-1 , соответственно 1 мм-1 = 100 см-1 = 1000 м-1 .
Разница между волновым числом и угловым волновым числом
Угловое волновое число часто ошибочно называют просто волновым числом. Однако, угловое волновое число k является величиной волнового вектора k и связано с волновым числом ξ следующим образом: k = | k | = 2*π*ξ = ω / c = 2*π / λ . В этой формуле где ω представляет собой так называемую угловую частоту. Волновой вектор – это вектор, перпендикулярный волновому фронту волны. Эта формула показывает, что волновое число ξ также может быть вычислено из углового волнового числа k: ξ = k / 2*π .
Важно: Угловую частоту и частоту также нельзя путать друг с другом. Угловая частота ω связана с частотой f следующим образом: ω = 2*π*f .
Угловая частота ω связана с частотой f следующим образом: ω = 2*π*f .
Физический смысл волнового числа.
Волновое число численно равно числу периодов волны, укладывающихся в отрезок 2π метров. Это пространственный аналог круговой частоты ω (рад·с-1). Характеристика периодического процесса в пространстве.
Пример расчета волнового числа
Если мы наблюдаем электромагнитную волну с длиной волны λ = 500 нм и хотим вычислить по ней волновое число ξ, то поступаем следующим образом. Чтобы получить размерность м-1 сначала переведите длину волны в метры. То есть 500 нм = 500 * 10-9 м = 5*10-7 м.
Используя представленную выше формулу, вы можете определить соответствующее волновое число: ξ = 1 / λ = 1 / 5*10-7 = 2*106 м-1 .
На одном метре волна колеблется 2 миллиона раз. Если преобразовать единицу измерения, то можно сказать, что волна колеблется 2000 раз на одном миллиметре: 2 * 106 м-1 = 0,001 * 2 * 106 мм-1 = 2000 мм-1 .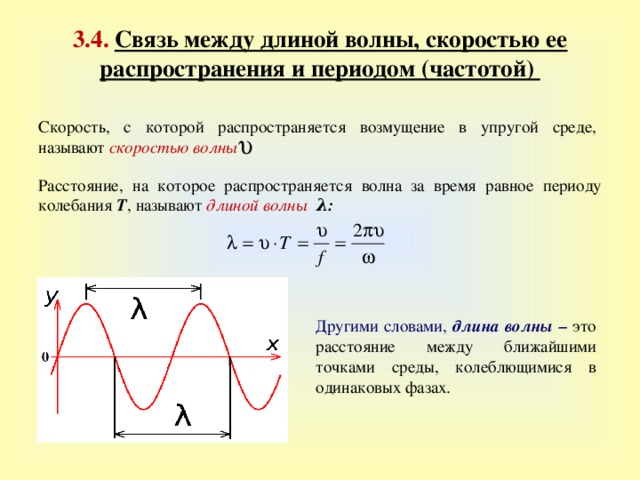
Пример расчета углового волнового числа
Если использовать ту же длину волны λ = 500 нм =5 *10-7 м, как в предыдущем примере, и подставьте это значение в формулу для расчета углового волнового числа, то это приведет к следующим результатам: k = 2 * π / λ = 2 * π / 5 *10-7 м = 1,2566 * 107 м-1 .
Легко видеть, что угловое волновое число k отличается от волнового числа ξ из предыдущего примера:
ξ = 2*106 м-1 ↔ k = 1,2566 * 107 м-1
Преобразование длины волны в волновой число
В следующей таблице показаны два направления преобразования из длины волны в волновое число и наоборот. Кроме того, в последней колонке перечислены некоторые области применения спектроскопии:
| Волновое число в 1/мм | Волновое число в 1/см | Волновое число в 1/м | Длина волны в нм | Длина волны в мкм | Длина волны в мм | Применение |
| 1 000 | 10 000 | 1 000 000 | 1 000 | 1 | 0,001 | Инфракрасная спектроскопия |
| 100 | 1 000 | 100 000 | 10 000 | 10 | 0,01 | Инфракрасная спектроскопия/терагерцовая спектроскопия |
| 10 | 100 | 10 000 | 100 000 | 100 | 0,1 | Терагерцовая спектроскопия |
| 1 | 10 | 1 000 | 1 000 000 | 1 000 | 1 | Микроволновая спектроскопия |
| 0,1 | 1 | 100 | 10 000 000 | 10 000 | 10 | Микроволновая спектроскопия/электронный спиновый резонанс |
Список использованной литературы
- Мартин Шапер, Mehrdimensionale Ortsfiltertechnik, Springer-Verlag 2014, ISBN 3-658-04944-8
- Физическая энциклопедия.
 В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин. — М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.
В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин. — М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.
Связь между частотой и длиной волны
Волна определяется как возмущение в материале, которое переносит энергию, не вызывая чистого движения частиц. Они путешествуют в периодическом повторяющемся движении, передавая энергию от источника к месту назначения. Волны делятся на два типа: поперечные волны и продольные волны. Поперечные волны — это волны света и воды, а продольные волны — это звуковые волны и волны сжатия.
Какая частота?
Количество колебаний волны в единицу времени определяется как частота (Гц). Это величина, обратная времени, обозначается знаком f. Его единица измерения — герц. Его размерная формула: [M 0 L 0 T -1 ].
Что такое длина волны?
Расстояние между двумя ближайшими точками в фазе друг с другом определяется как длина волны. Он представлен символом (лямбда). Это произведение расстояния, пройденного волной за единицу времени, и общего времени, затраченного на это движение. Его единица измерения – метры. Его размерная формула записывается как [M 0 L 1 T 0 ].
Он представлен символом (лямбда). Это произведение расстояния, пройденного волной за единицу времени, и общего времени, затраченного на это движение. Его единица измерения – метры. Его размерная формула записывается как [M 0 L 1 T 0 ].
Частота и длина волны косвенно пропорциональны друг другу. Больше длина волны, меньше частота и наоборот. Скорость, с которой распространяется волна, равна произведению ее частоты на длину волны, что оправдывает связь между этими двумя параметрами.
V = λ f
где,
V – скорость волны,
f — частота волны,
λ — длина волны.
Вывод
Примеры задачСвязь между частотой и длиной волны можно вывести, используя формулы для этих двух величин.
Мы знаем, что частота — это время, необходимое для совершения одного колебания вне времени t.
Итак, мы имеем,
f = 1/t …….. (1)
Также известно, что скорость волны – это отношение пройденного волной расстояния ко всему времени, затраченному ею.
V = λ/t
V = λ (1/t)
Используя (1), получаем,
V = λ f
Это выводит соотношение между частотой и длиной волны волны.
Задача 1. Вычислить частоту волны, если волна совершает один цикл за 0,02 с.
Решение:
Имеем,
Время (t) = 0,02 с
Используя формулу, которую имеем,
f = 1/t
f = 1/0,02
f = 50 Гц
Задача 2. Вычислить длину волны, бегущей со скоростью 250 м/с и имеющей частоту 600 Гц.
Решение:
Мы имеем,
В = 250,
F = 600
Используем формулу, которую мы имеем,
В = λ
=> 250 = λ (600)
.
=> λ = 250/600
=> λ = 5/12
=> λ = 0,416 м
Задача 3. Вычислить длину волны волны, бегущей со скоростью 32 м/с и имеющей частоту 800 Гц.
Решение:
Мы имеем,
В = 32,
F = 800
Используем формулу, которую мы имеем,
В = λ
=> 32 = λ (800)
. => λ = 32/800
=> λ = 1/25
=> λ = 0,04 м
Задача 4. Вычислить частоту волны, бегущей со скоростью 70 м/с и имеющей длину волны 2 м.
Решение:
У нас есть,
В = 70,
λ = 2
Используя формулу, которую мы имеем,
В = λ f
=> 70 = 2f
=> f = 70/2
5 Hz =2 => f
Задача 5. Вычислить частоту волны, бегущей со скоростью 135 м/с и имеющей длину волны 10 м.
Решение:
Имеем,
V = 135,
λ = 10
Используя формулу, которую имеем,
V = 0 3 λ f
2 => 135 = 10f
=> f = 135/10
=> f = 13,5 Гц
Задача 6.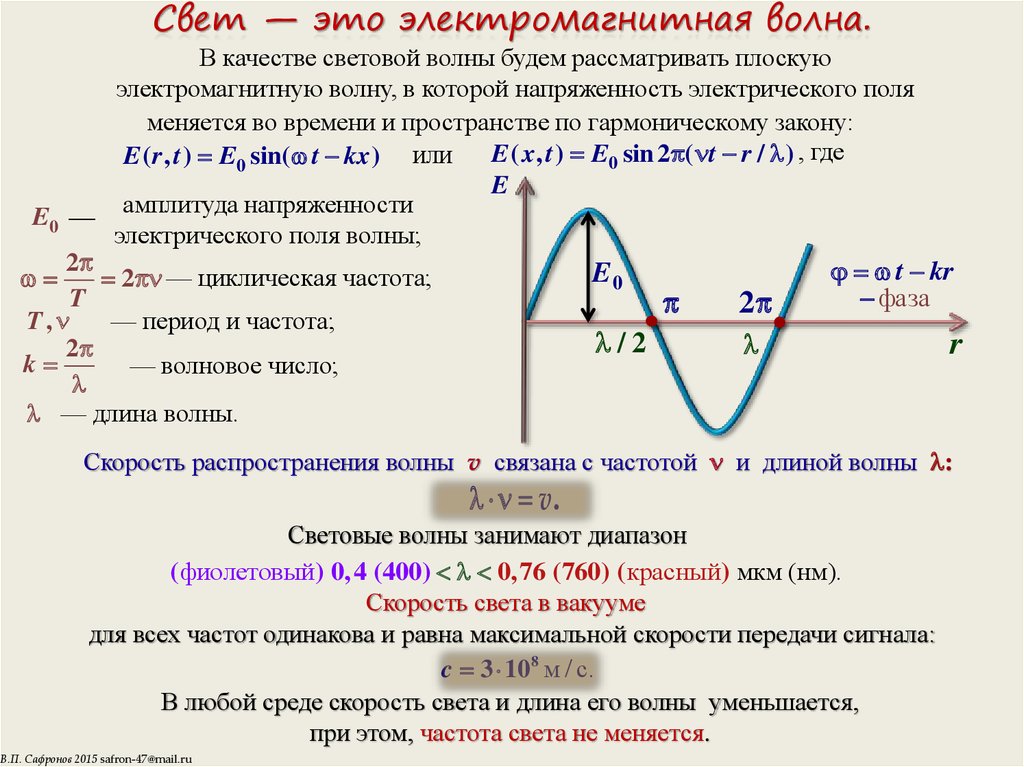 Вычислить время, за которое волна проходит расстояние 0,2 м со скоростью 350 м /с.
Вычислить время, за которое волна проходит расстояние 0,2 м со скоростью 350 м /с.
Решение:
Мы имеем,
В = 350,
λ = 0,2
Используя формулу, которую мы имеем,
В = λ F
=> 350 = 0,2 F
=>> λ F
=> 350 = 0,2 F
=>> λ F
=> 350 = 0,2 F
=> f = 350/0,2
=> f = 1750 Гц
Найдите затрачиваемое время по формуле f = 1/t.
t = 1/f
= 1/1750
= 0,00057 с
Задача 7. Вычислить скорость волны, прошедшей расстояние 2,5 м за 8 с.
Решение:
Мы имеем,
λ = 2,5,
T = 8,
Найти частоту с помощью формулы,
F = 1/T
= 1/8
= 0,125 Гц
Используя формулу, которую мы имеем,
В = λ f
В = (2,5) (0,125)
В = 0,3125 м/с
Связь между длиной волны и частотой
15 ноября 2015 г.
от Nipun
5 минут чтения
Длина волны и частота – взаимосвязь
Волны можно описать с помощью ряда различных характеристик волны. Двумя такими характеристиками являются длина волны и частота. Соотношение между длиной волны и частотой состоит в том, что частота волны, умноженная на ее длину волны, дает скорость волны , как мы увидим ниже.
Что такое длина волны
Мы обсуждали значение длины волны, когда обсуждали разницу между длиной волны и периодом. Резюмировать; каждая точка волны колеблется. То есть каждая точка на волне показывает какое-то регулярное, повторяющееся изменение некоторого значения. Например, если вы создаете волну, покачивая веревку вверх и вниз, то молекулы, из которых состоит веревка, постоянно движутся вверх и вниз. Если взять электромагнитную волну, то величина электрического и магнитного полей, обусловленных волной, в точке всегда меняется. Если рассматриваемая волна представляет собой не просто короткий импульс, то в любой момент времени на волне может быть несколько точек, находящихся на одной и той же стадии колебаний. Например, две точки на волне, которые одновременно достигают своего максимального значения в колебаниях, колеблются в унисон. Такие точки, которые всегда находятся на одной и той же стадии колебаний, называются 9.0005 в фазе друг с другом. Длина волны – это расстояние между двумя ближайшими точками, которые находятся в фазе друг с другом вдоль волны. Таким образом, два соседних пика или две соседние впадины на волне разделены расстоянием в одну длину волны. Часто мы используем греческую букву лямбда () для обозначения длины волны:
Например, две точки на волне, которые одновременно достигают своего максимального значения в колебаниях, колеблются в унисон. Такие точки, которые всегда находятся на одной и той же стадии колебаний, называются 9.0005 в фазе друг с другом. Длина волны – это расстояние между двумя ближайшими точками, которые находятся в фазе друг с другом вдоль волны. Таким образом, два соседних пика или две соседние впадины на волне разделены расстоянием в одну длину волны. Часто мы используем греческую букву лямбда () для обозначения длины волны:
Длина волны, создаваемой раскачиванием веревки вверх и вниз
это просто формальность, потому что существует бесконечно много путей, по которым можно перейти из одной точки в другую. В некоторых определениях длины волны может не упоминаться конкретно кратчайший путь , но в данном случае в определении подразумевается кратчайшее расстояние.
Что такое частота
Частота ( ) — это число полных колебаний , которое волна совершает за единицу времени . Измеряется в герцах (Гц). Для звуковых волн частота связана с высотой звука. Чем выше частота, тем выше высота звука. Например, нота «средняя до» — это звуковая волна с частотой 261,63 Гц. Это означает, что для создания этой ноты молекулы, создающие или передающие звуковую волну, должны колебаться 261,63 раза в секунду. Средняя нота D, которая имеет более высокий тон, чем средняя C, имеет частоту 29.3,66 Гц. Люди могут слышать звуки с частотами от 20 до 20000 Гц. Звуки с частотами ниже слышимого диапазона называются инфразвуком , а звуки с частотами выше диапазона человеческого слуха называются ультразвуком .
Измеряется в герцах (Гц). Для звуковых волн частота связана с высотой звука. Чем выше частота, тем выше высота звука. Например, нота «средняя до» — это звуковая волна с частотой 261,63 Гц. Это означает, что для создания этой ноты молекулы, создающие или передающие звуковую волну, должны колебаться 261,63 раза в секунду. Средняя нота D, которая имеет более высокий тон, чем средняя C, имеет частоту 29.3,66 Гц. Люди могут слышать звуки с частотами от 20 до 20000 Гц. Звуки с частотами ниже слышимого диапазона называются инфразвуком , а звуки с частотами выше диапазона человеческого слуха называются ультразвуком .
Какая связь между длиной волны и частотой
Вы можете создать волну с более высокой частотой на веревке, покачивая вверх и вниз с большей скоростью. При этом вы заметите, что длина волны становится короче. Ясно, что существует связь между длиной волны и частотой, и сейчас мы попытаемся выяснить, в чем именно заключается эта связь.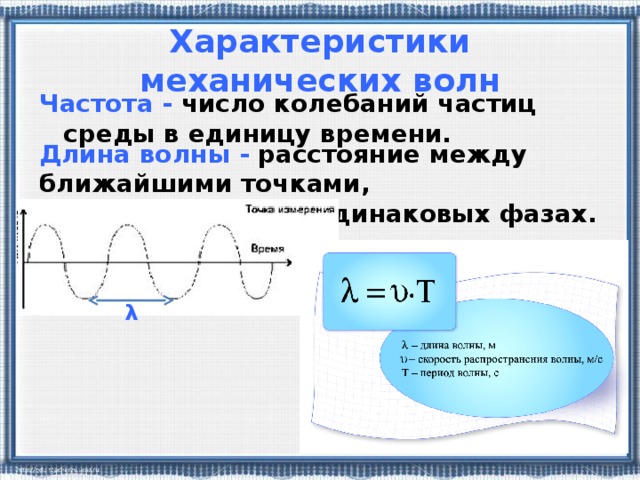
Период ( ) — еще одна величина, которую мы можем использовать для характеристики волны. Период – это время, необходимое для одного полного колебания . Поскольку частота измеряет количество колебаний волны в единицу времени, отсюда следует, что
Поскольку волна совершает одно полное колебание в течение одного периода, все точки волны возвращаются к одним и тем же значениям через один период. Это происходит в результате того, что каждая «стадия колебаний», проходя расстояние в одну длину волны в течение одного периода, оказывается в точке, которая находилась на той же стадии колебаний одним периодом ранее. Другими словами, в течение одного периода гребень перемещается в положение, которое предыдущий гребень занимал за один период до этого, и так далее.
Скорость волны () — это расстояние, которое волна проходит за единицу времени. Учитывая, что волна проходит расстояние в одну длину волны за один период,
Мы это знаем.
То есть скорость волны равна ее частоте, умноженной на длину волны. Это соотношение между длиной волны и частотой.
Электромагнитные волны, распространяющиеся в вакууме, имеют скорость 3×10 8 мс -1 . Эта скорость является фундаментальной константой в физике и обозначается буквой . Поэтому это уравнение иногда записывают как для электромагнитного путешествия в вакууме.
Это уравнение очень полезно. Например, мы знаем, что электромагнитные волны могут замедляться при переходе из воздуха в стекло. Частота
Скорость и длина волны изменяются при переходе из одной среды в другую.
Это объясняется анимацией в видео ниже:


 В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин. — М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.
В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин. — М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.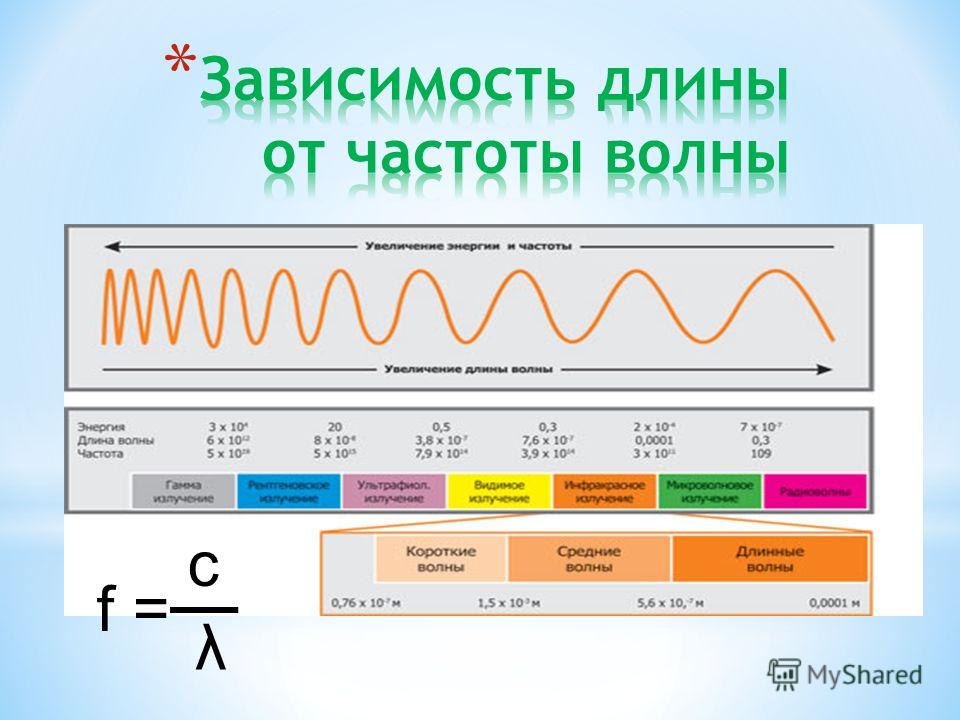 Итак, мы имеем,
Итак, мы имеем,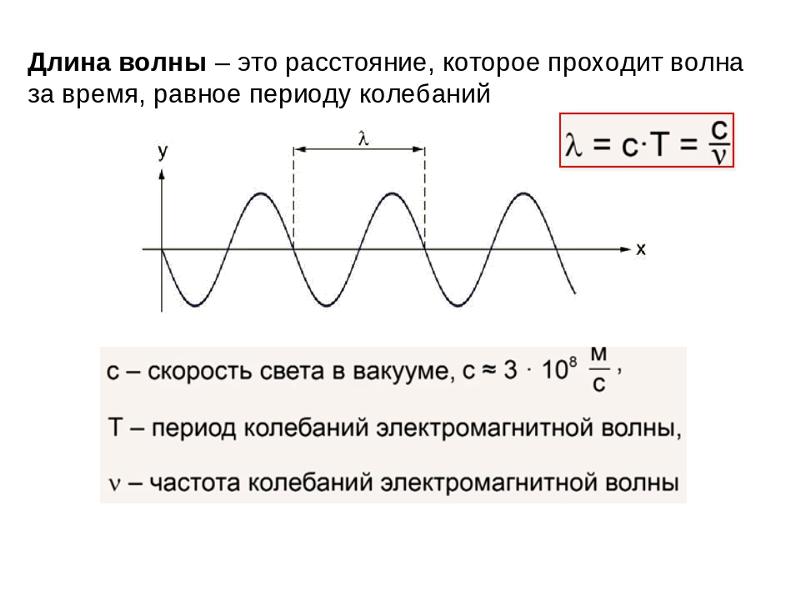 => λ = 250/600
=> λ = 250/600