Эффективные значения тока и напряжения. Эффективное, действующее напряжение, сила тока
Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.
Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.
Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемпри
.
 Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:
.
Сила тока в цепи изменяется по синусоидальному закону
,
.
Опуская вычисления, связанные с интегрированием, запишем окончательный результат
.
Если бы по
цепи шёл некоторый постоянный ток
,
то за время, равное,
выделилось бы тепло
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов
(4.28)
Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:
(4. 29)
29)
Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:
,
.
Тогда мгновенное значение мощности, выделяемой на участке цепи,
Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):
С использованием известной тригонометрической формулы
.
Величину
усреднять не нужно, так как она не зависит
от времени, следовательно:
.
За длительное
время значение косинуса много раз
успевает измениться, принимая как
отрицательные, так и положительные
значения в пределах от (1)
до 1. Понятно, что среднее во времени
значение косинуса равно нулю
Понятно, что среднее во времени
значение косинуса равно нулю
,
поэтому
(4.30)
Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим
. (4.31)
Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением . Например,
если участок цепи состоит из одного
только активного сопротивления, то
. Если участок цепи содержит только индуктивность или только ёмкость, то
и
.
Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т. д. Именно по той причине, что
на индуктивном и ёмкостном сопротивлениях
средняя расходуемая генератором энергия
равна нулю, их назвали реактивными. На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).
Пример 4.7. К генератору переменного
синусоидального тока подключён резистор
с сопротивлением.
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением
а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность
(см. формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
.
В результате средняя расходуемая генератором мощность
.
Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора
.
Тогда средняя мощность, расходуемая генератором
Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.
Переменный
ток долгое время не находил практического
применения. Это было связано с тем,
что первые генераторы электрической
энергии вырабатывали постоянный ток,
который вполне удовлетворял технологическим
процессам электрохимии, а двигатели
постоянного тока обладают хорошими
регулировочными характеристиками.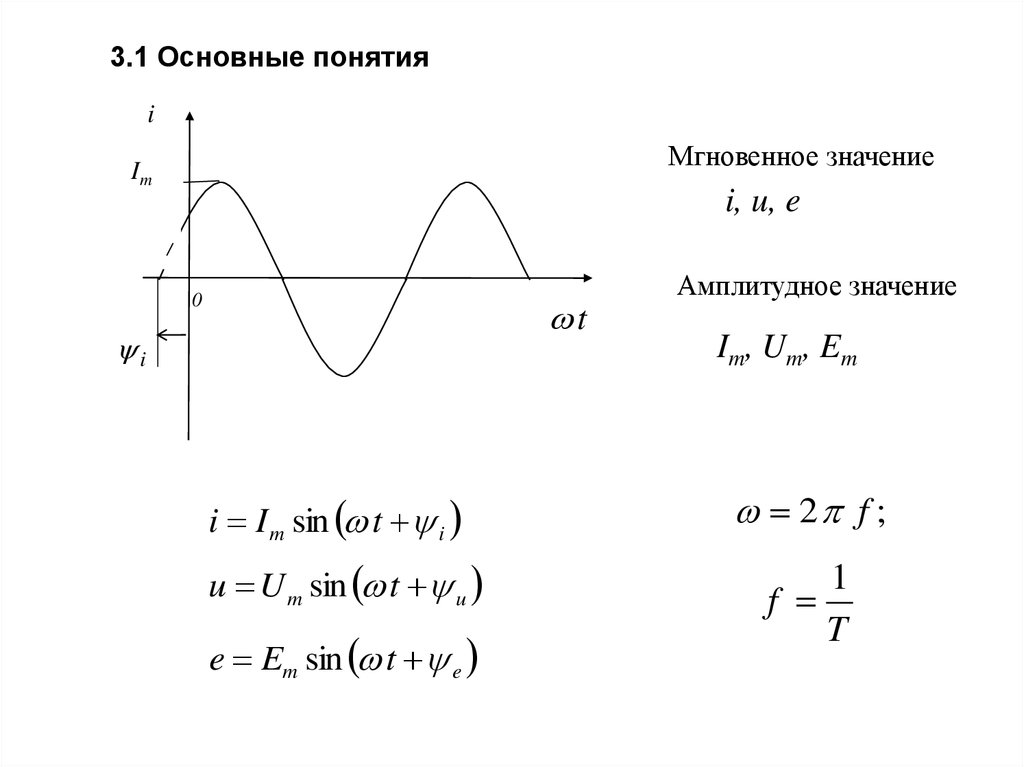
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным
током (напряжением, ЭДС и т. д.)называется
ток (напряжение, ЭДС и т.д.), изменяющийся
во времени. Токи, значения которых
повторяются через равные промежутки
времени в одной и той же последовательности,
называются
д.)называется
ток (напряжение, ЭДС и т.д.), изменяющийся
во времени. Токи, значения которых
повторяются через равные промежутки
времени в одной и той же последовательности,
называются
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .
Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:
i — мгновенное значение тока ;
u – мгновенное значение напряжения ;
е — мгновенное значение ЭДС ;
р — мгновенное значение мощности .
Наибольшее
мгновенное значение переменной величины
за период называется амплитудой (ее
принято обозначать заглавной буквой с
индексом m ).
Амплитуда тока;
Амплитуда напряжения;
Амплитуда ЭДС.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные
токи и напряжения можно изобразить
графически, записать при помощи уравнений
с тригонометрическими функциями,
представить в виде векторов на декартовой
плоскости или комплексными числами.
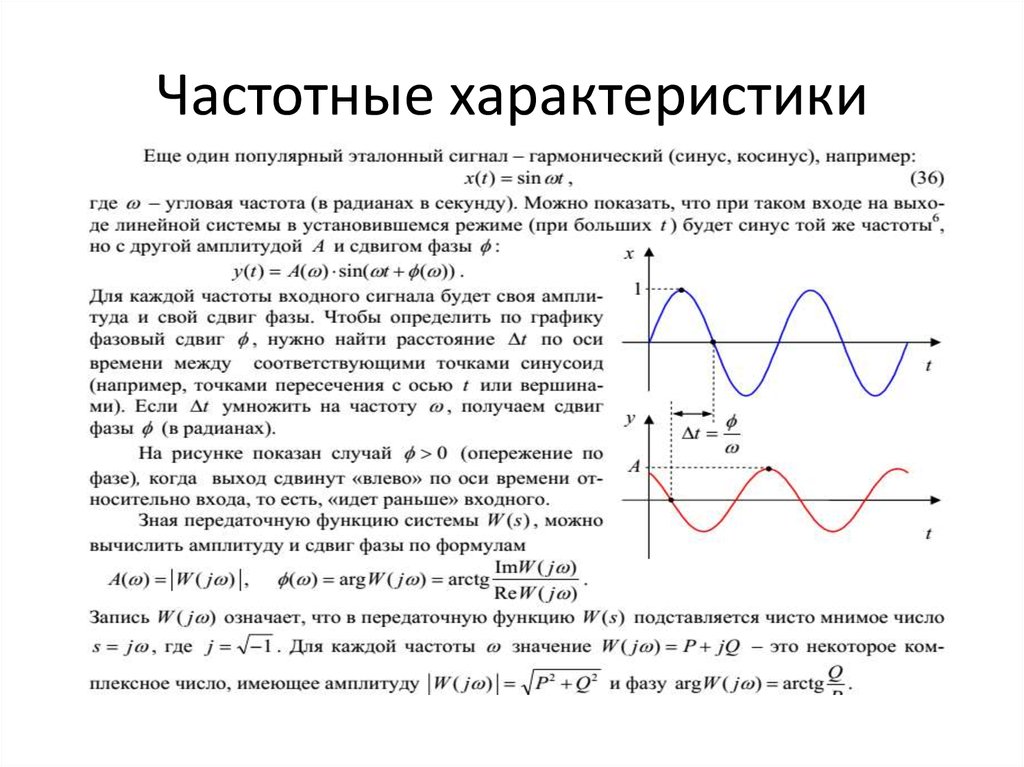
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:
Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и —начальной фазой ( ).
Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .
Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:
Векторное изображение синусоидально изменяющихся величин
На
декартовой плоскости из начала координат
проводят векторы, равные по модулю
амплитудным значениям синусоидальных
величин, и вращают эти векторы против
часовой стрелки (в
ТОЭ данное направление принято за
положительное )
с угловой частотой, равной w . Фазовый угол при вращении отсчитывается
от положительной полуоси абсцисс.
Проекции вращающихся векторов на ось
ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис.
3). Совокупность векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения и токи, называют векторными
диаграммами. При
построении векторных диаграмм векторы
удобно располагать для начального
момента времени (t =0), что
вытекает из равенства угловых частот
синусоидальных величин и эквивалентно
тому, что система декартовых координат
сама вращается против часовой стрелки
со скоростью w .
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные
диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их
применение делает расчет цепи более
наглядным и простым. Это упрощение
заключается в том, что сложение и
вычитание мгновенных значений величин
можно заменить сложением и вычитанием
соответствующих векторов.
Фазовый угол при вращении отсчитывается
от положительной полуоси абсцисс.
Проекции вращающихся векторов на ось
ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис.
3). Совокупность векторов, изображающих
синусоидально изменяющиеся ЭДС,
напряжения и токи, называют векторными
диаграммами. При
построении векторных диаграмм векторы
удобно располагать для начального
момента времени (t =0), что
вытекает из равенства угловых частот
синусоидальных величин и эквивалентно
тому, что система декартовых координат
сама вращается против часовой стрелки
со скоростью w .
Таким образом, в этой системе координат
векторы неподвижны (рис. 4). Векторные
диаграммы нашли широкое применение при
анализе цепей синусоидального тока. Их
применение делает расчет цепи более
наглядным и простым. Это упрощение
заключается в том, что сложение и
вычитание мгновенных значений величин
можно заменить сложением и вычитанием
соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:
Рассмотрим следующую цепь.
Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.
Активное сопротивление
Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:
U = Um*cos(ω*t).
Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.
I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).
Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует. 2) = Um/√2.
2) = Um/√2.
Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:
Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний — такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.
Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.
Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Действия тока не определяются ни амплитудным, ни мгновенным значениями. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.
Мощность P постоянного тока I , проходящего через сопротивление r , будет
P = I 2 × r .
Мощность переменного тока выразится как средний эффект мгновенной мощности i 2 × r за целый период или среднее значение от (I m × sin ωt ) 2 × r за то же время.
Пусть среднее значение i 2 за период будет M . Приравнивая мощность постоянного тока и мощность при переменном токе, имеем:
I 2 × r = M × r ,
Величина I называется действующим значением переменного тока.
Среднее значение i 2 при переменном синусоидальном токе определим следующим образом. Построим синусоидальную кривую изменения тока (рисунок 1).
Рисунок 1. Действующее значение синусоидального тока
Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости i 2 от времени. Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника M будет соответствовать среднему значению i 2 за период. Это значение за период, вычисленное при помощи высшей математики, будет равно .
Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника M будет соответствовать среднему значению i 2 за период. Это значение за период, вычисленное при помощи высшей математики, будет равно .
Следовательно,
Так как действующее значение переменного тока I равно , то окончательно формула примет вид
Аналогично зависимость между действующим и амплитудным значениями для напряжения U и E имеет вид:
Действующие значения переменных величин, то есть действующее значение напряжения, тока и электродвижущей силы, обозначаются прописными буквами без индексов (U , I , E ).
На основании изложенного выше, можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.
Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующее значение тока и напряжения.
При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в раз. От этого расположение векторов на диаграмме не изменится.
В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток .
- Переменный электрический ток — это ток, сила и направление которого периодически меняются.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,
где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Исходя из этого можно дать еще такое определение:
- Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п.
Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира.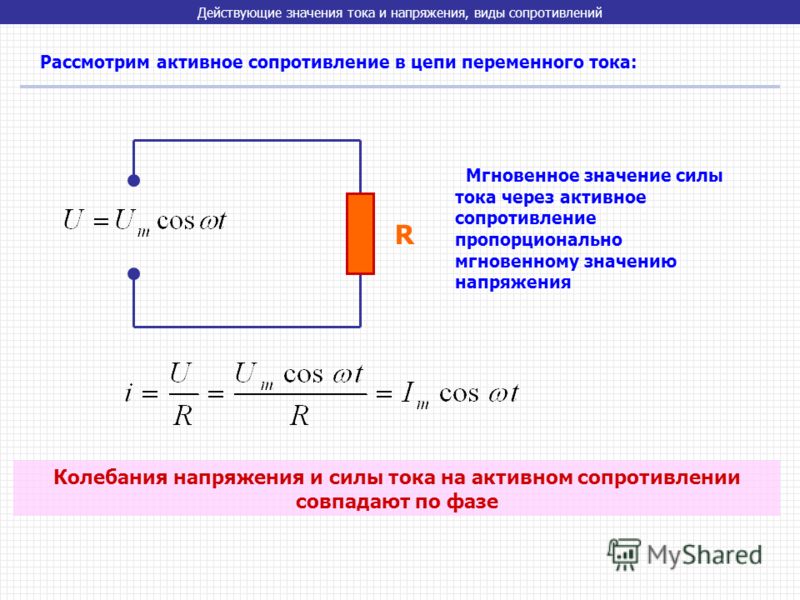 В США частота промышленного тока 60 Гц.
В США частота промышленного тока 60 Гц.
Генератор переменного тока
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.
- Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора изменяется по синусоидальному закону
\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)
где \({\rm E}_{m} =B\cdot S\cdot \omega\) — амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R , через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке
\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)
где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) — амплитудное значение силы тока.
Основными частями генератора являются (рис. 1):
1):
- индуктор — электромагнит или постоянный магнит, который создает магнитное поле;
- якорь — обмотка, в которой индуцируется переменная ЭДС;
- коллектор со щетками — устройство, посредством которого снимается с вращающихся частей или подается по ним ток.
Неподвижная часть генератора называется статором , а подвижная — ротором . В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.
На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока.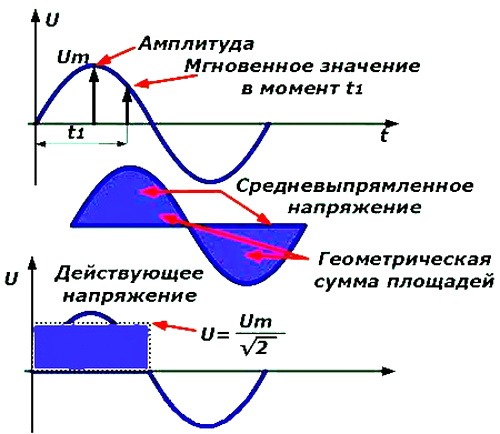 Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.
Из истории . Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» — спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».
*Принцип действия
Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).
рис. 1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то
\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)
где ω — угловая скорость вращения рамки, ν — частота ее вращения.
В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом
\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)
Тогда согласно закону Фарадея индуцируется ЭДС индукции
\(e=-\Phi «(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Действующие значения силы тока и напряжения
Пусть источник тока создает переменное гармоническое напряжение
\(u=U_{m} \cdot \sin \omega \cdot t. \;\;\;(1)\)
\;\;\;(1)\)
Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R , подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)
где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и силы тока . Зависящие от времени значения напряжения u и силы тока i называют мгновенными .
Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения .
- Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
 {2}}{R}.\)
{2}}{R}.\)Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.
Среднеквадратичное напряжение формула
Все мы знаем, что дома в розетках у нас напряжение В. Но не каждый знает, какое именно это напряжение. Давайте же разберемся с этой ситуацией. Для упрощения рассматриваемого примера будем считать, что вид напряжения — синусоида, то есть переменное напряжение с определенной периодичностью меняет значение с положительного на отрицательное. Рисунок 1 — Вид переменного напряжения. На рисунке 1 изображен вид идеального синусоидального напряжения одного периода Т.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.Содержание:
- Действующее значение переменного напряжения
- Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)
- Расчет среднего и среднеквадратичного значений тока/напряжения
- Среднее и действующее значения переменного тока и напряжения
- Система обогрева на резистивных элементах
- Переменный ток
- Напряжение переменного тока после выпрямителя формула. Среднеквадратичное значения напряжения
- Электрическое напряжение
- Действующие значения напряжения
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Амплитудное и действующее значения напряжения
youtube.com/embed/fp_-LJRbPfI» frameborder=»0″ allowfullscreen=»»/>Действующее значение переменного напряжения
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками.
Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе.
 Цепи с изменяющимися — переменными — токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Цепи с изменяющимися — переменными — токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.Переменным током напряжением, ЭДС и т. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем. Диапазон частот, применяемых в технике: от сверхнизких частот 0. Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:. Наибольшее мгновенное значение переменной величины за период называется амплитудой ее принято обозначать заглавной буквой с индексом m.
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:.
 На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки в ТОЭ данное направление принято за положительное с угловой частотой, равной w.
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки в ТОЭ данное направление принято за положительное с угловой частотой, равной w.Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 рис. Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами.
Таким образом, в этой системе координат векторы неподвижны рис. Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока.
Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов. Пусть, например, в точке разветвления цепи рис. Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин.

Значительно проще это осуществляется с помощью векторной диаграммы. На рис. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:. Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты:.
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока. Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов. Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Среднеквадратичное значение устар. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением В, работают светят, греют точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения. Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока. В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы.
Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени с квадратичным детектором или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени.

Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением. Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом. В электротехнике используется редко, но сравнительно часто используется в радиотехнике ток смещения и напряжение смещения. Геометрически это разность площадей под и над осью времени, делённая на период.
Для синусоидального сигнала смещение равно нулю. На практике используется редко, однако большинство измерительных приборов переменного тока — магнитоэлектрической системы т. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку.
В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
 Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения.При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой. Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров постоянного и переменного тока.
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.
Теория синусоидального тока является ключом к пониманию теории других цепей. Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
 Так как фазовый угол синусоиды за время одного периода Т изменяется на рад.
Так как фазовый угол синусоиды за время одного периода Т изменяется на рад.При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Синусоидальный ток напряжение характеризуется среднеквадратичным заначением. Узнать амплитудное напряжение легко. Амплитудное напряжение для однофазного тока больше эффетивоного в корень из двух 1. Это необходимо учитывать при проектировании блоков питания — конденсаторы в сглаживающем фильтре выпрямителя должны быть расчитанаы на напряжение выше амплитудного напряжения выпрямляемого тока. Амплитудное — это максимальное значение.
Если сиснусоиду хитро проинтегрировать, то так корень из двух и получишь. Полный цикл этих изменений называется периодом. Период измеряется в секундах и обозначается буквой Т. Количество периодов переменного тока за 1 секунду, есть частота f. Частота переменного тока f измеряется в герцах.
Наибольшее значение изменяющегося переменного напряжения — тока называется амплитудным значением или амплитудой.
 На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный.Выделение тепла не зависит от направления тока в цепи. Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки. Введено понятие действующего значения переменного напряжения Uд и тока Iд. Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.
Следовательно действующее или эффективное значение переменного тока будет равно:. После выпрямительных диодов оно принимает вид как на рисунке 2. Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования. Значение Ua примем за единицу.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
 Она отсекает верхнюю часть половинок синусоид.
Она отсекает верхнюю часть половинок синусоид.Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I. Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах. В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно вольт. Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей. Переменный ток AC — Alternating Current — электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
 Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте. В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей DC для периодически меняющегося электрического тока любой формы.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте. В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей DC для периодически меняющегося электрического тока любой формы.Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC. Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка. Суммируются мощности. Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.
 Величина переменного тока, как и напряжения, постоянно меняется во времени.
Величина переменного тока, как и напряжения, постоянно меняется во времени.Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)
Изучите соотношение среднеквадратичного напряжения и тока — формула и как найти. Читайте определение среднеквадратичного значения, применение, уравнения. Среднеквадратичное напряжение или ток — усредненное по времени напряжение или ток в системе переменного тока. В ситуациях с переменным током поток электрического заряда периодически меняет направление.
Измерение фазограммы (огибающей среднеквадратичного напряжения к полосе 1 кГц по формуле (), в которой ∆f2 принимается равной 1 кГц.
Расчет среднего и среднеквадратичного значений тока/напряжения
Теория и практика. Кейсы, схемы, примеры и технические решения, обзоры интересных электротехнических новинок. Уроки, книги, видео. Профессиональное обучение и развитие. Сайт для электриков и домашних мастеров, а также для всех, кто интересуется электротехникой, электроникой и автоматикой.
 Что такое действующее, среднеквадратичное, эффективное напряжение или ток. Среднее значение переменного синусоидального напряжения или тока. Говоря о величине, изменяющейся по синусоидальному гармоническому закону, можно за половину периода определить ее среднее значение. В результате получим:. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:.
Что такое действующее, среднеквадратичное, эффективное напряжение или ток. Среднее значение переменного синусоидального напряжения или тока. Говоря о величине, изменяющейся по синусоидальному гармоническому закону, можно за половину периода определить ее среднее значение. В результате получим:. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:.Среднее и действующее значения переменного тока и напряжения
Для питания электронных устройств требуется постоянное напряжение различных значений. Наиболее распространенным источником электрической энергии является промышленная сеть переменного напряжения частотой 50 Гц. Для преобразования переменного напряжения в постоянное однополярное применяют выпрямительные устройства. Существует однополупериодное и двухполупериодное выпрямление переменного тока.
Целью данной статьи является ознакомление пользователей с особенностями эксплуатации, монтажа и хранения танталовых конденсаторов.
 Статья содержит описание механизмов пробоя танталовых конденсаторов, предлагает вариант расчета допустимых уровней рабочих токов и напряжений для различных частотных диапазонов.
Статья содержит описание механизмов пробоя танталовых конденсаторов, предлагает вариант расчета допустимых уровней рабочих токов и напряжений для различных частотных диапазонов.Система обогрева на резистивных элементах
Самый непосредственный способ получить теплоту из электричества — это приложить напряжение к резистивному элементу, т. Если это сделать, то теплота будет генерироваться в виде инфракрасного ИК излучения. Обогреватели на резистивных элементах иногда используются в местностях, где зима не очень холодная. Они не слишком хороши как единственный источник тепла для тех районов, где зимы суровые, хотя и могут служить в качестве дополнения к основной системе отопления. В некоторых летних домиках используются обогреватели на резистивных элементах для того, чтобы подогреть воз дух весной, осенью или в ночное время.
Переменный ток
Поскольку напряжение синусоидальной волны изменяется во времени , оно не равно ее пиковому напряжению. Эффективное напряжение переменного тока является его эквивалентностью в виде напряжения постоянного тока и может быть рассчитано только с помощью RMS True RMS приборов.
 Эта формула упрощена прибором для учета только положительного пика синусоиды:. Среднеквадратичное измерение надежно, когда синусоидальная волна идеальна, потому что это измерение учитывает только пиковое значение формы волны. Итак, что происходит, когда синусоида не идеальна? RMS измерения нельзя считать надежными, потому что в настоящее время в любой установке имеется множество источников шума , из-за которых форма волны переменного тока никогда не бывает идеальной. В измерении True RMS истинное среднеквадратичное значение используются более сложные математические формулы, которые позволяют приблизить значение к реальности, чем RMS.
Эта формула упрощена прибором для учета только положительного пика синусоиды:. Среднеквадратичное измерение надежно, когда синусоидальная волна идеальна, потому что это измерение учитывает только пиковое значение формы волны. Итак, что происходит, когда синусоида не идеальна? RMS измерения нельзя считать надежными, потому что в настоящее время в любой установке имеется множество источников шума , из-за которых форма волны переменного тока никогда не бывает идеальной. В измерении True RMS истинное среднеквадратичное значение используются более сложные математические формулы, которые позволяют приблизить значение к реальности, чем RMS.Как известно, емкость конденсатора определяется по формуле: . Максимально допустимое среднеквадратичное напряжение.
Напряжение переменного тока после выпрямителя формула. Среднеквадратичное значения напряжения
Сравнив статистику посещения сайта за два месяца ноябрь и декабрь года , в MediaTek выяснили, что число посетителей ресурса из России увеличилось в 10 раз, а из Украины? Таким образом, доля русскоговорящих разработчиков с аккаунтами на labs.
 Амбициозная цель компании MediaTek — сформировать сообщество разработчиков гаджетов из специалистов по всему миру и помочь им реализовать свои идеи в готовые прототипы.
Амбициозная цель компании MediaTek — сформировать сообщество разработчиков гаджетов из специалистов по всему миру и помочь им реализовать свои идеи в готовые прототипы.Электрическое напряжение
ВИДЕО ПО ТЕМЕ: Урок 251. Измерение напряжения и силы тока
Действующее эффективное значение переменного тока равно величине такого постоянного тока , который за время, равное одному периоду переменного тока, произведёт такую же работу тепловой или электродинамический эффект , что и рассматриваемый переменный ток. Иначе говоря, действующее значение переменного тока можно определить по формуле:. Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.
Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим.
Действующие значения напряжения
Как вы помните из предыдущей статьи , переменное напряжение — это напряжение, которое меняется со временем.
 Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами. Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами. Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.Регистрация Вход. Ответы Mail. Вопросы — лидеры Квадрокоптер летит токо в верх модель YH 1 ставка. Не взлетает квадрокоптер 1 ставка.
RMS Voltage of AC Waveform
Переменный сигнал или сигнал переменного тока, связанный с переменным током, представляет собой периодический сигнал, который чередует положительные и отрицательные значения. Синусоидальная или синусоидальная волна является наиболее распространенной изменяющейся во времени волной, которая используется для представления формы волны переменного тока.
[adsense1]
В случае постоянного тока значения напряжения и тока обычно стабильны во времени.
 Легко выразить величину напряжения или тока, т. е. сколько напряжения или тока присутствует в любой части цепи.
Легко выразить величину напряжения или тока, т. е. сколько напряжения или тока присутствует в любой части цепи.В случае переменного тока, в отличие от постоянного, они не могут быть охарактеризованы одной величиной, так как амплитуда сигнала переменного тока непрерывно изменяется во времени.
Существует множество способов представления амплитуды сигнала переменного тока. Некоторые из них
- Мгновенное значение
- Пиковое значение
- Значение размаха
- Среднее значение
- Среднеквадратичное значение
В предыдущих разделах мы рассмотрели среднее значение напряжения и мгновенные значения сигнала переменного тока. Здесь описана еще одна важная тема о форме волны переменного тока, среднеквадратичное напряжение формы волны переменного тока.
[adsense2]
Outline
Среднеквадратичное напряжение формы волны переменного тока
Среднеквадратичное значение означает «среднеквадратичное» значение.
 Среднеквадратичное значение напряжения определяется как «квадратный корень из средних квадратов всех мгновенных напряжений в волне форма». Среднеквадратичное значение можно найти следующим образом: входные данные возводятся в квадрат и вычисляется среднее значение.
Среднеквадратичное значение напряжения определяется как «квадратный корень из средних квадратов всех мгновенных напряжений в волне форма». Среднеквадратичное значение можно найти следующим образом: входные данные возводятся в квадрат и вычисляется среднее значение.Это дает среднюю мощность. Для расчета напряжения берется квадратный корень из ранее полученного среднего значения. Следовательно, это называется среднеквадратичным напряжением.
Среднеквадратичное значение используется для получения постоянного эквивалента переменного тока, который будет рассеивать такое же количество тепла, когда любое значение применяется к резистору. Переменный ток с максимальным значением 1,4 ампера будет выделять такое же тепло через резистор, как и постоянный ток 1 ампер.
Следовательно, среднеквадратичное значение также иногда называют эквивалентным значением или эквивалентным значением постоянного тока. Измерение среднеквадратичного значения напряжения или тока формы волны переменного тока — лучший способ соотнести величины переменного и постоянного тока.

Среднеквадратичное значение также называется «действующим значением», которое эквивалентно значению постоянного тока, тока или напряжения, при котором переменный сигнал производит ту же мощность, что и постоянный ток.
Как правило, напряжение сети представляет собой среднеквадратичное значение. В Индии, например, напряжение питания находится в пределах 220-240В. На самом деле это среднеквадратичное значение переменного тока, которое эквивалентно производству той же мощности, что и 220–240 В постоянного тока.
Среднеквадратичное значение используется только для обозначения сигналов переменного тока, т. е. изменяющихся во времени синусоидальных сигналов, таких как переменное напряжение, переменный ток или других сложных сигналов, амплитуда которых изменяется со временем. Среднеквадратичное значение не применимо к цепям постоянного тока, где величина постоянна во времени.
Процесс определения среднеквадратичного значения напряжения очень похож на процесс определения среднего значения напряжения.
 Существует два метода определения среднеквадратичного значения напряжения сигнала. Это: графический метод и аналитический метод.
Существует два метода определения среднеквадратичного значения напряжения сигнала. Это: графический метод и аналитический метод.Графический метод
В этом методе мы найдем среднеквадратичное значение напряжения, используя средние координаты или мгновенные значения напряжения формы переменного сигнала.
Четкий вывод среднеквадратичного значения включает несколько этапов, показанных ниже.
ШАГ 1
В каждой форме волны переменного тока у нас есть много мгновенных напряжений, и количество мгновенных напряжений зависит от длительности синхронизации. Например, если форма волны разделена на n средних ординат, то в момент времени t = 2 мгновенное напряжение формы волны переменного тока равно V2.
Аналогично, в экземпляре t = n мгновенное напряжение равно van и т. д. Итак, сначала мы находим мгновенные значения напряжения каждого экземпляра периодической формы волны, например V1, V2, V3 и Vn.
Чтобы найти среднеквадратичное напряжение формы волны, мы должны найти квадратные значения каждого значения напряжения формы волны переменного тока.
 Это дает «квадратную» часть среднеквадратичного значения.
Это дает «квадратную» часть среднеквадратичного значения.V1 2 +V2 2 +V3 2 +V4 2 +—-
ШАГ 2
Нахождение среднего значения суммы квадратов значений напряжения. Делим сумму квадратов на количество середин ординат. Это дает «среднюю» часть RMS.
Среднее значение всех значений напряжения формы волны переменного тока периодической формы волны даст нам наиболее точное значение среднеквадратичного значения напряжения. Как правило, во всех математических приближениях мы устанавливаем средние значения, чтобы не допустить ошибок и установить наиболее точное значение вычислений.
Если у нас есть Vn значений напряжения в n экземплярах, среднее значение рассчитывается, как показано ниже.
Квадратный корень из этого значения дает среднеквадратичное значение формы волны переменного тока. Формула для расчета среднеквадратичного значения напряжения показана ниже.
Где n — количество экземпляров,
V1, V2, V3, V4 ….
 — мгновенные значения напряжения сигнала.
— мгновенные значения напряжения сигнала.Пример
Если у нас есть переменный сигнал с максимальной амплитудой 20 Вольт, давайте найдем его среднеквадратичное значение напряжения.
Мы делим сигнал на 10 средних значений ординаты следующим образом.Таким образом, среднеквадратичное значение напряжения переменного тока с пиковым напряжением 20 В составляет 14,15 В.
Графический метод является очень эффективным методом определения среднеквадратичных значений всех типов сигналов, включая сигналы сложной формы.
Аналитический метод
Другим методом, используемым для определения среднеквадратичного значения напряжения (или тока) периодической формы волны переменного тока, является аналитический или математический метод. Этот метод подходит для волн синусоидальной формы.
В этом методе среднеквадратичное значение напряжения вычисляется путем анализа площади под кривой сигнала переменного тока. Этот метод проще, чем графический, при работе с чистыми синусоидальными сигналами.

Периодический синусоидальный сигнал с периодом времени Т определяется выражением СКЗ = √[1/T ∫ 0 t В м 2 cos 2 (ωt) dt]
Для одного полного цикла или периода формы волны пределы интегрирования составляют от 0 до 360 0 . Таким образом, интегрируя через нижний и верхний пределы, мы получаем
Комплексное уравнение можно еще больше упростить, разделив его на ω = 2π / T. Тогда сокращенное уравнение для среднеквадратичного значения напряжения будет следующим:
В Среднеквадратичное значение = В м /2 = В м *0,707
Уравнение среднеквадратичного напряжения
Среднеквадратичное значение напряжения рассчитывается с использованием других значений напряжения формы волны, таких как пиковое напряжение, размах напряжения и среднее напряжение.
В пересчете на значение пикового напряжения
Среднеквадратичное значение напряжения переменного тока составляет 0,707 или 1/√2 пикового значения напряжения.
 Среднеквадратичное значение можно рассчитать, разделив пиковое напряжение на квадратный корень из 2 (почти 0,707).
Среднеквадратичное значение можно рассчитать, разделив пиковое напряжение на квадратный корень из 2 (почти 0,707).В СКЗ = В ПИКОВОЕ x 1 /√2
В СКЗ = В ПИКОВОЕ x 0,707
Расчетное значение напряжения от пика до пика5 можно умножить на
размах напряжения с 1/22 или 0,35355. Размах напряжения представлен как V
PP .V ОБЗОР = V P-P-P x 1 / 2√2
V ОБЗОР = V P-P x 0,353
С точки зрения среднего значения напряжения
. Ольтрализопа раз по сравнению со средним значением напряжения.
V ОБЗОР = V AVG x π / 2√2
V ОБЗОР = V AVG x 1.1107
Значение RMS
- В ТРЕБОВАЕ КРЕСТОВ, КАРТЫ ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА, ГАРТИТА. выражаются в виде среднеквадратичных значений.
- Обычно мы говорим, что напряжение в бытовой сети составляет около 220 Вольт переменного тока.
 Фактически это означает, что среднеквадратичное напряжение бытовой сети составляет 220 В. Значение
Фактически это означает, что среднеквадратичное напряжение бытовой сети составляет 220 В. Значение - RMS дает значения, эквивалентные постоянному току формы волны переменного тока.
- Все измерительное оборудование, такое как амперметры и вольтметры, измеряет только среднеквадратичное значение. В некоторых дорогих вольтметрах сначала вычисляется пиковое напряжение и затем, умножая его на 0,707, получаем среднеквадратичное значение напряжения, наиболее точно.
- Среднеквадратичное значение используется для определения коэффициента амплитуды и коэффициента формы сигнала переменного тока, которые являются ключевыми факторами, определяющими производительность системы.
Форм-фактор и пик-фактор
Для сигнала переменного тока, такого как синусоидальный сигнал, среднеквадратичное значение, пиковое значение и среднее значение являются тремя важными величинами, которые описывают амплитуду. Эти три значения зависят друг от друга.
Помимо этих трех величин, существуют некоторые отношения, которые обычно определяются между этими тремя основными измерениями.
 Это форм-фактор и пиковый (или пиковый) фактор.
Это форм-фактор и пиковый (или пиковый) фактор.Форм-фактор
«Форм-фактор — это отношение среднеквадратичного значения напряжения переменного сигнала к его среднему напряжению». 9Форм-фактор 0097 представлен K f .
Форм-фактор = среднеквадратичное напряжение / среднее напряжение
K f = В среднеквадратичное значение / В AVG
От отношения между средним значением напряжения и среднеквадратичным значением синусоидальной формы волны переменного тока к пику (или макс. ), мы можем рассчитать форм-фактор как
K f = 0,707 В МАКС. / 0,637 В МАКС. его среднеквадратичное значение напряжения». Мы также называем это «пиковым фактором» или «амплитудным фактором».
Крест-фактор представлен KP.
Крест-фактор = Пиковое напряжение / Среднеквадратичное напряжение
KP = В ПИКОВОЕ (или В МАКС. ) / В Среднеквадратичное значение как
KP = V MAX / 0,707 VMAX
= 1,414
Итог
- Сигналы, которые периодически чередуются относительно оси, называются «переменным сигналом» или «переменным сигналом».

- Среднеквадратичное значение напряжения означает среднеквадратичное значение напряжения. Среднеквадратичное значение определяется как «квадратный корень из средних значений квадратов мгновенных напряжений в форме волны, изменяющейся во времени».
- Представление среднеквадратичного значения является стандартным способом измерения переменного тока и напряжения, поскольку оно дает эквивалентные значения постоянного тока.
- Существует два метода расчета среднеквадратичного значения напряжения сигнала: графический метод и аналитический метод.
- Формула для среднеквадратичного значения напряжения в графическом методе равна
- Формула для среднеквадратичного значения напряжения в аналитическом методе:
В СКЗ = √[1/T ∫ 0 t В м 2 cos 2 (ωt) dt]
- Уравнения среднеквадратичного значения напряжения в терминах других значений напряжения:
VRMS = Vпик x 1 / √2
VRMS = Vпик-пик x 1 / 2√2
VRMS = Vavg x π / 2√2
- Мы можем измерить коэффициент амплитуды и коэффициент формы переменного сигнала где коэффициент амплитуды представляет собой отношение пикового значения к среднеквадратичному значению, а коэффициент формы представляет собой отношение среднеквадратичного значения к среднему значению.

Как получить среднеквадратичное значение формы импульса и прямоугольного сигнала – Mastering Electronics Design
Адриан С. Настасе
Среднеквадратичное значение формы импульсного сигнала можно легко рассчитать, начиная с определения среднеквадратичного значения. Форма импульсного сигнала показана на рисунке 1. Отношение t1/T представляет собой коэффициент заполнения импульсного сигнала. Как показано в других статьях на этом веб-сайте (MasteringElectronicsDesign.com: Как получить среднеквадратичное значение трапециевидной формы волны и MasteringElectronicsDesign.com: Как получить среднеквадратичное значение треугольной формы волны), определение среднеквадратичного значения представляет собой интеграл за период сигнала. как в уравнении (1).
Рисунок 1
(1) Импульсная функция с переменной «время» является константой, которая представляет собой амплитуду сигнала между 0 и t1 и нулем от t1 до T, как в (2).

(2) , где с u1(t) я отметил функцию формы сигнала на рисунке 1. После замены u1(t) в уравнении (1) мы можем найти среднеквадратичное значение в квадрате, как в следующем выражении.
(3) Следовательно, среднеквадратичное значение импульсного сигнала равно
(4) Это выражение также можно найти как (5)
(5) где с D я отметил коэффициент заполнения импульсного сигнала, D = t1/T.
Что делать, если импульсный сигнал биполярный, как на рис. 2? 9Рис. 2 Чтобы вычислить среднеквадратичное значение, давайте разделим сигнал на две части: от 0 до t1 и от t1 до T, как в (6).

(6) где с u11(t) и u12(t) я отметил два участка сигнала на рисунке 2.
Среднеквадратичное значение u11(t) идентично показанному в уравнении (3).
(7) Аналогичным образом можно рассчитать среднеквадратичное значение u12(t):
(8) Затем вычисляется общее среднеквадратичное значение формы биполярного импульса путем применения квадратного корня из суммы квадратов u11 RMS и u12 RMS .
(9) После расчетов среднеквадратичное значение биполярного импульса составляет
(10) Как видите, среднеквадратичное значение биполярного импульса не зависит от его скважности и равно его амплитуде.

Зная среднеквадратичное значение импульсного сигнала, мы можем легко вычислить среднеквадратичное значение периодического прямоугольного сигнала. Прямоугольная волна на рисунке 3 представляет собой импульсный сигнал с коэффициентом заполнения 50%. Его среднеквадратичное значение можно рассчитать из уравнения (5), где D = 1/2. Его среднеквадратичное значение приведено в (11).
Рисунок 3
(11) >>> <<<
Мы используем файлы cookie и другие технологии отслеживания, чтобы улучшить ваш просмотр на нашем сайте, показывать персонализированный контент и таргетированную рекламу, анализировать трафик сайта и понимать, откуда приходит наша аудитория. Чтобы узнать больше, нажмите ссылку Узнать больше. Кроме того, ознакомьтесь с нашей Политикой конфиденциальности, которая также была обновлена и вступила в силу 24 мая 2018 г.



 {2}}{R}.\)
{2}}{R}.\)
 Цепи с изменяющимися — переменными — токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Цепи с изменяющимися — переменными — токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ. На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки в ТОЭ данное направление принято за положительное с угловой частотой, равной w.
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки в ТОЭ данное направление принято за положительное с угловой частотой, равной w.

 Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад.
Так как фазовый угол синусоиды за время одного периода Т изменяется на рад. На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Она отсекает верхнюю часть половинок синусоид.
Она отсекает верхнюю часть половинок синусоид.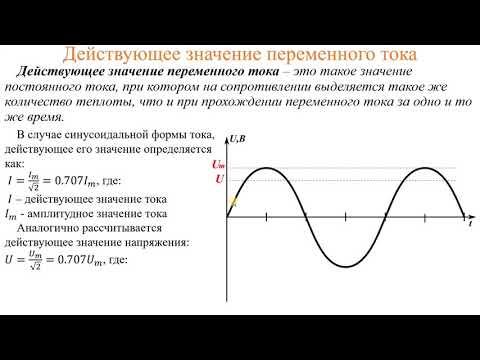 Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте. В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей DC для периодически меняющегося электрического тока любой формы.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте. В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей DC для периодически меняющегося электрического тока любой формы. Величина переменного тока, как и напряжения, постоянно меняется во времени.
Величина переменного тока, как и напряжения, постоянно меняется во времени. Что такое действующее, среднеквадратичное, эффективное напряжение или ток. Среднее значение переменного синусоидального напряжения или тока. Говоря о величине, изменяющейся по синусоидальному гармоническому закону, можно за половину периода определить ее среднее значение. В результате получим:. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:.
Что такое действующее, среднеквадратичное, эффективное напряжение или ток. Среднее значение переменного синусоидального напряжения или тока. Говоря о величине, изменяющейся по синусоидальному гармоническому закону, можно за половину периода определить ее среднее значение. В результате получим:. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:. Статья содержит описание механизмов пробоя танталовых конденсаторов, предлагает вариант расчета допустимых уровней рабочих токов и напряжений для различных частотных диапазонов.
Статья содержит описание механизмов пробоя танталовых конденсаторов, предлагает вариант расчета допустимых уровней рабочих токов и напряжений для различных частотных диапазонов. Эта формула упрощена прибором для учета только положительного пика синусоиды:. Среднеквадратичное измерение надежно, когда синусоидальная волна идеальна, потому что это измерение учитывает только пиковое значение формы волны. Итак, что происходит, когда синусоида не идеальна? RMS измерения нельзя считать надежными, потому что в настоящее время в любой установке имеется множество источников шума , из-за которых форма волны переменного тока никогда не бывает идеальной. В измерении True RMS истинное среднеквадратичное значение используются более сложные математические формулы, которые позволяют приблизить значение к реальности, чем RMS.
Эта формула упрощена прибором для учета только положительного пика синусоиды:. Среднеквадратичное измерение надежно, когда синусоидальная волна идеальна, потому что это измерение учитывает только пиковое значение формы волны. Итак, что происходит, когда синусоида не идеальна? RMS измерения нельзя считать надежными, потому что в настоящее время в любой установке имеется множество источников шума , из-за которых форма волны переменного тока никогда не бывает идеальной. В измерении True RMS истинное среднеквадратичное значение используются более сложные математические формулы, которые позволяют приблизить значение к реальности, чем RMS. Амбициозная цель компании MediaTek — сформировать сообщество разработчиков гаджетов из специалистов по всему миру и помочь им реализовать свои идеи в готовые прототипы.
Амбициозная цель компании MediaTek — сформировать сообщество разработчиков гаджетов из специалистов по всему миру и помочь им реализовать свои идеи в готовые прототипы. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами. Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами. Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму. Легко выразить величину напряжения или тока, т. е. сколько напряжения или тока присутствует в любой части цепи.
Легко выразить величину напряжения или тока, т. е. сколько напряжения или тока присутствует в любой части цепи. Среднеквадратичное значение напряжения определяется как «квадратный корень из средних квадратов всех мгновенных напряжений в волне форма». Среднеквадратичное значение можно найти следующим образом: входные данные возводятся в квадрат и вычисляется среднее значение.
Среднеквадратичное значение напряжения определяется как «квадратный корень из средних квадратов всех мгновенных напряжений в волне форма». Среднеквадратичное значение можно найти следующим образом: входные данные возводятся в квадрат и вычисляется среднее значение.
 Существует два метода определения среднеквадратичного значения напряжения сигнала. Это: графический метод и аналитический метод.
Существует два метода определения среднеквадратичного значения напряжения сигнала. Это: графический метод и аналитический метод.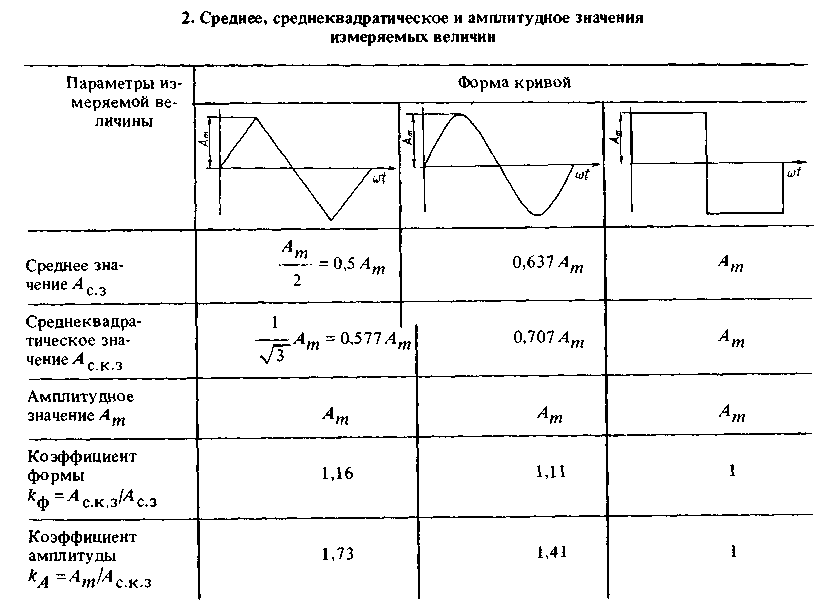 Это дает «квадратную» часть среднеквадратичного значения.
Это дает «квадратную» часть среднеквадратичного значения. — мгновенные значения напряжения сигнала.
— мгновенные значения напряжения сигнала.
 Среднеквадратичное значение можно рассчитать, разделив пиковое напряжение на квадратный корень из 2 (почти 0,707).
Среднеквадратичное значение можно рассчитать, разделив пиковое напряжение на квадратный корень из 2 (почти 0,707). Фактически это означает, что среднеквадратичное напряжение бытовой сети составляет 220 В.
Фактически это означает, что среднеквадратичное напряжение бытовой сети составляет 220 В. Это форм-фактор и пиковый (или пиковый) фактор.
Это форм-фактор и пиковый (или пиковый) фактор.