Сложение и вычитание двух векторов — онлайн калькулятор
В результате сложения двух векторов a и b получается вектор с, все элементы которого равны попарной сумме соответствующих элементов слагаемых векторов. При вычитании тех же векторов все элементы результирующего вектора с равны попарной разности соответствующих элементов.
Нахождение суммы и разности векторов онлайн позволяет обойтись без самостоятельного проведения расчетов. Нужно просто задать векторы (точками или координатами), выбрать действие (сложение или вычитание) и нажать кнопку «рассчитать». После этого онлайн-калькулятор выдаст результат вместе с подробными промежуточными выкладками
Как сложить и вычесть векторы с помощью онлайн-калькулятора
Чтобы сложить или вычесть векторы при помощи онлайн калькулятора, достаточно лишь задать необходимые векторы. Для этого:
- Опеделитесь, с какими векторами вы хотите работать.
 Это могут быть векторы на плоскости или векторы в пространстве.
Это могут быть векторы на плоскости или векторы в пространстве.В рассматриваемом примере, оставим размерность «2». То есть, мы работаем с векторами на плоскости.
- Теперь нужно выбрать форму представления векторов: их можно задать координатами либо точками:
Для наглядности, зададим один вектор точками, а второй – координатами.
- Теперь в поле «Значение вектора» нужно ввести соответствующие значения. Зададим векторы произвольным образом:
- Осталось нажать «Рассчитать» и получить ответ. Отметим, что складываемые и вычитаемые векторы можно также умножать на число. Для наглядности, умножим первый вектор a на 3 и сложим результат с вектором b:
Материалы, которые помогут вам лучше разобраться в теме:
- Векторы на плоскости и в пространстве — основные определения
- Операции над векторами и их свойства: сложение и умножение
- Координаты вектора в декартовой системе координат (ДСК)
- Нахождение координат вектора через координаты точек
- Векторное произведение — определения, свойства, формулы, примеры и решения
- Операции над векторами в прямоугольной системе координат
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Длина вектора. Модуль вектора
- Векторное произведение векторов
- Умножение вектора на число
- Угол между векторами
- Смешанное произведение векторов
- Скалярное произведение векторов
- Определение вектора по двум точкам
- Разложение вектора по базису
- Проверить являются ли вектора базисом
- Ортогональность векторов
- Компланарность векторов
- Коллинеарность векторов
- Проекция вектора на вектор
- Площадь треугольника, построенного на векторах
- Площадь параллелограмма, построенного на векторах
Как найти сумму и разность векторов без онлайн-калькулятора
Рассмотрим пример с применением формулы для суммы векторов на плоскости. Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления:
Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления:
c→=a→+b→=(ax+bx;ay+by)a→+b→=(3+4;5+3)=(7;8)
Правильность решения можно проверить с помощью онлайн-калькулятора.
Данный сервис будет полезен школьникам и студентам при самостоятельной подготовке к экзаменам и контрольным по векторной алгебре.
Понравился калькулятор? Поделись с друзьями!
Как сложить несколько векторов… -reshimne.ru
Новые вопросы
Ответы
Рассмотрим правила сложения векторов. Если слагаемые векторы путем их параллельного переноса последовательно пристраивать один за другим так, что начало последующего вектора, совпадает с концом предыдущего, то вектор, замыкающий получившуюся ломаную, является суммой данных слагаемых, причём его начало совпадает с началом первого из слагаемых векторов, а конец – с концом последнего. На рисунке 3 показано сложение четырёх векторов a, b, c и d.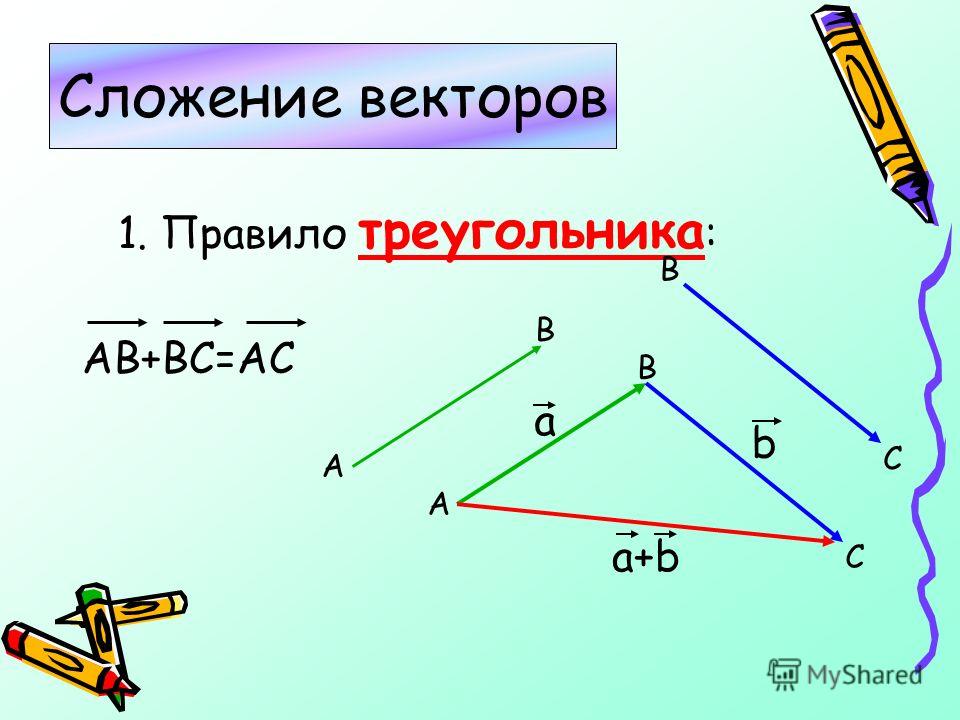 Символически это записывается в виде равенства f = a + b + c + d, где вектор f и является суммой указанных векторов.Рис. 3При сложении двух векторов часто используют так называемое «правило параллелограмма». При этом строят параллелограмм, используя слагаемые векторы в качестве его смежных сторон. Диагональ параллелограмма, проведённая из точки, где соединяются начала векторов, и является искомой суммой (рис. 4, слева).
Символически это записывается в виде равенства f = a + b + c + d, где вектор f и является суммой указанных векторов.Рис. 3При сложении двух векторов часто используют так называемое «правило параллелограмма». При этом строят параллелограмм, используя слагаемые векторы в качестве его смежных сторон. Диагональ параллелограмма, проведённая из точки, где соединяются начала векторов, и является искомой суммой (рис. 4, слева).
Похожие вопросы
Какие физические тела вы можете назвать? приведите примеры…
Чему равен периуд колебаний при циклической частоте 25 рад сек?…
Как складываются и вычитается скалярные физические величины…
Какие физические тела вы можете назовите ? приведите пример. ..
..
Поезд длиной 240 м , двигаясь равномерно, прошёл мост длиной 360 м за 2 мин. Чему равна скорость поезда? Ответ……… м/с. ПОМОГИТЕ ПОЖАЛУЙСТА….
С какой скоростью упадет на землю мяч с высокой 2м…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
История
Обществознание
Окружающий мир
География
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
8 класс.
 Геометрия. Векторы. Применение векторов к решению задач. — Сложение и вычитание векторов.Комментарии преподавателя
Геометрия. Векторы. Применение векторов к решению задач. — Сложение и вычитание векторов.Комментарии преподавателяСложение и вычитание векторов
На предыдущем уроке мы определили понятие вектора, сказали, какие векторы называются равными, коллинеарными, сонаправленными и противонаправленными.
Теперь пусть задано два вектора – вектора и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: (см. Рис. 1).
Рис. 1
Данное определение можно объяснить так: пусть был задан груз, и сначала на него подействовала сила – он переместился из точки А в точку В, после этого подействовала сила – груз переместился из точки В в точку С. Но в результате действия двух этих сил груз переместился из точки А в точку С.
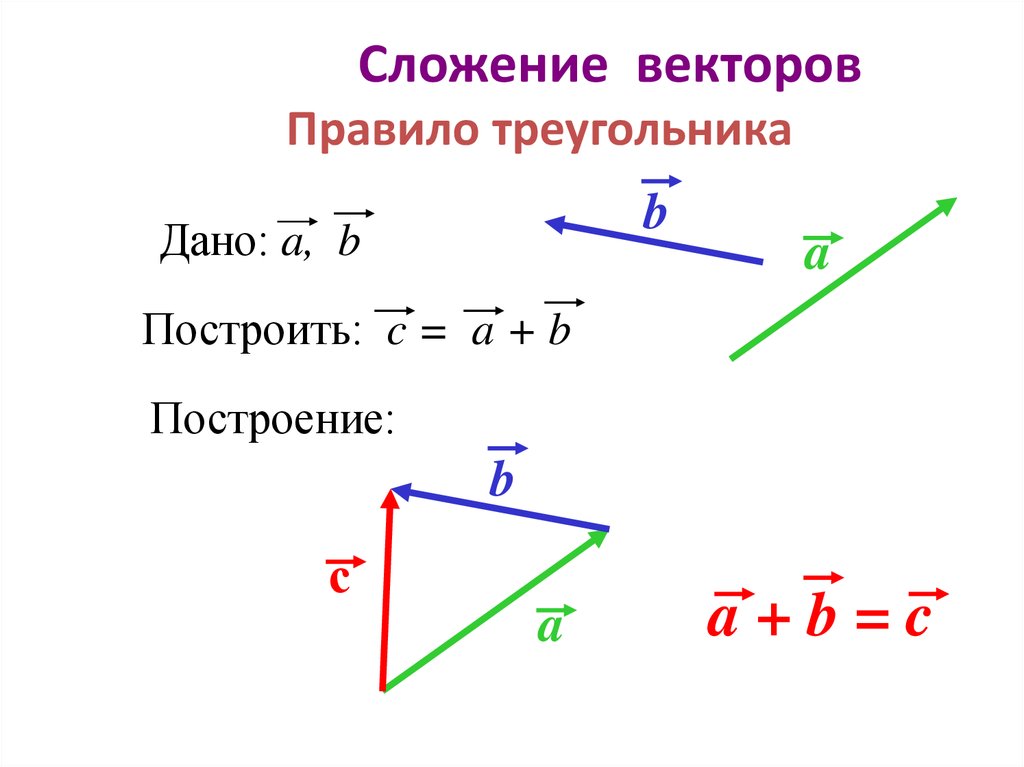
Таким образом, мы получили определение суммы двух векторов – правило треугольника.
Правило треугольника
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
Можно провести аналогию с числами. Мы ввели понятие числа, научились складывать числа, определили законы сложения и так далее. Теперь мы ввели понятие вектора, научились находить равные вектора, складывать вектора. Теперь нужно определить законы сложения.
Законы сложения векторов
Для любых векторов , и справедливы следующие равенства:
– переместительный закон.
Доказательство: отложим из точки сначала вектор , получаем точку В, из нее откладываем вектор , получаем точку С и вектор .
Теперь отложим из точки А сначала вектор получим точку В, из нее отложим вектор, получим точку С и вектор .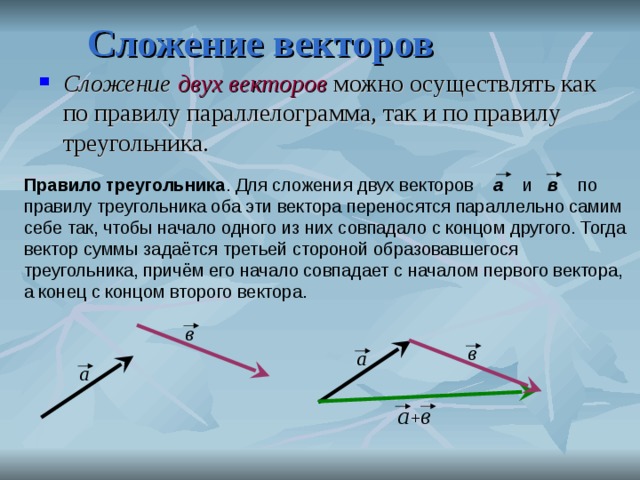
Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
Рис. 2
Откладываем из точки А вектор и вектор . Из точки В откладываем вектор , вектора и равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма. , таким образом, мы доказали переместительный
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.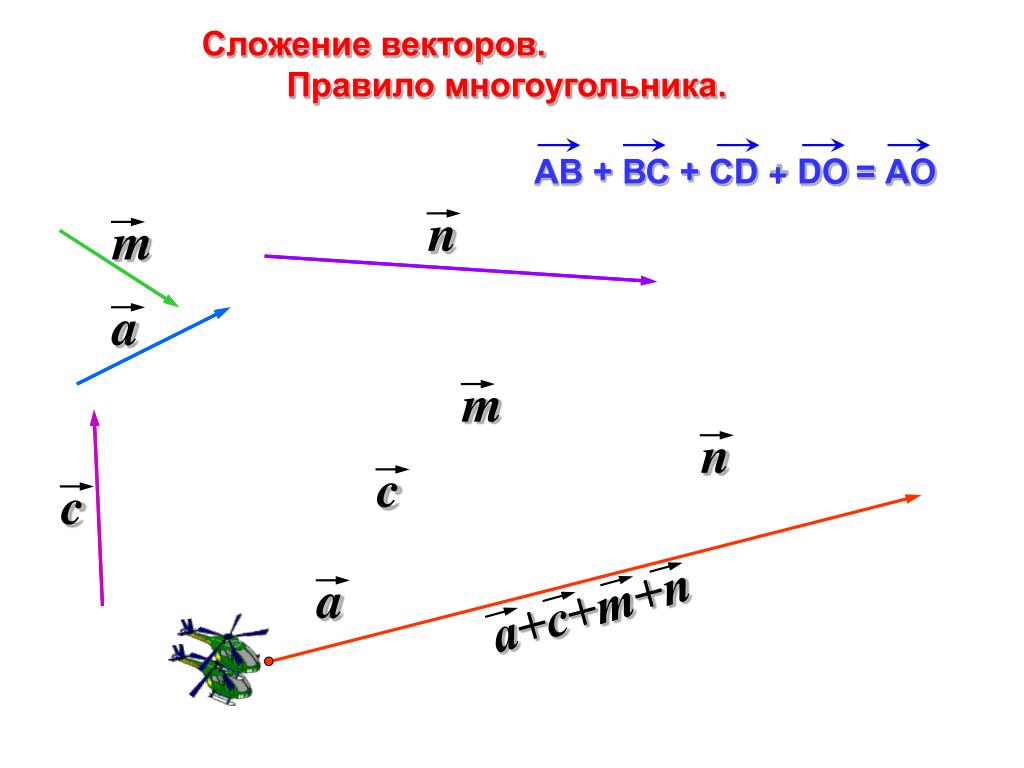
– сочетательный закон;
Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат (см. Рис. 4).
Рис. 4
В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору и получили результат: (см. Рис. 5).
Таким образом, мы доказали сочетательный закон сложения векторов.
Рис. 5
Правило многоугольника
Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов (см. Рис. 6).
Рис. 6
По аналогии с действительными числами после того, как мы научились их складывать, нужна обратная операция – вычитание.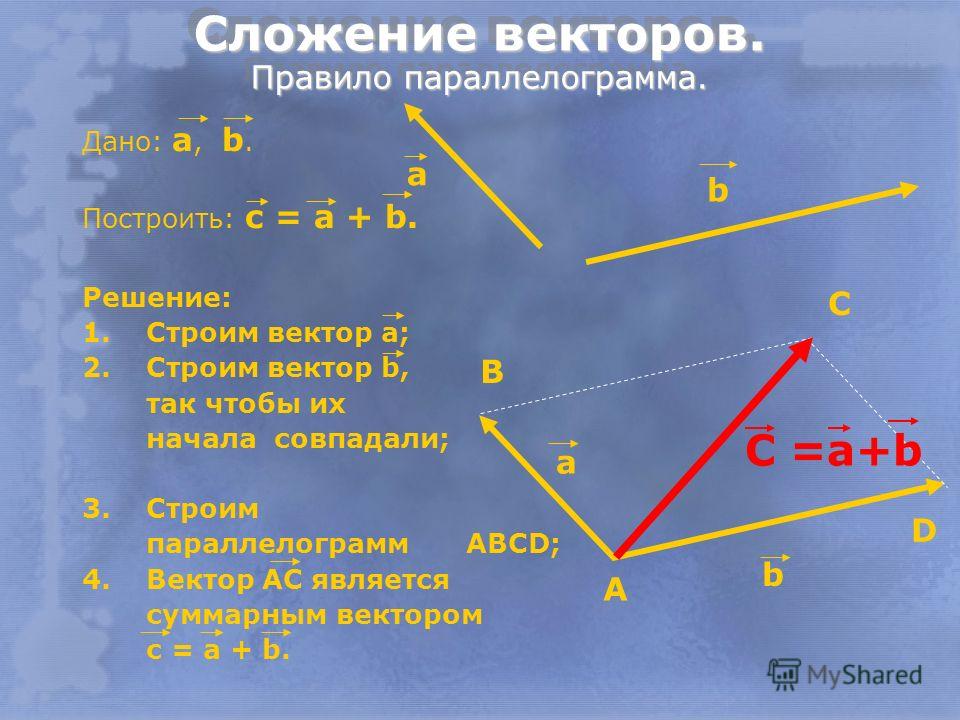
Пусть задано два вектора – векторы и . Найдем разность этих двух векторов .
Определение
Разностью двух векторов и называют такой третий вектор, сумма которого с вектором равна вектору .
Если задан вектор , то можно построить противоположный ему вектор , который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор: . Таким образом, .
Отложим из произвольной точки вектор , из его конца отложим вектор , получим в результате вектор (см. Рис. 7).
Рис. 7
Рассмотрим вычитание векторов на параллелограмме. Из точки А отложим векторы и . Из точек В и D отложим векторв и соответственно. Диагональ АС – это сумма векторов и : . Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору вектор , получим вектор (см. Рис. 8).
Рис. 8
Итак, на данном уроке мы вывели правила сложения и вычитания векторов при помощи треугольника и параллелограмма, сформулировали законы сложения векторов.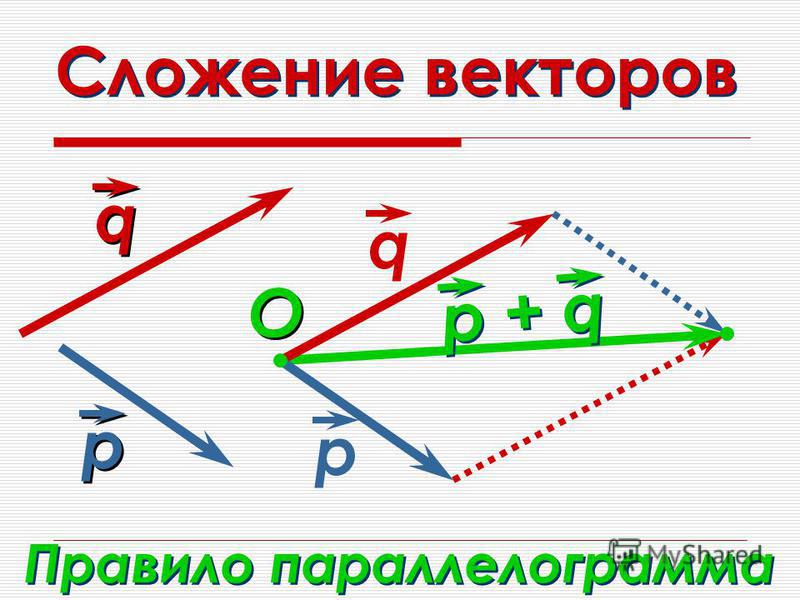
ИСТЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/vektory/slozhenie-i-vychitanie-vektorov
http://www.youtube.com/watch?v=r8icqcsv5AQ
http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/4-test-po-geometrii-9-klass-tema-slozhenie-i-vychitanie-vektorov-variant-1.html
http://gdz-matem.ru/8class/25-9.2-slozhenie-i-vychitanie-vektorov.html
http://www.lenbaza.ru/baza/pict/111.jpg
20.4 Методы сложения векторов | Векторы и скаляры
20.4 Методы сложения векторов (ESAGP)
Теперь, когда вы узнали о математических свойствах векторов, мы вернемся к сложению векторов более подробно. деталь. Существует ряд методов сложения векторов. Эти методы делятся на две основные категории: графические и алгебраические методы.
Графические методы (ESAGQ)
Графические методы включают построение точных масштабных диаграмм для обозначения отдельных векторов и их результатов.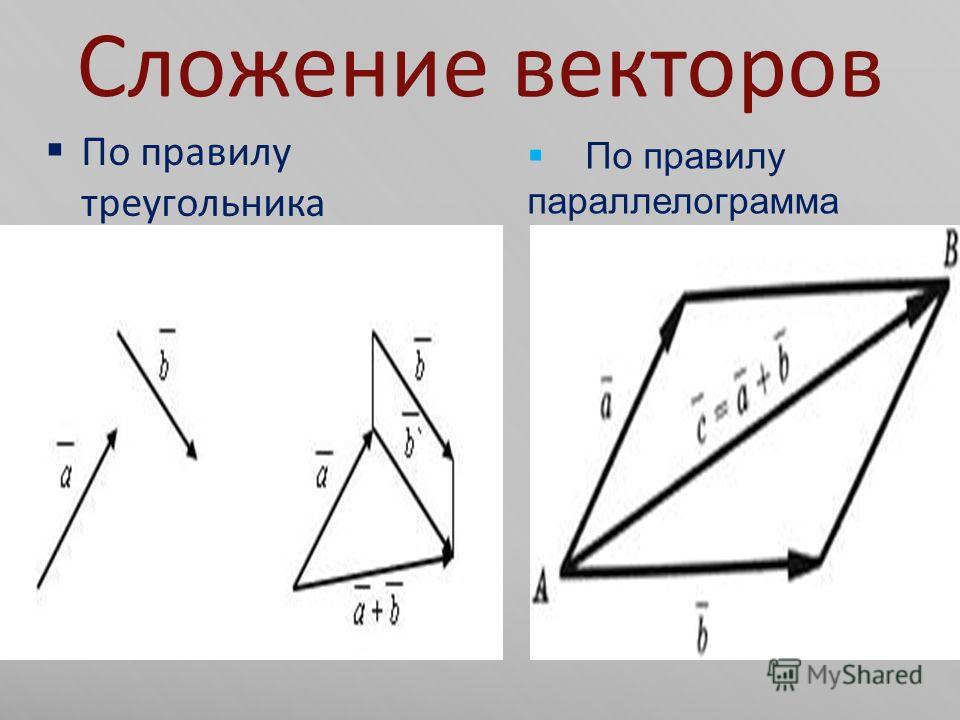 Мы рассмотрим только один графический метод: метод «голова к хвосту».
Мы рассмотрим только один графический метод: метод «голова к хвосту».
Метод: метод сложения векторов «голова к хвосту»
Нарисуйте грубый набросок ситуации.
Выберите масштаб и укажите опорное направление.
Выберите любой из векторов и нарисуйте его в виде стрелки в правильном направлении и правильной длины – не забудьте поставить стрелку на конце, чтобы обозначить его направление.
Возьмите следующий вектор и нарисуйте его в виде стрелки, начинающейся с острия первого вектора в правильном направлении. направлении и правильной длины.
Продолжайте, пока не нарисуете каждый вектор, каждый раз начиная с головы предыдущего вектора. Таким образом, добавляемые векторы рисуются один за другим, голова к хвосту.

Результатом является вектор, проведенный от конца первого вектора к началу последнего. Его величину можно определить по длине его стрелки с помощью шкалы. Его направление тоже может быть определяется по масштабной диаграмме.
Рассмотрим еще несколько примеров сложения векторов с использованием перемещений. Стрелки подскажут вам, как далеко двигаться и в каком направлении. Стрелки вправо соответствуют шагам вперед, а стрелки влево — шагам вперед. шаги назад. Посмотрите на все приведенные ниже примеры и проверьте их.
В этом примере говорится, что \(\text{1}\) шаг вперед, а затем еще один шаг вперед — это то же самое, что стрелка в два раза длиннее – два шага вперед.
В этом примере говорится, что \(\text{1}\) шаг назад, а затем еще один шаг назад — это то же самое, что стрелка дважды длинный – два шага назад.
Иногда возможно, что вы вернетесь к тому, с чего начали. В этом случае чистый результат того, что у вас есть
сделано то, что вы никуда не ушли (ваши начальная и конечная точки находятся в одном и том же месте). В этом случае ваш
результирующее смещение представляет собой вектор нулевой длины. Мы используем символ \(\vec{0}\)
В этом случае чистый результат того, что у вас есть
сделано то, что вы никуда не ушли (ваши начальная и конечная точки находятся в одном и том же месте). В этом случае ваш
результирующее смещение представляет собой вектор нулевой длины. Мы используем символ \(\vec{0}\)
Таким же образом проверьте следующие примеры. Стрелки вверх по странице можно рассматривать как шаги влево, а стрелки вниз страница как шаги вправо.
Попробуйте пару, чтобы убедиться в этом!
Важно понимать, что направления не являются особыми – «вперед и назад» или «влево и правильно» трактуются одинаково. То же самое верно для любого набора параллельных направлений:
В приведенных выше примерах отдельные смещения были параллельны друг другу. Однако то же самое с ног на голову Метод сложения векторов может применяться к векторам в любом направлении.
Рабочий пример 3: сложение головы к хвосту 1
На дороге ломается машина, и вы с другом, который случайно проходите мимо, помогаете водителю
нажмите-запустите его. Вы и ваш друг стоите вместе в задней части автомобиля. Если надавить с силой
\(\text{50}\) \(\text{N}\) и ваш друг толкает с силой \(\text{45}\) \(\text{N}\), что
результирующая сила, действующая на автомобиль? Используйте метод «голова к хвосту», чтобы вычислить ответ графически.
Вы и ваш друг стоите вместе в задней части автомобиля. Если надавить с силой
\(\text{50}\) \(\text{N}\) и ваш друг толкает с силой \(\text{45}\) \(\text{N}\), что
результирующая сила, действующая на автомобиль? Используйте метод «голова к хвосту», чтобы вычислить ответ графически.
Нарисуйте грубый набросок ситуации
Выберите масштаб и опорное направление
Выберем направление вправо в качестве положительного направления. Масштаб может быть \(\text{1}\) \(\text{см}\) = \(\text{10}\) \(\text{N}\).
Выберите один из векторов и нарисуйте его в виде стрелки нужной длины в правильном направление
Начните с вектора силы и нарисуйте стрелку, указывающую вправо, которая равна \(\text{5}\) \(\text{см}\)
длинный (т. е. \(\text{50}\) \(\text{N}\) = \(\text{5}\) \(\times\)\(\text{10}\) \(\text {N}\), поэтому вы
также необходимо умножить масштаб \(\text{см}\) на \(\text{5}\)).
Возьмите следующий вектор и нарисуйте его, начиная со стрелки предыдущего вектора.
Поскольку ваш друг толкает в том же направлении, что и вы, векторы ваших сил должны указывать в одном и том же направлении. направление. Используя масштаб, эта стрелка должна быть \(\text{4,5}\) \(\text{см}\) в длину.
Нарисуйте равнодействующую, измерьте ее длину и найдите направление
В этой задаче всего два вектора, поэтому результирующий вектор нужно провести из хвоста (т.е. начальная точка) первого вектора в начало второго вектора.
Результирующий вектор измеряет \(\text{9,5}\) \(\text{см}\) и указывает вправо. Следовательно, результирующий сила должна быть \(\text{95}\) \(\text{N}\) в положительном направлении ( или вправо).
Рабочий пример 4: сложение головы к хвосту 2
Используйте графический метод «голова к хвосту», чтобы определить результирующую силу, действующую на игрока в регби, если два игрока на
его команда толкает его вперед силами \(\vec{{F}_{1}} = \text{60}\text{ N}\) и \(\vec{{F}_{2}}
= \текст{90}\text{ N}\) соответственно, и два игрока противоположной команды толкают его назад с
силы \(\vec{{F}_{3}} = \text{100}\text{ N}\) и \(\vec{{F}_{4}} = \text{65}\text {N}\) соответственно.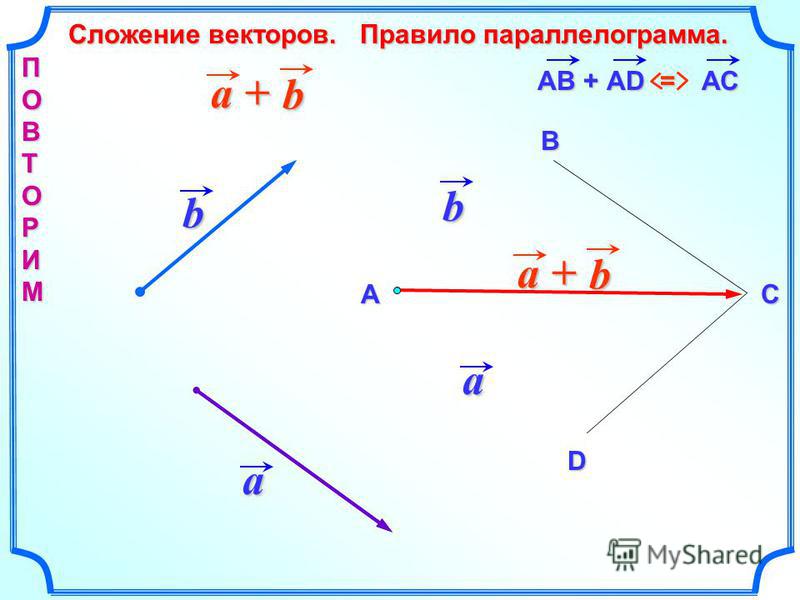
Выберите масштаб и базовое направление
Выберем масштаб \(\text{0,5}\) \(\text{см}\)= \(\text{10}\) \(\text{ N}\) и для нашей диаграммы мы будет определять положительное направление как вправо.
Выберите один из векторов и нарисуйте его в виде стрелки правильной длины в правильном direction
Мы начнем с рисования вектора \(\vec{{F}_{1}}= \text{60}\text{ N}\), указывающего в положительную сторону направление. Используя нашу шкалу \(\text{0,5}\) \(\text{см}\) = \(\text{10}\) \(\text{N}\), длина стрелка должна быть \(\text{3}\) \(\text{cm}\) и указывать вправо.
Возьмите следующий вектор и нарисуйте его, начиная со стрелки предыдущего вектора
Следующий вектор — \(\vec{{F}_{2}} = \text{90}\text{ N}\) в том же направлении, что и \(\vec{{F}_{1}} \). С использованием
шкале, стрелка должна быть \(\text{4,5}\) \(\text{см}\) длинной и указывать вправо.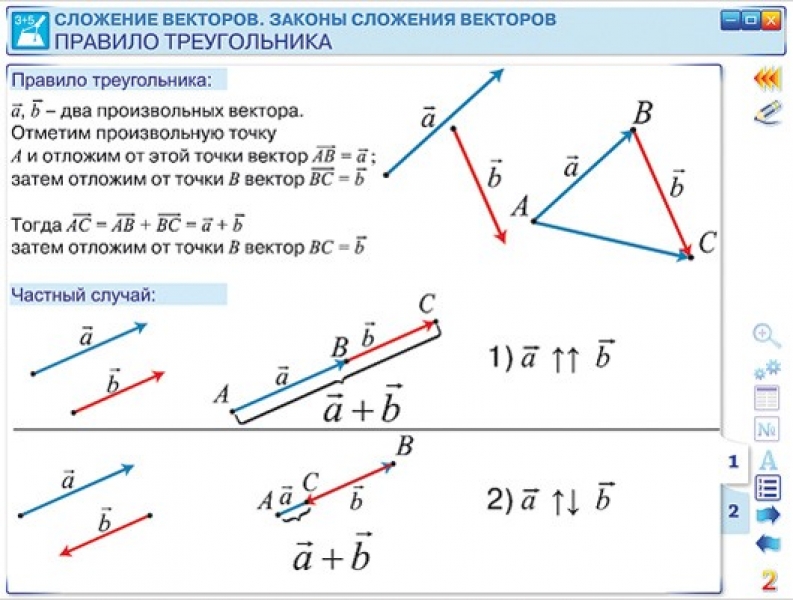
Возьмите следующий вектор и нарисуйте его, начиная со стрелки предыдущего вектора
Следующий вектор равен \(\vec{{F}_{3}} = \text{100}\text{ N}\) в в противоположном направлении . С использованием масштабе, эта стрелка должна быть \(\text{5}\) \(\text{см}\) длинной и указывать на осталось .
Примечание: Мы работаем в одном измерении, поэтому эта стрелка будет нарисована поверх первой. вектора влево. Это будет запутанно, поэтому мы нарисуем его рядом с фактической линией, чтобы показать вам, что это выглядит как.
Возьмите следующий вектор и нарисуйте его, начиная со стрелки предыдущего вектора
Четвертый вектор равен \(\vec{{F}_{4}} = \text{65}\text{ N}\) также в противоположное направление. С использованием масштаб, эта стрелка должна быть \(\text{3,25}\) \(\text{см}\) в длину и указывать влево.
Нарисуйте равнодействующую, измерьте ее длину и найдите ее направление.
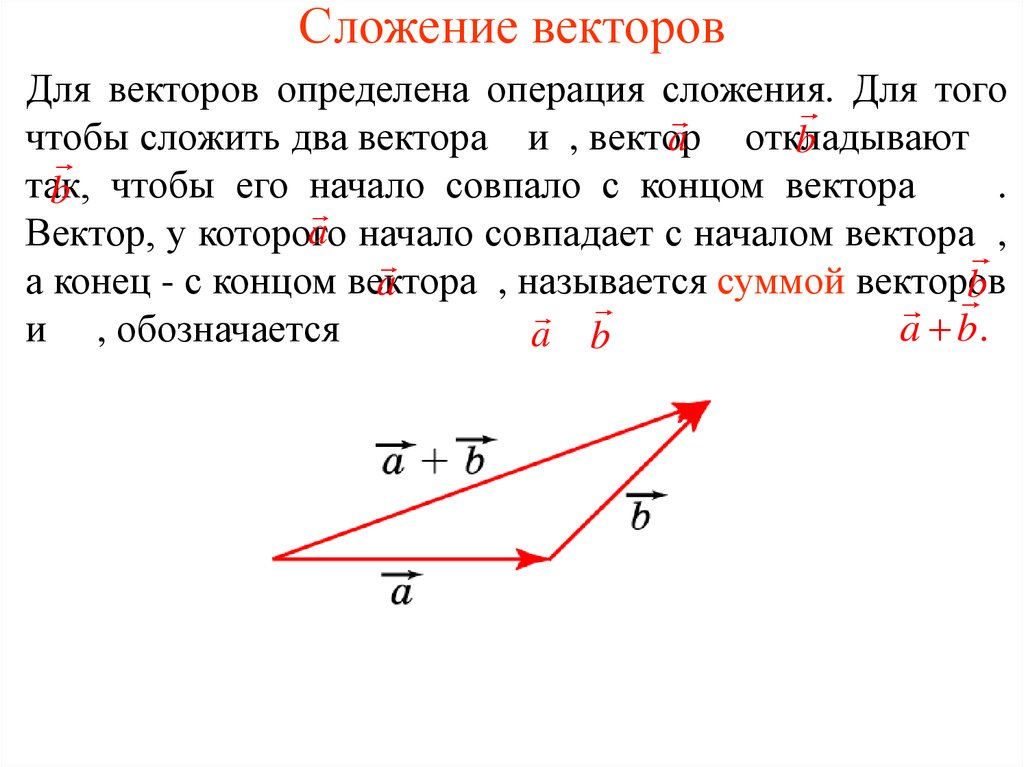
Теперь мы нарисовали все векторы сил, действующих на игрока. Результирующий вектор стрелка, которая начинается в конце первого вектора и заканчивается в начале последнего нарисованного вектора.
Результирующий вектор измеряет \(\text{0,75}\) \(\text{см}\), что при использовании нашей шкалы эквивалентно \(\text{15}\) \(\text{N}\) и указывает влево ( или отрицательное направление или направлении, в котором продвигаются члены противоположной команды).
временный текстАлгебраические методы (ESAGR)
Векторы по прямой линии
Всякий раз, когда вы сталкиваетесь со сложением векторов, действующих по прямой линии (т. е. некоторые из них направлены влево, а некоторые вправо, или некоторые действуют вверх, а другие вниз) вы можете использовать очень простой алгебраический метод:
Метод: сложение/вычитание векторов по прямой
Выберите положительное направление.
 Например, для ситуаций, связанных со смещением в западном направлении.
и восток, вы можете выбрать запад в качестве положительного направления. В этом случае смещения на восток отрицательны.
Например, для ситуаций, связанных со смещением в западном направлении.
и восток, вы можете выбрать запад в качестве положительного направления. В этом случае смещения на восток отрицательны.Затем просто добавьте (или вычтите) величину векторов, используя соответствующие знаки.
На заключительном шаге указать направление равнодействующей словами (положительные ответы в положительное направление, в то время как отрицательные результирующие имеют отрицательное направление).
Рассмотрим несколько примеров.
Рабочий пример 5: алгебраическое сложение векторов 1
Теннисный мяч катится к стене, которая находится на расстоянии \(\text{10}\) \(\text{m}\) от мяча. Если после
ударившись о стену, мяч катится дальше \(\text{2,5}\) \(\text{m}\) по земле от
стены, рассчитайте алгебраически результирующее перемещение мяча.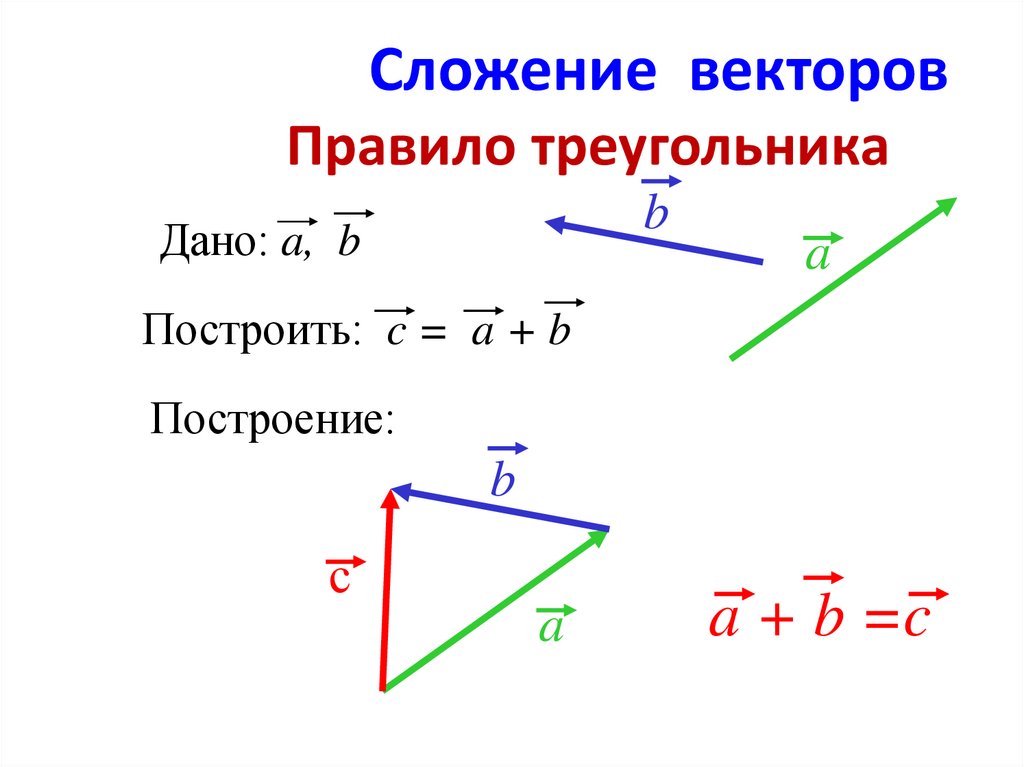
Нарисуйте грубый набросок ситуации
Решите, какой метод использовать для вычисления результирующего
Мы знаем, что результирующее смещение шара (\(\vec{x_{R}}\)) равно сумме перемещений шара отдельные смещения (\(\vec{x_{1}}\) и \(\vec{x_{2}}\)):
\[\vec{x_{R}} = \vec{x_{1}} + \vec{x_{2}}\]
Поскольку движение мяча прямолинейное (т. е. мяч движется к стене и от нее), мы можем использовать только что объясненный метод алгебраического сложения.
Выберите положительное направление
Давайте выберем положительное направление к стене. Это означает, что отрицательное направление от стены.
Теперь определим наши векторы алгебраически
С правым положительным:
\начать{выравнивать*} \vec{x_{1}} & = + \text{10,0}\text{м} \\ \vec{x_{2}} & = -\text{2,5}\text{м} \конец{выравнивание*}
Складываем векторы
Затем мы просто складываем два смещения, чтобы получить результат:
\начать{выравнивать*} \vec{x_{R}} & = \left(+\text{10,0}\text{m}\right) + \left(-\text{2,5}\text{m}\right) \ \ & = \влево(+\текст{7,5}\текст{м}\вправо) \конец{выравнивание*}
Цитата из результата
Наконец, в этом случае к стене является положительным направлением , поэтому: \(\vec{x_{R}} =
\text{7,5}\text{ м}\) к стене. 9{-1}$}\). Определить изменение скорости мяча.
9{-1}$}\). Определить изменение скорости мяча.
Нарисуйте набросок
Быстрый набросок поможет нам разобраться в проблеме.
Решите, какой метод использовать для расчета результата
Помните, что скорость является вектором. Изменение скорости мяча равно разности между начальной и конечной скоростями мяча:
\[\Delta \vec{v} = \vec{v_{f}} — \vec{v_{i}}\]
Так как мяч движется по прямой линии (то есть влево и вправо), мы можем использовать алгебраический метод Вычитание векторов только что обсуждалось.
Выберите положительное направление
Выберите положительное направление к стене. Это означает, что отрицательное направление от стены.
Теперь определим наши векторы алгебраически
\начать{выравнивать*} \vec{v_{i}} & = +\text{3}\text{ m·s$^{-1}$} \\ \vec{v_{f}} & = -\text{2}\text{м·с$^{-1}$} \end{выравнивание*} 9{-1}$}\) от стены.
Рабочий пример 7: алгебраическое сложение векторов 2
Мужчина прикладывает силу \(\text{5}\) \(\text{N}\) к ящику. Ящик отталкивает человека с сила \(\text{2}\) \(\text{N}\). Вычислите алгебраически результирующую силу, приложенную человеком к ящик.
Нарисуйте набросок
Быстрый набросок поможет нам разобраться в проблеме.
Решите, какой метод использовать для расчета результата
Помните, что сила — это вектор. Поскольку ящик движется по прямой линии (то есть влево и вправо), мы можно использовать только что обсуждавшийся алгебраический метод сложения векторов.
Выберите положительное направление
Выберите положительное направление к ящику (т.е. в том же направлении, что и
мужчина толкает). Это означает, что отрицательное направление направлено в сторону от ящика (т.е.
против направления, которое толкает мужчина).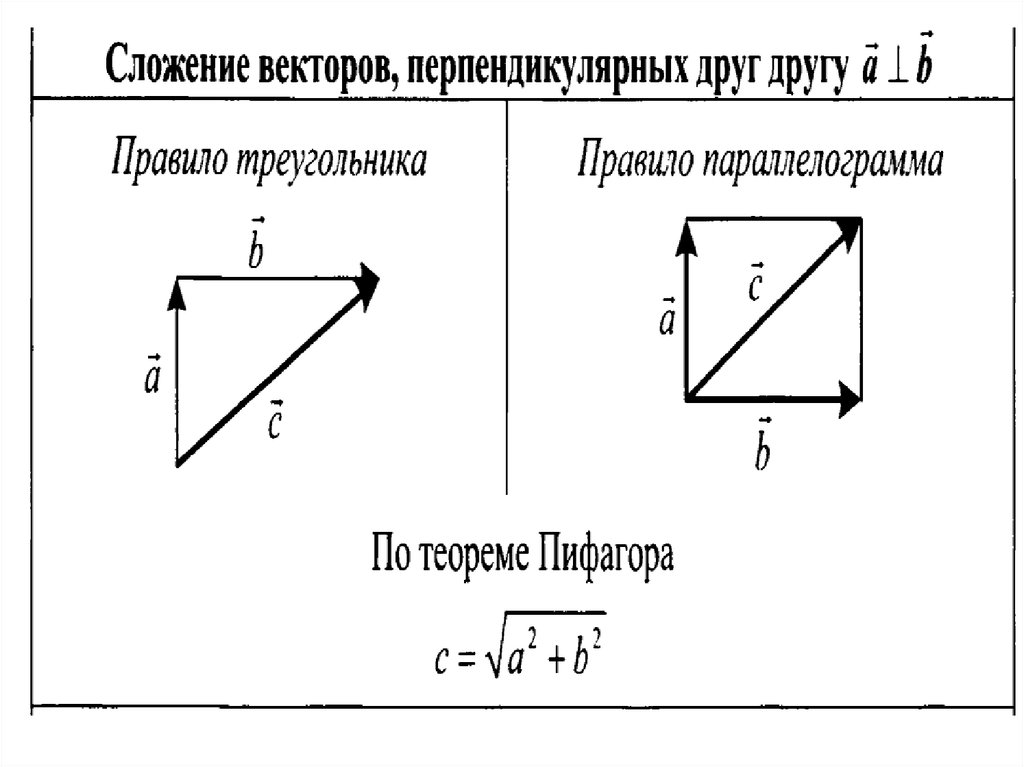
Теперь определим наши векторы алгебраически
\начать{выравнивать*} \vec{F_{\text{человек}}} & = +\text{5}\text{N} \\ \vec{F_{\text{ящик}}} & = -\text{2}\text{N} \конец{выравнивание*}Вычесть векторы
Таким образом, результирующая сила равна:
\начать{выравнивать*} \vec{F_{\text{человек}}} + \vec{F_{\text{ящик}}} & = \left(\text{5}\text{N}\right) + \left(\text{ 2}\текст{ Н}\справа)\\ & = \текст{7}\текст{N} \конец{выравнивание*}
Приведите результирующую
Помните, что в этом случае по направлению к ящику означает положительную силу : \(\text{7}\) \(\text{N}\) к ящику.
Помните, что только что обсуждавшаяся техника сложения и вычитания может быть применена только к векторам, действующим
по прямой линии. {-1}$}\) по азимуту \(\text{230}\)\(\text{°}\ ). Рассчитать
ее результирующую скорость, используя точные чертежи в масштабе. 9{-1}$}\). Найдите результирующую скорость лягушки, используя соответствующие вычисления.
Включите грубый набросок ситуации в свой ответ.
{-1}$}\) по азимуту \(\text{230}\)\(\text{°}\ ). Рассчитать
ее результирующую скорость, используя точные чертежи в масштабе. 9{-1}$}\). Найдите результирующую скорость лягушки, используя соответствующие вычисления.
Включите грубый набросок ситуации в свой ответ.
Решение пока недоступно
Mpihlonhle идет в магазин, идя \(\text{500}\) \(\text{m}\) на северо-запад, а затем \(\text{400}\) \(\text{m}\) N \(\text{30}\)\(\text{°}\) E. Определите ее результирующее перемещение, выполнив соответствующие расчеты.
Решение пока недоступно
Как складывать векторы с помощью аналитических методов
Сделать 7 минут чтения
Содержание
- Как складывать векторы с помощью аналитических методов
- Шаг 1. Определите оси x и y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей.
- Шаг 2.
 Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси.
Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси. - Шаг 3. Чтобы получить величину \(R\) равнодействующей, используйте теорему Пифагора:
- Шаг 4. Чтобы получить направление равнодействующей:
- Пример: сложение векторов с помощью аналитических методов
К посмотрите, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рисунок ниже, на котором векторы \(\mathbf{A}\) и \(\mathbf{B}\) складываются для получения результирующего \(\mathbf{R} \).
Векторы \(\mathbf{A}\) и \(\mathbf{B}\) — это два участка пути, а \(\mathbf{R}\) — равнодействующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления \(\mathbf{R}\).
Если \(\mathbf{A}\) и \(\mathbf{B}\) представляют два этапа ходьбы (два перемещения), то \(\mathbf{R}\) является полным перемещением. Человек, совершающий прогулку, оказывается на вершине \(\mathbf{R}. \) Есть много способов попасть в одну и ту же точку. В частности, человек мог пройти сначала в направлении x , а затем в направлении y . Этими путями являются x — и y -компоненты результирующей, \({\mathbf{R}}_{x}\) и \({\mathbf{R}}_{y}\). 9{–1}\left({A}_{y}/{A}_{x}\right)\). Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
\) Есть много способов попасть в одну и ту же точку. В частности, человек мог пройти сначала в направлении x , а затем в направлении y . Этими путями являются x — и y -компоненты результирующей, \({\mathbf{R}}_{x}\) и \({\mathbf{R}}_{y}\). 9{–1}\left({A}_{y}/{A}_{x}\right)\). Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Используйте уравнения \({A}_{x}=A\phantom{\rule{0.25em}{0ex}}\text{cos}\phantom{\rule{0.25em}{0ex}}\theta \ ) и \({A}_{y}=A\phantom{\rule{0.25em}{0ex}}\text{sin}\phantom{\rule{0.25em}{0ex}}\theta \), чтобы найти компоненты. На рисунке ниже это компоненты \({A}_{x}\), \({A}_{y}\), \({B}_{x}\) и \({B} _{у}\). Углы, которые векторы \(\mathbf{A}\) и \(\mathbf{B}\) образуют с x — оси \({\theta}_{\text{A}}\) и \({\theta}_{\text{B}}\) соответственно.
Чтобы добавить векторы \(\mathbf{A}\) и \(\mathbf{B}\), сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы \({\mathbf{A}}_{x}\), \({\mathbf{A}}_{y}\), \({\mathbf{B}}_{x} \) и \({\mathbf{\text{B}}}_{y}\), показанные на изображении.
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси .То есть, как показано на рисунке ниже,
\({R}_{x}={A}_{x}+{B}_{x}\)
и
\({R }_{y}={A}_{y}+{B}_{y}\text{.}\)
Величина векторов \({\mathbf{A}}_{x}\) и \({\mathbf{B}}_{x}\) добавляют, чтобы получить величину \({R}_{x}\) результирующего вектора в горизонтальном направлении. Точно так же величины векторов \({\mathbf{A}}_{y}\) и \({\mathbf{B}}_{y}\) складываются, чтобы получить величину \({R}_{ y}\) результирующего вектора в вертикальном направлении.
Компоненты вдоль одной оси, скажем, оси x , являются векторами вдоль одной линии и, таким образом, могут складываться друг с другом, как обычные числа.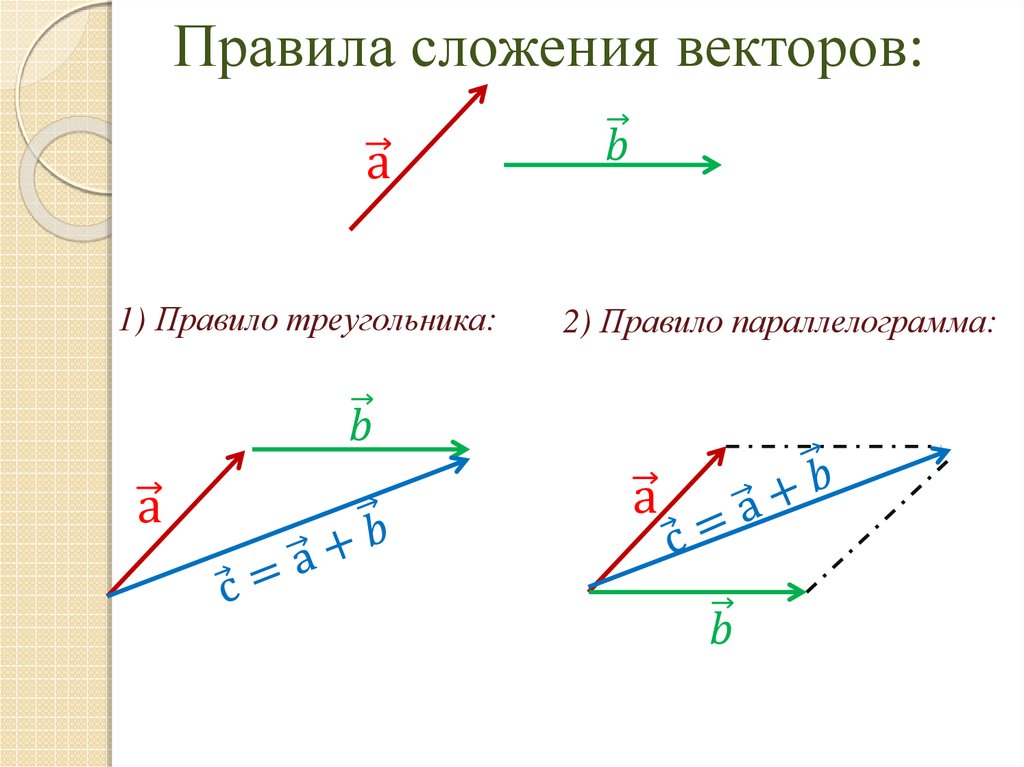 То же самое верно для компонентов вдоль оси y . (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток, а вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.)
То же самое верно для компонентов вдоль оси y . (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток, а вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.)
Итак, разложение векторов на компонентов вдоль общих осей упрощает их добавление. Теперь, когда компоненты \(\mathbf{R}\) известны, можно найти его величину и направление. 9{-1}\left({R}_{y}/{R}_{x}\right)\text{.}\)
Следующий пример иллюстрирует этот метод сложения векторов с использованием перпендикулярных компонентов.
Пример: добавление векторов с использованием аналитических методов
Добавьте вектор \(\mathbf{A}\) к вектору \(\mathbf{B}\), показанному на рисунке ниже, используя перпендикулярные компоненты вдоль x – и и — оси. Оси x и y проходят соответственно с востока на запад и с севера на юг.
Вектор \(\mathbf{A}\) представляет первый этап прогулки, в которой человек идет \(\text{53}\text{.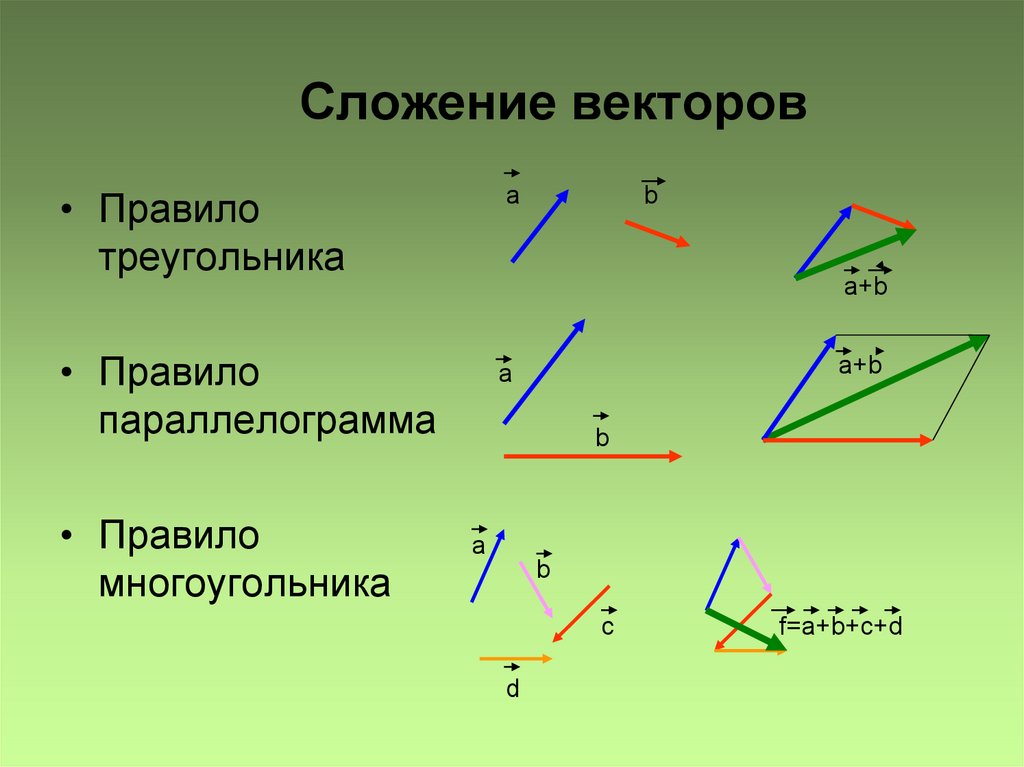 }\text{0 м}\) в направлении \(\ text{20}\text{.}0\text{º}\) к северу от востока. Вектор \(\mathbf{B}\) представляет второй отрезок, смещение \(\text{34}\text{.}\text{0 м}\) в направлении \(\text{63}\text {.}0\text{º}\) к северу от востока.
}\text{0 м}\) в направлении \(\ text{20}\text{.}0\text{º}\) к северу от востока. Вектор \(\mathbf{B}\) представляет второй отрезок, смещение \(\text{34}\text{.}\text{0 м}\) в направлении \(\text{63}\text {.}0\text{º}\) к северу от востока.
Вектор \(\mathbf{A}\) имеет величину \(\text{53}\text{.}\text{0 м}\) и направление \(\text{20}\text{.}0º\ ) к северу от оси x. Вектор \(\mathbf{B}\) имеет величину \(\text{34}\text{.}\text{0 m}\) и направление \(\text{63}\text{.}0\text{ º}\) к северу от оси x. Вы можете использовать аналитические методы для определения величины и направления \(\mathbf{R}\).
Стратегия
Компоненты \(\mathbf{A}\) и \(\mathbf{B}\) вдоль осей x — и y представляют собой ходьбу строго на восток и строго на север, чтобы получить до той же конечной точки. После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, сначала находим компоненты \(\mathbf{A}\) и \(\mathbf{B}\) по осям x — и y . Обратите внимание, что \(A=53,0 м\текст{}\), \({\theta}_{\text{A}}=20,0º\), \(B=34,0 м\текст{}\) и \ ({\ тета } _ {\ текст {B}} = 63,0º \). Мы находим 9{\circ})\)
Обратите внимание, что \(A=53,0 м\текст{}\), \({\theta}_{\text{A}}=20,0º\), \(B=34,0 м\текст{}\) и \ ({\ тета } _ {\ текст {B}} = 63,0º \). Мы находим 9{\circ})\)
\(B_{y} = (34,0\text{m})(0,891) = 30,3\text{m}\)
x — и y -компоненты результирующие, таким образом,
\({R}_{x}={A}_{x}+{B}_{x}=\text{49}\text{.}8 m\text{}+\text {15}\text{.}4 м\text{}=\text{65}\text{.}2 м\text{}\)
и
\({R}_{y}={A }_{y}+{B}_{y}=\text{18}\text{.}1 m+\text{30}\text{.}3 m=\text{48}\text{.}4 m\text{.}\)
Теперь мы можем найти величину равнодействующей по теореме Пифагора: 9{-1}\left(0\text{.}\text{742}\right)=\text{36}\text{.}6º\text{.}\)
Используя аналитические методы, мы видим, что величина \(\mathbf{R}\) равна \(\text{81}\text{.}\text{2 м}\), а его направление равно \(\text{36}\text{.}6º\ ) к северу от востока.
Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов.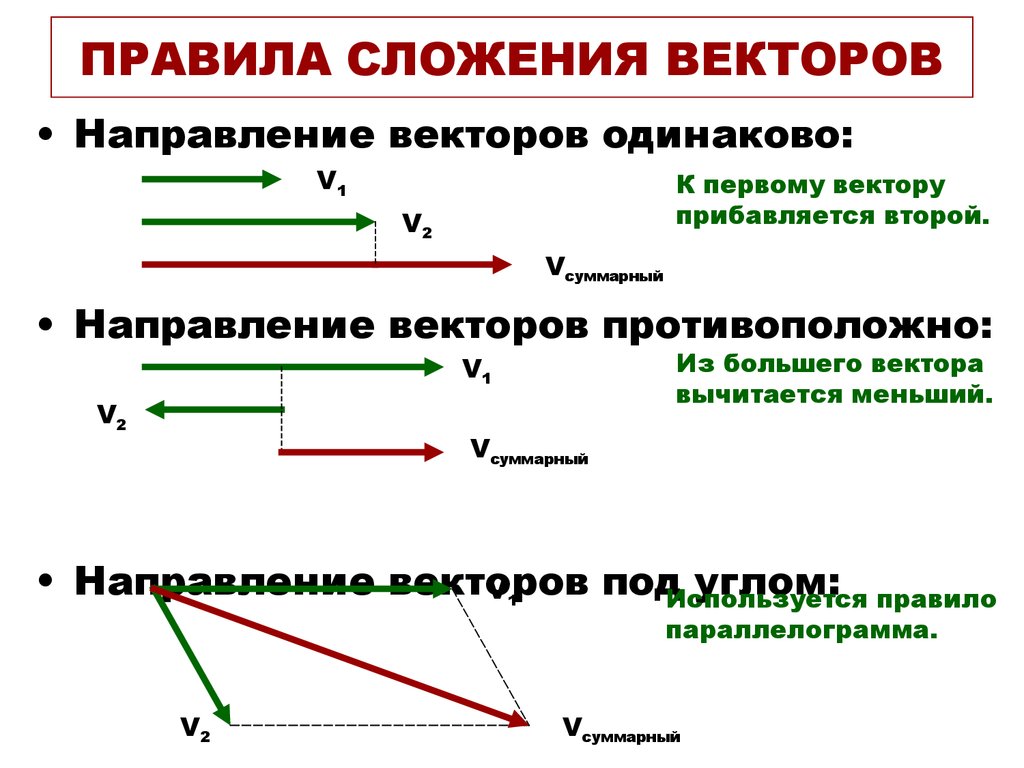 Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. То есть \(\mathbf{A}-\mathbf{B}\equiv \mathbf{A}+\left(\mathbf{–B}\right)\). Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты \(\mathbf{\text{–B}}\) являются минусами компонентов \(\mathbf{B}\). Таким образом, x — и y -компоненты результирующего \(\mathbf{A}-\text{B = R}\) равны
\({R}_{x}={A}_{ x}+\left(–{B}_{x}\right)\)
и
\({R}_{y}={A}_{y}+\left(–{B}_ {y}\right)\)
, а в остальном описанный выше метод идентичен методу сложения. (См. рисунок ниже.)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующая тема, Projectile Motion, — одна из многих, в которой использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.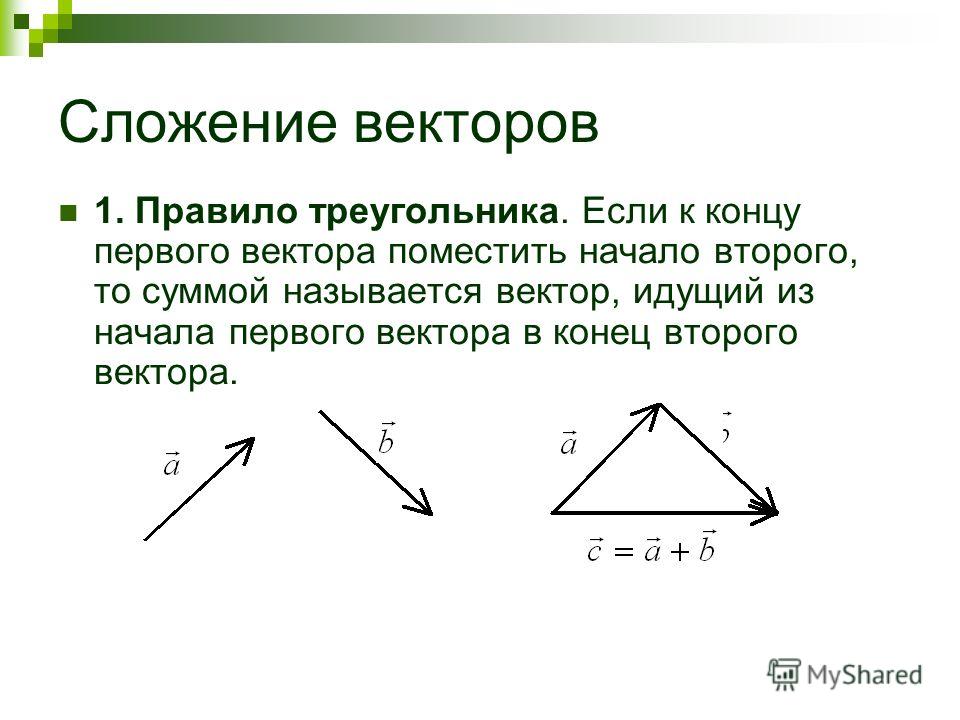
Вычитание двух векторов, показанных ранее. Компоненты \(\mathbf{\text{–B}}\) являются минусами компонентов \(\mathbf{B}\). Метод вычитания такой же, как и для сложения. 9{c}\)
\(a_{b}\)
\(\sqrt{a}\)
\(\sqrt[b]{a}\)
\(\frac{a}{ б}\)
\(\cfrac{a}{b}\)
\(+\)
\(-\)
\(\times\)
\(\div\)
\(\pm\)
\(\cdot\)
\(\amalg\)
\(\ast\)
\(\barwedge\)
\(\bigcirc\)
\( \bigodot\)
\(\bigoplus\)
\(\bigotimes\)
\(\bigsqcup\)
\(\bigstar\)
\(\bigtriangledown\)
\(\bigtriangleup\)
\(\blacklozenge\)
\(\blacksquare\)
\(\blacktriangle\)
\(\
4\) \(\bullet\)
\(\cap\)
\(\cup\)
\(\circ\)
\(\circledcirc\)
\(\dagger\)
\( \ddagger\)
\(\diamond\)
\(\dotplus\)
\(\lozenge\)
\(\mp\)
\(\ominus\)
\(\oplus \)
\(\oslash\)
\(\otimes\)
\(\setminus\)
\(\sqcap\)
\(\sqcup\)
\(\square\)
5
\(\star\)\(\triangle\)
\(\triangledown\)
\(\triangleleft\)
\(\Cap\)
\(\Cup\)
\( \upplus\)
\(\vee\)
\(\veebar\)
\(\клин\)
\(\wr\)
\(\следовательно\)
\(\left ( a \right )\)
\(\left \| a \right \|\)
\(\влево [ a \вправо ]\)
\(\влево \{ a \вправо \}\)
\(\влево \lceil a \вправо \rceil\)
\(\влево \ lfloor a \right \rfloor\)
\(\left ( a \right )\)
\(\vert a \vert\)
\(\leftarrow\)
\(\leftharpoondown\)
\(\leftharpoonup\)
\(\leftrightarrow\)
\(\leftrightharpoons\)
\(\mapsto\)
\(\rightarrow\)
\(\rightharpoondown\)
\( \правый гарпунвверх\)
\(\rightleftharpoons\)
\(\to\)
\(\Leftarrow\)
\(\Leftrightarrow\)
\(\Rightarrow\)
\(\overset{a}{ \leftarrow}\)
\(\overset{a}{\rightarrow}\)
\(\приблизительно \)
\(\asymp\)
\(\cong \)
\(\dashv \)
\(\doteq \)
\(= \)
\(\equiv \)
\(\frown \)
\(\geq \)
\(\geqslant \)
\(\гг\)
\(\gt \)
\(| \)
\(\leq \)
\(\leqslant \)
\(\ll \)
\(\lt \)
\( \models\)
\(\neq \)
\(\ngeqslant \)
\(\ngtr \)
\(\nleqslant \)
\(\nless \)
\(\not \equiv \)
\(\overset{\underset{\mathrm{def}}{}}{=} \)
\(\parallel \)
\(\perp \)
\(\prec \)
\(\preceq \)
\(\sim \)
\(\simeq\)
\(\smile\)
\(\succ\)
\(\succeq\)
\(\vdash\)
\(\in\)
\ (\ni \)
\(\notin \)
\(\nsubseteq \)
\(\nsupseteq \)
\(\sqsubset \)
\(\sqsubseteq \)
\(\ sqsupset \)
\(\sqsupseteq \)
\(\subset \)
\(\subseteq \)
\(\subseteqq \)
\(\supset \)
\supseteq )\(\supseteqq \)
\(\emptyset\)
\(\mathbb{N}\)
\(\mathbb{Z}\)
\(\mathbb{Q}\)
\(\mathbb{R}\)
\(\mathbb{C}\)
\(\alpha\)
\(\beta\)
\(\gamma\)
\(\delta \)
\(\эпсилон\)
\(\дзета\)
\(\эта\)
\(\тета\)
\(\йота\)
\(\каппа\)
\(\lambda\)
\(\mu\)
\(\nu\)
\(\xi\)
\(\pi\)
\(\rho\)
\(\sigma\)
\(\tau\)
\(\upsilon\)
\(\phi\)
\(\chi\)
\(\psi\)
\(\omega\)
\(\Gamma\)
\(\Delta\)
\(\Theta\)
\( \Lambda\)
\(\Xi\)
\(\Pi\)
\(\Sigma\)
\(\Upsilon\)
\(\Phi\)
\(\Psi \)
\(\Омега\)
\((а)\)
\([а]\) 9{} a\)
Редактировать математику с помощью TeX:
Предварительный просмотр математики:
Калькулятор сложения векторов: сложение и вычитание векторов
Этот бесплатный калькулятор сложения векторов позволяет вычислить сумму двух векторов (с кратными или без кратных) в 2D и 3D системы координат.
«Величина, представленная величиной и направлением, известна как вектор»
Графическое представление:На рисунке выше:
- Прямая линия представляет величину вектора
- Направление вектора указано стрелкой
Векторы представлены в виде координат или кратных координат. Ниже приведены формулы векторной суммы, которые используются для отображения комбинации векторов в целом. Давайте пройдем через это!
Без кратных: Система 2D:(a,b) + (d,e) = (a + d, b + e)
Система 3D:(a,b,c) + (d,e,f ) = (a + d, b + e, c + f)
Наш бесплатный калькулятор сложения векторов также учитывает формулы для сложения или вычитания векторов соответственно.
С кратными: Теперь представьте, что вы столкнулись с кратными, которые помогают вам составить сумму векторов более чем в два раза. Просто возьмем пример:
Просто возьмем пример:
Предположим, у вас есть выражение следующим образом:
a+b*2
Приведенное выше выражение означает, что вы, вероятно, добавите 2 копии изображения b к a. С нашим бесплатным калькулятором суммы векторов вы можете легко решать задачи сложения или вычитания векторов с кратными или без них.
Правило «голова к хвосту»:Это еще одно правило сложения векторов, позволяющее считать сумму векторов без координат вообще. Давайте сначала прольем свет на правило:
» Предположим, что у вас есть два вектора a и b. Чтобы добавить их, соедините хвост вектора b с головой вектора a. Теперь возьмем результирующий вектор c так, чтобы его хвост совпадал с хвостом вектора a, а голова с головой вектора b. Этот вектор c представляет собой сумму двух векторов, которые вы также можете определить с помощью этого бесплатного онлайн-вектора 9.0011 ”
Графическое представление: Правило параллелограмма: Помимо правила сложения векторов «голова к хвосту», это еще одно правило, которое считается более надежным, чем все остальные.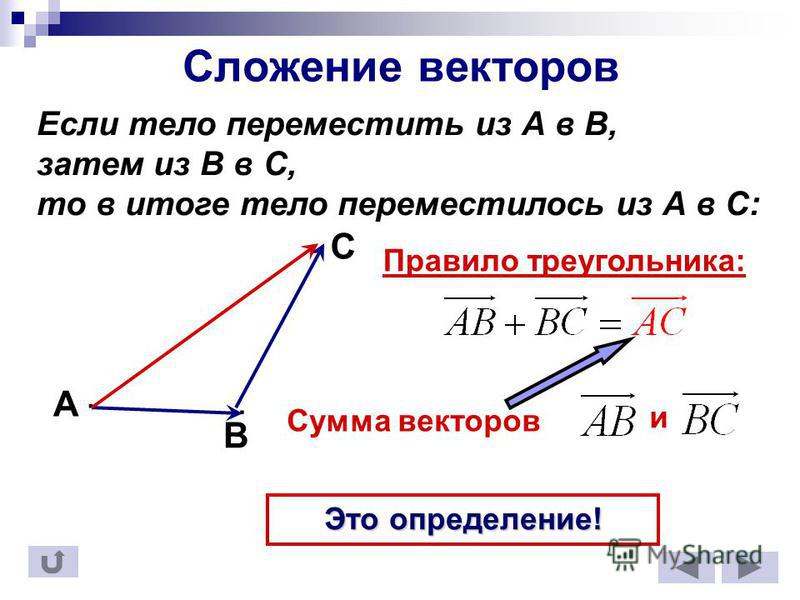 Теперь давайте поясним, что какой бы метод или правило вы ни выбрали для расчетов, этот бесплатный калькулятор сложения векторов сделает это за вас за пару секунд, сохраняя при этом точность. Кроме того, вы также можете использовать наш лучший калькулятор цифр, чтобы получить максимальную точность для любого расчета или числа.
Теперь давайте поясним, что какой бы метод или правило вы ни выбрали для расчетов, этот бесплатный калькулятор сложения векторов сделает это за вас за пару секунд, сохраняя при этом точность. Кроме того, вы также можете использовать наш лучший калькулятор цифр, чтобы получить максимальную точность для любого расчета или числа.
“ Если вы хотите сложить два вектора a и b, соедините их оба так, чтобы их хвосты совпадали друг с другом. Теперь создайте пунктирную линию напротив объединенных векторов. Наконец, диагональ параллелограмма будет представлять собой сумму векторов, которые вы также можете определить с помощью этого бесплатного 2D-калькулятора сложения векторов. ”
Графическое изображение: Как вычитать векторы? Без сомнения, вы можете использовать бесплатный калькулятор вычитания векторов, чтобы вычесть один вектор из другого, но здесь мы также познакомим вас с краткой концепцией.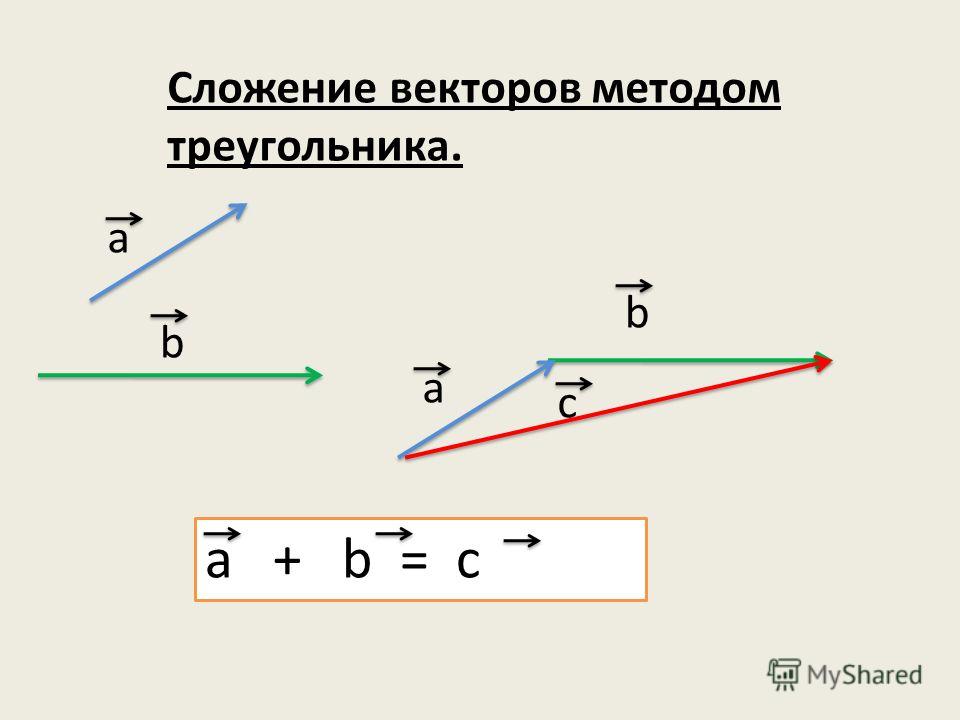
Посмотрите на картинку выше! Что ты видишь? Давайте объясним!
У нас есть два вектора a и -a , где a — положительный вектор, а -a — отрицательный вектор.
«Отрицательный вектор — это вектор, имеющий ту же величину, что и исходный вектор, но направление, противоположное ему»
Теперь, когда вы хотите вычесть два вектора, это означает, что вам нужно добавить исходный вектор к его противоположному вектору. Для векторов a и -a имеем:
a-a = a+(a-)
Вы также можете легко сложить два вектора с помощью этого калькулятора вычитания векторов.
Как сложить или вычесть два вектора?Давайте разберем пример, чтобы лучше понять концепцию векторной суммы или минус!
Пример № 01:
Как сложить векторы, указанные ниже:
Вектор A = (1, 4)
Вектор B = (6, 8)
Решение:
0 0 формула сложения 904:590 вектора Вектор А + Вектор В = (1, 4) + (6, 8)Вектор А + Вектор В = (1+6, 4+8)
Вектор А + Вектор В = (7, 14)
Для мгновенной проверки вы можете доверять расчетам нашего бесплатного векторного сумматора.
Давайте узнаем, как можно использовать этот калькулятор сложения векторов для сложения и вычитания двух векторов с кратными или без них.
Ввод:
- Из первого выпадающего списка выберите размерность векторов
- После этого выберите тип сложения или вычитания, который вы хотите выполнить (с множителями или без них)
- Теперь запишите координаты векторов в соответствующие поля
- Наконец, нажмите кнопку расчета
Вывод:
Бесплатный графический калькулятор сложения векторов выполняет следующие вычисления:
- Сумма векторов
- Вычитание векторов
- Калькулятор добавления векторов также отображает пошаговые расчеты для лучшего понимания решения
В реальной жизни существует огромное количество векторных приложений. Просто рассмотрим пример лодки и ее двигателя. Когда двигатель прикладывает силу в одном конкретном направлении для движения лодки, приливы будут прилагать силу, противоположную направлению движения лодки. И чтобы понять фактическое направление этих сил, вы можете использовать другой калькулятор векторной проекции, чтобы получить точные результаты.
Просто рассмотрим пример лодки и ее двигателя. Когда двигатель прикладывает силу в одном конкретном направлении для движения лодки, приливы будут прилагать силу, противоположную направлению движения лодки. И чтобы понять фактическое направление этих сил, вы можете использовать другой калькулятор векторной проекции, чтобы получить точные результаты.
В области инженерных наук у вектора действительно есть важная теория. Это помогает найти векторную сумму и вычитание для большинства физических или механических величин, таких как сила, работа, крутящий момент и т. д., и теперь вы также можете использовать этот бесплатный калькулятор векторной суммы для анализа добавления таких векторных параметров в кратчайшие сроки без снижение точности результатов.
Что вы подразумеваете под величиной вектора? Проще говоря, величина вектора — это длина вектора от начальной до конечной точки.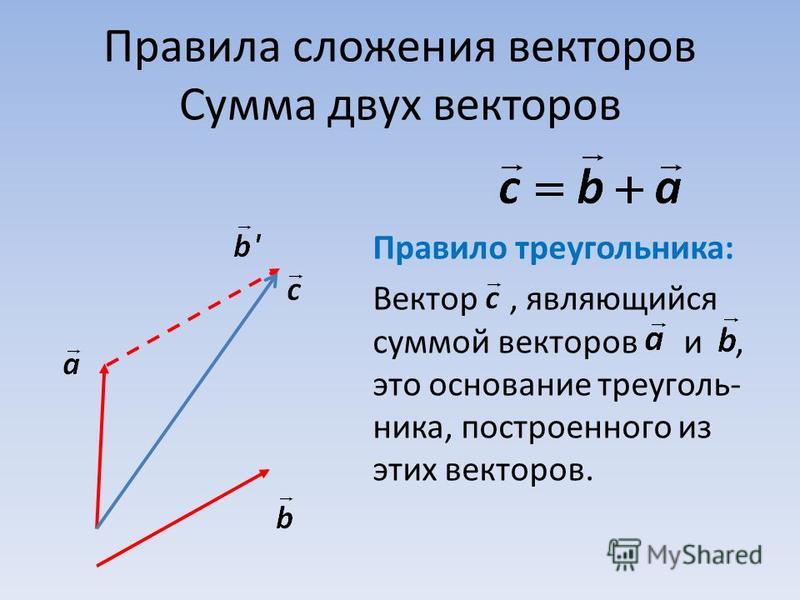


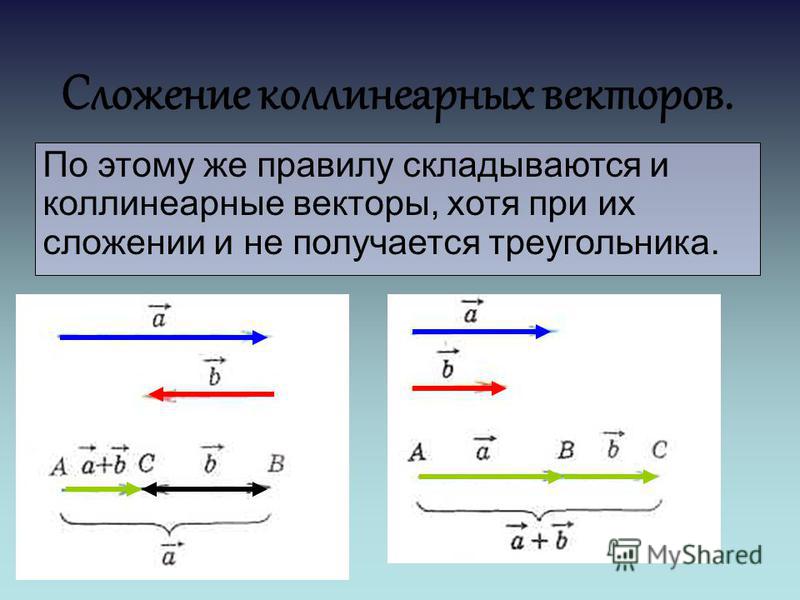 Например, для ситуаций, связанных со смещением в западном направлении.
и восток, вы можете выбрать запад в качестве положительного направления. В этом случае смещения на восток отрицательны.
Например, для ситуаций, связанных со смещением в западном направлении.
и восток, вы можете выбрать запад в качестве положительного направления. В этом случае смещения на восток отрицательны. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси.
Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси.