Как сложить три вектора из одной точки — kak.manesu.com
§ 2. Сложение векторов.
Известные из механики законы сложения векторных величин (сил, ускорений, скоростей) служат основанием следующего определения сложения векторов. Суммой двух векторов А и В называют такой третий вектор С, выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются слагаемые векторы (рис. 94), и обозначают:
Рис. 94.
Если два вектора А и В после приведения их к общему началу лежат на одной прямой, то сумма их С есть по определению вектор, длина которого равна сумме длин слагаемых векторов и направление совпадает с направлением этих векторов, если последние одинаково направлены; если же слагаемые векторы направлены в разные стороны, то сумма их С есть вектор, длина которого равна разности длин слагаемых векторов и направление совпадает с направлением вектора, имеющего большую длину. В случае равенства длин противоположно направленных векторов их сумма еегь особый «вектор», длина которого равна нулю. Такой вектор называют нулевым вектором и обозначают символом 0.
Посмотрим теперь, будет ли сложение векторов удовлетворять основным законам, которым подчиняется сложение чисел. Для сложения чисел мы имеем два основных закона.
1. Закон переместительности.
т. е. сумма не зависит от порядка слагаемых.
2. Закон сочетательности:
т. е. чтобы прибавить сумму, можно прибавить последовательно каждое слагаемое.
Первый закон, очевидно, удовлетворяется, что непосредственно вытекает из определения сложения векторов:
Чтобы перейти ко второму закону (сочетательности), следует предварительно выяснить понятие суммы нескольких слагаемых.
Рис. 95.
С этой целью упростим сначала самое построение суммы двух векторов. Мы условились считать равными векторы, имеющие одинаковую длину, параллельные и одинаково направленные. В силу этого векторы ОВ и АС (рис. 94) равны между собой. Отсюда вытекает такое правило сложения двух векторов: в конце первого слагаемого строим второе слагаемое. Вектор, замыкающий эту ломаную, есть сумма. Начало его совпадает с началом первого слагаемого, а конец — с концом второго.
Это правило треугольника нетрудно теперь распространить на любое число слагаемых. Пусть, например, требуется найти сумму трех векторов А, В и С:
причем под их суммой мы будем подразумевать результат последовательного прибавления к А сначала В и затем С. Другими словами, если
то согласно определению будет:
По предыдущему правилу треугольника строим сначала сумму  (рис. 95), т. е. в точке
(рис. 95), т. е. в точке  строим вектор
строим вектор  и соединяем
и соединяем
точку О с точкой  Затем к полученной сумме прибавляем вектор С, т. е. в конце ОЕ строим вектор ED — Q, и соединяем точку О с точкой
Затем к полученной сумме прибавляем вектор С, т. е. в конце ОЕ строим вектор ED — Q, и соединяем точку О с точкой 
Тогда
Отсюда вытекает такое правило сложения векторов: чтобы построить сумму любого числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго построить третий и т. д. Вектор, замыкающий полученную ломаную линию, представляет искомую сумму. Начало его совпадает с началом первого слагаемого, а конец — с концом последнего.
Рис. 96.
В случае сложения трех векторов, не параллельных одной плоскости, сумму их можно получить и другим способом. Пусть векторы А, В, С приведены к общему началу 
Построим на этих векторах параллелепипед (рис. 96). По предыдущему правилу
но отрезок OD является диагональю параллелепипеда, таким образом сумма данных векторов равна вектору-диагонали параллелепипеда, ребрами которого являются слагаемые векторы.
Рис. 97.
Заметим, что если бы слагаемые векторы были параллельны одной плоскости (такие векторы называются компланарными), то мы не могли бы построить на них параллелепипед.
Теперь перейдем к доказательству закона сочетательности:
По правилу сложения векторов (рис. 97)
но тому же вектору OD равна и сумма  так как
так как
Итак, равенство (3) доказано.
Из переместительного и сочетательного законов вытекает, что при нахождении суммы любого числа векторов можно складывать данные векторы в произвольном порядке.
Заметим, что по отношению к обычной сумме чисел существуют еще различные законы монотонности — о сравнительной величине слагаемых и суммы, как, например, сумма положительных слагаемых больше каждого из слагаемых. Все эти законы не имеют смысла для суммы векторов, потому что понятия «больше» и «меньше» неприложимы к векторам.
Рис. 98.
Source: scask.ru
Читайте также
Сложение и вычитание векторов. Видеоурок. Геометрия 8 Класс
Тема: Векторы
Урок: Сложение и вычитание векторов
На предыдущем уроке мы определили понятие вектора, сказали, какие векторы называются равными, коллинеарными, сонаправленными и противонаправленными.
Теперь пусть задано два вектора – вектора  и
и  . Найдем сумму этих двух векторов
. Найдем сумму этих двух векторов 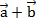
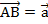 . Из точки В отложим вектор
. Из точки В отложим вектор 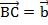 . Тогда вектор
. Тогда вектор 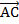 называют суммой заданных векторов:
называют суммой заданных векторов: 
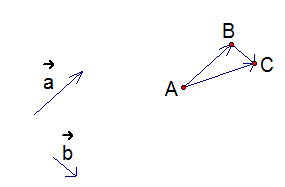
Рис. 1
Данное определение можно объяснить так: пусть был задан груз, и сначала на него подействовала сила  – он переместился из точки А в точку В, после этого подействовала сила
– он переместился из точки А в точку В, после этого подействовала сила 
Таким образом, мы получили определение суммы двух векторов – правило треугольника.
Правило треугольника
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
Можно провести аналогию с числами. Мы ввели понятие числа, научились складывать числа, определили законы сложения и так далее. Теперь мы ввели понятие вектора, научились находить равные вектора, складывать вектора. Теперь нужно определить законы сложения.
Законы сложения векторов
Для любых векторов  ,
,  и
и  справедливы следующие равенства:
справедливы следующие равенства:
 – переместительный закон.
– переместительный закон.
Доказательство: отложим из точки сначала вектор 
 , получаем точку С и вектор
, получаем точку С и вектор  .
.Теперь отложим из точки А сначала вектор  получим точку В, из нее отложим вектор
получим точку В, из нее отложим вектор
 .
.Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
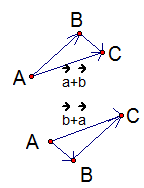
Рис. 2
Откладываем из точки А вектор 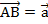 и вектор
и вектор  . Из точки В откладываем вектор
. Из точки В откладываем вектор 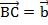 , вектора
, вектора  и
и  равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.  , таким образом, мы доказали переместительный
, таким образом, мы доказали переместительный
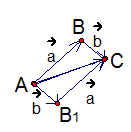
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
 – сочетательный закон;
– сочетательный закон;
Из произвольной точки А отложим вектор  , прибавим к нему вектор
, прибавим к нему вектор  , получим их сумму
, получим их сумму 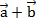 . К этой сумме прибавим вектор
. К этой сумме прибавим вектор  , получим результат
, получим результат 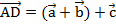 (см. Рис. 4).
(см. Рис. 4).
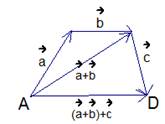
Рис. 4
В правой части выражения мы сначала получили сумму векторов  , после прибавили ее к вектору
, после прибавили ее к вектору  и получили результат:
и получили результат:  (см. Рис. 5).
(см. Рис. 5).
Таким образом, мы доказали сочетательный закон сложения векторов.
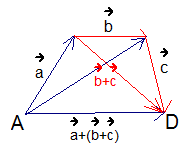
Рис. 5
Правило многоугольника
Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов (см. Рис. 6).

Рис. 6
По аналогии с действительными числами после того, как мы научились их складывать, нужна обратная операция – вычитание.
Пусть задано два вектора – векторы  и
и  . Найдем разность этих двух векторов
. Найдем разность этих двух векторов  .
.
Определение
Разностью двух векторов  и
и  называют такой третий вектор, сумма которого с вектором
называют такой третий вектор, сумма которого с вектором  равна вектору
равна вектору  .
.
Если задан вектор  , то можно построить противоположный ему вектор
, то можно построить противоположный ему вектор  , который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор:
, который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор:  . Таким образом,
. Таким образом,  .
.
Отложим из произвольной точки вектор  , из его конца отложим вектор
, из его конца отложим вектор  , получим в результате вектор
, получим в результате вектор  (см. Рис. 7).
(см. Рис. 7).
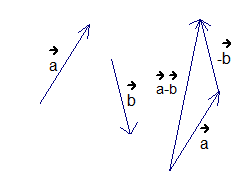
Рис. 7
Рассмотрим вычитание векторов на параллелограмме. Из точки А отложим векторы 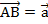 и
и  . Из точек В и D отложим векторв
. Из точек В и D отложим векторв 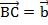 и
и  соответственно. Диагональ АС – это сумма векторов
соответственно. Диагональ АС – это сумма векторов  и
и  :
:  . Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору
. Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору  вектор
вектор 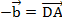 , получим вектор
, получим вектор  (см. Рис. 8).
(см. Рис. 8).

Рис. 8
Итак, на данном уроке мы вывели правила сложения и вычитания векторов при помощи треугольника и параллелограмма, сформулировали законы сложения векторов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Emomi.com (Источник).
- Prosto-o-slognom.ru (Источник).
- Изучение математики онлайн (Источник).
Домашнее задание
- Задание 1: дан треугольник
 , найдите сумму векторов:
, найдите сумму векторов:  и
и  ;
;  и
и  ;
;  и
и  ;
;  и
и  .
. - Задание 2: турист прошел 20 км на восток из города А в город В, а потом 30 км на восток в город С. Выбрав подходящий масштаб, начертите векторы
 и
и  Равны ли векторы
Равны ли векторы  и
и  ?
? - Задание 3: начертите попарно неколлинеарные векторы
 ,
,  и
и  и постройте векторы
и постройте векторы  ,
,  ,
,  .
.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькуляторВ механике существуют два типа величин:
Рассмотрим сначала алгебраический подход к сложению векторов. Покоординатное сложение векторов. Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.): Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле: В двумерном случае все абсолютно анологично, просто отбрасываем третью координату. Теперь перейдем к геометрическому смыслу сложения двух векторов: . При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Процедура сложения векторов по правилу параллелограмма заключается в следующем:
Правило треугольника Сложение векторов по правилу треугольника заключается в следующем:
Тригонометрический способ |
Законы сложения векторов. Правило параллелограмма
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Законы сложения векторов. Правило параллелограмма
Теорема
Доказательство
Дано:  ,
,  и
и 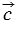 .
.
Доказать: 10.  +
+  =
=  +
+  ; 20. (
; 20. ( +
+  ) +
) + 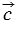 =
=  + (
+ ( +
+ 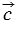 ).
).
Доказательство:
10. Пусть векторы  и
и  коллинеарны.
коллинеарны.
От произвольной точки А отложим векторы 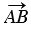 =
=  и
и 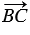 =
=  , т.е. векторы
, т.е. векторы  и
и  будут лежать на одной прямой и на той же прямой от точки А отложим векторы =
будут лежать на одной прямой и на той же прямой от точки А отложим векторы =  и
и 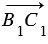 =
=  .
.
 +
+  =
=  ,
,  +
+  =
= 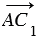 , тогда
, тогда 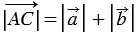 ,
, 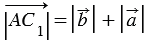 , при этом
, при этом 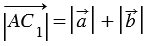 , так как модуль вектора — это длина отрезка, следовательно,
, так как модуль вектора — это длина отрезка, следовательно, 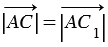 . Поэтому точки С и С1 совпадают, значит,
. Поэтому точки С и С1 совпадают, значит,  =
= 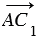 (по определению равных векторов), значит,
(по определению равных векторов), значит,  +
+  =
=  +
+  .
.
Пусть теперь векторы  и
и  не коллинеарны.
не коллинеарны.
От произвольной точки А отложим векторы 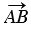 =
=  и =
и =  и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы
и на этих векторах построим параллелограмм АВСD. Противоположные стороны ВС и АD параллелограмма равны, при этом векторы 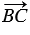 и сонаправлены, следовательно,
и сонаправлены, следовательно, 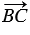 = =
= =  (по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы и
(по определению равных векторов), также DC = АВ (противоположные стороны параллелограмма) и векторы и 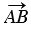 сонаправлены, следовательно, =
сонаправлены, следовательно, = 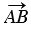 =
=  .
.
По правилу треугольника  =
= 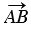 +
+ 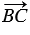 =
=  +
+  . Аналогично
. Аналогично  = + =
= + =  +
+  , поэтому
, поэтому  +
+  =
=  +
+  .
.
20. От произвольной точки А отложим вектор 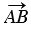 =
=  , от точки В — вектор
, от точки В — вектор 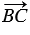 =
=  , а от точки С — вектор =
, а от точки С — вектор = 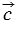 .
.
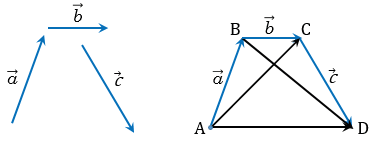
Применяя правило треугольника, получим:
( +
+  ) +
) + 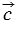 = (
= (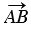 +
+ 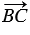 ) + =
) + =  + = ,
+ = ,
 + (
+ ( +
+ 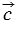 ) =
) = 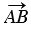 + (
+ (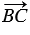 + ) =
+ ) = 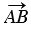 +
+ 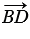 = .
= .
Следовательно, ( +
+  ) +
) + 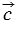 =
=  + (
+ ( +
+ 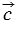 ).
).
Теорема доказана.
Правило параллелограмма
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 762, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 763, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 765, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 770, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 784, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 785, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 808, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 906, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 907, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Сложение векторов — PhysBook
Скаляры можно складывать, умножать и делить так же, как обычные числа.
Поскольку вектор характеризуется не только числовым значение, но и направлением, сложение векторов не подчиняется правилам сложения чисел. Например, пусть длины векторов a = 3 м, b = 4 м, тогда a + b = 3 м + 4 м = 7 м. Но длина вектора \(\vec c = \vec a + \vec b\) не будет равна 7 м (рис. 1).
Рис. 1.Для того, чтобы построить вектор \(\vec c = \vec a + \vec b\) (рис. 2), применяются специальные правила сложения векторов.
Рис. 2.А длину вектора суммы \(\vec c = \vec a + \vec b\) определяют по теореме косинусов \(c = \sqrt{a^2+b^2-2a\cdot b\cdot \cos \alpha}\), где \(\alpha\,\) – угол между векторами \(\vec a\) и \(\vec b\).
Правило треугольника
В зарубежной литературе этот метод называют «хвост к голове».
Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) (рис. 3, а) нужно переместить вектор \(\vec b\) параллельно самому себе так, чтобы его начало совпадало с концом вектора \(\vec a\) (рис. 3, б). Тогда их суммой будет вектор \(\vec c\), начало которого совпадает с началом вектора \(\vec a\), а конец — с концом вектора \(\vec b\) (рис. 3, в).
а б в Рис. 3.Результат не поменяется, если перемещать вместо вектора \(\vec b\) вектор \(\vec a\) (рис. 4), т.е. \(\vec b + \vec a = \vec a + \vec b\) (свойство коммутативности векторов).
а б в Рис. 4. <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-treug-1.swf</swf> «Правило треугольников» Пример 1 Увеличить Flash <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-treug-2.swf</swf> «Правило треугольников» Пример 2 Увеличить Flash Рис. 5.При помощи правила треугольника можно сложить два параллельных вектора \(\vec a\) и \(\vec b\) (рис. 6, а) и \(\vec a\) и \(\vec d\) (рис. 7, а). Суммы этих векторов \(\vec c = \vec a + \vec b\) и \(\vec f = \vec a + \vec d\) изображены на рис. 6, б и 7, б. Причем, модули векторов \(c = a + b\) и \(f=\left|a-d\right|\).
а б Рис. 6. а б Рис. 7.Правило треугольника можно применять при сложении трех и более векторов. Например, \(\vec c = \vec a_1 + \vec a_2 +\vec a_3 +\vec a_4\) (рис. 8).
Рис. 8.Правило параллелограмма
Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) (рис. 9, а) нужно переместить их параллельно самим себе так, чтобы начала векторов \(\vec a\) и \(\vec b\) находились в одной точке (рис. 9, б). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 9, в). Тогда суммой \(\vec a+ \vec b\) будет вектор \(\vec c\), начало которого совпадает с общим началом векторов, а конец — с противоположной вершиной параллелограмма (рис. 9, г).
а б в г Рис. 9. <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-paral-1.swf</swf> «Правило параллепипеда» Увеличить Flash Рис. 10.Вычитание векторов
Для того чтобы найти разность двух векторов \(\vec a\) и \(\vec b\) (рис. 11) нужно найти вектор \(\vec c = \vec a + \left(-\vec b \right)\) (см. Умножение вектора на скаляр) по правилу треугольника (рис. 12) или по правилу параллелограмма (рис. 13).
Рис. 11 а б в Рис. 12. а б б в Рис. 13.Разложение вектора по трём некомпланарным векторам. Задачи
На данном уроке мы напомним основные определения и рассмотрим типовые задачи на компланарные векторы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Тема: Векторы в пространстве
Урок: Разложение вектора по трем некомпланарным векторам. Задачи
Определение:
Вектором называется направленный отрезок. У вектора  точка А – начало вектора, точка В – конец.
точка А – начало вектора, точка В – конец.
Для вектора важна не только длина, но и направление.
Определение:
Коллинеарными называют векторы, принадлежащие одной и той же или параллельным прямым.
Коллинеарные векторы могут быть сонаправленными и противонаправленными.
Определение:
Равными называют коллинеарные сонаправленные векторы, длины которых равны.
Любой вектор можно единственным образом отложить от произвольной точки.
Для сложения векторов применяются правила треугольника, параллелограмма, многоугольника и параллелепипеда.
При умножении вектора на положительное число его длина умножается на это число, а направление остается неизменным. При умножении вектора на отрицательное число его длина умножается на это число, а направление меняется на противоположное.
Новым для векторов в пространстве относительно векторов на плоскости является понятие компланарности.
Определение:
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам (рис. 1, 2):

Рис. 1. Векторы на плоскости

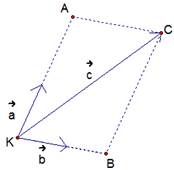
Рис. 2. Разложение вектора через два неколлинеарных
Данный факт легко доказывается. Пусть 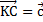 . Из точки С проводим прямую CB, параллельно вектору
. Из точки С проводим прямую CB, параллельно вектору 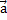 . Получаем вектор
. Получаем вектор  , коллинеарный вектору
, коллинеарный вектору 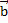 . Аналогично из точки С проводим прямую CА, параллельно вектору
. Аналогично из точки С проводим прямую CА, параллельно вектору 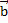 . Получаем вектор
. Получаем вектор 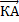 , коллинеарный вектору
, коллинеарный вектору 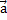 . Это означает, что существуют такие два числа х и у, причем единственные, что:
. Это означает, что существуют такие два числа х и у, причем единственные, что:
Сумма нескольких векторов | Формулы и расчеты онлайн
Сумма нескольких векторов а1, а2, а3, … , аn, это вектор, получающийся после ряда последовательных сложений: к вектору а1 прибавляется вектор а2, к полученному вектору прибавляется вектор а3 и т.д.
Из определения вытекает такое построение

Сумма нескольких векторов
Правило многоугольника или правило цепи
Из произвольного начала О строим вектор ОА1 = а1, из точки А1, как из начала, строим вектор А1А2 = а2, из точки А2 строим вектор А2А3 = а3 и т.д. Вектор ОАn (на рисунке n = 6) есть сумма векторов а1, а2, … , аn.
Сумма векторов а1, а2, а3, а4, а5, а6 обозначается
\[ \vect{a_1}+\vect{a_2}+\vect{a_3}+\vect{a_4}+\vect{a_5}+\vect{a_6} \]
Свойство сочетательности
Слагаемые векторы можно группировать как угодно.
Так, если найти сначала сумму векторов
\[ \vect{a_2}+\vect{a_3}+\vect{a_4}+\vect{a_5}+\vect{a_6} = \vect{A_1 A_6} \]
и к ней прибавить вектор а1 (ОА1), то получим то же вектор:
\[ \vect{a_1}+(\vect{a_2}+\vect{a_3}+\vect{a_4}+\vect{a_5}+\vect{a_6}) =
= \vect{a_1}+\vect{a_2}+\vect{a_3}+\vect{a_4}+\vect{a_5}+\vect{a_6} \]
Правило параллелепипеда
Если три вектора а, b, с после приведения к общему началу не лежат в одной плоскости, то сумму а+b+c можно найти таким построением:

Правило параллелепипеда — Сумма нескольких векторов
Из любого начала О строим векторы ОА = а, ОВ = b, ОС = с, на отрезках ОА, ОВ, ОС, как на ребрах, строим параллелепипед. Вектор диагонали OD есть сумма векторов a, b, и c (так как ОА = а, АК = ОВ = b, KD = OC = c и OD = OA + AK + KD).
В помощь студенту
Сумма нескольких векторов |
стр. 172 |
|---|


 , найдите сумму векторов:
, найдите сумму векторов: 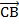 ;
; 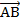 и
и  и
и  Равны ли векторы
Равны ли векторы  и
и  ,
, 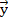 и
и  и постройте векторы
и постройте векторы  ,
,  ,
, 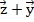 .
.