Векторы 9 класс онлайн-подготовка на Ростелеком Лицей
Определение вектора
Жизнь бесконечна, но для того, чтобы решать конкретные практические задачи, мы пытаемся приблизить реальность моделью с интересующей нас степенью точности. Описывать человека можно очень долго, но если нужно сшить костюм, то описание сузится до набора чисел – рост, длина рукавов, обхват груди и т. д. Похожая ситуация и с погодой – про нее можно рассказывать с любой степенью подробности. Но в прогнозе погоды обычно ограничиваются несколькими важными параметрами: температура воздуха, скорость ветра, атмосферное давление и т. д.
В рассмотренных примерах для описания объектов выбранной модели мы должны измерить характеристики этих объектов (например, рост человека или температуру воздуха). В некоторых случаях достаточно измерить одну величину. Так, покупая на рынке яблоки, мы их только взвешиваем. Нас не интересует диаметр яблок или их температура.
Но в примерах с костюмом или погодой измерением одной величины не обойтись. Т. е. один объект может описываться набором значений нескольких характеристик (двух, трех и т. д.). Такая ситуация нам уже встречалась и в математике: треугольник мы однозначно определяли длинами трех сторон или длинами двух сторон и угла между ними.
Т. е. один объект может описываться набором значений нескольких характеристик (двух, трех и т. д.). Такая ситуация нам уже встречалась и в математике: треугольник мы однозначно определяли длинами трех сторон или длинами двух сторон и угла между ними.
Ваш друг рассказал, что выехал из Москвы и проехал 170 км. Где он может находиться? Понятно, что его путь составил 170 км. Но куда он переместился? Он мог оказаться около Твери, Калуги, Тулы, Рязани, Владимира и т. д. Если бы речь шла об идеальной ситуации – движении в чистом поле, то он мог бы оказаться в любой точке окружности с центром в Москве и радиусом 170 км (см. рис. 1). Конкретное местоположение зависит от выбранного направления.
Рис. 1. Окружность с центром в Москве и радиусом 170 км
Перемещение на юг приведет нас в Тулу, а на северо-запад – в Тверь. Соединим Москву с Тулой отрезком и отметим стрелкой направление (см. рис. 2). Такой направленный отрезок называется перемещением (вспомните уроки физики: это направленный отрезок, соединяющий начало и конец движения).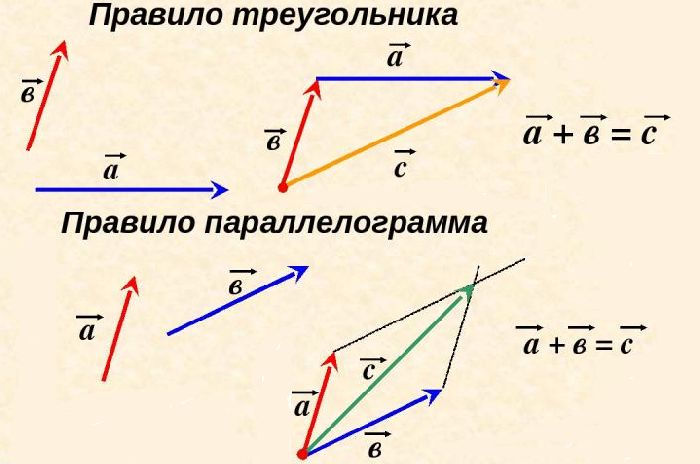
Рис. 2. Перемещение Москва – Тула
Теперь Москву с Тверью тоже соединим направленным отрезком (см. рис. 3). Это другое перемещение. Длины этих перемещений равны. Но направления у них были разные. Поэтому сами перемещения тоже являются разными.
Рис. 3. Перемещения Москва – Тула и Москва – Тверь одинаковы по длине, но имеют разные направления
Понятно, что если одинаковыми будут только направления, но длины перемещений окажутся разными, то и сами перемещения тоже окажутся разными. Посмотрите на перемещения Москва – Владимир и Москва – Нижний Новгород. У них практически одинаковые направления, но у второго в два раза больше длина.
Рис. 4. Перемещения Москва – Владимир и Москва – Нижний Новгород имеют практически одинаковые направления, но разные длины
Рассмотрим два последовательных перемещения: Москва – Владимир и Владимир – Рязань. Откуда и куда мы в итоге переместились? Из Москвы в Рязань. Два последовательных перемещения дают нам новое (см. рис. 5). И, как видим, длина итогового перемещения здесь не равна сумме длин исходных.
рис. 5). И, как видим, длина итогового перемещения здесь не равна сумме длин исходных.
Рис. 5. Два последовательных перемещения Москва – Владимир и Владимир – Рязань дают новое – Москва – Рязань
Т. е. для итогового перемещения не важна траектория, по которой мы двигались. Важны начальная и конечная точки. Например, последовательные перемещения Москва – Владимир – Калуга – Рязань – Тула эквивалентны простому перемещению Москва – Тула (см. рис. 6).
Рис. 6. Перемещение Москва – Владимир – Калуга – Рязань – Тула эквивалентно перемещению Москва – Тула
Рассмотрим еще один пример. Два человека несут сумку. Каждый из них прикладывает определенную силу к ручкам сумки. Результат их взаимодействия будет зависеть как от величины сил, так и от их направления (см. рис. 7).
Рис. 7. Результат взаимодействия людей, которые несут сумку, зависит и от величины сил, и от их направления
Силу, как и перемещение, удобно изображать направленным отрезком: чем длиннее отрезок, тем больше численное значение силы; направление действия силы совпадает с направлением отрезка.
И таких величин, которые можно описать, используя числовое значение и направление, достаточно много. Кроме перемещения и силы, таким образом можно описывать, например, скорость и ускорение тела .
Ну а раз есть целый класс подобных объектов, то для их описания был придуман удобный инструмент, который назвали вектором. Величины, которые описываются с помощью векторов, как вы уже слышали на уроках физики, называются векторными величинами.
Сформулируем строгое определение: вектор – это направленный отрезок, т. е. отрезок, для которого указаны начало и конец (задано направление).
Изображается в виде отрезка со стрелкой на конце. Обозначается либо большими буквами со стрелкой наверху: , либо одной маленькой тоже со стрелкой наверху: (см. рис. 8).
Рис. 8. Обозначения вектора
Часто вектор изображают без буквенных обозначений (см. рис. 9):
Рис. 9. Вектор без буквенных обозначений
Мы ввели вектор как инструмент для описания перемещения, силы, скорости и т.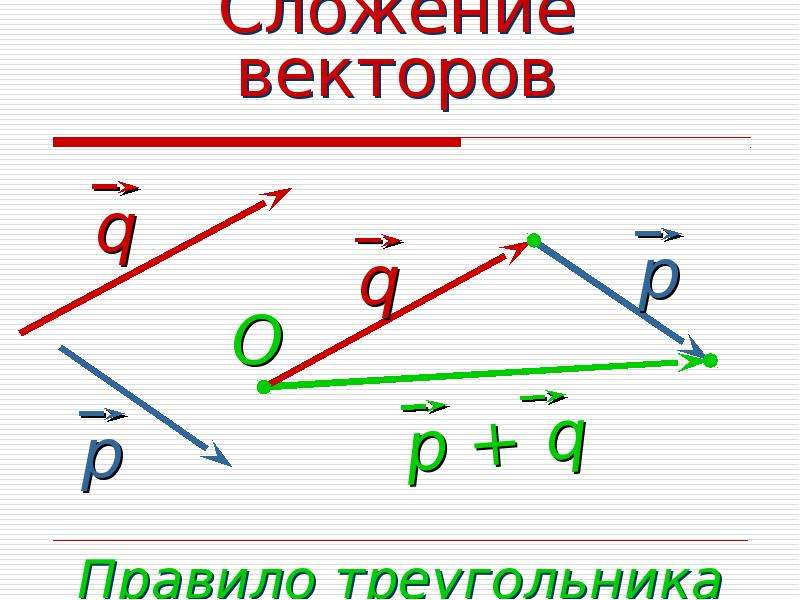 д. Но для решения различных задач нужно отработать технику работы с векторами. Мы уже сталкивались с такой ситуацией – ввели натуральные числа как удобный инструмент описания количества, а затем начали изучать технику работы с числами – сложение, умножение и т. д.
д. Но для решения различных задач нужно отработать технику работы с векторами. Мы уже сталкивались с такой ситуацией – ввели натуральные числа как удобный инструмент описания количества, а затем начали изучать технику работы с числами – сложение, умножение и т. д.
Равные векторы
Что можно делать с векторами? Мы уже рассмотрели несколько примеров задач, в которых необходимо сложить перемещения или силы, следовательно, нужно научиться складывать векторы. В дальнейшем мы поговорим и о других операциях, которые можно делать с векторами, а также о различных свойствах векторов, т. е. мы переходим непосредственно к технике работы с векторами.
Итак, пусть дан вектор (см. рис. 10):
Рис. 10. Вектор
Длину отрезка назовем модулем вектора или просто длиной вектора. Обозначение такое же, как для модуля числа . Модуль вектора соответствует численному значению физической величины: длине перемещения (расстоянию между начальной и конечной точками), величине силы и т. д.
д.
Модуль вектора можно найти так же, как и длину отрезка, если задан масштаб (см. рис. 11). Например, , (выбираем в качестве единицы измерения длины клетку). Модуль вектора можем найти, используя теорему Пифагора, как гипотенузу соответствующего прямоугольного треугольника: .
Рис. 11. Длину вектора можно найти, если задан масштаб
Как сравнивать длины векторов понятно – в этом смысле задача сравнения сводится к задаче сравнения длин соответствующих отрезков, которую мы уже умеем решать. А как сравнивать (и можно ли вообще это делать) направления разных векторов?
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (см. рис. 12). Векторы , , коллинеарны друг другу. Вектор не коллинеарен ни одному другому. Если совсем просто, то коллинеарность – это параллельность векторов.
Рис. 12. Коллинеарные векторы , ,
Коллинеарные векторы могут быть сонаправлены, как и , или противоположно направлены, как и или и .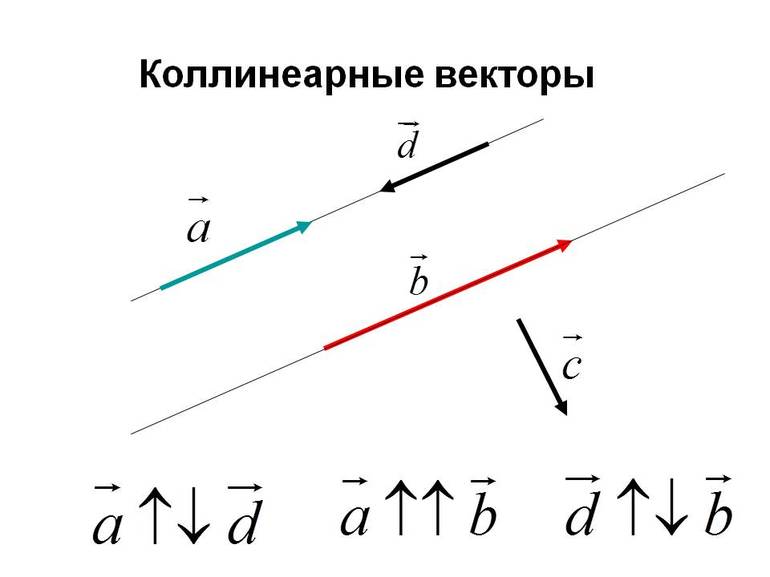 Обозначаются двумя стрелками в одну или разные стороны соответственно: , , .
Обозначаются двумя стрелками в одну или разные стороны соответственно: , , .
Поскольку векторы определяются двумя характеристиками – модулем и направлением, то они будут равны, если у них совпадают оба эти параметра. Т. е. равными будут векторы, у которых равны длины и которые являются сонаправленными.
Прежде чем формулировать строгое определение, посмотрим, согласуется ли это определение с логикой и жизненным опытом. Рассмотрим в качестве примера перемещение.
Нарисуем на листе бумаги два одинаковых вектора (см. рис. 13):
Рис. 13. Одинаковые векторы и
Накроем лист бумаги стеклом и посадим муху над точкой . Пусть муха переползет в точку (см. рис. 14). Вектор перемещения .
Рис. 14. Вектор перемещения
Вернем муху назад и сдвинем под стеклом лист так, чтобы муха оказалась над точкой , а затем повторила свой предыдущий путь. В результате она окажется в точке (см. рис. 15). Вектор перемещения .
Рис. 15. Вектор перемещения
Но ведь муха совершала одно и то же перемещение по стеклу. Она могла даже не видеть листа бумаги под стеклом. Конечно, разумно считать два рассмотренных перемещения одинаковыми, равными.
Она могла даже не видеть листа бумаги под стеклом. Конечно, разумно считать два рассмотренных перемещения одинаковыми, равными.
Векторы называются равными, если они сонаправлены и их длины равны (равенство векторов записывается как ):
Обратите внимание, что отдельно равенство модулей векторов или их сонаправленность не дают нам оснований говорить о равенстве векторов.
Действительно, в примере с другом, который отъехал от Москвы на 170 км, мы говорили о разных векторах одинаковой длины. Понятно, что перемещения, которые из одной и той же точки приводят нас в совершенно разные места, нельзя считать одинаковыми.
Аналогично в ситуации с сонаправленными векторами – можно выехать в одном направлении, но проехать 10 км, а можно – 100 км. Понятно, что перемещения, а значит, и векторы в этих случаях будут разными.
Правило треугольника
Мы определили равные векторы, т. е. ввели классы эквивалентности. Теперь можно поговорить об операциях, которые можно выполнять с векторами. Мы уже говорили, что несколько последовательных перемещений – это сложение перемещений, одновременное приложение к одному телу нескольких сил – это сложение сил. Если вы идете по движущемуся эскалатору, то ваша скорость относительно Земли – это сложение вашей скорости относительно эскалатора и скорости эскалатора относительно Земли.
Мы уже говорили, что несколько последовательных перемещений – это сложение перемещений, одновременное приложение к одному телу нескольких сил – это сложение сил. Если вы идете по движущемуся эскалатору, то ваша скорость относительно Земли – это сложение вашей скорости относительно эскалатора и скорости эскалатора относительно Земли.
Понятно, что для решения задач необходимо ввести операцию сложения для векторов. Перемещение естественным образом подсказывает нам, как складывать векторы.
Пусть мы переместились из точки в точку . Вектор перемещения . Далее мы переместились из точки в точку . Вектор перемещения . Итоговое перемещение складывается из двух первых перемещений (см. рис. 16). Тогда: .
Рис. 16. Перемещение складывается из перемещений и
Такое правило сложения двух векторов называют правилом треугольника. Оно непосредственно следует из того, что два последовательных перемещения эквивалентны перемещению из начальной точки в конечную.
Обратите внимание, что если точка не принадлежит отрезку , то сумма длин векторов всегда больше длине вектора суммы (неравенство треугольника). И только если точка принадлежит отрезку , то сумма длин векторов равна длине суммы. Можно сформулировать это так:
Можем ли мы применять правило треугольника для сложения двух произвольных векторов? Конечно. Рассмотрим векторы и (см. рис. 17):
Рис. 17. Рассматриваемые векторы и
Построим четырехугольник так, чтобы вектор был равен вектору (см. рис. 18). Полученный четырехугольник является параллелограммом, т. к. , .
Рис. 18. Параллелограмм
Т. к. векторы равны, то (по правилу треугольника) (см. рис. 19).
Рис. 19. Сумма векторов и равна вектору
Операцию, которую мы выполнили с вектором , чтобы получить равный ему вектор , называют параллельным переносом (см. рис. 20). Подробнее о ней мы поговорим чуть позже.
Рис. 20. Параллельный перенос
Частным, более простым случаем является сложение коллинеарных векторов. Если векторы сонаправлены, то, совместив параллельным переносом конец одного и начало другого, мы получим новый вектор, направленный в ту же сторону, что и слагаемые, и длина которого равна сумме длин слагаемых (см. рис. 21).
Если векторы сонаправлены, то, совместив параллельным переносом конец одного и начало другого, мы получим новый вектор, направленный в ту же сторону, что и слагаемые, и длина которого равна сумме длин слагаемых (см. рис. 21).
Рис. 21. Сложение сонаправленных коллинеарных векторов
Если векторы разнонаправленны, то после совмещения конца одного и начала другого мы получим короткий вектор суммы, который направлен в ту сторону, куда был направлен более длинный вектор, и длина суммы будет равна разности длин исходных векторов (см. рис. 22). Эта ситуация очень напоминает сумму двух чисел одного знака в первом случае и сумму двух чисел с разными знаками во втором случае.
Рис. 22. Сложение разнонаправленных коллинеарных векторов
Правило параллелограмма
Пример со сложением сил будет отличаться от сложений перемещений. Все дело в том, что перемещения могут быть последовательными. А о сумме сил мы говорим в тех случаях, когда две силы приложены к одному телу одновременно.
Если на горизонтальной поверхности человек тянет сани, то они движутся в ту же самую сторону, куда направлен вектор силы тяги. Если два человека тянут сани чуть в разных направлениях, то сани движутся по направлению между этими двумя этими векторами (см. рис. 23). Мы это интуитивно хорошо понимаем, когда выполняем вдвоем подобного рода работу (ранее рассматривали пример с сумкой, которую несут двое).
Рис. 23. Если два человека тянут сани в разных направлениях, то сани движутся по направлению между этими двумя этими векторами
Задача сложения сил сводится к задаче сложения векторов, которые имеют общее начало. Рассмотрим сумму векторов . Построим вектор , равный вектору (см. рис. 24).
Рис. 24. Векторы и имеют общее начало, векторы
Мы уже знаем, что по правилу треугольника:
Но что такое вектор ? Рассмотрим четырехугольник (см. рис. 25).
Рис. 25. Рассматриваемый четырехугольник
В нем , (в силу равенства векторов ). Значит, по признаку параллелограмма, – параллелограмм.
Значит, по признаку параллелограмма, – параллелограмм.
Т. е. суммой векторов с общим началом будет вектор диагонали параллелограмма, построенного на этих двух векторах, имеющий то же начало (см. рис. 26). Это правило называется правилом параллелограмма.
Рис. 26. Правило параллелограмма
Так как же складывать два вектора, по правилу треугольника или параллелограмма? Мы получили правило параллелограмма через правило треугольника. Т. е. оба правила верны. Какое из правил применять, зависит от ситуации – если нам нужно сложить векторы, у которых конец одного совпадает с началом другого, то удобнее пользоваться правилом треугольника. Если же мы складываем векторы с одинаковым началом, то – правилом параллелограмма. В остальных случаях можно выбрать любое из двух правил, которое покажется более удобным.
Вычитание векторов
Для чисел после операции сложения мы естественным образом ввели обратную операцию – вычитание. По аналогии поступим и с векторами.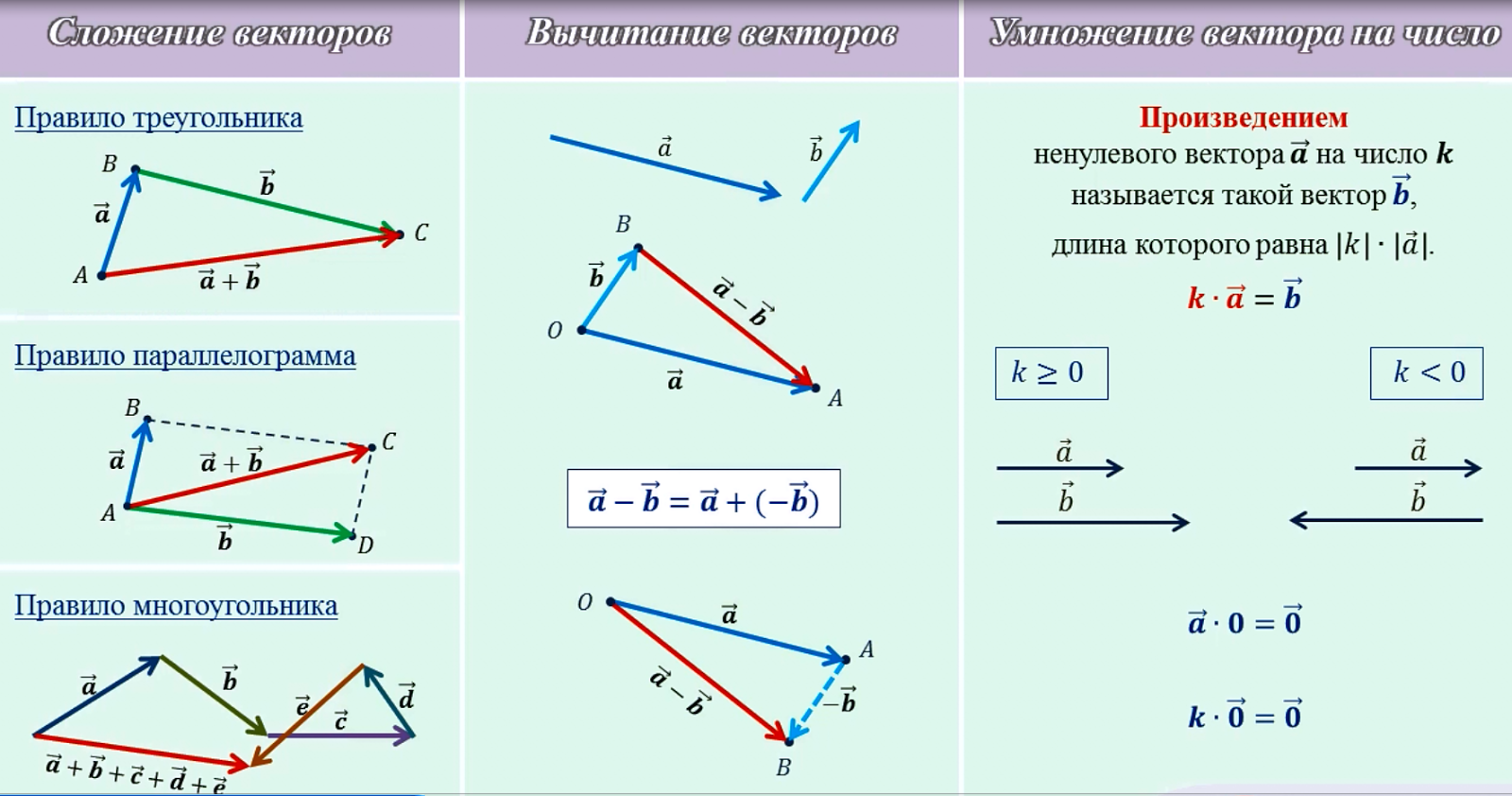
Т. к. , то естественно считать, что . Теперь можно сформулировать алгоритм вычитания векторов.
Пусть нужно из вектора вычесть вектор . Совместим их начала. Соединим концы векторов и направим к уменьшаемому, т. е. к вектору . Полученный вектор и есть разность двух векторов (см. рис. 27).
Рис. 27. Разность векторов и
Изобразим операцию сложения и вычитания векторов на одной картинке. Пусть два вектора и имеют общее начало. Достроим рисунок до параллелограмма.
Тогда одна диагональ является суммой векторов , а вторая – разностью (см. рис. 28).
Рис. 28. Сумма и разность векторов и
Иногда при решении задач забывают, в какую сторону направить вектор разности. Здесь есть очень простой совет: проверьте себя сложением. Если , значит, все в порядке.
Умножение вектора на число
Мы поговорили о сложении и вычитании векторов. Если продолжать аналогию с числами, то следующий шаг – введение операции умножения. Вспомним, что умножение – это краткая запись сложения одинаковых элементов: .
Вспомним, что умножение – это краткая запись сложения одинаковых элементов: .
Если тело совершило раза одно и то же перемещение, равное , то можно сказать, что оно переместилось в том же направлении на расстояние, равное .
Другой пример: если говорят, что машина увеличила скорость в раза, то обычно это означает, что направление не изменилось, а увеличилось численное значение скорости в раза. Описанные операции называются умножением вектора на число.
Сложим вектор с самим собой раза: – получаем вектор, длина которого в раза больше, а направление совпадает с . Новый вектор мы так и обозначили: . Это хорошо согласуется с понятием умножения как многократного сложения одинаковых элементов. В самом деле, если вектор сложить с самим собой раза, то как раз получится такой вектор (см. рис. 29).
Рис. 29. Сложение вектора с самим собой раза
Если умножить вектор на , то его длина увеличится в раза, а направление снова останется прежним (см.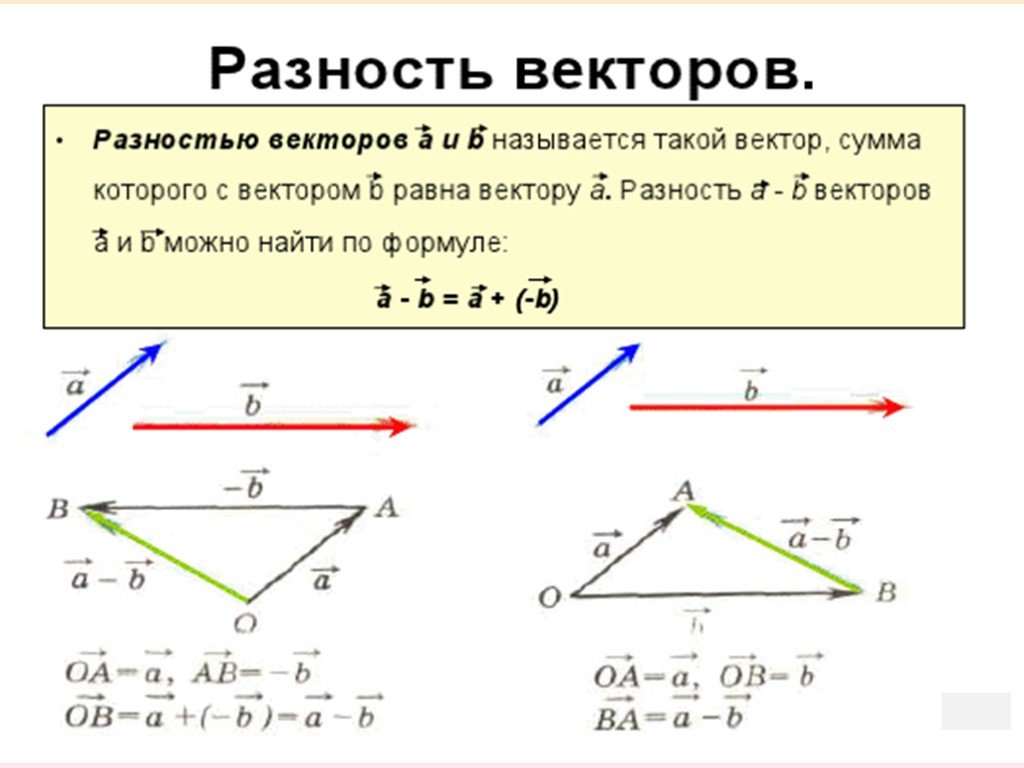 рис. 30).
рис. 30).
Рис. 30. Умножение вектора на
Умножение вектора на число ноль дает нам вектор нулевой длины. Назовем его нулевым вектором:
Нулевой вектор – это вектор нулевой длины. Начало и конец этого вектора совпадают. Направление у него не определено.
Давайте теперь подумаем, что может означать умножение на отрицательное число.
Возьмем для примера умножение на . Вспомним умножение чисел. Если умножить любое число на , получим противоположное ему число: , т. е. число, которое в сумме с данным дает ноль: .
Используем это определение и для векторов: для вектора назовем противоположным такой вектор , чтобы они в сумме давали ноль-вектор:
Вернемся к примеру с перемещением. Ноль-вектор – это перемещение, начало и конец которого – одна и та же точка . Пусть мы переместились из точки в точку . Каким должно быть перемещение, чтобы в итоге мы снова оказались в точке ? Понятно, что это перемещение из точки в точку . Получаем, что: .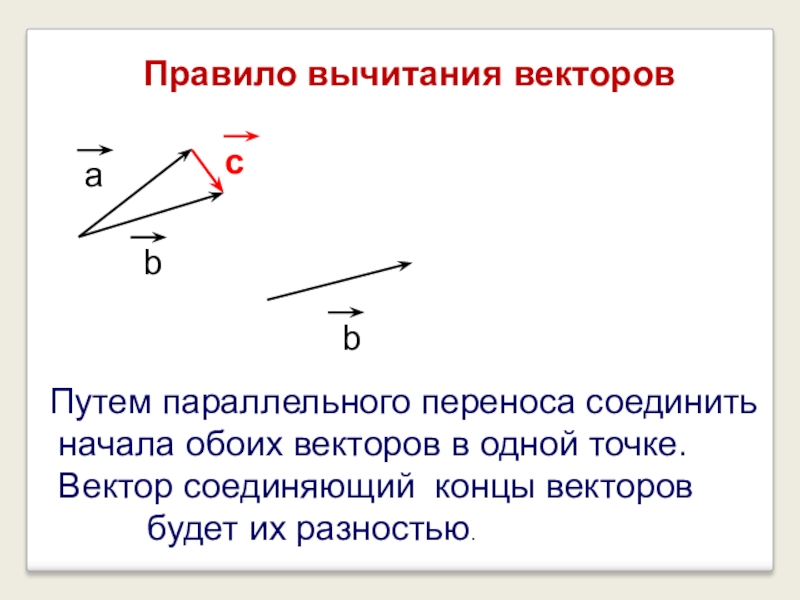
Тогда, по аналогии с числами, умножение вектора на число дает противоположный вектор:
Тогда при умножении вектора на произвольное отрицательное число будем получать вектор, противоположно направленный, длина которого – это длина первого вектора, умноженная на модуль этого числа (см. рис. 31).
Рис. 31. Умножение вектора на
Например, при умножении вектора на получим противоположно направленный вектор в раза длиннее, а при умножении на тоже противоположно направленный, но в раза короче:
Заметим, что векторы и всегда коллинеарны:
- если , то сонаправлены;
- если , то противоположно направлены
Оказывается, верно и обратное утверждение: если векторы и коллинеарны, то существует такое число , что:
Действительно, если векторы и сонаправлены, то в качестве , если противоположно направлены, то (в силу определения умножения вектора на число).
Заключение
Мы рассмотрели умножение вектора на число. А можно ли умножать векторы между собой? Оказывается, можно, причем разными способами. Но подробнее об этом мы поговорим на следующих уроках.
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия. 9 класс. Учебник. – М.: «Просвещение», 2014.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия. 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия. 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «onlinemschool.com» (Источник)
- Интернет-портал «math34.ru» (Источник)
- Интернет-портал «yaklass.ru» (Источник)
Домашнее задание
- Стороны правильного треугольника равны .
 Найти длину вектора .
Найти длину вектора . - Две стороны прямоугольника равны и . Найти длину суммы .
- Найти длину вектора:
Действия над векторами: сложение векторов
Представим себе пешехода на перекрестке двух улиц, которому надо перейти с угла, обозначенного $M_{1}$ (рис.), на угол $M_{2}$. Он мог бы направиться непосредственно к этому углу по прямой $M_{1}M_{2}$. Тогда мы сказали бы, что перемещение пешехода равно $\vec{M_{1}M_{2}}$. Но на улицах с оживленным движением такой переход запрещен. Поэтому дисциплинированный пешеход перейдет сначала из точки $M_{1}$ в точку $A$, а затем из точки $A$ в точку $M_{2}$. Конечный результат будет таким же, как если бы он прошел по прямой $M_{1}M_{2}$. Перемещение $\vec{M_{1}M_{2}}$ достигнуто в результате двух перемещений: $\vec{M_{1}A}$ и $\vec{AM_{2}}$. Эти перемещения заменили одно. Естественно считать, что перемещение $\vec{M_{1}M_{2}}$ есть сумма двух перемещений $\vec{M_{1}A}$ и $\vec{AM_{2}}$:$\vec{M_{1}M_{2}} = \vec{M_{1}A } + \vec{AM_{2}}$.
Этот пример ясно показывает, как складываются векторы. На рисунке векторы-слагаемые расположены так, что конец одного из них примыкает к началу другого. А вектор-сумма, или, как говорят, результирующий вектор, — это вектор, соединяющий начало одного из слагаемых с концом другого.
Это общее правило сложения любых векторов, а не только векторов перемещения.
Чтобы сложить два вектора, нужно их расположить так, чтобы конец первого вектора примыкал к началу второго. Вектор, соединяющий начало первого вектора с концом второго, есть сумма обоих векторов.
рис. 1
При выполнении этих построений векторы можно переносить параллельно самим себе (например, векторы $\vec{a}$ и \vec{b}$ на рис. 1а). Их можно также менять местами (рис. 1б). От этого ни модуль, ни направление результирующего вектора не изменяются.
рис. 2
Есть и другой способ сложения двух векторов. Вместо того чтобы располагать складываемые векторы один за другим, как мы только что делали, их располагают так, чтобы они исходили из одной точки (рис. 2). Затем, считая, что расположенные таким образом векторы образуют две стороны параллелограмма, достраивают параллелограмм (как показано пунктиром на рис.2) и проводят диагональ из точки, в которой были совмещены начала складываемых векторов. Эта диагональ и есть результирующий вектор. Приведенное правило сложения векторов называется правило м параллелограмма. Оба способа дают, конечно, один и тот же результат.
2). Затем, считая, что расположенные таким образом векторы образуют две стороны параллелограмма, достраивают параллелограмм (как показано пунктиром на рис.2) и проводят диагональ из точки, в которой были совмещены начала складываемых векторов. Эта диагональ и есть результирующий вектор. Приведенное правило сложения векторов называется правило м параллелограмма. Оба способа дают, конечно, один и тот же результат.
Таким образом, в отличие от чисел (скалярных величин) векторы складываются геометрически и результирующий вектор — это геометрическая сумма векторов. Модуль этой суммы векторов (как видно из рассмотренных нами примеров) оказывается меньше суммы модулей этих векторов, так как сумма двух сторон треугольника больше его третьей стороны.
рис. 3
Если складываются не два, а больше векторов, правило сложения остается прежним. Пусть, например, точка совершила последовательно перемещения из $OA$ в $A$, оттуда в $B$, затем в $C, D$ и $E$ (рис.3). Все эти перемещения могут быть заменены одним-единствекным перемещением из $O$ в $E$ по прямой $OE$.
Следовательно, чтобы сложить несколько векторов, надо расположить их так, чтобы конец первого вектора примыкал к началу второго, конец второго — к началу третьего и т. д. Результирующим будет вектор, направленный от начала первого вектора к концу последнего.
рис. 4
рис. 5
Рассмотрим частный случай, когда векторы направлены вдоль одной и той же прямой (рис. 4) или параллельно друг другу (рис. 5). Правило сложения остается и здесь тем же: векторы-слагаемые надо расположить так, чтобы конец одного примыкал к началу другого. Тогда вектор, соединяющий начало первого вектора с концом второго, и будет векторной суммой обоих векторов. Что же касается модуля суммы векторов, то, как видно из рисунка 4, он равен сумме модулей складываемых векторов. Если складываемые параллельные векторы направлены в противоположные стороны, то из рисунка 6 видно, что модуль их суммы равен разности модулей складываемых векторов, этот результирующий вектор направлен в сторону большего по модулю вектора.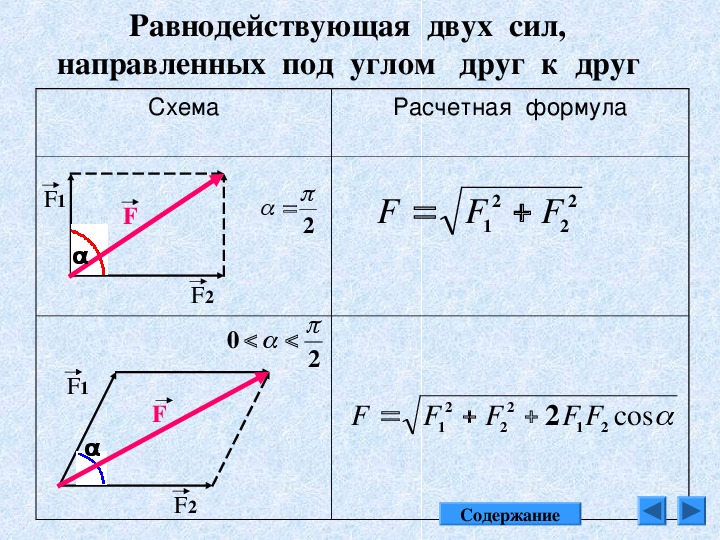
Отсюда следует, что параллельные векторы складываются так, как будто бы они являются алгебраическими величинами. Для этого нужно одному из направлений приписать знак «+», а противоположному — знак «-».
рис. 6
Как найти проекцию вектора, являющегося суммой нескольких векторов? На рисунке 6 приведены векторы $\vec{a}, \vec{b}$ и $\vec{c}$. Найдем их результирующий вектор $\vec{f}$:
$\vec{f} = \vec{a} + \vec{b} + \vec{c}$.
Спроецируем все складываемые векторы и результирующий вектор на какую-нибудь ось, например на ось $X$ (см. рис. 6). Из рисунка видно, что проекции векторов $\vec{a}$ и $\vec{b}$ на ось $X$ положительны, потому что их составляющие по оси $X$ ($\vec{AB}$ и $\vec{BC}$) направлены так же, как ось $X$; проекция же вектора с отрицательна, так как его составляющая по оси $X$ ($\vec{CD}$) направлена против этой оси. Составляющая результирующего вектора — это вектор $\vec{AD}$, а проекция этого вектора равна алгебраической сумме проекций $a_{x}, b_{x}$ и $c_{x}$. Следовательно,
Следовательно,
$f_{x} = a_{x} + b_{x} + c{x}$.
Проекция суммы векторов на данную ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Поэтому, для того чтобы найти проекцию суммы векторов, нет необходимости приставлять их друг к другу и находить результирующий вектор. Надо просто сложить проекции всех векторов, учитывая их знаки.
параллельных векторов — определение, примеры, формулы т. е. для любого вектора
a сам вектор и противоположный ему вектор -a являются векторами, которые всегда параллельны a . Расширяя это далее, любой скаляр, кратный a , параллелен a. т. е. вектор a и k a всегда являются параллельными векторами, где k — скаляр (действительное число).Давайте узнаем больше о параллельных векторах вместе с их определением, формулой и примерами.
1. | Что такое параллельные векторы? |
| 2. | Как найти параллельные векторы? |
| 3. | Скалярное произведение параллельных векторов |
| 4. | Перекрестное произведение параллельных векторов |
| 5. | Формула параллельных векторов |
| 6. | Единичный вектор, параллельный заданному вектору |
| 7. | Свойства параллельных векторов |
| 8. | Часто задаваемые вопросы о параллельных векторах |
Что такое параллельные векторы?
Два вектора называются параллельными тогда и только тогда, когда угол между ними равен 0 градусов. Параллельные векторы также известны как коллинеарные векторы. т. е. два параллельных вектора всегда будут параллельны одной и той же прямой, но они могут быть либо в одном направлении, либо в совершенно противоположном направлении. На следующем изображении векторы, показанные на крайнем левом рисунке, НЕ параллельны, поскольку они имеют разные направления (т. Е. Ни одно и то же, ни противоположные направления).
На следующем изображении векторы, показанные на крайнем левом рисунке, НЕ параллельны, поскольку они имеют разные направления (т. Е. Ни одно и то же, ни противоположные направления).
Параллельные векторы, направленные в противоположные стороны, иногда также называют антипараллельными векторами. На изображении выше последний рисунок показывает антипараллельные векторы. Но как математически идентифицировать параллельные векторы? Давайте посмотрим.
Как найти параллельные векторы?
Два вектора a и b называются параллельными векторами, если один из них кратен другому. т. е. a = k b , где k — скаляр (действительное число). Здесь «k» может быть положительным, отрицательным или 0. В этом случае
- a и b имеют одинаковые направления, если k положительно.
- a и b имеют противоположные направления, если k отрицательно.

Вот несколько примеров параллельных векторов:
- a и 3 a параллельны и имеют те же направления, что и 3 > 0.
- v и (-1/2) v параллельны и имеют те же направления, что и (-1/2) < 0.
- a = <1, -3> и b = <3, -9> параллельны, поскольку b = <3, -9> = 3 <1, -3> = 3 a .
В приведенных выше примерах пример 2 относится к антипараллельным векторам.
Скалярное произведение параллельных векторов
Скалярное произведение любых двух параллельных векторов равно произведению их величин. Рассмотрим два параллельных вектора а и б . Тогда угол между ними равен θ = 0. По определению скалярного произведения
a · b = | и | | б | cos θ
= | и | | б | 0
= | и | | б | (1) (потому что cos 0 = 1)
= | и | | б |
Следовательно, скалярное произведение двух параллельных векторов равно произведению их величин.
Перекрестное произведение параллельных векторов
Перекрестное произведение любых двух параллельных векторов является нулевым вектором. Рассмотрим два параллельных вектора a и b . Тогда угол между ними равен θ = 0. По определению перекрестного произведения
a × b = | и | | б | грех θ \ (\ шляпа {n} \)
= | и | | б | грех 0 \(\шляпа{п}\)
= | и | | б | (0) \(\шляпа{n}\) (поскольку sin 0 = 0)
= 0
Обратите внимание, что 0 здесь является вектором, а не скаляром. Таким образом, векторное произведение двух параллельных векторов является нулевым вектором (не просто нулем).
Формула параллельных векторов
Параллельные векторы можно определить с помощью скалярного множителя, скалярного произведения или перекрестного произведения. Вот формула параллельных векторов в соответствии с ее значением, объясненным в предыдущих разделах.
Вот формула параллельных векторов в соответствии с ее значением, объясненным в предыдущих разделах.
Единичный вектор, параллельный заданному вектору
Единичный вектор, параллельный заданному вектору a , обозначается \(\hat{a}\) и задается как \(\hat{a}\) = a / | и |. Здесь обратите внимание на две вещи:
- и и и / | и | (что равно 1/| a | · a) являются скалярными кратными друг другу. Следовательно, a и \(\hat{a}\) параллельны.
- Величина / | и | есть | и | / | и | = 1. Следовательно, \(\hat{a}\) — единичный вектор.
Следовательно, a / | и | является единичным вектором, параллельным a . Он получается делением вектора на его величину.
Пример: Найдите единичный вектор, параллельный вектору a = 3 i + 4 j .
Решение:
Дано, что a = 3 i + 4 j .
Его величина | и | = √(3 2 + 4 2 ) = √(25) = 5,
Таким образом, единичный вектор, параллельный a , равен
\(\hat{a}\) = / | и |
= (3 i + 4 j ) / 5
= (3/5) i + (4/5) j
Свойства параллельных векторов
- Два вектора a и b параллельны друг другу тогда и только тогда, когда a = k b , где k — скаляр.
- Здесь a и b находятся в направлениях, если k > 0, и в противоположных направлениях, если k < 0.

- Каждый вектор a параллелен самому себе, так как a = 1 a.
- Два вектора a и b называются параллельными, если их векторное произведение равно нулю. то есть а × б = 0 .
- Для любых двух параллельных векторов a и b их скалярное произведение равно произведению их модулей. т. е. a · b = | и | | б |.
☛ Похожие темы:
- Векторные формулы
- Компоненты вектора
- Типы векторов
- Калькулятор результирующего вектора
Часто задаваемые вопросы о параллельных векторах
Что такое определение параллельных векторов?
Два вектора a и b называются параллельными векторами , если выполняется одно из условий:
- Если один вектор кратен другому.
 т. е. a = k b , где k — скаляр.
т. е. a = k b , где k — скаляр. - Если их векторное произведение равно 0, то есть a × b = 0 .
- Если их скалярное произведение равно произведению их величин. т. е. a · b = | и | | б |.
Как найти вектор, параллельный заданному вектору?
Чтобы найти вектор, параллельный заданному вектору a , просто умножьте его на любой скаляр. Например, 3 a , -0,5 a , √2 a и т. д. параллельны вектору a .
Как определить, параллельны ли два вектора?
Чтобы определить, параллельны ли два заданных вектора, просто посмотрите, можно ли взять общий множитель из одного вектора так, чтобы он был кратен другому вектору. Другой способ — проверить, равно ли их векторное произведение 0.
В чем разница между перпендикулярными и параллельными векторами?
Вот различия между перпендикулярными и параллельными векторами.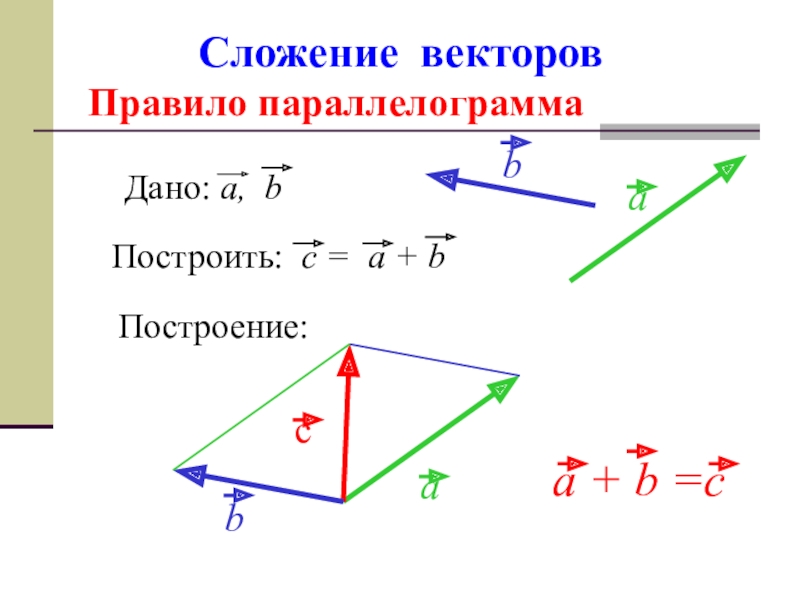
| Перпендикулярные векторы | Параллельные векторы |
|---|---|
| Два вектора называются перпендикулярными, если угол между ними равен 90 градусов. | Два вектора называются параллельными, если угол между ними равен 0 градусов. |
| Скалярное произведение двух перпендикулярных векторов равно 0. | Перекрестное произведение двух параллельных векторов равно 0 . |
| Если a и b перпендикулярны, то | а × б | = | и || б |. | Если a и b параллельны, то a · b = | и || б |. |
Параллелен ли вектор самому себе?
Каждый вектор a кратен самому себе.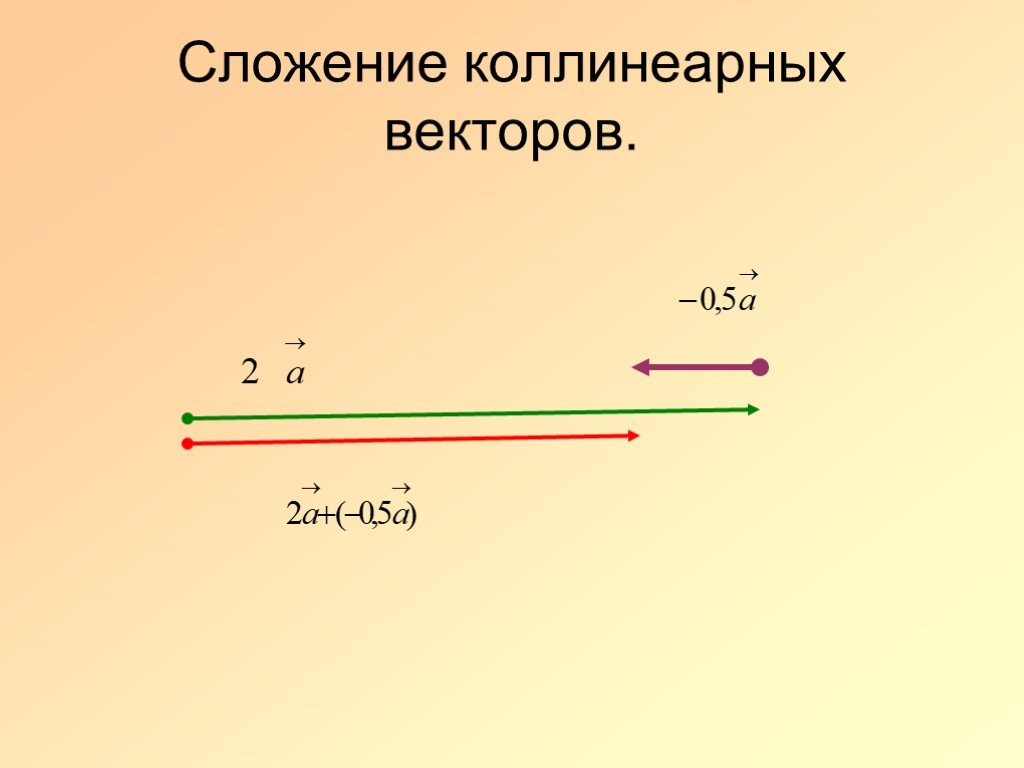 т. е. a = 1 a . Таким образом, каждый вектор параллелен самому себе. Кроме того, угол между вектором и самим собой всегда равен 0 градусов. Таким же образом мы можем сказать, что вектор параллелен самому себе.
т. е. a = 1 a . Таким образом, каждый вектор параллелен самому себе. Кроме того, угол между вектором и самим собой всегда равен 0 градусов. Таким же образом мы можем сказать, что вектор параллелен самому себе.
Какая формула для единичного вектора, параллельного результирующим векторам?
Мы знаем, что единичный вектор, параллельный вектору a , равен a / | и |. Таким образом, единичный вектор, параллельный равнодействующей двух векторов a и b , равен ( a+b) / | а+б |.
В чем разница между параллельными векторами и наклонными линиями?
Параллельные векторы и наклонные линии находятся в трехмерном пространстве. Параллельные прямые никогда не пересекаются и параллельны относительно координат x, y и z. Наклонные линии также находятся в трехмерном пространстве, но не параллельны и не пересекаются. Наклонные линии — это линии, присутствующие в разных плоскостях.
Наклонные линии — это линии, присутствующие в разных плоскостях.
Что такое равные и параллельные векторы?
Равные векторы имеют одинаковую величину и одинаковое направление. Параллельные векторы могут иметь разные величины, но они имеют одинаковые/противоположные направления. Например:
- a и a равные векторы.
- a и 3 a — параллельные векторы.
Что такое антипараллельный вектор
Антипараллельный вектор противоположен параллельному вектору. Поскольку антипараллельный вектор противоположен вектору, скалярное произведение одного вектора будет отрицательным, а уравнение другого вектора будет отрицательным по отношению к предыдущему. Антипараллельные векторы являются подмножеством всех параллельных векторов. Они также известны как антипараллельные векторы, поскольку они всегда противоположны направлению данного вектора и никогда не пересекают его.
Антипараллельные векторы:
Два параллельных вектора в Евклидовом пространстве, направленные в противоположные стороны, называются антипараллельными векторами. При этом один из векторов можно положить равным произведению другого вектора на любое отрицательное число. Как уже известно, для того, чтобы два вектора были параллельными, они не обязательно должны иметь одинаковую длину, а должны иметь только одну и ту же составляющую направления. Точно так же, чтобы два вектора были антипараллельными, они не обязательно должны иметь одинаковую длину; они должны быть параллельны и противоположны по направлению.
Производные отношения/Примеры антипараллельных векторов:
В этом треугольнике ABC высота равна AD. Теперь в ∆ABD прямой угол образован BD, а в ∆ADC прямой угол образован DC. Вместо этого считайте эти линии векторами. Тогда по закону сложения векторов треугольника BD и DC будут иметь противоположные направления. Они также имеют угол 180° между собой, что является требованием для антипараллельных векторов. Следовательно, теоретически известно, что BD и DC являются антипараллельными векторами.
Они также имеют угол 180° между собой, что является требованием для антипараллельных векторов. Следовательно, теоретически известно, что BD и DC являются антипараллельными векторами.
Это изображение описанной окружности треугольника ABC, где DE — касательная описанной окружности в вершине треугольника. Существует теорема о том, что DE будет иметь направление, противоположное направлению BC в векторной форме. Более того, они оба являются параллельными векторами. Следовательно, DE и BC являются антипараллельными векторами, так как они противоположны по направлению. O
На том же рисунке, если O — центр окружности, то OA будет радиусом описанной окружности в вершине, и она будет перпендикулярна DE. Поэтому в евклидовой математике существует теорема о том, что радиус описанной окружности в вершине будет перпендикулярен всем антипараллельным векторам ВС (точно так же перпендикулярен и DE).

Разница между антипараллельными векторами и противоположными векторами:
Два вектора называются противоположными или отрицательными, если они имеют одинаковую величину, но действуют в противоположном направлении друг к другу. С другой стороны, антипараллельные векторы не обязательно должны иметь одинаковую величину, но должны указывать в противоположных направлениях, а также иметь между собой угол 180°. Это означает, что один из двух векторов должен быть равен отрицательному ненулевому скалярному множителю первого вектора.
Например: À и -À являются противоположными или отрицательными векторами. Однако векторы À и -7À являются антипараллельными векторами, а вектор -7 отличен от нуля и является скалярным.
Набор отрицательных векторов всегда антипараллелен, но обратное может быть неверным.
Разница между параллельными и антипараллельными векторами:
Параллельные векторы указывают в одном направлении, тогда как антипараллельные векторы указывают в разных направлениях. Между параллельными векторами угол 0°, тогда как у антипараллельных векторов угол 180°.
Между параллельными векторами угол 0°, тогда как у антипараллельных векторов угол 180°.
Условия антипараллельности двух векторов:
Условия антипараллельности вектора:
Они должны указывать в противоположных направлениях.
Они должны иметь угол 180°
Первый вектор должен быть ненулевым скаляром, кратным второму.
Заключение
Антипараллельные векторы параллельны по природе, но противоположны по направлению. В них один из векторов является ненулевым скалярным множителем другого вектора. Условием антипараллельности векторов является то, что они направлены в противоположные стороны друг к другу и имеют между собой угол 180°. Любой вектор, имеющий любой другой угол, не может быть антипараллельным вектором. Это означает, что наклоны антипараллельных векторов будут одинаковыми. Антипараллельные векторы можно заключить фразой, что они параллельны и противоположно направлены.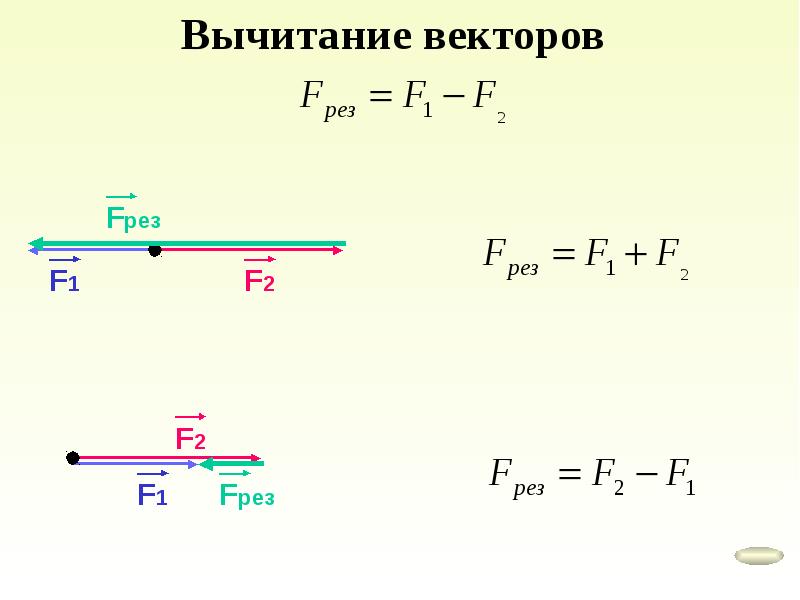


 Найти длину вектора .
Найти длину вектора .

 т. е. a = k b , где k — скаляр.
т. е. a = k b , где k — скаляр.