Примеры решения задач с векторами

Векторы используются во многих науках, таких как: математика, физика, геометрия и многие другие прикладные науки. На практике они позволяют не выполнять ненужных операций и сокращают время на выполнение задач. Поэтому для будущих специалистов очень важно понять теорию векторов и научиться решать с ними проблемы.

Прежде чем изучать примеры решения проблем, советуем вам изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.

Векторные координаты

пример

Запись \(\ \overline{a}=(5 ;-2) \) означает, что вектор \(\ \overline{a} \) имеет следующие координаты: абсцисса равна 5, ордината равна -2.

пример

Задание.

Векторы и дан \(\ \overline{a}=(-3 ; 5) \) и \(\ \overline{b}=(0 ;-1) \) . Найти векторные координаты \(\ \overline{c}=\overline{a}+\overline{b} \)

Решение.

\(\ \overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4) \)

Пример

Задание. {\circ} \)

Разложение вектора по ортам координатных осей

пример

Задание.

Зная разложение вектора \(\ \overline{a} \) на базисной системе векторов: \(\ \overline{a}=3 \overline{i}-\overline{k} \)запишите координаты этого вектора в пространстве.

Решение.

Коэффициенты ортов являются координатами вектора, поэтому из того, что \(\ \overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k} \) мы получаем \(\ \overline{a}=(3 ; 0 ;-1) \)

Пример

Задание.

Вектор \(\ \overline{a} \) определяется его координатами: \(\ \overline{a}=(2 ;-1 ; 5) \) запишите разложение этого вектора по осям осей.

Решение.

Координаты вектора представляют собой коэффициенты по осям координатных осей при разложении вектора в основную систему векторов, поэтому требуется разложение:

\(\ \overline{a}=2 \overline{i}-\overline{j}+5 \overline{k} \)

Скалярное произведение векторов

Пример

Задание.

Рассчитайте скалярное произведение векторов \(\ \overline{a} \) и \(\ \overline{b} \) , если их длины равны 2 и 3 соответственно, а угол между ними равен 60 °. {\circ}=6 \cdot \frac{1}{2}=3 \)

Пример

Задание.

Найти скалярное произведение векторов \(\ \overline{a}=(3 ;-1) \) и \(\ \overline{b}=(-2 ; 7) \)

Решение.

Скалярное произведение

\(\ \overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13 \) Векторное произведение векторов пример

Задание.

Найти векторное произведение векторов \(\ \overline{a}=(6 ; 7 ; 10) \) и \(\ \overline{b}=(8 ; 5 ; 9) \)

Решение.

Составляем определитель и вычисляем его:

\(\ \overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|= \)

\(\ =\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)= \)

\(\ =13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26) \)

Смешанное произведение векторов

Пример

Задание.

Рассчитать объем пирамиды, построенной на векторах \(\ \overline{a}=(2 ; 3 ; 5), \overline{b}=(1 ; 4 ; 4), c=(3 ; 5 ; 7) \)

Решение.

Мы находим смешанное произведение указанных векторов, для этого составляем определитель, в строки которого записываем координаты векторов \(\ \overline{a}, \overline{b} \) и \(\ \overline{c} \):

\(\ (\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{ccc}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3- \)

\(\ -3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4 \)

\(\ V_{\mathrm{пир}}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}(\mathrm{куб} . \mathrm{ед.}) \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Действия над векторами и свойства векторов Смешанное произведение векторов Векторное произведение векторов Скалярное произведение векторов

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Применение векторов к решению задач

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Сущность векторного метода для решения геометрических задач

2. Общая схема для решения геометрических задач векторным методом

3. Примеры типов задач, которые решаются векторным методом

4. Примеры задач на применение векторного метода

Сущность векторного метода для решения геометрических задач

Векторный метод решения задач основан на решении задач с использованием аппарата векторной алгебры.

Применение векторной алгебры к решению геометрических задач основано на следующих основных утверждениях.

Утверждение 1

(Необходимое и достаточное условие коллинеарности векторов): Два ненулевых вектора $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны тогда и только тогда, когда существует действительное число $k\ne 0$, такое, что удовлетворяется следующее равенство

Утверждение 2: Если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ не коллинеарны, то любой вектор $\overrightarrow{c}$, компланарный с данными векторами можно представить в виде линейной комбинации и притом единственным образом:

Утверждение 3: Любой вектор $\overrightarrow{d}$ в трехмерном пространстве можно разложить по трем некомпланарным векторам $\overrightarrow{a}$, $\overrightarrow{b}$ и $\overrightarrow{c}$:

При решении задач векторным методом также применяются такие понятия, как сложение, вычитание векторов, умножение вектора на число, а также понятие скалярного произведения векторов.

Общая схема для решения геометрических задач векторным методом

При решении геометрических задач векторным методом рекомендуется пользоваться следующей схемой:

1. Провести анализ условия задачи:

   а) Выяснить в какой системе координат (двумерной или трехмерной) рассматривается данная задача;

   б) Записать, что нам дано, что нужно найти или доказать, а также построить чертеж по условию задачи.

2. Перевести условие задачи и требования к векторному виду.

3. Составить векторные соотношения, соответствующие тому, что дано в задаче и привести их к векторным соотношениям, соответствующим требованиям задачи.

4. Перевести полученный результат на геометрический язык.

Примеры типов задач, которые решаются векторным методом

Приведем теперь примеры классических задач, решаемых с помощью векторного метода (Не приводя их решений).

1. Задачи на доказательство параллельности.

2. Задачи на нахождение отношений, в котором точка делит отрезок.

3. Задачи на доказательство принадлежности трех точек одной прямой.

4. Задачи на доказательство принадлежности четырех точек одной плоскости.

5. Задачи на доказательство перпендикулярности.

6. Задачи на вычисление длины отрезка.

7. Задачи на нахождение величины угла.

8. Задачи на вычисление площадей и объемов геометрических фигур.

Примеры задач на применение векторного метода

Далее рассмотрим ряд задач, которые решаются с помощью векторного метода.

Пример 1

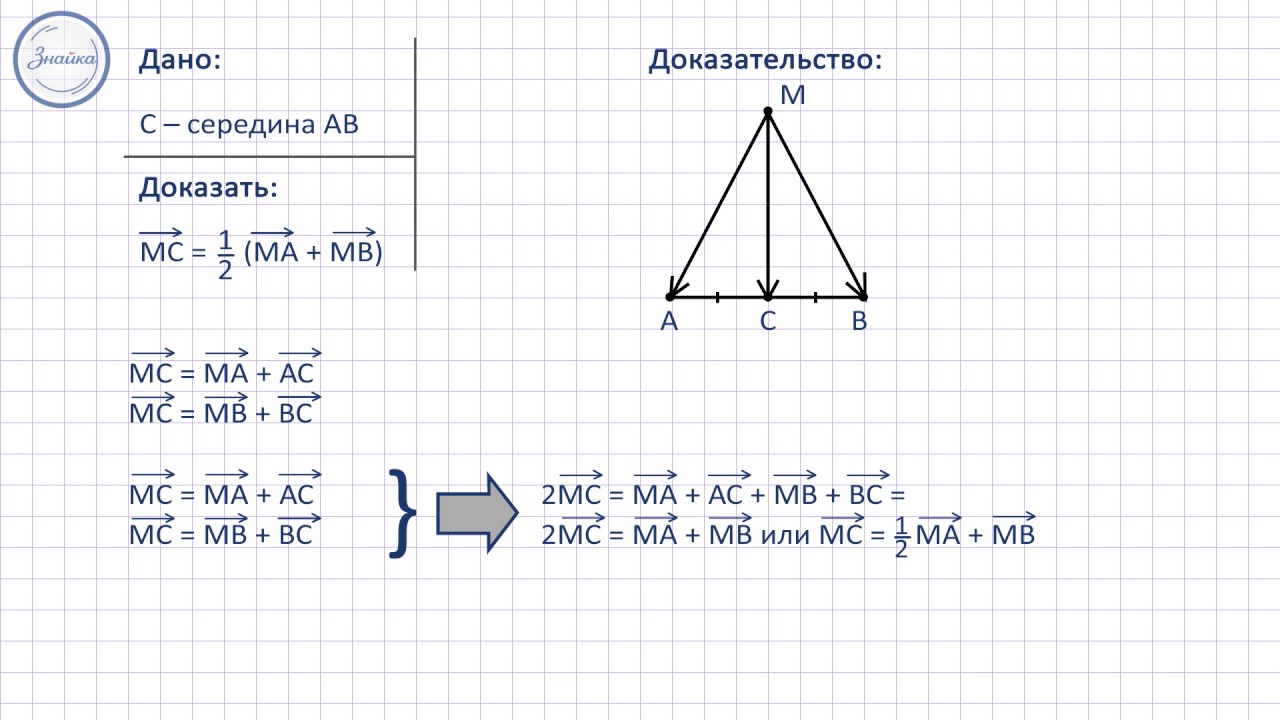
Доказать, что линия, соединяющая середины диагоналей произвольной трапеции параллельна основаниям этой трапеции и равна их полуразности.

Доказательство.

Пусть нам дана трапеция $ABCD.$ $MN$ — отрезок, соединяющий середины диагоналей данной трапеции (рис. 1).

Рисунок 1.

Докажем, что $MN=\frac{AD-BC}{2}$ и $MN||AD$

Рассмотрим вектор $\overrightarrow{MN}$. Используя правило многоугольника для сложения векторов, с одной стороны, получим

\[\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}\]

С другой стороны

\[\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CB}+\overrightarrow{BN}\]

Сложим два последних равенства:

\[2\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}+\overrightarrow{MC}+\overrightarrow{CB}+\overrightarrow{BN}\]

Так как $MN$ — отрезок, соединяющий середины диагоналей, то

\[\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0},\ \overrightarrow{DN}+\overrightarrow{BN}=\overrightarrow{0}\]

Тогда получим

\[2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{CB}=\overrightarrow{AD}-\overrightarrow{BC}\]

То есть

\[\overrightarrow{MN}=\frac{\overrightarrow{AD}-\overrightarrow{BC}}{2}\]

Так как $\overrightarrow{AD}\ и\ \overrightarrow{BC}$ сонаправлены, то $\overrightarrow{MN}||\overrightarrow{AD}$.

Из этого получаем, что $MN=\frac{AD-BC}{2}$ и $MN||AD$

ч. т. д.

Пример 2

На сторонах треугольника $ABC$ взяты точки $L,\ M,\ K$, так что $\left|BL\right|=3\left|AL\right|,\ \left|BM\right|=2\left|CM\right|,\ \left|AK\right|=2|CK|$. Найти, в каком отношении прямая $KL$ делит отрезок $AM$.

Решение.

Обозначим через точку $E$ — точку пересечения отрезка $AM$ с прямой $KL$(рис. 2).

Рисунок 2.

Найдем $\left|AE\right|:|EM|$

Введем, для удобства, следующие обозначения: $\overrightarrow{AB}=\overrightarrow{b},\ \overrightarrow{AC}=\overrightarrow{c}$, $\overrightarrow{AE}=x\overrightarrow{AM},$ $\overrightarrow{LE}=y\overrightarrow{LK}$

Воспользуемся далее правилом треугольника для сложения векторов. С одной стороны получим

\[\overrightarrow{AE}=x\overrightarrow{AM}=x\left(\overrightarrow{AB}+\overrightarrow{BM}\right)=x\left(\overrightarrow{b}+\frac{2}{3}\left(\overrightarrow{c}-\overrightarrow{b}\right)\right)=\frac{2}{3}x\overrightarrow{c}-\frac{1}{3}x\overrightarrow{b}\]

С другой стороны

\[\overrightarrow{AE}=\overrightarrow{AL}+\overrightarrow{LE}=\overrightarrow{AL}+y\overrightarrow{LK}=\frac{1}{4}\overrightarrow{b}+y\left(\frac{2}{3}\overrightarrow{c}-\frac{1}{4}\overrightarrow{b}\right)=\frac{2}{3}y\overrightarrow{c}+\frac{1}{4}\overrightarrow{b}-\frac{1}{4}y\overrightarrow{b}\]

Тогда

\[\frac{2}{3}x\overrightarrow{c}-\frac{1}{3}x\overrightarrow{b}=\frac{2}{3}y\overrightarrow{c}+\frac{1}{4}\overrightarrow{b}-\frac{1}{4}y\overrightarrow{b}\]

Получаем систему:

Рисунок 3.

$\overrightarrow{AE}=\frac{3}{7}\overrightarrow{AM}$, следовательно

Ответ: $3:4.$

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 01.04.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Решения и примеры для физики

Векторы могут использоваться для решения множества задач, включающих такие величины, как ускорение, импульс, сила, скорость и перемещение.

В чем разница между скалярами и векторами?

Скаляр — это величина, у которой нет направления . Это просто шкала таких величин, как килограммы или сантиметры. Например, ваш вес и рост выражаются через количество и единицу измерения, но не имеют направления. Примерами скалярных величин являются скорость, масса, температура, энергия, длина и расстояние.

Вектор , , с другой стороны, имеет величину и направление . Импульс объекта, например, равен его массе на ускорение и имеет направление, которое делает его векторной единицей. Примерами векторных величин являются скорость, ускорение, импульс, смещение и сила, включая вес.

Разложение векторов на компоненты

Разложение векторов на компоненты помогает нам, когда мы имеем дело с сложными векторными задачами . Чтобы разложить вектор на его компоненты, нам нужно измерить горизонтальную и вертикальную длину вектора и укажите эти длины как две отдельные величины. Давайте посмотрим на пример ниже, чтобы лучше понять концепцию.

Найдите компоненты вектора, показанного ниже.

Чтобы найти компоненты этого вектора, нам нужно начать с определения его горизонтальной и вертикальной длины.

Как видите, длина по горизонтали равна 12, а по вертикали — 10. Когда мы разлагаем вектор на его компоненты, мы всегда получаем одно значение по горизонтали и одно по вертикали. Длины, которые мы измерили, являются величинами компонентов вектора.

Как видите, компонентами этого вектора являются два вектора, горизонтальный и вертикальный, с величинами 12 и 10.

Можем ли мы разложить вектор на его компоненты, если мы не можем измерить его горизонтальная и вертикальная длина? Да, можем, но давайте посмотрим, как это делается.

Рис. 3. Вектор v и его компоненты. Источник: Огулкан Тезкан, StudySmarter.

Если мы знаем угол градиента вектора, мы можем определить величину его горизонтальной и вертикальной составляющих. Для приведенного выше вектора v угол градиента равен a. Затем мы можем определить соотношение между углом и величиной компонентов с помощью тригонометрии.

Определим величину горизонтальной составляющей v _x . Мы знаем, что:

Если мы решим уравнение для v _x , мы получим:

Теперь определим величину вертикальной составляющей v _y . Опять же, мы знаем, что:

Если мы решим уравнение для v _y , мы получим:

Сложение векторов вместе

Сложение двух векторов вместе называется нахождением их равнодействующей. Есть два способа сложения векторов. В первом задействовано с использованием масштабных диаграмм , а второй использует тригонометрию .

Определение результирующих векторов с использованием масштабных диаграмм

Чтобы найти результирующие векторы с помощью масштабных диаграмм, нам нужно нарисовать масштабную диаграмму векторов, которые мы хотим сложить вместе, соединив векторы ‘ кончик к хвосту ‘.

Следующий пример иллюстрирует концепцию.

Человек сначала проходит на северо-восток 11,40 м, затем продолжает идти на восток 6,6 м и, наконец, проходит на северо-запад 21,26 м, прежде чем остановиться. Определить полное перемещение человека.

Чтобы определить полное перемещение человека, нам нужно указать длины, которые он прошел, в виде векторов, каждый из которых имеет правильное направление и величину. Назовем его первое движение вектором А, второе — вектором В, а третье — вектором С.

Рисунок 4. Общее перемещение человека. Источник: Огулкан Тезкан, StudySmarter.

Если вы измерите линейкой общее перемещение, то увидите, что оно составляет 23,094 метра в северном направлении, хотя человек прошел 390,26 метра. Давайте докажем это математически, разложив векторы на их компоненты. В этом конкретном примере нам нужны только вертикальные компоненты, поскольку общее смещение является только вертикальным.

Рис. 5. Компоненты вектора. Источник: Огулкан Тезкан, StudySmarter.

Чтобы определить A _y , , мы применяем уравнение для разложения векторов на их компоненты:

Нам не нужно определять компоненты B, так как этот пример не включает вертикальную компоненту . Для определения C _y , мы применяем то же уравнение.

Полное перемещение равно сумме A _y и C _y , которое можно рассчитать следующим образом: другой, мы можем найти равнодействующую с помощью тригонометрии. Давайте снова посмотрим на пример.

Двое друзей толкают коробку. Две силы, которые они прикладывают, перпендикулярны друг другу. Один из друзей прикладывает силу в 3 ньютона (F ₁ ) в восточном направлении, а другой прикладывает силу в 4 ньютона (F ₂ ) в северном направлении. Определите результирующий вектор полной силы, действующей на коробку.

Рис. 6. Две перпендикулярные силы, воздействующие на коробку. Источник: Огулкан Тезкан, StudySmarter.

Две силы, F ₁ и F ₂ , перпендикулярны друг другу, а это означает, что модуль F _total равен гипотенузе треугольника, образованного этими векторами.

Задачи векторов — основные выводы

• В физике векторы используются для выражения любой величины, имеющей направление и величину.
• Чтобы разложить вектор на его компоненты, нам нужно измерить горизонтальную и вертикальную длины вектора и выразить их как два отдельных вектора.
• Чтобы сложить векторы вместе, мы можем использовать масштабные диаграммы или тригонометрию.
• Чтобы определить результирующие векторы с помощью масштабных диаграмм, нам нужно соединить векторы «кончик к хвосту».
• Если два вектора перпендикулярны друг другу, мы можем найти равнодействующую, используя теорему Пифагора.

линейная алгебра — Как решить векторное уравнение $\mathbf{r} + \mathbf{r} \times \mathbf{d} = \mathbf{c}$?

$\begingroup$

Учитывая следующее векторное уравнение в трех измерениях

$\mathbf{r} + (\mathbf{r} \times \mathbf{d}) = \mathbf{c}$

где $\mathbf{c}$ и $\mathbf{d}$ являются фиксированными заданными векторами, как найти все решения для $\mathbf{r}$?

---

До сих пор я пробовал следующие шаги, чтобы показать, что $\mathbf{r}$ должен лежать в заданной плоскости.

Взяв скалярное произведение с $\mathbf d$ с обеих сторон, мы получим

$$\mathbf{r} + (\mathbf{r} \times \mathbf{d}) = \mathbf{c} \ следует (\mathbf{r} + (\mathbf{r} \times \mathbf{d})) \cdot \mathbf{d} = \mathbf c \cdot \mathbf d.$$

Так как $\mathbf r \ раз \mathbf d$ перпендикулярно $\mathbf d$, их скалярное произведение равно нулю, поэтому мы получаем следующее (Уравнение $\ast$)

$$\mathbf r \cdot \mathbf d = \mathbf c \cdot \mathbf d$$

из чего можно сделать вывод, что $\mathbf r$ (как позиционный вектор) лежит в плоскости, содержащей $\ mathbf c$ и нормальна к вектору $\mathbf d$.

Однако это не обязательно означает, что все точки этой плоскости являются правильными решениями для $\mathbf r$. Я не понимаю, как уравнение ($\ast$) можно подставить обратно в исходное уравнение, чтобы каким-то образом устранить член в $\mathbf r$ или упростить его. Как решить это уравнение, убедившись, что вы нашли все решения для $\mathbf r$?

• линейная алгебра
• векторы

$\endgroup$

1

$\begingroup$

У вас есть 3 направления в пространстве.