Задание 2 из ЕГЭ по информатике

Русский язык Математика (профильная) Обществознание Физика История Биология Химия Английский язык Информатика Литература

Задания Варианты Теория

Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 Задание 22 Задание 23 Задание 24 Задание 25 Задание 26 Задание 27

Бесплатный интенсив по информатике

3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.

Курс стартует 27 марта.

Подробнее об интенсиве

За это задание вы можете получить 1 балл на ЕГЭ в 2023 году

Разбор сложных заданий в тг-канале:

Посмотреть

Задача 1

ДЛЯ 2022

Дядя Миша заполнял таблицу истинности функции F:

¬(𝑦→𝑤)∨(𝑥≡𝑧)∨𝑥

но как обычно ничего не успевает и заполнил лишь фрагмент из трёх различных её строк, даже не указав, какому…

Задача 2

Каждое из логических выражений A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности обоих выражений совпадают ровно 10 строк. Каково максимально возможно…

Задача 3

Логическая функция F задаётся выражением (x → y) → (w → g). Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F ложно.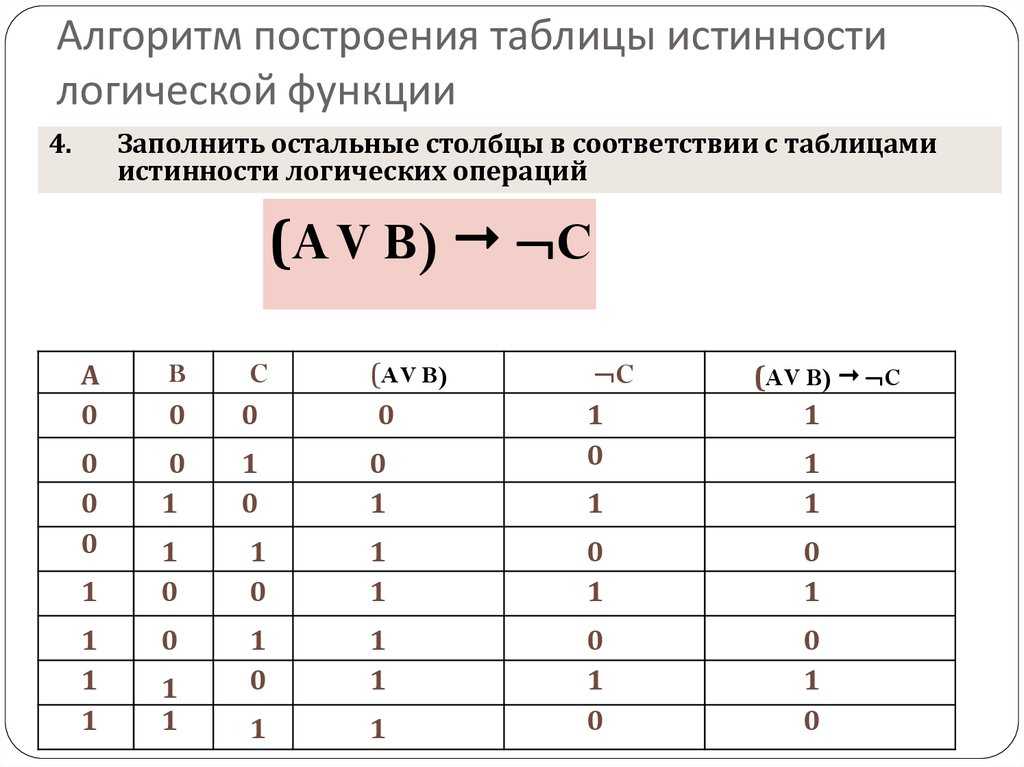 Определите, какому…

Задача 4

Логическая функция F задаётся выражением ¬x ⋁ y ⋁ (z ⋀ ¬w). Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F ложно.

Определите, какому…

Задача 5

Логическая функция F задаётся выражением (¬x⋀y)⋁(z⋀¬y)⋁ w. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Определите, …

Задача 6

Логическая функция F задаётся выражением (x⋁y)⋀(¬y ≡ z)⋀ w. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Определите,…

Задача 7

Логическая функция F задаётся выражением ((¬z⋁¬x)⋀z)⋁w⋁¬y. Ниже приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Опред…

Задача 8

Логическая функция F задаётся выражением ((x ⋀ z) ⋁ ¬x) ⋀ ¬w ⋀ y.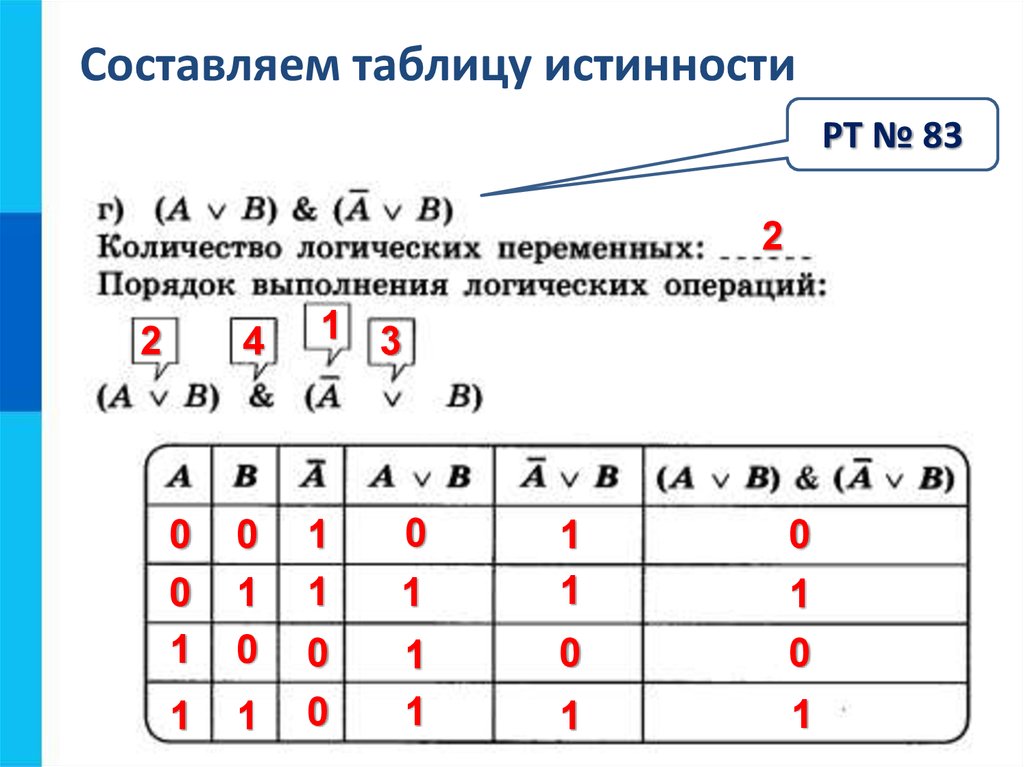

Ниже приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истин…

Задача 9

Логическая функция F задаётся выражением (y ⋀ (w → x)) → g. Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F ложно. Определите, какому…

Задача 10

Логическая функция F задаётся выражением ¬(x → z) ⋀ (¬y ⋁ w). Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F истинно. Определите, ка…

Задача 11

Логическая функция F задаётся выражением y ⋀ (x → z) ⋀ ¬w. Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F истинно. Определите, каком…

Задача 12

Логическая функция F задаётся выражением (x = y) ⋁ ¬(x → w)⋁ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Определ…

Задача 13

Логическая функция F задаётся выражением ((y → x)⋀(¬x → z))⋁ ¬w. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Опреде…

Задача 14

Логическая функция F задаётся выражением (x = y) ⋁ ¬(y → w) ⋁ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Опреде…

Задача 15

Логическая функция F задаётся выражением (x → y)⋀(¬y⋁w)⋀z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.

Определите, …

Задача 16

Укажите значения логических переменных X, Y, Z, T , при которых логическое выражение (X → Y ) ∨ ((X ∧ ¬Z) → T ) ложно.

Ответ запишите в виде строки из четырёх значений переменных X…

Задача 17

Дан фрагмент таблицы истинности выражения F:

…

x1	x2	x3	x4	x5	x6	x7	x8	F
0	0	0	1	0	0	0	1	0
0	0	1	1	1	1	0	0	1
0	1	0	1	1	0	1	1	1
0	1	1	0	0	1	0	1	0
1	0	0	0	1	1	0	0	0
1	0

Задача 18

Логическая функция F задаётся выражением (x → ¬y) ≡ (z ∨ y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Переменная 1 ???…

Задача 19

Логическая функция F задаётся выражением ¬x∧(y → z).Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Переменная 1 ???

Переменн…

Задача 20

Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (¬y ∧ ¬z). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Переменная 1 ?…

1 2

Второе задание экзамена по информационным технологиям проверяет, как выпускники умеют строить таблицы истинности различных логических выражений.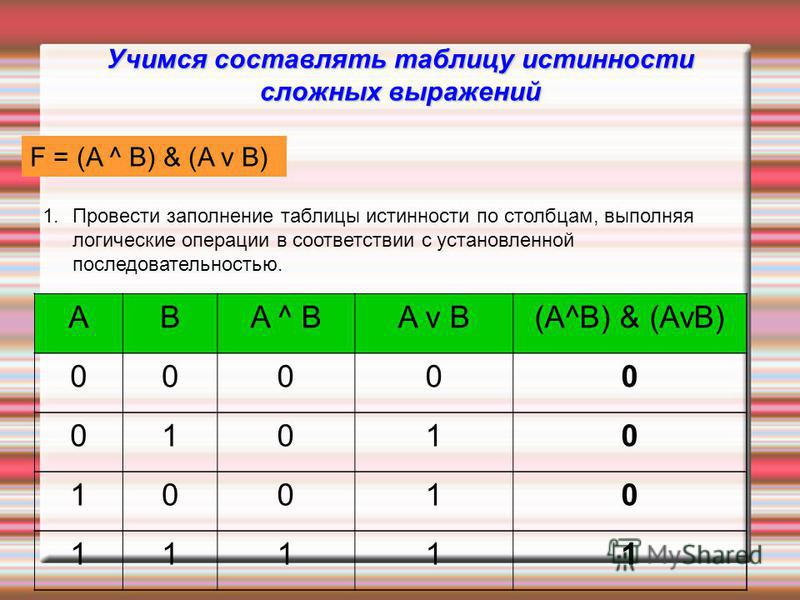

Количество переменных в примерах для решения может быть более трех. В части задач схемы уже частично построены, и вопросы касаются пустых ячеек. Как правило, ответ в таких случаях нужно выбрать из предложенных версий. Для этого типа задач правильный вариант всегда только один.

Если таблица истинности не имеет пустых клеток, вопрос может быть сформулирован следующим образом: «Что за высказывание может соответствовать F?» или «Выберите из предложенных версий ту, которая больше всего подходит под ячейку F».

Задача под номером два по праву считается одной из труднейших в экзамене по информатике. Эксперты советуют не сидеть над ней дольше пяти минут, а переходить к следующим заданиям. Второй вопрос часто оставляют на потом, возвращаясь к нему после решения более простых задачек.

Теория к заданию 2 по информатике: Алгебра логики. Таблицы истинности

<< Задание 1

Задание 3 >>

Популярные материалы

ЕГЭ по информатике — Задание 2 (Мощнейший метод)

Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.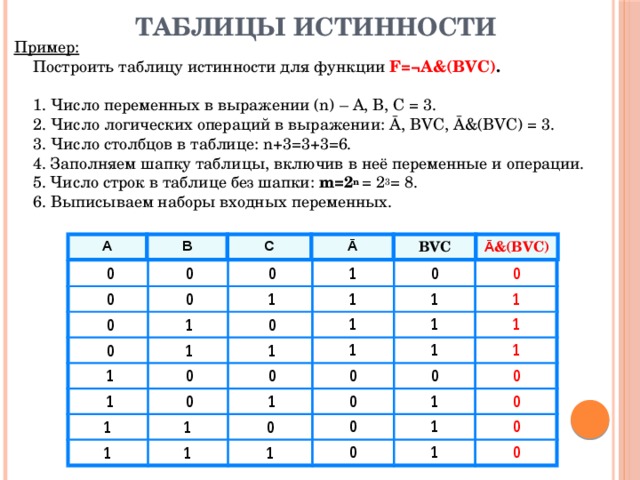

Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения:

0 (Ложь) или 1 (Истина).

С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.

Порядок выполнения логических операций:

1. () — операции в скобках
2. ¬ — логическое отрицание
3. ∧ — логическое умножение
4. ∨ — логическое сложение
5. ⟶ — следование
6. ≡ — равнозначность

Так же на ЕГЭ по информатике будет полезно знать логические формулы :
Ещё соотношения:

Передём к решению задач из ЕГЭ по информатике

Задача 1 (лёгкая)

Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x).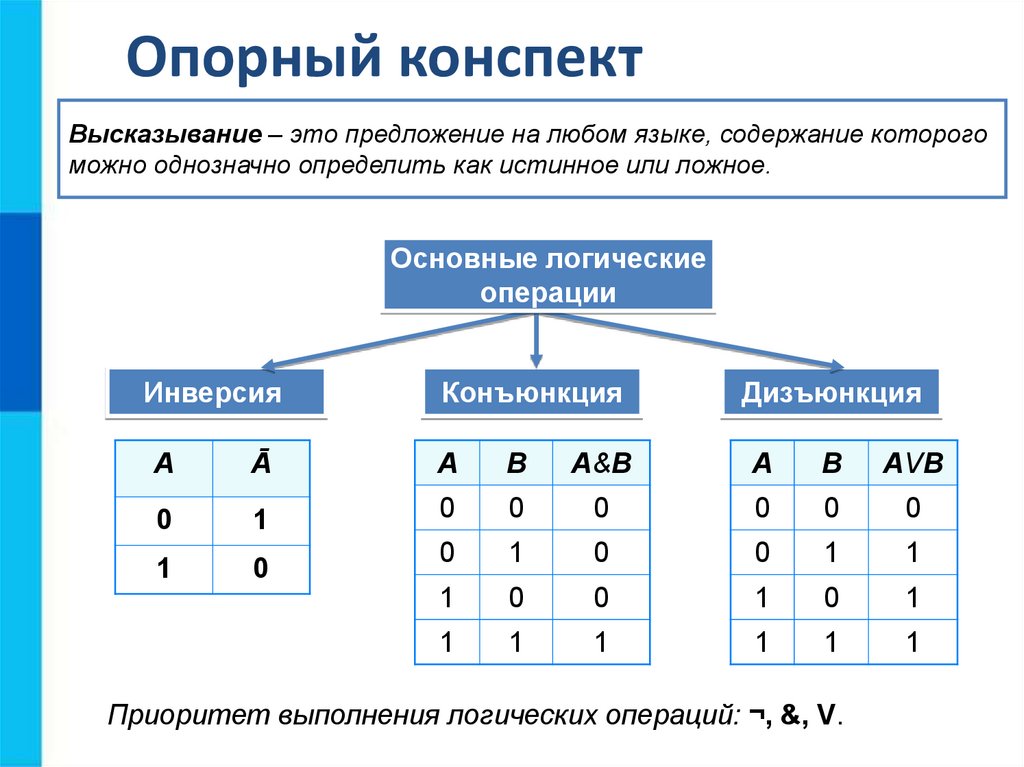 Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:

Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.

Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.

Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.

Ответ: zyxw

Задача 2 (средний уровень)

Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:

Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.

Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).

Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.

Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!

Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).

Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).

Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.

Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.

Тогда ответ будет равен yxwz.

Ответ: yxwz

Мощнейший метод для решения второго задания из ЕГЭ по информатике

Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).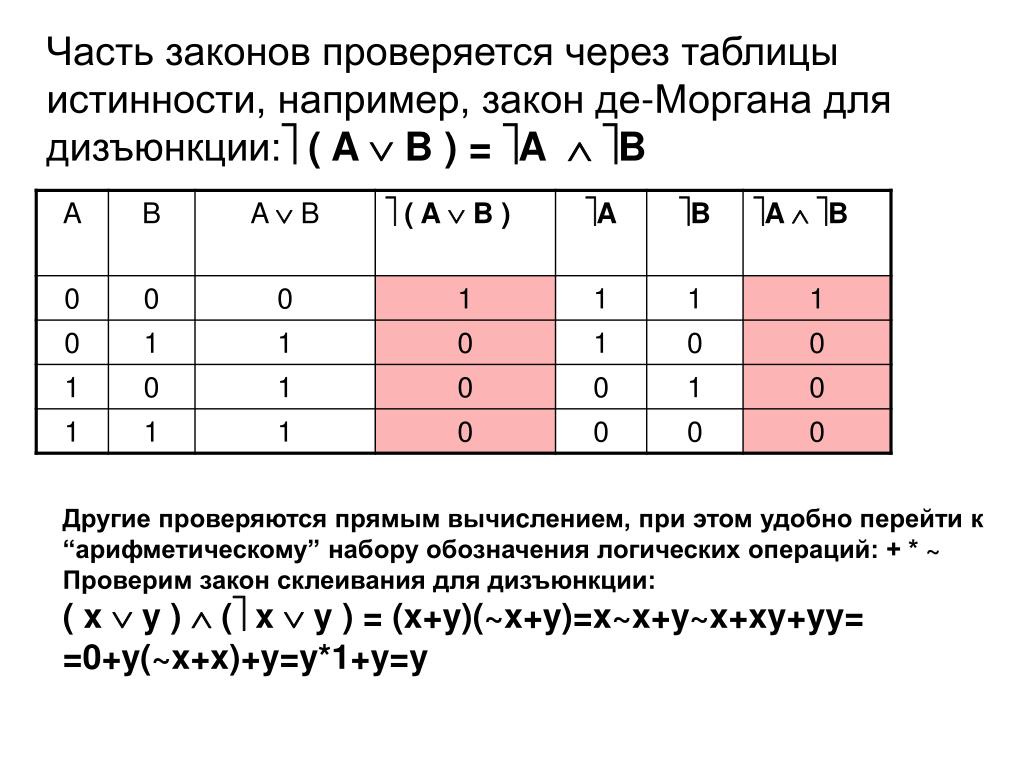
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:

Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.

Решение:

«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).

Тогда каждое выражение должно равняться 0(нулю).

Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 2⁴).

Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).

При небольшой тренировке анализ подобных выражений занимает сущие секунды!

У нас получается 4 строчки, которые удовлетворяют нашей функции:

Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).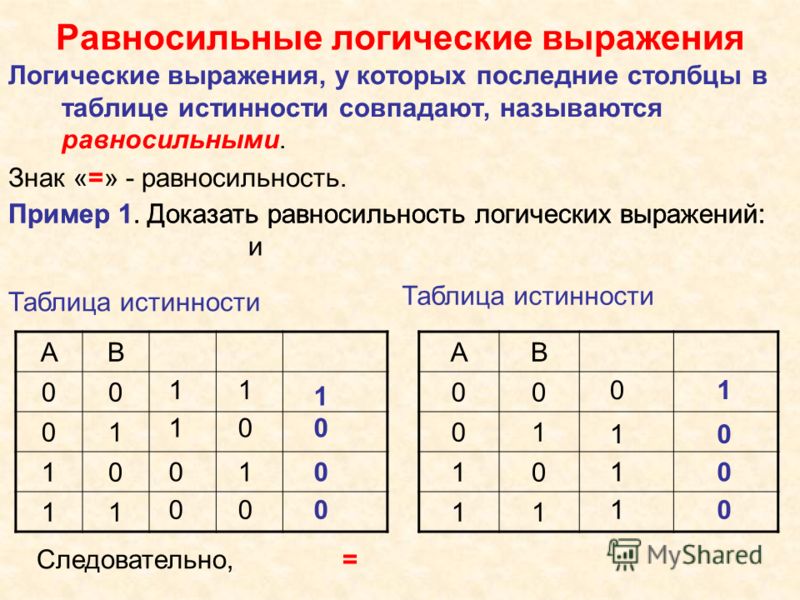

Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.

Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец

Ответ: ywzx.

На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!

Пока!

Символическая логика с таблицами истинности.

Мы рассмотрели основы символьной логики… | Бретт Берри | Математические приемы

Пример

Мы рассмотрели основы символьной логики в последнем посте . Теперь давайте воспользуемся этими навыками, решив оператор символьной логики.

Последнее сообщение

Введение в таблицы истинности и булеву алгебру

Таблица истинности — это небольшой удобный логический прибор, который используется не только в математике, но также в информатике и…

medium.com

Генерация таблицы истинности для (A ∧ ~B) → (C ∨ D)

Ключ к решению этой проблемы состоит в том, чтобы разбить ее на простейшие компоненты и решать по частям. .

Шаги 1 и 2

Шаг 1: У нас есть 4 переменные, поэтому нам нужно 4 столбца. Нам также понадобится 16 рядов, так как их по два варианта для каждого.

Самый простой способ скомпоновать таблицу — использовать шаблон с чередованием T/F .

В первой колонке заполните первую половину буквой T, а вторую половину буквой F. Затем чередуйте T/F через каждые 8÷2 или 4 во второй колонке. Продолжайте следовать шаблону, чередуя T/F каждые 2 в третьем столбце и каждый второй пробел в последнем столбце. Это охватывает все возможные перестановки.

Шаг 2: Нам нужно ~B вместо B, поэтому переверните все значения истинности в столбце B. Если вы используете карандаш, вы можете стереть столбец B и просто заменить его на ~B.

Шаг 3: Далее нам нужно вычислить (A ∧ ~B) и (C ∨ D). Для этих вычислений мы добавим в нашу таблицу еще два столбца.

Для логической конъюнкции, т. е. оператора И, нам нужно, чтобы и A, и ~B были истинными, чтобы получить истинный результат. Для ИЛИ нам нужно, чтобы только один из C или D был True, чтобы получить True. Используйте эти знания, чтобы заполнить последние два столбца.

Шаг 3

Шаг 4: Это последний шаг! Добавьте еще один столбец в конец для нашего окончательного вычисления: (A ∧ ~ B) → (C ∨ D).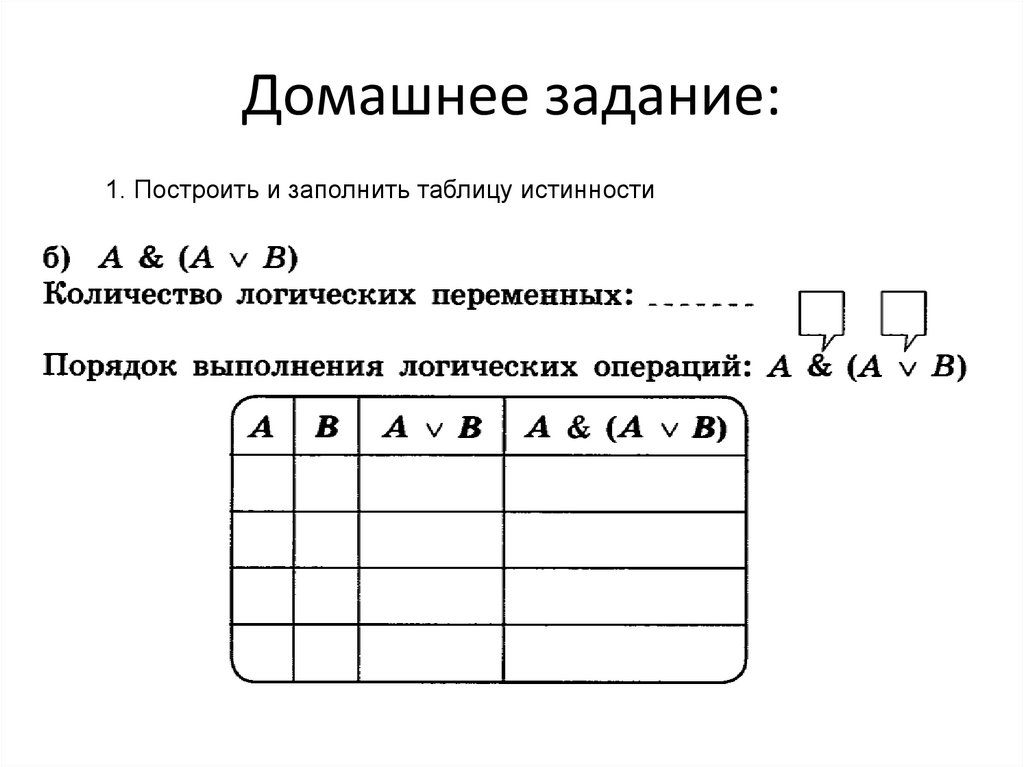

Мы знаем, что только в одном случае импликация (→) ложна, и это когда T → F. Поэтому проверьте столбцы (A ∧ ~B) и (C ∨ D) для этого случая. В нашей таблице есть только одна строка, где это происходит. Отметьте этот результат как F, а остальные как T.

Решение: Таблица истинности для (A ∧ ~B) → (C ∨ D)

Как бы запутанно это ни казалось на первый взгляд, это всего лишь простое применение определений. представлены в последнем посте. Просто не забывайте всегда брать его по одному кусочку за раз.

→ Чтобы увидеть больше уроков по математике, , посмотрите Math Hacks на YouTube! ←

Математические лайфхаки

Добро пожаловать во второй сезон математических лайфхаков! В этом сезоне мы рассмотрим темы из алгебры и тригонометрии, а также…

www.youtube.com

Введение в таблицы истинности и булевую алгебру

по математике, но также и по компьютерным наукам и…

Medium. com

Топ 10 секретов Triangle’s Pascal’s Triangle

Биномиальная теорема, Fibonacci Sequence, Sierpinski Triangle & More

Medium.com

Комбинации VS Permations

9007 Medium.com

. , и, как правило, неправильным образом. Мы говорим что-то вроде: «Эй, что у тебя…

medium.com

Таблица истинности — И, ИЛИ, НЕ-И, НЕ-ИЛИ, условное и биусловное

Таблица истинности используется для выполнения логических операций в математике. Эти операции включают булеву алгебру или булевы функции. В основном он используется для проверки того, является ли пропозициональное выражение истинным или ложным в соответствии с входными значениями. Это основано на булевой алгебре. Он состоит из столбцов для одного или нескольких входных значений, скажем, P и Q, и одного назначенного столбца для выходных результатов. Вывод, который мы получаем здесь, является результатом унарной или бинарной операции, выполненной над заданными входными значениями. Некоторыми примерами бинарных операций являются AND, OR, NOR, XOR, XNOR и т. д. Здесь мы изучим все операции с их соответствующей таблицей истинности.

Содержание:

• Таблица истинности для унарных операций
  • Логическая истина
  • Логическая Ложь
  • Логическая идентификация
  • Логическое отрицание
• Таблица истинности для бинарных операций
  • И и НЕ-И
  • ИЛИ И ИЛИ
  • Исключающее ИЛИ
  • Условное и биусловное
• Пример

Таблица истинности для унарной операции

Унарные состоят из одного входа, который либо Истина, либо Ложь. Для этих входных данных есть четыре унарные операции, которые мы собираемся выполнить здесь. Их:

• Логическая истина (только истина)
• Логическая ложь (только ложь)
• Логическая идентификация
• Логическое согласование

Логический Истинно

В этой операции вывод всегда истинен, несмотря на любое входное значение. Предположим, что P обозначает входные значения, а Q обозначает выходные данные, тогда мы можем записать таблицу как;

П	Q→T
Т	Т
Ф	Т

Где T=Истина и F=Ложь

Логическая Ложь

В отличие от логической истины, выходные значения для логической ошибки всегда ложны. Также говорят, что это unary falsum . Создадим таблицу истинности для этой операции.

П	Q→F
Т	Ф
Ф	Ф

Где T=Истина и F=Ложь

Логическая идентификация

В этой операции выходное значение остается таким же или равным входному значению. Выясним с помощью таблицы.

П	Q→P
Т	Т
Ф	Ф

Итак, здесь видно, что даже после выполнения операции над входным значением его значение остается неизменным.

Логическое отрицание

Когда мы выполняем операцию логического согласования над одним логическим значением или пропозициональным значением, мы получаем значение, противоположное входному значению, в качестве выхода. Давайте посмотрим на таблицу истинности для этого:

П	Q→~P
Т	Ф
Ф	Т

Символ «~» означает отрицание значения.

Таблица истинности для двоичных операций

Двоичная операция состоит из двух переменных для входных значений. Здесь также выходной результат будет основан на операции, выполненной над входными значениями или значениями предложения, и это может быть значение True или False. Основные бинарные операции:

• И
• ИЛИ
• НЕ-И
• НИ
• Исключающее ИЛИ
• Условное или «Если-то»
• Биусловный

Составим сводную таблицу истинности для всех бинарных операций, взяв в качестве входных значений P и Q.

П	Q	И (∧)	ИЛИ (∨)	НЕ-И (~∧)	НОР (~∨)	Исключающее ИЛИ (⊻)	Условный (⇒)	Биусловный (⇔)
Т	Т	Т	Т	Ф	Ф	Ф	Т	Т
Т	Ф	Ф	Т	Т	Ф	Т	Ф	Ф
Ф	Т	Ф	Т	Т	Ф	Т	Т	Ф
Ф	Ф	Ф	Ф	Т	Т	Ф	Т	Т

Где T означает True, а F — False.

Теперь давайте обсудим каждую бинарную операцию здесь одну за другой.

И и НЕ-И Операция

Из таблицы видно, что для операции И вывод имеет значение Истина, только если оба входных значения истинны, в противном случае вывод будет ложным. Оператор И обозначается символом (∧).

Принимая во внимание, что отрицание операции AND дает результат вывода для NAND и обозначается как (~∧).

ИЛИ и НЕ-ИЛИ Операция

Оператор OR указывает, что если любое из двух входных значений равно True, выходной результат всегда равен TRUE. Он представлен символом (∨).

Но операция НЕ-ИЛИ дает результат, противоположный операции ИЛИ. Это означает, что утверждение, которое истинно для ИЛИ, является ложным для НЕ. И выражается как (~∨).

Операция XOR

Эта операция указывает, что входные значения должны быть точно True или False. Символ XOR — (⊻).

Условная и биусловная операция

Условный оператор, также известный как оператор «если-то», дает результаты как «Истина» для всех входных значений, за исключением случаев, когда «Истина» подразумевает «Ложь». Обозначается знаком «⇒». Эта операция логически эквивалентна операции ~P ∨ Q. Докажем здесь;

Р	Q	~P	~П ∨ Q
Т	Т	Ф	Т
Т	Ф	Ф	Ф
Ф	Т	Т	Т
Ф	Ф	Т	Т

Вы можете сопоставить значения P⇒Q и ~P ∨ Q. Оба равны.

Двойное условие также известно как логическое равенство. Если оба значения P и Q равны True или False, то он генерирует вывод True, иначе результат будет ложным.