Get Vector Components — Unreal Development Kit (UDK)
Get Vector Components ( получить компоненты вектора ) данный элемент Unreal Kismet позволяет разложить координаты точки на 3 отдельных переменных (X Y Z) в виде дробных значений типа Float. Узлы данного элемента позволяют настроить следующие параметры:
Пример использования: Давайте будем следить за нашим персонажем а именно выводить координаты точки где он находиться. Для этого воспользуемся элементом Get Location and Rotation который может вернуть нам координаты обьекта в мире которым и станет на персонаж. Для этого откроем Unreal Kismet выбрав пункт меню View -> UnrealKismet Добавим в Unreal Kismet событие загрузки уровня после загрузки уровня будем запускать сложение друх чисел.
Целью получения координат будет наш игрок ( Player ) создадим переменную которая будет хранить всю информацию о нашем игроке из нее мы и получим координаты его расположения. Создадим переменную в которую функция вернет значение вектора Location расположение игрока.
Если попась мышкой по выходу Location и нажать правую кнопку мыши то можно создать переменную нужного типа которая буде сразу привязана к этому узлу. Результат Далее воспользуемся компонентом Get Vector Components для получения координат из этого вектора. Добавим его в Unreal Kismet и свяжем с нашей схемой. Теперь создадим 3 переменных типа Float в которые сохраним координаты где стоит наш персонаж И свяжем их с узлами функции Get Vector Components. Осталось добавить вывод координат на экран для этих целей подойдет компонет Log. Добавляем элемент в нашу схему. Добавляем в лог 2 узла 1) вывод нашей координаты типа Float 2) Вывод текста что это за значение например Coord X Введем значение этой переменной Нажав кнопку Ctrl выделяем компонент Log и переменную копируем его 3 раза для вывода трех координат. И меняем в тексте букву на X Y Z Связываем полученные параметры из функции Get Vector Components с с выводом их в лог Запустим игру и посмотрим что получилось. Отлично работает но что если нужно получать координаты игрока например раз в секунду для этих целей можно применить компонет Unreal Kismet под названием Delay (1.00). Он будет выполнять задержку в 1 секунду перед следующим вызовом функции получения координат Связжем его вот таким образом Теперь функция будет бесконечно следить за нашим игроком Вот как то так |
Как найти орт вектора? Ответ на webmath.ru
Содержание:
- Формула
- Примеры нахождения орта вектора
Формула
Чтобы найти орт $\bar{e}$ вектора $\bar{a}$, нужно вектор $\bar{a}$ поделить на его длину:
$$\bar{e}=\frac{\bar{a}}{|\bar{a}|}$$
Если вектор задан на плоскости своими координатами $\bar{a}=\left(a_{x} ; a_{y}\right)$, то его орт вычисляется по формуле:
$$\bar{e}=\frac{\bar{a}}{|\bar{a}|}=\frac{a_{x} \cdot \bar{i}+a_{y} \cdot \bar{j}}{\sqrt{a_{x}^{2}+a_{y}^{2}}}=\left(\frac{a_{x}}{\sqrt{a_{x}^{2}+a_{y}^{2}}} ; \frac{a_{y}}{\sqrt{a_{x}^{2}+a_{y}^{2}}}\right)$$
Если вектор задан в пространстве и имеет координаты $\bar{a}=\left(a_{x} ; a_{y} ; a_{z}\right)$, то его орт вычисляется по формуле:
$$\bar{e}=\frac{\bar{a}}{|\bar{a}|}=\frac{a_{x} \cdot \bar{i}+a_{y} \cdot \bar{j}+a_{z} \cdot \bar{k}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}=$$ $$=\left(\frac{a_{x}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} ; \frac{a_{y}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} ; \frac{a_{z}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}\right)$$
Примеры нахождения орта вектора
Пример
Задание.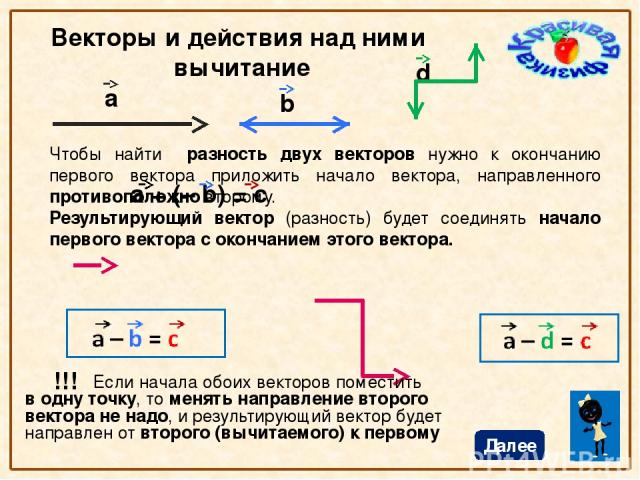
{2}}}=\frac{-2 \cdot \bar{i}+2 \cdot \bar{j}}{\sqrt{4+4}}=\frac{-2 \cdot \bar{i}+2 \cdot \bar{j}}{\sqrt{8}}=$$
$$=\frac{-2 \cdot \bar{i}+2 \cdot \bar{j}}{2 \sqrt{2}}=-\frac{1}{\sqrt{2}} \cdot \bar{i}+\frac{1}{\sqrt{2}} \cdot \bar{j}$$
Таким образом, искомый орт вектора $\bar{a}$ имеет координаты $\bar{e}=\left(-\frac{1}{\sqrt{2}} ; \frac{1}{\sqrt{2}}\right)$
Ответ. $\bar{e}=\left(-\frac{1}{\sqrt{2}} ; \frac{1}{\sqrt{2}}\right)$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны точки $A(3 ;-1 ; 4)$ и $B(2 ; 0 ; 2)$ . Найти орт вектора $\overline{A B}$
Решение. Найдем координаты вектора $\overline{A B}$, для этого из координат конца вектора (точки $B$ ) вычтем соответствующие координаты начала (точки $A$ ):
$$\overline{A B}=(2-3 ; 0-(-1) ; 2-4)=(-1 ; 1 ;-2)$$
Для нахождения орта полученного вектора воспользуемся формулой
$$\bar{e}=\frac{a_{x} \cdot \bar{i}+a_{y} \cdot \bar{j}+a_{z} \cdot \bar{k}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$$
Подставим в неё координаты вектора $\overline{A B}$, будем иметь:
$$\bar{e}=\frac{-1 \cdot \bar{i}+1 \cdot \bar{j}-2 \cdot \bar{k}}{\sqrt{(-1)^{2}+1^{2}+(-2)^{2}}}=\frac{-1 \cdot \bar{i}+1 \cdot \bar{j}-2 \cdot \bar{k}}{\sqrt{1+1+4}}=$$ $$=\frac{-1 \cdot \bar{i}+1 \cdot \bar{j}-2 \cdot \bar{k}}{\sqrt{6}}=-\frac{1}{\sqrt{6}} \cdot \bar{i}+\frac{1}{\sqrt{6}} \cdot \bar{j}-\frac{2}{\sqrt{6}} \cdot \bar{k}$$
Таким образом, орт вектора $\overline{A B}$ имеет координаты $\bar{e}=\left(-\frac{1}{\sqrt{6}} ; \frac{1}{\sqrt{6}} ;-\frac{2}{\sqrt{6}}\right)$
Ответ.
$\bar{e}=\left(-\frac{1}{\sqrt{6}} ; \frac{1}{\sqrt{6}} ;-\frac{2}{\sqrt{6}}\right)$
Читать дальше: как найти вектор по точкам.
linear алгебра — Как разделить вектор-строку $1 \times n$ на вектор $n \times 1$ и результат такого деления
Деление на вектор не определено. Позвольте мне дать вам некоторое представление о матрицах, чтобы понять, почему. Обычно матрицу можно рассматривать как оператор. Грубо говоря, матрица — это то, что действует на векторы и возвращает другой вектор.
У вас есть вектор-строка (она же матрица 1xn) и векторы-столбцы (она же матрица nx1). Если вы используете вектор-строку, то вы пишете $xA = y$, а затем мы говорим, что матрица A манипулировала вектором-строкой x для получения вектора-строки y. Если вы используете векторы-столбцы, вы пишете $Ax = y$, и мы говорим, что мы манипулировали x для получения вектора y. Обратите внимание, что с векторами-столбцами мы умножаем справа.
В большинстве математических и инженерных областей люди используют векторы-столбцы, и мы умножаем их на матрицы, чтобы манипулировать этими векторами, чтобы изменить, например, направление векторов по оси x или по оси y и т.
д. В других областях математики, таких как теория вероятностей, люди используют векторы-строки и вы умножаете по схеме $xA = y$.
Позже, я полагаю, люди обобщили определение умножения матрицы на вектор и добавили такие функции, как умножение матрицы на матрицу (которое в основном дает — в случае умножения двух матриц — в качестве вывода именно тот результат, который вы получили бы, если бы вы использовал бы оператор дважды). Причина, по которой у вас так много плюсов в вашем определении умножения матриц, заключается в том, что вы хотите просмотреть все возможные комбинации (и принять во внимание каждую комбинацию выход-вход).
Еще позже люди снова обобщили это понятие, а также разрешили перемножать отдельные строки и столбцы (просто отдельные векторы) друг с другом. У этого также были интересные факты, потому что у него были хорошие приложения, такие как скалярное произведение строки, умноженной на столбец.
В истории выше то, что я написал, возможно, исторически неверно, но история имеет смысл и помогает понять интуицию, стоящую за этими вещами.
Возвращаясь к вашему вопросу. В моей истории есть место только умножениям, так как только они подходят к моей истории преобразования векторов. Также знайте, что матрицы — очень своеобразные вещи и что многие вещи с матрицами невозможны. Например, матрицы вообще не обладают свойством коммутативности, поэтому даже для 2 заданных nxn квадратных матриц скажем A и B, $A * B \neq B * A$. 9{-1}$, но здесь это не всегда возможно. Однако некоторые матрицы имеют обратные, и такие матрицы называются обратимыми или неособыми.
Добавлено позже в связи с правкой: Это то, о чем вы говорите? (см. на 9 минуте)
Удачи.
Разделить каждую строку на элемент вектора с помощью NumPy
Улучшить статью
Сохранить статью
- Уровень сложности: Базовый
- Последнее обновление: 03 окт, 2022
Улучшить статью
Сохранить статью
В следующей статье показано, как разделить каждую строку на элемент вектора с помощью NumPy.
Элемент вектора может быть одним элементом, несколькими элементами или массивом. Оператор деления ( / ) используется для реализации требуемой функциональности. Мы можем разделить строки одномерных, двумерных или даже более типов массивов с помощью векторных элементов, и следующие примеры помогут вам лучше понять:
В примере мы разделим строки массива 1-D Numpy на элемент вектора, то есть [15]
Python3
9007 |
array([ Output:
Divide each by a vector element in двумерный массив Numpy
В этом примере мы делим каждую строку на элемент вектора двумерного массива Numpy с векторным элементом, т.е.0070 import numpy as np
n_arr = np.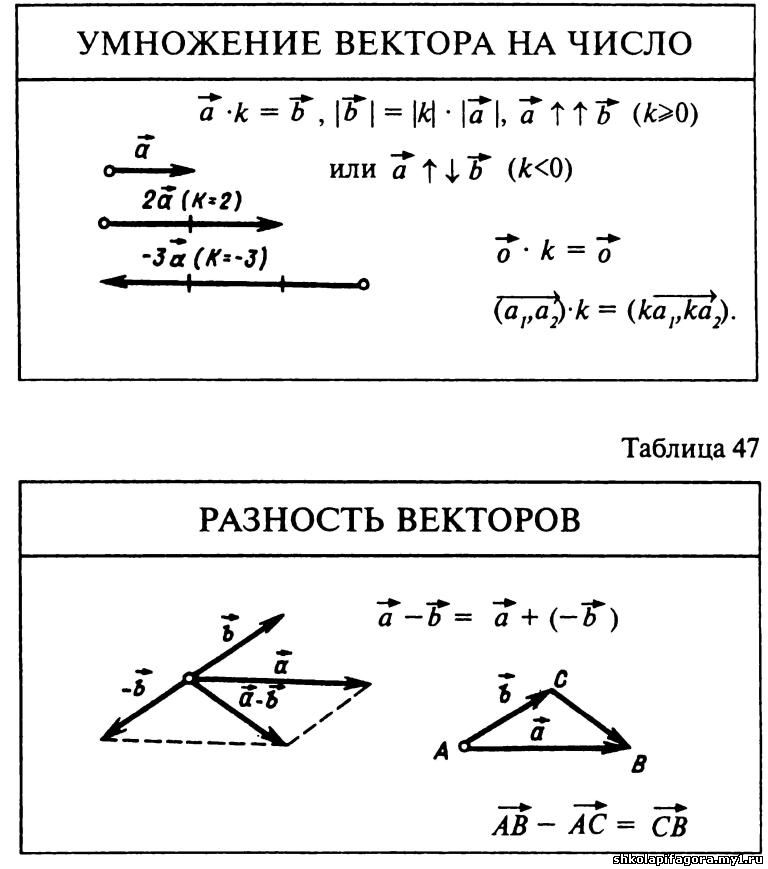 
array([[ 20 , 35 , 40 ],
[ 10 , 51 , 25 ]])
Выход: Печать ( 111070 : " ( 1".0003 Печать (N_ARR) VEC = NP.ARRAY ( 2,5 ]) 9 0003 2,5 ]) 9 0003 171717171717 гг. ) print (vec) print ( "\nResultant Array" ) print (n_arr / VEC [: Нет ])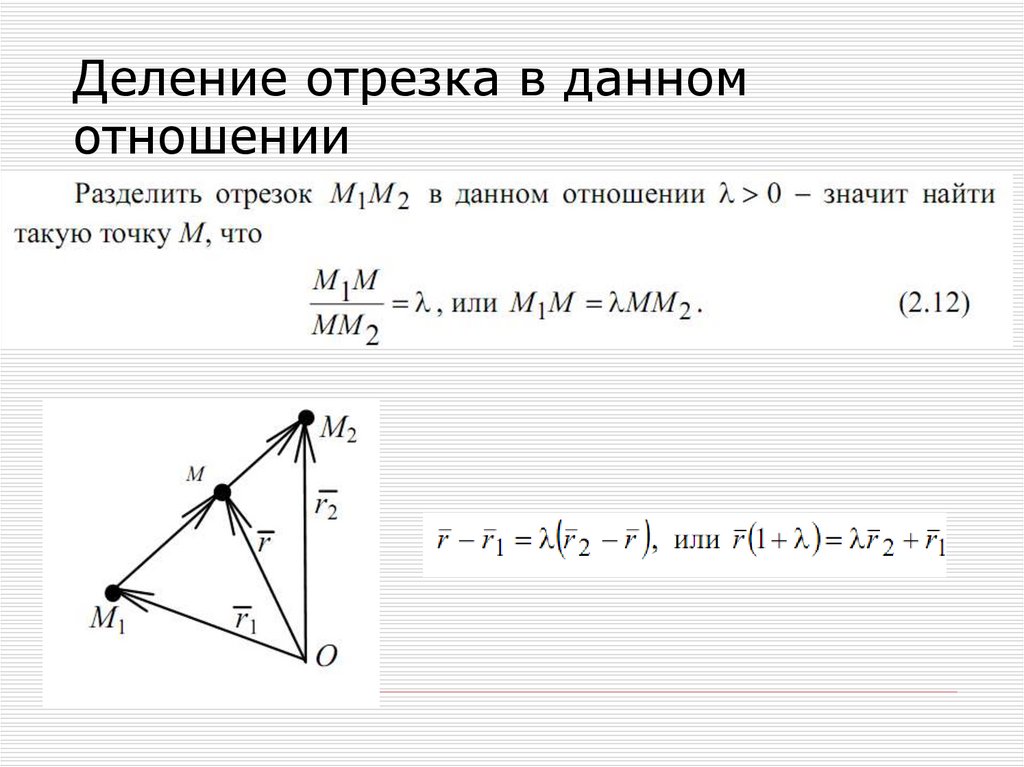 
На пример WES-Element Element в 3-делите NUMPY . В примерной дивикторе WE VECTOR. Пример . В примерной дивизии WE 3-DAM20. the rows of a 3-D Numpy array with a vector element i.e [3, 3]
Python3
. |
