Делитель напряжения: теория и принцип действия

Делитель напряжения позволяет получить меньшее напряжение из большего, напряжение может быть как постоянным, так и переменным.

Рис. 1. Схема простейшего делителя напряжения

Простейшая схема делителя напряжения содержит минимум два сопротивления. Если величины сопротивлений одинаковы, то согласно закону Ома, на выходе делителя будет получено напряжение, в два раза меньшее, чем на входе, так как падение напряжений на резисторах будет одинаковым. Для других случаев величина падения напряжений на резисторах делителя определяется по формулам

U_R1 = I*R1; U_R2 = I*R2       (1)

где U_R1, U_R2 — падения напряжения на резисторах R1 и R2 соответственно, I — ток в цепи. В схемах делителей выходное напряжение обычно снимают с нижнего по схеме резистора.

Сумма падений напряжений U_R1, U_R2 на резисторах равна напряжению источника питания. Ток в цепи будет равен напряжению источника питания, делённому на сумму сопротивлений резисторов R1 и R2:

I = U_пит / (R1 + R2)       (2)

Рассмотрим практическую схему делителя постоянного напряжения (рис.2)

Рис. 2. Делитель постоянного напряжения.

Ток, протекающий в этой схеме, согласно формуле (2) будет равен

I = 10 / (10000+40000) = 0,0002 А = 0,2 мА.

Тогда согласно формуле (1) падение напряжения на резисторах делителя напряжения будет равно:

U_R1 = 0,0002*10000 = 2 В;
U_R2 = 0,0002*40000 = 8 В.

Если из формулы (1) вывести ток:

I = U_R1 / R1       (3)

И подставить его значение в формулу (2), то получится универсальная формула для расчёта делителя напряжения:

U_R1 / R1 = U_пит / (R1 + R2)

Откуда

U_R1 = U_пит * R1 / (R1 + R2)       (4)

Подставляя значения напряжения и сопротивлений в формулу (4), получим величину напряжения на резисторе R1:

U_R1 = 10 * 10000 / (10000+40000) = 2 В,

и на резисторе R2:

U_R2 = 10 * 40000 / (10000+40000) = 8 В.

Делитель напряжения с реактивными элементами в цепи переменного тока

В вышеприведённой схеме делителя напряжения (рис. 2) были использованы активные элементы — резисторы, и питание схемы осуществлялось постоянным напряжением (хотя схему можно питать и переменным током). Делитель напряжения может содержать так же и реактивные компоненты (конденсаторы, катушки индуктивности), но в этом случае для нормальной работы потребуется питание синусоидальным током (рис. 3).

Рис. 3. Ёмкостный делитель напряжения в цепи переменного тока.

Изображённый на рисунке 3 ёмкостный делитель напряжения работает аналогично резистивному делителю, но рассчитывается несколько иначе, поскольку реактивное сопротивление конденсаторов обратно пропорционально их ёмкости:

R_c = 1/(2 * π * f * C)

Здесь R_c — реактивное сопротивление конденсатора;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
C — ёмкость конденсатора, Фарад.

То есть чем больше ёмкость конденсатора, тем меньше его сопротивление, и следовательно в схеме делителя напряжения на конденсаторе с большей ёмкостью падение напряжения будет меньше, чем на конденсаторе с меньшей ёмкостью. Следовательно, формула (4) для ёмкостного делителя напряжения примет следующий вид:

U_С1 = U_пит * С2 / (С1 + С2)       (5)

U_С1 = 10 * 40*10^-9 / (10*10^-9+40*10^-9) = 8 В,
U_С2 = 10 * 10*10^-9 / (10*10^-9+40*10^-9) = 2 В.

Индуктивный делитель напряжения (рис. 4.) так же как и ёмкостный требует для своей работы синусоидальное питающее напряжение.

Рис. 4. Индуктивный делитель напряжения в цепи переменного тока.

Поскольку реактивное сопротивление катушки индуктивности в цепи переменного тока пропорционально номиналу катушки:

R_L = 2 * π * f * L

Здесь R_c — реактивное сопротивление катушки индуктивности;
π — число Пи = 3,14159…;
f — частота синусоидального напряжения, Гц;
L — индуктивность катушки, Генри.

То следовательно и формула для расчёта индуктивного делителя напряжения будет точно такой же, как и формула для расчёта резистивного делителя напряжения (4), где вместо сопротивлений будут использоваться индуктивности:

U_L1 = U

пит * L1 / (L1 + L2)       (6)

Подставив в эту формулу параметры элементов из рисунка 4, получим:

U_L1 = 10 * 10*10^-6 / (10*10^-6+40*10^-6) = 2 В,
U_L2 = 10 * 40*10^-6 / (10*10^-6+40*10^-6) = 8 В.

В заключении следует отметить, что во всех расчётах величина нагрузки была принята равной бесконечности, поэтому полученные значения верны при работе рассмотренных делителей на сопротивление нагрузки, во много раз большее, чем величина собственных сопротивлений.

BACK

Делитель напряжения | Электронные печеньки

Что такое делитель напряжения?

Делитель напряжения — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. Делитель можно представить, как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Чаще всего делитель напряжения строится из двух резисторов. Такой делитель называют резисторным. Каждый резистор в таком делителе называют плечом. Плечо соединённое с землёй называют нижним, то что соединено с плюсом — верхним. Точка соединения двух резисторов называется средним плечом или средней точкой. Если говорить совсем упрощённо, то можно представить среднее плечо, как бассейн. Делитель напряжения позволяет нам управлять двумя «шлюзами», «сливая» напряжение в землю (уменьшая сопротивление нижнего плеча) или «подливая» напряжения в бассейн (уменьшая сопротивление верхнего плеча). Таким образом, делитель может использоваться для того, чтобы получить из исходного напряжения лишь его часть.

Принципиальная схема делителя напряжения

В рассматриваемом примере на вход (Uвх) подаётся напряжение 9В. Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?

Расчёт делителя напряжения

Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.

Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:

Rобщ = R1 + R2 = 400 + 500 = 900 Ом

По закону Ома находим силу тока, протекающего через резисторы:

I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА

Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):

Uвых = I * R2 = 0.01А * 500 Ом = 5В

Или упрощая цепочку вычислений:

Uвых = Uвх * (R2 / (R1+R2))

Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:

R1 = (Uвх-Uвых)/Iд+Iн

R2 = Uвых / Iд

Здесь Iд и Iн — ток делителя и ток нагрузки соответственно. В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд = 0.01 А (10 мА), а Iн = 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:

R1 = (Uвх-Uвых) * 100

R2 = Uвых * 100

P.S. Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель.

Проверяем:

Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:

R1 = (9-5) * 100 = 400 Ом

R2 = 5 * 100 = 500 Ом

Всё сходится!

Применение делителя напряжений

В основном делитель напряжения используется там, где нужно измерить изменяющееся сопротивление. На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.

Делитель напряжения — Википедия

Дели́тель напряже́ния — устройство , в котором входное и выходное напряжение связаны коэффициентом передачи 0⩽a⩽1{\displaystyle 0\leqslant a\leqslant 1}.

[1]

Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое — верхним^[2]. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента a{\displaystyle a} нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.

[1] Сопротивление может быть как активным, так и реактивным, а также и вовсе нелинейным, как, например, в параметрическом стабилизаторе напряжения.

Резистивный делитель напряжения

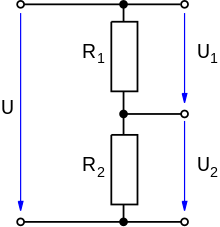Схема простейшего резистивного делителя напряжения

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

 U=IR{\displaystyle \ U=IR}.

Для каждого резистора имеем:
{U1=IR1U2=IR2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:

U1+U2=I(R1+R2).{\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}

Далее:

I=U1+U2R1+R2=UR1+R2.{\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}

Из этого следует:

{U1=IR1=UR1R1+R2U2=IR2=UR2R1+R2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R2{\displaystyle R_{2}}, можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U{\displaystyle U}. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R1+R2{\displaystyle R=R_{1}+R_{2}}. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.

Применение

Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.

Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.^[1]

Цепи обратной связи в усилителях

С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.

Простейшие электрические фильтры

RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.

Усилитель напряжения

Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если |R2|⩾|R1|{\displaystyle |R_{2}|\geqslant |R_{1}|}, а R1{\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.

Параметрический стабилизатор напряжения

Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.

Ограничения в применении резистивных делителей напряжения

Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.

Нормативно-техническая документация

• ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока

См. также

Примечания

1. ↑ ^{1 2 3} Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
2. ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.

Ссылки

Делитель напряжения

Господа, всем здрасьте!

Сегодняшняя статья будет не очень большой, но достаточно важной. Сейчас я бы хотел поведать вам про такую интересную вещь, как делитель напряжения. Эта вундервафля встречается практически в любой схеме, причем часто в очень больших количествах. Поэтому надо уметь виртуозно с ним обращаться и быстро пересчитывать в ту или в другую сторону.

Итак, что же такое делитель напряжения? Как подсказывает капитан Очевидность, он должен как-то делить напряжение. А это вполне может делать цепочка из двух последовательно соединенных резисторов. Причем входное напряжение мы подаем на вход этой цепочки, а выходное снимаем с нижнего резистора. Взгляните на рисунок 1 и вам все станет понятно.

Рисунок 1 – Делитель напряжения

Пусть у нас откуда-то приходит некоторое входное напряжение U_вх. Оно попадает на цепочку из двух последовательно соединенных резисторов R1 и R2.

Очевидно, входное напряжение каким-то образом распределяется между двумя резисторами R1 и R2. Напряжением U_вых, которое нам интересно, мы снимаем как раз-таки с нижнего резистора R2. Как его найти? Довольно просто, как оказывается. Что для этого надо сделать?

• Зная отдельные сопротивления R1 и R2 найти общее сопротивление цепочки как сумму этих сопротивлений;
• Зная общее сопротивление цепочки и приложенное к ней напряжение U_вх, с помощью закона Ома найти ток через резисторы цепочки;
• Зная ток через резистор R2 и его сопротивление, находим искомое напряжение U_вых.

Проделаем все это!

Используя закон Ома находим ток через делитель напряжения

Этот ток I течет как через резистор R1, так и через резистор R2 (мы помним, что если резисторы соединены последовательно, то через оба течет один и тот же ток). Теперь, если взглянуть на дело со стороны резистора R2, окажется, что мы легко найдем напряжение на нем. Действительно, вы ведь знаем сопротивление резистора и ток через него. Тогда согласно тому же самому закону Ома можно записать

Или, что абсолютно тоже самое

Вот по этой самой формулке можно посчитать напряжение на выходе делителя напряжения. Если хотите, можно ее запомнить, но если что она очень быстро выводится на основе элементарных соображений, поэтому, например, я ее не знаю наизусть.

Давайте теперь решим обратную задачу. Допустим, нам известно напряжение U_вых и надо найти напряжение U_вх. Такая задача тоже часто имеет место на практике. Например, когда на АЦП приходит напряжение не непосредственно от источника, а через делитель напряжения. Тогда мы с помощью АЦП производим измерение пришедшего напряжения U_вых и потом в микроконтроллере или еще где делаем пересчет для определения искомого значения U_вх.

Итак, как же, зная значение сопротивлений R1 и R2, а также напряжение U_вых, найти U_вх? Очень просто. Давайте по закону Ома найдем ток через резистор R2, раз уж нам известно напряжение U_вых на нем.

Идем дальше. Как вы помните, при последовательном соединении резисторов R1 и R2, через них будет протекать один и тот же ток, а данном случае I_R2. То есть найденный ток I_R2 течет и через резистор R1 тоже.

Это позволяет нам легко найти напряжение U_вх.

Надеюсь, особых пояснений не надо?  Мы просто умножаем ток, протекающий через цепочку резисторов, на общее сопротивление этой цепочки и таким образом получаем напряжение на входе цепочки.

Господа, а сейчас я бы хотел рассмотреть еще один скользкий момент. Мы пока что ни слова не говорили, а куда, собственно, идет это найденное нами напряжение U_вых? Действительно, куда? Ответ может быть, например, таким: на какой-нибудь высокоомный вход приемника сигнала U_вх. Что значит высокоомный в данном случае? А то, что входное сопротивление этого входа (которое считается как отношение приложенного напряжения ко входу к току входа) во много раз больше нашего сопротивления R2. Ну, хотя бы раз в десять, а лучше в сто. То есть допустим вариант, когда входное сопротивление приемника сигнала равно, например, 1 МОм, а R2=100 кОм. Тогда зачастую допустимо считать по приведенным выше формулам, однако следует понимать, что чем ближе сопротивление R2 к сопротивлению входа, тем больше будет погрешность..

А что делать, если входное сопротивление приемника соизмеримо с R2? Скажу сразу, это не очень хороший случай и лучше стараться его избегать, например, уменьшая сопротивления R1 и R2. Если же этого никак нельзя избежать, остается только включить в расчет это входное сопротивление. Как это сделать – смотрите рисунок 2

Рисунок 2 – Делитель напряжения с конечным входным сопротивлением

На рисунке 2 есть компонент R*, который как раз и представляет собой это самое сопротивление входа. Мы видим, что он соединен параллельно с нижним сопротивлением R2. Преобразуем это соединение в эквивалентное R2*, используя знания из предыдущей статьи

Наглядное представление этого преобразования показано на рисунке 3.

Рисунок 3 – Преобразование делителя

Теперь мы можем применять все ранее полученные формулы, подставляя в них вместо R2 полученное выражение R2*.

В заключении давайте попробуем решить практическую инженерную задачу по синтезу делителя напряжения. Пусть нам надо измерить напряжение, максимальное значение которого равно 15 В. Измерять будем с помощью микроконтроллера со встроенным АЦП, максимально допустимое напряжение на входе которого равно 3,3 В. Посчитать делитель напряжения для этого случая.

Расчет надо с чего-то начать. Например, в качестве нижнего резистора R2 выберем сопротивление в 10 кОм. Почему вдруг так? Да просто . Это считается не слишком много и не слишком мало и весьма ходовой номинал, найти который не проблема. А вообще можно выбрать в принципе любой резистор. Этим резистором мы задаем ток делителя, который не очень критичен в данном случае. Не следует брать слишком маленькие величины – десятки-сотни Ом, поскольку будут неоправданно большие потери мощности из-за малого сопротивления и резисторы делителя будут сильно греться. Кроме того, не следует брать слишком большие сопротивления в мегаомы. На них легко наводятся всякие паразитные напряжения из-за большого импеданса и АЦП будет мерить некорректно. Кроме того, они в совокупности с емкостями могут очень сильно интегрировать и искажать сигнал…но об этом не сейчас. Сейчас важно запомнить, что в подавляющем большинстве случаев величина сопротивлений резисторов делителя должна лежать в диапазоне единицы-десятки кОм. Есть, конечно, и исключения, но пока их не трогаем.

Итак, нижнее плечо делителя у нас R2=10 кОм, а максимально допустимое напряжение на резисторе R2 у нас U_{вых.макс}=3,3 В. Помня, что на пределе мы никогда не работаем положим, что пусть при заданных 15 В у нас на резисторе R2 будет не 3,3 В, а U_вых=3,0 В. Таким образом у нас есть небольшой запас: если входное напряжение будет чуть больше 15 В ничего страшного не произойдет и мы его даже сможем измерить. Итак, у нас на R2=10 кОм в худшем случае падает 3 В. Какой там ток по закону Ома течет через R2 в этом случае?

Теперь нам остается найти величину сопротивления R1 и делитель готов. Как это сделать? Очень просто! Что бы найти сопротивление, надо знать напряжение и ток. Ток мы только что нашли, он будет таким же, как и через R2. А напряжение на R1 будет равно разности входного напряжения U_вх и напряжения на R2 U_вых. Об этом бодро рапортуем наш с вами друг капитан Очевидность! Это следует непосредственно из логики работы делителя напряжения. Итак

Теперь легко считаем сопротивление R1

Именно такого номинала в продаже нет, зато можно купить резистор с сопротивлением 39 кОм. Этот резистор нам тоже подходит, просто в процессе расчетов необходимо будет учитывать этот факт.

Итак, господа, наш делитель напряжения, который позволит измерять напряжение до 15 В с помощью микроконтроллера состоит из резисторов R1=39 кОм и R2=10 кОм. По-хорошему после выбора конкретной марки резистора надо еще сделать проверку, не превышена ли максимально допустимая мощность, которая на нем рассеивается. Эта задача тривиальна и мы уже решали подобную вот в этой вот статье, поэтому сейчас, с вашего позволения, я не буду повторяться. Кому интересно, может сделать это сам и если будут вопросы с удовольствием обсужу это в комментариях. Ну а пока на сегодня все, господа. Удачи вам всем и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Шаг 3. Что такое делитель напряжения?

В самом простом случае делитель напряжения представляет собой два последовательно соединенных резистора (могут быть и конденсаторы — такой делитель будет работать для переменного напряжения). Казалось бы, что тут такого. Но изюминка в том, что можно с его помощью «разделить» напряжение, и получить на выходе напряжение, которое меньше входного. На сколько меньше? Это зависит от трех переменных: напряжения поданного на вход делителя и резисторов R₁-R₂. Если тебе лень разбираться, можно просто пользоваться формулой выше. А мы пойдём дальше. 

Чтобы понять как возможно такое «разделение» напряжения следует вспомнить правила Кирхгофа и что такое падение напряжения на элементе цепи. 

Падение напряжения

 Это вообще просто. Напряжением же называется разность потенциалов. U_R1 =φ1 — φ2. Так вот если измерить напряжение, к примеру, до резистора R₁ и после него, то после R₁ напряжение будет меньше — оно «упало» (закон Ома!). Поэтому напряжение, измеренное на выводах какого-либо компонента схемы и называют падением напряжения. 

Правила Киргофа

Их всего два. Во-первых, в узлах цепи сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Таким образом токи в узлах не теряются — сколько вошло, столько же вышло.

Во-вторых, сумма ЭДС замкнутой цепи равняется сумме падений напряжений вдоль этой цепи. Звучит замудрённо. Для схемы на картинке выше второе правило Кирхгофа будет выполняться так: U_вх = U_R1+U_R2, — т.е. напряжение никуда просто так не исчезает. Оно «падает» на компонентах цепи и сумма «падений» напряжения будет равна исходному значению напряжения. В нашем случае U_вх. 

Вывод формулы

Как я уже говорил, можно просто пользоваться формулой на картинке выше. Она работает. Но тебе же этого мало? Хочется понять почему так? 

По первому правилу Кирхгофа следует что через R₁, R₂ будет протекать один и тот же ток I. Тогда по второму правилу Кирхгофа: 

U_вх = U_R1+U_R2 = I*R₁ + I*R₂ = I*(R₁ + R₂). Выразим ток и получим: I = U_вх / (R₁ + R₂).
Пользуясь законом Ома: U_R2 = U_вых = I*R2 = U_вх / (R₁ + R₂) * R2

Всё просто!

Где применять?

Хочется того или нет, делители напряжения используются повсеместно. Но чаще всего специально думать о них не приходиться, кроме тех случаев, когда нужен делитель с определенным коэффициентом деления. Кстати, всем известные переменные резисторы могут использоваться как делители напряжения. 

Открою секрет. Есть ещё делители тока. Простейший делитель тока — это два резистора, соединенных параллельно.

Делитель напряжения — это… Что такое Делитель напряжения?

Дели́тель напряже́ния — устройство, в котором входное и выходное напряжение связаны коэффициентом передачи .^[1]

В качестве делителя напряжения обычно применяют регулируемые сопротивления (потенциометры). Можно представить как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним, а другое — верхним. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.^[1] Сопротивление может быть как активным, так и реактивным.

Резистивный делитель напряжения

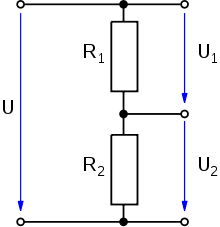Схема простейшего резистивного делителя напряжения

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

.

Для каждого резистора:


Разделив выражение для на выражение для в итоге получаем:
Таким образом, отношение напряжений и в точности равно отношению сопротивлений и .
Используя равенство
, в котором , а
И, выражая из него соотношение для тока:

Получим формулу, связывающую выходное ( ) и входное ( ) напряжение делителя:

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где  — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .

Применение

Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.

Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.^[1]

Усилитель напряжения

Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если , а  — отрицательно, например как на участке вольт-амперной характеристики туннельного диода^{[источник не указан 213 дней]}

Ограничения в применении резистивных делителей напряжения

• Номинал сопротивлений делителя должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки.

• Малые значения сопротивлений, являющихся делителем напряжения, приводят к возникновению больших токов в делителе. Снижается КПД схемы из-за нагрева сопротивлений.

• Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы.

Нормативно-техническая документация

• ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока

Примечания

1. ↑ ^{1 2 3} Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5

Ссылки

Резистивный делитель напряжения. Расчет делителя напряжения на резисторах

При проектировании электрических цепей возникают случаи, когда необходимо уменьшить величину напряжения (разделить его на несколько частей) и только часть подавать на нагрузку. Для этих целей используют делители напряжения. Они основаны на втором законе Кирхгофа.

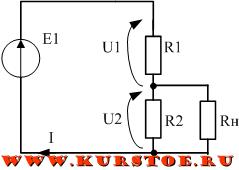
Самая простая схема — резистивный делитель напряжения. Последовательно с источником напряжения подключаются два сопротивления R1 и R2.

 

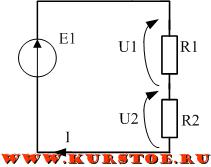
При последовательном подключении сопротивлений через них протекает одинаковый ток I.

 

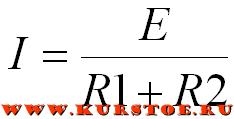
В результате, согласно закону Ома, напряжения на резисторах делится пропорционально их номиналу.

    

Подключаем нагрузку параллельно к R1 или к R2. В результате на нагрузке будет напряжение равное U_R2.

Примеры применения делителя напряжения 

1. Как делитель напряжения. Представьте, что у Вас есть лампочка, которая может работать только от 6 вольт и есть батарейка на 9 вольт. В этом случае при подключении лампочки к батарейке, лампочка сгорит. Для того, чтобы лампочка работала в номинальном режиме, напряжение 9 В необходимо разделить на 6 и 3 вольта. Данную задачу выполняют простейшие делители напряжения на резисторах.
2. Датчик параметр — напряжение. Сопротивление резистивных элементов зависит от многих параметров, например температура. Помещаем одно из сопротивлений в среду с изменяющейся температурой. В результате при изменении температуры будет изменяться сопротивление одного из делителей напряжения. Изменяется ток через делитель. Согласно закону Ома входное напряжение перераспределяется между двумя сопротивлениями.
3. Усилитель напряжения. Делитель напряжения может использоваться для усиления входного напряжения. Это возможно, если динамическое сопротивление одного из элементов делителя отрицательное, например на участке вольт-амперной характеристики туннельного диода.

Ограничения при использовании резистивных делителей напряжения

• Номинал сопротивлений делителя напряжения на резисторах должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки, подключаемой к делителю. В противном случае сопротивление нагрузки уменьшит величину разделенного делителем напряжения.
• Малые значения сопротивлений, являющихся делителем напряжения, приводят к большим потерям активной мощности. Через делитель протекают большие токи. Необходимо подбирать сопротивления, чтобы они не перегорали и могли рассеять такую величину отдаваемой энергии в окружающую среду.
• Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы, индукционные печи.
• Снижение КПД схемы за счет потерь на активных элементах делителя напряжения.
• Для получения точных результатов в делителе напряжения необходимо использовать прецизионные (высокоточные) сопротивления.