Построение таблиц истинности для логических выражений

Похожие презентации:

Основы логики. Таблица истинности. Равносильные логические выражения

Алгебра высказываний. Определение высказывания. Таблица истинности для высказываний. Логические тождества. (Лекция 2)

Построение таблиц истинности сложных высказываний

Логика высказываний

Логические основы ЭВМ. Алгоритмы логики. Построение таблиц истинности

Логика высказываний. Таблицы истинности

Логическое высказывание. Виды сложных высказываний

Построение таблиц истинности. 8 класс

Логическая модель. Логика высказываний. Основы логики высказываний

Формулы алгебры высказываний

Тема урока:
«Построение таблиц истинности для
логических выражений»
Цель: Формирование навыков применения технологии
построения таблиц истинности для составных логических
выражений.

2. Построение таблицы истинности

Таблица истинности – это таблица, показывающая
истинность сложного высказывания при всех возможных
значениях входящих переменных.
Последовательность действий:
1. Определить количество строк в таблице:
• количество строк = 2n+1,
где n – количество
логических переменных, 1 – строка заголовков
2. Определить количество столбцов в таблице:
• количество столбцов = количеству логических
переменных + количество логических операций
3. Расставить приоритеты действий:
• приоритеты: ( ), ¬, &, V, импликация, эквиваленция;
4. Заполнить столбцы входных переменных наборами
значений.
5. Заполнить таблицу истинности, выполняя логические
операции в соответствии с приоритетами действий.

3. В составных высказываниях логические операции выполняются в следующем порядке:

1.
2.
3.
4.
5.
6.
В составных высказываниях логические
операции выполняются в следующем
порядке:
Действия в скобках
Отрицание (не)
Конъюнкция (и)
Дизъюнкция (или)
Импликация
Эквиваленция

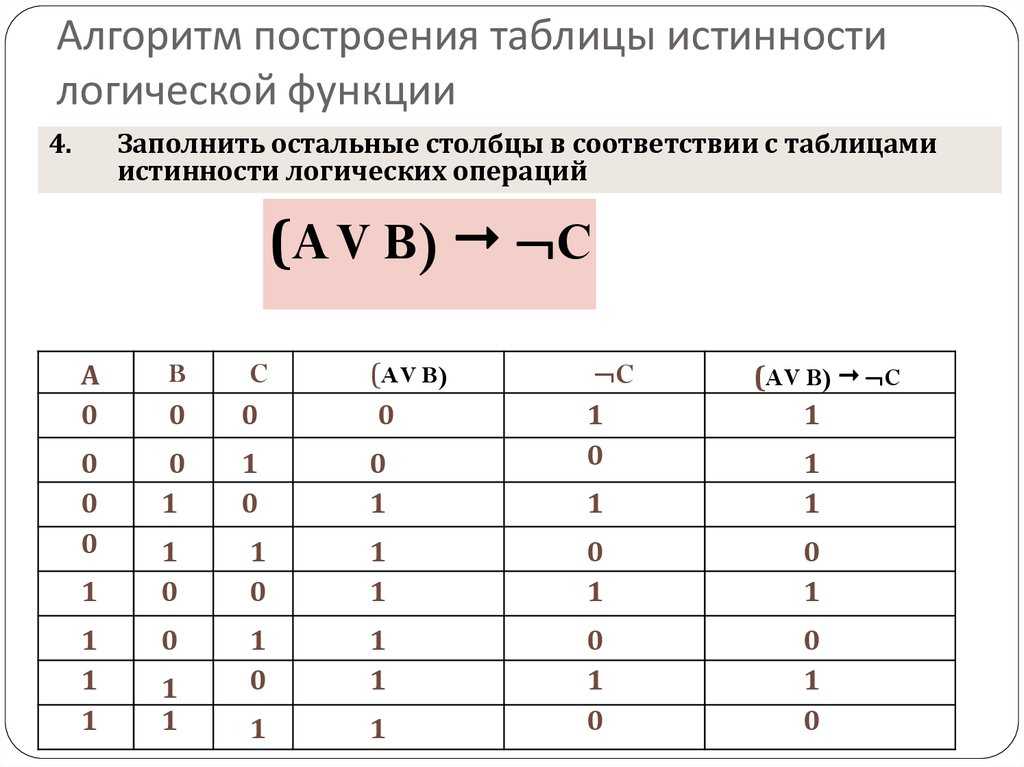
4. Заполнение таблицы истинности

22+1=5
¬( A&B)
A
B
A&B
¬( A&B)
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
2+2=4
Наборы входных переменных, во избежание ошибок,
рекомендуют вводить следующим образом:
1) разделить столбец значений первой переменной
пополам и заполнить верхнюю часть колонки нулями, а
нижнюю — единицами;
2) разделить столбец значений второй переменной на
четыре части и заполнить четверти чередующимися
группами нулей и единиц, начиная с группы нулей;
3) продолжать деление столбцов значений последующих
переменных на 8, 16 и т. д. частей и заполнение их
группами нулей или единиц до тех пор, пока группа нулей
(единиц) не будет состоять из одного символа.

6. например:

Построить таблицу истинности для выражения:
F=(A
А
В
0
0
0
А
В
B)&(A
B)
А
В
А
В
0
1
1
1
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
F

7. РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, у которых
таблицы истинности совпадают,
называют равносильными.

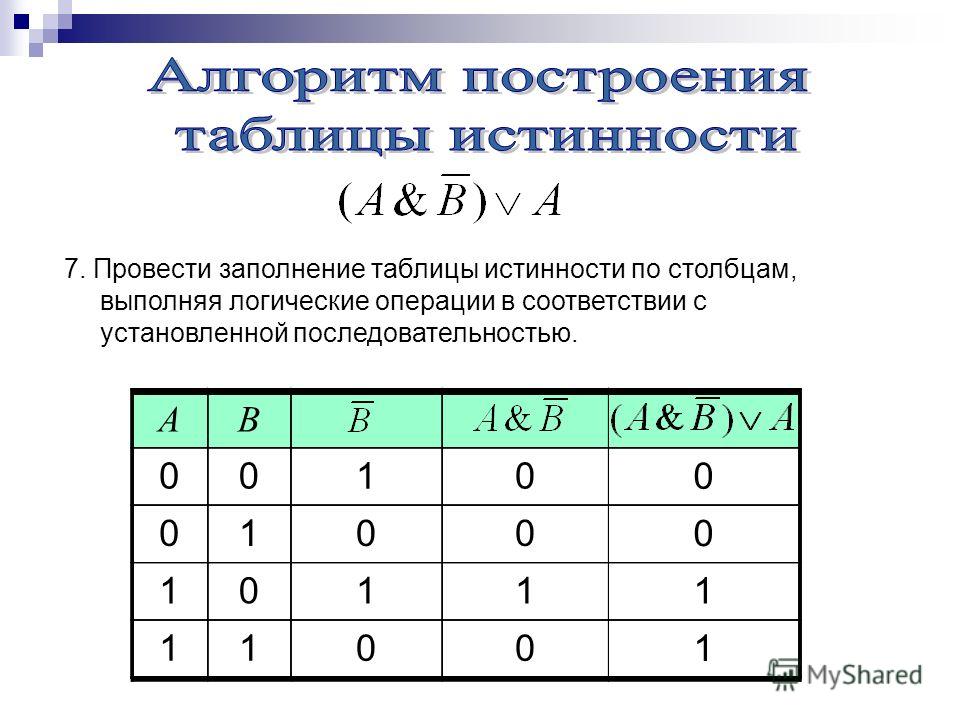
8. Доказать, что логические выражения: А & В и А В, равносильны

Доказать, что логические выражения:
А & В и А В, равносильны
Таблица истинности для А&В
Таблица истинности для А v В
А
В
А
В
А & В
А
В
А
В
А
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
1
1
0
0
0
1
1
1
0
Таблицы истинности совпадают, следовательно, логические
выражения равносильны.
В
Построим таблицу истинности для логического выражения A v А & В.
В нём две переменные, две операции, причём сначала выполняется
конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре
столбца:
Наборы входных переменных — это целые числа от 0 до 3

представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со
столбцом А. В таком случае говорят, что логическое выражение A v А& В
равносильно логической переменной А.
Таблица Для 3 переменных
(А В С)
А
В
С
С
В С
А В С (А В С)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
1
0
1
1
1
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
1
0
1
1
1
0
0
1
0
Свойства логических операций
Законы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B

English     Русский Правила

НОУ ИНТУИТ | Лекция | Минимизация логических схем

Аннотация: Рассматривается взаимосвязь различных способов описания работы логических схем и принципы их минимизации.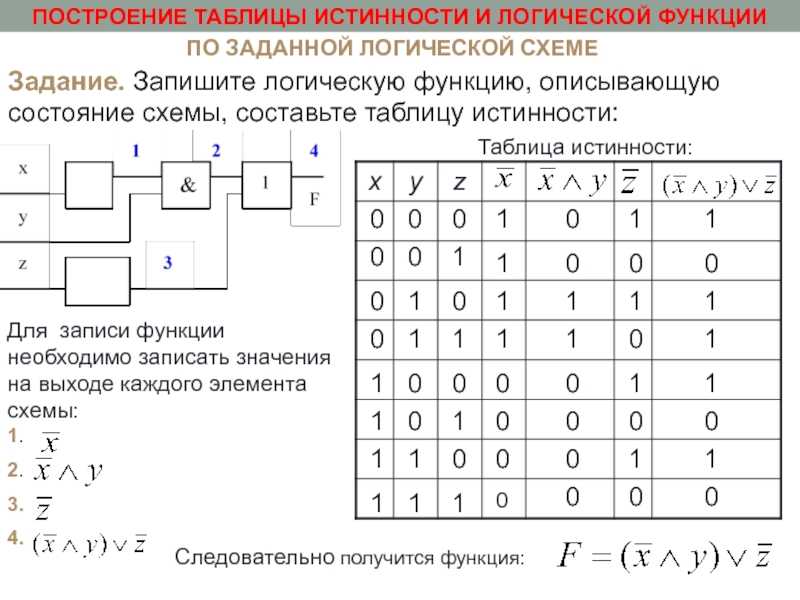

Ключевые слова: диаграмма Вейча, представление, выражение, Произведение, значение, переменная, решение обратной задачи, метод минимизации, логическая схема, КНФ

Составление логических выражений по таблице истинности

Каноническая сумма минтермов

Минтерм — это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1.

Каноническая сумма минтермов — это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.Она составляется в следующей последовательности:

1. В заданной таблице истинности подсчитывается — количество строк таблицы, в которой значение функции равно 1.
2. Затем записывается логическая сумма полных произведений.
3. Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы.

Для примера, представленного на рис. 1.6, каноническая сумма минтермов будет выглядеть так:

( 2.1)

Из сравнения (1.1) и (2.1) видно, что одной и той же таблице истинности (рис. 1.6,б) соответствуют два разных логических выражения, причем (1.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рис.

1.6, a.

Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча, диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.

Минимизация с помощью карт Карно

Карта Карно — графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности. По осям карты расставляются сочетания переменных, а внутри карты — значения функции.

Назначение карты Карно — найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например, , такая сумма равна при любом значении : при это будет , при это . Поэтому при вынесении за скобки в выражении:

intuit.ru/2010/edi»>- сумму можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты

:

1. Вертикальная ось размечается независимо от горизонтальной.
2. Начинать разметку можно с любого сочетания переменных.
3. Все сочетания переменных должны быть перечислены.
4. Для соседних клеток карты сочетание переменных должно отличаться не более чем одним знаком, причем соседними являются крайние клетки строки (столбца).

Для функции двух переменных карта Карно — это квадрат 2×2 клетки. В этих клетках размещаются 4 значения функции из последнего столбца

таблицы истинности (рис. 2.2).

Рис. 2.2. Таблица истинности (а) и карта Карно (б) для функции 2 переменных.

Для функции трех переменных карта Карно — это прямоугольник 2×4 или 4×2 клетки. В этих клетках размещаются 8 значений функции из последнего столбца таблицы истинности (рис. 2.3). При разметке большей из осей нужно четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции четырех переменных карта Карно — это квадрат 4×4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рис. 2.4). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.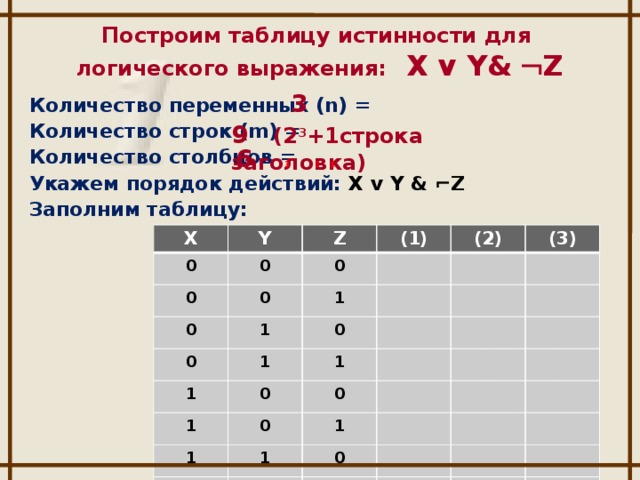

Для функции пяти переменных карта Карно представляет собой уже объемную фигуру — куб 4x4x4 клетки, поэтому для минимизации логических выражений она не применяется.

увеличить изображение
Рис. 2.3. Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных.

увеличить изображение
Рис. 2.4. Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных.

В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. Затем рассматриваются только те клетки, которые заполнены

единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:

1. intuit.ru/2010/edi»>Контуры должны быть прямоугольными и содержать количество единиц, равное , где — целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц.
2. Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть «разорванными».
3. Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица — это контур, которому соответствует полное логическое произведение всех переменных.

После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений.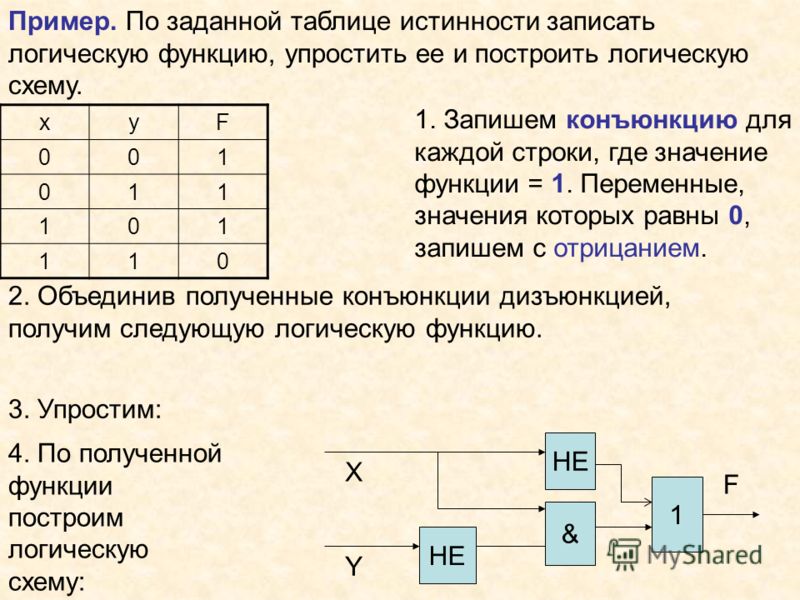 Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными.При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.

Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.5,а и нарисовать по нему логическую схему.

При одном варианте разметки осей (рис. 2.5,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рис. 2.5,в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рис. 2.5,б представлена развертка такого цилиндра, «разрезанная» между комбинациями , равными и .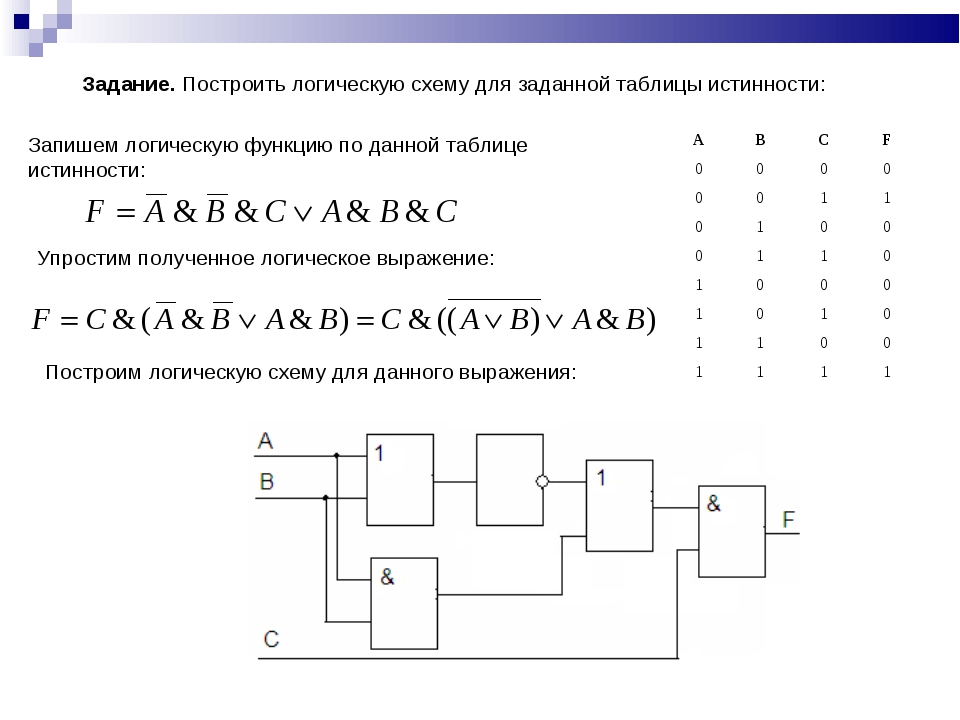 А на рис. 2.5,в представлена развертка этого же цилиндра, «разрезанная» между произведениями , равными и .

Первый контур охватывает четыре единицы, ему соответствует сумма минтермов: , в которой не изменяется только переменная . Второй контур охватывает две единицы. Ему соответствует сумма минтермов , в которой переменная принимает оба возможных значения, а произведение остается неизменным. Таким образом, получаем минимальное выражение:

( 2.2)

Ему соответствует логическая схема на рис. 2.5,г.

Рис. 2.5. Минимизация функции трех переменных

intuit.ru/2010/edi»>Для сравнения запишем максимальное выражение:

( 2.3)

Разница между (2.2) и (2.3) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (2.3), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рис. 2.5,г.

Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.6,а, и нарисовать по нему логическую схему.

Рис. 2.6. Минимизация функции четырех переменных

При первоначально выбранной разметке осей (рис. 2.6,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рис. 2.7, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры — квадрата. Для этого надо сначала соединить мысленно крайние строки — получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рис. 2.6,б представлена развертка такого торроида, «разрезанная» между комбинациями , равными и и между сочетаниями , равными и . А на рис. 2.7 представлена развертка этого же торроида, «разрезанная» между комбинациями , равными и и между произведениями , равными и . После анализа контуров получим минимальное выражение . Соответствующая ему схема приведена на рис. 2.8.

Рис. 2.7. К минимизации логической функции четырех переменных

Рис. 2.8. Логическая схема для минимизированного логического выражения

как составить таблицу истинности из логического выражения

A, B, C и D являются булевыми переменными, что означает, что каждая из них принимает значение «правда или ложь». Более сложные выражения имеют значение «истина» или «ложь». в зависимости от значений этих переменных, так, например, A’BD’ истинно, если А ложно, В истинно, D ложно, С либо истинно, либо ложно.

Сказать, что F = G, где F и G комплексные выражения, означает, что нет независимо от того, какие значения имеют логические переменные, значение F одинаково как значение G (то есть F и G либо оба истинны, либо оба ложны). Так, например, у нас есть

 АВ + АС = А(В+С)
 

, потому что если А истинно и либо В, либо С истинно, то обе стороны верны, а в любом другом случае обе стороны ложны—нет возможности присвоить значения для A, B, C так, чтобы две стороны вышли по-разному.

Как упоминалось в предыдущих постах, вы всегда можете доказать (или опровергнуть!) равенство, перебирая все возможные присваивания «true» и «false» переменные. Цель, кажется, состоит в том, чтобы доказать «теоремами», то есть используя операции, ранее подтвержденные. Как вы говорите, мы можем либо манипулировать одну сторону уравнения, пока она не примет вид другой стороны, или мы мог манипулировать обеими сторонами и привести их в общую форму.

В этом случае первое, на что следует обратить внимание, это то, что правая сторона (RHS) является копией LHS с некоторыми дополнительными элементами, прикрепленными к концу. Для этого причина, по которой проще всего манипулировать только RHS, чтобы избавиться от избыток! Мы можем начать с этой основной теоремы:

, если Q истинно всякий раз, когда истинно P, то Q = Q + P
 

Мы можем доказать эту теорему, систематически рассматривая все возможности для P и Q.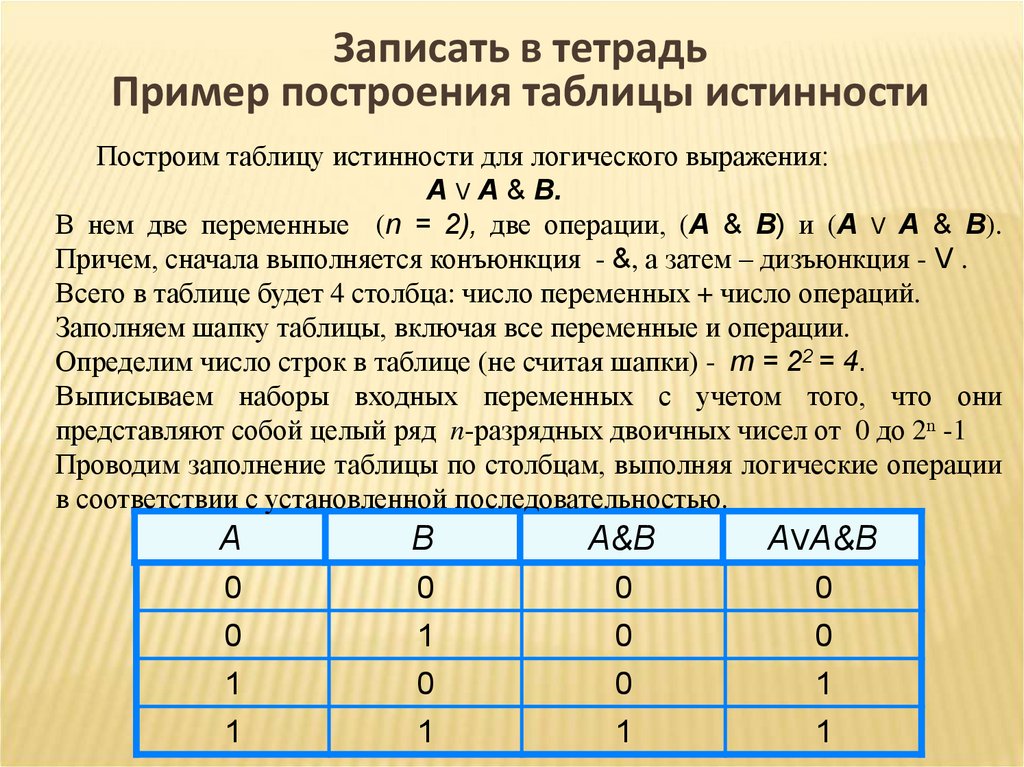 Или посмотрите на это так: если Q истинно, то обе части уравнение верно. А если Q ложно, то и P должно быть ложно (поскольку по предположение, если бы P было истинным, Q было бы истинным), следовательно, обе стороны ложны.

Учитывая эту теорему, мы доказываем:

 XY + X'Z = XY + X'Z + YZ
 

Доказательство: пусть P будет YZ, а Q будет XY+X’Z. Предположим, что P истинно, то есть Y и Z оба верны. Но если Y и Z оба истинны, то XY+X’Z должны быть истинны. (Причина: если X истинно, то, поскольку Y истинно, XY истинно. И если X истинно ложно, тогда, поскольку Z истинно, X’Z истинно. Таким образом, в любом случае XY+X’Z равно верно.) Итак, мы показали, что Q истинно всякий раз, когда истинно P, следовательно, предыдущую теорему Q = Q + P, которую в данном случае мы и хотели доказать.

Теперь мы можем доказать

 A'D' + AC' = A'D' + AC' + C'D'
 

Это то же самое, что и предыдущая теорема, полагая A вместо X, D’ вместо Y, и C’ вместо Z.

Из последней теоремы следует, что

 B(A'D' + AC') = B(A'D' + AC' + C'D')
 

то же, что и

 A'BD' + ABC' = A'BD' + ABC' + BC'D'
 

Учитывая это, мы можем взять правую часть оригинала и заменить A’BD’ + ABC’ для A’BD’ + ABC’ + BC’D’, то есть мы можем опустить термин BC’D’.

Шагами, аналогичными описанным выше, мы можем доказать эти две теоремы:

 A'BD' + BCD = A'BD' + BCD + A'BC
 BCD + ABC' = BCD + ABC' + ABD
 

, которые позволяют нам опустить последние два члена RHS оригинала, завершение доказательства.

логика — Как преобразовать таблицу истинности в логическое выражение?

Задавать вопрос

спросил 7 лет, 7 месяцев назад

Изменено 7 лет, 7 месяцев назад

Просмотрено 6к раз

$\begingroup$

Если у меня есть огромная таблица истинности, мне сложно составить выражение. Я знаю проблематичный метод, дизъюнктивную нормальную форму. Но я обнаружил, что не могу уменьшить огромное выражение.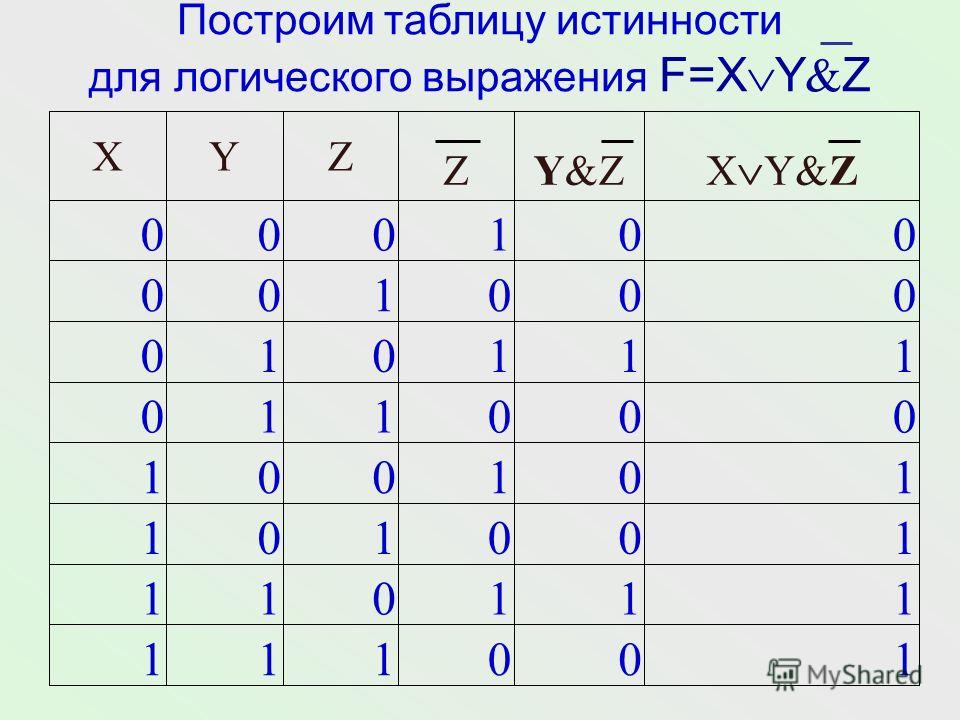

\begin{массив}{с | с | с | с || в} \hline p&q&r&s&\phi\\hline 1 и 1 и 1 и 1 и 0 \\ 1 и 1 и 1 и 0 и 0 \\ 1 и 1 и 0 и 1 и 1 \\ 1 и 1 и 0 и 0 и 1 \\ 1 и 0 и 1 и 1 и 0 \\ 1 и 0 и 1 и 0 и 0 \\ 1 и 0 и 0 и 1 и 0 \\ 1 и 0 и 0 и 0 и 1 \\ 0 и 1 и 1 и 1 и 1 \\ 0 и 1 и 1 и 0 и 1 \\ 0 и 1 и 0 и 1 и 1 \\ 0 и 1 и 0 и 0 и 1 \\ 0 и 0 и 1 и 1 и 0 \\ 0 и 0 и 1 и 0 и 1 \\ 0 и 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 0 и 1 \\ \hline \конец{массив}

• логика
• булевская алгебра

$\endgroup$

0

$\begingroup$

Вам следует поискать карты Карно

С помощью карт Карно вы можете преобразовать любую таблицу истинности в минимально сложное выражение без особых усилий. Я бы написал это в комментарии, но пока не могу комментировать.