Векторное умножение векторов. Python, Numpy
Вопрос задан
Изменён 1 год 1 месяц назад
Просмотрен 773 раза
Мне нужно узнать перпендикуляр к плоскости образованной двумя векторами в пространстве. Я нашел в интернете, что это можно вычислить через векторное умножение трехмерных векторов.
В коде это у меня выглядит вот так:
def get_normal(translated_vec):
line1 = translated_vec[1] - translated_vec[0]
line2 = translated_vec[2] - translated_vec[0]
normal = np.array([line1[1] * line2[2] - line1[2] * line2[1],
line1[2] * line2[0] - line1[0] * line2[2],
line1[0] * line2[1] - line1[1] * line2[0]])
l = np.linalg.norm(normal)
if l != 0:
normal /= l
else:
normal += 1.
0
return normal
Пример входных данных:
translated_vec = np.array([[ 0.07243389, -0.462265, 4.87585974],
[ 0.13487457, -0.3653465, 5.06419032],
[ 0.20468741, -0.1275775, 4.95642205]])
Это конечно работает, но работает слишком медленно, я хотел бы как-то это ускорить с помощью numpy, узнал что там есть функция vdot, но она мне не подходит, так как получая на вход два вектора, она выводит не новый вектор, а число. Т. е. мне нужно сделать быструю функцию которая вычисляет это.
- python
- python-3.x
- numpy
- vector
- вектор
Воспользуйтесь функцией np.cross(a, b, axisa=- 1, axisb=- 1, axisc=- 1, axis=None):
Return the cross product of two (arrays of) vectors.
The cross product of
aandbin is a vector perpendicular to bothaandb.If
aandbare arrays of vectors, the vectors are defined by the last axis ofaandbby default, and these axes can have dimensions 2 or 3. Where the dimension of eitherora bis 2, the third component of the input vector is assumed to be zero and the cross product calculated accordingly. In cases where both input vectors have dimension 2, thez-component of the cross product is returned.
12
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
#11.
 Произведение матриц и векторов, элементы линейной алгебры
Произведение матриц и векторов, элементы линейной алгебры
Смотреть материал на видео
Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую:
a = np.arange(1, 10).reshape(3, 3) b = np.arange(10, 19).reshape(3, 3) a*b
В консоли увидим результат:
array([[
10, 22, 36],
[ 52, 70, 90],
[112, 136,
162]])
Матричное умножение
Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:
то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду:
np.dot(a, b)
Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:
array([[ 84, 90, 96],
[201,
216, 231],
[318, 342,
366]])
Тот же результат можно получить и с помощью функции:
np.matmul(a, b)
Считается, что этот вариант предпочтительнее использовать при умножении матриц.
Векторное умножение
Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:
то их умножение можно реализовать в двух видах:
и
Первое умножение реализуется либо через функцию:
a = np.arange(1, 10) b = np.ones(9) np.dot(a, b) # значение 45
Либо, более предпочтительной функцией для внутреннего умножения векторов:
np.inner(a, b) # 45
Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции:
np.outer(a, b)
получим результат в виде следующей матрицы:
array([[1.,
1., 1., 1., 1., 1., 1., 1., 1.],
[2., 2., 2., 2., 2., 2., 2., 2., 2.],
[3., 3., 3., 3., 3., 3., 3., 3., 3.],
[4., 4., 4., 4., 4., 4., 4., 4., 4.],
[5., 5., 5., 5., 5., 5., 5., 5., 5.],
[6., 6., 6., 6., 6., 6., 6., 6., 6.],
[8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])
Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul:
a @ b # значение 45
или, с использованием матриц:
a.resize(3, 3) b.resize(3, 3) a @ b # аналог np.matmul(a, b)
Умножение вектора на матрицу
Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:
или
Для реализации первого способа, зададим одномерный вектор и двумерную матрицу:
a = np.array([1,2,3]) b = np.arange(4,10).reshape(3,2) # матрица 3x2
И, затем, воспользуемся уже знакомой нам функцией dot:
np.dot(a, b) # array([40, 46])
При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.
Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку:
np.dot(b, a) # несогласованность размеров
Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:
Определим массивa в два элемента и умножим на матрицу b:
a = np.array([1, 2]) np.dot(b, a) # array([14, 20, 26])
Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде:
a.shape = -1, 1 # вектор-столбец 2x1
Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец:
np.dot(b, a) # вектор-столбец 3x1
Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):
a @ b # вектор-столбец 3x1
Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.
Элементы линейной алгебры
Из высшей
математики хорошо известно, что матрицы можно использовать для решения систем
линейных уравнений.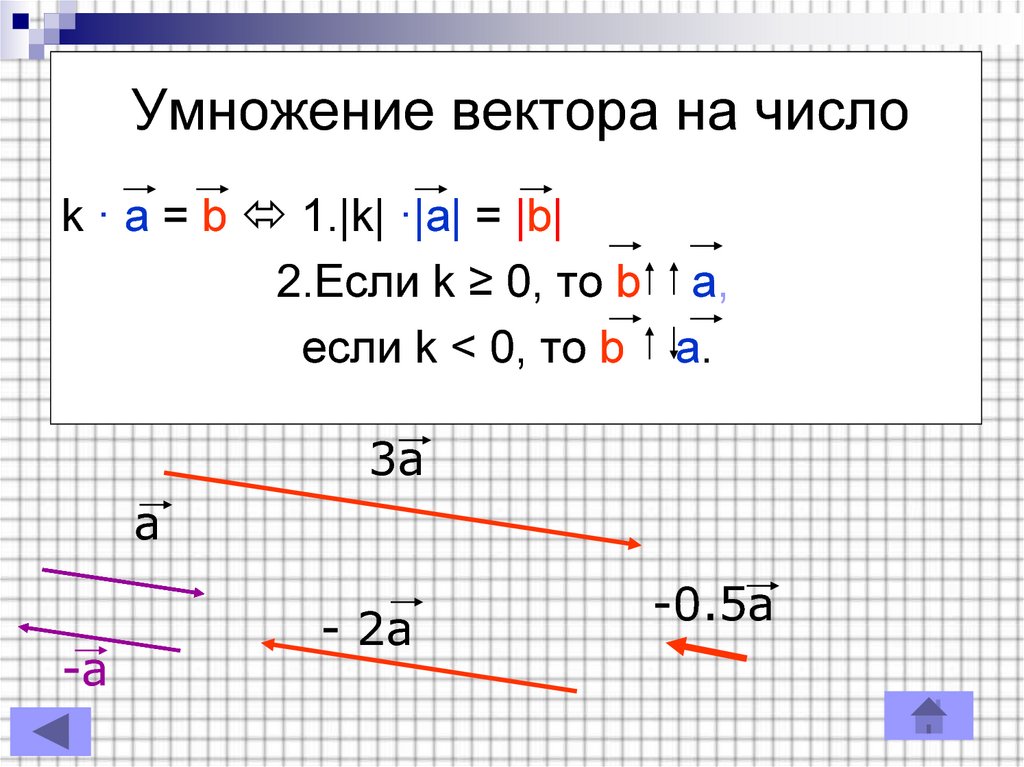
Предположим, имеется квадратная матрица 3×3:
a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])
Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов:
np.linalg.matrix_rank(a) # рангравен 3
Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:
Здесь - некие числа линейного уравнения. Например, возьмем их равными:
y = np.array([10, 20, 30])
Тогда корни уравнения можно вычислить с помощью функции solve:
np.linalg.solve(a, y) # array([-5. , 10. , -1.66666667])
Другой способ
решения этой же системы линейных уравнений возможен через вычисление обратной
матрицы.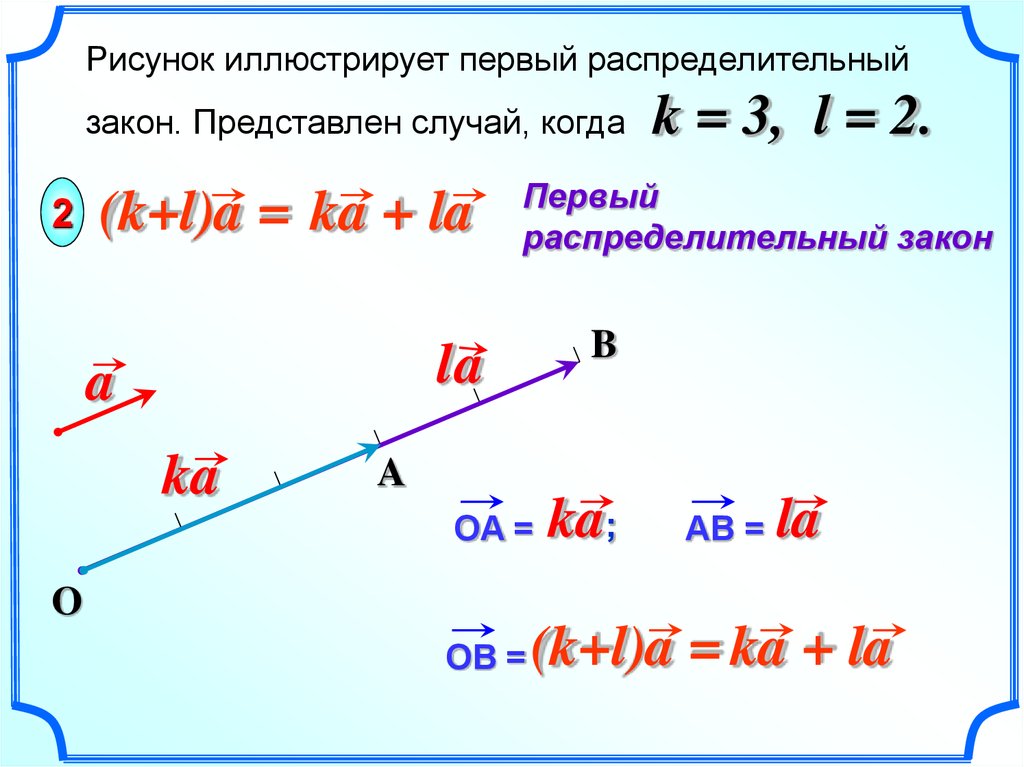 Изначально, уравнение можно записать в векторно-матричном виде:
Изначально, уравнение можно записать в векторно-матричном виде:
Откуда получаем решения :
На уровне пакета NumPy это делается так:
invA = np.linalg.inv(a) # вычисление обратной матрицы invA @ y # вычисление корней
Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.
|
Функция |
Описание |
|
linalg.cholesky() |
Разложение Холецкого |
|
linalg. |
QR-разложение матрицы |
|
linalg.svd() |
Сингулярное (SVD) разложение матрицы |
|
linalg.norm() |
Норма матрицы или вектора |
|
linalg.cond() |
Число обусловленности матрицы |
|
linalg.det() |
Определитель (детерминант) матрицы |
|
linalg.matrix_rank() |
Вычисление ранга матрицы по алгоритму SVD |
|
np.trace() |
Сумма диагональных элементов массива |
|
linalg. |
Вычисление собственных значений и правых собственных векторов |
|
linalg.eigvals() |
Вычисление собственных значений матрицы |
|
linalg.solve() |
Решение линейного матричного уравнения |
|
linalg.tensorsolve() |
Решение линейного тензорного уравнения |
|
linalg.lstsq() |
Решает задачу поиска наименьших квадратов для линейного матричного уравнения |
|
linalg.inv() |
Вычисление обратной матрицы |
|
linalg. |
Вычисление псевдообратной (Мура-Пенроуза) матрицы |
|
linalg.tensorinv() |
Вычисление обратного тензора (N-мерного массива) |
Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:
https://numpy.org/doc/stable/
Видео по теме
#1. Пакет numpy — установка и первое знакомство | NumPy уроки
#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки
#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки
#4. Свойства и представления массивов, создание их копий | NumPy уроки
#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки
#6. Объединение и разделение массивов | NumPy уроки
Объединение и разделение массивов | NumPy уроки
#7. Индексация, срезы, итерирование массивов | NumPy уроки
#8. Базовые математические операции над массивами | NumPy уроки
#9. Булевы операции и функции, значения inf и nan | NumPy уроки
#10. Базовые математические функции | NumPy уроки
#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки
#12. Множества (unique) и операции над ними | NumPy уроки
#13. Транслирование массивов | NumPy уроки
Все о типах умножения векторов
Операция умножения векторов включает скалярное произведение и векторное произведение, оба из которых являются фундаментальными подходами к векторным операциям.
В этой статье будут подробно рассмотрены два типа векторного умножения, а также различия между ними. Держите свои заметки по следующим темам под рукой, потому что нам может понадобиться обратиться к ним при изучении векторного умножения, поэтому обязательно держите их под рукой.
Очень важно решить, хотите ли вы скалярную или векторную величину при умножении двух или более векторов, потому что результат будет другим. Стратегия, которую нам нужно будет использовать, будет определяться нашим ответом на этот вопрос. (или векторный) продукт. Умножение векторов — это математическая операция, заключающаяся в умножении двух векторов на скалярный коэффициент.
- К этому моменту мы должны были узнать о распределении скалярных компонентов по вектору, что является первым процессом, который мы рассмотрим в этом разделе.
- Как вы могли догадаться, скалярное произведение, также известное как скалярное произведение, дает одну скалярную величину.
- Подобно foreach, перекрестное произведение дает векторную величину.
Наше объяснение будет ограничено двумя последними стратегиями, а именно скалярными произведениями и перекрестными произведениями. Поскольку их операторы изображают точку (.) и крестик (x), эти имена помогут вам определить операцию, которую необходимо выполнить.
Поскольку их операторы изображают точку (.) и крестик (x), эти имена помогут вам определить операцию, которую необходимо выполнить.
Два товара будут давать различные результаты и проходить различные процессы. Вот почему важно понимать, что представляют собой точечные и перекрестные произведения в уравнении.
Скалярное произведение и его правилаСкалярное произведение — это математическое выражение, представляющее проекцию одного вектора на другой вектор. Рассмотрим случай, когда у нас есть и, где скалярное произведение и является просто проекцией на интересующий вектор.
Взгляните на эту иллюстрацию, чтобы увидеть, что происходит, когда мы находим скалярное произведение и и Что происходит, когда мы берем компонент вектора A вдоль направления B и умножаем его на величину компонента вектора B
A.B= (Acos θ)B=ABcos θ
В результате скалярное произведение A и B (A. B) есть просто произведение величин двух векторов, умноженное на косинус угла между ними.
B) есть просто произведение величин двух векторов, умноженное на косинус угла между ними.
Поскольку конечный продукт представляет собой скалярное число, то скалярное произведение часто называют скалярным числом. Ниже приведены некоторые важные свойства скалярного произведения, которые следует учитывать при его использовании:
- Скалярное произведение коммутативно следующим образом:
A.B=B.A
- Скалярное произведение обладает распределительным свойством:
A.(B+C)=B.(A+C)
- Когда вы берете скалярное произведение двух перпендикулярных векторов, результат всегда будет равен 0 (поскольку cos 90° равно 0).
Другой метод вычисления скалярного произведения двух векторов заключается в умножении их соответствующих декартовых компонентов друг на друга. Предполагая, что и являются единичными векторами вдоль осей и соответственно, мы можем вычислить произведение A и B, как показано ниже.
A=A1i +A2j+A2k
B=B1i+ B2j +B3k
A.B= A1B1+A2B2+A3B3
Перекрестное произведение и его правила , мы используем оператор x, и результирующее произведение является вектором. В результате перекрестное произведение или векторное произведение требует от нас учитывать направление.Отличный способ увидеть векторное произведение двух векторов — вычислить площадь параллелограмма путем перемножения векторов.
Перекрестное произведение A и B равно произведению Asin θ и B, как мы видим из этого.
AxB =(Asin θ)B=ABsin θn
Имейте в виду, что единичный вектор n — это просто вектор, перпендикулярный и к, и к. Это означает, что если у нас есть два вектора и угол между ними, мы можем найдите перекрестное произведение, умножив величины двух векторов, которое является перекрестным произведением. Затем результат можно умножить на синус угла, образованного двумя рассматриваемыми векторами.
Свойства перекрестного произведенияВот некоторые из наиболее важных характеристик векторных или перекрестных произведений, о которых вам следует знать:
- Векторные или перекрестные произведения являются антикоммутативными в следующих отношениях: x B= -B x A
- Векторное произведение имеет распределительное преимущество перед сложением:
Ax(B+C) = AxB +AxC
- Перекрестное произведение двух параллельных векторов всегда будет равно 0,
Операция векторного умножения включает скалярное произведение и перекрестное произведение, оба из которых являются фундаментальными подходами к векторным операциям.
 (или скалярное) произведение и перекрестное (или векторное) произведение. Умножение векторов — это математическая операция, включающая умножение двух векторов на скалярный коэффициент. Скалярное произведение — это математическое выражение, представляющее проекцию одного вектора на другой вектор. Когда вы берете скалярное произведение двух перпендикулярных векторов, результатом всегда будет равен 0 (поскольку cos 90° равно 0). Возможно, здесь уже проявляется закономерность: для перекрестных произведений мы используем оператор x, и результирующее произведение является вектором. В результате перекрестное произведение или векторное произведение требует от нас учитывать направление. Перекрестное произведение двух параллельных векторов всегда будет равно 0.
(или скалярное) произведение и перекрестное (или векторное) произведение. Умножение векторов — это математическая операция, включающая умножение двух векторов на скалярный коэффициент. Скалярное произведение — это математическое выражение, представляющее проекцию одного вектора на другой вектор. Когда вы берете скалярное произведение двух перпендикулярных векторов, результатом всегда будет равен 0 (поскольку cos 90° равно 0). Возможно, здесь уже проявляется закономерность: для перекрестных произведений мы используем оператор x, и результирующее произведение является вектором. В результате перекрестное произведение или векторное произведение требует от нас учитывать направление. Перекрестное произведение двух параллельных векторов всегда будет равно 0.Умножение векторов на скалярную величину с примерами
Вектор связывает два данных точки. Это математическая величина, имеющая как Величину, так и направление.
Умножение векторов
Умножение векторов может быть двух типов:
(i) Скалярное умножение
(ii) Умножение на вектор
Здесь мы обсудим только скалярное умножение на
.
Умножение векторов на скаляр:
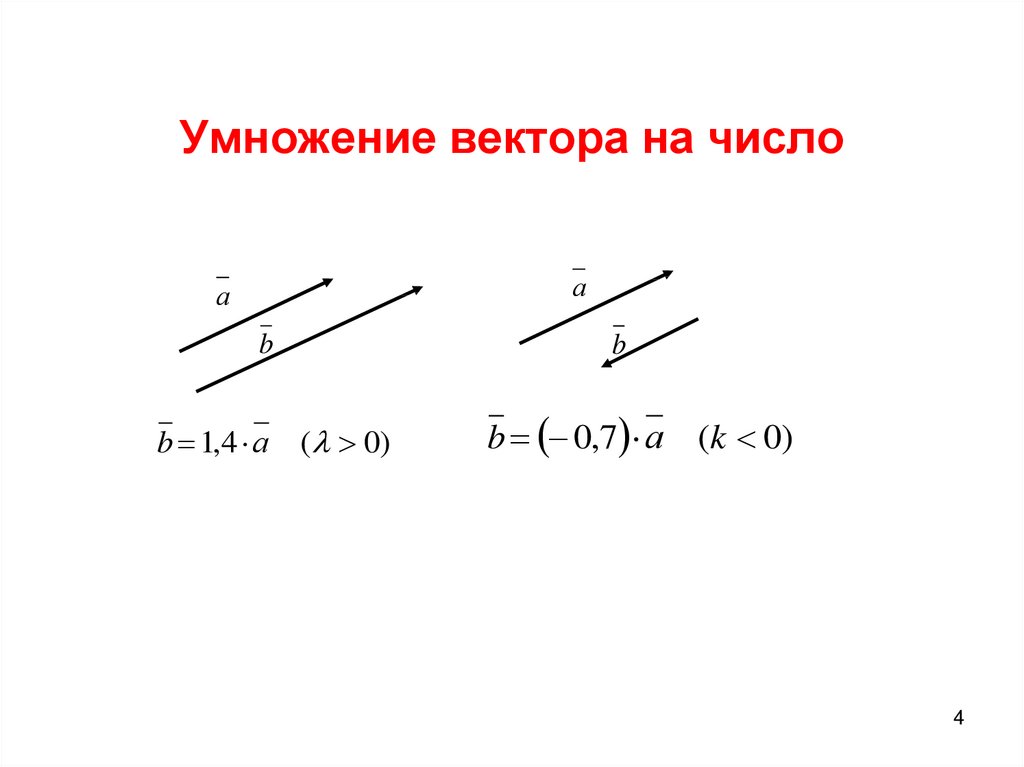
Когда вектор умножается на скалярную величину, величина вектора изменяется в соответствии с величиной скаляра, но направление вектора остается неизменным.
Предположим, у нас есть вектор
\(\begin{array}{l} \overrightarrow {a} \end{array} \)
, то если этот вектор умножить на скалярную величину k то мы получим новый вектор с величиной как |\(\begin{array}{l} \overrightarrow {ka} \end{array} \)
|и направление остается таким же, как у вектора\(\begin{array}{l} \overrightarrow {a} \ end{array} \)
, если k положительно и если k отрицательно, то направление k становится прямо противоположным направлению вектора\(\begin{array}{l} \overrightarrow {a} \end{array} \)
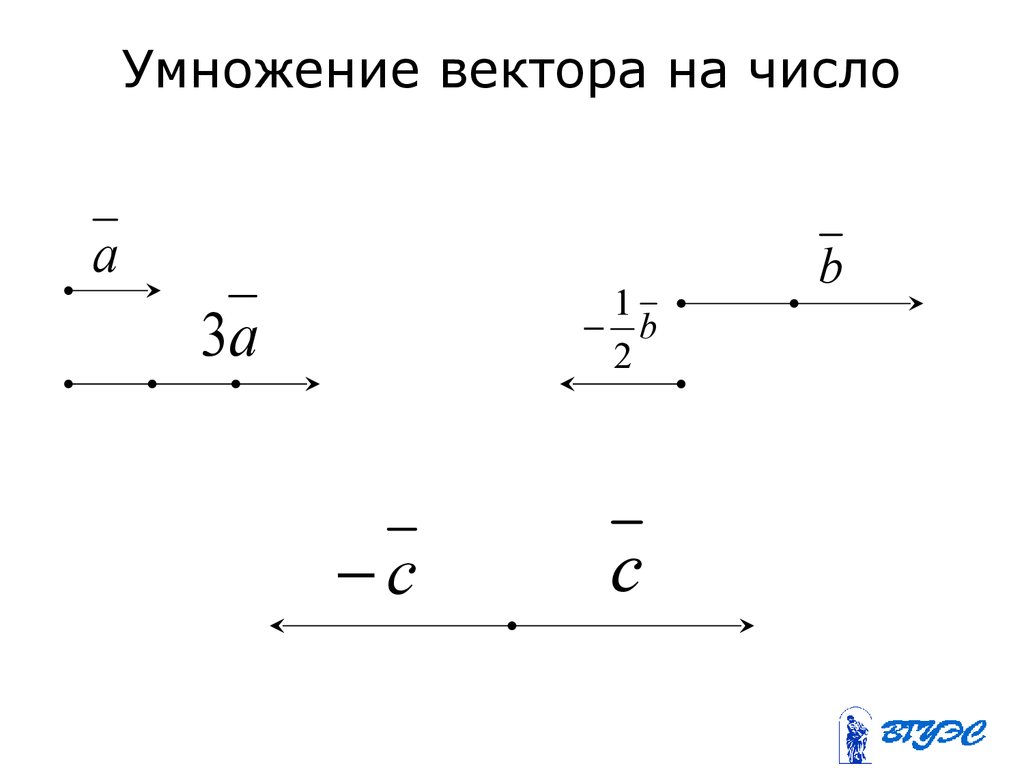
.Теперь разберемся визуально со скалярным умножением вектора
Возьмем значения ‘k’ равными = 2,3,-3,
\(\begin{array}{l} \frac {-1}{2}\end{array} \)
и скоро.
Из приведенного набора векторов видно, что направление вектора
\(\begin{array}{l} \overrightarrow {a} \end{array} \)
остается неизменным, когда значение скаляра положительное, и направление становится прямо противоположным, когда значение скаляра отрицательно, и в обоих случаях величина продолжает изменяться в зависимости от значений скалярного множителя.Как видно из приведенных выше обсуждений,
\(\begin{массив}{l}~~~~~~~~\end{массив} \)
|\(\begin{array}{l} \overrightarrow {ka} \end{array} \)
|=k|\(\begin{array}{l} \overrightarrow {a} \end{array} \)
|Предположим, что если значение скалярного множителя k равно -1, то путем скалярного умножения мы знаем, что результирующий вектор равен
\(\begin{array}{l} \overrightarrow {-a} \end{array} \)
, затем\(\begin{array}{l} \overrightarrow {a} \end{array} \)
+ (\(\begin{array}{l} \overrightarrow {-a} \end {массив} \)
) = 0 . Вектор
Вектор\(\begin{array}{l} \overrightarrow {-a} \end{array} \)
представляет отрицательный или аддитивный обратный вектору\(\begin{массив}{l} \overrightarrow {a} \end{массив} \)
.Теперь предположим, что значение k =
\(\begin{array}{l} \frac {1}{|a|} \end{array} \)
при условии, что значение\(\begin {array}{l} \overrightarrow {a} \ne 0\end{array} \)
тогда по свойству скалярной кратности векторов имеем\(\begin{array}{l} \overrightarrow {ka} \ конец {массив} \)
= |k|\(\begin{array}{l} \overrightarrow {a} \end{array} \)
=\(\begin{массив}{l} \frac {1}{|a|} \end{массив} \)
× |\(\begin{array}{l} \overrightarrow {-a} \end{array} \)
| .Кроме того, согласно приведенному выше обсуждению, если k = 0, тогда вектор также становится равным нулю.
Давайте рассмотрим пример, чтобы прояснить этот момент,
Пример: Вектор представлен в ортогональной системе как
\(\begin{array}{l} \overrightarrow {a} \end{array} \)
=\(\begin{array}{l} 3 \ шляпа i + \ шляпа j + \ шляпа k \ конец {массив} \)
.



 If
If  dot(a, b)
dot(a, b)
 resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b)
resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b) array([1, 2])
np.dot(b, a) # array([14, 20, 26])
array([1, 2])
np.dot(b, a) # array([14, 20, 26])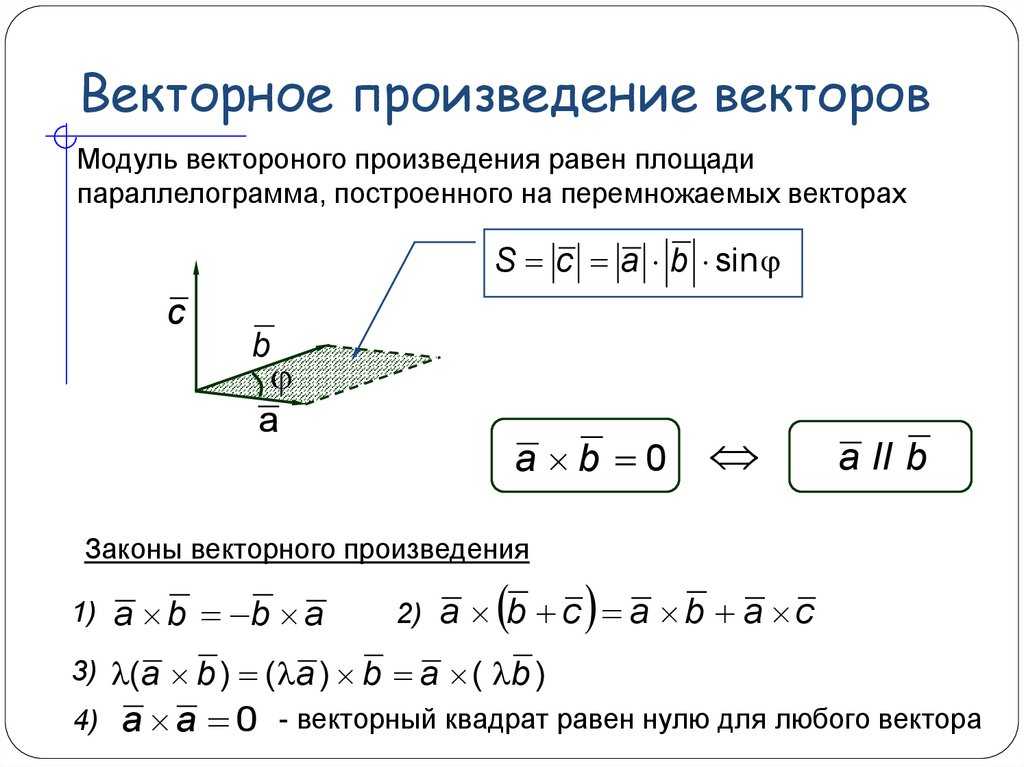 qr()
qr()
 eig()
eig()
 pinv()
pinv()
 (или скалярное) произведение и перекрестное (или векторное) произведение. Умножение векторов — это математическая операция, включающая умножение двух векторов на скалярный коэффициент. Скалярное произведение — это математическое выражение, представляющее проекцию одного вектора на другой вектор. Когда вы берете скалярное произведение двух перпендикулярных векторов, результатом всегда будет равен 0 (поскольку cos 90° равно 0). Возможно, здесь уже проявляется закономерность: для перекрестных произведений мы используем оператор x, и результирующее произведение является вектором. В результате перекрестное произведение или векторное произведение требует от нас учитывать направление. Перекрестное произведение двух параллельных векторов всегда будет равно 0.
(или скалярное) произведение и перекрестное (или векторное) произведение. Умножение векторов — это математическая операция, включающая умножение двух векторов на скалярный коэффициент. Скалярное произведение — это математическое выражение, представляющее проекцию одного вектора на другой вектор. Когда вы берете скалярное произведение двух перпендикулярных векторов, результатом всегда будет равен 0 (поскольку cos 90° равно 0). Возможно, здесь уже проявляется закономерность: для перекрестных произведений мы используем оператор x, и результирующее произведение является вектором. В результате перекрестное произведение или векторное произведение требует от нас учитывать направление. Перекрестное произведение двух параллельных векторов всегда будет равно 0.
 Вектор
Вектор