Метод микрокаротажного зондирования (МКЗ)

Микрокаротаж основан на измерении кажущегося удельного электрического сопротивления прискважинной зоны двумя микрозондами (градиент – микрозондом A0.025M0.025N и потенциал – микрозондом A0.05M), установленными на прижимном изоляционном башмаке. Также метод микрокаротажа регистрирует кривую среднего диаметра. Радиус исследования градиент-микрозонда приблизительно равен его длине (3,75 см), а потенциал-микрозонда в 2-2,5 раза больше его длины, т. е. составляет 10-12 см. Вертикальная разрешающая способность метода: микроградиент зонд – 4 см, микропотенциал зонд – 5 см; горизонтальная разрешающая способность метода: микроградиент зонд – 4 см, микропотенциал зонд – 10 см.

Боковой микрокаротаж основан на регистрации кажущегося удельного электрического сопротивления прискважинной зоны фокусированным микрозондом, установленном на прижимном изоляционном башмаке. Радиус исследования около – 10 см. Вертикальная разрешающая способность метода – 5 см, горизонтальная разрешающая способность метода – 10 см

.

Типовые условия применения метода:

• скважины необсаженные, вертикальные и слабонаклонные, заполненные пресной жидкостью;
• ограничением в применении метода является существенное изменение диаметра и формы сечения ствола скважины, препятствующее плотному прилеганию башмака к стенке скважины, а также наличие раствора в скважине с удельным электрическим сопротивлением менее 0,05 Ом*м;
• ограничениями в применении метода являются растворы на углеводородной основе;
• наиболее широкое применение БМК находит при исследовании разрезов скважин, заполненных минерализованной ПЖ.

ПРИМЕНЕНИЕ:

определение электрического сопротивления части пласта, непосредственно прилегающей к скважине, и детального расчленения разреза; выделение коллекторов, литологическое расчленение разреза; определение эффективной толщины пластов; определение удельного электрического сопротивления промытой зоны; оценка сопротивления промывочной жидкости в интервале каверн; расчленение разреза с высокой точностью; определение кривой среднего диаметра.

ТЕХНИЧЕСКИЕ ОСОБЕННОСТИ:

Прибор МК+БМК-2Р	исследования в скважинах диаметром от 110 до 400 мм; диапазон измерения кажущегося сопротивления: 0,5 — 800 Ом*м; одновременная регистрация с МБК и МКВ; возможность применения в составе модульной сборки; возможность обеспечения надежного контакта регистрирующего «башмака» даже при больших углах наклонах скважины (35°).
Прибор МК-1Т	возможность работы в глубоких и сверхглубоких скважинах при аномально-высоких термобарических условиях.
Прибор МК-БМК-К-90	исследования в скважинах диаметром от 110 до 400 мм; диапазон измерения кажущегося сопротивления: 0,5 — 800 Ом*м; одновременная регистрация с МБК и МКЗ; возможность применения в составе модульной сборки.

Обозначение прибора: Т – термобаростойкий БМК – боковой микрокаротаж

Регистрируемые параметры: Эффективное электрическое сопротивление. Диаметр скважины.

Единицы измерения: Ом*м м

ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ

	Прибор МК+БМК-2Р1	Прибор МК-1Т	Прибор МК-БМК-К-90
Длина, м	3,95	4,65	4,7
Диаметр, мм	90	90	90
Масса, кг	85	122	130
Максимальная рабочая температура, °С	120	120	120
Максимальное рабочее давление, МПа	80	140	80
Максимальная скорость записи, м/ч в интервале М 1:200 (детальных исследований)	900	900	900
Диаметр исследуемых скважин, мм	от 110 до 400	от 110 до 400	от 110 до 400
Положение в скважине	прижимается	прижимается	прижимается
Комбинируемость	концевой	концевой	концевой
Диапазон измерения, Ом*м
МГЗ и МПЗ	0,1 – 50	0,1 – 50	0,1 – 50
зонда БМК	0,5 – 800	0,5 – 800	0,5 – 800
Относительная погрешность измерения, %
для МГЗ и МПЗ	5+7,5/x*	5+7,5/x*	5+7,5/x*
для БМК	5+40/x*	5+40/x*	5+40/x*
диаметра скважины	2. 5+1000/x*	2.5+1000/x*	2.5+1000/x*

ПРИНЦИПИАЛЬНАЯ КОНСТРУКЦИЯ ЗОНДА

Микрозонд КС представляет собой трехэлектродную измерительную установку с небольшими (2,0-2,5 см) расстояниями между электродами. Электроды микрозонда, изготовленые из латунного стержня диаметром 10 мм, размещены на внешней стороне башмака из изоляционного материала. Для исключения влияния скважины на результаты измерений башмак внешней стороной прижимается к стенке скважины управляемым рычажным устройством. В таком микрозонде башмак с электродами шарнирно укрепляется на одной из двух пар рычагов, которые прижимаются спиральной пружиной к стенке скважины любого диаметра с постоянным усилением. Одновременно с кривыми микрозондов это устройство позволяет регистрировать кривую изменения диаметра скважины с глубиной – микрокавернограмму.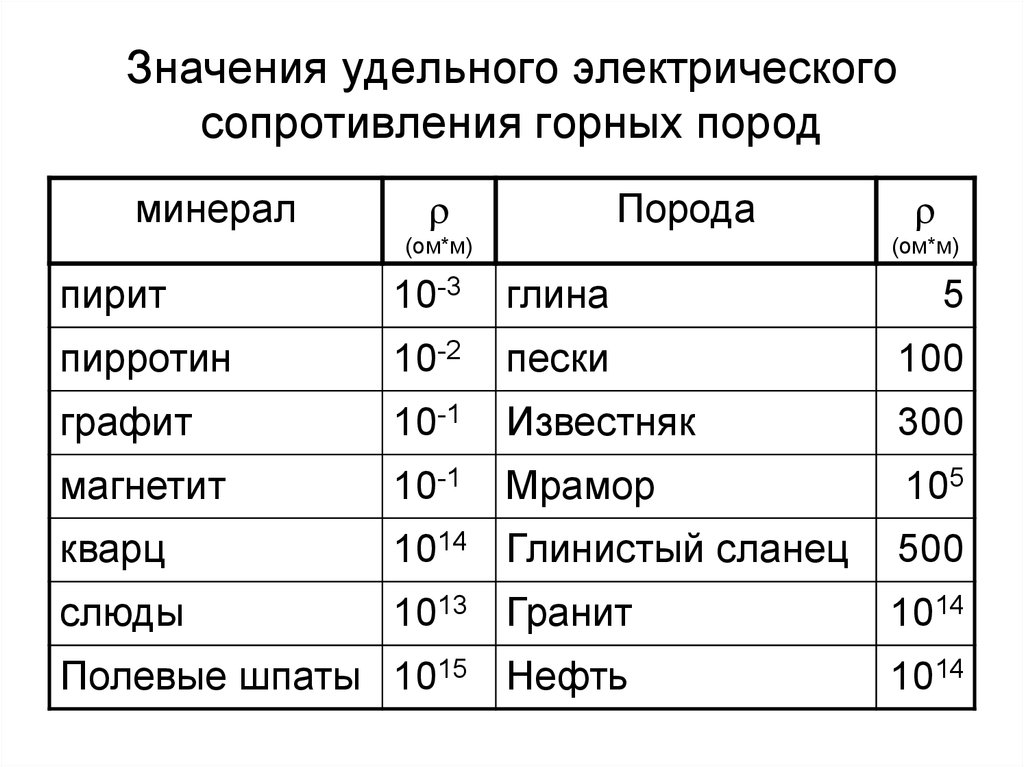

¹MCFL — аналог аппаратуры компании Schlumberger

§ 7.3. Закон Ома для постоянного тока

Сила тока I в проводнике пропорциональна приложенному напряжению или разности потенциалов на конце проводника U и обратно пропорциональна сопротивлению R проводника.

. (7.4)

Из формулы (7.4) определяется единица сопротивления 1 Ом (или 1 ).

1 Ом − сопротивление такого проводника, в котором при напряжении 1Вольт течет постоянный ток 1 Ампер. (1 Ом = 1В/1А).

Учитывая (7.3), закон Ома для неоднородного участка цепи, т.е. для цепи, где помимо сопротивления R присутствует источник тока с ЭДС ε₁₂ , имеет вид: .

Сопротивление (активное) проводника зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине ℓ и обратно пропорционально площади его поперечного сечения S (рис. 7.1 ).

.

О тсюда переход к равенству осуществляется коэффициентом пропорциональности ρ, который характеризует материал проводника и называется удельным электрическим сопротивлением: .

Единица измерения удельного сопротивления – Ом·м.

Вещества, у которых удельное сопротивление ρ < 10⁻⁷Ом·м, хорошо проводят электрический ток, поэтому они называются проводниками. У диэлектриков ρ > 10⁸ Ом·м, поэтому они обычно непреодолимы для электрических зарядов. Удельное сопротивление большинства веществ лежит между указанными пределами. Характерной особенностью этих веществ, называемых полупроводниками, является возрастание электрической проводимости ρ (уменьшение электрического сопротивления R) с увеличением температуры.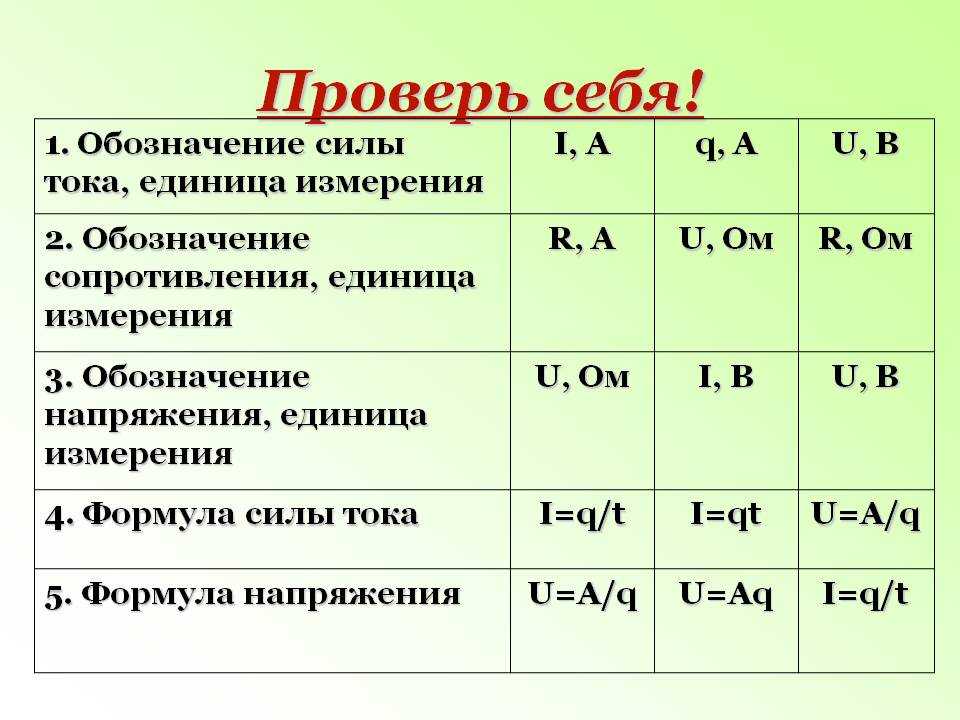

Как и у металлов, проводимость твердых полупроводников обусловлена перемещением электронов. Однако условия перемещения электронов в металлах и полупроводниках различны. В металлах эти электроны полностью оторваны от своих атомов и свободно перемещаются внутри металла, совершая хаотичное движение, средняя скорость которого зависит от температуры проводника. Когда появляется внешнее электрическое поле или разность потенциалов на концах проводника, на электроны действует дополнительная кулоновская сила, под воздействием которой они приобретают еще и направленное движение (против направления напряженности электрического поля). С повышением температуры увеличивается и средняя скорость хаотичного движения ионов, взаимодействием с которыми обусловлено сопротивление проводника. Поэтому с повышением температуры у проводников увеличивается активное сопротивление.

Опыт показывает, что в первом приближении у проводников изменение активного сопротивления с температурой описывается линейным законом:

R(t)=R₀(1+αt), где R(t) и R₀ сопротивления проводника при температурах t и 0⁰C соответственно, α – температурный коэффициент сопротивления (для большинства чистых металлов при не очень низких температурах α≈ 1/273 К⁻¹≈ 0,0037 К⁻¹, хотя может колебаться (2÷7) 10⁻³ или иметь другие значения, например для ртути α ≈ 0,0009 К⁻¹).

У чистых (без примесей) полупроводников при низких и нормальных температурах имеется небольшое число свободных электронов: подавляющее большинство электронов связано (хотя весьма слабо) с атомами. Этим объясняется плохая проводимость (так называемая электронная проводимость) полупроводников при таких температурах. Для того чтобы связанный электрон стал свободным и участвовал в создании электрического тока, нужна дополнительная энергия, т.е. необходимо увеличить его кинетическую энергию. Это происходит при повышении температуры полупроводника. Увеличение концентрации свободных электронов повышает проводимость и соответственно снижает сопротивление полупроводника. Правда, с ростом температуры усиливается хаотическое движение атомов полупроводника, тем самым затрудняется упорядоченное движение электронов, что вызывает увеличение сопротивления полупроводника. Однако влияние роста концентрации свободных электронов на сопротивление полупроводника преобладает над влиянием хаотического движения атомов. Причем влияние изменения температуры сказывается на изменении сопротивления больше у полупроводников, чем у металла (при изменении температуры на 1 К сопротивление металла возрастает в среднем на 0,004, а сопротивление полупроводника уменьшается в среднем на 0,06 сопротивления при нормальных температурах).

Помимо электронной проводимости, в полупроводниках существует и другой механизм проводимости (дырочный), при котором вместо оторванного электрона в атоме образуется разорванная связь (дырка), которая играет роль положительного заряда, т.е.становится блуждающим положительным зарядом.

Существенным преимуществом полупроводника является то, что даже небольшое количество примесей может очень сильно изменить сопротивление полупроводника (сотые доли процента примеси могут изменить сопротивление полупроводника в десятки раз).

У некоторых металлов (алюминий, цинк, свинец и др. ) при Т<10 К (Т_max≈ 22,3 K) сопротивление R скачкообразно уменьшается до нуля: металл становится абсолютным проводником (так называемое явление сверхпроводимости). Ток в таких цепях циркулирует сутками(!) (незатухающий ток) и может достигать 10⁷ А·м^-2, без выделения тепла. Сверхпроводниками могут быть и диэлектрики, например водород, ксенон — газы, переведенные в твердое состояние (при очень низких температурах и высоких давлениях).

Сверхпроводимость уже применяется в практике, например, для создания очень сильных магнитных полей, но для ее широкого применения препятствуют низкие температуры, необходимые для осуществления сверхпроводимости. Сейчас ведется интенсивный поиск таких веществ, для которых сверхпроводимость протекла бы при более высоких (например, при комнатных) температурах.

Явление сверхпроводимости объясняется в рамках квантовой теории.

Физические свойства электрического элемента наглядно демонстрирует зависимость силы тока I, протекающего через этот элемент, от напряжения U, приложенного к нему (так называемая вольт-амперная характеристика — ВАХ).

Вид ВАХ нам подсказывает, с каким электрическим элементом мы имеем дело: линейным или нелинейным. У линейных элементов сопротивление в данном диапазоне изменений значений напряжения U остается постоянной R=U/I=const, а это означает, что зависимость I от U линейна (на рис. 7.2, а)). Нелинейными называются такие элементы, для которых отношение на-

пряжения U к силе тока I не остается постоянным при изменении U и I, т.е. R=U/I≠const; тогда ВАХ представляет собой кривую линию (рис. 7.2, б)).

Что такое электрическое сопротивление? Определение и единица сопротивления

Определение сопротивления

Свойство вещества сопротивляться протеканию через него электрического тока называется сопротивлением. Единицей сопротивления является Ом. В проводниках свободные электроны движутся беспорядочно внутри металла, и при приложении напряжения электроны начинают двигаться из точки с более низким потенциалом в точку с более высоким потенциалом.

При дрейфе электронов происходит столкновение между электронами и атомом и молекулой проводника, и это столкновение затрудняет путь потока электронов. Это препятствие потоку электронов, вызванное столкновением электронов с атомом и молекулой, создает препятствие. Электрическая помеха на пути протекания тока представляет собой электрическое сопротивление.

Когда мы подаем напряжение в цепь, ток течет через сопротивление. Пусть напряжение на сопротивлении равно V, а ток, протекающий в цепи, равен I.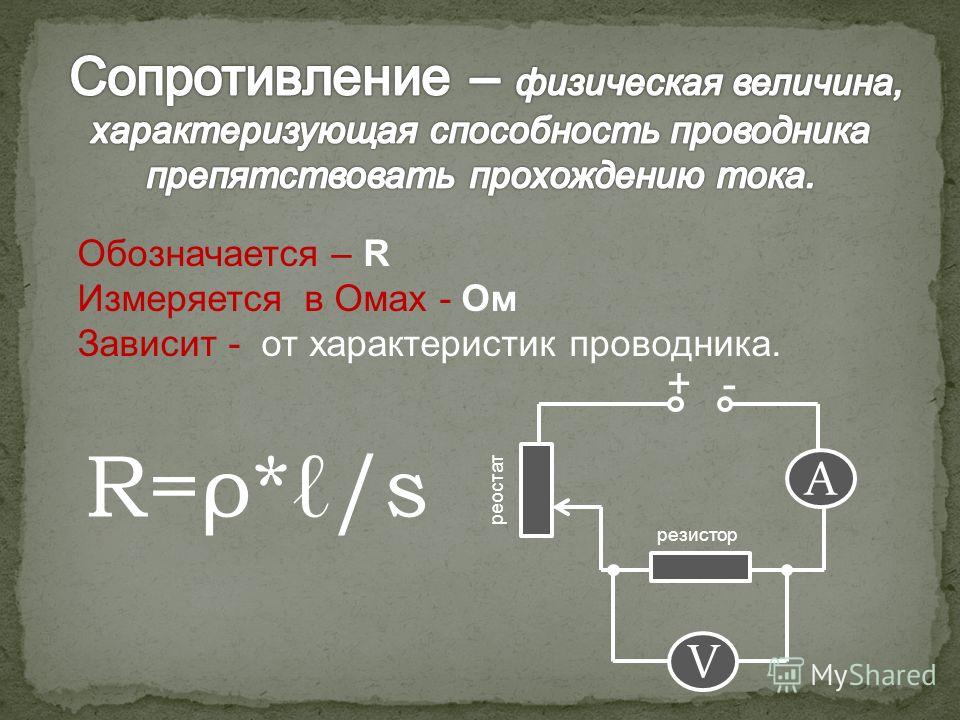 Напряжение на сопротивлении пропорционально протеканию электрического тока. По закону Ома;

В ∝  I
В =  RI
R = V/I Где
В – напряжение
I – ток
R – Сопротивление вещества  

Следовательно, мы можем определить сопротивление как отношение приложенного напряжения к ток через вещество.

R = V/I

Единица сопротивления

При приложении разности потенциалов в один вольт к сопротивлению через него протекает ток силой 1 ампер, тогда сопротивление равно 1 Ом . Единицей сопротивления является вольт на ампер o r ом , названный в честь Джорджа Ома . Символ Ома — омега (Ω ). Единицей измерения сопротивления в системе СИ является Ом ( Ом )

R = V/I (закон Ома)
= 1 Вольт/1 ампер

R = 1 Ом (Ом)

Различные единицы сопротивления

Более крупные единицы сопротивления: килоом, мегаом и гигаом. Меньшие единицы сопротивления: мОм, микроОм и наноОм.

Соотношение между различными единицами сопротивления приведено ниже. Различные единицы сопротивления:

9006 4OLOD 9006,973 9006 4та 9006,974 4,3,9006 4 000)963963

Единица измерения сопротивления	Значение в Ом (Ом)
1 GIGA OHM (GOT)	10 ω
1 MEGA OHM (M ω)	10 6 ω
1 KILO OHM (K ω
4 7,3,9006 4,3,9006 4,3,9006.
1 Milli OHM (M ω)	10 -3 ω
1 Micro OHM (μ Ом)	10 -6 ω	3	-6 ω	3	-6 ω	3	9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 9004 -6 ω
-6 ω
-6 . -9   Ом

Related Posts

• Закон Ома-Утверждение, Формула, Решенные Примеры
• Как сопротивление зависит от диаметра?
• Что такое тензодатчик и как он работает
• Электропроводность | Определение, символ, формула, единица измерения 
• Удельное электрическое сопротивление | Определение, формула, символ, единицы измерения
• Контактное сопротивление и его значение

Похожие посты:

Подпишитесь на нас и поставьте лайк:

Измерение сопротивления — WikiLectures

Спасибо за ваши комментарии.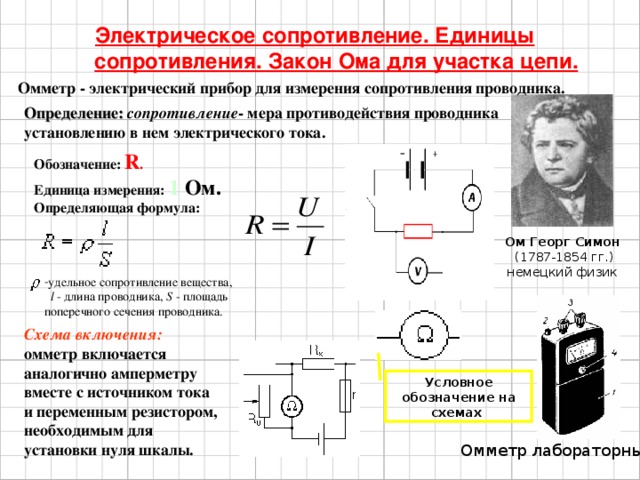

Спасибо за рецензирование этой статьи.

Ваш отзыв не вставлен (допускается один отзыв на статью в день)!

Электрическое сопротивление — это свойство конкретного проводящего тела. Для простоты предположим, что такое тело снабжено двумя токопроводящими выводами и что в него больше нигде не входит электрический ток. Будет электрический ток U между клеммами и электрический ток I будет протекать по питающему проводу. Электрическое сопротивление можно ввести, например, используя закон Ома (тоже в интегральной форме) как константу пропорциональности между приложенным напряжением U и протекающим током I :

[math]\displaystyle{ U = R\cdot I }[/math]

Единицей электрического сопротивления является Ом  [ Ом ], часто используются множители кОм и МОм . Обратная величина электрического сопротивления называется электропроводностью G , ее единица измерения равна Сименс [ S ].

И электрическое сопротивление, и электрическая проводимость являются константами, характеризующими конкретное тело, помимо материала, на них также влияет его геометрическая конфигурация. Величины используются для характеристики конкретного материала:

• удельное электрическое сопротивление (проводимость) γ  [ См·м ^-1 ]
• удельное электрическое сопротивление (удельное сопротивление) ρ  [ Ом·м ]

Измерение электрического сопротивления[править | править источник]

Метод Ома[править | править источник]

Электрическое сопротивление обычно измеряют непосредственно по закону Ома (его так называемая интегральная форма), то есть пропуская через тело электрический ток и измеряя падение напряжения, возникающее на теле. Затем сопротивление рассчитывается по соотношению:

[math]\displaystyle{ R= \frac{U}{I} }[/math]

Мы измеряем электрический ток амперметром и напряжение вольтметром . Поскольку обычно необходимо одновременно измерять напряжение и ток, возможны два варианта:

Однако обе схемы по-своему проблематичны. В случае соединения А вольтметр показывает действительное напряжение на измеряемом сопротивлении, а амперметр показывает сумму токов, проходящих через измеряемое сопротивление и вольтметр. Такая схема удобна там, где ток, проходящий через измеряемое сопротивление, значительно выше, чем ток, проходящий через вольтметр, т. е. если измеряемое сопротивление будет относительно небольшим. При известном значении сопротивления вольтметра R _V можно сделать поправку и вычислить неизвестное сопротивление по соотношению:

[math]\displaystyle{ R_X = \frac{U}{I — \frac{U}{R_V}} }[/math]

В соединении B ток, протекающий через сопротивление измеряется точно, но измеренное падение напряжения увеличивается на падение напряжения на амперметре. Такая схема будет уместна там, где падение напряжения на измеряемом сопротивлении значительно превышает падение напряжения на амперметре, т. е. при относительно больших значениях измеряемого сопротивления. При известном значении внутреннего сопротивления амперметра можно сделать поправку:

[math]\displaystyle{ R_X = \frac{U-R_A\cdot I}{I} }[/math]

Метод замены[edit | править источник]

Подстановочный метод измерения электрического сопротивления реализуется путем подключения неизвестного сопротивления к источнику постоянного электрического напряжения и измерения протекающего электрического тока. После этого подключают калиброванный переменный резистор (обычно резисторную декаду) и экспериментально устанавливают его номинал так, чтобы по цепи протекал такой же ток, как и при включении в цепь неизвестного резистора. Если течет тот же ток, значение на декаде сопротивления равно неизвестному сопротивлению. Таким образом, неизвестное сопротивление заменяется известным сопротивлением, если можно выбрать сопротивление, через которое протекает тот же самый ток.

Аналогично можно проводить измерения с источником постоянного электрического тока.