Определить Токи Электрической Схемы — tokzamer.ru

Подставив 1.

Рассчитайте схему цепи

Рекомендуем: Подключение 2 х клавишного выключателя

Основные понятия

Рассмотрим пример. В заданной схеме, см.

Токи в резисторах В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю. Выполняем все поэтапно.

В табл.

Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.

Пусть, например, задана величина приложенного к току напряжения U и требуется определить ток в цепи и распределение напряжений на ее участках. Последовательное соединение нелинейных элементов. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.

Примеры решения задач на законы Кирхгофа

В схеме рис. После проведенных преобразований рис.

Приступаем к основному этапу — составлению системы уравнений контурных токов. Про комплексные числа можно подробнее прочитать на нашем сайте. Определим параметры электрической цепи рис. Уравнения по второму закону составляют для независимых контуров. Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур.

Переменный ток.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.

Последним этапом находим действительные токи, для этого нужно записать для них выражения. Работа активного двухполюсника под нагрузкой в номинальном режиме определяется уравнением 1.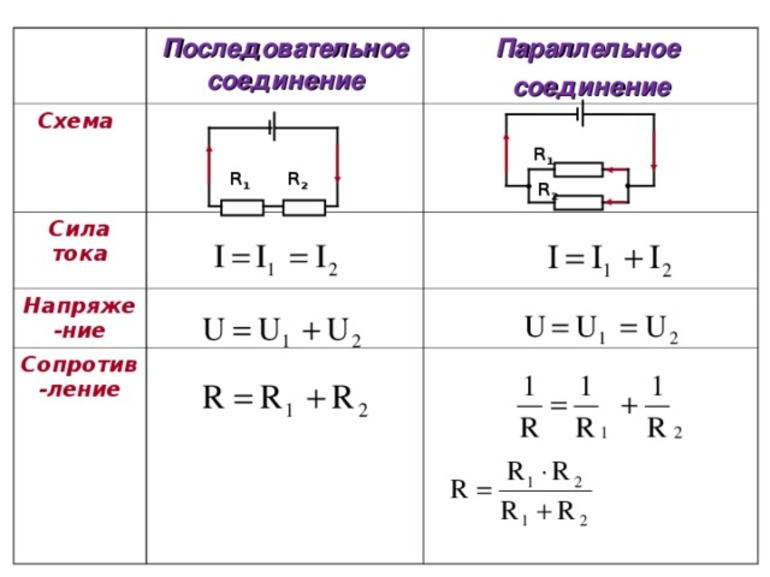

Определим параметры электрической цепи рис. Неуправляемые нелинейные элементы имеют одну вольт-амперную характеристику; управляемые — семейство характеристик.

Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора. Чтобы решить такую систему можно воспользоваться программой MathCad. В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.

Читайте дополнительно: Нормы прокладки кабеля под землей

АГЗ МЧС РГР №1 Расчёт линейных цепей постоянного тока

Уравнения по второму закону составляют для независимых контуров. Определим параметры электрической цепи рис. Контурный ток равен действительному току, который принадлежит только этому контуру. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.

Направление обхода контура совпадает с направлением контурных токов. Режим работы электрической цепи рис. Переменный синусоидальный ток или напряжение задается уравнением: Здесь Im — амплитуда тока. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.

Определить токи во всех ветвях схемы на основании метода наложения.

Эта вольт-амперная характеристика строится по двум точкам 1 и 2 рис. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Следовательно, схема источника тока рис. Вычислим коэффициент подобия.

1.1.3 Определить токи во всех ветвях схемы на основании метода наложения

По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

а) Определяем частные токи от ЭДС Е₁ при отсутствии ЭДС Е₂, т. е. рассчитываем цепь по

Показываем направление частных токов от ЭДС E₁ и обозначаем буквой I с одним штрихом (I’). Решаем задачу методом «свертывания»

Ток источника

Определяем частные токи от ЭДС Е₂ при отсутствии ЭДС Е₁

Ток источника

Вычисляем токи ветвей исходной цепи выполняя алгеб­раическое сложение частных токов, учитывая их направление:

1.1.4 Составить баланс мощностей для заданной схемы

Источники Е₁ и Е₂ вырабатывают электрическую энергию, т. к. на­правление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи запишется так:

Подставляем числовые значения и вычисляем

С учетом погрешности расчетов баланс мощностей получился.

1.1.5 Результаты расчетов токов по пунктам 1 и 2 представить в виде таблицы и сравнить

Ток ветви	I1 A	I2 A	I3 A	I4 A	I5 A	I6 A
Метод расчета
Метод контурных токов	0,429	0,081	0,510	0,291	0,219	0,138
Метод наложения	0,429	0,081	0,509	0,189	0,05	0,239

1.

1.6 Построить потенциальную диаграмму для любого замкнутого контура, включающего обе эдс

Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:

Возьмем контур АВCА. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю

Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А.

Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат -потенциалы точек с учетом их знака.

1.2 Расчет нелинейных электрических цепей постоянного тока Задание

Построить входную вольтамперную характеристику схемы нелиней­ной электрической цепи постоянного тока. Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики.

R3=45 Ом; U=140В.

ВАХ нэ1-б нэ2-в.

ВАХ линейного элемента строим по уравнению. Она представляет собой прямую, проходящую через начало координат. Для определения координаты второй точки ВАХ линейного элемента задаемся произ­вольным значением напряжения. Например, U_R = 90 В, тогда соответствующее значение тока

Соединив полученную точку с началом координат, получим ВАХ линейного элемента.

Далее строится общая ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически «сворачиваем» цепь. Начинаем с разветвленного участка. Нелинейные элемент нэ2 и линейный R1 соединены параллельно, их ВАХ I₁=f(U₁) и I₂=f(U₂). С учетом этого строим общую для них ВАХ. Для этого задаемся напряжением и складываем токи при этом напряжении I₃=I₁+I₂. Точка пересечения этих значений тока и напряжения дает одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ I

3=f(U₁₂).

Далее мы имеем характеристики нелинейного элемента I₃=f(U₃) и нелинейного элемента (нэ12) I₃=f(U₁₂), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I₃=f(U).

Дальнейший расчет цепи производим по полученным графикам.

Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значение напряжения, равное 140 В (точка

«а»). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ I₃=f(U), получим точку «в». Из точки «в» опускаем перпендикуляр на ось тока (точка «с»). Отрезок «ос» дает нам искомое значение общего тока I₃=0,9 А. Когда опускаем перпендикуляр из точки «в» на ось тока, то пересекаем ВАХ I₃=f(U₃) и I₃=f(U₁₂) в точках «f’ и «d» соответственно. Опуская перпендикуляры из этих точек на ось напряжения, получим напряжения на каждом участке цепи: U ₃=110В и U₁₂=30 В, но U₁₂=U₁=U₂, т. к. нелинейные элементы соединены параллельно. Чтобы найти токи I₁ и I₂ при U₁₂=81 В, опустим перпендикуляр из на ось напряжений до пересечения с ВАХ I₁=f(U₁) и I₂=f(U₂) в точках «N» и «М». Опустив из этих точек перпендикуляры на ось токов, получим I₂ = 0,5 А и I₁ = 0,4 А. В результате имеем следующие значения токов и напряжений на всех элементах цепи: I₁=0,4 А; I₂ =0,5 А; I₃ = 0,9 A; U₁=30 В; U₂=30 В; U₃=110 В.

Маркировка напряжений, токов и узлов

Ultimate Electronics: практическое проектирование и анализ схем

---

≡ Оглавление

«

2. 13

Закон напряжения Кирхгофа и закон тока Кирхгофа

»

2.15

Решающие схемы

Правила определения конкретных токов и напряжений для обеспечения правильного применения уравнений KCL и KVL. 16 мин чтение

Как обсуждалось в предыдущем разделе, закон Кирхгофа для напряжения и закон Кирхгофа для тока — это правила, которые описывают, как формировать уравнения тока и напряжения из связного графа цепи. По сути, они представляют собой

бухгалтерских или бухгалтерских правил, устанавливающих баланс между зарядом и потенциальной энергией.

Сами по себе правила не очень сложны, но, как и бухгалтерия, новички в электронике быстро запутываются из-за двух моментов:

1. Маркировка напряжений и токов последовательно и
2. Постоянное отслеживание знака или направления.

---

Мы можем пометить каждый двухконтактный компонент напряжением и током. Обычное соглашение состоит в том, чтобы определить ток как положительный при входе в положительный вывод элемента схемы:

Линейные элементы с маркировкой тока и напряжения на клеммах

Circuitlab. com/cv5q6274rxjyv

Править — Имитация

Для источника напряжения положительная клемма четко обозначена знаком + знак на условном обозначении. Ток определяется как положительный переход в + Терминал.

Для источника тока символ показывает заостренную головку и тонкий конец стрелки, указывающей направление тока. На рисунке, показанном здесь, мы решили определить положительную клемму как хвост источника тока. Это удобно, потому что, если мы снова определим ток как положительный, идущий

в этого терминала, то ток будет таким же, как определенное значение источника.

Для резистора нет направленности компонента. Тем не менее, мы указываем положительную и отрицательную клемму для напряжения v9 как показано, и мы указываем направление для текущего i9 . Наш выбор в какой терминал звонить + был произвольным, но до тех пор, пока нынешний i9 определяется как положительный переход в этого терминала, тогда закон Ома v9=i9R9 будет применяться без изменения знака. (Если мы изменим направление текущего i9без переназначения + терминал, нам нужно было бы написать v9=−i9R9 .)

Условное обозначение тока как положительного при протекании в + Терминал произволен, но некоторые вещи с ним выполняются просто и последовательно:

1. Во-первых, отношения V-I, такие как определение закона Ома, не нуждаются в знаке минус.
2. Во-вторых, потребляемая мощность определяется правильно с P=vi , где Р>0 для обычных компонентов, которые потребляют энергию, например резистор, и P<0 для компонентов, которые обеспечивают питание, например аккумулятор.

---

Решая схему на бумаге, мы можем обозначить токи и напряжения вокруг схемы любыми именами, которые нам нравятся, при условии, что мы позаботимся о том, чтобы отслеживать их направление и знак.

Но при решении с использованием программного обеспечения для моделирования цепей, такого как CircuitLab, каждый вывод каждого компонента имеет встроенное имя, которое можно использовать для ссылки на его ток. В этом простом примере мы явно обозначили эти токи:

.

Маркированные терминальные токи

Circuitlab.com/cbcmg28t4burj

Править — Моделирование

Компонент, такой как источник напряжения «V1», имеет две клеммы с именами «V1.nA» и «V1.nB». Мы можем попросить симулятор показать текущий в конкретного терминала, запросив, например, «I (V1.nA)». Мы также можем показать напряжение на клемме относительно земли , запросив, например, «V(V1.nA)».

Для таких компонентов, как резисторы, может быть неочевидно, какая клемма «nA», а какая «nB». Однако, если вы запустите симуляцию постоянного тока, а затем наведете курсор мыши на схему, вы сможете навести курсор мыши на каждый отдельный терминал, и он покажет имя терминала, напряжение и ток.

Вы также можете добавить собственные выражения для расчета, такие как «V(R1.nA)-V(R1.nB)», которые будут вычислять падение напряжения на резисторе R1.

Вам предлагается щелкнуть схему выше, запустить эту простую симуляцию и поэкспериментировать с различными выражениями для определения токов и напряжений в цепи.

В примере схемы, показанном выше, присутствует ряд равенств, потому что у нас есть несколько имен для одних и тех же величин.

Например, для всех компонентов с двумя клеммами ток на одну клемму должен выходить из другой клеммы, поэтому:

I(V1.nA)=-I(V1.nB)I(R1.nA)=-I(R1.nB)I(R2.nA)=-I(R2.nB)

(Обратите внимание, что численно бывает, что в этой цепи имеется только одно значение тока, потому что это простая одиночная петля, но так будет не всегда.)

Напряжения в каждом узле цепи могут быть обозначены как один или несколько компонентов терминалы, которые подключаются к этому узлу, или как узел с явным именем (см. метки «A», «B» и «C») выше. Ссылка на них любым из этих способов идентична симулятору, но для вашего удобства вам рекомендуется помечать полезные узлы там, где это уместно. А для земли эти напряжения автоматически устанавливаются равными нулю:

V(A)=V(V1.nA)=V(R1.nA)V(B)=V(R1.nB)=V(R2.nA)V(C)=V(V1.nB)= V(R2.nB)=0

В предыдущем разделе, посвященном закону напряжения Кирхгофа, мы обсуждали определение различных путей и то, как обозначение vAB указывает напряжение в узле A по отношению к узлу B. В среде моделирования все отдельные именованные узлы привязаны к земле. Таким образом, если мы хотим найти в CircuitLab относительное напряжение узла, мы должны написать выражение:

vAB=V(A) — V(B)

Вот пошаговая инструкция решения для vAB :

1. Щелкните схематическое изображение «Маркированные клеммные токи» несколькими абзацами выше. Программное обеспечение CircuitLab откроется в новой вкладке браузера.
2. В нижней части экрана нажмите Simulate , чтобы переключиться в режим имитации.
3. На вкладке DC нажмите кнопку + Добавить выражение . Введите «V(A) — V(B)» (без кавычек, но с заглавными буквами!) и нажмите ввод. Это выражение будет добавлено в список.
4. Нажмите кнопку Запустить DC Solver .

Следуйте инструкциям, чтобы убедиться, что вы умеете пользоваться средой моделирования для определения определенных токов и напряжений.

---

Рассмотрим немного более сложный пример:

Маркированные клеммные токи — с BJT и светодиодом

Circuitlab.com/cj55dff4nv229

Править — Имитация

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему.

Эта цепь имеет 5 узлов (обозначенных A, B, C, D и заземление) и 6 элементов.

Клеммы светодиода с именем D1 называются «D1.nA» и «D1.nK», где «nA» — анод, а «nK» — катод.

Выводы биполярного транзистора с именем Q1 называются «Q1.nB» для базы, «Q1.nC» для коллектора и «Q1.nE» для эмиттера.

В то время как приведенные выше правила для компонентов с двумя выводами просто предусматривали, что ток, проходящий через один вывод, равен отрицательному току, проходящему через другой вывод, для устройств с тремя (или более) выводами правило немного отличается. В случае транзистора Q1 имеется три терминальных тока: ток в базу, ток в коллектор и ток в эмиттер. Нас может заинтересовать любой из них, и в следующих главах мы будем им интересны. Тем не менее, по-прежнему применяется правило сохранения, поскольку модель с сосредоточенными элементами запрещает хранение чистого заряда в любом элементе схемы или в любом узле. Как следствие, общий ток в любом компоненте равен нулю, поэтому для транзистора Q1:

I(Q1.nB)+I(Q1.nC)+I(Q1.nE)=0

Для любого двухполюсника, даже такого нелинейного, как светодиод D1, есть только одно значение величины тока через устройство, поэтому мы обычно просто называем это, например, током через диод, не уточняя, что это «анодный ток» или «катодный ток», поскольку они тривиально связаны. Поскольку 2 терминальных тока имеют 1 уравнение, связывающее их, существует только 2−1=1 степень свободы (т. е. одно значение тока для устройства), а остальное — просто вопрос указания знака и направления.

Однако для любого N-терминального компонента существует N различных клеммных токов, которые могут нас заинтересовать. В общем, они делают очень разные вещи! Увеличение тока базы Q1 на 1 мА оказывает гораздо большее влияние на схему, чем увеличение тока коллектора Q1 на 1 мА. Тем не менее, существует 1 уравнение, связывающее сумму всех токов со всеми клеммами компонента, в результате чего остается N−1 степени свободы.

---

При анализе или проектировании схемы принято «задавать вопросы» о различных токах и напряжениях в цепи. (Какое напряжение VB ? Каков ток в базе Q1, I(Q1.nB) ?) Мы можем сформулировать «решение схемы» с точки зрения нахождения любых ответов (неизвестных), которые мы ищем.

В цепи с N узлов (включая 1, определенный как земля), T терминалы компонентов и C компонентов, мы можем задать много вопросов:

1. [Для каждого N2 пара узлов:] Какова разность напряжений Vij ?
2. [Для каждого T Терминал компонента:] Каков ток на этом терминале?
3. [Для каждого T клемма компонента:] Какой ток выходит из этой клеммы?

Из этих трех случаев имеем N2+2T «вопросы», которые мы могли бы задать. Даже для схемы среднего размера возникает много возможных вопросов, но все они являются действительными вопросами , на которые мы сможем ответить после решения схемы.

Однако, чтобы уменьшить размерность нашей проблемы, мы пытаемся упростить это большее количество вопросов (неизвестных) до меньшего числа, чтобы его было легче решать. (См. также: Системы уравнений.)

Например, для разности напряжений мы знаем, что существует нулевая разность напряжений. Vii для любой пары одного и того же узла дважды (i,i) . Кроме того, из закона Кирхгофа о напряжении мы знаем, что циклы напряжений в сумме равны нулю, поэтому мы можем использовать определенную опорную землю для преобразования парных разностей напряжений в разности точечных напряжений между узлом и землей.

1. [Для каждого из N−1 незаземленные узлы:] Какое напряжение в данном узле Vi (относительно земли)?

Вместо N2 вопросы о попарных разностях напряжений, теперь у нас есть N−1 вопросов – резко меньшее количество. Важно отметить, что как только мы ответим на эти N−1 вопросы (т.е. решить для этих неизвестных), мы можем легко найти ответы на исходный N2 вопросов.

Для токов 2T вопросы, касающиеся «входа» и «выхода» из конкретного терминала, также легко сводятся к Т вопросы, учитывая только версию «в». Важно отметить, что как только мы ответим на эти T вопросы, мы можем легко ответить на вопросы «из» простым отрицательным знаком.

Теперь мы уменьшили исходное значение N2+2T. вопросы к (N−1)+T вопросов — гораздо меньше.

Теперь мы можем применить текущие отношения терминала компонента.

Как обсуждалось выше, каждый компонент с двумя выводами имеет тривиальное соотношение между токами двух выводов: одно уравнение. И каждый компонент с несколькими клеммами также имеет единственное уравнение, связывающее токи его клемм. В общем, хотя по-прежнему справедливо «задавать вопрос» отдельно о токах базы, коллектора и эмиттера в транзисторе Q1, дело в том, что если мы знаем значение любых двух из трех, мы также знаем и третье.

Это означает, что T вопросы о терминальных токах на C компоненты на самом деле имеют только T−C возможных степеней свободы. Как только мы узнаем значения (правильного подмножества) T−C терминальные токи, остальное мы знаем.

Даже не взглянув на структуру конкретной схемы, мы теперь знаем, что можем отобразить схему из N узлов (включая 1, определенный как земля), T терминалы компонентов и C компонентов из исходного большего пространства:

N2+2T

возможные вопросы по току и напряжению в гораздо меньшее пространство всего:

(N-1)+T-C

вопроса. Основная идея заключается в том, что гораздо проще решить систему уравнений с меньшим числом неизвестных. И что особенно важно, поиск ответов на это меньшее подмножество позволяет нам (очень легко) отбрасывать ответы на оставшиеся вопросы по мере необходимости.

Например, если у нас есть даже очень простая схема с N=8 узлов, Т=20 клеммы и C=10 компонентов (предположим, что все 10 компонентов являются двухконтактными устройствами), у нас будет 82+2∗20=104 вопросы, которые мы можем задать о различных попарных разностях напряжений и терминальных токах.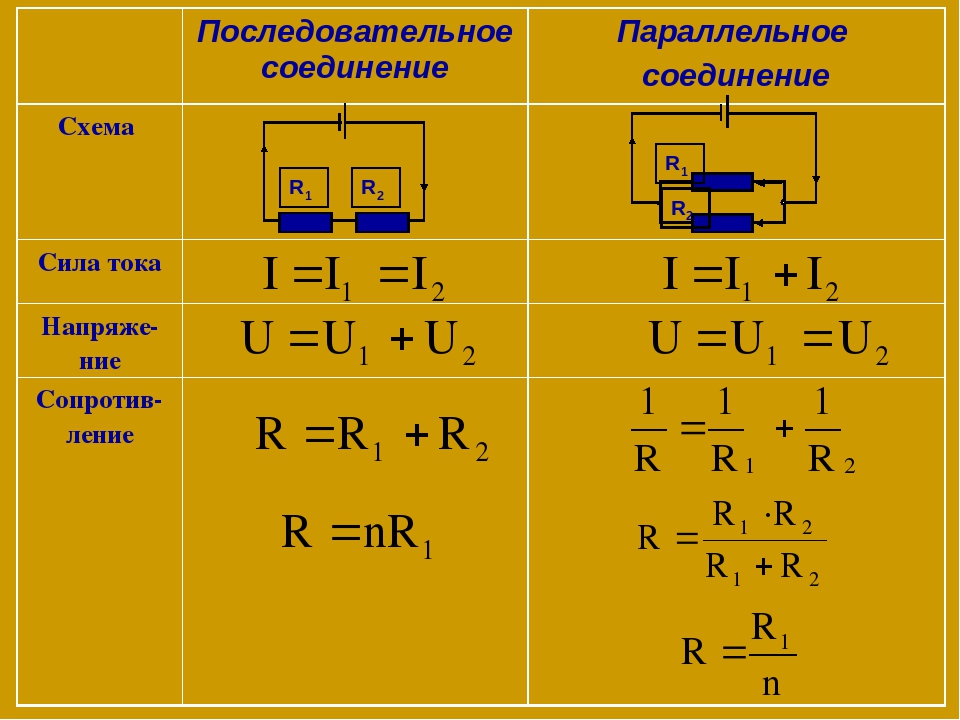 Однако мы можем сопоставить эту схему с гораздо меньшим набором (8−1)+20−10=17. вопросы, из которых мы можем легко восстановить ответы на любой из первоначальных 104 вопросов! И мы добились этого значительного сокращения, даже не взглянув на компоненты или их расположение.

Этот процесс сокращения широко используется как программным обеспечением для моделирования цепей, таким как CircuitLab, так и при решении схем вручную. (На самом деле, это часто полностью замалчивается, оставляя новичков в замешательстве относительно того, как было выполнено такое упрощение и как вернуться к ответам на вопросы, которые нас в конечном итоге интересуют, поэтому мы решили сделать это здесь более подробно.)

---

Как показывают два примера цепей с помеченными токами на клеммах выше, мы можем пометить T различных токов на клеммах в цепи с T общим количеством клемм, но они не уникальны.

В нашем предыдущем обсуждении закона тока Кирхгофа мы смогли обсудить текущие потоки, не ссылаясь на какие-либо конкретные компоненты или терминалы. Мы достигли этого, вручную пометив токи, а также поместив стрелку, чтобы указать определенное направление обычного потока тока (в отличие от потока электронов). Например:

Пример KCL с тремя узлами

Circuitlab.com/c4e7f729tv5s3

Править — Simulate

Мы вручную пометили стрелку тока через каждый из четырех показанных компонентов, и это само по себе позволило нам написать три уравнения KCL (по одному в каждом узле A, B, C), описывающих структуру схемы. (Обратите внимание, что, хотя было сгенерировано 3 уравнения, только 2 из них являются линейно независимыми. Просмотрите раздел KCL, чтобы просмотреть эти уравнения.) На самом деле, в простом последовательно соединенном наборе элементов мы могли бы сразу понять, что i1 = i2 и использовать только одну переменную, если направление везде одинаково.

Процесс ручной маркировки текущих переменных (и произвольного назначения направления) включает в себя большую часть только что описанных процессов редукции.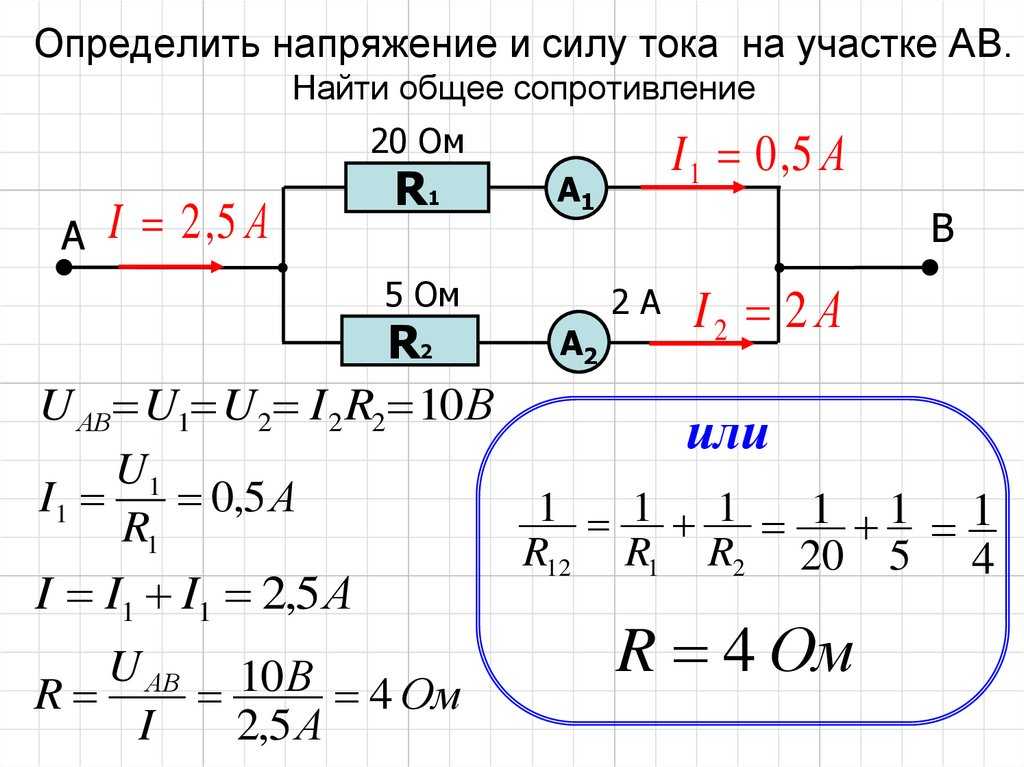 Мы по-прежнему можем задавать все возможные текущие вопросы (т. е. клеммные токи в каждом компоненте или из него), но теперь мы можем ссылаться на эти клеммных токов в терминах этих вручную выбранных токовых переменных, иногда называемых ответвленными токами .

Симулятор цепей обычно не представляет мир с точки зрения токов ветвей, а вместо этого вычисляет токи клемм для различных компонентов. Тем не менее, они явно тесно связаны и могут быть отображены туда и обратно, просто определяя правильный ток ветви, который отображается на клемму, и применяя знак минус, если стрелка тока ветви выходит «из» этой клеммы, а не в обычном определении. клеммных токов, являющихся положительными для потока «в» клемму.

---

Мы можем маркировать токи ветвей и в более сложных цепях, как это часто делается при ручном решении. Например, мы можем обозначить наш пример с несколькими терминалами выше: (щелкните, чтобы открыть в новой вкладке)

.

Маркированные токи клемм и ответвлений — с BJT и светодиодом

Circuitlab.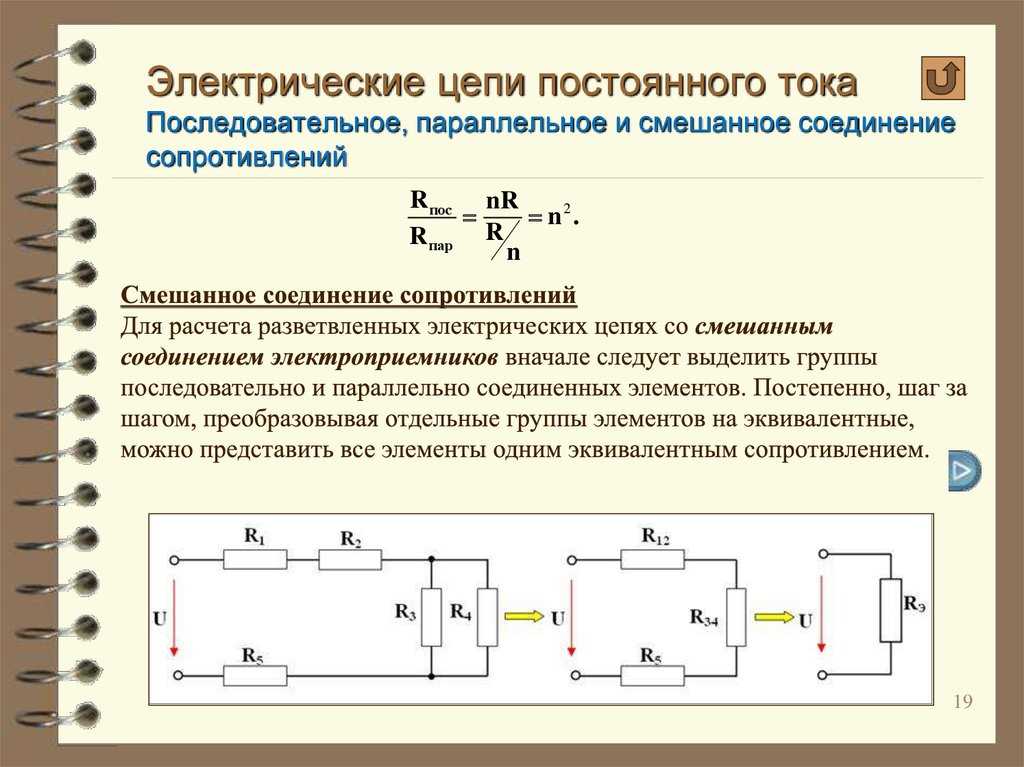 com/c95w3f4e3n69c

Править — Моделирование

Мы пометили 6 ветвей тока, с i1 по i6. . В общем, на схеме мы не будем так явно обозначать как токи ветвей, так и клеммные токи, но мы делаем это здесь, чтобы быть очень явными и показать сопоставление между ними.

Просто наблюдая направления стрелок вдоль каждой ветви цепи, мы можем написать множество уравнений, связывающих токи ветвей с токами клемм. Например, для i1 , мы можем видеть, что это описывает ток, протекающий через источник напряжения V1, и направление стрелки i1 противопоставляется I(V1.nA) но находится в том же направлении, что и I(V1.nB) . Это позволяет нам записать:

i1=-I(V1.nA)i1=I(V1.nB)

или проще:

i1=-I(V1.nA)=I(V1.nB)

Мы можем повторить этот процесс для каждого из 6 токов ветвей, пока не сопоставим все 13 токов клемм с 6 токами ветвей:

i1=−I(V1.nA)=I(V1.nB)i2 =I(R2.nA)=-I(R2.nB)i3=I(D1.nA)=-I(D1.nK)=I(Q1.nC)i4=I(Q1.nB)i5=I( R3.nA)=-I(R3. nB)i6=-I(Q1.nE)=I(R1.nA)=-I(R1.nB)

Каждый ток ответвления просто сопоставляется со всеми терминальными токами на этом ветвь, возможно, со знаком минус, указывающим на несоответствие направления стрелки. Ветвь продолжается до тех пор, пока не произойдет «расщепления», когда ток может идти двумя путями.

Для схемы с 13 терминалами это позволяет нам ответить на 26 возможных текущих вопросов (т. е. ток в любой терминал или из него) только с 6 базовыми переменными.

Процесс сопоставления тока ветви имеет тенденцию автоматически обрабатывать узлы, где встречаются только два терминала (например, узлы C и D), поскольку мы помечаем их как одну непрерывную ветвь, поэтому мы назначаем только одну текущую переменную. Для узлов, где встречаются 3 или более клемм (таких как A и B), мы можем применить закон тока Кирхгофа к токам ветвей:

i1-i2-i3=0i2-i4-i5=0

Кроме того, процесс сопоставления тока ответвления имеет тенденцию заботиться о сохранении потока заряда в устройствах с двумя выводами, поскольку они помечены одним и тем же током ответвления. Однако для компонентов с тремя или более клеммами мы можем явно сгенерировать правило суммирования дополнительных токов, заметив, что суммарные входные токи ветвей должны равняться суммарным выходным токам ветвей. Например, для транзистора Q1:

i3+i4−i6=0

Это дополнительное и, возможно, ценное ограничение при ручном решении схемных задач. Однако в программном обеспечении для моделирования цепей, таком как CircuitLab, все многополюсные устройства эффективно моделируются внутренне как набор различных (возможно, нелинейных и взаимодействующих) двухвыводных устройств, поэтому дополнительное ограничение не требуется.

---

Еще один способ осмыслить процесс маркировки и сокращения — рассмотреть, как мы будем эффективно проводить измерения цепи. Для этого мы снова обратимся к гидравлической аналогии воды под давлением, протекающей через сеть труб и других компонентов. (Пока мы игнорируем практические вопросы точности и т. д. и рассматриваем только теоретическую модель. )

Мы можем задать вопрос о разнице напряжений (т. е. разности давлений) между любыми двумя точками в сети и в гидравлической системе. системы, мы могли бы купить дифференциальные манометры и установить их между каждой парой точек, которые нас интересуют. Однако, если у нас есть N очков, у нас есть N2 пар точек (или, возможно, N(N−1)2 пар, если игнорировать Vii=0 и разрешено измерять Vab=-Vba ). Дифференциальный манометр подобен вольтметру с двумя выводами и показывает только относительную разницу давлений. Однако для этого необходимо провести множество дифференциальных измерений, а покупка и установка этих датчиков стоит дорого! Вместо этого мы можем просто установить N−1 манометры перепада давления (взяв 1 узел за точку отсчета), а затем вычитать, когда это необходимо, чтобы ответить на любые вопросы об относительных различиях. Для небольшой гидравлической схемы, состоящей всего из 10 узлов, это разница между 45 и 9 узлами.датчики установить и читать!

Точно так же мы могли бы установить амперметр (т. е. устройство для измерения расхода) на каждом выводе каждого компонента, но явно не имеет смысла устанавливать расходомер с обеих сторон одного двухвыводного компонента, поскольку скорость потока будет такой же при условии отсутствия утечек. Вместо этого мы должны установить только одно измерение скорости потока на ответвление. (И, если есть 3+ терминальных компонента, мы можем быть даже более умными и установить меньше, чем один расходомер на ответвление, используя сохранение расхода, как показано выше.) Это гораздо меньшее количество расходомеров для покупки, установки, и монитор.

Точно так же, как мы естественным образом применяем эти упрощения при измерении электрической (или гидравлической) цепи, мы применяем их и при постановке задачи для алгебраического решения, потому что они значительно упрощают этот процесс.

---

В следующем разделе «Решение систем цепей» мы поговорим об объединении нашего маркированного структурного представления схемы с уравнениями на уровне отдельных компонентов для полной настройки и решения схем любой сложности.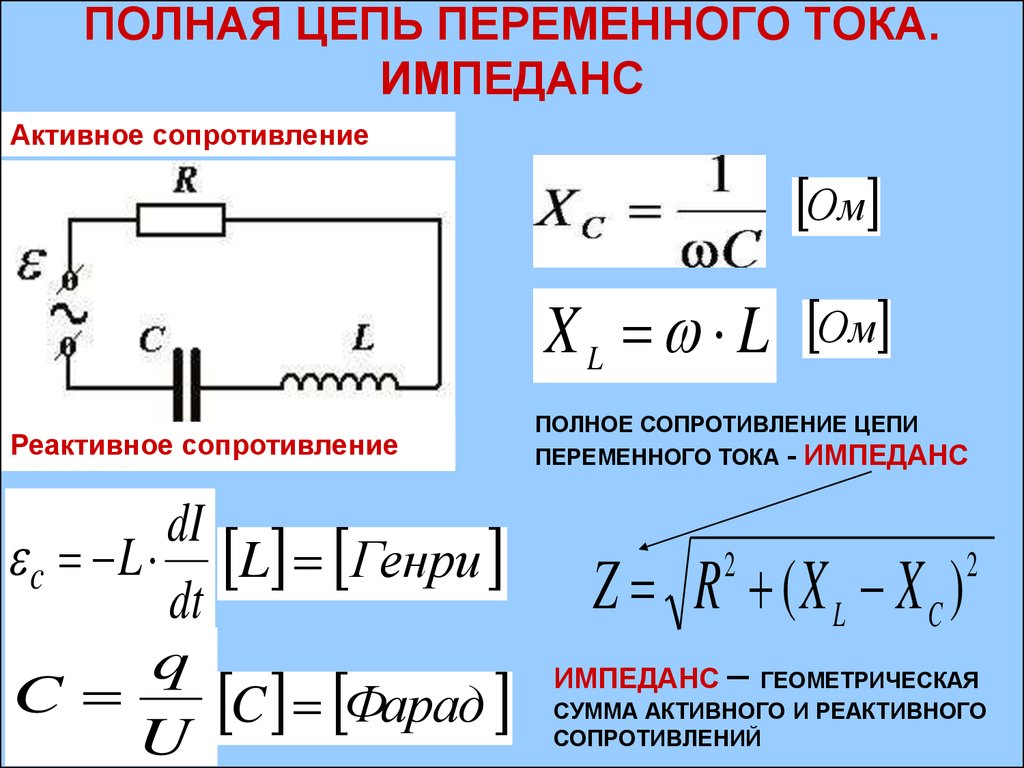

≡ Оглавление

«

2.13

Закон напряжения Кирхгофа и закон тока Кирхгофа

»

2.15

Решающие схемы

---

Роббинс, Майкл Ф. Абсолютная электроника: проектирование и анализ практических схем. CircuitLab, Inc., 2021, Ultimateelectronicsbook.com. Доступ . (Авторское право © 2021 CircuitLab, Inc.)

Что?, Последовательное или параллельное, Измерение тока и напряжения

29 ноября, 2022 17 августа 2022

В этом посте

Мы собираемся перейти к схемам и их компонентам. Следующие символы используются для обозначения компонентов схемы, которые обычно используются в физике.

Вы должны быть знакомы с этими символами, как вы увидите, и, возможно, вам придется использовать эти символы или их небольшие вариации в экзаменационных вопросах по электричеству и цепям.

Электрические цепи всегда включают в себя источник электроэнергии для обеспечения напряжения, провода, обеспечивающие путь прохождения тока, и компонент, который можно использовать для демонстрации того, что ток распространяется по цепи. Лампы и светодиоды ( светодиоды) являются примерами компонентов, которые можно использовать для индикации наличия тока в цепи.

Оба эти компонента загораются или светятся только тогда, когда через них проходит ток. Если компоненты подключены к цепи, но не светятся, это указывает на то, что ток не течет и должен быть либо обрыв в проводе, либо отсутствие напряжения, толкающего электроны по цепи.

Последовательные и параллельные цепи и их применение

Электрические цепи могут быть соединены последовательно или параллельно . Эти различные типы схем имеют ключевые сходства и различия, которые делают их подходящими для различных целей. Вы должны быть в состоянии объяснить, почему последовательная или параллельная схема более подходит для конкретных приложений.

Последовательные цепи

В последовательной цепи компоненты соединяются один за другим в линию. Ток, протекающий через каждый компонент, всегда одинаков, независимо от их положения в цепи. На приведенной ниже схеме показан пример последовательной цепи:

Электричество проходит по всем проводам цепи. Это означает, что электричество должно пройти через каждый компонент цепи и вернуться к исходной точке. Если один компонент в последовательной цепи будет удален или отключен, цепь будет разорвана, и электричество больше не сможет течь.

Например, рассмотрим набор елочных огней, соединенных последовательно. Если одна из лампочек сломалась, электричество не может пройти к следующей лампочке. Цепь будет разорвана, и ни один из огней не загорится. Поэтому было бы очень трудно определить, какая лампочка неисправна. Понятно, почему последовательная схема была бы плохим выбором для домашнего освещения!

P параллельные цепи

В параллельной цепи каждый компонент может быть размещен на отдельных петлях, параллельных друг другу. Напряжение на всех компонентах в параллельной цепи одинаково, а ток — нет. Ток распределяется поровну между всеми отдельными ветвями цепи. Сумма токов, измеренных на каждой ветви цепи, должна быть равна общему току, протекающему по цепи. Это означает, что общий ток, протекающий по цепи, распределяется между каждой параллельной ветвью компонента. На приведенной ниже схеме показан пример параллельной цепи:

Поскольку каждый компонент в параллельной цепи находится на отдельном контуре цепи, при обрыве одного компонента ток все еще может проходить по другим неразрывным ветвям. Таким образом, компоненты в других ветвях по-прежнему смогут работать. Вернемся к нашему предыдущему примеру с елочными огнями. Если бы лампы были соединены в параллельную цепь и одна из лампочек вышла из строя, остальные лампы продолжали бы гореть. Тогда было бы очень легко определить и заменить сломанную лампочку. Параллельные цепи используются в бытовом освещении по той же причине. Например, если на кухне перегорела лампочка, остальные лампы в доме останутся гореть.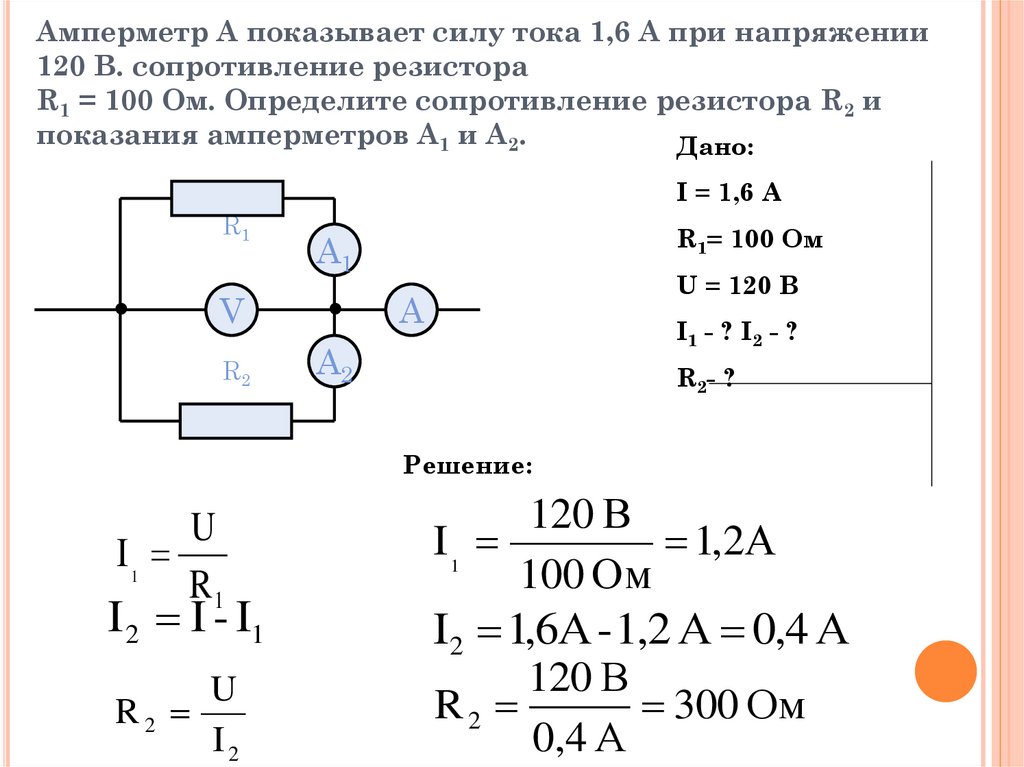 Последовательные и параллельные схемы имеют разные характеристики, что делает их подходящими для разных приложений.

В последовательной цепи:

• Один переключатель может одновременно включать и выключать все компоненты.
• Если одна лампочка или устройство сломается, все остальные лампочки или устройства перестанут работать.
• Напряжение, подаваемое элементом или сетью, распределяется между всеми компонентами. Чем больше лампочек добавлено в последовательную цепь, тем тусклее они будут.
• Чем больше сопротивление любого компонента, тем больше доля напряжения в цепи.

В параллельной цепи:

• Выключатели могут быть размещены в разных частях цепи для индивидуального включения и выключения каждой лампочки.
• Если одна лампочка или устройство сломается, пострадают только лампочки на той же ветке.
• Каждая ветвь цепи получает одинаковое напряжение, поэтому, если в цепь параллельно добавить дополнительные лампочки, их яркость не изменится.

Декоративные гирлянды обычно соединяются последовательно. Это потому, что каждой лампочке нужно только низкое напряжение. Если напряжение от сети распределяется между каждой лампочкой, они все равно получают достаточно энергии для производства света. Если одна из лампочек неправильно установлена ​​в патроне или сломается, цепь больше не будет замкнутой, и ни одна из лампочек не загорится.

Свет в ваших домах подключен параллельно. Каждая лампочка может включаться и выключаться отдельно, и яркость лампочек не меняется, когда другие лампочки включены или выключены. Если одна лампочка сломается или будет удалена, вы все равно сможете использовать другие лампочки в доме.

Ток и напряжение в последовательных и параллельных цепях

Ток в цепи обычно измеряют с помощью устройства, называемого амперметром. Амперметр помещают последовательно с компонентом, через который проходит ток, и поэтому он становится частью цепи. Он способен измерять величину тока, протекающего через него.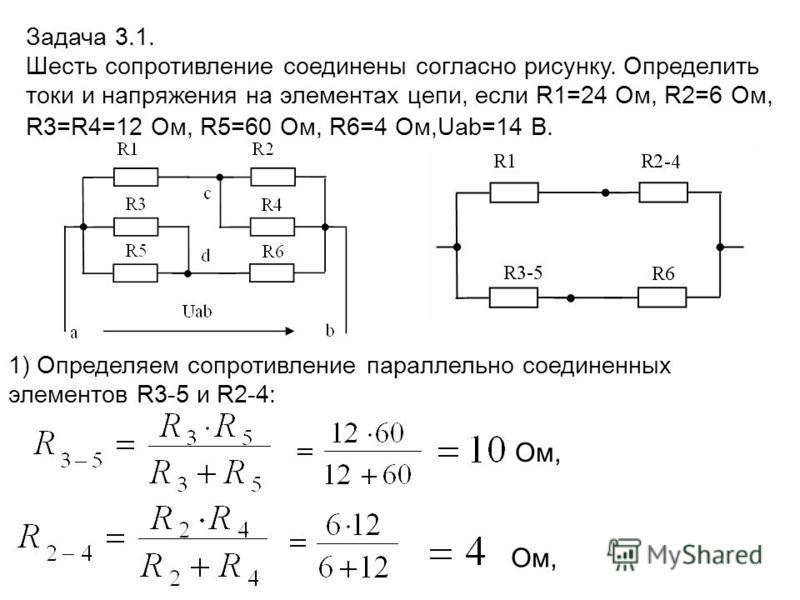

Амперметр должен иметь низкое сопротивление, так как в противном случае ток уменьшится, и измеренное значение будет неточным. На диаграмме напротив показано типичное положение амперметра по отношению к цепи.

Для измерения разности потенциалов или напряжения на компонентах в цепи, таких как элементы или лампы, мы используем устройство, известное как вольтметр. Вольтметры должны быть подключены параллельно или параллельно компоненту, на котором мы измеряем разность потенциалов.

Вольтметр, подключенный параллельно компоненту, измеряет количество энергии, передаваемой каждому кулону заряда, прошедшего через него. На диаграмме напротив показано типичное положение вольтметра в цепи, где он расположен параллельно компоненту, на котором он измеряет разность потенциалов.

Ток и напряжение в последовательной цепи

В последовательной цепи ток, протекающий через все компоненты, одинаков. Поэтому, если ток измерялся в какой-либо точке цепи, он всегда должен быть равен. Например, если в начале цепи был измерен ток 0,4 А, то ток, измеренный в любой другой точке цепи, также должен быть равен 0,4 А.

Величина тока зависит от общего напряжения, выдаваемого элементами или батареями, а также от количества и характера компонентов, включенных в цепь. Если добавить больше компонентов, ток уменьшится, поскольку каждый из них оказывает сопротивление потоку электричества.

Напряжение в последовательной цепи не одинаково для всех компонентов. Напряжение распределяется поровну между компонентами цепи, если их сопротивления равны. Например, если батарея в последовательной цепи производит 6 В, и у нас есть три компонента в цепи, напряжение, измеренное на каждом компоненте, будет 2 В. Если сопротивления компонентов неодинаковы, напряжение, измеренное на компонентах, будет различным.

Посмотрите на изображения двух последовательных цепей выше. Тот, что слева, показывает результаты размещения вольтметра в цепи в разных точках, и мы видим, что 6 вольт — это мощность от батареи. Затем он разделяется между компонентами, так что каждый из них имеет измерение 3 В. На изображении справа показана та же схема, но на этот раз с показаниями амперметра. Мы видим, что ток (измеряемый в амперах) одинаков по всей цепи.

Ток и напряжение в параллельной цепи

В параллельной цепи ток делится по разным ветвям, а затем снова объединяется при возвращении в батарею. Ток, измеренный до и после ветвей, должен быть одинаковым. Каждая ветвь цепи будет измеряться в процентах от начального тока. Сумма токов, измеренных на всех ветвях, должна быть равна общему току, измеренному в начале и конце цепи.

Например, рассмотрим параллельную цепь с двумя ответвлениями, где начальный измеренный ток равен 0,4 А. Каждая из двух ветвей имеет только одну луковицу. Ток будет проходить через обе ветви и обе лампы одинаково, поэтому ток, измеренный на обеих ветвях, будет 0,2 А, как показано на диаграмме выше.

Напряжение или разность потенциалов (p. d.) между компонентами, соединенными в параллельную цепь, всегда равны. Каждая ветвь будет иметь точно такой же p.d. и это значение не меняется, в отличие от последовательной цепи. Например, на приведенной выше схеме показана параллельная цепь с двумя ответвлениями. Аккумулятор имеет р.д. 6 В, и каждая ветвь также имеет p.d. 6В

Как измерить ток

Для измерения тока, протекающего по цепи, мы используем амперметр. Амперметр подключается последовательно с компонентами и измеряет скорость, с которой заряд течет по цепи.

Как мы уже говорили, электрический заряд измеряется в кулонах (Кл). Один кулон эквивалентен примерно шести миллионам, миллионам, миллионам электронов. Это должно дать вам представление о том, насколько крошечными на самом деле являются электроны! Один кулон заряда, проходящий через объект каждую секунду, равен одному амперу.

Для расчета заряда, проходящего через провод, мы используем уравнение:

Q=I×t
где Q= заряд (в кулонах), I= ток (в амперах) и t= время (в секундах)

Вы должны быть в состоянии изменить это уравнение, чтобы найти ток, заряд или время в зависимости от значений, указанных в экзаменационном вопросе.

Чтобы найти ток, заряд и время, мы можем использовать формулу треугольника, как показано на диаграмме ниже. Значение, которое вы хотите рассчитать, закрыто, и вы смотрите на два оставшихся значения. Если они показаны один поверх другого, то вам нужно разделить верхнее число на нижнее число. Если они отображаются рядом, то вы должны умножить два значения.

Пример

Если по проводу протекает ток 12 А в течение 8 секунд, рассчитайте заряд.

Здесь мы используем наше уравнение Q=I×t и подставляем ток и время:

Q=I×t
Q=12A×8s
Q=96 кулонов

Пример

Если заряд 120C и затраченное время составило 12 секунд, рассчитайте необходимый ток. Здесь мы перестраиваем уравнение, чтобы получить I = Q  t, и подставляем значения:

Передача энергии

Как обсуждалось ранее, энергия, переданная компонентам (в джоулях), может быть рассчитана с использованием приведенного ниже уравнения: также можно рассчитать с помощью уравнения:

Пример

Рассчитайте энергию, переданную за период 45 секунд, если ток равен 30 А, а напряжение равно 5 В.

Передаваемая энергия = 30 А x 5 В x 45 с

Передаваемая энергия = 6750 Дж

Исследование взаимосвязи между током и напряжением

Зависимость между напряжением и током можно исследовать экспериментально для различных компонентов. Метод такого эксперимента описан следующим образом:

1. Соберите последовательную цепь, содержащую батарею, амперметр, тестируемый компонент, вольтметр, помещенный на компонент, и переменный резистор.
2. Запишите начальный ток и напряжение, показанные на амперметре и вольтметре.
3. Измените настройку переменного резистора, чтобы изменить ток, протекающий по цепи, и напряжение на компоненте.
4. Сделайте еще одно показание измененного тока и напряжения.
5. Повторите шаги 3 и 4 не менее пяти раз, чтобы собрать несколько измерений тока и напряжения.
6. Дважды повторите шаги 2–5 и рассчитайте среднее напряжение для каждого тока.
7. Поменяйте местами провода так, чтобы клеммы ячейки поменялись местами, и повторите шаги 2–6.