ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ И ОПРЕДЕЛЕНИЕ МОМЕНТА СИЛЫ ТРЕНИЯ
⇐ ПредыдущаяСтр 9 из 19Следующая ⇒
Цель работы: построить для маховика график зависимости углового ускорения b от момента силы натяжения Мн и определить из него момент силы трения Мтр и момент инерции маховика J.
Оборудование: маховик, штангенциркуль, набор грузов, секундомер, линейка.
Общие сведения
Согласно основному уравнению динамики вращательного движения угловое ускорение прямо пропорционально сумме моментов внешних сил, действующих на тело, и обратно пропорционально моменту инерции

Здесь 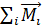 – векторная сумма моментов сил, которую называют результирующим моментом сил;
– векторная сумма моментов сил, которую называют результирующим моментом сил;
В настоящей работе экспериментально изучается эта зависимость.
Описание установки и метода измерений
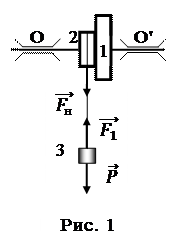
Маховик состоит из диска 1 и шкива 2, насаженных на вал (рис. 1). Вал может вращаться около горизонтальной оси OO’. На шкив намотана нить, к свободному концу которой подвешен груз 3.
При падении груза маховик начинает вращаться с угловым ускорением b.
Результирующий момент, создающий это ускорение, складывается из момента Мн силы натяжения нити и момента

Если момент инерции маховика и момент силы трения остаются постоянными, то зависимость углового ускорения от момента силы натяжения линейная и графически изображается прямой линией (рис 2).
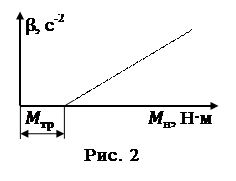 Из уравнения (2) следует, что при покоящемся маховике (b=0) Мн = Мтр. Только когда момент силы натяжения становится больше максимального момента силы трения покоя, маховик начинает вращаться равноускоренно. Прямая на графике пересекает ось абсцисс (рис. 2) в точке, которая определяет
Из уравнения (2) следует, что при покоящемся маховике (b=0) Мн = Мтр. Только когда момент силы натяжения становится больше максимального момента силы трения покоя, маховик начинает вращаться равноускоренно. Прямая на графике пересекает ось абсцисс (рис. 2) в точке, которая определяет
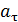 точек боковой поверхности шкива, которое равно ускорению a падающего груза:
точек боковой поверхности шкива, которое равно ускорению a падающего груза:

где r и D – радиус и диаметр шкива.

где h – путь, пройденный грузом за время t.
Подставив выражение (4) в уравнение (3), получим формулу, по которой можно рассчитать на опыте угловое ускорение маховика

Модуль момента силы натяжения числено равен произведению силы натяжения Fн на плечо силы, которое является радиусом шкива:
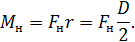
Силу натяжения нити найдем, рассматривая движение груза3. На него действуют сила тяжести P и сила реакции нити F1. По второму закону Ньютона 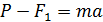 , где m – масса подвешенного к нити груза.
, где m – масса подвешенного к нити груза.
Учитывая, что сила натяжения нити, действующая на шкив и сила реакции, действующая на груз, одинаковы по величине (Fн = F1), получим
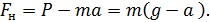
Тогда

Подставив в уравнение (6) выражение (4) для ускорения a, получим формулу

по которой можно рассчитать на опыте момент силы натяжения нити, действующей на маховик.
Порядок выполнения работы
1. Измерить штангенциркулем диаметр D шкива.
2. Вращая маховик, поднять висящий на нити груз на высоту
3. Отпустив маховик и, одновременно включив секундомер, определить время t опускания груза с высоты h. Измерение времени провести три раза. Результаты опыта занести в табл. 1.
Таблица 1
| Номер опыта | Масса m, кг | Высота h, м | Время t, c | Момент силы натяжения Мн, Н·м | Угловое ускорение b, с-2 | |||
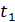 | 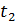 | 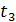 | 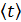 | |||||
4. Повторить опыт с пятью различными грузами. Массы грузов указаны на них.
5. По формулам (5) и (7) вычислить для каждого груза угловое ускорение b и момент силы натяжения
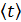 ).
).
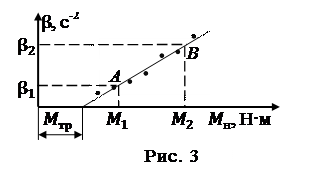 6. Результаты опыта изобразить графически на листе миллиметровой бумаги. Для этого по оси ординат в определенном масштабе отложить значения b, а по оси абсцисс также в определенном масштабе – значения Мн (масштабы по осям координат выбираются независимо друг от друга и должны быть нанесены на координатные оси). Полученные точки соединить прямой линией. Проводить прямую следует так, чтобы она лежала возможно ближе к точкам и по обе ее стороны оказывалось приблизительно равное их количество (см. рис. 3).
6. Результаты опыта изобразить графически на листе миллиметровой бумаги. Для этого по оси ординат в определенном масштабе отложить значения b, а по оси абсцисс также в определенном масштабе – значения Мн (масштабы по осям координат выбираются независимо друг от друга и должны быть нанесены на координатные оси). Полученные точки соединить прямой линией. Проводить прямую следует так, чтобы она лежала возможно ближе к точкам и по обе ее стороны оказывалось приблизительно равное их количество (см. рис. 3).
7. Продлить прямую до пересечения с осью абсцисс, определить по графику момент силы трения.
Для определения момента инерции маховика нужно на экспериментальной прямой, взять точки A и B и провести через них прямые, параллельные осям координат (рис. 3). Момент инерции рассчитать по формуле
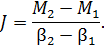
Записать окончательные результаты опыта
М
Контрольные вопросы
1. Что называется моментом инерции материальной точки? Единицы его измерения. От чего зависит момент инерции тела? Какую роль он играет во вращательном движении?
2. Что называется моментом силы относительно точки, неподвижной оси? Как определить направление момента силы? В каких единицах он измеряется?
3. Дать определения угловой скорости и углового ускорения. Как определить их направления?
4. Какова связь между линейными и угловыми скоростями и ускорениями?
5. Вывести основное уравнение динамики вращательного движения.
7. Почему движение подвешенного к нити груза и вращение маховика являются равноускоренными?
8. Вывести расчетные формулы (5) и (7).
9. Объяснить, как графически находят момент силы трения и момент инерции маховика.
10. Проведите аналогию между величинами и формулами, описывающими поступательное и вращательное движение.
Библиографический список
1. Детлаф, А. А. Курс физики / А. А. Детлаф, Б. М. Яворский. – М.: Высш. шк., 1999. – § 4.1–4.3.
2. Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 6, 16, 18.
3. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев. – СПб.: Лань, 2005. – § 38, 39.
4. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл.7 § 7.1, 7.3, 7.4, 7.6.
5. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 30, 32–38.
6. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.31– 1.34.
ЛАБОРАТОРНАЯ РАБОТА № 9
Лабораторная работа № 4 проверка основного закона динамики для вращающихся тел
КРАТКАЯ ТЕОРИЯ. Вращательным движением называется движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой (ось вращения).
Вращательное движение можно описать с помощью угловых кинематических величин.
1. Вектор
углового перемещения 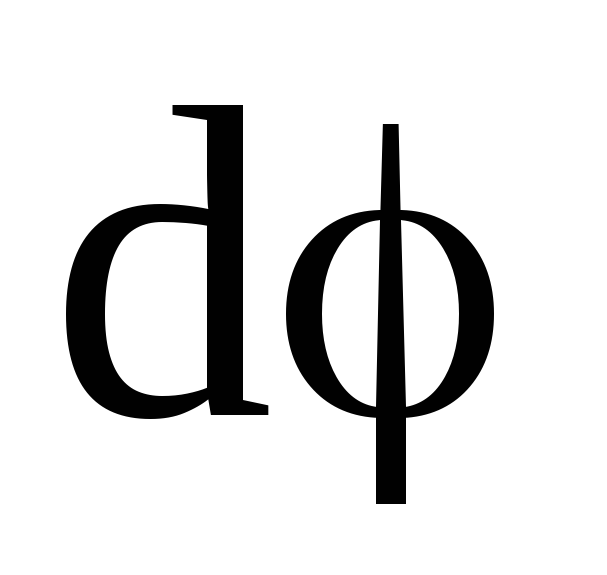
физическая векторная величина, модуль
которой равен углу поворота (углу между
двумя радиусами, проведенными в начальное
и конечное положение материальной
точки). Вектор углового перемещения
направлен перпендикулярно плоскости,
в которой произошел поворот, так, что с
конца вектора вращение наблюдается
происходящим против часовой стрелки.
Направление вектора углового перемещения
может быть найдено по правилу правого
буравчика (рис. 1). Угловое перемещение
измеряется в радианах.
физическая векторная величина, модуль
которой равен углу поворота (углу между
двумя радиусами, проведенными в начальное
и конечное положение материальной
точки). Вектор углового перемещения
направлен перпендикулярно плоскости,
в которой произошел поворот, так, что с
конца вектора вращение наблюдается
происходящим против часовой стрелки.
Направление вектора углового перемещения
может быть найдено по правилу правого
буравчика (рис. 1). Угловое перемещение
измеряется в радианах.
2. Угловая
скорость 
физическая величина, показывающая
угловое перемещение, совершаемое за
единицу времени:
физическая величина, показывающая
угловое перемещение, совершаемое за
единицу времени: 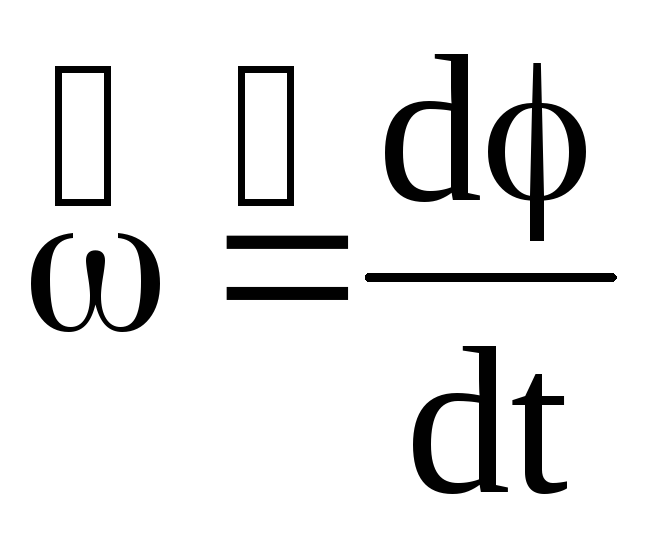 .
.
Вектор
угловой скорости совпадает по направлению с вектором
углового перемещения.
совпадает по направлению с вектором
углового перемещения.
3. Угловое
ускорение 
физическая величина, показывающая
изменение угловой скорости за единицу
времени:
физическая величина, показывающая
изменение угловой скорости за единицу
времени:
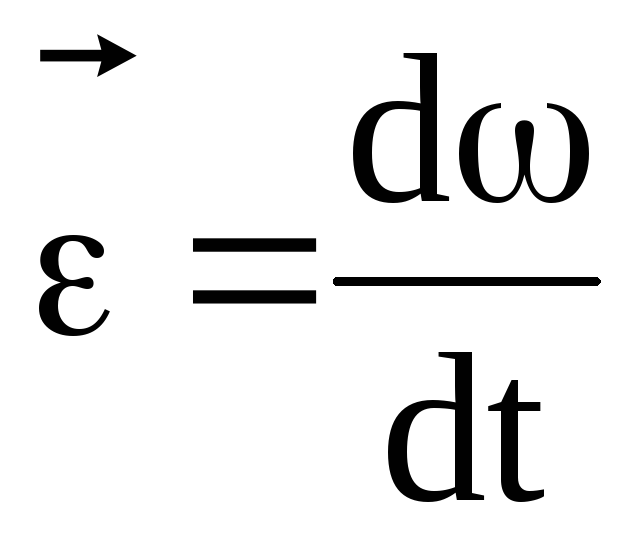 .
.
Вектор углового ускорения совпадает по направлению с вектором изменения угловой скорости. При ускоренном вращении векторы угловой скорости и углового ускорения направлены в одну сторону, при замедленном – в противоположные.
Угловые кинематические величины связаны с линейными следующими векторными произведениями:

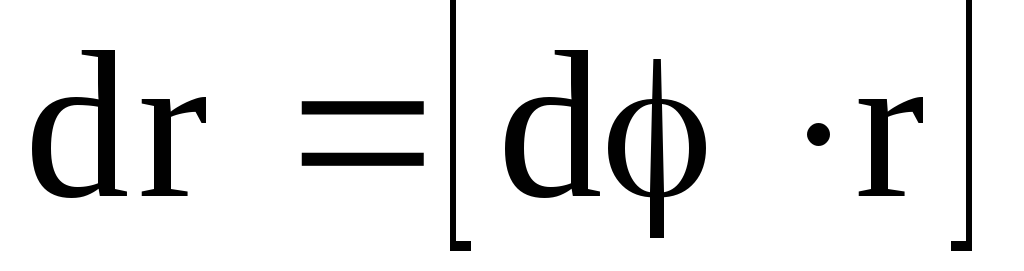 ,
, 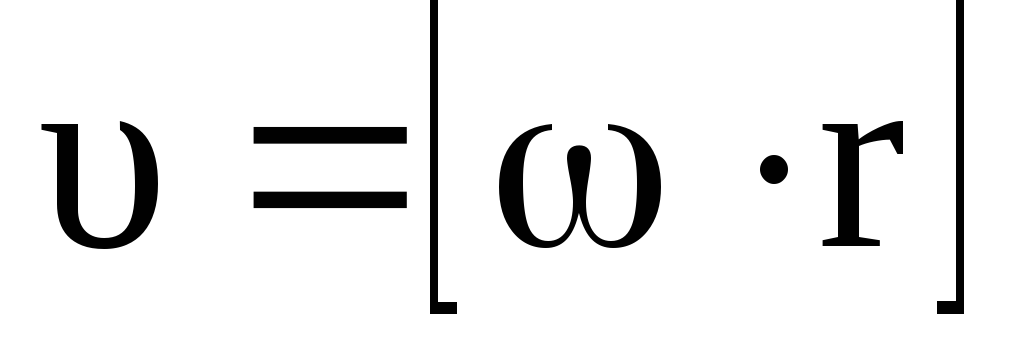 ,
,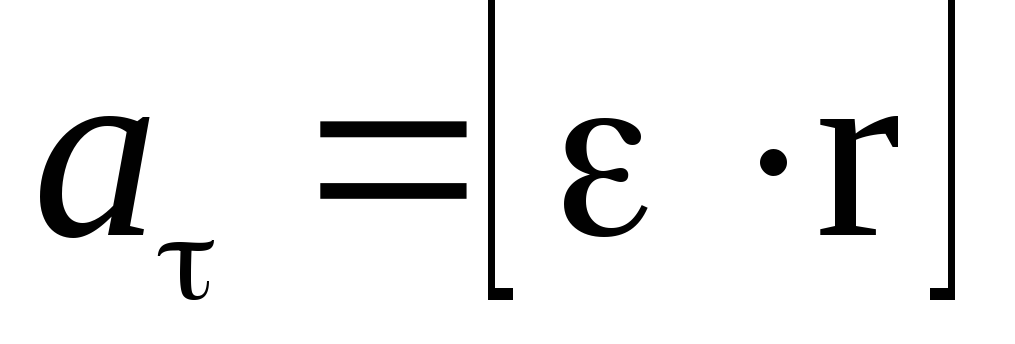 ,
,
где dr – элемент дуги окружности, описываемой точкой, r – радиус этой окружности, — линейная скорость точки, а — тангенциальное ускорение точки.
Векторы 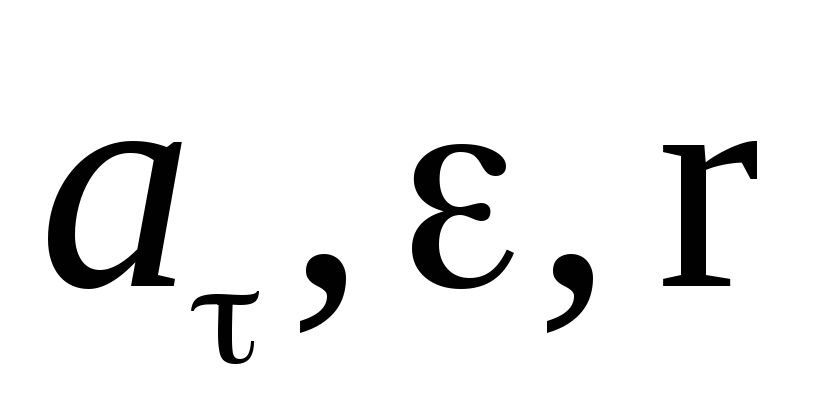 взаимно перпендикулярны. Угловое
ускорение по модулю может быть найдено,
если известно тангенциальное ускорение
какой-либо точки тела и ее расстояние
от оси вращения:
взаимно перпендикулярны. Угловое
ускорение по модулю может быть найдено,
если известно тангенциальное ускорение
какой-либо точки тела и ее расстояние
от оси вращения:
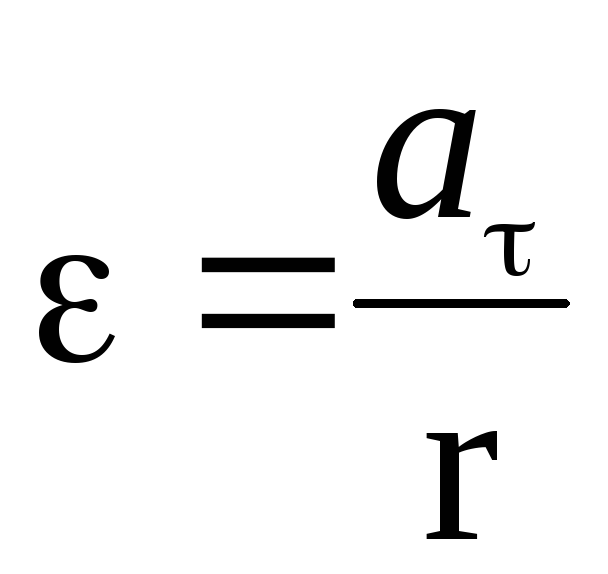 .
(1)
.
(1)
Если тело вращается вокруг неподвижной оси, то все кинематические и динамические векторные соотношения записываются в проекции на ось вращения, то есть в скалярном виде.
Причиной возникновения углового ускорения является воздействие на тело момента силы относительно оси вращения. Моментом силы называется физическая величина, равная векторному произведению радиусвектора на силу:
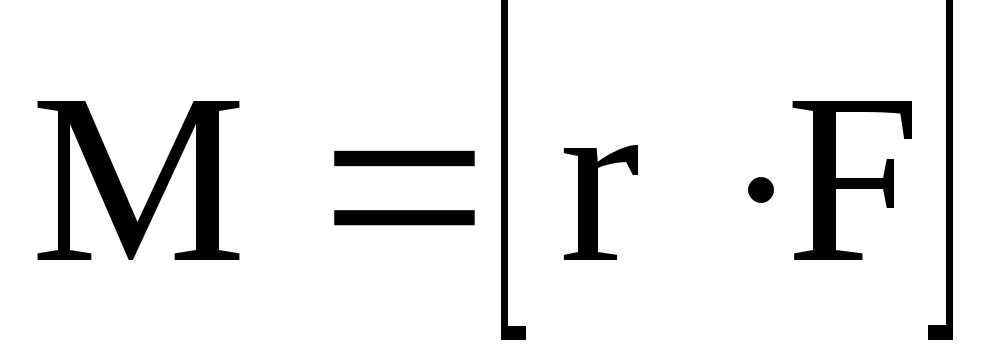 .
.
В скалярном виде момент силы относительно оси вращения равен произведению силы на плечо:
M = Fl, (2)
где l плечо кратчайшее расстояние от оси вращения до линии действия силы.
Основной закон динамики для вращающихся тел:угловое ускорение тела прямо пропорционально моменту силы, действующей на тело, и обратно пропорционально моменту инерции тела:
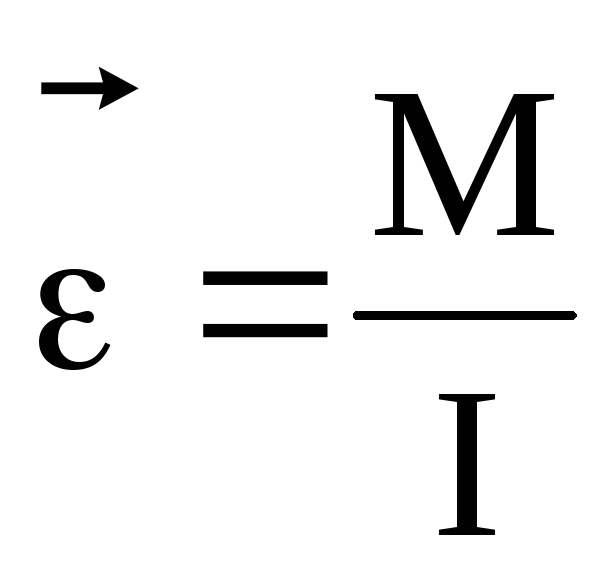 .
(3)
.
(3)
Момент инерции тела является мерой инертности вращающегося тела и зависит от массы тела и ее распределения относительно оси вращения:
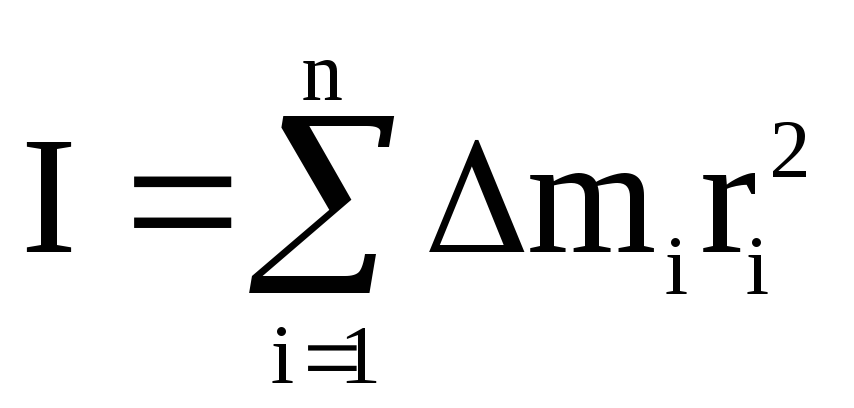 ,
(4)
,
(4)
где 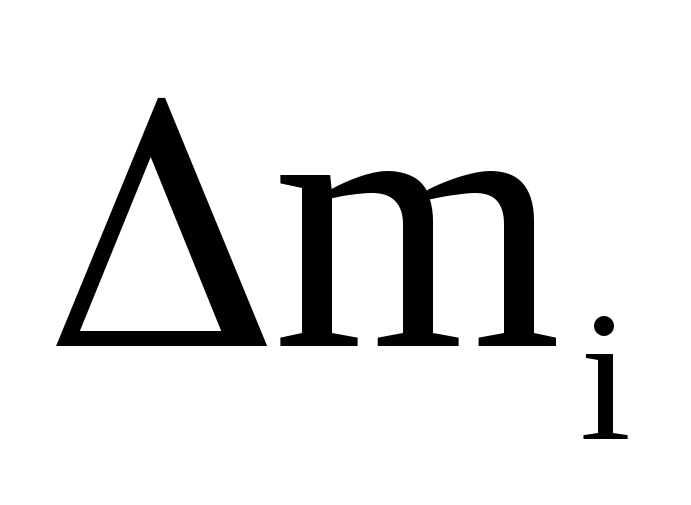 — масса небольшого элемента тела,
— масса небольшого элемента тела,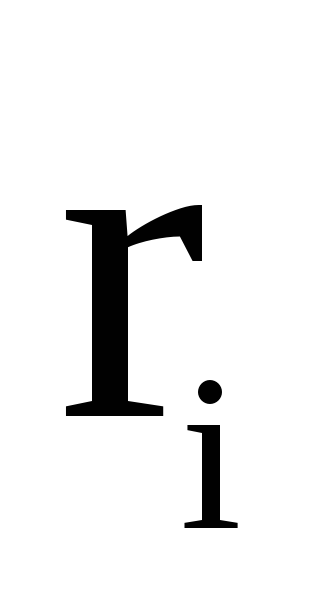 — расстояние от этого элемента до оси
вращения.
— расстояние от этого элемента до оси
вращения.
Момент инерции можно изменить, изменив массу тела или передвинув какие-либо части тела на другое расстояние от оси вращения.
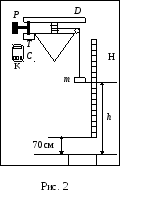
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для проверки зависимости углового ускорения от момента силы и момента инерции используется экспериментальная установка, в которой изучается вращение диска-платформы относительно вертикальной оси (рис.2). Момент инерции диска-платформы изменяется путем наложения на платформу дополнительных стальных дисков.
Установка собрана на вертикальном щите, укрепленном на стене. Кроме вращающегося тела на щите установлен электронный хронометр С, шкала высоты Н, кнопка пуска К и нижняя педаль П, являющаяся началом отсчета высоты.
Тело
приводится во вращение нитью, намотанной
на шкив радиуса r. К другому концу нити привязан груз массы 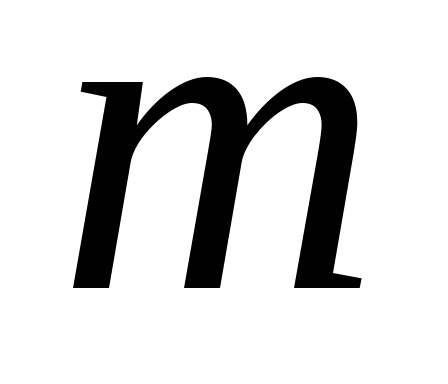 ,
к которому с помощью резьбы прикрепляются
дополнительные грузики. Диск снабжен
электромагнитным тормозом Т, включение
которого производится рукояткой Р.
,
к которому с помощью резьбы прикрепляются
дополнительные грузики. Диск снабжен
электромагнитным тормозом Т, включение
которого производится рукояткой Р.
| Опыт проводится в следующем порядке: Нить
наматывается на шкив виток к витку.
Груз m устанавливается на определенной
высоте h над нижней педалью П. Установка
фиксируется в этом положении
тормозом Т. Хронометр устанавливается
на нуль кнопкой сброса, расположенной
на его корпусе. Кнопкой пуска
выключается тормоз и одновременно с
этим включается хронометр. Платформа
ускоренно вращается, груз равноускоренно
опускается. Хронометр выключается
в тот момент, когда груз достигает
педали П. Ускорение груза, опускающегося
с высоты |
Тангенциальное
ускорение точек, расположенных на
поверхности шкива, равно ускорению
груза 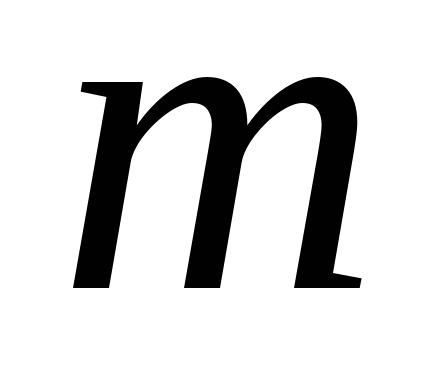 .
Поэтому, в соответствии с формулой (1),
угловое ускорение вращающегося тела
вычисляется по формуле:
.
Поэтому, в соответствии с формулой (1),
угловое ускорение вращающегося тела
вычисляется по формуле:
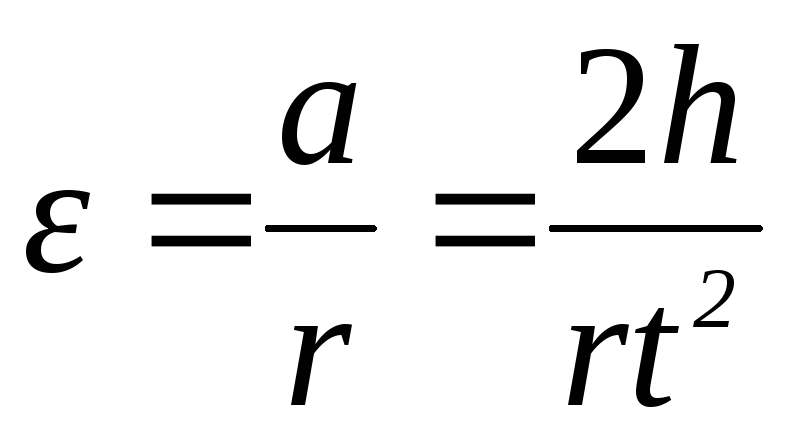 .(6)
.(6)
Угловое
ускорение вращающегося тела в данном
случае сообщается результирующим
действием момента силы натяжения нити 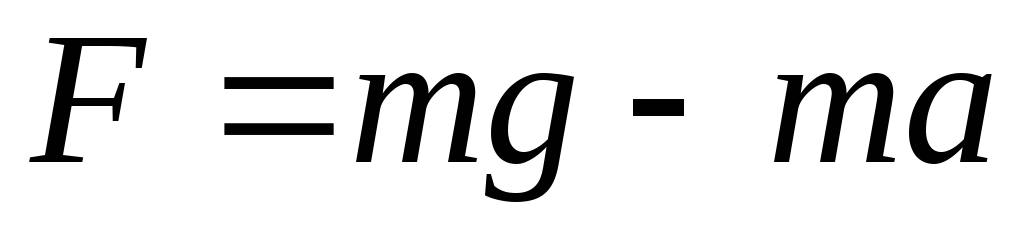 и момента сил трения в подшипниках Мтр:
и момента сил трения в подшипниках Мтр:
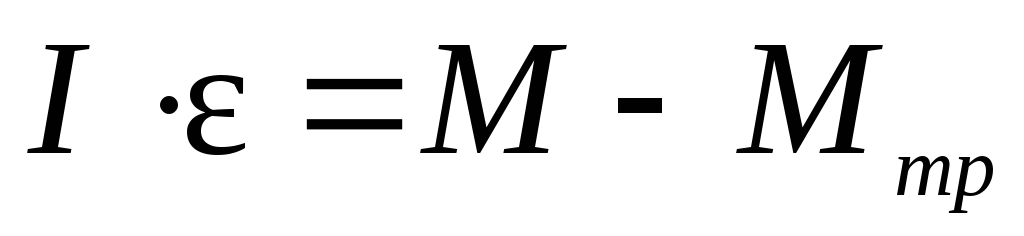 ,
,
где 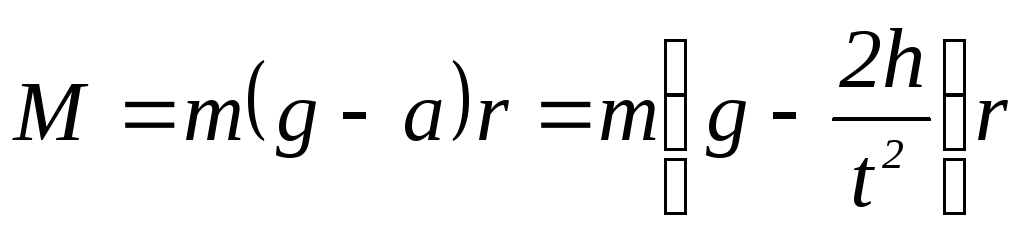 ,
(7)
,
(7)
т.к.
плечо силы натяжения равно радиусу
шкива 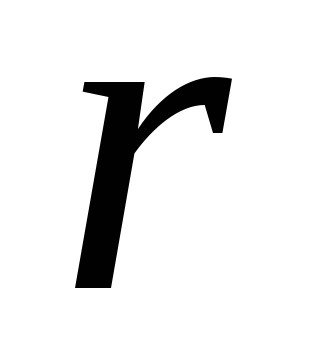 .
.
| П
В каждом случае вычисляется момент силы по формуле (7) и угловое ускорение по формуле (6). По результатам опытов строится график зависимости углового ускорения от вращающего момента М (рис. 3). Точка пересечения прямой (а) с осью моментов определяет значение момента сил трения в подшипниках установки. |
Зависимость углового ускорения от вращающего момента, которая должна получиться в отсутствии трения, выражается прямой (б) (рис.3). Параллельная экспериментальному графику (а) прямая (б) проходит через начало координат. Значение момента инерции установки вычисляется как котангенс угла наклона графика к оси моментов. Для этого на графике (б) выбирается какая-либо точка с координатами M1 и 1. Момент инерции вычисляется как отношение:
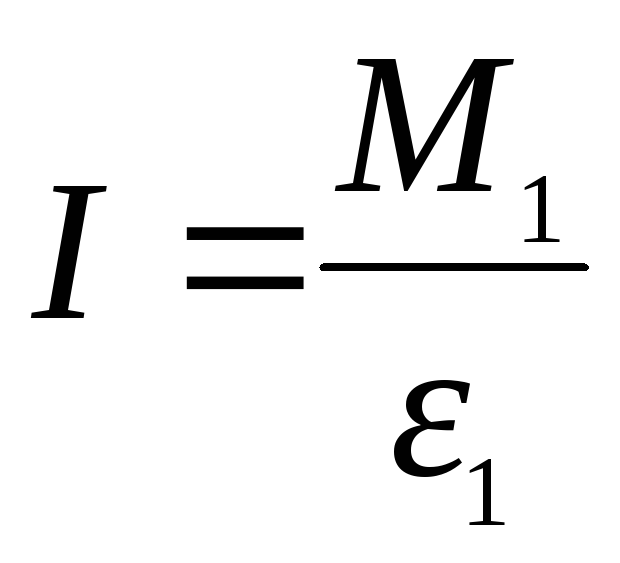 .
(8)
.
(8)
Для исследования зависимости углового ускорения от момента инерции проводятся несколько опытов при различных количествах дополнительных дисков.
момента инерции платформы с различным числом дополнительных дисков при постоянном вращающем моменте М.
ЗАДАНИЕ.
1. При постоянном значении момента силы и момента инерции несколько раз измерить время опускания груза m с одной и той же высоты. Результаты занести в таблицу 1. Оценить случайную погрешность в определении времени t.
2. Для ненагруженной платформы (без дополнительных дисков) измерить время опускания грузов различной массы с заданной преподавателем высоты h, вычислить угловое ускорение по формуле (6) и момент силы по формуле (7). Результаты измерений и вычислений занести в таблицу 2. Рассчитать по формуле (8) момент инерции ненагруженной платформы для каждого груза, найти среднее значение момента инерции и абсолютную погрешность измерений.
3. Построить график зависимости углового ускорения от момента силы М ( = f(M)) и определить момент инерции I1 ненагруженной платформы по отношению соответствующих катетов треугольника (см. рис.4 и формулу (8)).
4. Изменить момент инерции вращающейся платформы с помощью дополнительных дисков. Проделать такие же опыты и вычисления для двух новых значений момента инерции вращающейся части установки. Результаты измерений и вычислений занести в соответствующие таблицы 3 и 4. На графике = f(M) построить зависимости углового ускорения от момента силы М и определить моменты инерции I2 и I3 по формуле (8).
5. Построить график зависимости углового ускорения от момента инерции I (( = f(I) при произвольно выбранном постоянном значении момента силы М.
5. Оценить погрешность в определении величин I1, I2 и I3 .
Внимание! Во всех опытах нить на шкив наматывается в одном направлении.
Как определить момент сил трения?
Когда решают любые задачи по физике, в которых имеются движущиеся объекты, то всегда говорят о силах трения. Их либо учитывают, либо ими пренебрегают, но факт их присутствия ни у кого не вызывает сомнения. В данной статье рассмотрим, что такое момент сил трения, а также приведем проблемы, для устранения которых воспользуемся полученными знаниями.
Сила трения и ее природа
Каждый понимает, что если одно тело движется по поверхности другого совершенно любым способом (скользит, катится), то всегда существует некоторая сила, которая препятствует этому перемещению. Она называется динамической силой трения. Причина ее возникновения связана с тем фактом, что любые тела имеют микроскопические шероховатости на своих поверхностях. Когда соприкасаются два объекта, то их шероховатости начинают взаимодействовать друг с другом. Это взаимодействие носит как механический характер (пик попадает во впадину), так и происходит на уровне атомов (дипольные притяжения, ван-дер-ваальсовые и другие).
Когда соприкасаемые тела находятся в покое, то, чтобы привести их в движение относительно друг друга, необходимо приложить усилие, которое больше такового для поддержания скольжения этих тел друг по другу с постоянной скоростью. Поэтому помимо динамической также рассматривают статическую силу трения.
Свойства силы трения и формулы для ее вычисления
В школьном курсе физики говорится, что впервые законы трения изложил французский физик Гийом Амонтон в XVII веке. На самом деле это явление стал изучать еще в конце XV века Леонардо да Винчи, рассматривая движущийся предмет по гладкой поверхности.
Свойства трения могут быть кратко изложены следующим образом:
- сила трения всегда действует против направления перемещения тела;
- ее величина прямо пропорциональна реакции опоры;
- она не зависит от площади контакта;
- она не зависит от скорости перемещения (для небольших скоростей).
Эти особенности рассматриваемого явления позволяют ввести следующую математическую формулу для силы трения:
F = μ*N, где N — реакция опоры, μ — коэффициент пропорциональности.
Значение коэффициента μ зависит исключительно от свойств поверхностей, которые трутся друг о друга. Таблица значений для некоторых поверхностей приведена ниже.
Для трения покоя формула используется та же самая, что приведена выше, однако значения коэффициентов μ для тех же поверхностей будут совершенно иные (они больше по величине, чем для скольжения).
Особый случай представляет трение качения, когда одно тело катится (не скользит) по поверхности другого. Для силы в этом случае применяют формулу:
F = f*N/R.
Здесь R — радиус колеса, f- коэффициент качения, который согласно формуле имеет размерность длины, что его отличает от безразмерного μ.
Момент силы
Перед тем как отвечать на вопрос, как определить момент сил трения, необходимо рассмотреть само физическое понятие. Под моментом силы M понимают физическую величину, которая определяется как произведение плеча на значение силы F, приложенной к нему. Ниже приведен рисунок.
Здесь мы видим, что приложение F к плечу d, которое равно длине гаечного ключа, создает крутящий момент, приводящий к откручиванию зеленой гайки.
Таким образом, для момента силы справедлива формула:
M = d*F.
Заметим, что природа силы F не имеет никакого значения: она может быть электрической, гравитационной или вызванной трением. То есть определение момента силы трения будет тем же самым, что приведено в начале пункта, и записанная формула для M остается справедливой.
Когда появляется момент сил, вызванный трением?
Эта ситуация возникает, когда выполняются три главных условия:
- Во-первых, должна иметь место вращающаяся система вокруг некоторой оси. Например, это может быть колесо, движущееся по асфальту, или крутящаяся на оси горизонтально расположенная музыкальная пластинка патефона.
- Во-вторых, должно существовать трение между вращающейся системой и некоторой средой. В примерах выше: на колесо действует трение качения при его взаимодействии с поверхностью асфальта; если положить музыкальную пластинку на стол и раскрутить ее, то она будет испытывать трение скольжения о поверхность стола.
- В-третьих, возникающая сила трения должна действовать не на ось вращения, а на крутящиеся элементы системы. Если сила имеет центральный характер, то есть действует на ось, то плечо равно нулю, поэтому она не будет создавать момента.
Как найти момент силы трения?
Чтобы решить эту задачу, необходимо сначала определить, на какие вращающиеся элементы действует сила трения. Затем следует найти расстояние от этих элементов до оси вращения и определить, чему равна сила трения, действующая на каждый элемент. После этого необходимо выполнить умножение расстояний ri на соответствующие величины Fi и сложить полученные результаты. В итоге суммарный момент сил трения вращения вычисляется по формуле:
M = ∑nri*Fi.
Здесь n — количество сил трения, возникающих в системе вращения.
Любопытно отметить, что хотя M — это величина векторная, поэтому при сложении моментов в скалярной форме следует учитывать ее направление. Трение всегда действует против направления вращения, поэтому каждый момент Mi=ri*Fi будет иметь один и тот же знак.
Далее решим две задачи, где используем рассмотренные формулы.
Вращение диска болгарки
Известно, что когда диск болгарки радиусом 5 см режет металл, то он вращается с постоянной скоростью. Необходимо определить, какой момент сил создает электромотор прибора, если сила трения о металл диска равна 0,5 кН.
Поскольку диск вращается с постоянной скоростью, то сумма всех моментов сил, которые на него действуют, равна нулю. В данном случае мы имеем всего 2 момента: от электромотора и от силы трения. Поскольку они действуют в разных направлениях, то можно записать формулу:
M1 — M2 = 0 => M1 = M2.
Поскольку трение действует только в точке соприкосновения диска болгарки с металлом, то есть на расстоянии r от оси вращения, то ее момент силы равен:
M2 = r*F=5*10-2*500 = 25 Н*м.
Поскольку электромотор создает такой же по модулю момент, получаем ответ: 25 Н*м.
Качение деревянного диска
Имеется диск из дерева, его радиус r равен 0,5 метра. Этот диск начинают катить по деревянной поверхности. Необходимо рассчитать, какое расстояние способен он преодолеть, если начальная скорость вращения его ω составляла 5 рад/с.
Кинетическая энергия вращающегося тела равна:
E = I*ω2/2.
Здесь I — момент инерции. Сила трения качения будет приводить к замедлению движения диска. Работу, совершаемую ей, можно вычислить по следующей формуле:
A = M*θ.
Здесь θ — угол в радианах, на который сможет повернуться диск в процессе своего движения. Тело будет катиться до тех пор, пока вся его кинетическая энергия не расходуется на работу трения, то есть можно приравнять выписанные формулы:
I*ω2/2 = M*θ.
Момент инерции диска I равен m*r2/2. Чтобы вычислить момент M силы трения F, следует заметить, что она действует вдоль края диска в точке его соприкосновения с деревянной поверхностью, то есть M = r*F. В свою очередь F = f*mg/r (сила реакции опоры N равна весу диска mg). Подставляя все эти формулы в последнее равенство, получим:
m*r2*ω2/4 = r*f*mg/r*θ => θ=r2*ω2/(4*f*g).
Поскольку пройденное диском расстояние L связано с углом θ выражением L=r*θ, то получаем конечное равенство:
L=r3*ω2/(4*f*g).
Значение f можно посмотреть в таблице для коэффициентов трения качения. Для пары дерево-дерево он равен 1,5*10-3 м. Подставляем все величины, получаем:
L=0,53*52/(4*1,5*10-3*9,81) ≈ 53,1 м.
Для подтверждения правильности полученной конечной формулы можно проверить, что получаются единицы измерения длины.
Порядок выполнения работы
1. Передвигая грузы Свдоль стержней, добиться безразличного равнове-сия маятника.
2. Измерить диаметр шкива и рассчитать его радиус R.
3. Определить высоту падения грузов h.
4. Найти массу груза 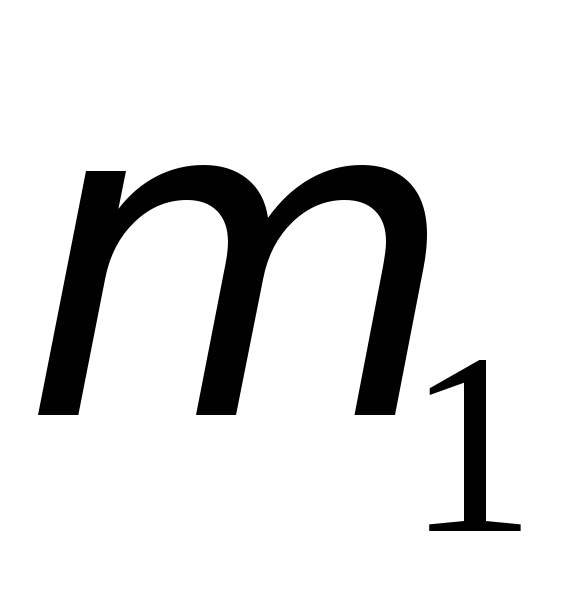 ,
уравновешивающего момент силы трения.
,
уравновешивающего момент силы трения.
5. Поместив на платформу груз массой m, определить время его падения не менее 3-х раз.
6. Указанное в п. 5 проделать тремя грузами (указанными преподавателем).
7. Данные измерений занести в таблицу
8. Предварительно убедившись, что  <<
<< ,
рассчитать для каждого из грузоввращающий момент по формуле (1.8).
,
рассчитать для каждого из грузоввращающий момент по формуле (1.8).
9. Рассчитать угловое ускорение маятника Обербека по формуле (1.9).
10. Убедиться в выполнении равенств (1.2).
11. Построить график зависимости углового
ускорения маятника  от вращающего момента
от вращающего момента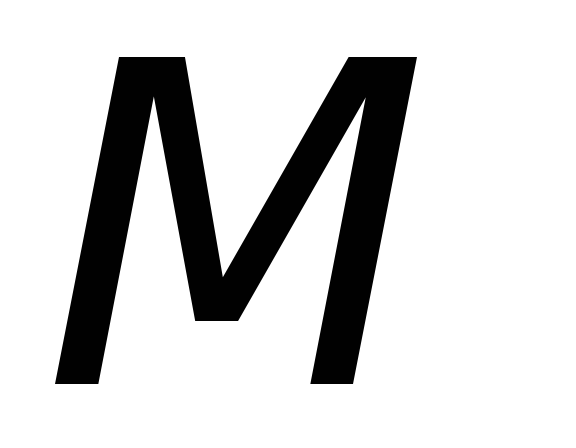 .
.
12. Определить момент инерции маятника с помощью графика и сравнить полученное значение со средним значением, рассчитанным по формуле (1.1).
13. По указанию преподавателя оценить
погрешности измерения величин  и
и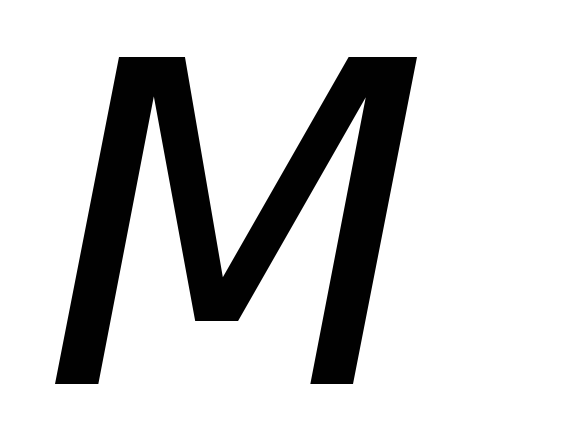 и показать их на графике.
и показать их на графике.
Контрольные вопросы
Дайте определение момента инерции тела. Поясните его физический смысл. В каких единицах измеряется момент инерции? Как можно изменить момент инерции маятника в данной работе?
Чему равен момент силы относительно неподвижной оси? Что он характеризует? В каких единицах измеряется?
Что называется плечом силы?
Что такое угловая скорость, угловое ускорение? Каков смысл этих величин? В каких единицах они измеряются?
Какие направления имеют в данной работе моменты сил трения и натяжения, угловая скорость, угловое ускорение?
Напишите основной закон динамики для поступательного и вращательного движений.
Выведите расчётные формулы для вращающего момента (1.7) и углового ускорения (1.8).
Литература
Савельев И. В. Курс физики. Т. 1. – М.: Наука, 1989. – С. 94–116.
Трофимова Т. И. Курс физики. – М.: Высш. шк., 2001. – С. 34–46.
Зисман Г. А., Тодес О. М. Курс обшей физики. Т. 1. – М.: Наука, 1972. – С. 59–70.
Работа 1.2
Определение момента инерции махового колеса
Цель работы: вычислить момент инерции махового колеса с помощью падающего груза.
Приборы и принадлежности: маховое колесо, набор грузов, масштабная линейка, штангенциркуль, секундомер.
Описание установки и метода измерений
Маховое колесо Ми шкив радиусаRнасажены на единую осьО(рис. 1.2). На
шкив навит шнурок, к которому прикреплён
груз массой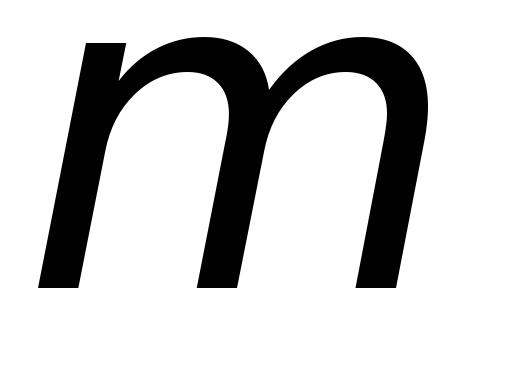 .
Грузу сообщают потенциальную энергию,
подняв его на высоту
.
Грузу сообщают потенциальную энергию,
подняв его на высоту 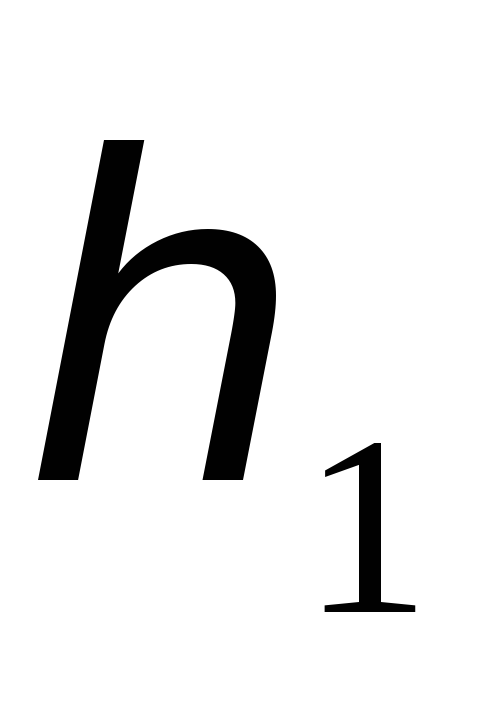 по отношению к некоторому уровню, высота
которого принята за ноль. При падении
груза его потенциальная энергия
по отношению к некоторому уровню, высота
которого принята за ноль. При падении
груза его потенциальная энергия  переходит в кинетическую энергию
поступательного движения груза
переходит в кинетическую энергию
поступательного движения груза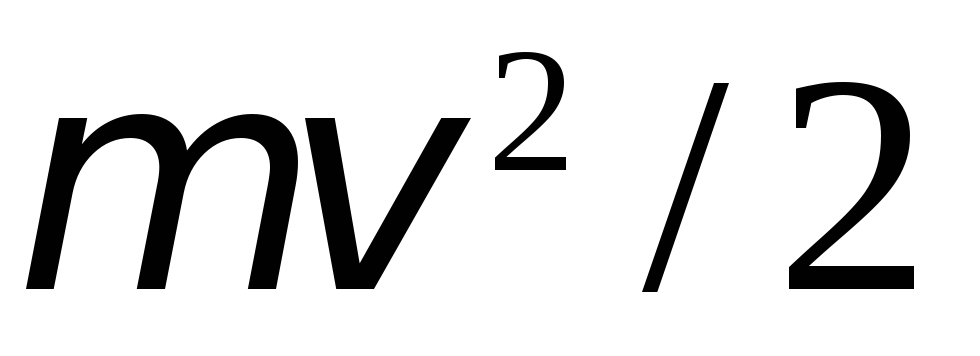 и кинетическую энергию вращательного
движения маховика
и кинетическую энергию вращательного
движения маховика 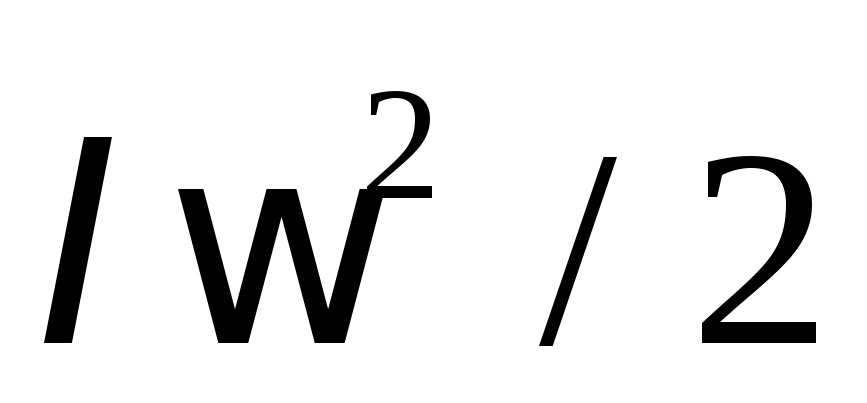 ,
а также расходуется на преодоление сил
трения в подшипнике. Таким образом,
закон сохранения механической энергии
для данной системы имеет вид
,
а также расходуется на преодоление сил
трения в подшипнике. Таким образом,
закон сохранения механической энергии
для данной системы имеет вид
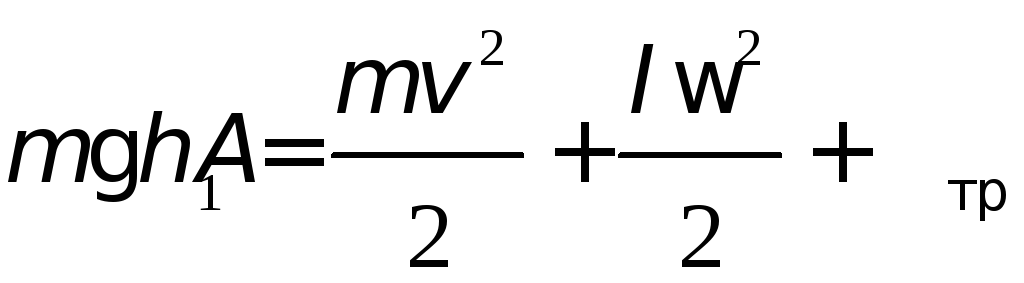 ,(2.1)
,(2.1)
где  – ускорение свободного падения,
– ускорение свободного падения,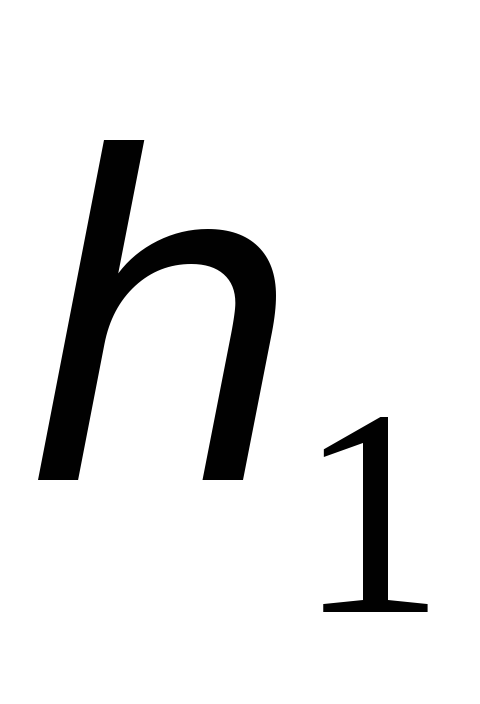 – высота, на которую поднят груз,
– высота, на которую поднят груз, – скорость груза в нижней точке падения,
– скорость груза в нижней точке падения, 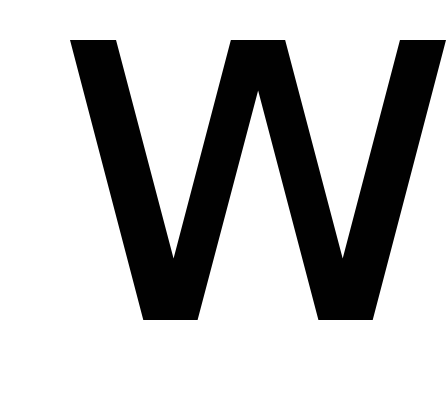 – угловая скорость маховика в тот же
момент времени,
– угловая скорость маховика в тот же
момент времени,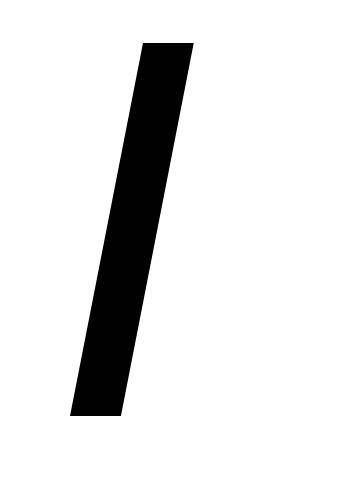 –
момент инерции махового колеса,
–
момент инерции махового колеса,  –
работа по преодолению сил трения в
подшипнике при движении груза вниз.
–
работа по преодолению сил трения в
подшипнике при движении груза вниз.
С помощью
уравнения (2.1) можно экспериментально
определить момент инерции махового
колеса, если известны остальные величины: 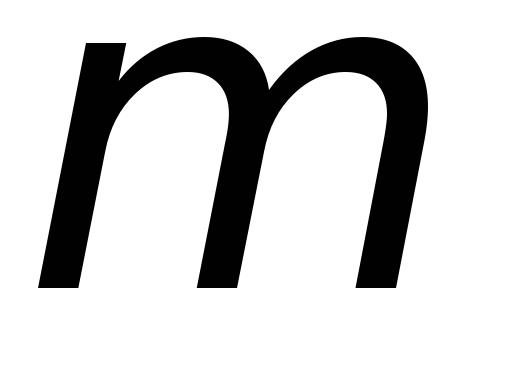 ,
, 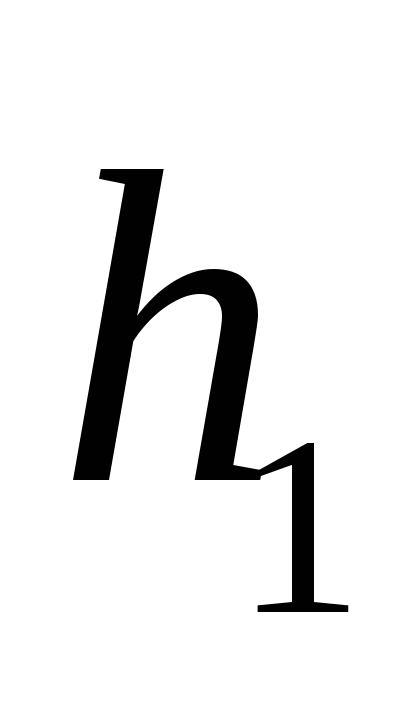 ,
, ,
,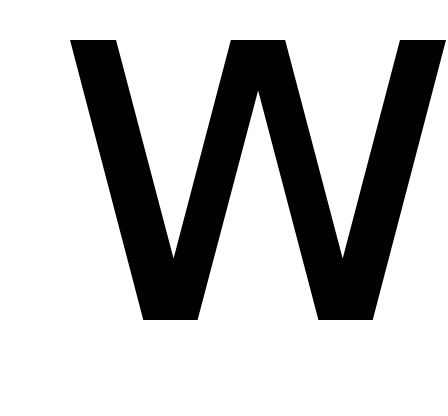 и
и .
.
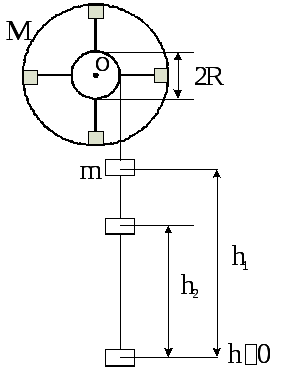
Рис. 2.1
Работа сил трения в подшипнике может быть найдена по формуле 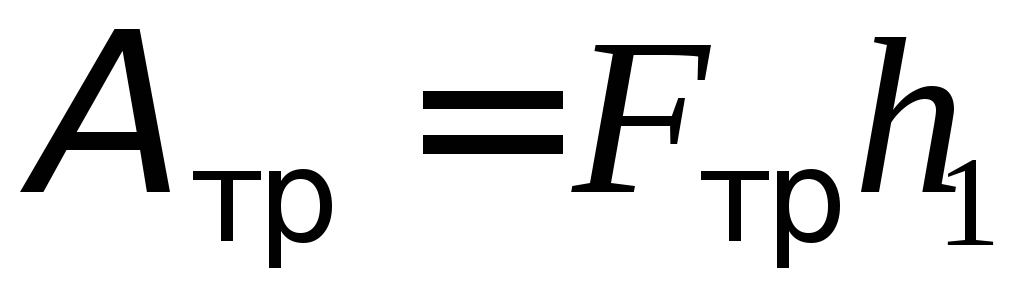 ,
(2.2)
,
(2.2)
где  – сила трения в подшипнике, которуюможно найти, исходя
из следующихсоображений.
Если колесо не остановить, то оно,
вращаясь по инерции, поднимет груз наменьшую высоту
– сила трения в подшипнике, которуюможно найти, исходя
из следующихсоображений.
Если колесо не остановить, то оно,
вращаясь по инерции, поднимет груз наменьшую высоту 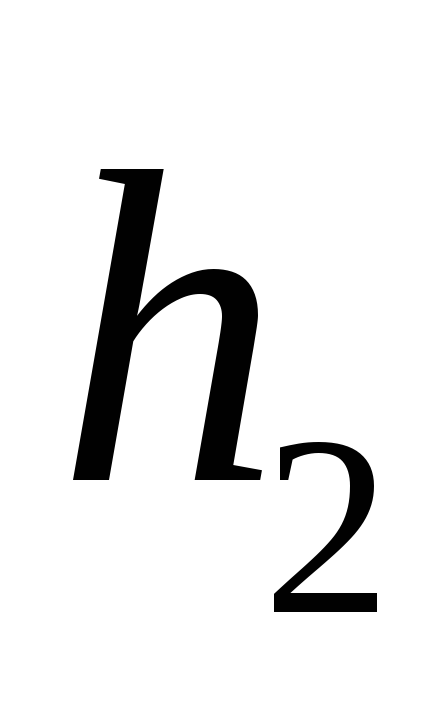 .
Работа силы трения навсем
пути
.
Работа силы трения навсем
пути 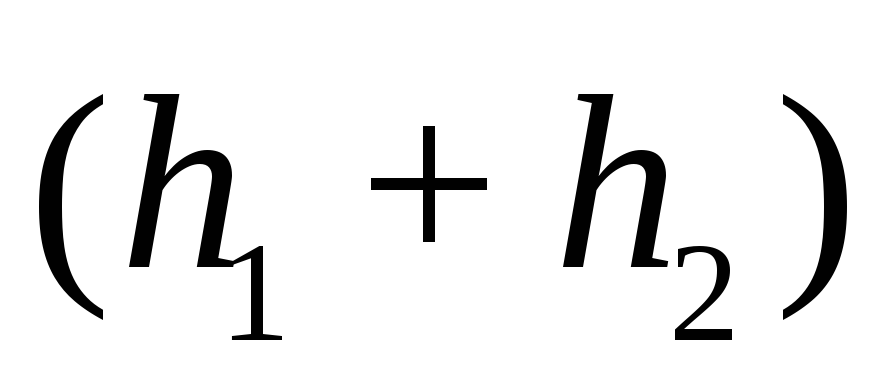 равна разности
потенциальных энергий груза в
конечном и начальном положениях, т. е.
равна разности
потенциальных энергий груза в
конечном и начальном положениях, т. е.
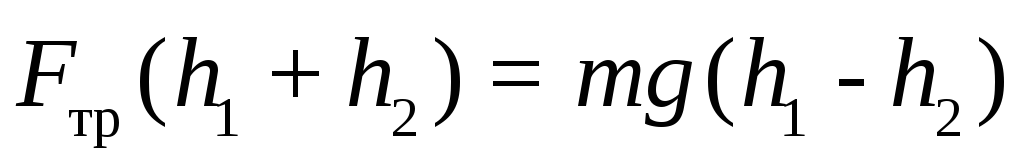 ,
,
откуда 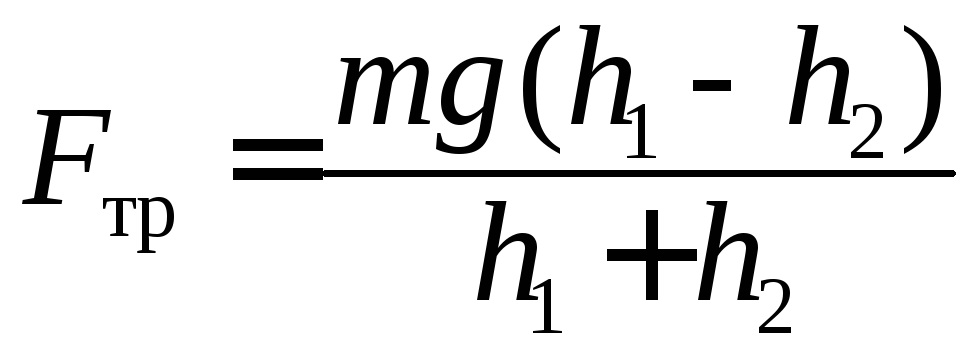 .
(2.3)
.
(2.3)
Подставив (2.3) в (2.2), получим формулу для расчета работы силы трения при движении груза вниз
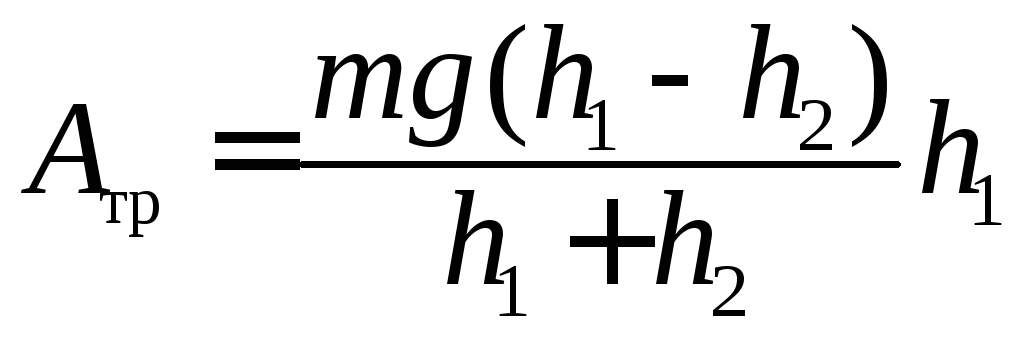 .
(2.4)
.
(2.4)
На груз действуют постоянные силы, поэтому его движение является равноускоренным и описывается уравнениями
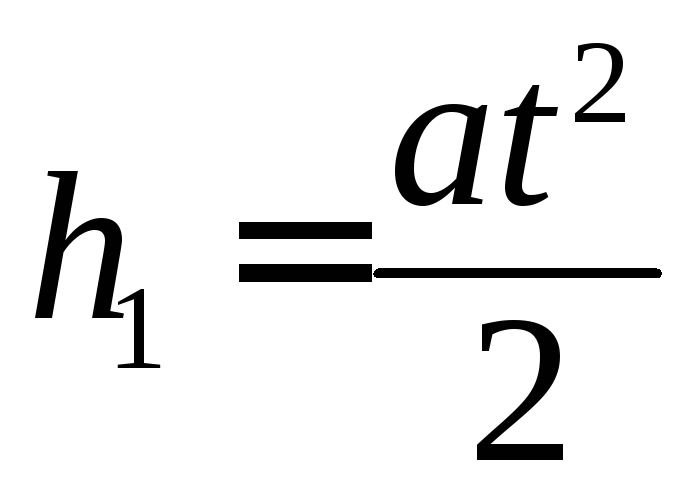 и
и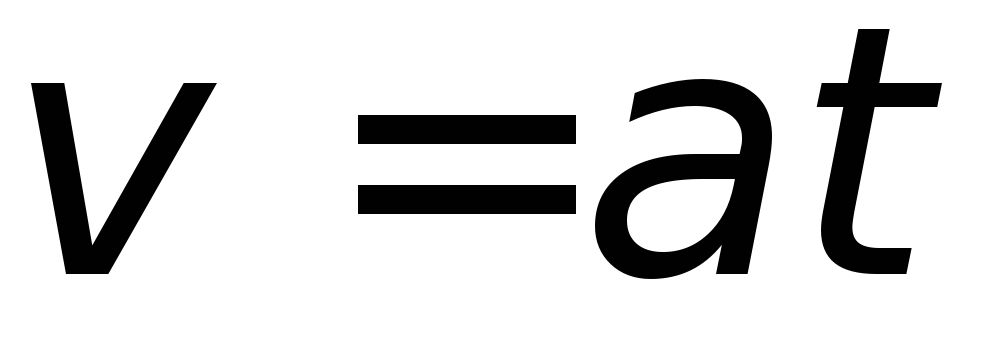 .
.
Исключив из этих уравнений ускорение, получим выражение для линейной скорости груза в нижней точке
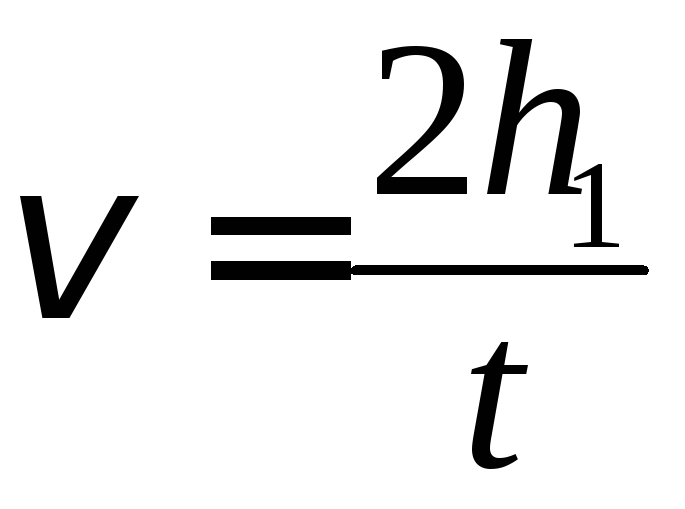 .
(2.5)
.
(2.5)
Нить, на которой
подвешен груз, практически нерастяжима,
следовательно,
линейная скорость точек обода шкива
равна скорости груза. И угловуюскорость махового колеса можно получить,
используя соотношение между линейной
и угловой скоростями (Т.5)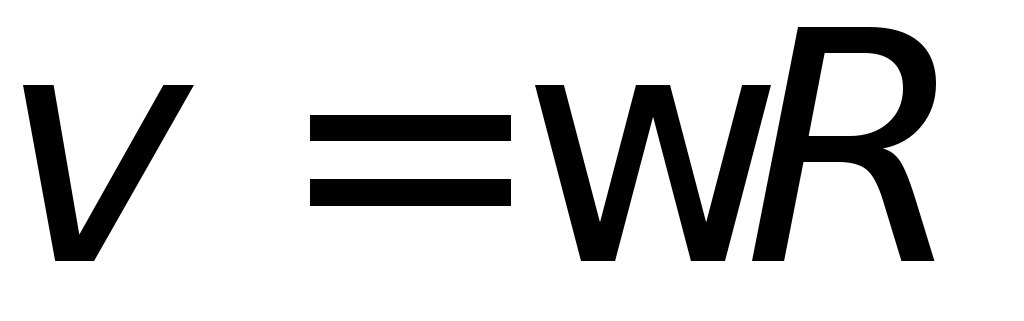 .
В момент, когда груз находится в нижней
точке траектории, угловая скорость
махового колеса равна
.
В момент, когда груз находится в нижней
точке траектории, угловая скорость
махового колеса равна
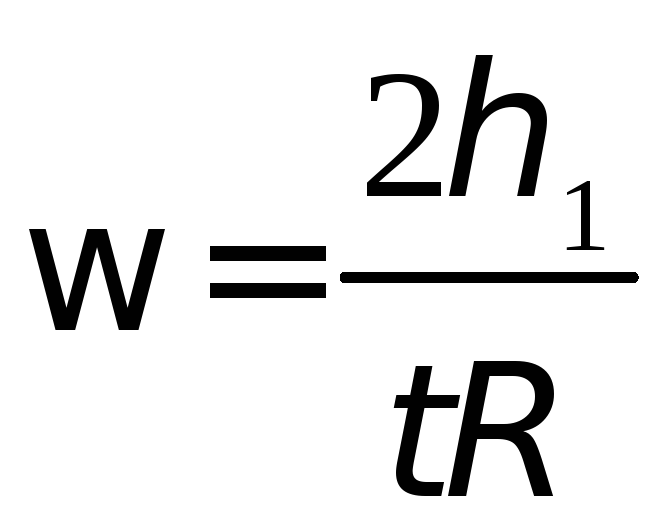 ,
(2.6)
,
(2.6)
где t – время падения груза с высоты h1.
Подставив выражение (2.4), а также выражения (2.5) и (2.6) в (2.1), получим формулу для вычисления момента инерции махового колеса в данной работе
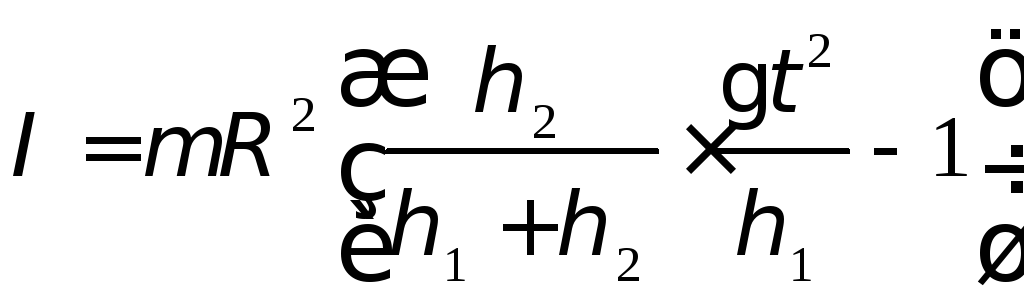 .
(2.7)
.
(2.7)
механика 7
ЛАБОРАТОРНАЯ РАБОТА № 7
МАЯТНИК ОБЕРБЕКА.
Принадлежности: лабораторная установка маятника Обербека, секундомер, грузы фиксированной массы, штан-
генциркуль.
Цель работы: изучение динамики вращательного движения, оцен ка влияния трения на точность результатов про ведённых измерений, проверка второго закона Ньютона для вращательного движения.
I. Теория маятника Обербека.
В работе изучается динамика вращательного движения. В частности, экспериментально проверяется уравнение моментов для вращения вокруг неподвижной оси
Je = Мвнеш (1)
где J — момент инерции тела; e — угловое ускорение;
Мвнеш — сумма проекций на ось вращения моментов внешних сил.
На рис.1. схематически показан прибор, с помощью которого удобно исследовать уравнение (1). Он называется маятником Обербе-
ка. Маятник состоит из четырёх стержней, укреплённых на втулке
под прямым углом друг к другу. Втулка и два шкива различных радиусов (r1 и r2) насажены на общую ось. Ось закреплена в подшипниках, так что вся система может свободно вращаться вокруг горизонтальной оси. Момент инерции прибора можно менять, передвигая закрепленные на стержнях цилиндрические грузы известной массы. Один конец нити прикреплён к шкиву, а ко второму концу, переброшенному через блок, подвешена платформа известной массы.
Если, намотав нить на шкив, приподнять платформу с грузом Р на высоту h, а затем отпустить, позволив ей свободно падать, то на маховик начнёт действовать вращающий момент М.
М = T*d / 2 (2)
Рис.1.
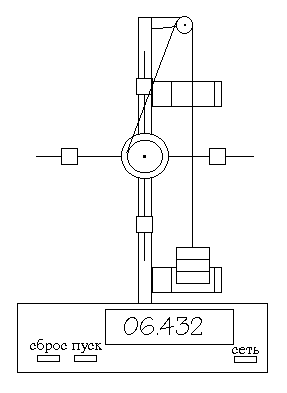
где d — диаметр шкива, Т — натяжение нити.
Под действием этого постоянного момента маховик начинает вращаться с угловым ускорением e. Очевидно, что вращение маховика и поступательное движение платформы с грузом происходит за счёт потен-
циальной энергии нагруженной платформы. Если не учитывать потерю
энергии вследствие трения в подшипниках осей маховика и блока, то
можно считать, что потенциальная энергия W полностью переходит в
кинетическую энергию поступательного движения платформы с грузом Wк‘
и кинетическую энергию вращения маховика Wк«. В момент, когда
платформа опустится с высотыh
Wn = Wк’ + Wк»
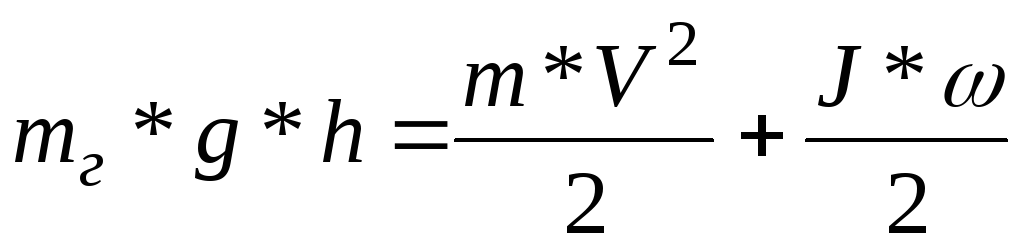 (3)
(3)
где J — момент инерции маховика,
mг — масса платформы с грузом,
g — ускорение свободного падения,
V — скорость поступательного движения платформы ( скорость на поверхности шкива).
w — угловая скорость вращения маховика (шкива).
Формулу (3) можно преобразовать, пользуясь связью между угловой и линейной скоростями:
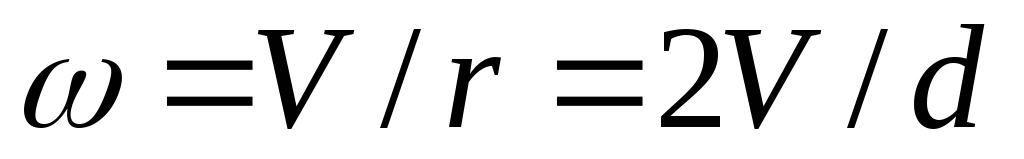 (4)
(4)
Подставляя (4) в (3), находим:
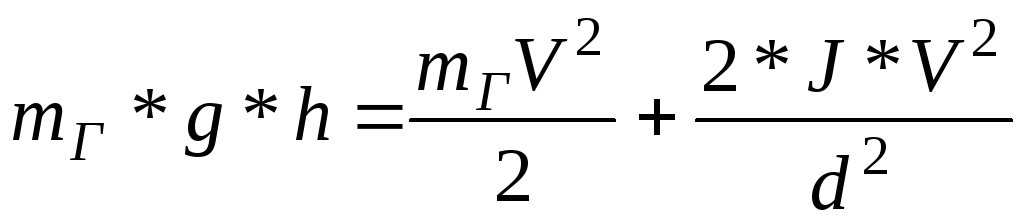 (5)
(5)
откуда
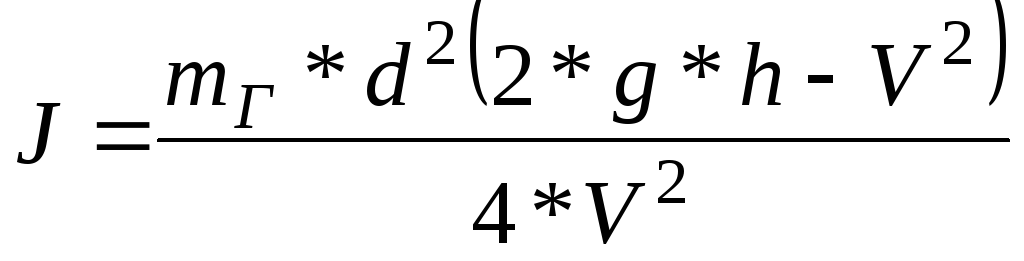 (6
(6
Движение платформы с грузом равноускоренное и, следовательно,
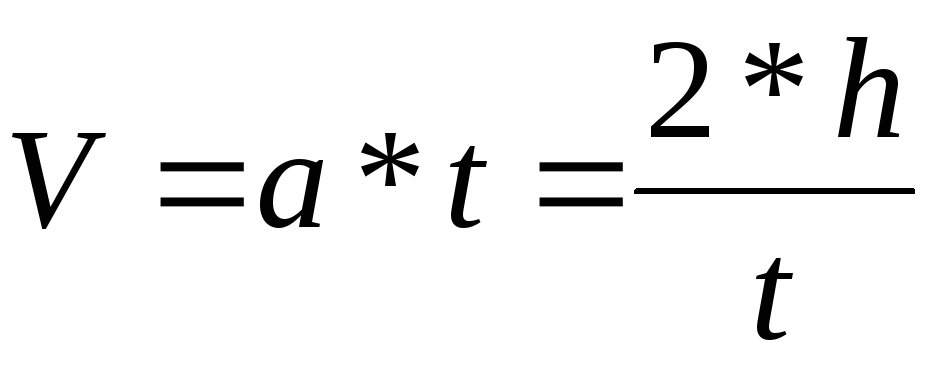
где а — ускорение платформы с грузом .
Подставив последнее выражение в формулу (6), получаем окончательную расчётную формулу для определения момента инерции маятника:
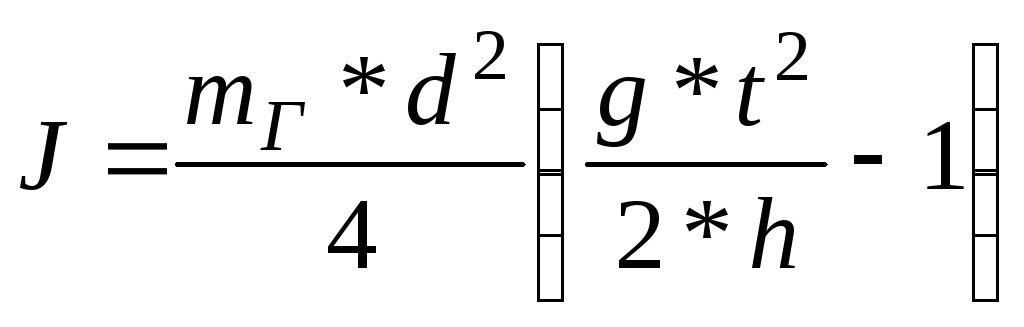 (7)
(7)
Чтобы вывести формулу для вычисления момента силы М, запишем второй закон Ньютона для груза Р (платформа с грузом):
mгa = Р — Т (8)
где m — масса платформы с грузом, a — её ускорение.
Из уравнений (2) и (8) получаем, что момент силы натяжения нити
М = Тr = mг(g — a)r. (9)
Ускорение a связано с угловым ускорением e соотношением
e = a/r (10)
Кроме того на маятник действует момент сил трения в оси Мтр. С учётом этого уравнения (1) имеет вид
mг(g — a)r — Mтр = Ja/r. (11)
Формула (11) дает связь между ускорением а, которое можно измерить опытным путем, и моментом инерции J. В уравнение (11)
входит ускорение a платформы. Это ускорение можно довольно просто
определить.
Действительно, измеряя время t, в течении которого платформа с грузом опускается на расстояние h, можно найти ускорение a:
a = 2h/t2 (12)
Тогда
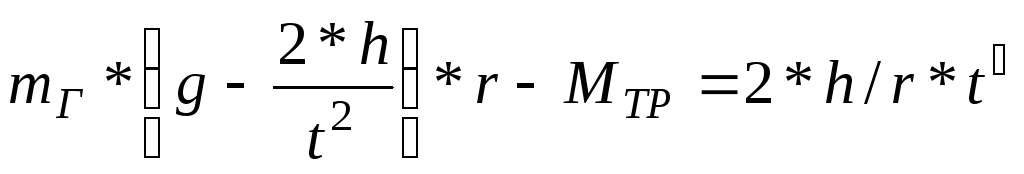 (13)
(13)
В формулу (13) входит неизвестная величина — момент силы трения Мтр. Хотя, интуитивно понятно, что момент силы трения мал,
тем не менее он не настолько мал, чтобы им в формуле (9) можно
было пренебречь. Если положить Мтр = 0, то можно убедиться, что
результаты опыта будут отличаться от зависимости (9). Можно по
порядку величины экспериментально определить Мтр и это нужно, конечно, сделать в начале работы. Для этого, с помощью нескольких грузов увеличивая силы натяжения Т нити, найдите минимальное значение mог, при которой маятник начнёт вращаться. Дальнейшие измерения нужно проводить с грузами массой mг > 10mог. На первый взгляд относительную роль момента силы трения можно уменьшить, если взять грузы массой mг >> mог, допустим, груз m = 102mог. Однако это не так по двум причинам. Первая — увеличение массы груза приводит к увеличению силы давления N на ось, а значит и к росту момента силы трения
Мтр = f*N*r,
где f — коэффициент трения,
r — плечо силы трения.
Вторая причина состоит в том,что увеличение m уменьшает время падения t, а значит, ухудшает точность измерения ускорения a.
По найденным значениям моментов инерции J1 и J2 и моментов сил М1 и М2 можно, исходя из основного уравнения вращательного движения , найти соответствующее значение угловых ускорений e1 и e2.
С другой стороны угловые ускорения e1 и e2 можно найти и
другим путём, исходя из чисто кинематических соображений, а именно, из (10) и (12)
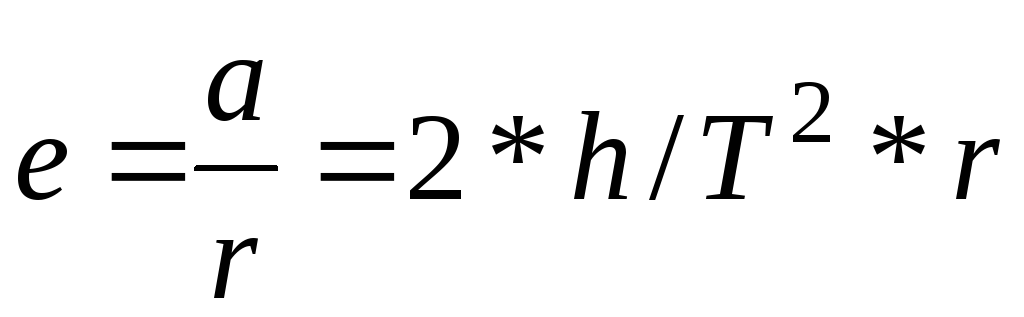 (14)
(14)
Найденные опытным путём значения моментов инерции маховика можно сравнивать с их значениями, вычисленные по общеизвестным
формулам.
Момент инерции маховика равен сумме моментов составных частей — крестовины, состоящей из четырех стержней, и насаженных на неё четырёх цилиндров:
J = Jкрест + 4Jцил = 4Jcт + 4Jцил
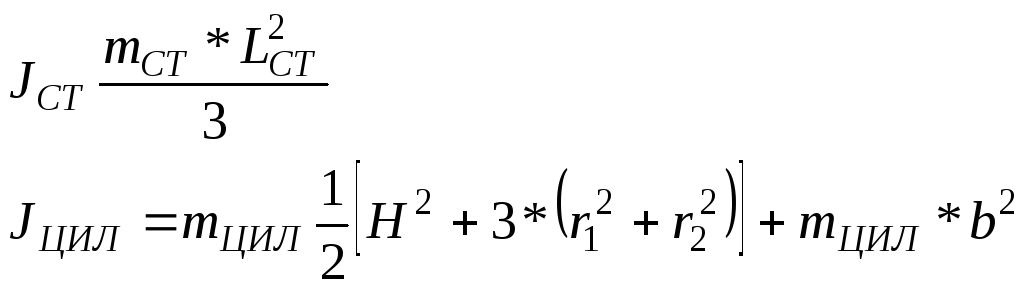
где: b — расстояние от риски, нанесённой на стержне крестовины до
оси вращения,
Н— высота цилиндра,
r1— внешний радиус цилиндра,
r2— внутренний радиус цилиндра .
Поскольку вывод формулы (7) производился в предположении что потеря энергии на преодоление сил трения пренебрежимо мала, зна-
чение моментов инерции, найденных на опыте, несколько превышает
расчётные, Jэксп > Jрасч.
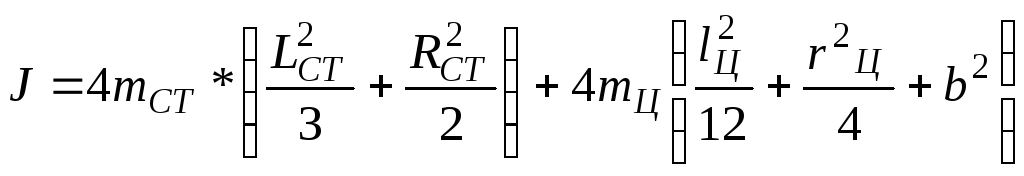 (15)
(15)
где
b — расстояние от оси вращения до грузов на крестовине;
mц — масса одного груза на крестовине;
Lст — длина стержня крестовины;
Rст — радиус стержня;
mст — масса стержня без груза;
rц — радиус цилиндрического груза на крестовине;
lц — образующая цилиндрического груза;
d — диаметр втулки;
II. Порядок измерений.
— с помощью регулируемых ножек основания привести колонну прибора к вертикальному положению. Проверить, не толкают ли грузы в корпус верхнего и нижнего фотоэлектрических датчиков;
— сдвинуть подвижный кронштейн на выбранную высоту, и так установить, чтобы грузы падая проходили через середину рабочего окна фотоэлектрических датчиков;
— соединить фотоэлектрические датчики 1 и 2 соответственно с гнездами 1 и 2 миллисекундомера;
— произвести заземление прибора;
— включить сетевой шнур измерителя в сеть питания;
— нажать клавишу (СЕТЬ), проверяя, показывают ли все индикаторы обоих фотоэлектрических датчиков;
— переместить грузы в верхнее положение и проверить, находится ли схема в состоянии покоя;
— нажать клавишу (ПУСК) и проверить, произошло ли движение схемы, миллисекундомер измерил время прохождения мути торможения
схемы;
— нажать клавишу (СБРОС) и проверить, произошло ли обнуление показаний измерителя и освобождение блокировки электромагнитом;
— перенести грузы в верхнее положение, отжать клавишу (ПУСК) и проверить, произошла ли повторная блокировка схемы.
III. Измерение.
Представляет интерес экспериментально исследовать две зависимости.
Первая — зависимость углового ускорения e от момента внешней силы Мвнеш = mgr при условии, что момент инерции J остаётся постоянным.
Если на оси ординат откладывать угловое ускорение e, а на
оси абсцисс — m *g*r, то, согласно (10), экспериментальные точки
должны ложиться на прямую. Из (11) видно, что наклон этой прямой
равен 1/J, а точка пересечения с осью абсцисс даёт Мтр.
Если экспериментальные данные подтверждают линейную зависимость e от mgr, то, можно приступить к изучению второй зависимости — зависимости момента инерции J от расстояния R грузов mц до оси вращения маятника (рис.18).
Согласно теореме Гюйгенса-Штейнера
J(R) = J0 + 4mцR2
Выясним, как проверить эту зависимость экспериментально. Для этого преобразуем соотношение (11), пренебрегая в нём малой величиной (моментом силы трения Мтр) по сравнению с моментом m*g*r. Из (10) и (11) имеем
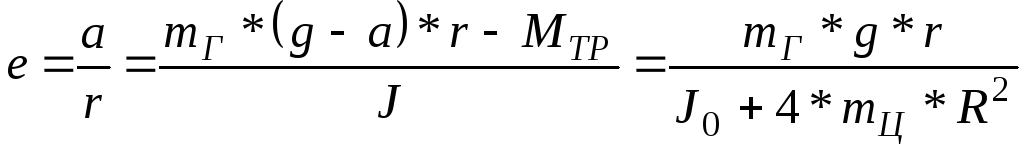 (16)
(16)
Следовательно
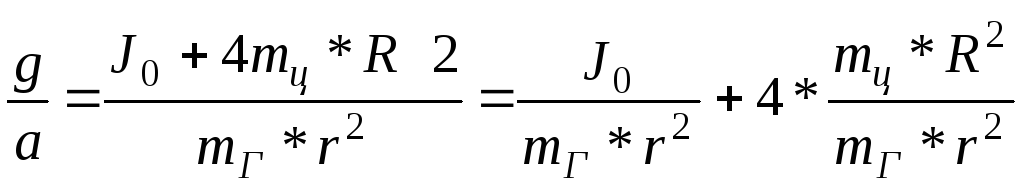 (17)
(17)
Из (17) понятно, как экспериментально проверить зависимость (17): нужно, выбрав постоянную массу mг груза, измерять ускорение a при различных положениях R грузов mц на спицах. Результаты измерений удобно изобразить в виде точек на координатной плоскости
XOY, где х = (R/r)2, y = g/a.
Если экспериментальные точки в пределах точности измерений ложатся на прямую, то это подтверждает зависимость (17), а зна-
чит и формулу
J(R) = J0 + 4mц*R2
Отметим, что при выводе формулы (17) мы пренебрегли моментом сил трения, т.е. считали, что Мтр << mgr. Значение Мтр получено из графика зависимости e от (mgr) при R = const. Это и позволяет выбрать массу перегрузка так, что неравенство mgr >> Мтр заведомо выполняется.
Роль момента сил трения можно оценить и иначе. Для этого заметим, что если маятник в начальный момент вращается с угловой скоростью wo, то к моменту остановки он повернётся на угол f, определяемый из соотношения
J*wo2/2 = Aтр= Mтр*f (18)
где Jwo2/2 — начальная кинетическая энергия вращающегося маятника, Атр — работа сил трения. В (18) предполагается, что момент сил трения является постоянной величиной и связан с угловым ускорением соотношением
J*eo = Мтр (19)
где eo — ускорение, определяемое только моментом сил трения.
Из (18) и (19) находим
wo2 = 2eo*f (20)
Пусть n — полное число оборотов, которое делает маятник до остановки, а To — период вращения маятника в начале движения. Тогда f = 2pn, wo = 2p/To и из (20) получаем
eo = p/(n*To2) (21)
Отсюда ясно, как на опыте определить eo: нужно измерить вре-
мя To, за которое совершается первый оборот, и полное число n
оборотов маятника до остановки. Во всех дальнейших измерениях
нужно следить, чтобы выполнялось неравенство eo << e.
IV. Задание.
1. Устанавливаем два груза на одинаковом расстоянии R1, на двух взаимно перпендикулярых спицах. Одну из спиц приводим в горизонтальное положение и, перемещая груз на противоположной спице, добиваемся равновесия, не меняя расстояния R1. Поворачиваем крестовину на 90o и добиваемся равновесия на других спицах. Убеждаемся, что крестовина уравновешена в любом положении грузов (поворачивая крестовину).
Полезно несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. Подумайте, как на основа-
нии этих опытов определить, хорошо ли сбалансирован маятник.
2. Определите приближённо минимальную массу mо, при которой маятник начинает вращаться, и оцените момент сил трения из соотношения
Мтр*Ё~ mo g*r,
где r — радиус шкива, на котором подвешен груз mo.
3. Оцените ускорение eo, возникающее под действием момента сил трения. Для этого приведите маятник во вращение, измерьте время To, за которое он совершает первый оборот, и полное число оборотов n маятника до полной остановки. Затем по формуле (21)
вычислите eo. Измерения повторите три раза и сравните соответс-
твующие им значения eoi.
4. Определите экспериментально зависимость углового ускорения e маятника от момента приложенной силы m*g*r. В этой серии измерений момент инерции маятника должен оставаться постоянным: J = const.
Для определении зависимости e = e*(m*g*r) измерьте время t, за которое груз m опускается на расстояние h. Измерение времени t
для каждого груза при постоянном значении h повторите три раза.
Затем найдите среднее значение времени падения груза по формуле
tср = 1/3 (t1 + t2 + t3)
и определите среднее ускорение груза их соотношения (12):
аср = 2h/tср2
Эти измерения и вычисления повторите для пяти значений массы m груза,причём для всех mг должно выполняться неравенство mг >>mo, где mo — масса перегрузка, страгивающего маятник (п.2). Результаты измерений запишите в табл.1.
Таблица 1.
t1 | t2 | t3 | tср | ∆t | mr | aср | ∆e | eср | mг*g*r |
h = , ∆h = , r = , R =
Полученные экспериментально точки отложите в координат ной плоскости x = mgr, y = e и по ним постройте график зависимости (рис. 2,а).
5. Проверьте экспериментально зависимость (17). Для этого, взяв постоянную массу груза mг >> mo, определите ускорение a груза m при пяти различных положениях R на спицах грузов mц.
В каждом положении R измерения времени падения t груза m с
высоты h повторите три раза.
Результаты измерений занесите в табл.2.
Полученные экспериментальные точки нанесите с учётом погрешностей в координатной плоскости x = (R/r)2, y = g/a и постройте график зависимости y = y(x) (рис.2,б).
Таблица 2.
R | (R/r)² | t1 | t2 | t3 | tср | ∆t | a | g/a |
r = , mг = , h = , ∆h =
V. Определение погрешности измерения момента инерции.
Относительная погрешность измерения момента инерции определяется по формуле:
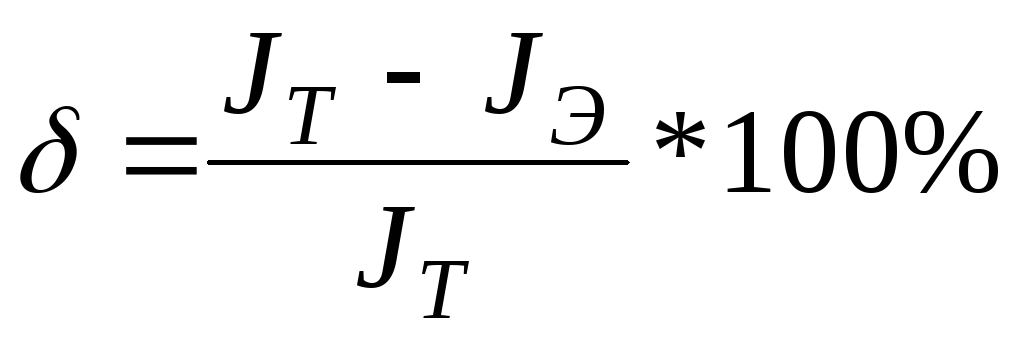
где Jт — теоретический момент инерции, определяемый по формуле
(15).
Jэ — экспериментальный момент инерции, определяемый по формуле (7).
VI. Точность измерений.
погрешность определения длины пути прохождения груза +1 мм
рабочая погрешность измерения времени не более 0,02 %
рабочая погрешность определения момента инерции не более 8 %
VII. Контрольные вопросы.
1. Что называется моментом сил? Какова размерность единицы его измерения в системе СИ?
2. Что называется моментом инерции тела относительно оси вращения?
3. Запишите основной закон вращательного движения.
4. Как определить момент силы, приводящей во вращение маятник Обербека?
5. Почему стремятся уменьшать момент сил трения? Казалось бы, даже большую величину Мтр можно легко учесть с помощью урав-
нения (11).
6. Какую из величин в данном эксперименте следует измерять с наибольшей точностью?
7. Сформулируйте и докажите теорему Гюйгенса-Штейнера.


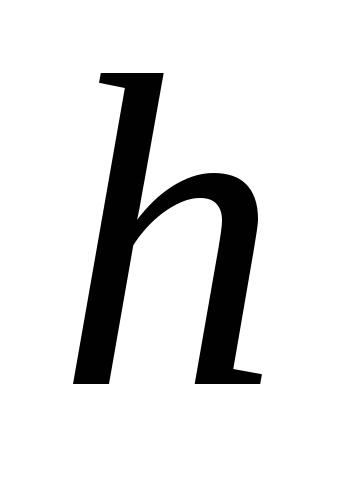 в течение времениt,
находится по формуле:
в течение времениt,
находится по формуле: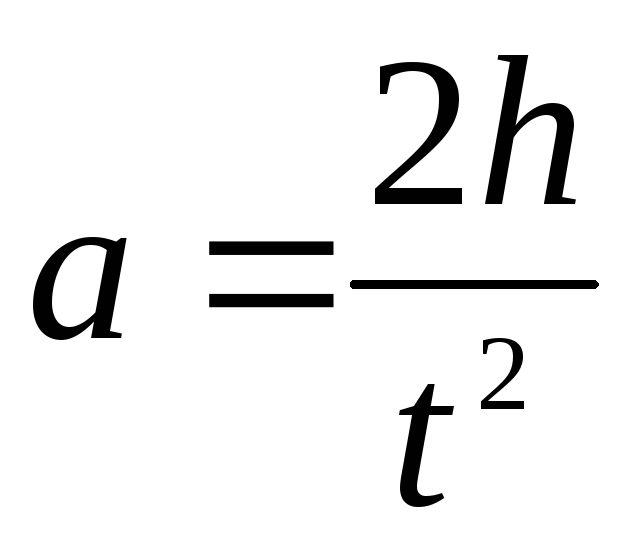 .(5)
.(5)
