Модуль силы Ампера – единица измерения, формула и определение кратко (11 класс)

4.6

Средняя оценка: 4.6

Всего получено оценок: 90.

Обновлено 15 Января, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 90.

Обновлено 15 Января, 2021

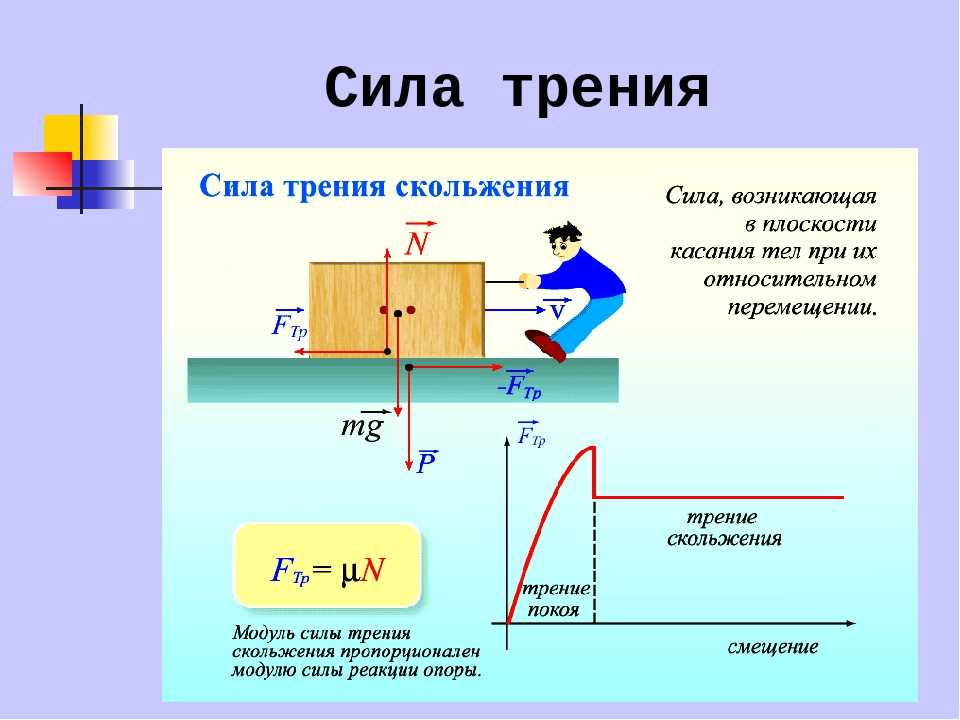
Из курса физики за 11 класс известно, что на проводник с током, находящийся в магнитном поле, действует сила, которая называется силой Ампера. Рассмотрим, от чего зависит эта сила, приведем ее формулу.

Сила Ампера

Как показывает опыт, магнитное поле не действует на покоящиеся электрические заряды. Однако, если заряд движется, то со стороны магнитного поля на него начинает действовать сила Лоренца, направленная перпендикулярно плоскости, которая образованна векторами скорости заряда и магнитной индукции. Электрический ток — это движение заряженных частиц. Для тока единицей измерения в физике принят ампер. Если проводник с током находится в магнитном поле, то на носители заряда действуют силы Лоренца, которые сливаются в общую силу, действующую на весь проводник в целом.

Такая сила называется силой Ампера. От чего она зависит?

Рис. 1. Действие магнитного поля на проводник с током.

Очевидно, что, во-первых, раз сила Ампера порождается магнитным полем, то она должна быть пропорциональна величине магнитной индукции.

Во-вторых, поскольку магнитное поле действует на заряды, то сила Ампера должна быть пропорциональна величине заряда, движущегося в проводнике.

В-третьих, поскольку магнитное поле действует на движущийся заряд, то сила Ампера должна зависеть от скорости движения заряда.

Две последних величины — заряд и скорость его движения — хорошо характеризует такая величина, как сила тока. Напомним, сила тока — это отношение заряда, проходящего по проводнику, ко времени прохождения.

Наконец, количество носителей заряда в проводнике зависит от длины проводника.

Таким образом, сила Ампера должна быть пропорциональна величине магнитной индукции, силе тока в проводнике и длине проводника.

Направление силы Ампера

У силы Ампера есть одна важная особенность. Ее направление зависит от ориентации проводника. Она направлена перпендикулярно плоскости, образованной векторами тока и магнитной индукции. Если магнитная индукция и ток направлены по одной прямой, то сила Ампера равна нулю. Максимальной сила Ампера будет в том случае, если магнитная индукция перпендикулярна направлению движения тока.

Для определения направление силы Ампера пользуются правилом левой руки:

Рис. 2. Правило левой руки для силы Ампера.

Следовательно, в формуле модуля силы Ампера должен быть еще один член — угол между направлениями магнитной индукции и тока.

Формула силы Ампера

С учетом всего перечисленного можно получить формулу силы Ампера, которую еще называют законом Ампера:

$$F= I |\overrightarrow B| Δl sin \alpha$$

Модуль силы Ампера равен произведению силы тока в проводнике, вектора магнитной индукции, длины проводника и синуса угла между направлениями векторов магнитной индукции и тока.

Рис. 3. Закон Ампера.

Что мы узнали?

Модуль силы Ампера пропорционален силе тока в проводнике, длине проводника, величине магнитной индукции и синусу угла между векторами магнитной индукции и тока.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Элиза Кубанычбекова

  5/5

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 90.

---

А какая ваша оценка?

Модуль силы тяготения

(12.2)

Закон тяготения в указанной форме (равенство 12.1) справедлив также для случаев:

а) тел со сферически-симметричным распределением массы, когда плотность (§18) является только функцией расстояния от центра тела; в этом случае r — расстояние между центрами масс тел;

б) тел, одно из которых, имеющее сферически-симметричное распределение массы, по размерам значительно превосходит второе. В этом случае r — расстояние между центром масс первого тела и вторым телом, которое можно рассматривать как материальную точку.

Сила тяжести F_тяж — сила, под действием которой все тела падают относительно поверхности Земли с ускорением свободного падения

g (без учета силы сопротивления воздуха):

F_тяж = mg. (12.3)

Вследствие вращения Земли вокруг своей оси система отсчета, связанная с поверхностью Земли, является неинерциальной и сила тяжести несколько отличается от силы тяготения. Однако это отличие мало, и для решения некоторых задач можно считать, что

F_тяг = mg. (12.4)

Модуль ускорения свободного падения на поверхности Земли

(12.5)

где M_з — масса Земли, R_з — радиус Земли.

Значение g = 9,806 м/с² принято в качестве стандартного.

Вес тела F_В — сила, с которой тело действует на опору (подвес), удерживающую (удерживающий) его от свободного падения.

Вес тела направлен противоположно силе реакции опорыR (на рис.12.4 брусок рассматривается как материальная точка), модули их равны:

F_В = R. (12.6)

Если опора неподвижна (или движется с постоянной скоростью) относительно поверхности Земли, то вес тела равен силе тяжести (но эти силы приложены

к разным телам):

F_В = mg. (12.7)

Если опора движется с ускорением а относительно поверхности Земли, то вес тела не равен силе тяжести:

F_В = m (g  a). (12.8)

Модуль веса тела может быть больше, меньше или равным модулю силы тяжести.

Состояние невесомости — состояние, при котором вес тела равен нулю.

Состояние невесомости выполняется при условии:

а = g, (12.9)

т.е. при свободном падении тела.

Состояние перегрузки — состояние, при котором модуль веса тела больше модуля силы тяжести.

Первая космическая скорость — скорость спутника планеты, радиус орбиты R_ор которого незначительно превышает радиус планеты R_пл:

(12. 10)

где h — высота спутника над поверхностью планеты (h  R_пл).

Первая космическая скорость для Земли

(12.11)

где g — ускорение свободного падения на поверхности Земли, R₃ — радиус Земли.

Тема 3. Законы сохранения

§13. Импульс

Импульс (количество движения) материальной точки p — ВФВ, равная произведению массы м.т. m на ее скорость v:

p = mv. (13.1)

Единица импульса — килограмм-метр в секунду: [p] = кгм/с.

Приращение (изменение) импульса материальной точки

p = p_к – p_н. (13.2)

На рис.13.1 показано приращение импульса м.т. при абсолютно упругом ударе о неподвижную плоскость.

Приращение импульса м. т. связано с приращением ее скорости v равенством:

p = mv. (13.3)

Второй закон Ньютона (с использованием импульса)

Скорость изменения импульса материальной точки относительно инерциальной системы отсчета (ИСО) равна приложенной к ней силе:

(13.4)

Если сила постоянна (F = const) на промежутке времени t, то приращение импульса материальной точки равно импульсу силы:

p = Ft (13.5)

(произведение постоянной силы на промежуток времени ее действия называется импульсом силы, единица которого Нс).

Скорость изменения импульса материальной точки относительно инерциальной системы отсчета (ИСО) при одновременном приложении к ней нескольких сил равна сумме всех приложенных сил (или равнодействующей силе):

(13.6)

Если равнодействующая сила постоянна (F_p = const) на промежутке времени t, то приращение импульса м.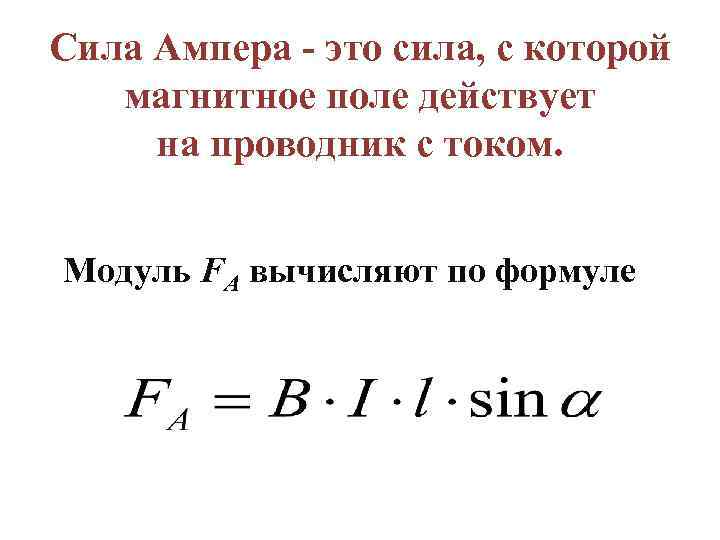

т. равно импульсу равнодействующей силы:

p = F_pt. (13.7)

Импульс системы материальных точек равен сумме импульсов всех м.т., принадлежащих данной системе:

(13.8)

где p_i — импульс i-й м.т. массой m_i, движущейся со скоростью v_i.

Центр масс (центр инерции) системы м.т. r_ц.м — точка, радиус-вектор которой определяется равенством:

(13.9)

где m_i, r_i — масса и радиус-вектор i-й м.т. соответственно, m_с — масса системы материальных точек:

(13.10)

Скорость центра масс системы материальных точек

(13.11)

Импульс системы м.т. может быть найден через произведение скорости центра масс и массы системы:

p_с = m_сv_{ц. м}. (13.12)

Если система м.т. незамкнута, то скорость изменения импульса системы относительно ИСО равна равнодействующей всех внешних сил:

(13.13)

при этом

(13.14)

где F_{p.внеш i} — равнодействующая внешних сил, действующих на i-ю материальную точку системы.

Если равнодействующая внешних сил постоянна (F_р.внеш = const) на промежутке времени t, то приращение импульса системы м.т. равно импульсу равнодействующей внешних сил:

p_c = F_р.внеш t. (13.15)

Равенству (13.15) эквивалентна система уравнений для проекций приращения импульса системы м.т. (при движении материальных точек в плоскости хОу):

(13.16)

Закон сохранения импульса системы материальных точек

Относительно инерциальной системе отсчета (ИСО) импульс замкнутой системы материальных точек с течением времени не изменяется:

p_{з. с} = const, (13.17)

при этом взаимодействие между материальными точками системы может приводить к изменению их импульсов.

Равенству (13.17) эквивалентно равенство:

p_з.с = 0. (13.18)

Скорость центра масс замкнутой системы относительно ИСО с течением времени не изменяется:

v_ц.м..з.с = const. (13.19)

Условие сохранения импульса незамкнутой системы материальных точек

Импульс незамкнутой системы м.т. p_с с течением времени не изменяется, если сумма всех внешних сил, приложенных к материальным точкам системы, равна нулю:

p_с = const при F_p.внеш = 0. (13.20)

Равенству (13.20) эквивалентно равенство:

p_с = 0 при F_{p. внеш} = 0. (13.21)

Условие сохранения проекции импульса незамкнутой системы материальных точек

Проекция импульса незамкнутой системы м.т. на какую-либо ось не изменяется, если проекция суммы всех внешних сил на эту ось равна нулю, например:

p_{с x} = const при F_{p.внеш x} = 0. (13.22)

Равенству (13.22) эквивалентно равенство:

p_{с x} = 0 при F_{p.внеш x} = 0. (13.23)

Как рассчитать модуль упругости

Обновлено 28 декабря 2020 г.

Автор: H.L.M. Lee

Если вы сдвинете концы резинового стержня друг к другу, вы приложите ​ сжимающую ​ силу и сможете немного укоротить стержень. Если потянуть за концы друг от друга, сила называется натяжением, и можно растянуть стержень вдоль. Если вы потянете один конец к себе, а другой конец от себя, используя так называемую сдвиговую силу, стержень растянется по диагонали.

Модуль упругости (​ E ​) является мерой жесткости материала при сжатии или растяжении, хотя существует также эквивалентный модуль сдвига. Это свойство материала и не зависит от формы или размера объекта.

Небольшой кусок резины имеет тот же модуль упругости, что и большой кусок резины.​ Модуль упругости ​, также известный как модуль Юнга, названный в честь британского ученого Томаса Янга, связывает силу сжатия или растяжения объекта с результирующим изменением длины.

Что такое стресс и напряжение?

​ Напряжение ​ (​ σ ​) представляет собой сжатие или растяжение на единицу площади и определяется как:

\sigma=\frac{F}{A}

площадь поперечного сечения, к которому приложена сила. В метрической системе напряжение обычно выражается в паскалях (Па), ньютонах на квадратный метр (Н/м ² ) или ньютонах на квадратный миллиметр (Н/мм ² ).

Когда к объекту прикладывается напряжение, изменение формы называется штамм. ​ В ответ на сжатие или растяжение ​ нормальная деформация ​ (​ ε ​) определяется пропорцией:

\epsilon=\frac{\Delta L}{L}

В этом случае Δ​ L ​ – изменение длины, ​ L ​ – исходная длина. Нормальная деформация, или просто деформация , безразмерна.

Разница между упругой и пластической деформацией

Пока деформация не слишком велика, такой материал, как резина, может растягиваться, а затем возвращаться к исходной форме и размеру при снятии силы; резина испытала упругая деформация, представляющая собой обратимое изменение формы. Большинство материалов могут выдерживать некоторую упругую деформацию, хотя она может быть незначительной в прочном металле, таком как сталь.

Однако, если напряжение слишком велико, материал будет подвергаться пластической деформации и необратимому изменению формы. Напряжение может даже увеличиться до такой степени, что материал порвется, например, когда вы тянете резиновую ленту, пока она не разорвется на две части.

Использование формулы модуля упругости

Уравнение модуля упругости используется только в условиях упругой деформации от сжатия или растяжения. Модуль упругости представляет собой простое напряжение, деленное на деформацию:

E=\frac{\sigma}{\epsilon}

в паскалях (Па), ньютонах на квадратный метр (Н/м ² ) или ньютонах на квадратный миллиметр (Н/мм ² ). Для большинства материалов модуль упругости настолько велик, что обычно выражается в мегапаскалях (МПа) или гигапаскалях (ГПа).

Для проверки прочности материалов инструмент тянет за концы образца с большей и большей силой и измеряет результирующее изменение длины, иногда до тех пор, пока образец не сломается. Площадь поперечного сечения образца должна быть определена и известна, чтобы можно было рассчитать напряжение от приложенной силы. Данные испытания мягкой стали, например, могут быть построены в виде кривой напряжения-деформации, которую затем можно использовать для определения модуля упругости стали.

Модуль упругости по кривой напряжения-деформации

Упругая деформация возникает при малых деформациях и пропорциональна напряжению. На кривой напряжение-деформация это поведение видно как прямолинейный участок для деформаций менее примерно 1 процента. Итак, 1 процент — это предел упругости или предел обратимой деформации.

Например, чтобы определить модуль упругости стали, сначала определите область упругой деформации на кривой напряжение-деформация, которая, как вы теперь видите, относится к деформации менее примерно 1 процента, или 92

Как рассчитать модуль Юнга

Обновлено 25 июня 2018 г.

Автор: Barbara Mascareno

Когда вы думаете о прочных материалах, поддерживающих мост или здание, вы можете не думать об эластичности.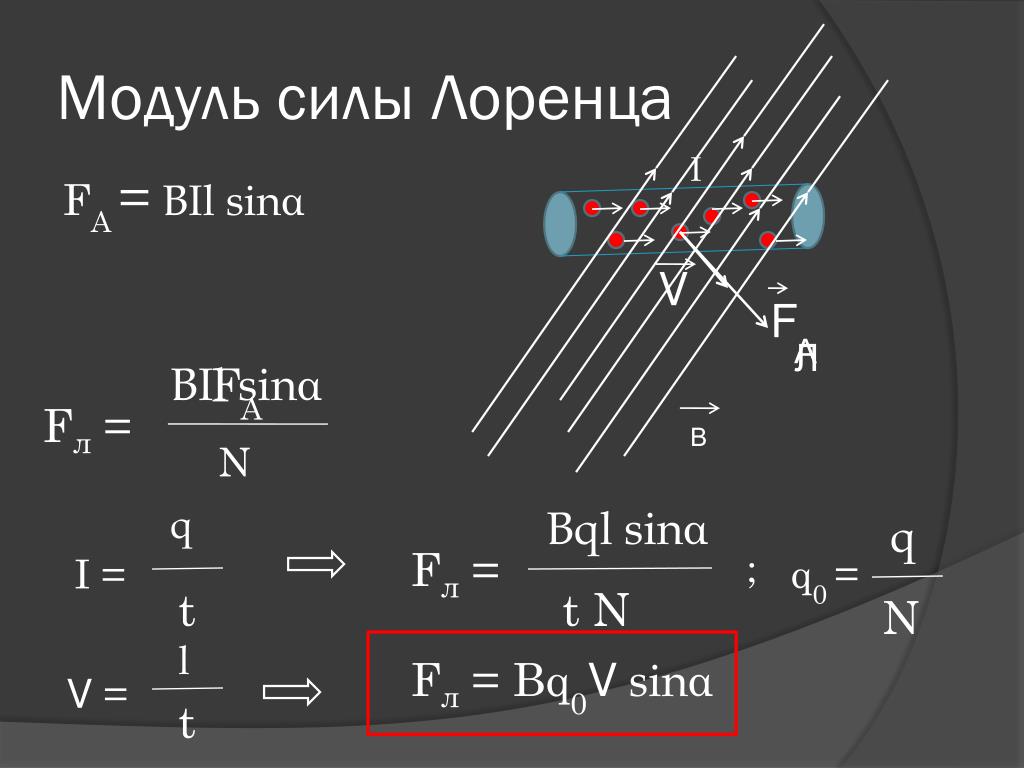 Помогая определить эластичность материалов, модуль Юнга определяет напряжение и деформацию. Эта механическая характеристика эластичности предсказывает, как прочный материал будет деформироваться под действием определенной силы. Поскольку существует прямо пропорциональная зависимость между напряжением и деформацией, график представляет соотношение между растягивающим напряжением и деформацией.

Расчет модуля Юнга относится к упругости

Расчет модуля Юнга зависит от приложенной силы, типа материала и площади материала. Напряжение среды связано с отношением приложенной силы к площади поперечного сечения. Кроме того, деформация учитывает изменение длины материала по отношению к его первоначальной длине.

Сначала вы измеряете начальную длину вещества. Используя микрометр, вы определяете площадь поперечного сечения материала. Затем тем же микрометром измерьте разные диаметры вещества. Затем используйте различные массы с прорезями, чтобы определить приложенную силу.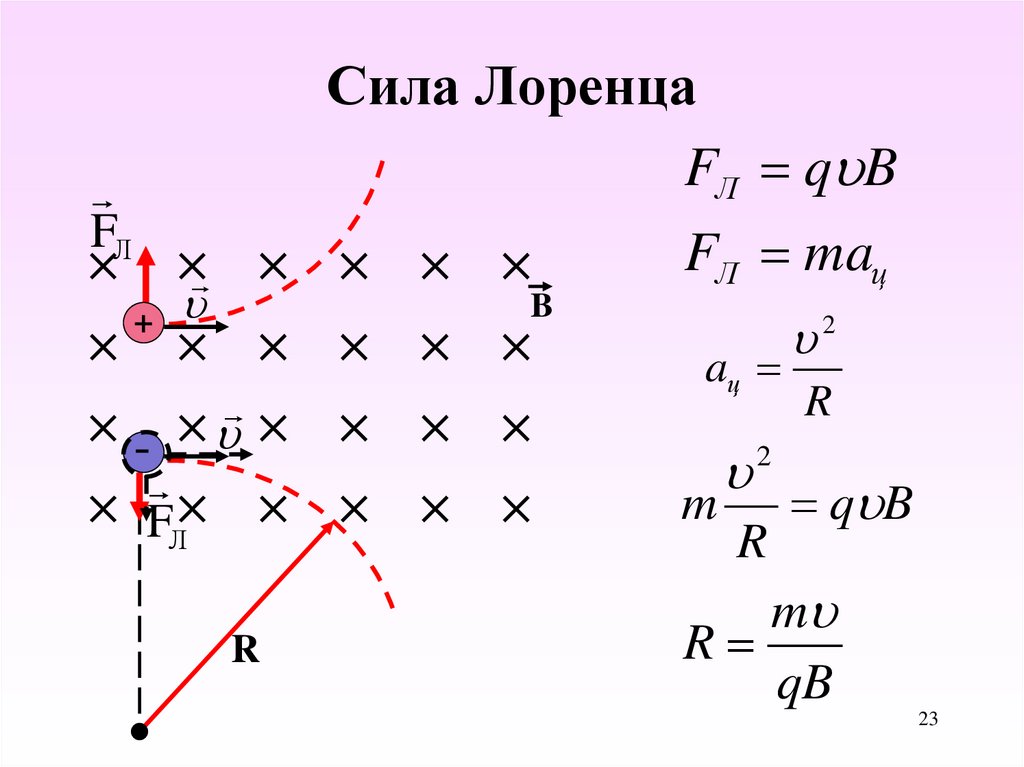

Поскольку компоненты имеют разную длину, используйте шкалу нониуса для определения длины. Наконец, постройте различные меры длины относительно приложенных сил. Уравнение модуля Юнга: E = растягивающее напряжение/деформация растяжения = (FL) / (A * изменение L), где F — приложенная сила, L — начальная длина, A — квадратная площадь, а E — модуль Юнга в паскалях. (Па). С помощью графика можно определить, проявляет ли материал эластичность.

Соответствующие приложения для модуля Юнга

Испытание на растяжение помогает определить жесткость материалов с помощью расчета модуля Юнга. Рассмотрим резинку. Когда вы растягиваете резинку, вы прикладываете усилие, чтобы ее удлинить. В какой-то момент резинка прогибается, деформируется или рвется.

Таким образом, испытание на растяжение позволяет оценить эластичность различных материалов. Этот тип идентификации в основном классифицирует эластичное или пластическое поведение.