От чего зависит индуктивность. Индуктивность катушки, её назначение, характеристики, формулы

Содержание

Что такое индуктивность

Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):

L = Ф/ I.

С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.

Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.

Самоиндукция

Индуктивность: формула

Если через замкнутый контур пропускать переменный ток, можно зарегистрировать с помощью простых экспериментов магнитное поле в окружающей среде. Изменение силовых параметров сопровождается появлением в цепи наведенной электродвижущей силы. Данное явление называют самоиндукцией.

Величину ЭДС можно вычислить по формуле:

Е = -L * (Δi/Δt).

Это выражение показывает зависимость напряжения от изменения тока за единицу времени. Поправочный коэффициент (L) обозначает особенности проводника (индукционной катушки). Знак «-» характеризует инерционные свойства явления.

При пропускании синусоидального сигнала следует учитывать отставание напряжения (векторное выражение) от тока на 90 градусов. Амплитуда будет прямо пропорциональна частоте (w):

E = L * I * w.

Расчёт поправки на собственную индуктивность витков

Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L

Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки

Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.

В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению

где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;

ω – число витков соленоида;

DСР – средний диаметр катушки, м;

I – коэффициент, зависящий от расположения витков катушки.

Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.

Для варианта а), провод намотан с небольшим коэффициентом заполнения

где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).

Для варианта б), провод намотан с большим коэффициентом заполнения

где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).

Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки

где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).

Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP

— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен

— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен

где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).

Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая

— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен

— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен

где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).

Индуктивность в электрических цепях

В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.

В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:

Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:

где ω является угловой частотой резонансной частоты F:

Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов.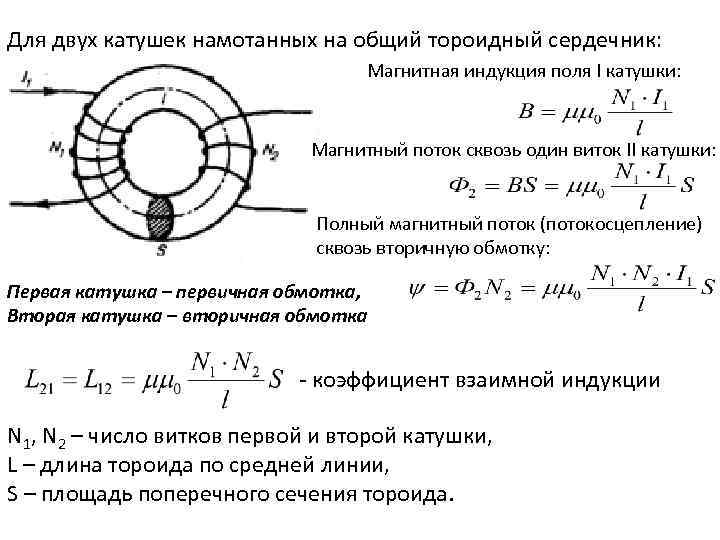 Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.

 Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.

Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:

Индуктивность и емкость в цепи переменного тока

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:

i = Iм sin ωt

u = Uм sin (ϕ + ωt),

e = Ɛm sin (ψ + ωt).

Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:

R=(pl/S)(1 + at).

В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

График и схема подключения

Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением.  Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:

ХL = ωL.

Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Катушки индуктивности

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток.  Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;

Хс = 1/ωС

Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:

Будет интересно➡  Фантомное питание для микрофона: схема подключения

X = XL—XC

и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.

В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:

P = IU cos ϕ.

Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:

Р = I2R

Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при XL=XC.)

Индуктивность

Показатель добротности

Добротность – это отношение между реактивным и индуктивным (активным) сопротивлением.

Активное – это показатель естественного сопротивления материала. Реактивное возникает, если изменения действующего значения напряжения, тока или емкости.

Для измерения используется следующее уравнение:

Q=2∙π∙f∙L/R,

Где:

• π– число Пи, равное 3,14;
• F – частотность;
• R – сопротивление.

Проблема может возникать с понятием «частота», т. к. многие не знают, что представляет собой колебательный контур. Это некоторая цепь, в которой присутствует катушка.

Как правило, колебательный контур состоит из источника питания, индукционного элемента и конденсатора. Определяется частота по формуле Томсона (она же формула резонансной частоты).

Чем выше показатель частотности, тем «добротнее» считается катушка.

Дроссель

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Лабораторная работа № 2.07 определение индуктивности катушки

Цель работы

Целью данной работы является изучение явления электромагнитной индукции и его законов, измерение индуктивности катушки, исследование зависимости индуктивности катушки от силы тока, протекающего по ее обмотке, а также индуктивности катушки, ее полного и индуктивного сопротивлений от частоты переменного тока.

Краткая теория.

Всякий контур, по которому течет ток, пронизывается магнитным полем, созданным этим током. Если сила тока в контуре меняется, то изменяется и сцепленный с контуром магнитный поток, поэтому вследствие явления электромагнитной индукции в контуре возникает ЭДС. Возникновение ЭДС в контуре при изменении силы тока в нем называется самоиндукцией.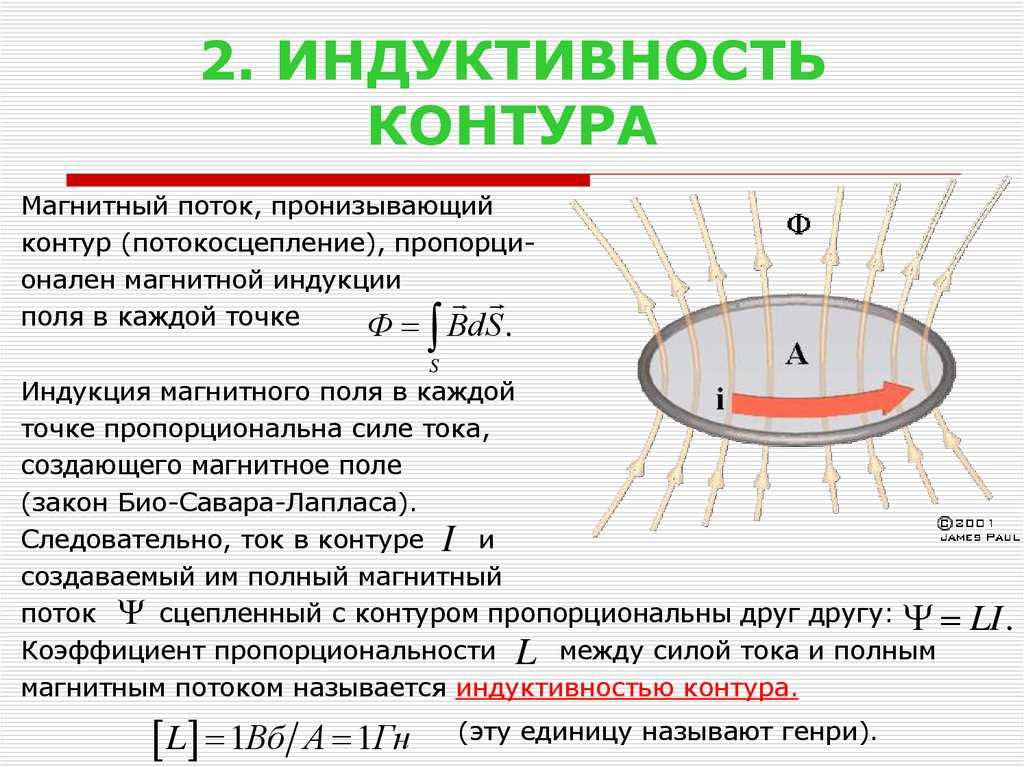 В соответствии с законом Фарадея величина ЭДС индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур, то есть,

(2.07.1)

Магнитный поток, создаваемый током, протекающим в контуре, называется потоком самоиндукции _s. Поток самоиндукции пропорционален индукции магнитного поля, создаваемого этим током, которая, в свою очередь, пропорциональна величине силы тока в контуре. Поэтому магнитный поток самоиндукции пропорционален величине силы тока

, (2.07.2)

где L – индуктивность контура.

Индуктивность контура – это скалярная физическая величина, характеризующая способность контура создавать поток самоиндукции и зависящая от его формы, размеров и магнитной проницаемости среды. Из (2.07.2) следует, что индуктивность контура измеряется величиной магнитного потока, сцепленного с контуром, при силе тока в нем равной 1 А. За единицу измерения индуктивности в системе СИ принимается 1 Гн – это индуктивность такого контура, с которым сцеплен магнитный поток в 1 Вб при силе тока в контуре, равной 1 А.

При неизменной индуктивности закон Фарадея для самоиндукции выглядит следующим образом:

(2.07.3)

т. е. ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре. В соответствии с законом Фарадея можно дать другое определение индуктивности. Индуктивность определяется величиной ЭДС, возникающей в контуре, при изменении в нем силы тока на 1 А за 1 с. Тогда, согласно (2.07.3), 1 Гн – это индуктивность такого контура, в котором индуцируется ЭДС, равная 1 В, при изменении в нем силы тока на 1 А за 1 с. Знак минус в формуле (2.07.3) отражает правило Ленца, согласно которому самоиндукция противодействует всякому изменению силы тока в контуре и представляет собой аналогию с инерцией в механике.

В электрической цепи наличие индуктивности приводит к возникновению добавочного индуктивного сопротивления катушки переменному току

, (2.07.4)

где  – частота переменного тока.

Модуль полного сопротивления Z катушки переменному току определяется по закону Ома

(2. 07.5)

где U и I – эффективные значения напряжения и силы тока в катушке.

Полное сопротивление катушки Z складывается из сопротивления катушки в цепи постоянного тока R (омического или активного сопротивления) и индуктивного сопротивления X_L в соответствии с формулой:

. (2.07.6)

или, подставив

(2.07.7)

из которого можно выразить индуктивность катушки L

(2.07.8)

Соотношение (2.07.8) лежит в основе опыта по определению индуктивности. Для того, чтобы определить индуктивность, необходимо измерить частоту переменного тока, действующее значение силы переменного тока, протекающего через катушку, действующее значения напряжения на катушке и омическое сопротивление катушки.

Индуктивность длинного соленоида с сердечником может быть рассчитана по формуле

, (2. 07.9)

где  – магнитная проницаемость сердечника; – магнитная постоянная;

n – число витков, приходящихся на единицу длины катушки; V – объем катушки.

Измеряя индуктивность катушки, можно определять магнитную проницаемость материала, из которого изготовлен сердечник. В частности, таким способом можно определять магнитную проницаемость горных пород. Определив индуктивность катушки с сердечником из исследуемой породы L_с и без сердечника L₀, по отношению этих индуктивностей L_С/L₀ определяют . Определение магнитной проницаемости горных пород и минералов необходимо для изучения вопросов, связанных с установлением качества железных руд и железистых пород, магнитным обогащением полезных ископаемых, с разведкой рудных тел, исследованием трещиноватости массива горных пород.

Выполнение работы

Необходимые приборы: лабораторный стенд, внутри которого смонтированы все элементы схемы; генератор периодических сигналов; цифровой вольтметр. Рабочая схема опыта показана на рис. 18 и на панели стенда.

Индуктивность | Физика

Цели обучения

К концу этого раздела вы сможете:

• Вычислять индуктивность катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Катушки индуктивности

Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9. 0019 индуктивность . Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.

Рисунок 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что » E ₂ индуцируемая» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, ∆ I / ∆ t , как на причине индукции. Изменение тока I ₁ в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС ₂ в другом. Мы выражаем это в форме уравнения как

[латекс] {\ текст {ЭДС}} _ {2} = — М \ гидроразрыва {\ Delta {I} _ {1}} {\ Delta t} \\ [/латекс] ,

, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют небольшой размер M по сравнению с катушками трансформатора на Рисунке 3 от компании Transformers. Единицами для M являются (В ⋅ с) / A = Ω ⋅ с, который назван Генри (H) в честь Джозефа Генри. То есть 1 Гн = 1 Ом⋅с. Природа здесь симметрична. Если мы изменим текущий I ₂ в катушке 2, мы индуцируем ЭДС ₁ в катушке 1, которая определяется как

[латекс]{\текст{ЭДС}}_{1}=-M\frac{\Delta { I}_{2}}{\Delta t}\\[/latex],

, где M то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M предназначен для противодействия катушкам, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)

Рис. 2. Нагревательные спирали электрической сушилки для белья можно намотать встречно, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.

Самоиндукция , также существует действие закона Фарадея об индукции устройства на себя. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока Δ I через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Он определяется как

[латекс]\текст{ЭДС}=-L\frac{\Delta I}{\Delta t}[/латекс],

, где л — собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рис. 3.

Рис. 3.

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность L устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большую L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо получить небольшую катушку L , например, путем встречной обмотки катушек, как показано на рис. 2. Катушка индуктивности 1 Гн является большой катушкой индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с л = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, определяемая как ЭДС = − L (Δ I /Δ t ), будет противиться изменению. Таким образом, будет индуцироваться ЭДС, определяемая как ЭДС = — л (Δ I / t ) = (1,0 Гн)[(10 А)/(1,0 мс)] = 10 000 В. Положительный знак означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока. Есть применение такому большому наведенному напряжению. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать L для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность L обычно заданное количество. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется по закону индукции Фарадея как ЭДС = — Н (Δ Φ / t ) и, по определению самоиндукции, как ЭДС = — л (Δ I / Δ t ). Приравнивание этих выходов

[латекс]\текст{ЭДС}=-N\frac{\Delta \Phi }{\Delta t}=-L\frac{\Delta I}{\Delta t}\\[/latex]

Решение для L дает

[латекс] L=N\frac{\Delta \Phi }{\Delta I}\\[/latex]

Это уравнение для собственной индуктивности L устройства всегда справедливо. Это означает, что собственная индуктивность L зависит от того, насколько эффективен ток в создании потока; тем эффективнее, чем больше Δ Φ / Δ I . Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Так как район A соленоида фиксирован, изменение потока Δ Φ = Δ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется как [латекс] B = {\ mu } _ {0} {nI} = {\ mu } _ {0} \ frac {NI} { \ell}\\[/латекс]. (Здесь n  =  N / ℓ , где N — количество витков, а ℓ — длина соленоида. ) Изменяется только ток, так что [латекс]\Delta \Phi =A\ Дельта B = {\ mu } _ {0} \ text {NA} \ frac {\ Delta I} {\ ell} \\ [/latex]. Подставляя Δ 9{2}A}{\ell}\text{(соленоид)}\\[/латекс].

Это собственная индуктивность соленоида с площадью поперечного сечения A и длиной ℓ . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример 1. Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками.

Стратегия 9{2}A}{\ell }\\[/latex]

Площадь поперечного сечения в этом примере  A = πr ² = (3,14…)(0,0200 м) ² = 1,26 × 10 ⁻³ м ² , N равно 200, а длина ℓ равна 0,100 м. Мы знаем, что проницаемость свободного пространства составляет мк ₀ = 4π × 10 ⁻⁷ Тл ⋅ м/А. {2}\right)}{0,100 \text{ м}}\\ & =& 0,632 \text{ мГн}\end{массив}\\[/latex].

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных приложений индуктивности используется в светофорах, которые могут определить, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.

Рисунок 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Энергия, запасенная в индукторе

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что 9{2}\right)=0.284 \text{ J}\end{array}\\[/latex]

Обсуждение

Этого количества энергии, безусловно, достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

Резюме раздела

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока Δ I ₁ /Δ t в одном индуцирует ЭДС ₂  во втором:

  [латекс]{\текст{ЭДС}}_{2}=-M\frac{\Delta {I}_{1}}{\Delta t}\\[/latex],

  , где M  определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.

• Симметрично изменение тока Δ I ₂ /Δt через второе устройство индуцирует ЭДС ₁  в первом:

  [латекс] {\ текст {ЭДС}} _ {1} = — М \ гидроразрыва {\ Delta {I} _ {2}} {\ Delta t} \\ [/ латекс],

  , где M  такая же взаимная индуктивность, как и в обратном процессе.

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Прибор называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна
  [латекс]\текст{ЭДС}=-L\frac{\Delta I}{\Delta t}\\[/latex],

  , где L — собственная индуктивность индуктора, а Δ I / Δ t — скорость изменения тока через него. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца.

• Единицей собственной и взаимной индуктивности является генри (Гн), где 1 Гн = 1 Ом⋅с.
• Собственная индуктивность L катушки индуктивности пропорциональна тому, насколько поток изменяется с током. Для катушки индуктивности N , 9{2}\\[/латекс].

Концептуальные вопросы

1. Как бы вы поместили две одинаковые плоские катушки в контакт, чтобы они имели наибольшую взаимную индуктивность? В мере?
2. Как бы вы придали проводу заданной длины такую ​​форму, чтобы обеспечить наибольшую самоиндукцию? В мере?
3. Проверить, как было сделано без доказательства в Примере 1 (выше), что единицы T ⋅ m ² / A  = Ω ⋅ s = H.

Задачи и упражнения

1. Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?

2. Если две катушки, расположенные рядом друг с другом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток 2,00 А в другой отключается через 30,0 мс?

3. Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

4. Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

5. Начиная с [latex]{\text{emf}}_{2}=-M\frac{\Delta {I}_{1}}{\Delta t}\\[/latex], покажите, что единицы индуктивности (В ⋅ с)/A = Ом ⋅ с.

6. Вспышки фотокамеры заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности.

За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

7. Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

8. (a) Рассчитайте собственную индуктивность соленоида длиной 50,0 см и диаметром 10,0 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

9. Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

10. Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и общее количество витков 400. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

11. Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению. Каково значение собственной индуктивности?

12. Как быстро может быть отключен ток 150 А через дроссель 0,250 Гн, если ЭДС индукции не может превышать 75,0 В?

13. Интегрированные концепции  Очень большой сверхпроводящий соленоид, такой как тот, который используется в МРТ-сканировании, сохраняет 1,00 МДж энергии в своем магнитном поле при токе 100 А. а) Найдите его индуктивность. (б) Если катушки «идут нормально», они приобретают сопротивление и начинают рассеивать тепловую энергию. Какой прирост температуры произойдёт, если вся накопленная энергия пойдет на нагрев магнита массой 1000 кг при средней удельной теплоемкости 200 Дж/кг · ºC?

14. Необоснованные результаты  Катушка индуктивности 25,0 Гн отключает ток 100 А за 1,00 мс. а) Какое напряжение индуцируется, чтобы противостоять этому? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?

Глоссарий

индуктивность

свойство устройства, описывающее, насколько эффективно оно создает ЭДС в другом устройстве

взаимная индуктивность

насколько эффективно пара устройств индуцирует ЭДС друг в друге 9{2}\\[/латекс]

Избранные решения задач и упражнений

1.  1,80 мГн

3. 3,60 В

7. (a) 31,3 кВ (b) 125 кДж (c) 1,56 МВт (d) Нет, это не удивительно, поскольку это мощность очень высокая.

9. (а) 1,39 мГн (б) 3,33 В (в) Ноль

11. 60,0 мГн

13. (а) 200 Гн (б) 500 ºC

 

Физический Колледж 2

Резюме

• Расчет индуктивности катушки индуктивности.
• Рассчитайте энергию, запасенную в катушке индуктивности.
• Рассчитайте ЭДС, создаваемую катушкой индуктивности.

Индукция – это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9. 0197 индуктивность .

Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.

Рис. 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Обратите внимание, что « E ₂ индуцируемая» представляет ЭДС индукции в катушке 2.)

Во многих случаях, когда геометрия устройств фиксирована, поток изменяется при изменении тока. Поэтому мы сосредоточимся на скорости изменения тока, [латекс]\жирныйсимвол{\Delta I / \Delta t}[/латекс], как на причине индукции. Изменение тока [latex]\boldsymbol{I_1}[/latex] в одном устройстве, катушка 1 на рисунке, индуцирует [latex]\boldsymbol{\textbf{emf}_2}[/latex] в другом.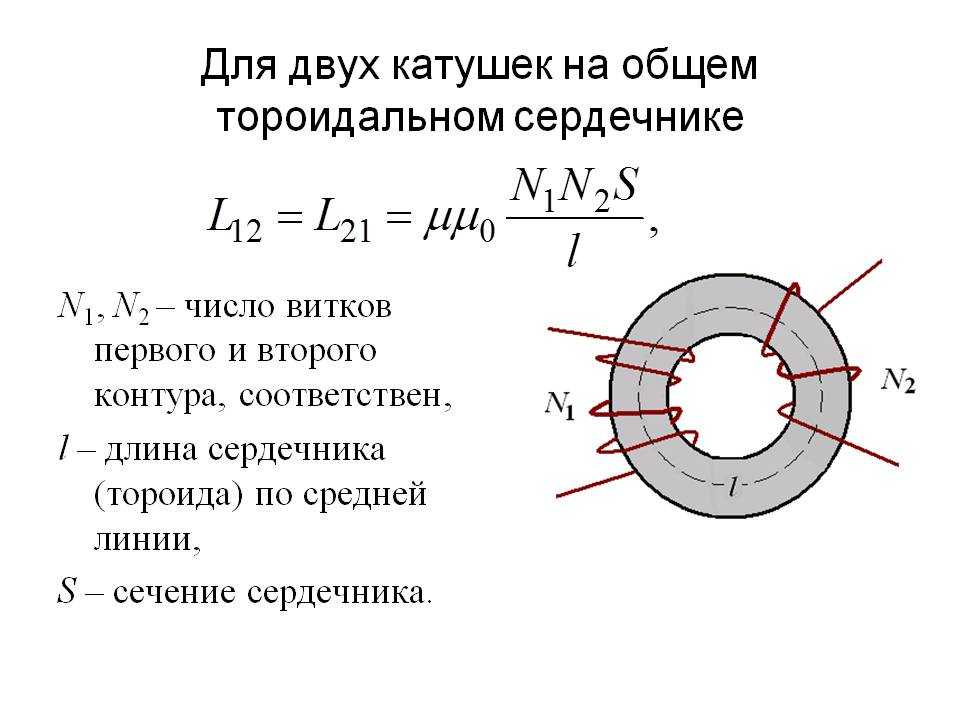 Выразим это в виде уравнения как

[латекс]\boldsymbol{\textbf{emf}_2 = -M}[/латекс] [латекс]\boldsymbol{\frac{\Delta I_1}{\Delta t}}[/латекс],

, где [латекс]\boldsymbol{M}[/латекс] определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность [латекс]\boldsymbol{M}[/латекс], тем эффективнее связь. Например, катушки на рисунке 1 имеют маленький [латекс]\жирныйсимвол{M}[/латекс] по сравнению с катушками трансформатора в главе 23.7. Рисунок 3. Единицы для [латекс]\жирныйсимвол{М}[/латекс] равны [ латекс]\boldsymbol{(\textbf{V} \cdot \;\textbf{s})/ \textbf{A} = \Omega \cdot \;\textbf{s}}[/latex], который называется Генри (H), в честь Джозефа Генри. То есть [латекс]\boldsymbol{1 \;\textbf{H} = 1 \Omega \cdot \;\textbf{s}}[/latex].

Природа здесь симметрична. Если мы изменим ток [latex]\boldsymbol{I_2}[/latex] в катушке 2, мы индуцируем [latex]\boldsymbol{\textbf{emf}_1}[/latex] в катушке 1, который определяется как

[латекс]\boldsymbol{\textbf{emf}_1 = -M}[/латекс] [латекс]\boldsymbol{\frac{\Delta I_2}{\Delta t}}[/латекс],

, где [latex]\boldsymbol{M}[/latex] — то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью [латекс]\boldsymbol{M}[/латекс] .

Большая взаимная индуктивность [латекс]\boldsymbol{M}[/латекс] может быть как желательной, так и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность [латекс]\boldsymbol{M}[/латекс] – это встречная обмотка катушек, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)

Рисунок 2. Нагревательные спирали электрической сушилки для белья могут быть намотаны встречно, так что их магнитные поля компенсируют друг друга, что значительно уменьшает взаимную индуктивность с корпусом сушилки.

Самоиндукция , действие закона Фарадея об индукции устройства на себя, также существует. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока [латекс]\boldsymbol{\Delta I}[/латекс] через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Это дается

[латекс]\boldsymbol{\textbf{emf}= -L}[/латекс] [латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/латекс],

, где [latex]\boldsymbol{L}[/latex] – собственная индуктивность устройства. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначено символом на рисунке 3.

Рис. 3.

Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность [латекс]\boldsymbol{L}[/латекс] устройства, тем больше его сопротивление любому изменению тока через него. Например, большая катушка с большим количеством витков и железным сердечником имеет большой [латекс]\жирныйсимвол{L}[/латекс] и не позволит току быстро измениться. Чтобы избежать этого эффекта, необходимо добиться небольшого [латекса]\жирного символа{L}[/латекса], например, путем встречной намотки катушек, как показано на рис. 2.9.0005

Катушка индуктивности 1 Гн представляет собой большую катушку индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с [латекс]\boldsymbol{L = 1,0 \;\textbf{H}}[/латекс], через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, заданная формулой [латекс]\жирныйсимвол{\текстбф{ЭДС} = -L(\Delta I/\Delta t)}[/латекс], будет препятствовать изменению. Таким образом, ЭДС будет индуцироваться следующим образом: A})/(1,0 \;\textbf{ms})]=10 000 \;\textbf{V}}[/latex]. Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.

Для такого большого наведенного напряжения есть применение. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)

Рис. 4. Благодаря быстрому переключению катушки индуктивности батареи на 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.

Можно рассчитать [латекс]\boldsymbol{L}[/латекс] для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность [латекс]\жирный символ{L}[/латекс] обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции задается законом индукции Фарадея как собственной индуктивности, как [латекс]\boldsymbol{\textbf{ЭДС}=-L(\Delta I/ \Delta t)}[/latex]. Приравнивая эти выходы

[латекс]\boldsymbol{\textbf{emf} = -N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta t}}[/латекс] [латекс]\boldsymbol{ = -L}[/latex] [латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/latex].

Решение для [латекс]\boldsymbol{L}[/латекс] дает

[латекс]\boldsymbol{L = N}[/латекс] [латекс]\boldsymbol{\frac{\Delta \phi}{\Delta I}}[/latex].

Это уравнение для собственной индуктивности [латекс]\boldsymbol{L}[/латекс] устройства всегда справедливо. Это означает, что самоиндукция [латекс]\boldsymbol{L}[/латекс] зависит от того, насколько эффективен ток в создании потока; чем эффективнее, тем больше [латекс]\boldsymbol{\Delta \phi \Delta I}[/latex].

Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь [латекс]\жирныйсимвол{А}[/латекс] соленоида фиксирована, изменение потока составляет [латекс]\жирныйсимвол{\Дельта \фи = \Дельта (ВА) = А \Дельта В}[/ латекс]. Чтобы найти [латекс]\boldsymbol{\Delta B}[/латекс], заметим, что магнитное поле соленоида определяется выражением [латекс]\жирный символ{В = \mu _0 nI = \mu 0 \frac{NI} {\ell}}[/латекс]. (Здесь [латекс]\boldsymbol{n = N/ \ell}[/latex], где [латекс]\boldsymbol{N}[/латекс] — количество витков, а [латекс]\boldsymbol{\ell}[/ латекс] — длина соленоида.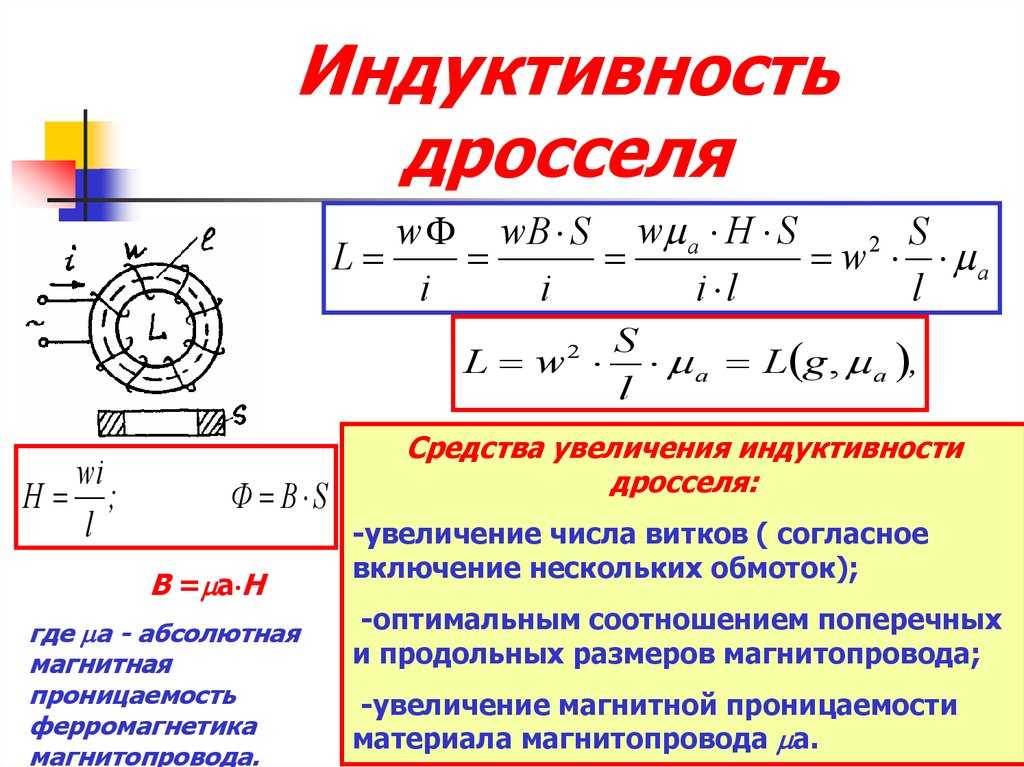 ) Изменяется только ток, так что [латекс]\жирныйсимвол{\Delta \phi = A \Delta B = \mu_0 NA \frac{\Delta I}{\ell}}[/latex] . Замена [латекс]\boldsymbol{\Delta \phi}[/latex] на [латекс]\boldsymbol{L = N \frac{\Delta \phi}{\Delta I}}[/latex] дает 92A}{\ell}}[/latex][latex]\boldsymbol{(\textbf{соленоид})}.[/latex]

Это собственная индуктивность соленоида с площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] и длиной [латекс]\boldsymbol{\ell}[/латекс]. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.

Пример 1. Расчет собственной индуктивности соленоида среднего размера

Рассчитайте собственную индуктивность соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками. 92) {0,100 \;\textbf{м}} \\[1em] & \boldsymbol{0,632 \;\textbf{мГн}} \end{массив}[/latex].

Обсуждение

Этот соленоид средних размеров. Его индуктивность около миллигенри также считается умеренной.

Одно из распространенных приложений индуктивности используется в светофорах, которые могут определить, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.

Рисунок 5 Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)

Из закона Ленца мы знаем, что индуктивности противодействуют изменениям тока. Есть альтернативный взгляд на эту оппозицию, основанный на энергии. Энергия хранится в магнитном поле. Требуется время, чтобы накопить энергию, и также нужно время, чтобы истощить энергию; следовательно, существует оппозиция быстрым изменениям. В индукторе магнитное поле прямо пропорционально току и индуктивности устройства. Можно показать, что 92 = 0,284 \;\textbf{J}}. \end{array}[/latex]

Обсуждение

Этого количества энергии определенно достаточно, чтобы вызвать искру, если ток внезапно отключится. Он не может быть построен мгновенно, если только потребляемая мощность не бесконечна.

• Индуктивность — это свойство устройства, которое показывает, насколько эффективно оно индуцирует ЭДС в другом устройстве.
• Взаимная индуктивность — это действие двух устройств, индуцирующих ЭДС друг в друге.
• Изменение тока [латекс]\boldsymbol{\Delta I_1 / \Delta t}[/латекс] в одном индуцирует ЭДС [латекс]\boldsymbol{\textbf{ЭДС}_2}[/латекс] во втором:

  [латекс]\boldsymbol{\textbf{emf}_2 = — M}[/latex][латекс]\boldsymbol{\frac{\Delta I_1}{\Delta t}}[/latex],

  , где [латекс]\жирныйсимвол{М}[/латекс] определяется как взаимная индуктивность между двумя устройствами, а знак минус соответствует закону Ленца.

• Симметрично изменение тока [латекс]\boldsymbol{\Delta I_2/ \Delta t}[/латекс] через второе устройство индуцирует ЭДС [латекс]\boldsymbol{\textbf{ЭДС}_1[/латекс] в первый:

  [латекс]\boldsymbol{\textbf{emf}_1 = — M}[/latex][латекс]\boldsymbol{\frac{\Delta I_2}{\Delta t}}[/latex] ,

  , где [латекс]\boldsymbol{M}[/латекс] — та же взаимная индуктивность, что и в обратном процессе.

• Текущие изменения в устройстве индуцируют ЭДС в самом устройстве.
• Самоиндукция — это эффект устройства, индуцирующего ЭДС само по себе.
• Прибор называется индуктором, а ЭДС, индуцируемая в нем изменением тока через него, равна

  [латекс]\boldsymbol{ЭДС = -L}[/латекс][латекс]\boldsymbol{\frac{\Delta I}{\Delta t}}[/latex],

  , где [latex]\boldsymbol{L}[/latex] — собственная индуктивность катушки индуктивности, а [latex]\boldsymbol{\Delta I / \Delta t}[/latex] — скорость изменения тока через Это. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца.

• Единицей собственной и взаимной индуктивности является генри (H), где [latex]\boldsymbol{1 \;\textbf{H} = 1 \Omega \cdot \;\textbf{s}}[/latex].
• Самоиндукция [латекс]\boldsymbol{L}[/латекс] катушки индуктивности пропорциональна тому, насколько поток изменяется с током. Для [латексного]\boldsymbol{N}[/латексного]-виткового индуктора

  [латекс]\boldsymbol{L = N}[/латекс][латекс]\boldsymbol{\frac{\Delta \phi}{\Delta T}}[/latex]

• Самоиндукция соленоида 92}[/латекс].

Задачи и упражнения

1: Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?

2: Если две катушки, расположенные рядом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной из них, когда ток 2,00 А в другой отключается через 30,0 мс?

3: Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?

4: Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?

5: Начиная с [латекс]\boldsymbol{\textbf{эдс}_2 = -M \frac{\Delta I_1}{\Delta t}}[/latex], покажите, что единицами измерения индуктивности являются [латекс ]\boldsymbol{(\textbf{V} \cdot \;\textbf{s})/ \textbf{A} = \Omega \cdot \;\textbf{s}}[/latex].

6: Вспышки камеры заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?

7: Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если ток 100 А через него отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?

8: (a) Рассчитайте собственную индуктивность соленоида длиной 50,0 см и диаметром 10,0 см, имеющего 1000 витков.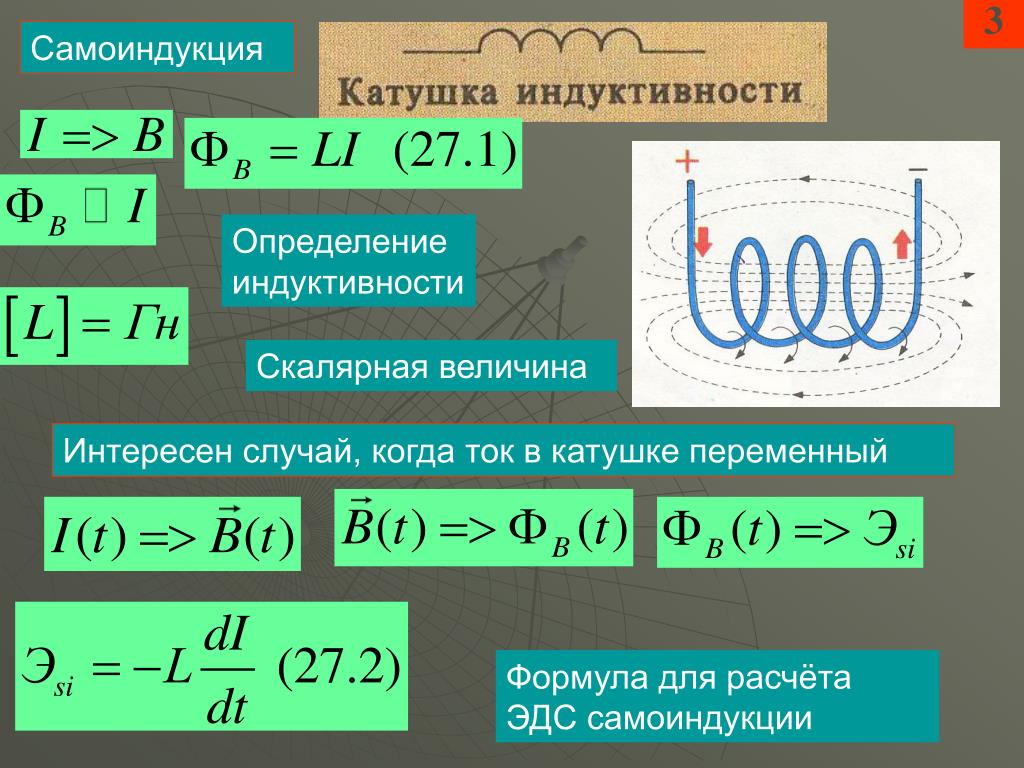 б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?

9: Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?

10: Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?

11: Когда ток 20,0 А через катушку индуктивности отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению.