РАДИО ВСЕМ, №12, 1926 год. Расчет емкости конденсаторов
РАДИО ВСЕМ, №12, 1926 год. Расчет емкости конденсаторов«Радио Всем», №12, декабрь 1926 год, стр. 20-21
М. А. Нюренберг.
Почти во всех случаях радиолюбительской практики приходится иметь дело с конденсаторами — постоянной и переменной емкости и их расчету мы посвящаем эту статью.
Конденсатор постоянной емкости.
Простейший конденсатор постоянной емкости (черт. 1) представляет собой две металлические обкладки, разделенные друг от друга каким-либо диэлектриком (воздухом, слюдой и пр.). Емкость такого конденсатора зависит от площади металлической обкладки; расстояния между обкладками (толщины диэлектрика) и свойств того диэлектрика, который применен в конденсаторе. Чем больше площадь обкладок, чем ближе расположены обкладки друг к другу, тем больше емкость конденсатора.
Свойства диэлектрика определяются величиной, носящей название
Черт. 1.
Емкость такого конденсатора определяется формулой:
C = ε·S 12,5d где C — емкость конденсатора в см.
S — плошадь одной обкладки в кв.см.
d — расстояние между обкладками в см.
ε — диэлектрическая постоянная (величины ε для различных диэлектриков приводятся ниже в таблице):
| Диэлектрик | ε = | Диэлектрик | ε = |
| Пустота…… | Бумага (сухая).. | 1,8—2,6 | |
| Воздух…… | 1,0006 | Каучук…… | 2,0—3,5 |
| Керосин…… | 2 | Парафин…… | 1,8—2,3 |
| Эбонит…… | Сера. ….. |
3,6—4,8 | |
| Маслян. бумага.. | 2 | Целлюлоид…… | 4 |
| Шеллак…… | 3,0—3,8 | Сургуч…… | 4 |
| 5—10 | Вода (химич. чистая)…… |
81 | |
| Слюда…… | 5—8 |
Конденсаторы, состоящие из двух обкладок, имеют очень незначительную емкость и потому применяются очень редко — в специальных схемах для коротких волн.
Обычно применяются конденсаторы, состоящие из нескольких обкладок, емкость которых может быть очень велика (черт.2).
Черт. 2.
Емкость таких конденсаторов зависит, кроме всего указанного ранее (для случая конденсатора с двумя обкладками), также от числа обкладок. Прибавляя к описанному ранее конденсатору одну, две, три и т. д. обкладок, мы будем увеличивать емкость конденсатора в 2, 3, 4 и т. д. раза.
Подсчитать емкость плоского конденсатора можно по номограмме черт. 3. В этой номограмме: dmm — толщина диэлектрика в мм. Fсм2 — площадь одной обкладки в кв. см., Cсм — емкость в см., n — общее число обкладок. Диэлектрическая постоянная ε — принята равной единице (воздух),
Последовательность соединения точек следующая: F — n — Z — d — C.
Черт. 2.
(увеличенное изображение)
В таблице II приведены значения емкости конденсатора в зависимости от числа обкладок и толщины диэлектрика при площади обкладки равной 1 кв. сантиметру. Для расчета емкости следует величину, взятую из таблицы, умножить на площадь обкладки в кв.
 ) |
Число пластин | |||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 11 | 12 | |||
| 0,005 | 31,9 | 63,8 | 95,7 | 127 | 159 | 191 | 223 | 255 | 287 | 319 | 351 | фин ε = 2.  |
| 0,01 | 15,9 | 31,9 | 47,8 | 63,7 | 79,6 | 95,5 | 111 | 127 | 143 | 159 | ||
| 0,03 | 5,3 | 10,6 | 15,9 | 21,2 | 26,5 | 31,9 | 37,2 | 42,5 | 47,8 | 53,2 | 58,5 | |
| 0,05 | 6,4 | 9,5 | 12,7 | 15,9 | 19,1 | 22,3 | 25,5 | 28,7 | 31,9 | 35,1 | ||
| 0,08 | 1,99 | 3,98 | 5,96 | 7,95 | 9,95 | 11,9 | 13,9 | 15,9 | 17,9 | 19,9 | 21,8 | |
| 0,1 | 1,59 | 3,19 | 4,78 | 6,37 | 7,96 | 9,55 | 11,1 | 12,7 | 14,3 | 15,9 | 17,5 | |
| 0,005 | 95,6 | 191 | 287 | 381 | 477 | 572 | 669 | 765 | 860 | 956 | 1050 | Слюда ε = 6.  |
| 0,01 | 47,7 | 95,6 | 143 | 191 | 239 | 286 | 333 | 381 | 428 | 476 | 524 | |
| 0,03 | 15,9 | 31,8 | 47,7 | 63,5 | 79,4 | 95,5 | 111 | 127 | 143 | 159 | 175 | |
| 0,05 | 9,6 | 19,2 | 28,7 | 38,1 | 47,7 | 57,2 | 66,9 | 76,5 | 86,0 | 95,6 | 105 | |
| 0,08 | 5,9 | 11,9 | 17,9 | 23,9 | 29,9 | 35,7 | 41,7 | 47,7 | 53,7 | 59,7 | 65,4 | |
| 0,1 | 4,7 | 9,5 | 14,3 | 19,1 | 23,9 | 28,6 | 33,3 | 38,1 | 42,8 | 47,6 | 52,4 | |
Формула для расчета емкости конденсатора, состоящего из нескольких обкладок, имеет следующий вид:
C = ε·S (n — 1) 12,5d Все обозначенные те же, что и в ранее приведенной формуле.
n — общее число обкладок (положительных и отрицательных).
Конденсатор переменной емкости.
Расчет конденсатора переменной емкости заключается в подсчете его максимальной емкости (при вдвинутых подвижных пластинах) и ничем не отличается от расчета плоского постоянного конденсатора. Начальная емкость (при выдвинутых подвижных пластинах) подсчету не поддается и обычно определяется экспериментальным путем.
Черт. 4.
При расчете конденсатора переменной емкости следует за площадь пластины принимать лишь ту площадь, которая взаимно перекрывается пластинами (подвижной и неподвижной). На черт. 4 эта площадь заштрихована.
Формула для расчета емкости переменного конденсатора, пластины которого имеют полукруглую форму, следующая:
C = ε (r12 — r22) (n — 1) 8d где r1 — радиус подвижной пластины в см.
r2 — внутренний радиус неподвижной пластины в см. (см. черт. 4).Остальные обозначения те же, что в ранее приведенных формулах.
Расчет емкости квадратичного конденсатора описан в № 11 «Радио Всем», где также описаны графики емкости конденсаторов, почему на этом вопросе мы останавливаться не будем.
Соединение конденсаторов.
При параллельном соединении нескольких конденсаторов (черт. 5) емкость всей группы будет равна сумме емкостей отдельных конденсаторов, т. е.
Черт. 5.
При последовательном соединении нескольких конденсаторов (черт.6) общая емкость группы будет меньше емкости любого из включенных в группу конденсаторов. Для двух последовательно включенных конденсаторов общую емкость легко подсчитать по номограмме черт.
7, где C1 и C2 — емкости отдельных конденсаторов, а C — общая емкость этих конденсаторов, включенных последовательно. Простым соединением помощью линейки C1 и C2 определяется в точке пересечения общая емкость C. Очевидно, что, пользуясь этой номограммой, можно определить емкость нескольких, последовательно включенных конденсаторов. Для этого последовательно определяются значения C при двух конденсаторах C1 и C2; полученное значение C для двух конденсаторов соединяется с третьим конденсатором C3 и т. д.
Черт. 6.
Формула для последовательно соединенных конденсаторов имеет вид:
1 = 1 + 1 + 1 + . C C1 C2 C3 где C — общая емкость группы
C1, C2, C3 … — емкости отдельных конденсаторов.Дпя двух конденсаторов формула имеет вид:
C = C1C2 C1 + C2
.. Черт. 7.
(увеличенное изображение)
Этой статьей мы заканчиваем первый цикл статей, посвященных расчетам деталей и в следующих номерах журнала перейдем к расчетам антенн и приемников.
1) Пример работы с номограммой приведен не в №8, а в №7 «Радио Всем» за 1926 год. (примечание составителя).
Электроемкость. Емкость конденсатора
Главная → Примеры решения задач ТОЭ → Электроемкость. Емкость конденсатора
Электроемкость. Емкость конденсатора
Основные положения и соотношения
1. Закон Кулона
F=Q1⋅Q24π⋅εa⋅R2, (1)
здесь
F — сила взаимодействия между зарядами;
Q1 и Q2 — точечные заряды;
R — расстояние между ними;
εa — абсолютная диэлектрическая проницаемость среды, равная ε0·εr;
εr — относительная диэлектрическая проницаемость;
ε0=14π⋅с2⋅10−7≈8,85418782⋅10−12 Фм – электрическая постоянная.
2. Напряженность электростатического поля точечного заряда Q на расстоянии R от него
E=Q4π⋅εa⋅R2. (2)
Напряженность поля в любой точке между пластинами плоского конденсатора вдалеке от краев
E=Ud, (3)
здесь d — расстояние между пластинами конденсатора, U — напряжение.
Напряженность поля в точке, отстоящей на расстоянии r от бесконечно длинной заряженной оси с линейной плотностью τ
E=τ2π⋅εa⋅r. (4)
Напряженность поля в точке, отстоящей на расстоянии r от оси цилиндрического конденсатора (r1 <r < r2)
E=Ur⋅lnr2r1, (5)
здесь U — напряжение конденсатора, r1 и r2 — соответственно внутренний и внешний радиусы конденсатора.
Напряженность поля в точке, отстоящей на расстоянии R от центра сферического конденсатора (R1 < R < R2)
E=U⋅R1⋅R2R2⋅(R2−R1), (6)
здесь U — напряжение конденсатора, R1 и R2 — соответственно внутренний и внешний радиусы конденсатора.
3. Вектор электрического смещения
D→=εa⋅E→. (7)
4. Общее выражение емкости конденсатора
C=QU. (8)
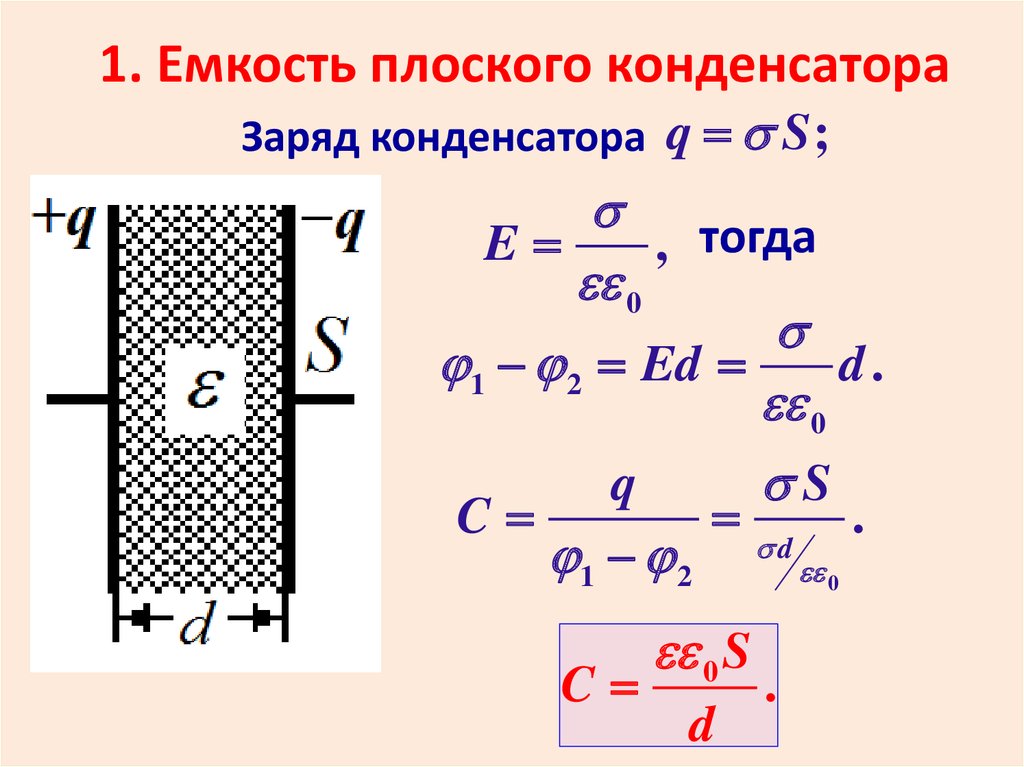
Емкость плоского конденсатора
C=εa⋅Sd=εr⋅ε0⋅Sd, (9)
здесь S — поверхность каждой пластины конденсатора; d — расстояние между ними.
Скачать статью Вывод формулы емкости плоского конденсатора
Емкость цилиндрического конденсатора
C=2π⋅εa⋅llnr2r1, (10)
здесь l — длина конденсатора, r1 и r2 — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости коаксиального кабеля
Емкость сферического конденсатора
C=4π⋅εa⋅R1⋅R2R2−R1, (11)
здесь R1 и R2 — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости сферического конденсатора
Емкость двухпроводной линии
C=π⋅εa⋅lln[D2a+(D2a)2−1], (12)
здесь l — длина линии, D — расстояние между осями проводов, a — радиус проводов.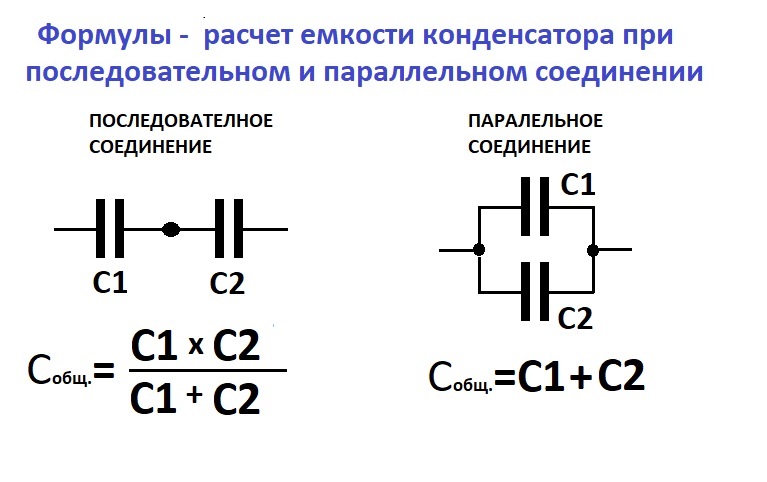
Емкость однопроводной линии
C=2π⋅εa⋅lln[ha+(ha)2−1], (13)
здесь l — длина линии, h — высота подвеса провода над землей, a — радиус провода.
5. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C=C1+C2+…+Cn=∑k=1nCk. (14)
При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1C=1C1+1C2+…+1Cn=∑k=1n1Ck. (15)
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет
C=C1⋅C2C1+C2, (16)
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям
U1=U⋅C2C1+C2; U2=U⋅C1C1+C2. (17)
6. Энергия электростатического поля конденсатора
W=C⋅U22=Q⋅U2=Q22C. (18)
Удельная энергия электростатического поля (на единицу объема диэлектрика) выражается следующим образом
w=dWdV=E⋅D2=εa⋅E22.
(19)
Общая величина энергии электростатического поля выражается интегралом величины удельной энергии по всему объему диэлектрика конденсатора
W=∫Vεa⋅E22dV. (20)
7. Расчет распределения зарядов в сложных цепях, содержащих источники э. д. с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=ΣQ′. (21)
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑k=1nEk=∑k=1nUC k=∑k=1nQkCk. (22)
Упражнения и задачи
Задача 1.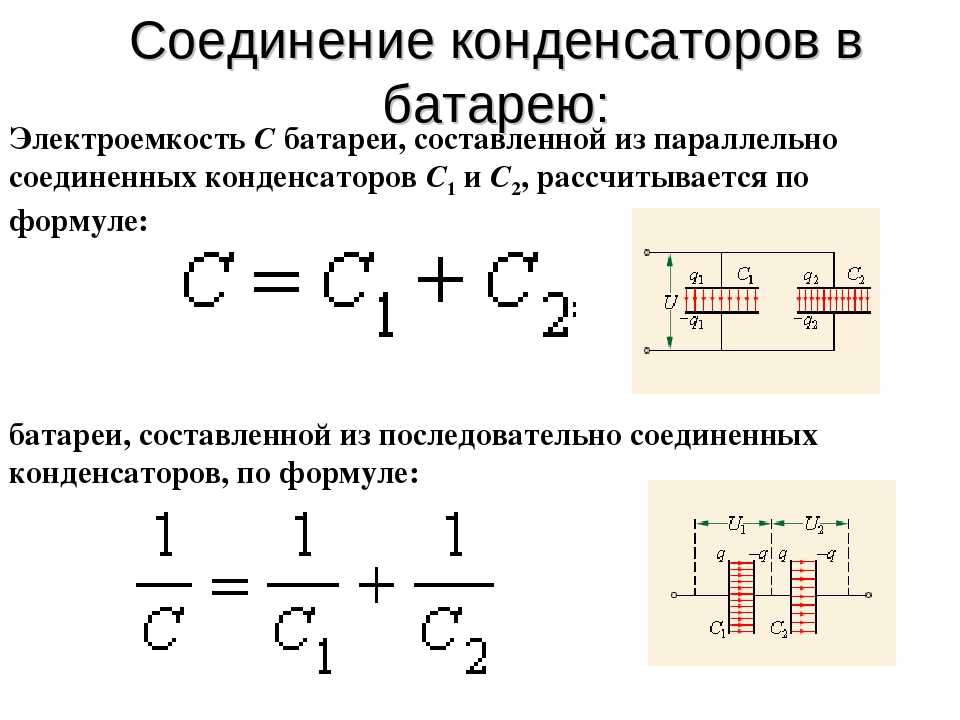
Имеется конденсатор переменной емкости от 500 до 1500 пФ. Указать, какой добавочный конденсатор с минимальным диапазоном переменной емкости следует взять и как его включить, чтобы эквивалентная емкость изменялась от 100 до 250 пФ.
Ответ: 125 — 300 пФ, включить параллельно.
Задача 2. Емкость плоского конденсатора, имеющего слюдяной диэлектрик, равна 44,3 пФ. Площадь каждой пластины конденсатора составляет 25 см2, расстояние между пластинами равно 3 мм.
Чему равна относительная диэлектрическая проницаемость слюды? Принимая пробивное напряжение слюды равным 80 кВ/мм, определить, при каком максимальном напряжении может работать этот конденсатор, чтобы он имел трехкратный запас прочности.
Начертить график изменения потенциала между пластинами конденсатора.
Ответ: εr = 6; Umax = 80 кВ; график падения потенциала вычерчивается по уравнению φ = U·(1 — x/d), здесь U — потенциал положительно заряженной обкладки, принятый равным напряжению конденсатора, d — расстояние между пластинами, x — переменное расстояние до положительной обкладки конденсатора.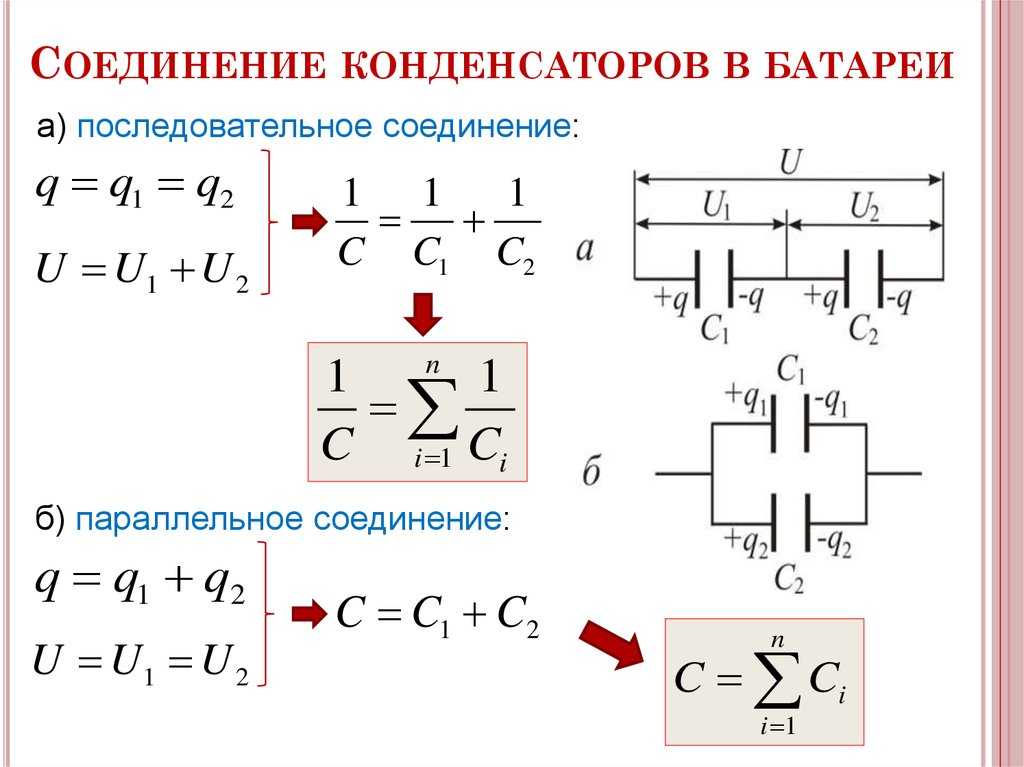
Задача 3. Доказать, что многопластинчатый конденсатор (рис. 1), состоящий из n одинаковых пластин, площадью S каждая, с рас стоянием между двумя соседними пластинами d, с диэлектриком, абсолютная диэлектрическая проницаемость которого ε, имеет емкость, равную
C=εa⋅S⋅(n−1)d.
Рис. 1
Подсчитать, сколько надо взять листов станиоля, каждый площадью S = 40 см2, чтобы получить многопластинчатый конденсатор емкостью 0,5 мкФ при условии, что диэлектриком является парафинированная бумага (εr = 1,8) толщиною 0,05 мм.
Ответ: 393 листа.
Задача 4. Плоский слоистый конденсатор (рис. 2), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
Рис. 2
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C=C1⋅C2C1+C2=εa1⋅Sd1⋅εa2⋅Sd2εa1⋅Sd1+εa2⋅Sd2=εa1⋅εa2⋅Sεa1⋅d2+εa2⋅d1.
Подставляя сюда числовые значения, предварительно заменив εa1 = ε0εr1 и εa2 = ε0εr2, получим
C=ε0⋅εr1⋅εr2⋅Sεr1⋅d2+εr2⋅d1=8,85⋅10−12⋅6⋅7⋅12⋅10−46⋅0,4⋅10−3+7⋅0,3⋅10−3=99⋅10−12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U1=QC1=C⋅Uпрεa1⋅Sd1=εa2⋅d1εa1⋅d2+εa2⋅d1⋅Uпр;U2=QC2=C⋅Uпрεa2⋅Sd2=εa1⋅d2εa1⋅d2+εa2⋅d1⋅Uпр.
Напряженности электростатического поля в каждом слое
E1=U1d1=εa2εa1⋅d2+εa2⋅d1⋅U′пр;E2=U2d2=εa1εa1⋅d2+εa2⋅d1⋅U″пр.
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U′пр=E1⋅εa1⋅d2+εa2⋅d1εa2=49,5 кВ;U″пр=E2⋅εa1⋅d2+εa2⋅d1εa1=27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 5. Вычислить емкость 1 км коаксиального кабеля типа 2,6/9,4. В этом кабеле изоляция осуществлена с помощью полиэтиленовых шайб (εr = 2,2) толщиною a = 2,2 мм, размещенных через равные промежутки b = 25 мм, остальное пространство между шайбами заполнено воздухом (рис.
3). Диаметр жилы d = 2,6 мм, внутренний диаметр наружного провода D = 9,4 мм.
Рис. 3
Указание. Емкость кабеля может быть подсчитана, исходя из того, что отдельные его участки соединены параллельно.
Ответ: 48·10–9 Ф/км = 48 нФ/км.
Задача 6. Силовой одножильный кабель с резиновой изоляцией в свинцовой оболочке марки СРГ имеет сечение жилы 25 мм2. Известно, что наибольшая напряженность электростатического поля в изоляции кабеля не должна превышать 6 кВ/мм. Определить толщину слоя резиновой изоляции, если при испытании кабеля между жилой и оболочкой включают напряжение, равное 10 кВ.
Принимая потенциал жилы кабеля равным U = 10 кВ, построить график падения потенциала в диэлектрике кабеля в зависимости от расстояния до центра кабеля.
Ответ: 2,25 мм. График строится по уравнению φ(r)=U⋅lnr2rlnr2r1.
Задача 7. Цилиндрический конденсатор длиною l = 5 см имеет двухслойный диэлектрик (рис.
4).
Рис. 4
Внутренний радиус r1 = 1 см, внешний — r2 = 3 см, радиус разграничения слоев диэлектриков r3 = 1.5 см. Относительные диэлектрические проницаемости: внутреннего слоя изоляции εr1 = 2, наружного εr2 = 4.
Вычислить емкость конденсатора и начертить кривые изменения напряженностей и потенциалов в каждом из слоев, если конденсатор находится под напряжением U = 2 кВ.
Указание. При помощи теоремы Гаусса находятся напряженности электростатического поля в каждом из слоев
E1=τ2π⋅εa1⋅r; E2=τ2π⋅εa2⋅r,
где τ — линейная плотность заряда (заряд на единицу длины конденсатора). Затем вычисляется напряжение между обкладками конденсатора по формуле
U=∫r1r3E1dr+∫r3r2E2dr.
Отсюда определяется линейная плотность заряда
τ=2π⋅U1εa1lnr3r1+1εa2lnr2r3.
Емкость конденсатора вычисляется по формуле (8). Потенциал φ1 в любой точке области первого слоя диэлектрика (r3 > r > r1) определяется из выражения
φr1−φ1=∫r1rE1dr,
а потенциал φ2 в любой точке области второго слоя (r2 > r > r3) диэлектрика вычисляется из выражения
φr2−φ2=∫r2rE2dr.
В последних формулах φr1 = U — потенциал внутренней обкладки конденсатора, φr2 — потенциал на границе раздела диэлектриков. Внешняя оболочка заземлена: φ2(r2) = 0.
Ответ:
C=2π⋅l1εa1lnr3r1+1εa2lnr2r3;E1(r)=Ur⋅(lnr3r1+εa1εa2lnr2r3); E2(r)=Ur⋅(εa2εa1lnr3r1+lnr2r3);φ1(r)=U⋅(1−lnrr1lnr3r1+εa1εa2lnr2r3); φ2(r)=U⋅εa1εa2lnr2rlnr3r1+εa1εa2lnr2r3.
Пример вывода формулы емкости двухслойного цилиндрического конденсатора при помощи теоремы Гаусса
Ремонт ноутбуков на карте рядом со, карты в красноярске.
Задача 8. Чему равен внешний радиус сферического конденсатора емкостью 20 пФ, внутренний радиус которого 2 см. а относительная Диэлектрическая проницаемость изоляции εr = 3. При каком напряжении конденсатор будет пробит, если пробивное напряжение изоляции равно 15 кВ/мм?
Ответ: 3 см, 100 кВ.
Задача 9. Найти емкость сферического конденсатора, изображенного на рис. 5.
Рис. 5
Даны радиусы R1, R2 и R3; изоляция однородная, ее абсолютная диэлектрическая проницаемость равна ε.
Указание. Данный конденсатор может быть рассмотрен как два Параллельно соединенных конденсатора.
Ответ: C=4π⋅εa⋅R22⋅(R3−R1)(R3−R2)(R2−R1).
Задача 10. К пластинам плоского двухслойного конденсатора приложено напряжение 3 кВ. Площадь пластины равна 5 см2. Толщины первого и второго слоев конденсатора равны соответственно 4 и 6 мм, а диэлектрические проницаемости — 6 и 1.
Построить графики изменения напряженности и потенциала между пластинами в зависимости от расстояния до положительной пластины, потенциал которой принять равным + 3 кв.
Задача 11. Имеется два одинаковых конденсатора переменной емкости. Емкость каждого конденсатора можно плавно изменять от 20 до 200 пФ.
Какие границы изменения емкости можно получить при различном соединении этих конденсаторов между собой?
Ответ: от 10 до 400 пФ.
Задача 12. Определить емкость воздушной двухпроводной линии длиной 2 км, если диаметр проводов равен 3 мм и расстояние между осями проводов составляет 30 см.
Задача 13. Определить емкость однопроводной телеграфной линии длиною 180 км, если диаметр провода равен 3 мм, а средняя высота подвеса провода над землей составляет 7 м.
Начертить кривую зависимости емкости этого провода в функции расстояния от земли.
Ответ: 1,1 мкФ.
Задача 14. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга.
Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W1=C1⋅U22=ε0⋅Sd1⋅U22,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C2=ε0⋅Sd2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т.
е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W2=ε0⋅Sd2⋅U222=ε0⋅S10d1⋅(10U)22=10⋅ε0⋅Sd1⋅U22=10⋅W1.
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W2−W1=9⋅W1=9⋅ε0⋅Sd1⋅U22=2,86⋅10−7 Дж.
Задача 15. Плоский конденсатор с воздушным диэлектриком заряжается от источника электрической энергии с напряжением U.
Определить, как изменится энергия конденсатора, если после отключения его от источника энергии расстояние между обкладками увеличить вдвое.
Ответ: энергия увеличится в два раза.
Задача 16. Плоский конденсатор с диэлектриком из эбонита (εr = 2,5) в виде пластинки толщиной d = 5 см присоединен к полюсам батареи. После зарядки эбонитовая пластинка вынимается.
Как нужно изменить расстояние между обкладками конденсатора, чтобы энергия конденсатора осталась без изменения?
Задачу решить в двух случаях: 1) если конденсатор остается присоединенным к батарее и 2) если конденсатор отключить от батареи.
Ответ: в обоих случаях пластины должны отстоять друг от друга на расстоянии 2 см.
Задача 17. Конденсатор емкостью C1 = 40 мкФ заряжен от сети до напряжения U1 = 220 В; другой конденсатор емкостью C2 = 10 мкФ заряжен от другой сети до напряжения U2 = 110 В.
Положительные зажимы конденсаторов после отсоединения от источников соединяются вместе:
а) Чему равна разность потенциалов между отрицательными зажимами конденсаторов?
б) Чему равны заряды до и после последующего соединения друг с другом отрицательных зажимов конденсаторов?
в) Чему равны напряжения на конденсаторах после соединения их отрицательных зажимов?
г) Чему равна энергия каждого конденсатора до.
и после соединения отрицательных зажимов?
Ответ: а) 110 В, б) до соединения: Q1 = 8800 мкКл, Q2 = 1100 мкКл; после соединения: Q′1 = 7920 мкКл, Q′2 = 1980 мкКл, в) 198 В, г) до соединения: W1 = 0,97 Дж, W2 = 0,06 Дж; после соединения: W′1 = 0,784 Дж, W′2 = 0,196 Дж.
Задача 18. Три последовательно соединенных конденсатора, емкости которых 2, 10 и 15 мкФ, заряжаются от сети с напряжением 120 В. После отключения от сети конденсаторы разъединяются друг от друга без потери заряда. Если затем конденсаторы соединить параллельно, то чему будет равно напряжение на их зажимах?
Ответ: 20 В.
Список литературы
1. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. — М.: Гардарики, 2001.– 317 с.
2. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: в 3-х тт.: Учебник для вузов. Том 3. –4-е изд. — СПб.: Питер, 2003. — 377 с.
3. Купалян С.Д. Теоретические основы электротехники / Под ред. Г.И. Атабекова. — М.-Л.: Госэнергоиздат, 1963. — ч. 3. Электромагнитное поле. — 112 с.
4. Теоретические основы электротехники. т. 2. Нелинейные цепи и основы теории электромагнитного поля. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. — М.: Высш. шк., 1976. — 383 с.
5. Поливанов, К.М. Теоретические основы электротехники: в 3-х ч. / К.М. Поливанов. ч. 3: Теория электромагнитного поля. — М.: Энергия, 1969. — 352 с.
6. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учебное пособие для вузов / Бессонов Л.А., Демидова И.Г. и др.; Под ред. Л.А. Бессонова. — М., Высшая школа, 2000. — 528с.: ил.
7. Колли Я.Н. и др. Задачник по теоретическим основам электротехники (теория поля).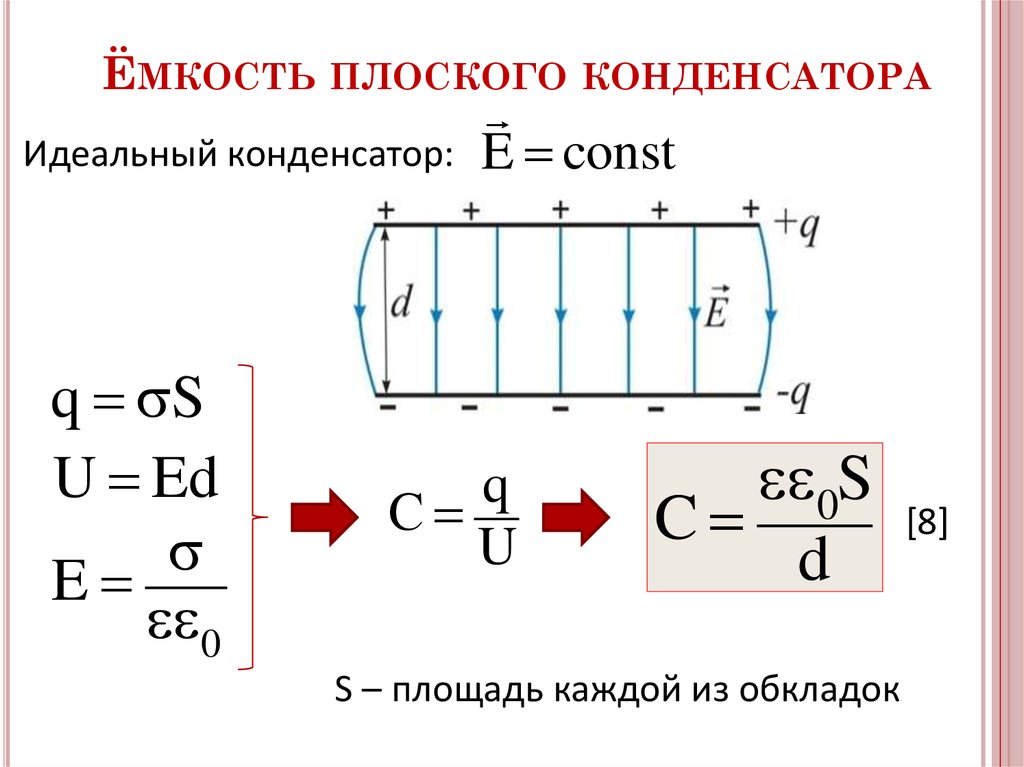
Уч. пособие для вузов. Под ред. Поливанова К.М. — М., «Энергия», 1972.
8. Ионкин П.А. Сборник задач и упражнений по теоретическим основам электротехники: Учебное пособие. — М., Энергоиздат, 1982. — 768с.
9. Татур Т.А. Основы теории электромагнитного поля: Справочное пособие. — М.: Высш. шк., 1989 . — 270 с.
электрическая постоянная, емкость конденсатора, электроемкость, емкость плоского конденсатора, емкость цилиндрического конденсатора, сферический конденсатор, емкость двухпроводной линии, емкость однопроводной линии, емкость коаксиального кабеля
домашнее задание и упражнения — Найти емкость конденсатора
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 1к раз
$\begingroup$
Дано: Рассмотрим конденсатор, подключенный к батарее напряжением V .
Пусть конденсатор имеет площадь А и расстояние между пластинами L. Предположим, что
конденсатор имеет слой линейного диэлектрика (с диэлектрической проницаемостью κ, так что
ε = κε0) толщиной L/2 на нижней пластине.Я обнаружил, что емкость равна $C=\frac{2\kappa\epsilon_0 A}{L}$. Я был прав насчет разделительного расстояния? В более распространенных примерах конденсатора они утверждают, что пластины плоские, между ними ничего нет. В этом случае высота линейного диэлектрика равна половине общего расстояния между пластинами. Правильно ли я использую оставшееся свободное пространство, а именно $L/2$, в качестве разделительного расстояния в уравнении? Для справки:
$$C=\frac{\kappa \epsilon_0 A}{d}$$
- домашние задания и упражнения
- емкость
- напряжение
$\endgroup$
$\begingroup$
Мгновенная проверка, показывающая, что ваш ответ неверен: установите $\kappa = 1$, как если бы диэлектрика не было, и вы не восстановите формулу для параллельных пластин для зазора $L$.
Как решить эту задачу:
Пусть напряжение на конденсаторе равно $V$, а напряжение сверху и снизу равно $V_t$ и $V_b$ соответственно, тогда $$V=V_t+V_b,$$ что подразумевает, что $$1/C=1/C_t+1/C_b$$, поскольку $V=Q/C$.
Таким образом, эта система состоит из двух последовательных конденсаторов. Один конденсатор — это верхний зазор, а другой — нижняя часть. Используйте формулу для пластинчатых конденсаторов дважды, с расстоянием $L/2$ в обоих случаях, затем получите общую емкость, используя формулу для двух последовательно соединенных конденсаторов. Задействована некоторая алгебра.
Вы можете снова проверить полученный ответ, установив $\kappa=1$ и посмотрев, восстановите ли вы обычную формулу тарелки.
$\endgroup$
5
$\begingroup$
Поле $\mathbf{D}$ между пластинами (как обычно, без учета эффекта интерференции) однородно и нормально к плоскости пластин (для простоты предположим, что в направлении z) и определяется выражением
$$\ mathbf{D} = \frac{Q}{A}\hat{\mathbf{z}}$$
, где пластины имеют заряд $Q$ и $-Q$ соответственно.
Электрическое поле (между пластинами) внутри диэлектрика равно
$$\mathbf{E_\kappa} = \frac{\mathbf{D}}{\kappa \epsilon_0}$$
а электрическое поле (между пластинами) в воздухе равно
$$\mathbf{ E} = \frac{\mathbf{D}}{\epsilon_0}$$
Таким образом, разность потенциалов между пластинами равна
$$V = \left(\frac{L}{2}\mathbf{E_ \ kappa} + \ frac {L} {2} \ mathbf {E} \ right) \ cdot \ hat {\ mathbf {z}} = \ left (\ frac {L} {2} \ frac {\ mathbf {D }}{\каппа\epsilon_0} + \frac{L}{2}\frac{\mathbf{D}}{\epsilon_0}\right)\cdot\hat{\mathbf{z}} = \left(\frac {L}{2}\frac{Q}{A\kappa\epsilon_0} + \frac{L}{2}\frac{Q}{A\epsilon_0} \right)$$
Тогда емкость равна
$$C = \frac{Q}{V} = \frac{1}{\frac{L/2}{A\kappa\epsilon_0} + \frac{L/2}{ A\epsilon_0}} = \frac{1}{\frac{1}{C_1}+ \frac{1}{C_2}}$$
, что является формулой для последовательно соединенных конденсаторов.
$\endgroup$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Преобразование емкости в импеданс и взаимосвязь между ними
Ключевые выводы
● Узнайте о формулах преобразования емкости в импеданс.
● Получите более полное представление о том, как взаимодействуют емкость и импеданс.
● Узнайте больше о важности импеданса при анализе цепей переменного тока.
Емкость и ее отношение к импедансу
Область электроники содержит различные параметры, которые измеряют, помогают и влияют на функциональность, а также на производительность каждого электронного устройства. Эти параметры влияют на исходные и окончательные проектные решения.
Такие параметры, как емкость и импеданс, должны оставаться в допустимых проектных пределах, иначе даже самый точный проект не сможет обеспечить желаемый функциональный результат.
Кроме того, бывают случаи, когда требуется преобразование одного параметра в эквивалент другого. Одно такое преобразование, такое как емкость в импеданс, является требованием детального анализа цепи переменного тока.
Конденсаторы и емкость
Компонент, связанный с емкостью, — это, конечно же, конденсатор, а способность системы накапливать электрический заряд называется емкостью. В физике это отношение изменения электрического заряда в системе к изменению ее электрического потенциала. В любом случае стандартной единицей измерения емкости является фарад.
Эти пассивные электронные компоненты накапливают энергию в виде электростатического поля. В чистом виде конденсатор состоит из двух проводящих пластин, разделенных изолирующим материалом, называемым диэлектриком. Емкость конденсатора прямо пропорциональна площади поверхности его пластин и обратно пропорциональна расстоянию между этими пластинами. Однако чистая емкость также зависит от диэлектрической проницаемости вещества, разделяющего пластины.
При преобразовании импеданса конденсатора мы используем формулу Z = -jX. Имейте в виду, что реактивное сопротивление является более однозначным параметром и определяет, какое сопротивление будет иметь конденсатор на определенной частоте. Как указывалось ранее, знание импеданса необходимо для детального анализа цепи переменного тока.
Катушка индуктивности и импеданс
Понимание импеданса в цепи переменного тока
Импеданс — это активное сопротивление электрической цепи или компонента переменному току из-за комбинированного воздействия реактивного сопротивления и омического сопротивления. Другими словами, импеданс является расширением принципов сопротивления в цепях переменного тока. Мы также определяем импеданс как любое препятствие или меру сопротивления электрического тока потоку энергии при подаче напряжения.
Более техническое определение — это полное противодействие электрической цепи потоку переменного тока одной частоты.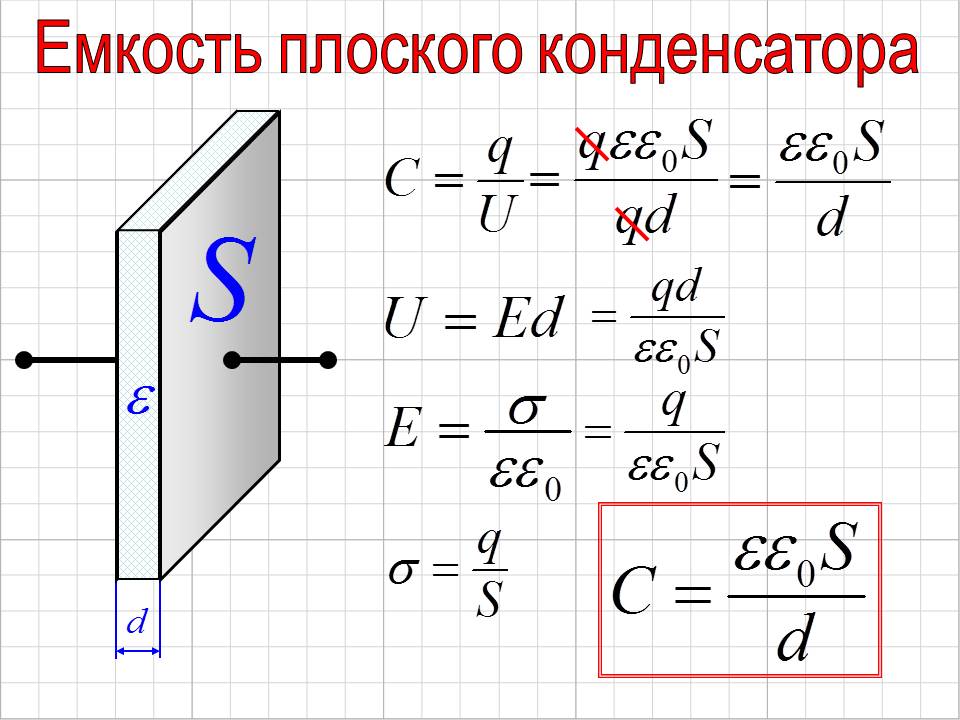
Таким образом, это комбинация реактивного сопротивления и сопротивления, которую мы измеряем в омах и обозначаем символом Z.
Реактивное сопротивление (X) выражает сопротивление компонента переменному току, тогда как импеданс (Z) указывает сопротивление компонента обоим переменного и постоянного тока. Мы показываем его как комплексное число с помощью следующей формулы: Z = R + jX. В идеале импеданс резистора равен его сопротивлению. В этих условиях реальная или действительная часть импеданса представляет собой сопротивление, а мнимая часть равна нулю или нулю.
Преобразование емкости в импеданс
Существуют калькуляторы емкостного реактивного сопротивления, которые позволяют определить полное сопротивление конденсатора при условии, что у вас есть значение его емкости (C) и частота сигнала, проходящего через него (f). Вы вводите емкость в фарадах, пикофарадах, микрофарадах или нанофарадах и частоту в единицах ГГц, МГц, кГц или Гц. Например, емкость в 2 фарад на частоте 100 герц даст импеданс 0,0008 Ом.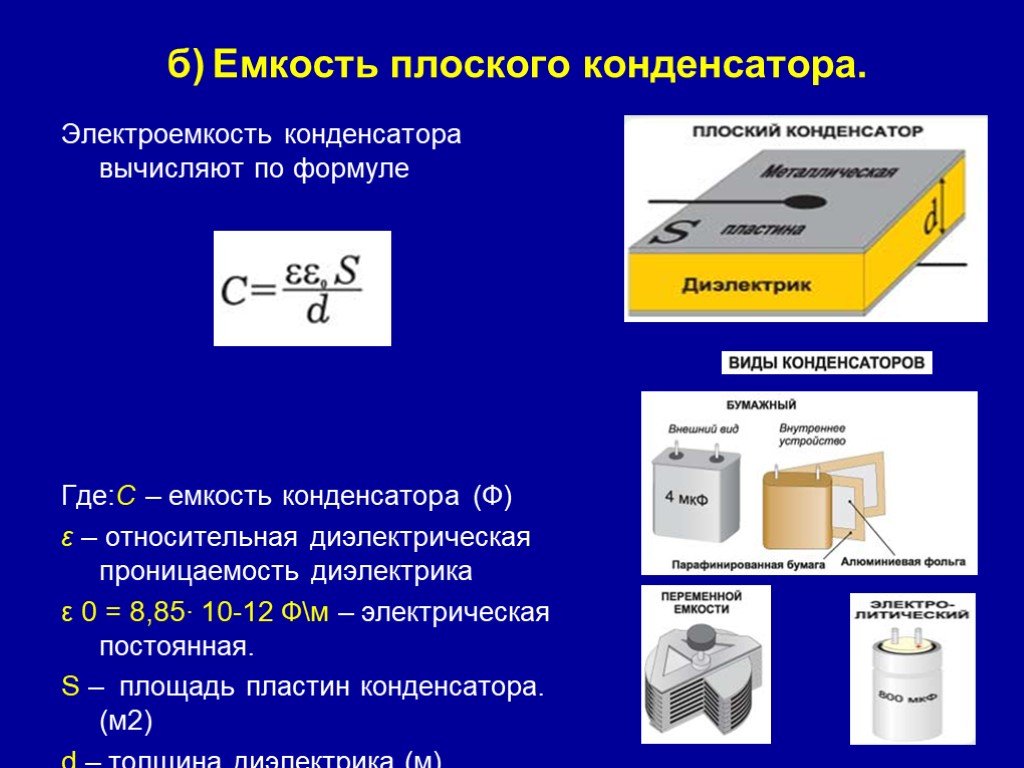
Ниже приведена формула, необходимая для расчета вышеуказанных значений:
Теперь мы понимаем параметры идеального резистора, когда его импеданс равен его сопротивлению. Однако полное сопротивление идеального конденсатора равно величине его реактивного сопротивления, хотя эти два параметра не идентичны. Мы выражаем реактивное сопротивление как обычное число в омах, а полное сопротивление конденсатора представляет собой реактивное сопротивление, умноженное на -j. Это соответствует следующей формуле: Z = -jX . В этом контексте термин -j представляет фазовый сдвиг на 90 градусов, который возникает между током и напряжением в чисто емкостной цепи.
Используя уравнение преобразования
Используя приведенное выше уравнение (XC = 1/ωC = 1/2πƒC), вы можете получить реактивное сопротивление конденсатора, а для преобразования его в импеданс конденсатора вы можете использовать формулу Z = -jX .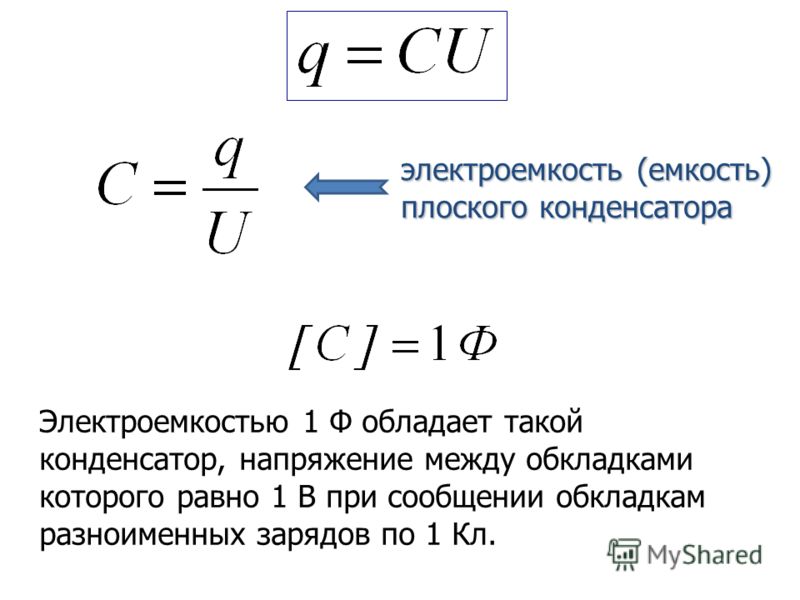
Помните, что реактивное сопротивление является более очевидным значением параметра, и оно определяет, какое сопротивление имеет конденсатор на определенной частоте.
Из приведенных выше уравнений видно, что реактивное сопротивление конденсатора обратно пропорционально емкости и частоте. Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Эта обратная связь между частотой и реактивным сопротивлением облегчает использование конденсаторов для блокирования низкочастотных составляющих сигнала и одновременного пропускания высокочастотных составляющих.
Емкость в цепи переменного тока легко различима, но для тщательного анализа цепи переменного тока требуется импеданс. Логически это означает, что первостепенное значение имеет более глубокое понимание того, как взаимодействуют эти два параметра.
Обмотка индуктора из медного провода
Наличие функциональных и надежных схем зависит от наличия подходящего набора программного обеспечения для проектирования и анализа, помогающего создавать схемы, имитационные модели и посадочные места.
