Электричество и магнетизм

При внесении незаряженного проводника во внешнее электрическое поле свободные заряды начинают двигаться и через небольшое время приходят в равновесие. Создается стационарное распределение зарядов, при котором на одной стороне проводника образуется избыток отрицательных зарядов, а на другой — избыток положительных. Это явление называется электростатической индукцией (рис. 2.5).

Рис. 2.5. Электростатическая индукция

Поле индуцированных (появившихся на поверхности проводника) зарядов полностью компенсирует внутри проводника внешнее поле. В противном случае внутри проводника происходило бы движение электри­ческих зарядов, и распределение не было бы стационарным. Итак, при равновесном состоянии суммарное поле (внешнее и индуцированных зарядов) внутри проводника равно нулю. Поэтому в отношении суммарного поля справедливы выводы, сделанные нами ранее для заряженных проводников в отсутствии внешнего поля.

Видео 2.8. Электростатическая индукция «natürlich».

В частности, электрическое поле будет отсутствовать во внутренней полости в материале проводника (рис. 2.6). На свойстве проводников экранировать внешние поля (не пропускать их внутрь области, окруженной проводником) основывается электростатическая защита от действия внешних электростатических полей (рис. 2.7).

Рис. 2.6. Появление индуцированных зарядов на поверхности проводника
при воздействии на него внешнего электрического поля

 

Рис. 2.7. Электростатическая защита. Поле в металлической полости равно нулю

Так, автомобиль является безопасным убежищем во время грозы, и не потому, что резина на колесах изолирует его от земли. Здесь мы должны быть благодарны теореме Остроградского — Гаусса. Однако следует подчеркнуть, что замкнутый полый проводник экранирует полость внутри себя только от внешних зарядов и полей.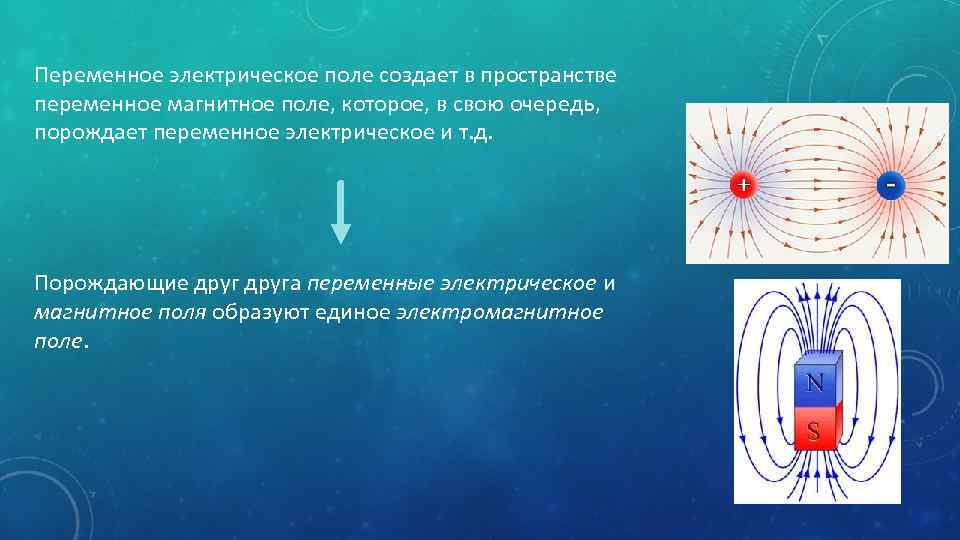

Если внести заряды внутрь полости, то там появится электрическое поле при том, что в самом проводнике поле, по-прежнему будет равно нулю.

Далее, суммарное поле вблизи проводника перпендикулярно его поверхности и равно

(2.3)

где  — плотность индуцированных зарядов (мы предполагаем, что про­водник в целом не заряжен).

На практике приходится решать следующую задачу. Дано некоторое внешнее поле. В него вносится проводник заданной формы. Надо найти распределение индуцированных на нем зарядов и те изменения суммарного поля вне проводника, к которым они приводят. Плотность зарядов при заданном потенциале проводника определяется кривизной поверхности:  растет с увеличением положительной кривизны (выпуклости) и убывает с увеличением отрицательной кривизны (вогнутости) (рис. 2.8).

Рис. 2.8. Электрическое поле (силовые линии и эквипотенциальные поверхности)
  незаряженной сферы вблизи точечного электрического заряда

Задача.  Дана сферическая металлическая оболочка с внутренним и внешним радиусами   и  соответственно.  В центр полости помещен заряд . Найти электрическое поле и потенциал системы, а также распределение зарядов на поверхности оболочки (рис. 2.9).

Рис. 2.9.   Электрическое поле положительного заряда  окруженного металлической оболочкой

Решение.   Благодаря сферической симметрии заряды расположатся на поверхностях оболочки с постоянной поверхностной плотностью:  — на внутренней и  — на внешней сторонах. Рассмотрим сначала поле внутри  оболочки.   Проведем воображаемую сферическую поверхность радиусом   Внутри нее находится только заряд . Следовательно, поле в полости оболочки будет таким же, как и для изолированного заряда . Возьмем теперь поверхность радиусом , где  . Так как поле в металле отсутствует, равен нулю поток через нашу поверхность. Это значит, что полный заряд внутри нее равен нулю. Он складывается из заряда  и полного заряда на внутренней поверхности, который, стало быть, равен . С другой стороны, заряд на вну­тренней поверхности можно определить как  , откуда следует  . Металлическая оболочка в целом была незаряженной, поэтому полный заряд , появившийся на ее внутренней поверхности, должен быть скомпенсирован полным зарядом , возникшим на внешней поверхности оболочки (сохранение электрического заряда). Поэтому плотность заряда  . Проведем наконец воображаемую поверхность вне металлической оболочки  . Полный заряд внутри поверхности складывается из 1) заряда , 2) заряда  на внутренней поверхности оболочки и 3) заряда  на ее внешней стороне. Поэтому внутри воображаемой поверхности находится заряд . Это значит, что электрическое поле вне оболочки снова совпадает с полем одиноч­ного точечного заряда .

Итак, мы установили, что электрическое поле направлено по радиус-вектору  и по абсолютной величине равно

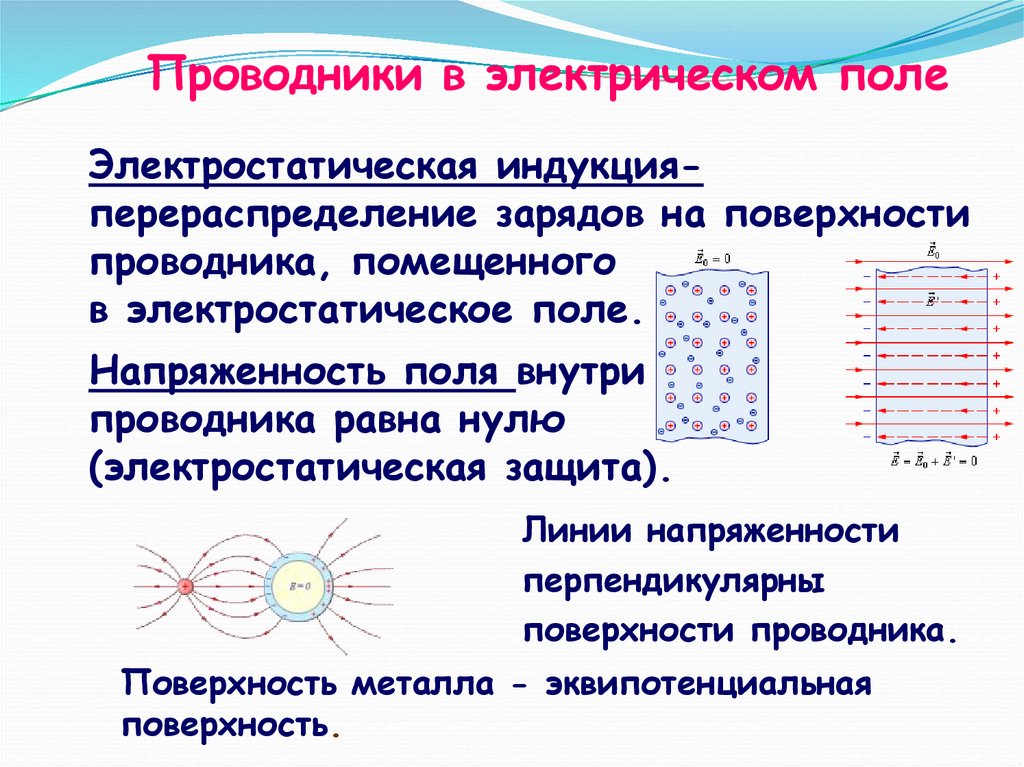
(2.4)

Нам осталось найти потенциал поля в различных точках системы. Вне оболочки потенциал совпадает с потенциалом точечного заряда:   На внешней поверхности оболочки потенциал ра­вен   Поскольку внутри оболочки поля нет, потенциал сохраняет это значение во всех точках внутри металла. Вну­три полости потенциал опять совпадает с потенциалом точечного за­ряда. Поскольку последний определен с точностью до константы, имеем  Значение этого потенциала на внутренней поверхности оболочки  должно совпасть со значением потенциала  на внешней оболочке. Отсюда можно найти постоянную  

Получаем в итоге:

(2. 5)

Графики зависимости напряженности поля и потенциала представлены на рис. 2.10.

 

Рис.  2.10.   Напряженность и потенциал электрического поля заряда q, 
окруженного металлической оболочкой с внутренним радиусом  и внешним радиусом 
Пунктирные линии соответствуют характеристикам поля одиночного заряда в отсутствие оболочки

 

Дополнительная информация 

http://e-lib.gasu.ru/eposobia/shitov1/R_1_3.html  — атмосферное электричество, грозовая активность на Земле;

http://elf.gi.alaska.edu/  — высотные атмосферные разряды;

http://www.spritesandjets.com/index.htm — различные типы высотных разрядов;

http://vlf.stanford.edu/ —  лаборатория изучения атмосферного электричества;

http://www.news-ingeneers.ru/softi32.html — электростатическая защита;

http://www.lii.ru/issledovaniya_i_zawita_letatel_nyh_apparatov_ot_molnii_i_statiche_skogo_elektrichestva_s_razdelom_poyas. html  — защита летательных аппаратов от молний и статического электричества.

Электрическое поле проводника с током

Details

26 October 2016

Господа, доброе всем время суток! Сегодня коротенечко рассмотрим затронутый в статье про силу тока вопрос, почему же лампочка вспыхивает мгновенно при столь малой скорости направленного движения заряженных частиц. Речь пойдет, как уже многие догадались, об

электрическом поле проводника с током. Мы попытаемся разобраться как это поле выглядит внутри и снаружи проводника и рассмотрим механизм его образования. Итак, погнали!

На самом деле мы сейчас рассмотрим довольно нетривиальные вещи. Дело в том, что когда речь заходит про электрическое поле часто возникает непонимание физики процессов и бесконечные споры о том, что же это такое, особенно если имеют место быть движущиеся заряды. В ход идет мощная артиллерия из целого каскада уравнений Максвелла и прочих дивергенций, однако и это не всегда приводит к однозначному пониманию происходящего.

Скажу честно, сначала я вообще не хотел писать статью на данную тему и затрагивать рассмотрение этого вопроса, тем более, что в инженерной практике он не имеет большого значения. Однако, поразмыслив, все-таки я решил кратко рассмотреть его для полноты картины, разумеется, на максимально простом уровне.

Прежде всего зададимся вопросом – а что же нужно для того, чтобы имел место электрический ток? По сути мы уже ответили на этот вопрос в статье про  силу тока. Нам нужно наличие свободных заряженных частиц

– электронов или ионов, а также некоторой силы, вызывающей это упорядоченное движение. Эта сила – электрическое поле. Да, именно благодаря электрическому полю и возникает электрический ток. 

Что именно такое электрическое поле, как оно создается, чем характеризуется и какие законы описывают поведение зарядов в нем мы рассмотрели вот в этой статье. На всякий случай еще раз напомню, что электрическое поле создается электрическими зарядами.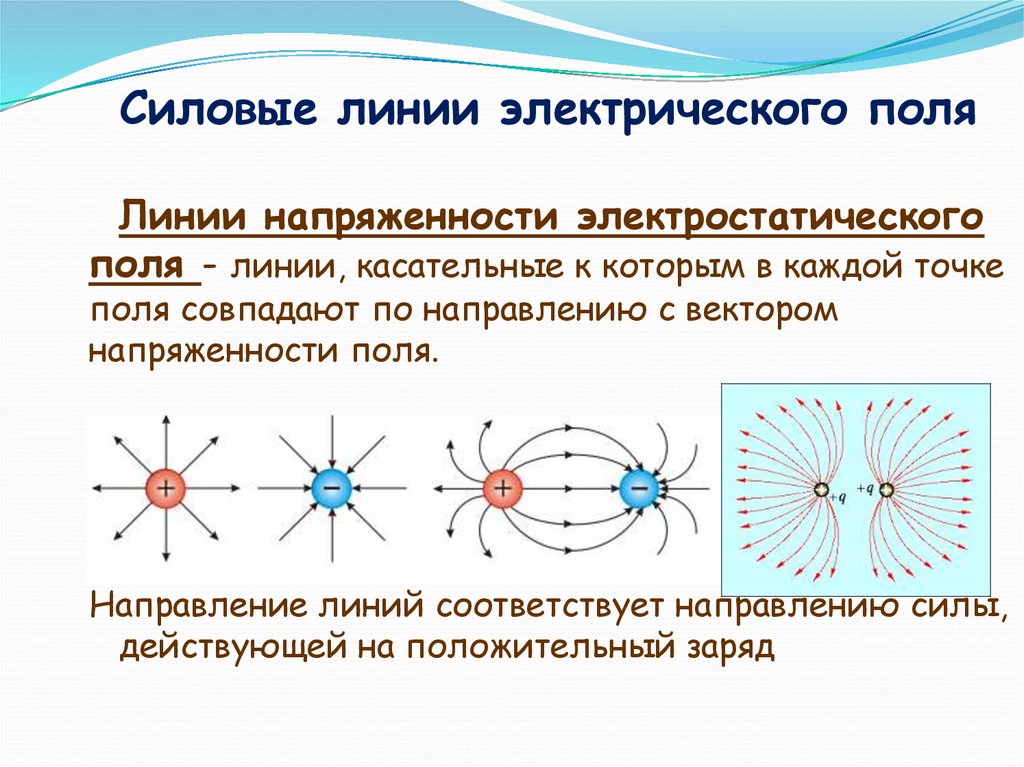

Итак, поле создается зарядами. Ок. Как же в итоге возникает ток в проводнике? Рассмотрим цепь, состоящую из проводника с нагрузкой и батарейки. Батарейка создает некоторое напряжение. На минусовой клемме батареи, очевидно, имеет место избыток электронов. Это минус и по определению там электронов больше, чем на плюсе. Эти заряды создают вокруг себя поле. Но что делать, если длина проводника несколько километров? Ведь поле затухает пропорционально квадрату расстояния, как мы помним из закона Кулона. При замыкании цепи эти электроны с минусовой клеммы начинают действовать на близлежащие электроны в проводнике, толкать их в стороны. Часть электронов будет двигаться вдоль оси проводника. Часть электронов достигнет поверхности проводника и скопится на ней. Образуется типа поверхностного заряда. Этот поверхностный заряд будет создавать поле в следующей участке проводника. Ну и так далее. Распространение поверхностного заряда иллюстрирует рисунок 1.

Рисунок 1 – Распространение поверхностного заряда

Дело в том, что распространяться этот самый заряд, ну, то есть, по сути поле, будет со скоростью света, которая, как известно, равна примерно 300 000 км/с. Очень быстро. Поэтому и загорится лампочка почти мгновенно. Это поле называется стационарным. Оно неизменно в течении времени. Да, заряды движутся. Но на их место приходят новые, точно такие же по величине.

Господа, как мы все помним из вот этой вот статьи для визуализации электрического поля и его наглядного представления принято использовать силовые линии. Как же выглядят силовые линии внутри проводника с током и снаружи от него? Ответ таков: внутри проводника с током силовые линии параллельны оси проводника, а снаружи — идут под углом к нему. Это показано на рисунке 2.

Рисунок 2 – Силовые линии проводника с током

Почему это так? Разберемся сначала с ситуацией вне проводника. Как мы уже выяснили на проводнике с током, на его поверхности, содержится поверхностный заряд. Причем (господа, внимание!),  этот заряд плавно уменьшается по длине проводника. Ясно, что рядом с минусом будет намного больший избыток электронов, чем рядом с плюсом, на котором, наоборот, их недостаток.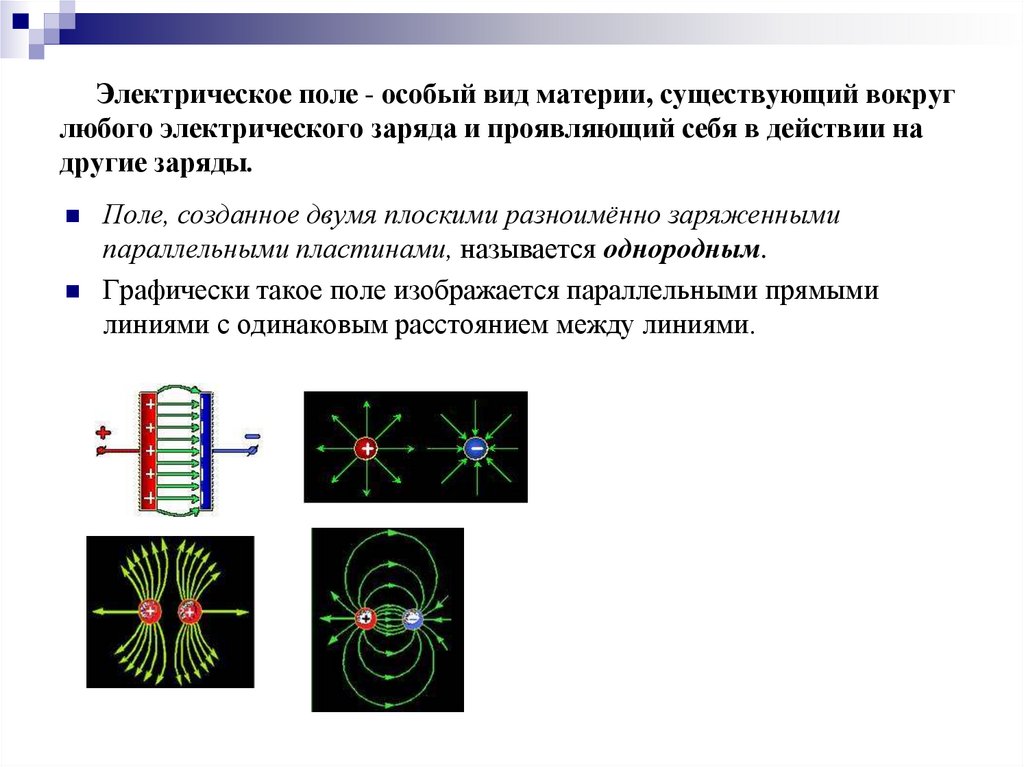   То есть есть продольная составляющая вектора напряженности. Кроме того, очевидно, есть составляющая вектора напряженности, перпендикулярная поверхности проводника. Поверхностный заряд ведь светит своей напряженностью вокруг себя. Итого, по правилу сложения векторов получаем, что вне проводника поле направлено под углом к нему. Господа, для тех, кто вдруг забыл, напоминаю правило сложения векторов. Оно показано на рисунке 3.

Рисунок 3 – Правило сложения векторов

Внутри же проводника создаются такие условия, что силовые линии напряженности направлены вдоль его оси. Почему это так? Ответ может быть такой. Очевидно, что в проводнике с током сила тока одинакова по всей длине проводника. Кто не верит — амперметр в лапки и вперед измерять. Это значит, что по всей длине проводника скорость зарядов одна и та же. Господа, это неопровержимо выведено в нашей самой первой статье про  силу тока. Если скорость одна и та же, то одинакова и сила, с которой поле действует на заряды. А раз одинакова сила, то будет одна и та же напряженность поля во всех сечениях проводника. Сила же зависит напрямую от напряженности! Причем одинакова сила будет при любой длине проводника. Это свидетельствует о том, что линии напряженности в проводнике параллельны оси проводника.

Уфф! Господа, чуть передохните и прочитайте предыдущий абзац еще разок. Знаю, там одно, цепляется за другое, потом другое за третье и в конце уже не помнишь, с чего начиналось. В таком случае лучше отдохнуть и перечитать еще разок перед тем, как читать дальше. Отдохнули? Тогда едем дальше!

Остался еще один скользкий вопрос. Как же распределена плотность тока в проводнике с постоянным током? По идее она должна быть у поверхности чуть больше: там ведь существует поверхностный заряд, то есть более высокая концентрация электронов. Однако в литературе я нигде не нашел ни подтверждения, ни опровержения данному доводу. Все почему-то обходят этот вопрос.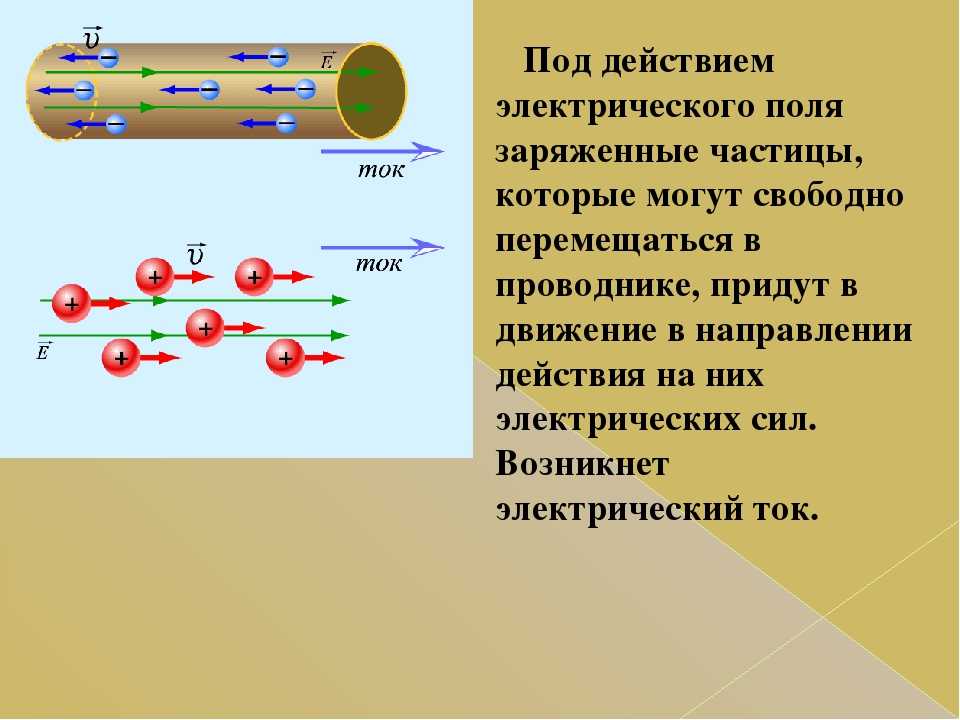 Рассмотрению подлежит только распределение плотности  в случае переменного тока, скин эффект там и прочее. Но здесь ведь это ни при чем. Здесь может быть только кулоновское расталкивание зарядов ближе к поверхности проводника… Господа, если у кого есть соображения по этому поводу, пожалуйста, напишите в комментарии.  Но что можно сказать однозначно, даже если и расталкивание есть, то оно минимально. На практике им пренебрегают, считая, что постоянный ток целиком, с одинаковой плотностью, течет по всему сечению проводника.

Но вернемся еще раз к вопросу, почему ток в цепи возникает практически мгновенно. Что бы стало совсем понятно, приведем аналогию из области гидравлики. Не пугайтесь, господа. Я в тоже в этой прекрасной науке мало шарю. Только если на практическом уровне: починить кран, заменить трубу, прикрутить вентиль. Так что оставьте ваши страхи, никаких уравнений Навье-Стокса и прочих Эйлеров не будет!  Возьмем водопровод в вашем доме. Вообще, как ни странно, очень многие вещи в электричестве можно лучше понять на примере этого самого водопровода. По сути протекание тока в проводниках чем-то схоже с протеканием воды в трубах.

Итак, водопровод наполнен водой (проводник наполнен свободными электронами). В системе водопровода есть давление (к проводнику приложено напряжение, в проводнике есть электрическое поле). Мы открываем кран (замыкаем электрическую цепь). Из крана начинает течь вода. Внимание, господа! В момент открывания крана начинает течь не та вода, которая на ближайшей водокачке. А та, которая уже в трубах, та, которая рядом с вами, и начинает она течь мгновенно (лампочка загорается мгновенно) при открытии крана, не смотря на то, что скорость течения воды может быть небольшой (мы помним наши выводы про скорость движения электронов).

Аналогия полнейшая, как мы видим. А что это значит – это значит, что даже если вы электронщик/электрик, сантехнику знать лишним тоже не будет! Эти две области имеют в себе больше общего, чем может показаться на первый неискушенный взгляд!

Итак, мы рассмотрели вопрос что же вызывает протекание тока в проводнике, объяснили, почему ток возникает во всей цепи практически мгновенно не смотря на крайне низкую дрейфовую скорость перемещения зарядов и показали, как формируется поле в проводнике с постоянным током. Господа, полагаю, на сегодня достаточною. Удачи вам всем и до скорых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Электрические поля: определение, напряженность, уравнение

Поле генерируется источником в пространстве вокруг него. Электрически заряженная частица создает электрическое поле. Протоны и электроны обладают электрическими полями и на определенном расстоянии притягивают или отталкивают другие заряженные частицы.

Определение электрического поля

Силы являются векторами, как и электрическое поле. E — векторная величина, измеряемая в Ньютонах/Кулонах или вольтах/м:

Здесь F и q — соответственно сила источника и заряд, к которому приложена эта сила. Если мы выразим силу через электрическое поле, результат будет:

Для изолированного положительного заряда электрическое поле вокруг него распространяется радиально наружу от заряда во всех направлениях, в то время как для изолированного отрицательного заряда электрическое поле вокруг него направлено радиально внутрь.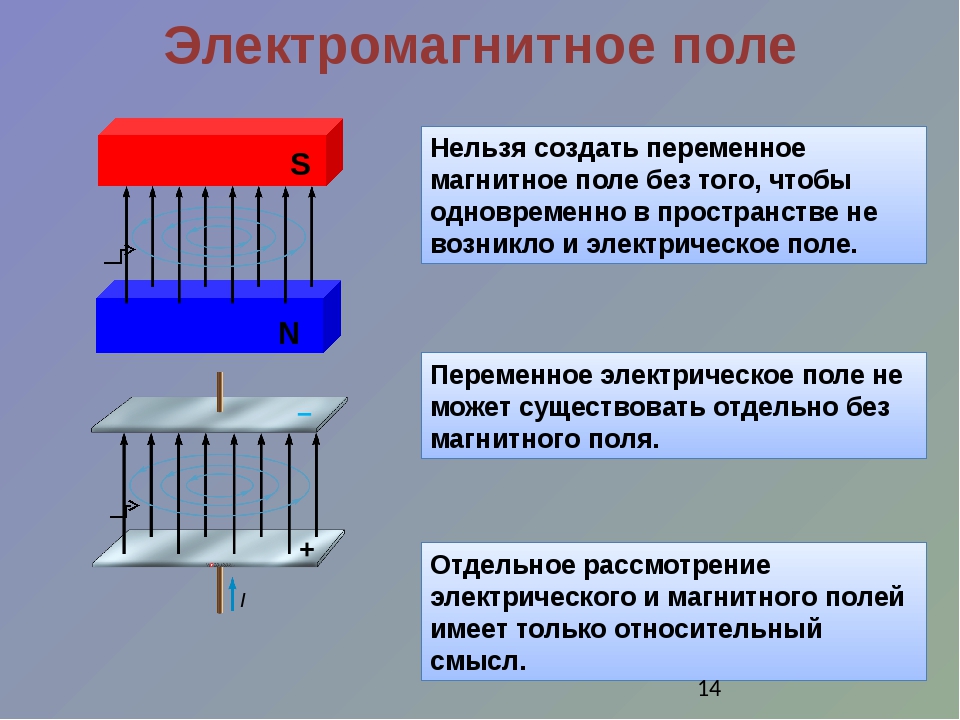 Когда дело доходит до сил, которые испытывают эти заряды, общее правило состоит в том, что положительные заряды испытывают силу в направлении электрического поля, а отрицательные заряды испытывают силу, противоположную направлению поля.

Закон Кулона и поле заряда 9-2.

Рис. 1. Электрическое поле частицы. Источник: StudySmarter.

Электрическое поле зависит от расстояния точки приложения от источника самого поля и от интенсивности заряда. В случае одиночной частицы мы находим эквипотенциальные концентрические сферы, где напряженность поля одинакова.

Электрическое поле множественных зарядов

При правильной корректировке терминов формула, используемая для описания одиночного заряда, также может быть использована для расчета более сложных случаев. В случае нескольких зарядов мы должны учитывать их влияние на точку приложения. Это рассчитывается путем сложения вклада каждого заряда.

Рис. 2. Поле двух частиц в некоторой точке на расстоянии равно сумме полей на этом расстоянии. Источник: StudySmarter.

Как видите, большой разницы с предыдущим примером нет. N здесь представляет собой общее количество зарядов, но вместо того, чтобы вычислять это один раз, вам нужно сложить результат этой формулы для всех зарядов (N). Обратите внимание, что важно соблюдать направление каждого вклада при выполнении векторной суммы.

Электрическое поле распределенных зарядов

Рассмотрим несколько более сложную ситуацию. Это также более полезно, поскольку нечасто можно найти движущиеся запасные частицы. Вместо этого рассмотрите предметы определенной формы и объема. Благодаря принципу суперпозиции здесь мы рассматриваем однородную плотность заряда ρ вместо заряда отдельной частицы. Расчет электрического поля заключается в выполнении интеграла, учитывающего распределение заряда внутри объекта:

Исходя из этого результата, можно пойти еще дальше и рассмотреть, например, неоднородную плотность заряда. Возьмем источник, заряд которого меняется по одному или нескольким измерениям в пространстве и по всему объему. Чтобы назвать эту плотность, мы добавляем размеры, от которых она зависит, между скобками. Например, случай плотности заряда, который изменяется в измерении x, представлен как ρ (x). Исчисление будет более сложным без какой-либо разницы в концепции.

Электрический потенциал

Иногда вам нужно рассчитать, что происходит в электрическом поле. Движение заряда в электрическом поле не такое же, как вне электрического поля. Кроме того, иногда в пространстве электрического поля есть и другие заряды, и интересно посмотреть, что между ними происходит. Электрический потенциал позволяет провести эти расчеты.

От электрического поля к электрическому потенциалу

Электрический потенциал – это количество энергии, необходимое для перемещения заряда в электрическом поле из точки А в точку В без потери или преобразования энергии. Чтобы определить электрический (или электростатический) потенциал, нам нужна точка отсчета. Первый является источником электрического поля. В случае одиночной частицы с пробным зарядом, погруженной в ее поле, потенциал равен:

Прежде всего следует отметить, что электрический потенциал является скалярной величиной. Более того, даже если формула очень близка к формуле силы, мы должны учитывать радиус, а не ее квадратную степень. Наконец, что важно, это количество зависит от тестового заряда. Нам нужно обратиться к абсолютной ссылке; таким образом, определение V:

. Рассмотрим две точки и разность между ними примем за разность потенциалов ΔV:

. становится меньше. Чем дальше b отдаляется от a, тем больше 1/rb приближается к нулю, вплоть до того, что b настолько далеко, что мы можем не рассматривать этот термин в скобках, а определение Va — Vb совпадает с определением U. Единица измерения мерой потенциала является вольт.

Электрические поля (только для A2) — ключевые выводы

• Поле генерируется источником в пространстве вокруг него. Электрическое поле создается электрически заряженной частицей.
• Источник, генерирующий электрическое поле, может быть дискретным или непрерывным.
• Эквипотенциальные поверхности поля — это поверхности, на которых воздействие самого поля на пробный заряд одинаково.
• Перемещение заряда в электрическое поле требует энергии, а количество энергии, необходимое для перемещения из точки А в точку В, называется электрическим потенциалом.
• Когда речь идет о потенциале между двумя точками, одна из них часто описывается как находящаяся в бесконечности, так что ее величина не зависит от заряда движущейся частицы.

электромагнетизм — Откуда берется электрическое поле в замкнутой цепи?

$\begingroup$

Что я понимаю до сих пор:

• Электрический потенциал (напряжение) – это потенциальная энергия, которой обладает заряд из-за его расположения в электрическом поле
• Электрическое и магнитное поле создается, когда ток проходит по проводу.
• Не электроны переносят энергию в цепи, а фотоны в электромагнитном поле переносят энергию.

Мой вопрос в том, откуда берется электрическое поле и почему оно ведет себя именно так. Насколько я понимаю, электрическое поле формируется из-за разницы электрических потенциалов между двумя точками. Но, однако, это не может быть правдой, потому что в противном случае между положительной и отрицательной клеммами батареи возникло бы электрическое поле, которое привело бы к ее короткому замыканию. Какое отношение настоящие электроны имеют к тому, как ведет себя поле и в каком направлении оно указывает? Как известно, скорость электронов просто дрейфует из-за того, что поле направлено от отрицательного полюса. Так что они не могут быть теми, кто несет энергию.

• электромагнетизм
• электростатика
• электрические цепи
• электрические поля

$\endgroup$

1

$\begingroup$

Но, однако, это не может быть правдой, потому что в противном случае между положительной и отрицательной клеммами батареи возникло бы электрическое поле, которое привело бы к ее короткому замыканию.

Нет, там — это электрическое поле, направленное от положительной клеммы батареи к отрицательной клемме внутри корпуса батареи. Химический состав батареи таков, что этого поля недостаточно, чтобы заставить (общий) заряд двигаться от положительного к отрицательному внутри батареи (батарея не является идеальным проводником!). Вместо этого заряд должен искать путь через нагрузку. И наоборот, «свежесмешанная» батарея без разделения зарядов и без макроскопического электрического поля самопроизвольно создаст его, поскольку химическая реакция разделяет заряды и откладывает их на клеммах. По мере того, как электрическое поле на батарее растет, химическая реакция перемещает меньше чистого заряда (обратная реакция становится более предпочтительной), а напряжение батареи — это напряжение, при котором реакция находится в равновесии.

Химический состав батареи перемещает электроны от одной клеммы к другой. Заряды на концах (избыточные протоны с одной стороны, избыточные электроны с другой) генерируют электрические поля. Движение этого заряда создает магнитные поля. Оба вносят вклад в плотность энергии в электромагнитном поле. Энергия движется в электромагнитном поле всякий раз, когда электрическое и магнитное поля не параллельны.

$\endgroup$

$\begingroup$

Когда цепь разомкнута, электроны в проводе занимают самые низкоэнергетические доступные состояния в зонной структуре. Каждому состоянию также соответствует импульс, и их распределение случайно. Чистого импульса нет.

Когда цепь замкнута, для продолжения электрохимической реакции внутри батареи требуется поток электронов от отрицательного полюса к положительному. Реакция является источником электрического поля. Из-за этого E-поля некоторые электроны в проводе переходят в более высокие энергетические состояния, и теперь у них есть чистый импульс.

Общий поток электронов приводит к возникновению магнитного поля вокруг провода.

Электроны — это не то, что переносит энергию в цепи, это фотоны в электромагнитном поле, несущие энергию.