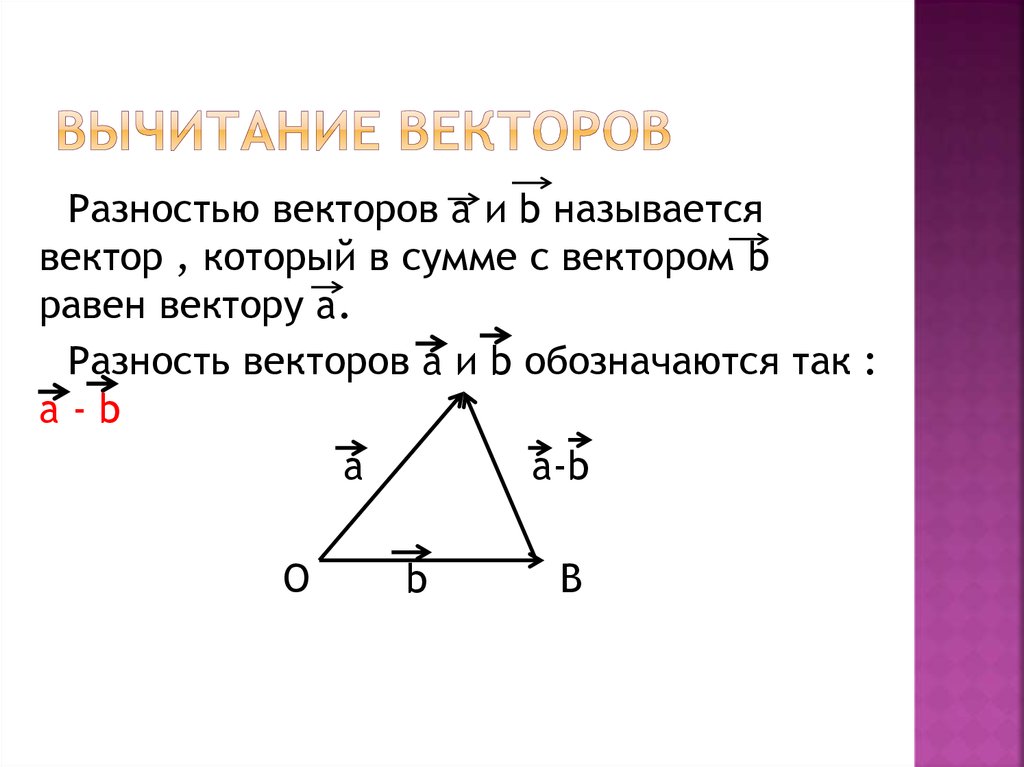
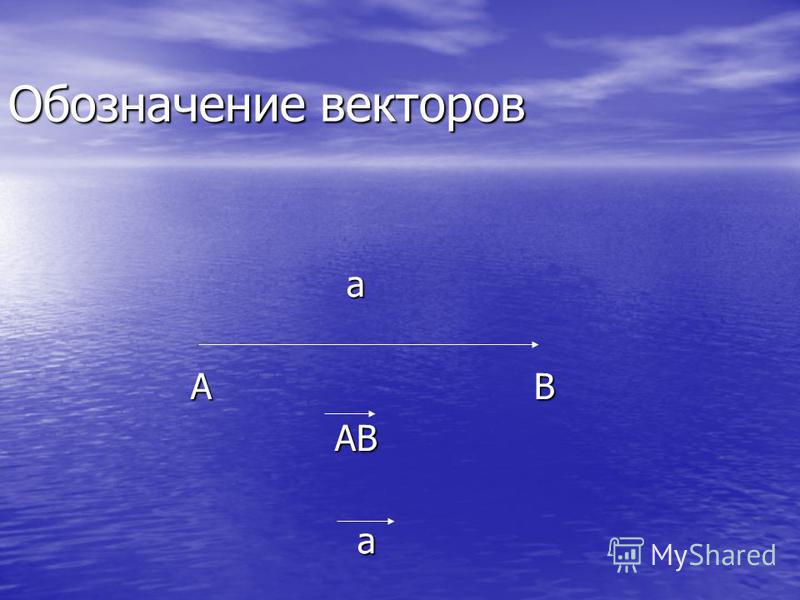
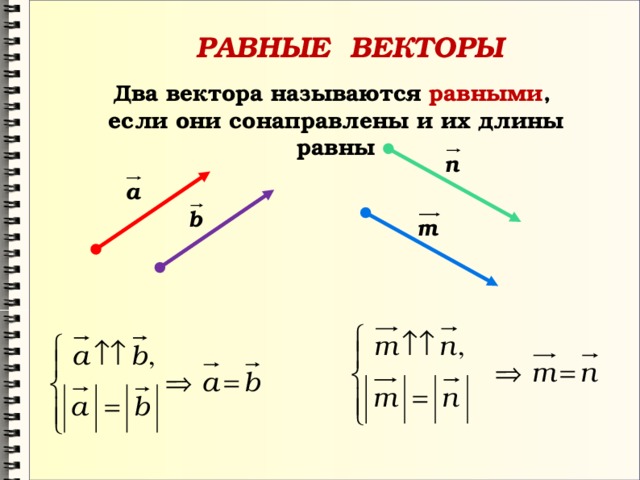
1.1. Что такое вектор?
Это «альфа» и «омега» аналитической геометрии.
Сначала вспомним школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка , а концом отрезка – точка . Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку на другой конец отрезка, то получится вектор , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института и выйти из дверей института – это две разные вещи.
Отдельные точки удобно считать так называемым нулевым вектором . У этого вектора начало и конец совпадают и его направление не определено.
Как многие помнят, в геометрии рассматривают векторы плоскости и векторы пространства, и излагаемые факты справедливы 
Обозначения: многие сразу обратили внимание на палочку без стрелочки в обозначении и сказали: «там же вверху еще стрелку ставят»! Верно, можно записать со стрелкой: , но допустима и запись , которую я буду использовать в дальнейшем. Такая привычка сложилась из практических соображений – слишком разнокалиберными и «мохнатыми» получались мои стрелки в школе и ВУЗе. В некоторых источниках векторы выделяют жирным шрифтом:, подразумевая тем самым, что это вектор.
Со стилистикой разобрались и теперь о главном:
1) Векторы можно записать двумя большими латинскими буквами:
2) Векторы также записывают маленькими латинскими буквами:
В частности, наш вектор можно для краткости переобозначить маленькой латинской буквой .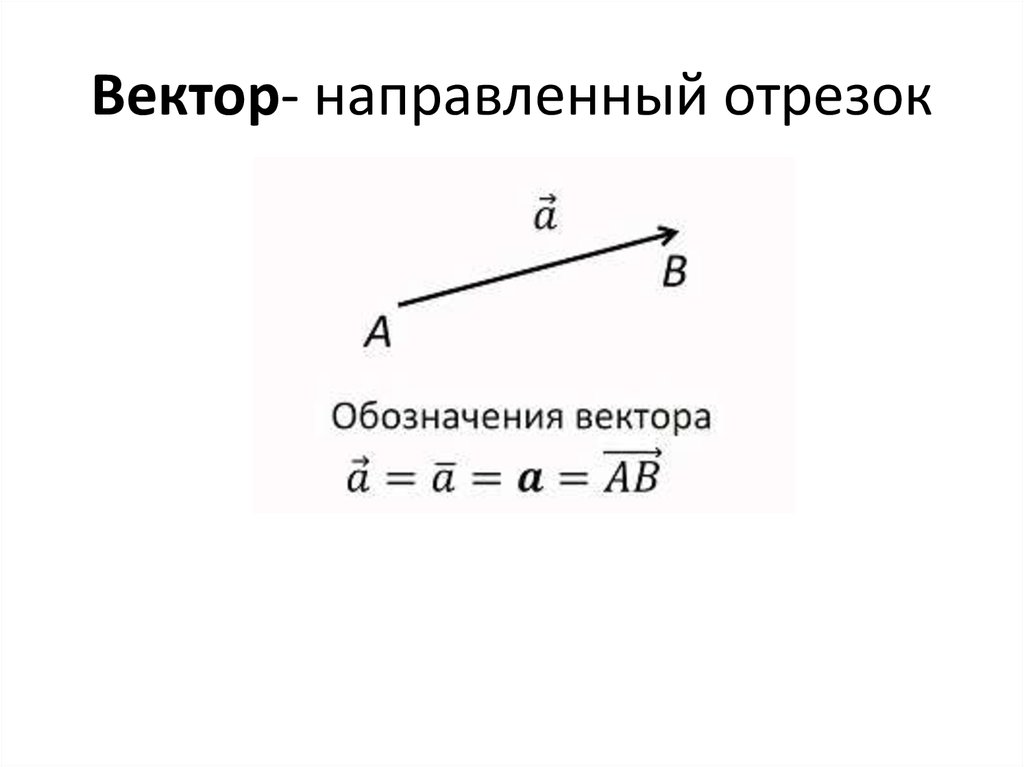
Длиной или модулем ненулевого вектора называется длина отрезка . Длина нулевого вектора равна нулю.
Длина вектора обозначается знаком модуля: ,
То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.
Свободный вектор – это множество сонаправленных отрезков равной длины:
Часто говорят, что «вектор, равный данному, можно отложить от любой точки», но далеко не все понимают настоящий смысл этого действия. С математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР. В чём состоит свобода? В ходе решения задачи вы можете «пристроить» направленный отрезок в ЛЮБУЮ, нужную вам точку плоскости или пространства. И это очень крутое свойство! Представьте направленный отрезок произвольной длины и направления – его можно «клонировать» в любой точке плоскости или пространства, по сути, он существует ВЕЗДЕ.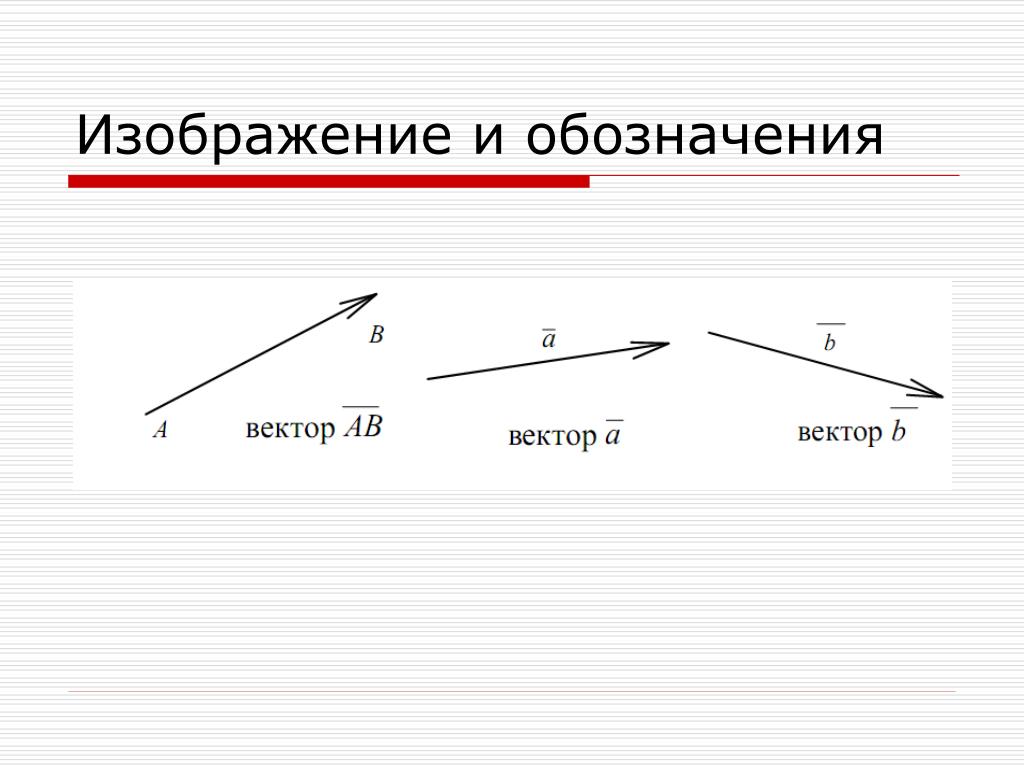
Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения вектора имеет значение. Ударьте кулаком по подушке и по кирпичу и почувствуйте разницу :). Кроме того, несвободные векторы рассматриваются и в некоторых разделах математики.
Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.
Вспоминаем ещё одно понятие:
1.2. Коллинеарность векторов
| Оглавление |
Автор: Aлeксaндр Eмeлин
Вектор на плоскости. Вектор длина.
- Альфашкола
- Статьи
- Векторы
Что такое вектор?
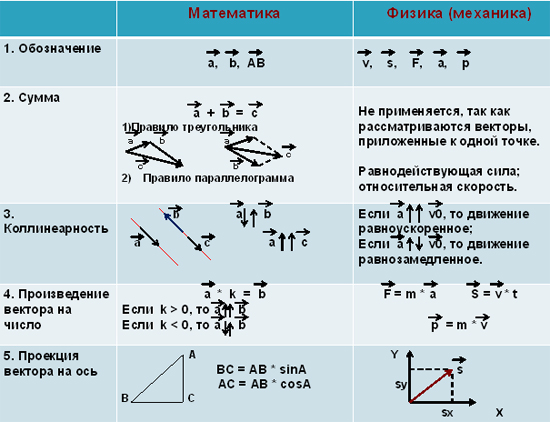
Векторы могут быть графически представлены направленными отрезками. Длина выбирается, согласно некоторому масштабу, а направление направленного отрезка линии представляет направление вектора. Например, если мы обозначим, что \(1\) см — \(5\) км/ч, то \(15\) км/ч ветер с северо-запада будет направленным отрезком \(3\) см, как показано на рисунке снизу.
Длина выбирается, согласно некоторому масштабу, а направление направленного отрезка линии представляет направление вектора. Например, если мы обозначим, что \(1\) см — \(5\) км/ч, то \(15\) км/ч ветер с северо-запада будет направленным отрезком \(3\) см, как показано на рисунке снизу.
Вектор на плоскости — это направленный отрезок. Два вектора считаются эквивалентны, если они имеют одинаковую величину и направление.
Рассмотрим вектор, взятый из точки \(A\) в точку \(B\). точка \(A\) называется начальной точкой вектора, а точка \(B\) называется конечной точкой. Символьная запись читается как вектор AB. Векторы также обозначаются английскими прописными буквами, такими как \(\overline{u},\overline{v}\) и \(\overline{w}\) или большими буквами \(\overline{AB}, \overline{CD}\)с чертой сверху. Чтобы определить, эквивалентны ли векторы, мы учитываем их величины и направления. Четыре вектора на рисунке сверху \(\overline{AB}, \overline{CD},\overline{OP},\overline{v}\) имеют одинаковую длину и направление.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Наталья Анатольевна Люфт
Репетитор по математике
Стаж (лет)
Образование:
Новосибирскй педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Тамара Анатольевна Меркулова
Репетитор по математике
Стаж (лет)
Образование:
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Мария Валерьевна Загребина
Репетитор по математике
Стаж (лет)
Образование:
Удмуртский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ОГЭ по математике
- Репетитор по геометрии
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по грамматике русского языка
- Репетитор грамматики английского языка
- Репетитор для подготовки к ЕГЭ по истории
- ВПР по математике
- Подготовка к ОГЭ по информатике
- Scratch
Похожие статьи
- Радианная мера угла
- Текстовые задачи.
 Задание №1 из ЕГЭ прошлых лет
Задание №1 из ЕГЭ прошлых лет - Решаем профильный ЕГЭ. №17. Оптимизация
- ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 3)
- Родители не пускают гулять с друзьями: что делать?
- 4 секрета подготовки к старшей школе
- Почему многие вкусные продукты вредные?
- Зачем кормить птиц зимой и как правильно это делать
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Как вы представляете векторы?
Недавно я говорил о векторах. В то время мне пришлось остановиться и вспомнить, как я представлял векторы. В идеале я должен придерживаться тех же обозначений, что и в «Основах: векторы и сложение векторов». Но позвольте мне рассмотреть различные способы представления вектора.
В то время мне пришлось остановиться и вспомнить, как я представлял векторы. В идеале я должен придерживаться тех же обозначений, что и в «Основах: векторы и сложение векторов». Но позвольте мне рассмотреть различные способы представления вектора.
Графический
Может быть, это слишком очевидно, но об этом нужно было сказать. Вы можете представлять векторы, рисуя их. На самом деле, это очень полезно концептуально, но, возможно, не слишком полезно для вычислений. Когда вектор представлен графически, его величина представлена длиной стрелки, а его направление представлено направлением стрелки. Вот пример:
Я думаю, что самым большим недостатком этого представления (помимо того, что сложно получить численные ответы для сложения) является то, что его не так просто представить в 3-х измерениях. Для следующих представлений я попытаюсь связать их с графическим представлением.
Величина и направление
Возможно, этот формат популярен в курсах по алгебре. По сути, вы просто указываете величину вектора и угол (от положительной оси x), на который указывает вектор. Вот пример (с использованием того же вектора, что и раньше):
По сути, вы просто указываете величину вектора и угол (от положительной оси x), на который указывает вектор. Вот пример (с использованием того же вектора, что и раньше):
И в формате величина-направление это будет:
Я не слишком нашел этот формат. Во-первых, если вы хотите добавить векторы, вам нужно найти компоненты. Во-вторых, студенты часто путаются с тем, что этот угол всегда измеряется от одной и той же оси (это не обязательно должна быть ось x, это просто то, что обычно). О, если вы хотите сделать это для трехмерного вектора, оно того не стоит. Вам понадобятся два угла. Что ж, в некоторых случаях это может быть оправдано.
Компоненты
С помощью метода компонентов идея состоит в том, чтобы просто задать величину вектора в каждом из координатных направлений. Вот пример.
Подожди. Я не закончил. Да, я записал эти компоненты в виде векторов, так что:
Часто вы увидите, что учебники останавливаются здесь. В этом случае они могут сказать что-то вроде:
В этом случае они могут сказать что-то вроде:
Важно понимать, что это обозначение НЕ является величиной вектора F над x означает, что это единичный вектор. Единичный вектор — это вектор, который имеет величину 1 без единиц измерения. Это означает, что вектор F x может быть записан как:
И, может быть, теперь вы понимаете, почему этот отрицательный знак важен. Вектор F x находится в направлении, противоположном вектору x-шляпы, и поэтому вам нужен отрицательный знак. Таким образом, используя это обозначение, вы можете записать вектор F как:
В некоторых учебниках вместо x и y используется буква you i и j — это будет выглядеть так:
То же самое, но другой вид. Однако не забывайте о единицах. Векторы имеют единицы измерения, если вы их не укажете, вы, вероятно, математик (шучу). Кроме того, эту нотацию можно расширить до трех измерений, добавив компонент z-hat или k-hat. Еще одна приятная вещь заключается в том, что все эти векторы настроены и готовы к добавлению. Если у вас есть вектор в компонентной нотации, вы готовы к работе.
Если у вас есть вектор в компонентной нотации, вы готовы к работе.
Я думаю, причина, по которой в некоторых учебниках используется формат величина-направление, заключается в том, что его легче соотносить с реальной жизнью. В реальной жизни я бы измерил величину и направление силы, а затем вычислил компоненты.
То же самое, но по-другому
Мне очень нравится учебник физики «Материя и взаимодействия» Рут Чабай и Брюса Шервуда. В учебнике векторы представлены следующим образом:
Мне нравится это обозначение. Он короткий и подчеркивает компоненты, а также идею о том, что все силы трехмерны. Короткая вещь действительно хороша для ленивых людей, таких как я. Кроме того, он очень хорошо сочетается с векторами в vpython. Вот как я бы написал этот вектор в vpython:
Представление вектора — примеры, величина, часто задаваемые вопросы
LearnPracticeDownload
Представление вектора выполняется с помощью стрелки. Мы знаем, что у стрелы есть острие и хвост. Наконечник стрелки обозначает направление вектора. Давайте узнаем больше о представлении вектора вместе с примерами.
Наконечник стрелки обозначает направление вектора. Давайте узнаем больше о представлении вектора вместе с примерами.
| 1. | Что такое представление вектора? |
| 2. | Представление векторов положения |
| 3. | Представление величины вектора |
| 4. | Представление векторных операций |
| 5. | Часто задаваемые вопросы о представлении вектора |
Что такое представление вектора?
Представление вектора выполнено направленным отрезком линии. Это стрела, у которой есть голова и хвост. здесь,
- Начальная точка вектора называется его хвостом (или) начальной точкой вектора.
- Конечная точка вектора называется его головой (или) конечной точкой вектора.
Голова вектора показывает его направление. Направление вектора — это угол, который он составляет с опорной линией. Вектор, который начинается в точке A и заканчивается в точке B, обозначается \(\overrightarrow{A B}\).
Направление вектора — это угол, который он составляет с опорной линией. Вектор, который начинается в точке A и заканчивается в точке B, обозначается \(\overrightarrow{A B}\).
Приведенный выше вектор также может быть представлен как — \(\overrightarrow{BA}\), который является отрицательным вектором \(\overrightarrow{AB}\).
Иногда векторы обозначаются одной строчной буквой со стрелкой над ней. Например, мы можем пометить указанный выше вектор \(\overrightarrow{AB}\) как \(\overrightarrow{a}\). Но мы не можем идентифицировать начальную точку и конечную точку вектора в этом представлении.
Представление векторов положения
Точки на координатной плоскости представлены векторами положения. На приведенном выше рисунке
- Точка A представлена вектором положения \(\overrightarrow{OA}\) = <-3, 2>
- Точка B представлена вектором положения \(\overrightarrow{OB}\) = <2, 1>
Здесь О — начало. Мы можем вычислить компоненты вектора \(\overrightarrow{AB}\), вычитая вектор положения начальной точки из вектора конечной точки. На приведенном выше рисунке
На приведенном выше рисунке
\(\overrightarrow{AB}\) = \(\overrightarrow{OB}\) — \(\overrightarrow{OA}\)
= <2, 1> — <-3, 2 >
= <2 -(-3), 1 - 2>
= <5, -1>
Таким образом, вектор, представляющий \(\overrightarrow{AB}\) на приведенном выше рисунке, равен <5, -1>.
Представление величины вектора
Величина вектора \(\overrightarrow{AB}\) представлена либо |\(\overrightarrow{AB}\)| или просто АБ. Мы используем AB для представления величины вектора \(\overrightarrow{AB}\), потому что величина есть не что иное, как его длина, а AB представляет собой длину отрезка, соединяющего A и B. Точно так же величина a вектор \(\overrightarrow{a}\) представлен либо как |\(\overrightarrow{a}\)| или просто «а». Мы можем найти величину вектора (когда нам известны его компоненты), взяв квадратный корень из суммы квадратов компонентов. Из последнего примера
\(\overrightarrow{AB}\) = <5, -1>
Его величина равна,
|\(\overrightarrow{AB}\)| (или) AB = √(5)² + (-1)² = √26
Представление векторных операций
Для любых трех векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\) и \(\overrightarrow{c}\):
- \(\overrightarrow{a}\) + \(\overrightarrow{b}\) представляет собой сумму векторов.

- \(\overrightarrow{a}\) — \(\overrightarrow{b}\) представляет разность векторов.
- \(\overrightarrow{a}\) · \(\overrightarrow{b}\) представляет скалярное произведение векторов.
- \(\overrightarrow{a}\) × \(\overrightarrow{b}\) представляет векторное произведение векторов.
- \(\widehat{a}\) представляет единичный вектор в направлении \(\overrightarrow{a}\).
- [\(\overrightarrow{a}\) \(\overrightarrow{b}\) \(\overrightarrow{c}\)] (или) \(\overrightarrow{a}\) · [ \(\overrightarrow{b }\) × \(\overrightarrow{c}\) ] (или) [\(\overrightarrow{a}\) × \(\overrightarrow{b}\) ] · \(\overrightarrow{c}\) называется скалярное тройное произведение.
☛ Связанные темы:
- Векторные формулы
- Калькулятор добавления векторов
- Калькулятор результирующего вектора
- Калькулятор угла между двумя векторами
Примеры представления векторов
Пример 1: Если вектор начинается в точке P = <-5, 4, 3> и заканчивается в <3, -4, 0>, то как его представить?
Решение:
Мы знаем, что вектор представлен стрелкой, расположенной над начальной точкой, за которой непосредственно следует конечная точка вектора.

Поскольку начальной и конечной точками данного вектора являются P и Q соответственно, вектор имеет вид \(\overrightarrow{PQ}\).
Ответ: \(\overrightarrow{PQ}\).
Пример 2: Найдите компоненты вектора \(\overrightarrow{PQ}\), упомянутого в Пример 1.
Решение:
Заданные векторы положения:
\(\overrightarrow{OP}\) = <-5, 4, 3>
\(\overrightarrow{OQ}\) = <3, -4, 0>
Мы знаем, что:
\(\overrightarrow{PQ}\) = \(\overrightarrow{OQ}\) — \(\overrightarrow{OP}\)
= <3, -4, 0> — <-5, 4, 3>
= <3 - (-5), -4 - 4, 0 - 3>
= <8, -8, -3>Ответ: <8, -8, -3>.
Пример 3: Найдите величину \(\overrightarrow{PQ}\), а также покажите, как ее можно представить.
Решение:
Величина \(\overrightarrow{PQ}\) представлена как |\(\overrightarrow{PQ}\)| (или) ПК.

PQ = √8² + (-8)² + (-3)²
= √64+64+9
= √137Ответ: PQ (или) \(\overrightarrow{PQ}\) = √137
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по представлению вектора
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о представлении вектора
Как представить вектор на диаграмме?
Представление вектора выполняется с помощью стрелки, конец которой является начальной точкой вектора, а вершина — конечной точкой вектора. Вектор, который начинается в P и заканчивается в Q, обозначается \(\overrightarrow{PQ}\).
Как представить вектор на графике?
Вектор имеет начальную и конечную точки.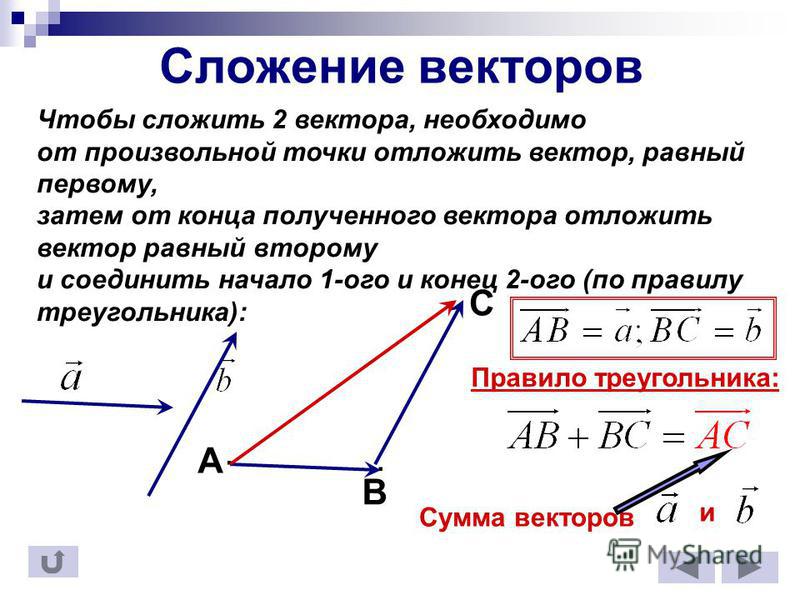 Чтобы изобразить его на графике, просто отметьте его начальную и конечную точки на листе графика и соедините их стрелкой так, чтобы хвост стрелки был в начальной точке, а ее конец в конечной точке.
Чтобы изобразить его на графике, просто отметьте его начальную и конечную точки на листе графика и соедините их стрелкой так, чтобы хвост стрелки был в начальной точке, а ее конец в конечной точке.
Как представить величину вектора?
Величина вектора представлена с помощью символа «модуль». т. е. величина вектора \(\overrightarrow{AB}\) обозначается |\(\overrightarrow{AB}\)| . Мы можем представить его просто без символа модуля и без знака вектора (стрелки), т. е. |\(\overrightarrow{AB}\)| = АБ.
Как представить векторное произведение?
Векторное произведение также известно как векторное произведение, а векторное произведение двух векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) обозначается как \(\overrightarrow{a}\) × \(\overrightarrow{b}\).
Что представляет собой векторная сумма?
По закону сложения треугольника сумма двух векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) представляет собой вектор, который начинается с хвоста вектора \(\overrightarrow{a}\) и заканчивается в начале \(\overrightarrow{b}\).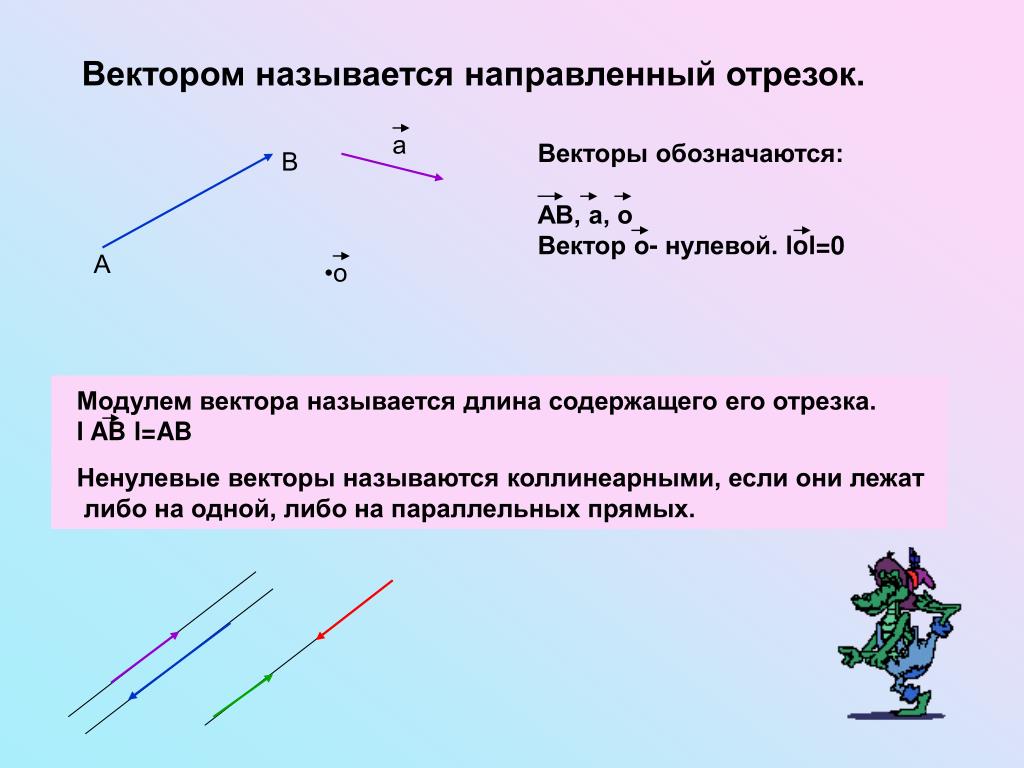


 Задание №1 из ЕГЭ прошлых лет
Задание №1 из ЕГЭ прошлых лет