3.2.1 Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции. Расчет электрических полей из принципа суперпозиции.

Если в пространство, окружающее любой электрический заряд внести другой заряд, то на него будет действовать кулоновская сила, т.е. в пространстве окружающем любой заряд существует силовое поле. Согласно современным представлениям наряду с веществом существуют особые формы существования материи посредством которой осуществляются взаимодействия различной природы между макротелами и микрочастицами. В случае взаимодействия зарядов говорят об электрическом поле.

Электрическое взаимодействие зарядов осуществляется через посредство электрического поля. Каждый заряд создает в окружающем пространстве электрическое поле и оно действует на другие заряды.

Электрическое поле – это

— особая форма существования материи посредством которой осуществляется взаимодействие между заряженными телами;

— объективная реальность, существующая вне наших знаний о ней;

— создаются поля заряженными телами;

— обнаружить поле или исследовать поле можно по действию на заряженные тела.

В этом разделе физики рассматривают только поля, создаваемые неподвижными зарядами – электростатические поля.

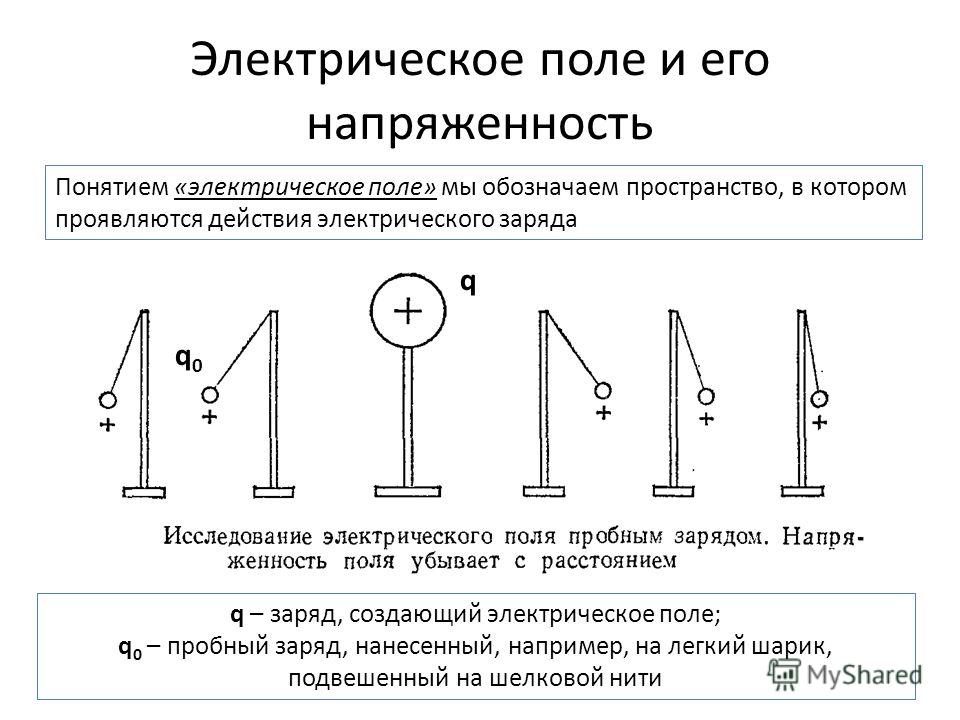
Электрические поля обнаруживают и исследуют с помощью электрического заряда, который называют «пробным зарядом». Для того, чтобы «пробный заряд» как можно меньше искажал исследуемое поле, он должен быть точечным и достаточно малым по модулю. «Пробный заряд» должен быть «положительным»( так договорились).

Из опыта следует, что сила, действующая на пробный заряд, помещенный в данную точку поля, зависит и от свойств поля в данной точке и от величины пробного заряда. Если же найти отношение силы, действующей на пробный заряд к величине этого пробного заряда, то это отношение зависит только от свойств поля в рассматриваемой точке и может служить характеристикой поля в этой точке.

Напряженность электрического поля в данной точке – это векторная физическая величина, являющаяся силовой характеристикой поля и равная силе, с которой поле действовало бы на единичный положительный точечный заряд, помещенный в данную точку поля:

.

Напряженность характеризует поле в каждой точке независимо от того, есть в этой точке пробный заряд или нет.

Поле называется однородным, если напряженность поля во всех его точках одинакова и по модулю и по направлению.

Формулу для вычисления напряженности поля, создаваемого точечным зарядом можно получить, используя закон Кулона. Запишем закон Кулона в векторном виде для взаимодействия заряда q, создающего поле, и пробного заряда q⁺: ,

где — радиус – вектор. Проведенный от заряда в точку. Где находится пробный заряд. Тогда по определению напряженности электрического поля получаем

.

Из этой формулы видно, что вектор напряженности поля, создаваемого зарядом q в каждой точке поля направлен по радиальной линии от заряда q , если заряд, создающий поле, положительный, и к заряду q , если этот заряд отрицательный ( см.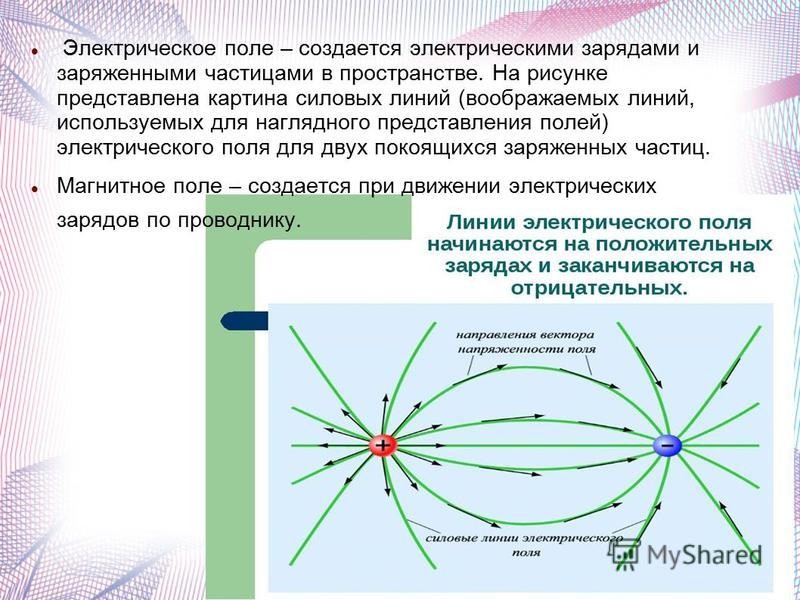 рис.).

Силовые линии электростатического поля и их свойства

Для того, чтобы наглядно представить себе распределение поля вокруг заряда, которое создает это поле, ввели понятие линии вектора напряженности

или силовые линии электрического поля. Линия вектора напряженности — это направленная линия в пространстве, касательная к которой в каждой точке совпадает с вектором . С помощью силовых линий можно охарактеризовать не только направления вектора , но и модуль этого вектора. Густота проведенных линий позволяет качественно оценивать, где поле более слабое, а где более сильное. Чем гуще расположены силовые линии, тем больше будет по величине напряженность электрического поля в этих областях.

Можно отметить следующие свойства линии напряженности электрического (силовых линий) поля:

– они конечны, т.е. они имеют начало и конец: начинаются на положительных зарядах и заканчиваются на отрицательных;

— линии напряженности электрического поля никогда не пересекаются, т.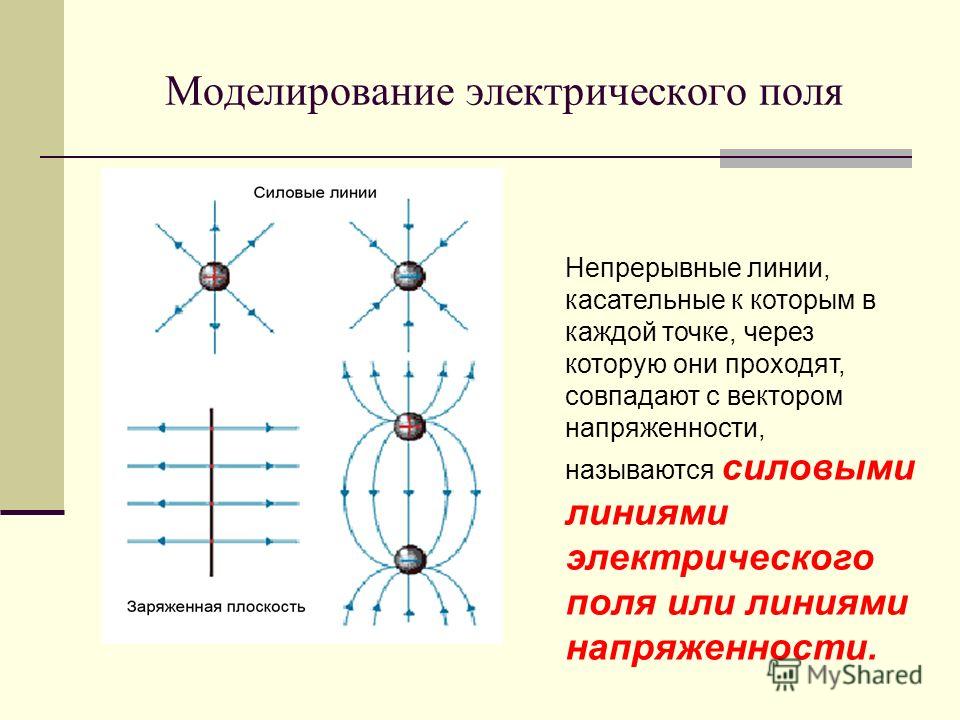 к. в каждой точке поля вектор — имеет единственное значение;

— линии однородного поля параллельны друг другу и расположены с одинаковой густотой; линии неоднородного поля непараллельные.

Принцип суперпозиции. Расчет электрических полей из принципа суперпозиции.

Электростатическое поле создается неподвижными электрическими зарядами и неразрывно с ними связано. Тела, обладающие зарядом, могут быть точечными или протяженными любой формы.

Пусть поле создается в вакууме системой точечных зарядов

q₁, q_2, q_{3, …} q_n. По принципу независимости действия сил каждый заряд в отдельности действует на пробный заряд , помещенный в данную точку поля, с отдельной силой: заряд q₁ действует с силой , заряд с силой и т.д. Результирующая сила, действующая на пробный заряд, равна векторной сумме сил …. :

.

Если это уравнение разделить на величину пробного заряда, то получим выражение для результирующей напряженности электрического поля, создаваемого системой точечных зарядов.

или

Это равенство выражает принцип суперпозиции( наложения) полей: напряженность электростатического поля в какой-либо точке пространства, создаваемая системой зарядов, равна геометрической сумме векторов напряжённостей полей, создаваемых каждым зарядом в отдельности в этой же точке.

В случае непрерывного распределения зарядов суммирование заменяется интегрированием, поскольку даже если заряды не точечные их можно свести к сумме точечных зарядов, и принцип суперпозиции полей надо будет записать в интегральной форме:

Основной задачей электростатики является расчет характеристик электростатических полей, имеющихся в различных реальных случаях, т. е. определение величины и направления вектора напряженности . В общем случае эта задача решается на основе закона Кулона и принципа суперпозиции полей.

В случае системы точечных зарядов расчет поля сводится к определению напряженностей, полей, создаваемых отдельными точечными зарядами, и к последующему их суммированию.

В случае непрерывного распределения заряда в пространстве его разбивают на бесконечно малые порции , которые можно считать точечными зарядами; вычисляют напряженность поля, создаваемого этим точечным зарядом, а затем, используя принцип суперпозиции находят напряженность поля, создаваемого непрерывно распределенным зарядом. При решении такого типа задач для того. чтобы выразить , надо знать как распределен заряд в пространстве.

В том случае, когда заряд распределен по объему, вводится характеристика: объемная плотность заряда ρ – заряд, приходящийся на единицу объема:

В том случае, когда заряд распределен по поверхности, вводится характеристика: поверхностная плотность заряда σ – заряд, приходящийся на единицу поверхности:

В том случае, когда заряд распределен по линии, вводится характеристика: линейная плотность заряда τ – заряд, приходящийся на единицу длины:

Напряженности полей простейших распределений зарядов нам известны. Используя формулы для вычисления напряжённостей полей некоторых простейших распределений зарядов, методом суперпозиции можно рассчитать напряженность поля, созданного сложным распределением зарядов.

Приведем формулы для вычисления модуля напряженности поля и картину силовых линий для некоторых распределений зарядов.

1. Поле точечного заряда

,

где r – кратчайшее расстояние от заряда q до той точки, в которой вычисляем поле, , ε — относительная диэлектрическая проницаемость среды. Силовые линии поля точечного заряда представляют собой радиальные линии, идущие во всех направлениях от заряда.

2. Поле бесконечной заряженной нити с линейной плотностью заряда τ.

,

где — линейная плотность зарядов,

r — кратчайшее расстояние от нити до точки, в которой считаем поле.

Силовые линии представляют собой радиальные линии, расположенные в плоскости, перпендикулярной к нити и при её положительном заряде они начинаются на нити и уходят в бесконечность. На рисунке показан ход силовых линий в плоскости, в которой расположена нить( рис.а) и в плоскости перпендикулярной нити ( рис.б)

3. Поле бесконечно протяженной плоскости с поверхностной плотностью заряда σ

,

где  — относительная диэлектрическая проницаемость среды вокруг плоскости,

₀ — 8,8510^-12 Ф/м – электрическая постоянная. Силовые линии поля плоскости расположены перпендикулярно плоскости в каждой точке, касательная к которой в каждой точке совпадает с вектором напряженности . Поле бесконечной заряженной плоскости является однородным, т.е. не зависит от расстояния до плоскости.

Если вспомнить, что по определению напряженность электростатического поля — это сила, с которой поле действует на пробный заряд (единичный, положительный, точечный), то можно представить себе, как идут силовые линии в простейших случаях, что и приведено на рисунках.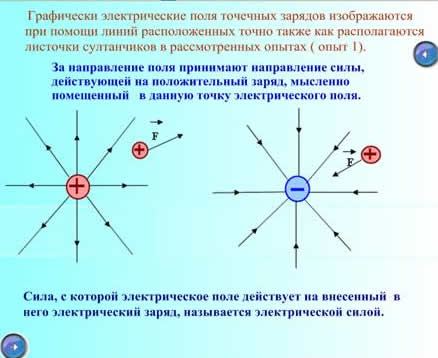

Урок по физике на тему «Электростатическое поле сферы»

МАОУ СОШ №37 Октябрьского района ГО г. Уфа РБ.

 

 

 

 

 

 

Разработка урока по физике.

Электростатическое поле заряженной сферы.

 

 

 

 

 

 

составила и провела:

учитель физики

Хаматнурова Э.М.

 

 

 

 

 

 

 

 

 

 

Тема урока:

Электрическое поле заряженной сферы.

Цель урока:

Продемонстрировать электрическое поле вне и внутри заряженной сферы. Рассчитать значение напряжённости электрического поля заряженной сферы в различных её точках.

Задачи урока:

1) сформировать умения и навыки практического характера: наблюдение за демонстрационным экспериментом, составление  умозаключения в ходе эксперимента, умение качественно описывать эксперимент и решать задачи.

2) развивать познавательный интерес к предмету на основных достижениях науки и техники, а также при наблюдении природных явлениях.

3) воспитывать ответственность за результаты учебного труда, понимание его значимости, соблюдение техники безопасности, санитарно-гигиенических условий труда.

ТСО:

1)    Интерактивная доска.

2)    Электрофорная машина, сосуд, дипольные индикаторы, металлический шар.

 

 

 

 

 

 

 

 

 

 

 

 

Физический диктант.

№	Вопрос	Ответ
1	Что такое электрическое поле?	Форма существования материи.
2	Назовите свойства электрического поля?	Поле материально, существует не зависимо от нас, обладает определёнными свойствами, которые позволяют не путать его с чем-либо другим в окружающем мире, создаётся только электрическим зарядом, неразрывно связано с зарядом.
3	Назовите количественную характеристику электрического поля?	Напряжённость электрического поля.
4	Как зависит напряжённость электрического поля, созданная точечным зарядом,  при удалении от заряда на расстояние?	Напряжённость электрического поля ослабевает с увеличением расстояния. Самое сильное поле у поверхности заряженного тела.
5	Как обнаружить в пространстве электрическое  поле?	Электрическое поле обнаруживается по силам, действующим на заряженное тело.
6	Дайте определение точечного заряда.	Точечный заряд- заряженное тело, размеры которого много меньше расстояния его возможного действия на другие тела.
7	Что является источником электростатического поля?	Неподвижный заряд.
8	Опишите принцип суперпозиции полей.	Напряжённость поля системы зарядов в данной точке равна геометрической(векторной) сумме напряжённостей полей, созданных в этой точке каждым зарядом в отдельности.
9	Дайте определение линиям напряжённости.	Линии напряжённости-линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряжённости электростатического поля в данной точке.
10	Дайте определение однородного электрического поля.	Электрическое поле, векторы напряжённости которого одинаковы во всех точках пространства, называется однородным.

 

 

Разноимённые заряды по 0,1 мкКл каждый находятся на расстоянии 6см друг от друга. Найдите напряжённость поля в точке, удалённой на 5 см от каждого из зарядов.

 

 

 

 

 

 

Демонстрационный эксперимент №1.

В сосуд наливаем немного подсолнечного масла и посыпаем его сверху манной крупой. Вводим один электрод, на который подаём заряд. Наблюдаем картину электрического поля одного заряда. В этот сосуд вводим  проводящий заряженный шарик. Наблюдаем, как первоначально хаотически ориентированные частички выстраиваются в упорядоченные линии.

Вывод

Частицы выстраиваются в линии потому, что со стороны электрического поля на них действуют силы. Поэтому линии между электродами, которые обозначают частицы, называют силовыми линиями электрического поля.

Демонстрационный эксперимент №2.

Изготавливаем несколько одинаковых дипольных индикаторов: полоски бумаги, согнутые под углом вдоль, устанавливаем на иглы по центру тяжести. В качестве подставок используем держатели для магнитных стрелок. С помощью этих индикаторов визуализируем электрическое поле: заряженного шара.

Вывод

Дипольные индикаторы позволяют визуализировать электрическое поле и помогают сформировать понятие силовых линий электрического поля.

 

О чём будет идти речь на уроке?

Тема урока: Электростатическое поле заряженной сферы.

Цель урока: Продемонстрировать электрическое поле вне и внутри заряженной сферы и рассчитать значение напряжённости электрического поля заряженной сферы в различных её точках.

 

 

 

 

 

Демонстрационный эксперимент №3.

Видео о заряженной сфере.

Вопросы по фильму:

1)    На какой фотографии электрического поля нет?

2)    На какой фотографии напряжённость электрического поля сферы сильнее?

3)    О чём свидетельствует угол отклонения нити от положения равновесия?

4)    Сможете расставить силы, действующие на пробный заряд.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пусть мы имеем заряженную сферу, известного радиуса. Найдём напряжённость поля в произвольной точке А (вне сферы), находящейся на расстоянии r от центра сферы, используя принцип суперпозиции полей.

1)    Мысленно разделим сферу на пары одинаковых точечных зарядов q₂ и q₂´, симметричных относительно отрезка ОА, т.к. сферу нельзя рассматривать как точечный заряд вблизи поверхности сферы.

2)    Любая пара зарядов создаёт напряжённость Е_А вдоль оси  ОА, поэтому результирующая напряжённость направлена радиально, от сферы.

3)    Электростатическое поле, созданное заряженной сферой, сосредоточено в определённой области пространства вне сферы.

4)    Линии напряжённости поля, созданные заряженной сферой, совпадают с линиями напряжённости точечного положительного заряда.

 

 

5)    Поэтому для расчёта напряжённости вне сферы применима формула напряжённости точечного заряда:

                                    

 

 

 

 

 

 

 

 

 

В центре сферы(стр. 383 по Касьянову)

Напряжённости поля, созданного любыми диаметрально противоположными зарядами q₁ и q₁´, одинаковы по модулю и противоположны по направлению.

Напряжённости полей в любой точке внутри сферы компенсируют друг друга.

 

 

 

 

 

 

Внутри заряженной сферы электростатическое поле отсутствует. Е=0.

 

 

 

 

 

 

 

 

 

 

 

 

Электростатическое поле, созданное заряженной сферой, сосредоточено в определённой области пространства вне сферы.

 

 

 

Построим график зависимости напряжённости электрического поля  сферы от расстояния до точки, в которой хотим узнать величину напряжённости электрического поля.

 

 

 

 

Физкультурная минута.

 

 

 

 

 

 

 

 

 

 

 

№1. Задание части В.

В точке А на поверхности равномерно заряженной сферы напряжённость её электрического поля равна Е_а . Чему равна напряжённость поля сферы в её центре О и в точке В, лежащей на середине отрезка ОА?

Установите соответствие между физическими величинами и их значениями.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Физическая величина:	Её значение:
А) напряжённость электрического поля сферы в точке О Б) напряжённость электрического поля сферы в точке В	1)    2Еа 2)     Еа 3)        Еа/2 4)     0

 

№2. Задание части А.

Если равномерно заряженный проводящий шар радиусом  5 см создаёт на расстоянии 10 см от его поверхности электрическое поле напряжённостью 4 В/м , то на расстоянии 10 см от центра шара напряжённость поля равна…

1)    4 В/м

2)    8 В/м

3)    9 В/м

4)    12 В/м

 

№3.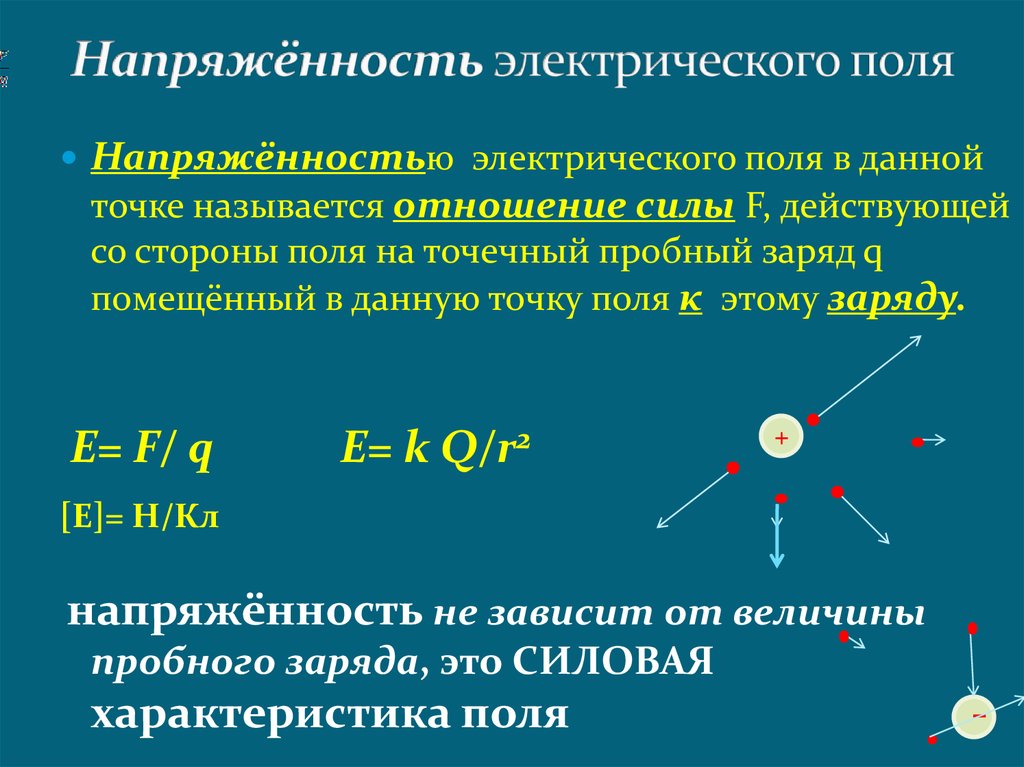 Задание части А.

Напряжённость электрического поля равномерно заряженной поверхности радиусом 0,2 м уменьшается в 6,25 раз при удалении от поверхности сферы на расстояние…

1)    0,1 м

2)    0,2м

3)    0,3м

4)    0,4 м

№4. Задание части А.

Размерность напряжённости электрического поля в системе СИ может быть выражена следующим образом…

1)    Кл / м2

2)    Кл / м

3)    Н / Кл

4)    Н*м / Кл

 

 

 

№5. Задание части А.

Шар радиусом R=5см, обладающий равномерно распределённым зарядом q_ш, покоится в масле с диэлектрической проницаемостью e=4. На расстоянии L=20см от поверхности шара находится точечный заряд q=5нКл. Сила взаимодействия между точечным зарядом и шаром по модулю равна F=12мкН. Величина заряда q_ш равна…

1)    43нКл

2)    67нКл

3)    84нКл

4)    216нКл

 

№6. Задание части А.

Одинаковые небольшие проводящие шарики, заряженные одноимёнными зарядами q1=20мКл и q2=40мКл, находятся на расстоянии r друг от друга. Затем половину заряда, находящегося на первом шарике, перенесли на второй. При этом сила взаимодействия между ними…

1)    Уменьшилась в 4 раза

2)    Уменьшилась в 1,6 раза

3)    Увеличилась в 1,6 раза

4)    Не изменилась

 

 

 

 

 

 

 

 

 

 

 

 

1)    Отгадайте загадку.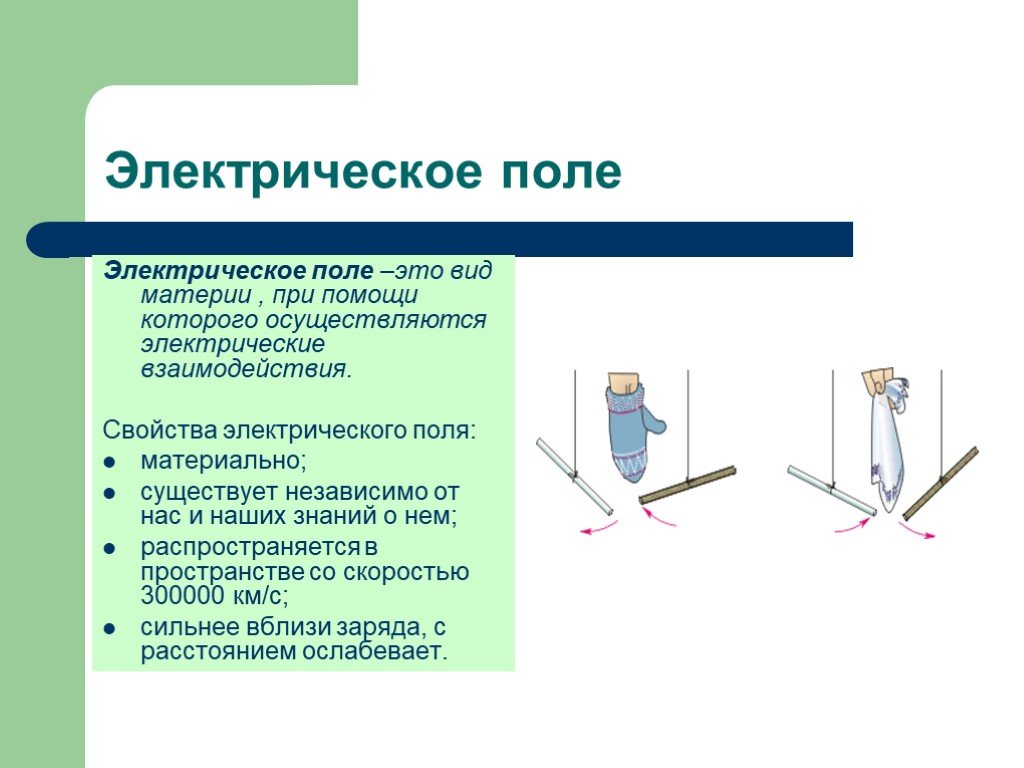

Летит огневая стрела, Никто её не поймает: Ни царь, ни царица, Ни красна девица.

Сверкнёт, мигнёт, кого-то позовёт.

Меня никто не видит, но всякий слышит,           а спутницу мою всяк может видеть, но никто не слышит.

Небесная лошадь скачет, из-под ног огонь сыплется.

2)    Задача по физике с использованием текстов из художественной прозы. Н.С.Лесков

«Реяли молнии; с грохотом нёсся удар за ударом, и вдруг Туберозов видит пред собою тёмный ствол дуба, и к нему плывёт светящийся, как тусклая лампа, шар; чудная искра посредине дерева блеснула ослепляющим светом, выросла в ком и разорвалась. В воздухе гряхнуло страшное бббах!.. Дерево было как ножом срезано у самого корня и лежало на земле…»

Какое явление вы узнаёте в этом эпизоде?

3)    Видео про шаровую молнию.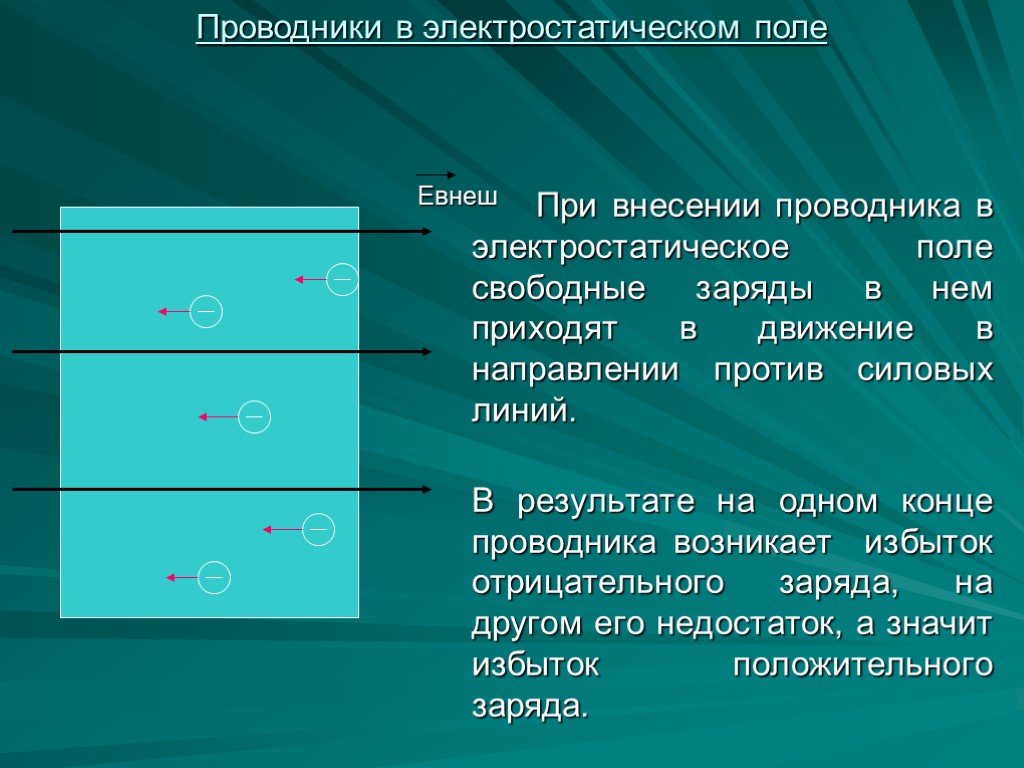

4)    Доклад про шаровую молнию.

Шарова́я мо́лния — светящийся плавающий в воздухе шар, уникально редкое природное явление, единой физической теории возникновения и протекания которого к настоящему времени не представлено. Существуют около 400 теорий, объясняющих явление, но ни одна из них не получила абсолютного признания в академической среде. В лабораторных условиях похожие, но кратковременные явления удалось получить несколькими разными способами, но вопрос о единственной природе шаровой молнии остаётся открытым. По состоянию на конец XX века не было создано ни одного опытного стенда, на котором это природное явление искусственно воспроизводилось бы в соответствии с описаниями очевидцев шаровой молнии.

Широко распространено мнение, что шаровая молния — явление электрического происхождения, естественной природы, то есть представляет собой особого вида молнию, существующую продолжительное время и имеющую форму шара, способного перемещаться по непредсказуемой, иногда удивительной для очевидцев траектории.

Во время грозы земля и объекты на ней заряжаются положительно, значит шаровая молния, обходящая объекты и копирующая рельеф, также заряжена положительно. Если встречается предмет, заряженный отрицательно, молния притянется к нему и скорее всего взорвётся.

С течением времени заряд в молнии может изменяться, и тогда меняется характер её движения. Шаровая молния чутко реагирует на электрическое поле вблизи поверхности Земли, на заряд, имеющийся на объектах. Молния стремится переместится в те области пространства, где напряжённость поля меньше, этим можно объяснить частое появление шаровых молний внутри помещения.

Шаровая молния обычно появляется в грозовую, штормовую погоду; зачастую, но не обязательно, наряду с обычными молниями. Но имеется множество свидетельств её наблюдения в солнечную погоду. Чаще всего она как бы «выходит» из проводника или порождается обычными молниями, иногда спускается с облаков, в редких случаях — неожиданно появляется в воздухе или, как сообщают очевидцы, может выйти из какого-либо предмета (дерево, столб).

В связи с тем, что появление шаровой молнии как природного явления происходит редко, а попытки искусственно воспроизвести его в масштабах природного явления не удаются, основным материалом для изучения шаровых молний являются свидетельства неподготовленных к проведению наблюдений случайных очевидцев, тем не менее некоторые свидетельства очень подробно описывают шаровую молнию и достоверность этих материалов не вызывает сомнений.

5)    Коваль-богатырь.(белорусская сказка)

Коваль-богатырь отправился искать Змея, убежавшего с поля боя. В пути его застала ночь.

«Улёгся Коваль-Богатырь под дубом, лежит и слышит- гром громыхает. Зашумел лес, загудел, заговорил на разные голоса. Но вот сверкнула молния и загремело так, что аж земля задрожала, налетел ветер. Дубы трещат, сосны стонут, а ели сгибаются чуть не до земли. А молния как сверкнёт, как блеснёт чуть не через всё небо, осветит тёмный лес, и снова тьма, как под Землёй. Разгулялся Перун, как хватит молнией в сосну, так и располосует её от верхушки до корней, ударит в дуб – расколет дуб…»

Правильно ли поступил Коваль-Богатырь, когда остался под дубом во время грозы?

6)    Физика в шутках и анекдотах.

Учитель спрашивает Жан-Луи:

-Скажи, ты знаешь разницу между молнией и электричеством?

-Да, мосье: молния-это бесплатное электричество.

7)    Пословицы и поговорки.

Молния не сверкнёт- грома не будет.

После того как молния сверкнула, боятся нечего.

Молния два раза в одно место не бьёт.

Чтобы уберечься от молнии, на голову ковш не надевают.

Зимой грома не бывает.

В грозу зонтик не защита.

Молния не всегда рождает гром.

Молния ударяет в высокое дерево.

Гроза застала в поле- садись на землю.

 

 

 

 

 

 

 

Исследователи раскрывают механизм обнаружения электрического поля в микроразмерных графеновых датчиках

Рисунок 1: Схематическая диаграмма, показывающая механизм определения электрического поля в графеновых датчиках для (а) положительного и (б) отрицательного электрических полей. В случае положительного электрического поля электроны притягиваются к графеновому каналу из слоя SiO2. Напротив, электроны переносятся из графенового канала на ловушки в слое SiO2 для отрицательного электрического поля. Предоставлено: Японский передовой институт науки и технологий.

Способность ощущать величину и полярность электрического поля представляет большой научный интерес. Приложения включают раннее предсказание молнии и обнаружение сверхзвуковых самолетов. В настоящее время в полевых мельницах широко используются датчики электрического поля. Хотя они могут обнаруживать электрические поля любой полярности и поля величиной всего 1 В/м, большой размер (> 1 м) препятствует их широкому использованию в реальных приложениях. Кроме того, двигатель внутри полевой мельницы, который позволяет обнаруживать электрическое поле, может выйти из строя. Были предприняты некоторые попытки миниатюризировать датчик электрического поля за счет внедрения датчиков на основе МЭМС. Хотя они небольшие и не содержат движущихся частей, сложный процесс изготовления делает эти датчики менее рентабельными.

Исследователи из Японского передового института науки и технологий (JAIST) и Otowa Electric Co., Ltd., ведущего производителя оборудования для молниезащиты, начали искать лучшую альтернативу. Их исследование привело к графену, двумерному материалу толщиной в один атом. «Хорошо известно, что плотность носителей в графене очень чувствительна к внешним возмущениям. Такое изменение плотности носителей отражается на токе стока. Хотя были некоторые попытки и предложения использовать графен в качестве датчика электрического поля, ни один из предыдущих работы установили основной механизм восприятия электрического поля в графене. Мы поняли, что жизненно важно сначала установить механизм, чтобы внести какие-либо улучшения в датчик, что стало нашей основной целью», — говорит старший преподаватель Манохаран Муруганатан.

С помощью серии экспериментов команда наконец установила механизм восприятия электрического поля в графене. Они обнаружили, что перенос зарядов между графеном и ловушками на границе раздела SiO ₂ /графен под действием электрического поля является ключевым явлением в механизме восприятия. Такой перенос зарядов и связанное с этим изменение плотности носителей отражаются как изменение тока стока. Направление переноса заряда зависит от полярности электрического поля. Электроны переносятся с ловушек на графен в положительном электрическом поле, а с графена на ловушки — в отрицательном электрическом поле. Таким образом, изменение тока стока под действием электрического поля противоположно положительному и отрицательному электрическому полю, что облегчает обнаружение полярности поля. Кроме того, количество переносимых между графеном и ловушками носителей заряда зависит от величины электрического поля. Чем сильнее электрическое поле, тем больше электронов перемещается между графеном и ловушками. Разница в количестве переданного заряда также отражается на токе стока. Таким образом, изменение тока стока при приложении электрического поля можно приравнять величине электрического поля.

Дополнительная информация: Афсал Карекуннан и др. «Пересмотр механизма измерения электрического поля в графеновых устройствах», ACS Omega (2021). DOI: 10.1021/acsomega.1c05530

Предоставлено Японский институт передовых наук и технологий

Цитата : Исследователи раскрывают механизм обнаружения электрического поля в микроразмерных графеновых датчиках (23 декабря 2021 г.) получено 24 ноября 2022 г. из https://phys.org/news/2021-12-uncover-mechanism-electric-field-microscale.html

Этот документ защищен авторским правом. Помимо любой добросовестной сделки с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в ознакомительных целях.

электромагнетизм — Почему мы можем обнаружить магнитное поле, но не электрическое поле вокруг переменного тока?

спросил 8 лет, 1 месяц назад

Изменено 8 лет, 1 месяц назад

Просмотрено 2к раз

$\begingroup$

Рассмотрим провод, по которому проходит переменный ток. Из-за переменного тока вокруг провода существует переменное магнитное поле, а из-за переменного магнитного поля существует электрическое поле, перпендикулярное магнитному полю, и это создает распространяющуюся электромагнитную волну.

Если их магнитное поле создает электрическое поле, и они объединяются, чтобы сформировать электромагнитные волны, почему компас показывает магнитное поле вокруг провода?

Причина моего вопроса:

Если электрическое и магнитное поля объединяются в электромагнитную волну, и мы обнаруживаем присутствие магнитного поля, то почему мы не можем обнаружить присутствие электрического поля, перпендикулярного ему?

• электромагнетизм
• магнитные поля

$\endgroup$

9

$\begingroup$

Если их магнитное поле создает электрическое поле и они объединяются в формируют электромагнитные волны, почему компас показывает магнитное поле вокруг провод?

Для создания электромагнитных волн нам нужно, чтобы ток изменялся во времени, так что магнитное поле изменялось во времени, что индуцировало изменяющееся во времени электрическое поле и т. д.

Однако это не тот случай, когда все магнитное поле, создаваемое изменяющийся во времени ток связан с ЭМ излучением.

В реактивном ближнем поле вблизи провода существуют изменяющиеся во времени электрические и магнитные поля, которые не связаны с электромагнитными волнами (которые переносят энергию), а, скорее, связаны с накоплением энергии. Из связанной статьи:

Например, ток , протекающий в антенне, создает чисто магнитное компонент в ближней зоне , который затем разрушается, когда антенна ток начинает меняться, вызывая передачу магнитного поля энергия возвращается электронам в антенне по мере изменения магнитного поля вызывает эффект самоиндукции на антенне, которая его создала. Этот возвращает энергию антенне регенеративным способом, так что она не потерял.

В целом все довольно сложно, но для низкой частоты, например, переменного тока 60 Гц по проводу в цепи преобладает синусоидально изменяющееся во времени магнитное поле.