- Логическое умножение
- Логическое умножение
- Логическое умножение — двуместная логическая операция, определяемая таблицей истинности:
-: 0 and 0 = 0
-: 0 and 1 = 0
-: 1 and 0 = 0
-: 1 and 1 = 1Синонимы: Конъюнкция
Синонимы английские: and , &
См. также: Логические операции
Финансовый словарь Финам.
.
- Логическое сложение
- Логограмма
Смотреть что такое «Логическое умножение» в других словарях:
логическое умножение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN logical multiplication … Справочник технического переводчика
логическое умножение — loginė daugyba statusas T sritis automatika atitikmenys: angl. logical multiplication vok. logische Multiplikation, f rus. логическое умножение, n pranc. multiplication logique, f … Automatikos terminų žodynas
Логическое умножение — Конъюнкция логическая операция, по своему применению максимально приближенная к союзу и . Синонимы: логическое И , логическое умножение, иногда просто И . Это бинарная инфиксная операция, то есть, она имеет два операнда и ставится между ними.… … Википедия
Логическое мышление — Логика (др. греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος «речь», «рассуждение») наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это… … Википедия
Логическое исчисление — Исчисление (формальная система), интерпретируемое в терминах какого либо фрагмента дедуктивной логики (См. Логика). Различные Л. и. служат базой для построения более богатых «нелогических» (например, математических) теорий. Примерами Л. и … Большая советская энциклопедия
Арифметическо-логическое устройство
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
БУЛЬ — (Boole) Джордж (род. 2 нояб. 1815, Линкольн – ум. 8 дек. 1864, Корк) англ, математик и логик, создатель т. н. «алгебраической логики» (см. Логистика). Осн. произв.: «The mathematical analysis of logik», 1847; «An analysis of the laws of thought» … Философская энциклопедия
Логические элементы — Логические элементы устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого «1» и низкого «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике,… … Википедия
Логический тип — По техническим причинам Bool перенаправляется сюда. О Bool можно прочитать здесь: stdbool.h. Логический, булев (англ. Boolean или logical data type) тип данных примитивный тип данных в информатике, которые могут принимать два возможных … Википедия
Логическое умножение Википедия
Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние, иногда просто «И»[1].
Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).
Обозначения
Наиболее часто встречаются следующие обозначения для операции конъюнкции:
a ∧ b , a & & b , a & b , a ⋅ b , a A N D b , min ( a , b ) {\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}
(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: a b {\displaystyle ab} [1]).
При этом обозначение
a
∧
b
{\displaystyle a\land b}
, рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &
Обозначение ⋀ для конъюнкции было использовано и в раннем языке программирования Алгол 60[6]. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения .AND. и & (с возможностью замены последнего на ключевое слово and[8][9]; в языках C и C++ применяются обозначения & для побитовой конъюнкции и && для логической конъюнкции[10]).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что 0 < 1 {\displaystyle 0<1} ), оказывается, что ( a ∧ b ) = min ( a , b ) . {\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: ( a ∧ b ) = a b ( mod k ) {\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае
Булева алгебра
Определение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).
Правило: результат равен наименьшему операнду.
Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества
{
0
,
1
}
{\displaystyle \{0,1\}}
. Результат также принадлежит множеству
{
0
,
1
}
{\displaystyle \{0,1\}}
. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений
0
,
1
{\displaystyle 0,1}
может использоваться любая другая пара подходящих символов, например
f
a
l
s
e
,
t
r
u
e
{\displaystyle false,true}
или
F
,
T
{\displaystyle F,T}
или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например,
t
r
u
e
>
f
a
l
s
e
{\displaystyle true>false}
, при цифровом обозначении старшинство естественно
1
>
0
{\displaystyle 1>0}
.
Таблицы истинности:
для бинарной конъюнкции
для тернарной конъюнкции
| a {\displaystyle a} | b {\displaystyle b} | c {\displaystyle c} | a ∧ b ∧ c {\displaystyle a\land b\land c} |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции[13].
Многозначная логика
Операции, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: m i n ( a , b ) {\displaystyle min(a,b)} , где a , b ∈ { 0 , … , k − 1 } , {\displaystyle a,b\in \{0,\dots ,k-1\},} а k {\displaystyle k} — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 0 {\displaystyle 0} и k − 1 {\displaystyle k-1} .
Название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.
Классическая логика
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a
∧
b
→
a
{\displaystyle a\land b\to a}
a
∧
b
→
b
{\displaystyle a\land b\to b}
a
→
(
b
→
(
a
∧
b
)
)
{\displaystyle a\to (b\to (a\land b))}
С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Схемотехника
Логический элемент «И»Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения[13]. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах есть «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе есть «0»
Теория множеств
С точки зрения теории множеств, конъюнкция аналогична операции пересечения.
Программирование
В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.
Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата f a l s e {\displaystyle false} или t r u e {\displaystyle true} . Например:
if (a & b & c)
{
/* какие-то действия */
};
Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:
a = false; b = true; c = true;
if (a && b && c)
{
/* какие-то действия */
};
Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.
Результат будет равен t r u e {\displaystyle true} , если оба операнда равны t r u e {\displaystyle true} (для числовых типов не равны 0 {\displaystyle 0} ). В любом другом случае результат будет равен f a l s e {\displaystyle false} .
При этом применяется стандартное соглашение: если значение левого операнда равно f a l s e {\displaystyle false} , то значение правого операнда не вычисляется (вместо b {\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
или выключающую
подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:
if (a != 0 && b / a > 3)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдёт деления на ноль.
Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 01100101 2 {\displaystyle 01100101_{2}} |
| b = | 00101001 2 {\displaystyle 00101001_{2}} |
| то | |
| a И b = | 00100001 2 {\displaystyle 00100001_{2}} |
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1 {\displaystyle 1} , а «ложь» как 0 {\displaystyle 0} . При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребёнка» — не то же самое, что «Мэри родила ребёнка и вышла замуж».
Примечания
- ↑ 1 2 3 Кондаков, 1975, с. 264—266, 534—536.
- ↑ Ampersand (неопр.). // Website Online Etymology Dictionary. Дата обращения 7 февраля 2016.
- ↑ Кондаков, 1975, с. 67.
- ↑ Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
- ↑ Earliest Uses of Symbols of Set Theory and Logic (неопр.). // Website Jeff Miller Web Pages. Дата обращения 7 февраля 2016.
- ↑ Кондаков, 1975, с. 30.
- ↑ Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- ↑ Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- ↑ Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- ↑ Эллис М.[en], Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- ↑ Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- ↑ Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
- ↑ 1 2 Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.
Литература
Логические элементы — Википедия
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x ( x n ) ∗ m {\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x {\displaystyle \ x} — основание системы счисления, n {\displaystyle \ n} — число входов (аргументов), m {\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2 ( 2 2 ) ∗ 1 = 2 4 = 16 {\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2 ( 2 3 ) ∗ 1 = 2 8 = 256 {\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2 ( 2 1 ) = 2 2 = 4 {\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC) 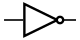 Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)| A {\displaystyle A} | ¬ A {\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение
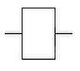
| A {\displaystyle A} | A {\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2 ( 2 2 ) = 2 4 = 16 {\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И

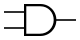
| A {\displaystyle A} | B {\displaystyle B} | A ∧ B {\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ

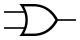
| A {\displaystyle A} | B {\displaystyle B} | A ∨ B {\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A {\displaystyle A} | B {\displaystyle B} | A | B {\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.
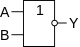
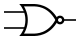
| A {\displaystyle A} | B {\displaystyle B} | A {\displaystyle A} ↓ B {\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
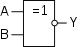 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC) 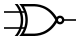 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)| A {\displaystyle A} | B {\displaystyle B} | A {\displaystyle A} ↔ B {\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

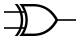
В англоязычной литературе XOR.
| A {\displaystyle A} | B {\displaystyle B} | A ⊕ B {\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A {\displaystyle A} | B {\displaystyle B} | A {\displaystyle A} → B {\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A {\displaystyle A} | B {\displaystyle B} | B {\displaystyle B} → A {\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A {\displaystyle A} | B {\displaystyle B} | f ( A , B ) {\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A {\displaystyle A} | B {\displaystyle B} | f ( A , B ) {\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
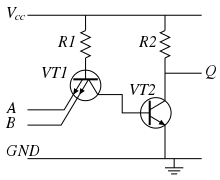 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
Тест по теме: «Основы логики» 10 класс
Тест по теме: «Основы логики»
10 класс
Составила учитель информатики – Глухова Татьяна Ивановна
Вариант 1
Наука, изучающая законы и формы мышления, называется:
1) алгебра; 3) философия;
2) геометрия; 4)логика
2. Какое из следующих высказываний являются истинным?
1) город Лондон – столица Франции ; 3) II+VI=VIII;
2) 5+4 = 6 +2; 4) томатный сок вреден.
3.Повествовательное предложение в котором что-то утверждается или отрицается называется:
1) выражение; 3) высказывание;
2) утверждение; 4) умозаключение.
4. Константа, которая обозначается «1» в алгебре логики называется:
1) ложь; 3) правда;
2)истина; 4) неправда.
5. Объединение двух высказываний в одно с помощью союза «и» называется:
1) инверсия; 3) импликация;
2) конъюнкция; 4) дизъюнкция.
6. Чему равно значение логического выражения (1v1) & (1v0)?
1) 1; 3) 2;
2) 10 4) 0.
7.Какая из логических операций не является базовой?
1) дизъюнкция; 3) конъюнкция;
2) инверсия; 4) импликация
8. Графическое изображение логического выражения называется:
1) схема; 3)график;
2) чертёж; 4) рисунок.
9. Двойное отрицание логической переменной равно:
1) 0 3) исходной переменной;
2) обратной переменной; 4)1.
10. Устройство, выполняющее базовые логические операции, называется:
1) регистр; 3) вентиль;
2) ячейка; 4) триггер.
11. Какое состояние триггера является запрещённым?
1) 1-1; 3)1-0;
2) 0-0; 4) 0-1
Ключ:
1-4
2-3
3-3
4-2
5-2
6-1
7-4
8-1
9-3
10-3
11-1
2 вариант
Что такое логика?
1) это наука о суждениях и рассуждениях;
2) это наука, занимающая изучением логических основ работы компьютера;
3) это наука о формах и законах человеческого мышления и, в частности, о законах доказательных рассуждений;
4) это наука, изучающая законы и методы накопления, обработки и сохранения информации с помощью ЭВМ
2. Логическая функция – это:
1)простое высказывание; 3) вопросительное предложение;
2) составное высказывание; 4) логическая операция.
3. Как кодируется логическая переменная, принимающая значение «ЛОЖЬ»?
1) 0; 3)2;
2) 1; 4) неправда.
4. Какие из следующих высказываний являются истинными?
1) 8+2=3+5; 3) III+V=VIII;
2)Число десять – нечётное; 4) город Париж – столица Англии.
5. Чему равно значение логического выражения (1v1)&(0v¬0)=?
1) 0; 3)10;
2)1; 4) 2.
6. Значение логического выражения ¬(АvВ) по закону Моргана равно?
1) ¬А&¬B; 3) ¬A&B;
2)A&¬B; 4) ¬Av¬B.
7. Логической операцией не является:
1) логическое деление;
2) логическое сложение;
3) логическое отрицание;
4) логическое умножение.
8. Объединение двух высказываний в одно с помощью оборота «если…,то…» называется:
1) дизъюнкция; 3) инверсия;
2) конъюнкция; 4)импликация.
9. Таблица, содержащая все возможные значения логического выражения называется:
1) таблица ложности;
2) таблица истинности;
3) таблица ответов;
4) таблица значений.
10. Для сложения одноразрядных двоичных чисел используется:
1) регистр; 3) полусумматор;
2) триггер; 4) сумматор.
11. Какое состояние триггера хранит информацию?
1) 1-0; 3)0-0;
2)0-1; 4) 1-1.
Ключ:
1-3
2-2
3-1
4-3
5-2
6-1
7-1
8-4
9-2
10-4
11-3
27 Логическое сложение и умножение.
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
A B F
1 1 1
1 0 0
0 1 0
0 0 0
2 Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
A B F
1 1 1
1 0 1
0 1 1
0 0 0
28 Основные законы алгебры логики.
Вот как трактует логику толковый словарь: «Логика — наука, изучающая способы обоснования суждений, доказательства, мышления и логического вывода. В математической логике используются для этого методы алгебры или теории алгоритмов». «Алгебра логики (булева алгебра) — раздел математики, изучающий методы оперирования логическими (булевыми) переменными, принимающими только два значения — истина и ложь. Предложен английским математиком Джорджем Булем». Добавим только, что помимо манипуляций константами «да» и «нет» логические переменные могут являться результатом применения к числам операторов отношения (меньше, больше, равно и т.п.).
В компьютерах булевы переменные представляются (кодируются) битами (разрядами двоичной системы счисления), где 1 обычно означает истину, а 0 — ложь. Вот ещё одно достоинство двоичной системы счисления!
В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.

Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.
1. Закон противоречия:

2. Закон исключенного третьего:

3. Закон двойного отрицания:

4. Законы де Моргана:
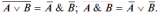
5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
6. Законы поглощения: A ∨ (A & B) = A; A & (A ∨ B) = A.
7. Законы исключения констант: A ∨ 1 = 1; A ∨ 0 = A; A & 1 = A; A & 0 = 0; B ∨ 1 = 1; B ∨ 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:

9. Закон контрапозиции: (A ⇔ B) = (B ⇔ A).
Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ∨ B = B ∨ A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ∨ (B ∨ C) = (A ∨ B) ∨ C.
3. Дистрибутивный закон: A & (B ∨ C) = (A & B) ∨ (A & C).
Основы логики, Джордж Буль, булева алгебра
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (⇒), эквиваленция (⇔)
Выполним преобразование, например, логической функции

применив соответствующие законы алгебры логики.
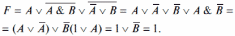
Дизъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».
Это бинарная инфиксная операция, то есть, она имеет два операнда и стоит между ними. Чаще всего встречаются следующие варианты записи: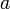 ||
|| 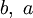 |
| 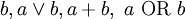 .
.
Булева алгебра
В булевой алгебре дизъюнкция — это функция двух переменных (они же — операнды операции). Переменные Правило: результат равен 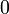 , если оба операнда равны
, если оба операнда равны 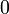 ; во всех остальных случаях результат равен
; во всех остальных случаях результат равен 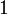 .
.
Многозначная логика
В многозначной логике операция дизъюнкции может определяться другими способами. Чаще всего применяется схема: 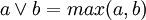 , где
, где ![~a, b \in [0, 1]](/800/600/https/dic.academic.ru/pictures/wiki/files/100/dfbf391a6408e74c7a9b40da50e8fffd.png) . Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов
. Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 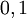 .
.
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространенных вариантов включает 3 аксиомы для дизъюнкции: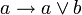
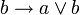
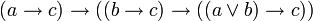
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
Программирование
В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++ логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|».
Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата 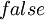 или
или 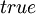 . Например:
. Например:
if (a || b)
{
/* какие-то действия */
};
Результат будет равен 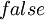 , если оба операнда равны
, если оба операнда равны 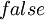 или
или 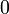 . В любом другом случае результат будет равен
. В любом другом случае результат будет равен 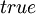 .
.
При этом применяется стандартное соглашение: если значение левого операнда равно 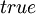 , то значение правого операнда не вычисляется (вместо
, то значение правого операнда не вычисляется (вместо 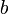 может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:
может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:
if (a == NULL || a->x == 0)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет разыменования нулевого указателя.
Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 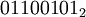 |
| b = | 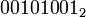 |
| то | |
| a ИЛИ b = | 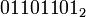 |
Связь с естественным языком
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — исключающего «ИЛИ».
См. также
Wikimedia Foundation. 2010.
логическое умножение — со всех языков на русский
См. также в других словарях:
Логическое умножение — двуместная логическая операция, определяемая таблицей истинности: : 0 and 0 = 0 : 0 and 1 = 0 : 1 and 0 = 0 : 1 and 1 = 1 Синонимы: Конъюнкция Синонимы английские: and , & См. также: Логические операции Финансовый словарь Финам … Финансовый словарь
логическое умножение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN logical multiplication … Справочник технического переводчика
логическое умножение — loginė daugyba statusas T sritis automatika atitikmenys: angl. logical multiplication vok. logische Multiplikation, f rus. логическое умножение, n pranc. multiplication logique, f … Automatikos terminų žodynas
Логическое умножение — Конъюнкция логическая операция, по своему применению максимально приближенная к союзу и . Синонимы: логическое И , логическое умножение, иногда просто И . Это бинарная инфиксная операция, то есть, она имеет два операнда и ставится между ними.… … Википедия
Логическое мышление — Логика (др. греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος «речь», «рассуждение») наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это… … Википедия
Логическое исчисление — Исчисление (формальная система), интерпретируемое в терминах какого либо фрагмента дедуктивной логики (См. Логика). Различные Л. и. служат базой для построения более богатых «нелогических» (например, математических) теорий. Примерами Л. и … Большая советская энциклопедия
Арифметическо-логическое устройство — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
БУЛЬ — (Boole) Джордж (род. 2 нояб. 1815, Линкольн – ум. 8 дек. 1864, Корк) англ, математик и логик, создатель т. н. «алгебраической логики» (см. Логистика). Осн. произв.: «The mathematical analysis of logik», 1847; «An analysis of the laws of thought» … Философская энциклопедия
Логические элементы — Логические элементы устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого «1» и низкого «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике,… … Википедия
Логический тип — По техническим причинам Bool перенаправляется сюда. О Bool можно прочитать здесь: stdbool.h. Логический, булев (англ. Boolean или logical data type) тип данных примитивный тип данных в информатике, которые могут принимать два возможных … Википедия
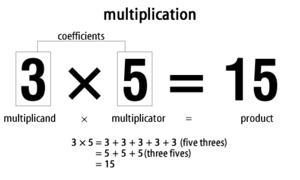
Умножение — это арифметическая операция для нахождения продукта из двух чисел. Умножение — это третья операция в математике после сложения, которая является первой, вычитание, которое является вторым, а затем происходит умножение.
С натуральными числами он сообщает вам количество плиток в прямоугольнике, где одно из двух чисел равно количеству плиток на одной стороне, а другое число равно количеству плиток на другой стороне.
С действительными числами он сообщает вам площадь прямоугольника, где первое число равно размеру одной стороны, а второе число равно размеру другой стороны.
Например, три, умноженные на пять, — это сумма пяти сумм, сложенных вместе, или три пятерки. Это может быть записано как 3 × 5 = 15, или произнесено как «трижды пять равно пятнадцать». Математики называют два числа, которые вы хотите, чтобы умножить «коэффициенты» вместе, или «умножить» и и «умножить» отдельно .Мультипликатор × мультипликатор = произведение.
Умножение между числами называется коммутативным — когда порядок чисел не влияет на стоимость продукта. Это верно для целых чисел (целых чисел), например, 4 × 6 — это то же самое, что и 6 × 4, а также для рациональных чисел (дробей) и для всех других действительных чисел (представляемых в виде поля в непрерывной линии), а также для комплексных чисел (чисел, представляемых в виде поля в плоскости). Это не верно для кватернионов (чисел, представимых в виде кольца в четырехмерном пространстве), векторов или матриц.
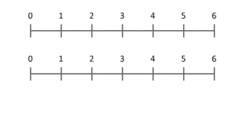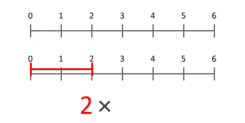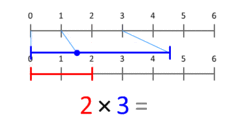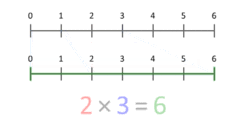
Определение умножения как повторного сложения дает возможность прийти к теоретико-множественной интерпретации умножения кардинальных чисел. Более точное представление — думать о нем как о масштабируемых величинах. Эта анимация показывает, что 3 умножается на 2, давая 6 в результате. Обратите внимание, что синяя точка в синем сегменте длины 3 размещается в позиции 1, а синий сегмент масштабируется таким образом, чтобы эта точка была размещена в конце красного сегмента длины 2.Для умножения на любой X синяя точка всегда начинается с 1 и заканчивается на X. Это работает даже для X, меньшего 1 или отрицательного.
Противоположностью умножения является деление.
Учителя обычно требуют, чтобы их ученики запомнили таблицу первых 9 чисел при обучении умножению.
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Addition ( + ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Назначение сложения ( x + = y ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Назначение ( x = y ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
асинхронная функция выражение | Chrome Полная поддержка 55 | Edge Полная поддержка 15 | Firefox Полная поддержка 52 | IE Нет поддержки № | Opera Полная поддержка 42 | Safari Полная поддержка 10.1 | WebView Android Полная поддержка 55 | Chrome Android Полная поддержка 55 | Firefox Android Полная поддержка 52 | Opera Android Полная поддержка 42 | Safari iOS Полная поддержка 10.3 | Samsung Интернет Android Полная поддержка 6,0 | nodejs Полная поддержка 7.6.0
| ||||||||||||||||||||
ждут | Chrome Полная поддержка 55 | Edge Полная поддержка 14 | Firefox Полная поддержка 52 | IE Нет поддержки № | Opera Полная поддержка 42 | Safari Полная поддержка 10.1 | WebView Android Полная поддержка 55 | Chrome Android Полная поддержка 55 | Firefox Android Полная поддержка 52 | Opera Android Полная поддержка 42 | Safari iOS Полная поддержка 10.3 | Samsung Интернет Android Полная поддержка 6,0 | nodejs Полная поддержка 7.6.0
| ||||||||||||||||||||
Побитовое И ( a & b ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Побитовое И присвоение ( x & = y ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Побитовое НЕ ( ~ ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Побитовое ИЛИ ( a | b ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Побитовое ИЛИ присвоение ( x | = y ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.b ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.= y ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 |
класс | Chrome Полная поддержка 42 | Edge Полная поддержка 13 | Firefox Полная поддержка 45 | IE Нет поддержки № | Opera Полная поддержка 29 | Safari Полная поддержка 7 | WebView Android Полная поддержка 42 | Chrome Android Полная поддержка 42 | Firefox Android Полная поддержка 45 | Opera Android Полная поддержка 29 | Safari iOS Полная поддержка 7 | Samsung Интернет Android Полная поддержка 4.0 | nodejs Полная поддержка 6.0.0
| ||||||||||||||||||||
| Оператор запятой | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 4 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Условный оператор ( c? T: f ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Decrement ( - ) | Chrome Полная поддержка 2 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 4 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 3.2 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
исключить | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 4 | Opera Полная поддержка 9 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
| Назначение по деструктурированию | Chrome Полная поддержка 49 | Edge Полная поддержка 14 | Firefox Полная поддержка 41
| IE Нет поддержки № | Opera Полная поддержка 36 | Safari Полная поддержка 8 | WebView Android Полная поддержка 49 | Chrome Android Полная поддержка 49 | Firefox Android Полная поддержка 41
| Opera Android Полная поддержка 36 | Safari iOS Полная поддержка 8 | Samsung Интернет Android Полная поддержка 5.0 | nodejs Полная поддержка 6.0.0 | ||||||||||||||||||||
Отделение (/) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Назначение отдела ( x / = y ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Равенство ( a == b ) | Chrome Полная поддержка 1 | Edge Полная поддержка 12 | Firefox Полная поддержка 1 | IE Полная поддержка 3 | Opera Полная поддержка 3 | Safari Полная поддержка 1 | WebView Android Полная поддержка 1 | Chrome Android Полная поддержка 18 | Firefox Android Полная поддержка 4 | Opera Android Полная поддержка 10.1 | Safari iOS Полная поддержка 1 | Samsung Интернет Android Полная поддержка 1.0 | nodejs Полная поддержка 0.1.100 | ||||||||||||||||||||
Возведение в степень ( ** ) | Chrome Полная поддержка 52 | Edge Полная поддержка 14 | Firefox Полная поддержка 52 | IE Нет поддержки № | Opera Полная поддержка 39 | Safari Полная поддержка 10.1 | WebView Android Полная поддержка 51 | Chrome Android Полная поддержка 52 | Firefox Android Полная поддержка 52 | Opera Android Полная поддержка 41 | Safari iOS Полная поддержка 10.3 | Samsung Интернет Android Полная поддержка 6,0 | nodejs Полная поддержка 7.0.0
|
Арифметика, Сравнение, Логика и многое другое.
Что такое операторы в python?
Операторы — это специальные символы в Python, которые выполняют арифметические или логические вычисления. Значение, с которым работает оператор, называется операндом.
Например:
>>> 2 + 3
5 Здесь + — оператор, выполняющий сложение. 2 и 3 являются операндами, а 5 являются выходными данными операции.
Арифметические операторы
Арифметические операторы используются для выполнения математических операций, таких как сложение, вычитание, умножение и т. Д.
| Оператор | Значение | Пример |
|---|---|---|
| + | Добавить два операнда или унарный плюс | х + у + 2 |
| — | Вычтите правый операнд из левого или одинарного минуса | x — y- 2 |
| * | Умножить два операнда | х * у |
| / | Разделите левый операнд на правый (всегда приводит к плавающему) | х / у |
| % | Модуль — остаток от деления левого операнда на правый | x% y (остаток от x / y) |
| // | Этажное деление — деление, которое приводит к целому числу, скорректированному слева в числовой строке | х // у |
| ** | Экспонента — левый операнд, возведенный в степень справа | х ** у (х до степени у) |
Пример 1: Арифметические операторы в Python
х = 15
у = 4
# Вывод: x + y = 19
печать ('x + y =', x + y)
# Вывод: x - y = 11
печать ('x - y =', x-y)
# Вывод: x * y = 60
печать ('x * y =', x * y)
# Вывод: х / у = 3.75
печать ('x / y =', x / y)
# Вывод: x // y = 3
print ('x // y =', x // y)
# Выход: x ** y = 50625
печать ('x ** y =', x ** y) Выход
х + у = 19 х - у = 11 х * у = 60 х / у = 3,75 х // у = 3 х ** у = 50625
Операторы сравнения
Операторы сравнения используются для сравнения значений. Возвращает True или False в зависимости от условия.
| Оператор | Значение | Пример |
|---|---|---|
| > | Больше — Истина, если левый операнд больше правого | х> у |
| < | Меньше — Истина, если левый операнд меньше правого | х 9009 |
| == | равно — истина, если оба операнда равны | х == у |
| ! = | Не равно — Истина, если операнды не равны | х! = У |
| > = | Больше или равно — Истина, если левый операнд больше или равен правому | x> = y |
| <= | Меньше или равно — Истина, если левый операнд меньше или равен правому | x <= y |
Пример 2: операторы сравнения в Python
х = 10
у = 12
# Вывод: x> y - False
print ('x> y is', x> y)
# Вывод: x = y - Ложь
print ('x> = y is', x> = y)
# Вывод: x <= y True
печать ('x <= y is', x <= y) Выход
x> у ложно х <у верно х == у Ложь х! = у верно x> = у ложно х <= у истина
Логические операторы
Логическими операторами являются операторы и , или , , а не .
| Оператор | Значение | Пример |
|---|---|---|
| и | Истинно, если оба операнда истинны | х и у |
| или | Истинно, если один из операндов истинен | х или у |
| не | True, если операнд false (дополняет операнд) | не х |
Пример 3: Логические операторы в Python
x = True
у = ложно
печать («х и у есть», х и у)
печать ('x или y is', x или y)
печать («не х есть», не х) Выход
х и у ложно х или у истина не х ложно
Вот таблица истинности для этих операторов.
Битовые операторы
Битовые операторы действуют на операнды, как если бы они были строками двоичных цифр. Они работают понемногу, отсюда и название.
Например, 2 - это 10 в двоичном формате, а 7 - 111 .
В приведенной ниже таблице: Позвольте x = 10 ( 0000 1010 в двоичном формате) и y = 4 ( 0000 0100 в двоичном виде)
| Оператор | Значение | Пример |
|---|---|---|
| и | побитового И | x & y = 0 ( 0000 0000 ) |
| | | побитовый ИЛИ | х | у = 14 ( 0000 1110 ) |
| ~ | побитовый НЕ | ~ x = -11 ( 1111 0101 ) |
| ^ | Побитовый XOR | x ^ y = 14 ( 0000 1110 ) |
| >> | Битовый сдвиг вправо | x >> 2 = 2 ( 0000 0010 ) |
| << | побитовый сдвиг влево | x << 2 = 40 ( 0010 1000 ) |
Назначение операторов
Операторы присваивания используются в Python для присваивания значений переменным.
a = 5 - это простой оператор присваивания, который присваивает значение 5 справа переменной a слева.
В Python есть различные составные операторы, такие как + + 5 , который добавляет переменную, а затем назначает ее. Это эквивалентно a = a + 5 .
| Оператор | Пример | Эквивалент |
|---|---|---|
| = | x = 5 | x = 5 |
| + = | x + = 5 | х = х + 5 |
| - = | x - = 5 | х = х - 5 |
| * = | x * = 5 | х = х * 5 |
| / = | х / = 5 | х = х / 5 |
| % = | x% = 5 | x = x% 5 |
| // = | х // = 5 | х = х // 5 |
| ** = | x ** = 5 | х = х ** 5 |
| & = | х & = 5 | х = х & 5 |
| | = | х | = 5 | х = х | 5 |
| ^ = | х ^ = 5 | х = х ^ 5 |
| >> = | x >> = 5 | х = х >> 5 |
| << = | х << = 5 | х = х << 5 |
Специальные операторы
Язык Python предлагает некоторые специальные типы операторов, такие как оператор идентификации или оператор членства.Они описаны ниже с примерами.
Идентификационные операторы
- это , а - это не , это операторы идентификации в Python. Они используются для проверки, находятся ли два значения (или переменные) в одной и той же части памяти. Две равные переменные не означают, что они идентичны.
| Оператор | Значение | Пример |
|---|---|---|
| это | Истинно, если операнды идентичны (относятся к одному и тому же объекту) | х истинно |
| не | Истинно, если операнды не идентичны (не относятся к одному и тому же объекту) | х не правда |
Пример 4. Идентификационные операторы в Python
x1 = 5
у1 = 5
x2 = «Привет»
y2 = 'Привет'
х3 = [1,2,3]
у3 = [1,2,3]
# Вывод: Ложь
печать (x1 не y1)
# Вывод: True
печать (x2 - y2)
# Вывод: Ложь
печать (x3 is y3) Выход
Неверно Правда Неверно
Здесь мы видим, что x1 и y1 являются целыми числами с одинаковыми значениями, поэтому они равны и идентичны.То же самое имеет место с x2 и y2 (строки).
Но x3 и y3 являются списками. Они равны, но не идентичны. Это потому, что интерпретатор находит их отдельно в памяти, хотя они равны.
Членство операторов
в и не в являются операторами членства в Python. Они используются для проверки того, найдено ли значение или переменная в последовательности (строка, список, кортеж, набор и словарь).
В словаре мы можем только проверять наличие ключа, а не значения.
| Оператор | Значение | Пример |
|---|---|---|
| из | Истинно, если значение / переменная найдены в последовательности | 5 х |
| не в | Истинно, если значение / переменная не найдены в последовательности | 5 не в х |
Пример № 5: операторы членства в Python
x = 'Привет, мир'
y = {1: 'a', 2: 'b'}
# Вывод: True
печать ('H' в х)
# Вывод: True
печать («привет» не в х)
# Вывод: True
печать (1 в год)
# Вывод: Ложь
печать («а» в у) Выход
True Правда Правда Неверно
Здесь 'H' находится в x , но 'hello' отсутствует в x (помните, Python чувствителен к регистру).Аналогично, 1 - это ключ, а 'a' - это значение в словаре y . Следовательно, 'a' в y возвращает False .

