PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

основные понятия, формулы, пример решения задачи

Когда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными размерами, вводя понятие материальной точки. Для другого типа задач, в которых рассматриваются покоящиеся или вращающиеся тела, важно знать их параметры и точки приложения внешних сил. В этом случае речь идет о моменте сил относительно оси вращения. Рассмотрим этот вопрос в статье.

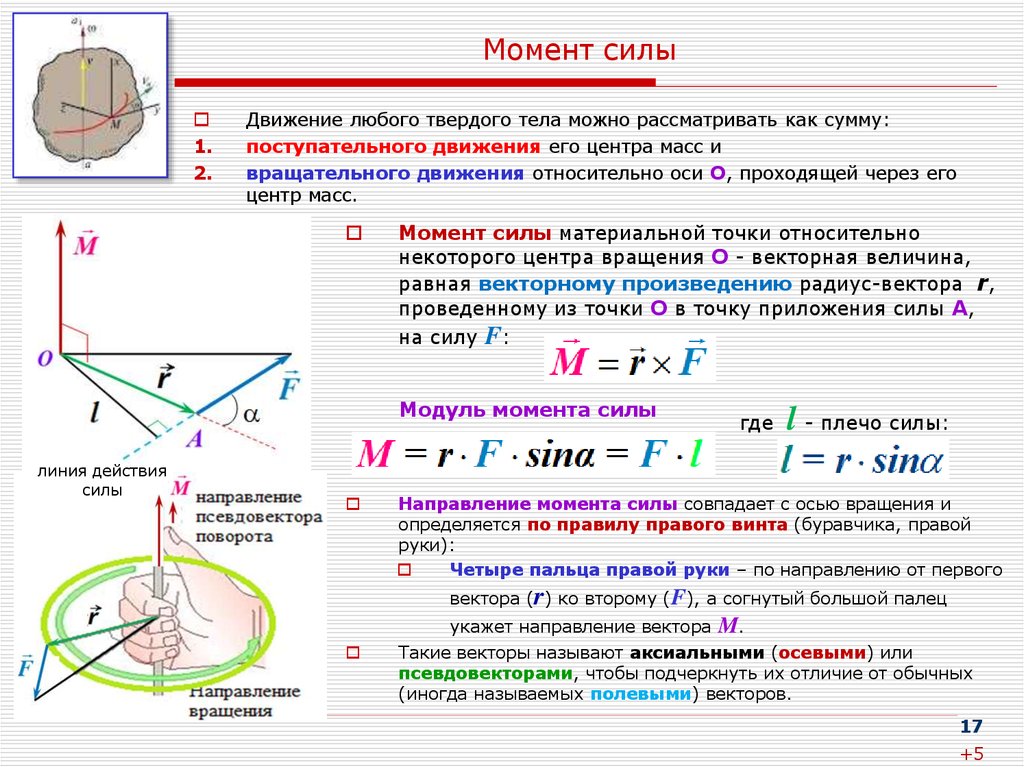
Понятие о моменте силы

Перед тем как приводить формулу момента силы относительно оси вращения неподвижной, необходимо пояснить, о каком явлении пойдет речь. Ниже дан рисунок, на котором изображен гаечный ключ длиной d, к концу его приложена сила F. Нетрудно представить, что результатом ее воздействия будет вращение ключа против часовой стрелки и откручивание гайки.

Согласно определению, момент силы относительно оси вращения представляет собой произведение плеча (d в данном случае) на силу (F), то есть можно записать следующее выражение: M = d*F. Сразу же следует оговориться, что приведенная формула записана в скалярном виде, то есть она позволяет рассчитать абсолютное значение момента M. Как видно из формулы, единицей измерения рассматриваемой величины являются ньютоны на метр (Н*м).

Как выше было оговорено, момент M в действительности представляет собой вектор. Для пояснения этого утверждения рассмотрим другой рисунок.

Здесь мы видим рычаг длиной L, который закреплен на оси (показано стрелкой). К его концу приложена сила F под углом Φ. Нетрудно себе представить, что эта сила будет вызывать подъем рычага. Формула для момента в векторной форме в этом случае запишется так: M¯ = L¯*F¯, здесь черта над символом означает, что рассматриваемая величина — это вектор. Следует пояснить, что L¯ направлен от оси вращения к точке приложения силы F¯.

Приведенное выражение является векторным произведением. Его результирующий вектор (M¯) будет направлен перпендикулярно плоскости, образованной L¯ и F¯. Для определения направления момента M¯ существуют несколько правил (правой руки, буравчика). Чтобы не заучивать их и не путаться в порядке умножения векторов L¯ и F¯ (от него зависит направление M¯), следует запомнить одну простую вещь: момент силы будет направлен таким образом, что если смотреть с конца его вектора, то воздействующая сила F¯ будет вращать рычаг против часовой стрелки. Это направление момента условно принято за положительное. Если же система совершает вращение по часовой стрелки, значит, результирующий момент сил имеет отрицательное значение.

Таким образом, в рассматриваемом случае с рычагом L величина M¯ направлена вверх (от рисунка к читателю).

В скалярной форме формула для момента запишется в виде: M = L*F*sin(180-Φ) или M = L*F*sin(Φ) (sin(180-Φ) = sin(Φ)). Согласно определению синуса, можно записать равенство: M = d*F, где d = L*sin(Φ) (см. рисунок и соответствующий прямоугольный треугольник). Последняя формула является аналогичной той, которая была приведена в предыдущем пункте.

Проведенные выше вычисления демонстрируют, как работать с векторными и скалярными величинами моментов сил, чтобы не допустить ошибок.

Физический смысл величины M¯

Поскольку два рассмотренных в предыдущих пунктах случая связаны с вращательным движением, то можно догадаться, какой смысл несет момент силы. Если сила, действующая на материальную точку, является мерой увеличения скорости линейного перемещения последней, то момент силы — это мера ее вращательной способности применительно к рассматриваемой системе.

Приведем наглядный пример. Любой человек открывает дверь, взявшись за ее ручку. Также это можно сделать, если толкнуть дверь в зоне ручки. Почему никто не открывает ее, толкая в области петель? Очень просто: чем ближе к петлям приложена сила, тем труднее открыть дверь, и наоборот. Вывод предыдущего предложения следует из формулы для момента (M = d*F), откуда видно, что при M = const величины d и F находятся в обратной зависимости.

Момент силы — аддитивная величина

Во всех рассмотренных выше случаях имела место лишь одна действующая сила. При решении же реальных задач дело обстоит гораздо сложнее. Обычно на системы, которые вращаются или находятся в равновесии, действуют несколько сил кручения, каждая из которых создает свой момент. В этом случае решение задач сводится к нахождению суммарного момента сил относительно оси вращения.

Суммарный момент находится путем обычной суммы отдельных моментов для каждой силы, однако, следует не забывать использовать правильный знак для каждого из них.

Пример решения задачи

Для закрепления полученных знаний предлагается решить следующую задачу: необходимо вычислить суммарный момент силы для системы, изображенной на рисунке ниже.

Мы видим, что на рычаг длиной 7 м действуют три силы (F1, F2, F3), причем они имеют разные точки приложения относительно оси вращения. Поскольку направление сил перпендикулярно рычагу, то нет необходимости применять векторное выражение для момента кручения. Можно рассчитать суммарный момент M, используя скалярную формулу и не забывая о постановке нужного знака. Поскольку силы F1 и F3 стремятся повернуть рычаг против часовой стрелки, а F2 — по часовой стрелке, то момент вращения для первых будет положительным, а для второй — отрицательным. Имеем: M = F1*7-F2*5+F3*3 = 140-50+75 = 165 Н*м. То есть суммарный момент является положительным и направлен вверх (на читателя).

4.1: Направление момента

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

70224

• Дэниел У. Бейкер и Уильям Хейнс
• Университет штата Колорадо via Engineeringstatics

В двумерной задаче направление момента можно легко определить путем проверки по часовой или против часовой стрелки. Вращение против часовой стрелки соответствует вектору момента, направленному за пределы страницы, и считается положительным.

В трехмерном пространстве вектор момента может указывать в любом направлении в пространстве, и его труднее визуализировать. Направление определяется правилом правой руки .

Чтобы применить правило правой руки, сначала установите0038 вектор положения \(\vec{r}\text{.}\), указывающий из центр вращения в точку приложения силы или другую точку на линии ее действия. Если вы выровняете большой палец с вектором положения, а указательный палец с вектором силы, то ваш средний палец укажет направление вектора момента \(\vec{M}\text{.}\) В качестве альтернативы, вы можете выровнять указательный палец палец с вектором положения и ваш средний палец с вектором силы, и ваш большой палец будет указывать в направлении вектора момента.

Рисунок 4.1.1. Два способа применения правила правой руки для определения направления момента.

Другим подходом является метод «точка-и-завиток». Начните с плоской руки и кончиков пальцев, направленных вдоль вектора положения \(\vec{r}\), указывающего от центра вращения до точки на линии действия силы. Отрегулируйте руку так, чтобы вектор силы \(\vec{F}\) скручивал пальцы. Затем ваш большой палец определяет направление момента \(\vec{M}\text{.}\)

      Рисунок 4.1.2. Техника правила правой руки «укажи и поверни» для моментов.

Любой из этих методов можно использовать для определения направления момента. Все они дают одинаковый результат, поэтому вам не нужно изучать их все, но убедитесь, что у вас есть хотя бы один метод, который вы можете использовать точно и последовательно.

---

Эта страница под названием 4.1: Direction of a Moment распространяется под лицензией CC BY-NC-SA 4.

0 и была создана, изменена и/или курирована Дэниелом У. Бейкером и Уильямом Хейнсом (Engineeringstatics) посредством исходного контента, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэниел В. Бейкер и Уильям Хейнс

   Лицензия

   СС BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@https://engineeringstatics. org

крутящий момент — Как определить направление моментов (путаница)?

Задавать вопрос

Спросил 1 год, 7 месяцев назад

Изменено 1 год, 7 месяцев назад

Просмотрено 577 раз

$\begingroup$

Мой учитель показывает мне несколько способов вычисления момента и его направления. В этом примере она собирается использовать принцип моментов, чтобы решить это (т.е. разложить на компоненты)

Но больше всего у меня проблем с определением направления момента.

Я читал описание в википедии (правило хвата правой рукой), но много раз пытался понять, почему сила x отрицательна? Мы используем соглашение, что против часовой стрелки = положительное и по часовой стрелке = отрицательное.

Может кто-нибудь объяснить и помочь мне визуализировать это?

обновление:

Я включил изображение своей руки (RHGR), чтобы показать вам, что я имею в виду. И, как вы можете видеть, это против часовой стрелки

• крутящий момент
• крутящий момент

$\endgroup$

$\begingroup$

Как и для большинства величин, связанных с вращением, вектор, представляющий момент (или крутящий момент), определяется как направленный вдоль оси вращения. (Ось обычно представляет собой одно направление, связанное с вращающимся объектом, которое не меняется со временем.) Выбор правила правой руки является произвольным (но общепринятым). Это легко запомнить. Согните пальцы правой руки вокруг оси в направлении вращения (которое будет вызвано крутящим моментом). Затем большой палец правой руки указывает направление (вдоль оси) вектора, представляющего крутящий момент. (То же правило можно использовать для угла, угловой скорости, углового ускорения и углового момента.