1. Электрический заряд. Закон кулона.

ОБЩИЕ СОВЕТЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

Можно решить любую задачу,

если смотреть на неё достаточно долго.

А. Б. Ходулёв

Сборник содержит свыше 400 задач разной степени трудности, систематизированных по разделам программы курса «Электромагнетизм», читаемого автором студентам специальности «Физика» Волгоградского государственного технического университета. Характер большинства задач рассчитан на то, что студенты владеют не только школьным материалом физики и математики, но и основами математического анализа, векторного анализа и дифференциальных уравнений.

Задачи в сборнике условно разделены на два уровня: простые (номера без звёздочек) и сравнительно сложные (со звёздочкой). Задачи первого уровня – это, как правило, типовые, «утешительные», решаемые в два-три действия очевидным применением основных законов или уравнений электромагнетизма.

Задачи второго уровня можно назвать «интересными». Чтобы отыскать их рациональное решение, требуется не только свободное владение соответствующими разделами электромагнетизма и математики, но и хорошая сообразительность, физическая интуиция, опыт. Их решение – это некоторое искусство, где невозможно ответить на вопрос «а как до этого догадаться?». Например, не вдруг сообразишь, как применить свойство аддитивности потенциала при решении задачи о потенциале изолированного нейтрального металлического шара, если вблизи него находится точечный заряд. Даже закон сохранения энергии в электромеханической или в чисто электрической системе записать правильно зачастую нелегко.

Все законы и соотношения электромагнетизма в данном сборнике записаны только в системе СИ. В этой системе следует решать и все предложенные задачи.

______________________________

При решении физических задач следует придерживаться следующих общих рекомендаций и советов.

1. Решение практически каждой задачи должно начинаться с рисунка или схемы, поясняющей её сущность. На рисунке (схеме) должны быть указаны основные величины, входящие в задачу. Если они не входят в условие, но нужны при решении, их надо ввести самим. Если задача связана, например, с определением токов или напряжений в электрической цепи, то совершенно необходимо ввести на схеме стрелки токов и напряжений, а также направления обхода контуров. Эти стрелки определяют знаки в уравнениях Кирхгофа. Если задача связана с электрическим или магнитным полями, то обязательно должны быть указаны направления этих полей. Правильный и аккуратно выполненный рисунок со стрелками и символами хорошо дополняет, а иногда и заменяет словесные комментарии к задаче (а комментарии в задаче совершенно необходимы!). Но самое главное – правильный рисунок или схема существенно облегчает и подсказывает само решение, помогает

подступиться к задаче.

2. Сделав рисунок и уяснив суть задачи, нужно кратко записать её условие: в столбик записывается, что дано и что требуется определить.

3. Необходимо твёрдо запомнить: просто «по формулам» задачи не решаются. Конечно, основные законы, определения физических величин, некоторые базовые формулы и уравнения знать надо, но для решения задачи этого недостаточно, как недостаточно знания ходов фигур для игры в шахматы. Для решения более или менее сложных задач рецептов нет. Необходимо овладеть искусством применения законов и определений, вúдением и пониманием физических процессов, связанных с данной задачей. Это достигается только личным упорством, тренировкой в решении ряда

типовых задач, в которых использование того или иного закона очевидно.

4. Каждую задачу надо решать, как правило, в общем виде, т. е. в буквенных обозначениях. Решение в общем виде не только позволяет «увидеть» поведение искомой величины, её зависимость от других параметров, но и судить о правильности решения.

5. Получив решение в общем виде, следует, прежде всего, проверить его размерность. Неверная размерность – первый признак того, что в преобразования где-то вкралась ошибка. Далее, если возможно, надо исследовать поведение решения в предельных частных случаях, которые обычно очевидны. Так например, если найден ток через какой-либо резистор, то при его сопротивлении

R ток через него должен стремиться к нулю. Такого рода проверки хотя и не гарантируют правильности решения, но вселяют уверенность в этом.

Особо внимательно следует относиться ко всякого рода разностям в знаменателях: при некотором соотношении между величинами знаменатель может обратиться в ноль. Нужно обязательно проанализировать, не приводит ли это к физической нелепости.

6. Убедившись в общей непротиворечивости аналитического (буквенного) решения и правильных размерностях, можно подставлять численные данные. Чтобы здесь не ошибиться, все данные надо подставлять в единой системе СИ, тогда и результат автоматически будет в системе СИ. Точность вычислений должна соответствовать точности исходных данных: обычно это 2-3 значащие цифры.

Доведение задачи «до числа» – это важный завершающий этап её решения. Не следует относиться к этой процедуре пренебрежительно.

7. Получив численный ответ, следует убедиться в его правдоподобности. Так например, если напряжение на каким-либо элементе цепи постоянного тока получилось больше напряжения генератора, то либо при решении, либо при вычислениях где-то сделана ошибка.

8. Выбранной в условии символики следует придерживаться на протяжении всей задачи. Так например, если в исходных данных ток обозначен буквой i, то далее нельзя тот же ток обозначать прописной I. Если напряжений в цепи много, то надо индексами указывать, какое именно напряжение имеется в виду: и₁, и₂ или, например, и_ab.

Вновь вводимые в задаче промежуточные символы должны быть обязательно описаны словами, например: «Пусть dB – поле малого элемента кольца с током i».

Неописанными символами оперировать нельзя. Некоторую символику допустимо и удобно вводить не словесно, а на аккуратно выполненных рисунках.

9. На обдумывание задачи не рационально тратить слишком много времени. Если за 20-30 минут упорных размышлений и поисков подступы к данной задаче не найдены, то, скорее всего, они не будут найдены и далее, так как наступает утомление. Только после этого можно посмотреть ответ или решение. Но лучше оставить задачу до следующего дня и попробовать подступиться к ней ещё раз. Не надо быстро сдаваться, каждая нерешённая задача должна задевать самолюбие, только так можно продвинуться вперёд. Если же заглядывать в ответы и решения сразу, едва прочитав условие, то вы не научитесь решать задачи никогда. Но решив задачу самостоятельно, свериться с ответом совершенно естественно и полезно.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

1.1. Базовые соотношения

Закон Кулона: F₂₁ == −F₁₂ , .

Определение электрического поля Е: E = F/q.

Принцип суперпозиции: Е ==Е₁ + Е₂ +…+ Е_N

.

Теорема Гаусса: ,div E = .

Электрические поля стандартных объектов:

а) поле точечного заряда: Е =,.

б) поле равномерно заряженной плоскости: .

в) поле равномерно заряженной нити: .

г) поле равномерно заряженной сферы: Е_in = 0, .

д) поле равномерно заряженного шара: ,

е) поле на оси заряженного кольца: .

1.2. Задачи

1.1. Каков суммарный заряд всех атомных ядер в песчинке углерода (угля, алмаза, графита) массой 1 мг? С какой силой отталкивались бы две такие песчинки на расстоянии 100 м, если бы у них были удалены все электроны?

1. 2. В некоторой области пространства поле Е отсутствовало, но когда туда поместили заряженный шарик, то на него стала действовать электрическая сила. Почему?

1.3. Положительный и отрицательный точечные заряды притягиваются друг к другу с силой F. Как изменится эта сила, если между ними поместить шар из металла или диэлектрика?

1.4. Могут ли два одноименно заряженных металлических шара притягиваться?

1.5. Два одинаковых маленьких шарика массами m имеют одинаковые заряды. Шарики подвешены на нитях одинаковой длины l, закрепленных в одной точке. В результате кулоновского отталкивания каждый шарик отклонился на угол  от вертикали. Определить заряд q каждого шарика.

1.6. Два одинаковых одноимённых точечных заряда q расположены на некотором расстоянии друг от друга. Какой заряд Q надо поместить между ними, чтобы вся система находилась в равновесии?

1. 7. Три одинаковых одноименных заряда q расположены в вершинах равностороннего треугольника. Какой заряд Q надо поместить в центр треугольника, чтобы система находилась в равновесии?

1.8. Четыре одинаковых одноименных заряда q расположены в вершинах квадрата. Какой заряд Q надо поместить в центр квадрата, чтобы система находилась в равновесии?

1.9*. Множество точечных зарядов (например, электронов) образует однородное тонкослойное сферическое облако, общий заряд которого равен q. Какой точечный заряд Q надо поместить в центр этого облака, чтобы удержать его от развала, т. е. чтобы система находилась в равновесии?

1.10. В вершинах равностороннего треугольника со стороной а находятся заряды +q, +q и – q. Вычислить напряженность поля Е в центре треугольника.

1.11. Заряд q₁ = +4q помещён в точке х₁ = 0 оси х, а заряд q₂ = –q – в точке х₂ = 6. Каков должен быть третий заряд q₃ и в какой точке х₃ его надо поместить, чтобы система находилась в равновесии?

1.12. Заряд q₁ = +4q помещён в точке х₁ = 0 оси х, а заряд q₂ = +q – в точке х₂ = 6. Каков должен быть третий заряд q₃ и в какой точке х₃ его надо поместить, чтобы система находилась в равновесии?

1.13. Доказать, что если два одинаковых металлических шарика, заряженные одноимённо неравными зарядами q₁и q₂, сдвинуть до касания, а затем вновь развести на исходное расстояние, то сила их отталкивания увеличится, и тем больше, чем больше разность (q₁ – q₂).

1.14. В центр тонкого проволочного кольца радиусом R с зарядом q поместили точечный заряд Q того же знака. Если Q ≫ q, то сила натяжения кольца будет вызвана в основном зарядом Q. Вычислить эту силу.

1.15*. Четыре положительных заряда q, Q, q и Q связаны четырьмя одинаковыми нитями, как показано на рис. 1.1. Вычислить угол , соответствующий равновесной геометрии системы, если Q = 2q.

1.16*. Четыре положительных заряда q, q и Q, Q связаны пятью одинаковыми нитями длиной l каждая, как показано на рис. 1.2. Определить натяжение F диагональной нити.

1.17. Кольцо радиусом R из тонкой проволоки имеет заряд q. Определить поле Е на оси кольца и изобразить график функции Е(х). Вычислить максимальное значение Е_max на оси и соответствующую координату х_m.

1.18*. Тонкий круглый диск радиусом R имеет заряд q, равномерно распределённый по его поверхности. Определить: 1) распределение поля Е(х) на оси диска (на оси х с нулём в центре диска) и построить соответствующий график; 2) поле Е вблизи поверхности диска, т. е. при х → 0.

1.19. Отрезок нити, заряженный с погонной плотностью γ, изогнут в виде полукольца радиусом R. Найти поле Е в центре этого полукольца.

1.20*. Вычислить напряжённость поля Е в центре полусферы радиусом R, по поверхности которой равномерно распределён заряд q.

1.21*. Полусфера равномерно заряжена по поверхности положительным зарядом. Применяя принцип суперпозиции, определить правильное направление вектора электрического поля Е в точке М экваториальной плоскости, показанной на рис. 1.3.

1.22. Используя принцип суперпозиции, вычислить поле Е тонкой прямой бесконечно длинной нити, равномерно заряженной с погонной плотностью γ.

1.23. Отрезок прямой нити длиной 2а имеет заряд q, равномерно распределённый по его длине. Определить поле Е на оси х, проходящей через середину отрезка и перпендикулярной ему.

1.24. Отрезок прямой нити длиной 2а имеет заряд q, равномерно распределённый по его длине. Определить поле Е на линии продолжения отрезка (вне его). Начало координат взять в центре отрезка.

1.25. Две длинные прямые параллельные нити равномерно заряжены каждая с погонной плотностью +γ. Расстояние между нитями равно 2а. Определить поле Е в плоскости симметрии между ними, т. е. Е(х), где х – ось, лежащая в этой плоскости и перпендикулярная нитям. Построить график Е(х). Вычислить расстояние х_m, где это поле максимально.

1.26. Две длинные прямые параллельные нити равномерно заряжены с погонными плотностями +γ и −γ. Расстояние между нитями равно 2а. Определить поле Е в плоскости симметрии между ними, т. е. Е(х), где х – ось, лежащая в этой плоскости и перпендикулярная нитям. Построить график Е(х). Вычислить расстояние х_m, где это поле максимально.

1.27*. Имеется полубесконечная прямая нить, равномерно заряженная с погонной плотностью γ (Кл/м). Соосно с ней, с центром на её основании находится тонкое кольцо радиусом R, несущее заряд q. Найти силу взаимодействия кольца и нити.

1.28. Полубесконечный круглый цилиндр радиусом R заряжен равномерно по поверхности с погонной плотностью заряда γ (Кл/м). В центре его основания помещён точечный заряд q. Какая сила действует на этот заряд?

1.29. Сплошной длинный цилиндр радиусом R равномерно заряжен с объёмной плотностью ρ. Вычислить его погонную плотность заряда γ. Определить поле Е внутри и вне этого цилиндра и изобразить график Е(r).

1.30. Заряд q равномерно распределён по объёму шара радиусом R. Найти поле Е внутри и вне шара и построить график E(r).

1.31*. Согласно одной из моделей, ядро атома водорода окружено сферически симметричной электронной оболочкой с плотностью отрицательного заряда ρ(r) = C, гдеа = 5·10⁻¹¹ м – эффективный радиус атома водорода, С – константа, определяемая из условия, чтобы общий заряд оболочки был равен «–е». Определить в единицах «е» заряд оболочки внутри сферы радиусом а. Определить величину поля Е на поверхности этой сферы с учётом наличия в ней точечного ядра водорода.

1.32*. Шар заряжен равномерно по объёму с объёмной плотностью ρ. В шаре имеется сферическая полость, центр которой смещён относительно центра шара на расстояние а (а – вектор смещения). Найти поле Е внутри полости. Влиянием вещества шара пренебречь.

1.33. Две параллельные плоскости, находящиеся на расстоянии d друг от друга, равномерно заряжены с поверхностными плотностями +3σ и –σ. Определить величину и направление поля Е между ними и вне их. Изобразить картину линий поля Е этой системы.

1.34*. Две параллельные плоскости имеют равномерно распределённые заряды с поверхностными плотностями +₀ и +2₀. Между ними параллельно им вдвинули незаряженную металлическую пластину. Найти поверхностную плотность зарядов ±, индуцированных на сторонах этой пластины.

1.35*. Две близко расположенные параллельные металлические пластины зарядили с плотностями +σ₀₁ и +σ₀₂ соответственно. Найти поверхностные плотности заряда на внешних (σ₁, σ₄) и на внутренних (σ₂, σ₃) сторонах пластин.

1.36*. Слева от бесконечной плоскости однородное электрическое поле равно Е₁, а справа Е₂ (рис. 1.4). Найти величину и «направление» давления p, которое испытывает плоскость со стороны электрического поля.

1.37*. Известно, что у поверхности длинной широкой ленты, несущей поверхностный заряд σ (Кл/м), электрическое поле Е = σ/(2ε₀). Чему равно поле Е₁ в плоскости ленты на расстоянии х от её края? Ширина ленты равна а. При каком х поле Е₁ = Е?

1.38*. Бусинка массой m, имеющая заряд q, может без трения двигаться по нити, натянутой горизонтально между двумя одинаковыми точечными зарядами Q того же знака. Длина нити 2l. Определить частоту ω малых продольных колебаний бусинки около положения равновесия.

1.39*. Согласно идее Томсона, атом представляет собою шарообразное облако, равномерно заряженное по объёму с общим зарядом е = +1,6·10^-19Кл. Внутри этого облака колеблется «точечный» электрон с зарядом –е и массой m = 0,9·10⁻³⁰ кг. Полагая, что положительное облако значительно тяжелее электрона и не деформируется при его колебаниях, а радиус облака R = 0,1 нм (это примерный размер реального атома), найти длину волны  (нм), излучаемой атомом Томсона при колебаниях электрона около центра облака.

1.40*. В прямой длинной трубке с закрытыми торцами помещены четыре шарика с одинаковыми зарядами, которые могут свободно двигаться вдоль трубки. Очевидно, что два крайних шарика будут прижаты к торцам трубки кулоновскими силами. Найти положения средних шариков.

Электрическое поле (к задачнику Рымкевича для 10-11 классов)

Электрическое поле к задачнику по физике за 10-11 классы «Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений» Рымкевич А.П.

Электрическое поле и электрический заряд — первичные понятия, которые не определяются аналогично понятиям точки и прямой в геометрии. Неподвижный заряд создает вокруг себя электрическое поле. Если замкнутая система обладала зарядом q, то при любых изменениях в ней заряд q сохраняется. Это фундаментальное утверждение носит название закона сохранения заряда.

Точечным зарядом называется заряд исчезающе малых размеров. Из эксперимента известно, что два точечных заряда q₁ и q₂ на расстоянии r взаимодействуют с силой F, значение которой определяется законом Кулона:

где

— коэффициент пропорциональности. Когда заряды одноименные, то они отталкиваются, когда разноименные — притягиваются.

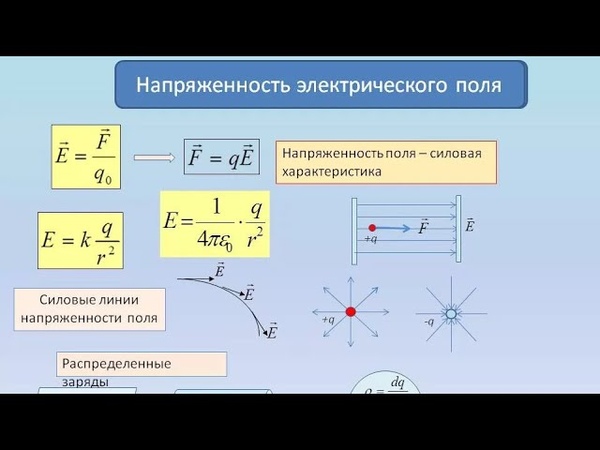
Силовой характеристикой электрического поля является вектор напряженности E;. Рассмотрим некоторый заряд q, внесенный в электрическое поле E;. Тогда на него будет действовать сила F;, которая определяется формулой: F; = qE;. Это формула может служить определением вектора напряженности электрического поля. Для графического представления электростатического поля пользуются понятием линий напряженности. Эти линии начинаются на положительных зарядах и заканчиваются на отрицательных. Касательная в каждой точке линии напряженности направлена также, как и вектор E; . Если имеется N зарядов, каждый из которых создает свое поле E₁;, E₂;,…, E_N; , то полная напряженность в любой точке пространства E; определяется как векторная сумма этих напряженностей (принцип суперпозиции):

Для точечного заряда q значение напряженности E в точке, удаленной от него на расстоянии r, выражается формулой:

Проводником называется тело, содержащее свободные заряды. Если мы сообщим проводнику некоторый заряд q, то он распределится по поверхности, а внутри проводника поле будет равно нулю. Поверхностной плотностью о называется отношение заряда к площади поверхности проводника

Поле заряженного проводящего шара снаружи от него совпадает с полем точечного заряда, а внутри него равно нулю. Поле бесконечной заряженной проводящей плоскости с поверхностной плотностью заряда о определяется формулой:

где ε₀ = 8,854⋅10^-12 Ф/м — электрическая постоянная.

Диэлектриком называется тело, в котором отсутствуют свободные заряды. При помещении диэлектрика в электрическое поле происходит его поляризация, при этом поле E в диэлектрике уменьшается в ε раз:

где E₀ — напряженность поля вне диэлектрика, ε — диэлектрическая проницаемость. При перемещении заряда q в электрическом поле E; на

расстояние

совершается работа A:

Изменение потенциальной энергии ΔW_P равно:

Потенциал φ — энергетическая характеристика электрического поля, он определяется формулой:

Эквипотенциальные поверхности — это такие поверхности, в каждой точке которых потенциал постоянен. Потенциал поля φ в некоторой точке пространства, созданный N зарядами, равен алгебраической сумме потенциалов φ₁, φ₂,…, φ_N созданных отдельными зарядами (принцип суперпозиции): φ = φ₁ + φ₂ + … +

φ_N— Потенциал поля точечного заряда q на расстоянии r от него определяется формулой:

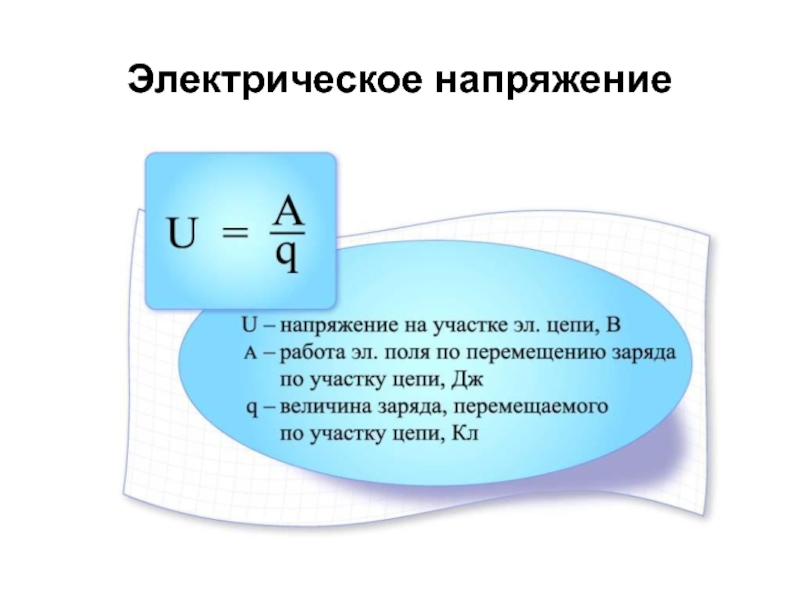
Напряжением U между точками A и B называется разность потенциалов:

где φ₁ — потенциал в точке A, φ₂ — потенциал в точке B. Напряжение U связано с напряженностью E электрического поля следующей формулой:

Конденсатором называется устройство, способное накапливать заряд. Емкость конденсатора C определяется как отношение заряда q на его обкладках к приложенному напряжению U:

Емкость не зависит от заряда и напряжения на нем, а определяется его геометрическими свойствами (формой и размером) и родом среды. Для плоского конденсатора емкость равна:

где ε — диэлектрическая проницаемость среды между обкладками, S — площадь обкладок, d — расстояние между обкладками. Энергия заряженного конденсатора W определяется формулой:

Плотность энергии ω электрического поля E выражается формулой:

Пересмотр концепции поля – Колледж физики, главы 1-17

18 Электрический заряд и электрическое поле

Резюме

• Описать силовое поле и рассчитать напряженность электрического поля, создаваемого точечным зарядом.
• Рассчитайте силу, действующую на пробный заряд со стороны электрического поля.
• Объясните взаимосвязь между электрической силой (F) на испытательном заряде и напряженностью электрического поля (E).

Контактные силы, такие как между бейсбольным мячом и битой, объясняются в малом масштабе взаимодействием зарядов в атомах и молекулах в непосредственной близости. Они взаимодействуют через силы, включающие Кулоновская сила . Действие на расстоянии — это сила между объектами, которые находятся недостаточно близко, чтобы их атомы могли «соприкоснуться». То есть они разделены более чем несколькими атомными диаметрами.

Например, заряженная резиновая расческа притягивает нейтральные кусочки бумаги на расстоянии под действием кулоновской силы. Очень полезно представить объект, окруженный в пространстве силовым полем . Силовое поле переносит силу на другой объект (называемый тестовым объектом) на некотором расстоянии.

Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. 2}[/latex], для точечный заряд (частица, имеющая заряд [латекс]\boldsymbol{Q}[/латекс]), действующий на пробный заряд [латекс]\boldsymbol{q}[/латекс] на расстоянии [латекс]\boldsymbol {r}[/latex] (см. [ссылка]). Как величина, так и направление кулоновского силового поля зависят от [латекс]\boldsymbol{Q}[/латекс] и пробного заряда [латекс]\boldsymbol{q}[/латекс].

Рис. 1. Поле кулоновских сил, обусловленное положительным зарядом Q , действует на два разных заряда. Оба заряда находятся на одинаковом расстоянии от Q . (a) Поскольку q ₁ положительна, сила F 1 , действующая на нее, является отталкивающей. (b) Заряд q ₂ отрицателен и больше по величине, чем q ₁ , поэтому сила F 9004 5 2 действует на него привлекательнее и сильнее, чем Ф ₁ . Таким образом, кулоновское силовое поле не является уникальным в любой точке пространства, поскольку оно зависит от пробных зарядов 9.0017 q ₁ и q ₂ а также плата Q .

Для упрощения мы бы предпочли иметь поле, которое зависит только от [латекс]\boldsymbol{Q}[/латекс] , а не от тестового заряда [латекс]\жирныйсимвол{q}[/латекс]. Электрическое поле определяется таким образом, что оно представляет собой только создающий его заряд и уникально в каждой точке пространства. В частности, электрическое поле [латекс]\boldsymbol{E}[/латекс] определяется как отношение кулоновской силы к пробному заряду:

[латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{F}{q}}[/латекс],

где [латекс]\boldsymbol{F}[/латекс] — электростатическая сила (или кулоновская сила), действующая на положительный пробный заряд
[латекс]\boldsymbol{q}[/латекс]. Понятно, что [латекс]\boldsymbol{E}[/латекс] находится в том же направлении, что и
[латекс]\жирныйсимвол{F}[/латекс]. 2 }[/латекс] . Таким образом, величина электрического поля [латекс]\boldsymbol{E}[/латекс] для точечного заряда равна 92}}[/латекс]

Таким образом видно, что электрическое поле зависит только от заряда [латекс]\boldsymbol{Q}[/латекс] и расстояния [латекс]\boldsymbol{r}[/латекс]; он полностью не зависит от тестового заряда [латекс]\boldsymbol{q}[/латекс].

Расчет электрического поля точечного заряда

Расчет напряженности и направления электрического поля [латекс]\boldsymbol{E}[/латекс], создаваемого точечным зарядом 2,00 нКл (нанокулонов) на расстоянии 5,00 мм от заряда. 95 \;\textbf{N} / \textbf{C}.} \end{array}[/latex]

Обсуждение

Эта напряженность электрического поля одинакова в любой точке на расстоянии 5,00 мм от заряда [latex]\boldsymbol{Q}[/latex], который создает поле. Он положительный, что означает, что он имеет направление, указывающее в сторону от заряда [латекс]\boldsymbol{Q}[/латекс].

Расчет силы, действующей на точечный заряд электрическим полем

Какую силу электрическое поле, найденное в предыдущем примере, действует на точечный заряд [латекс]\boldsymbol{-0,250 \;\mu \textbf{C}} [/латекс]?

Стратегия

Поскольку мы знаем напряженность электрического поля и заряд в поле, силу, действующую на этот заряд, можно рассчитать, используя определение электрического поля [латекс]\boldsymbol{\textbf{E} = \textbf{ F}/q}[/latex] заменены на [latex]\boldsymbol{ \textbf{F} = q \textbf{E}}[/latex]. 5}[/latex] N/C, таким образом, 95 \;\textbf{N} / \textbf{C})} \\[1em] & \boldsymbol{0.180 \;\textbf{N}.} \end{массив}[/latex]

Потому что [латекс] \boldsymbol{q}[/latex] отрицательна, сила направлена ​​против направления поля.

Обсуждение

Сила притяжения, как и ожидалось для разных зарядов. (Поле было создано положительным зарядом, а здесь действует на отрицательный заряд.) Заряды в этом примере типичны для обычного статического электричества, а полученная небольшая сила притяжения аналогична силам, возникающим при статическом прилипании и подобных ситуациях.

PhET Explorations: Electric Field of Dreams

Играй в мяч! Добавьте заряды в Поле Снов и посмотрите, как они реагируют на электрическое поле. Включите фоновое электрическое поле и отрегулируйте направление и величину.

Рисунок 2. Электрическое поле мечты

• Поле электростатической силы, окружающее заряженный объект, распространяется в пространстве во всех направлениях.
• Электростатическая сила, действующая точечным зарядом на пробный заряд на расстоянии [латекс]\boldsymbol{r}[/латекс], зависит от заряда обоих зарядов, а также от расстояния между ними.
• Электрическое поле [latex]\textbf{E}[/latex] определяется как

  [латекс]\boldsymbol{E =}[/латекс] [латекс]\boldsymbol{\frac{\textbf{F}}{q,}}[/латекс]

  , где [латекс]\textbf{F}[/латекс] — кулоновская или электростатическая сила, действующая на небольшой положительный пробный заряд [латекс]\boldsymbol{q}[/латекс]. [latex]\textbf{E}[/latex] имеет единицы N/C.

• Величина электрического поля [латекс]\textbf{E}[/латекс], создаваемого точечным зарядом [латекс]\boldsymbol{Q}[/латекс] , равна 92}}.[/латекс]

  , где [латекс]\boldsymbol{r}[/латекс] — расстояние от [латекс]\жирныйсимвол{Q}[/латекс]. Электрическое поле [латекс]\boldsymbol{E}[/латекс] является вектором, и поля из-за множественных зарядов складываются подобными векторами.

 

 

поле

карта величины и направления силы, действующей на другие объекты, простирающейся в космос

Точечная оплата

Заряженная частица, обозначенная как [латекс]\boldsymbol{Q}[/латекс], создающая электрическое поле

испытательный заряд

Частица (обозначается как [латекс]\жирный символ{q}[/латекс]) с положительным или отрицательным зарядом, помещенная в электрическое поле, создаваемое точечным зарядом

«Нажми и узнай» — сумма оплаты

Родительская категория: Наука 9

Количество заряда, Q

Расчет количества заряда объекта

Электрон — это частица, которая отвечает за заряд объекта. Движение электронов к объекту определяет тип заряда, который будет иметь объект. Объект будет заряжен положительно там, где происходит потеря электронов, отрицательно заряжен там, где есть прирост или избыток электронов, и нейтрален там, где положительный и отрицательный заряды равны.

Общее количество электронов, осажденных или удаленных из объекта, будет определять количество (количество) заряда на объекте.

Таким образом, заряд одного электрона определяется как фундаментальная единица заряда. Заряд является фундаментальным измерением, которое не может быть получено из каких-либо других измерений. Заряд измеряется в кулонах

Символ заряда — « Q », а символ Кулона — « C ».

Количество заряда на одном отдельном электроне может быть математически определено равным очень небольшому количеству заряда.

Этот небольшой заряд равен 1,6 X 10 ^-19 Кл . Это небольшое количество заряда известно как основной заряд, и его символ равен e (чтобы напомнить нам, что это заряд одного отдельного электрона).