Нахождение вектора, перпендикулярного данному вектору, примеры и решения
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
Определение 1При условии значения угла между двумя ненулевыми векторами равным 90°( π2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Теорема 1Скалярное произведение двух ненулевых векторов a→ и b→ равном нулю для выполнения равенства a→, b→=0 достаточно для их перпендикулярности.
Доказательство 1Пусть заданные векторы a→ и b→ перпендикулярны, тогда выполним доказательство равенства a⇀, b→=0.
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на
Как найти вектор перпендикулярный двум другим
Начнем с постановки задачи.
Пусть нам требуется найти координаты вектора в трехмерном пространстве, который одновременно перпендикулярен двум не коллинеарным векторам 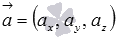 и
и 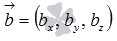 . Если векторы
. Если векторы  и
и 
 или
или  (о нахождении такого вектора мы говорили в предыдущем пункте).
(о нахождении такого вектора мы говорили в предыдущем пункте).Одно из решений такой задачи основано на использовании понятия векторного произведения векторов.
Нам известно, что векторное произведение векторов  и
и  представляет собой вектор, перпендикулярный одновременно и вектору
представляет собой вектор, перпендикулярный одновременно и вектору 
 . Таким образом, векторное произведение
. Таким образом, векторное произведение  является решением нашей задачи. В координатной форме оно имеет вид
является решением нашей задачи. В координатной форме оно имеет вид 
Разберем на примере.
Найдите координаты какого-нибудь вектора, перпендикулярного одновременно двум векторам 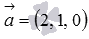
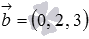 .
.Решением нашей задачи является векторное произведение заданных векторов. Найдем его (при необходимости смотрите статью вычисление определителя матрицы): 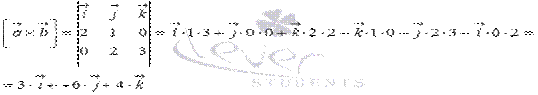
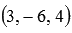 — один из векторов, одновременно перпендикулярный и вектору
— один из векторов, одновременно перпендикулярный и вектору 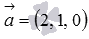 и
и 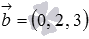 .
.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9816 —  | 7682 —
| 7682 —  или читать все.
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Скалярное произведение двух ненулевых векторов a → и b → равном нулю для выполнения равенства a → , b → = 0 достаточно для их перпендикулярности.
Пусть заданные векторы a → и b → перпендикулярны, тогда выполним доказательство равенства a ⇀ , b → = 0 .
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию a → и b → перпендикулярны, а, значит, исходя из определения, угол между ними 90 ° . Тогда имеем a → , b → = a → · b → · cos ( a → , b → ^ ) = a → · b → · cos 90 ° = 0 .
Вторая часть доказательства
При условии, когда a ⇀ , b → = 0 доказать перпендикулярность a → и b → .
По сути доказательство является обратным предыдущему. Известно, что a → и b → ненулевые, значит, из равенства a ⇀ , b → = a → · b → · cos ( a → , b → ) ^ найдем косинус. Тогда получим cos ( a → , b → ) ^ = ( a → , b → ) a → · b → = 0 a → · b → = 0 . Так как косинус равен нулю, можем сделать вывод, что угол a → , b → ^ векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство ( a → , b → ) = a x · b x + a y · b y , справедливое для векторов с координатами a → = ( a x , a y ) и b → = ( b x , b y ) , на плоскости и ( a → , b → ) = a x · b x + a y · b y для векторов a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .
Применим на практике и рассмотрим на примерах.
Проверить свойство перпендикулярности двух векторов a → = ( 2 , — 3 ) , b → = ( — 6 , — 4 ) .
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
( a → , b → ) = a x · b x + a y · b y = 2 · ( — 6 ) + ( — 3 ) · ( — 4 ) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → — j → и i → + 2 · j → + 2 · k → быть перпендикулярными.
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → — j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты ( 1 , — 1 , 0 ) и ( 1 , 2 , 2 ) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → — j → = 1 · 1 + ( — 1 ) · 2 + 0 · 2 = — 1 .
Выражение не равно нулю, ( i → + 2 · j → + 2 · k → , i → — j → ) ≠ 0 , а это означает, что векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны.
Даны векторы a → = ( 1 , 0 , — 2 ) и b → = ( λ , 5 , 1 ) . Найти значение λ , при котором данные векторы перпендикулярны.
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( — 2 ) · 1 = 0 ⇔ λ = 2
Ответ: векторы перпендикулярны при значении λ = 2 .
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
Дан треугольник А В С со сторонами А В = 8 , А С = 6 , В С = 10 см. проверить на перпендикулярность векторы A B → и A C → .
При перпендикулярности векторов A B → и A C → треугольник A B C считается прямоугольным. Тогда применим теорему Пифагора, где В С – гипотенуза треугольника. Равенство B C 2 = A B 2 + A C 2 должно выполниться. Отсюда следует, что 10 2 = 8 2 + 6 2 ⇔ 100 = 100 . Значит, А В и А С являются катетами треугольника А В С , следовательно, A B → и A C → перпендикулярны.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

Задан ненулевой вектор a → , лежащий на прямой а. Тогда заданный b → , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и a → . Если вектору i → перпендикулярен вектор j → или любой из векторов λ · j → при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b → , перпендикулярному a → = ( a x , a y ) , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a → = ( a x , a y ) . Для этого необходимо записать условие перпендикулярности векторов в такой форме a x · b x + a y · b y = 0 . Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = — a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = — a x · b x a y .
Дан вектор с координатами a → = ( — 2 , 2 ) . Найти перпендикулярный данному вектор.
Обозначим искомый вектор как b → ( b x , b y ) . Найти его координаты можно из условия перпендикулярности векторов a → и b → . Тогда получим: ( a → , b → ) = a x · b x + a y · b y = — 2 · b x + 2 · b y = 0 . Присвоим b y = 1 и подставим: — 2 · b x + 2 · b y = 0 ⇔ — 2 · b x + 2 = 0 . Отсюда из формулы получим b x = — 2 — 2 = 1 2 . Значит, вектор b → = ( 1 2 , 1 ) является вектором, перпендикулярным a → .
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a → = ( a x , a y , a z ) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .

Необходимо найти координаты b → , перпендикулярного ненулевому вектору a → = ( a x , a y , a z ) .
Пусть задан b → с координатами b x , b y и b z . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство a x · b x + a y · b y + a z · b z = 0 должно выполняться. Из условия a → — ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что a x ≠ 0 , ( a y ≠ 0 или a z ≠ 0 ). Следовательно, имеем право разделить на эту координату все неравенство a x · b x + a y · b y + a z · b z = 0 , получим выражение b x + a y · b y + a z · b z a x = 0 ⇔ b x = — a y · b y + a z · b z a x . Присваиваем координатам b y и b x любое значение, вычисляем значение b x , исходя из формулы, b x = — a y · b y + a z · b z a x . Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .
Рассмотрим доказательство на примере.
Дан вектор с координатами a → = ( 1 , 2 , 3 ) . Найти вектор, перпендикулярный данному.
Обозначим искомый вектор за b → = ( b x , b y , b z ) . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.
a ⇀ , b ⇀ = 0 ⇔ a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · b x + 2 · b y + 3 · b z = 0 ⇔ b x = — ( 2 · b y + 3 · b z )
Если значение b y = 1 , b z = 1 , тогда b x = — 2 · b y — 3 · b z = — ( 2 · 1 + 3 · 1 ) = — 5 . Отсюда следует, что координаты вектора b → ( — 5 , 1 , 1 ) . Вектор b → является одним из перпендикулярных векторов заданному.
Ответ: b → = ( — 5 , 1 , 1 ) .
Нахождение координат вектора, перпендикулярного двум заданным векторам
Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам a → ( a x , a y , a z ) и b → = ( b x , b y , b z ) . При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .
При решении применяется понятие векторного произведения векторов.
Векторным произведением векторов a → и b → называют вектор, одновременно перпендикулярный и a → и b → . Для решения данной задачи применяется векторное произведение a → × b → . Для трехмерного пространства имеет вид a → × b → = a → j → k → a x a y a z b x b y b z
Разберем подробнее векторное произведение на примере задачи.
Заданы векторы b → = ( 0 , 2 , 3 ) и a → = ( 2 , 1 , 0 ) . Найти координаты любого перпендикулярного вектора данным одновременно.
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 — k → · 1 · 0 — j → · 2 · 3 — i → · 0 · 2 = 3 · i → + ( — 6 ) · j → + 4 · k →
Ответ: ( 3 , — 6 , 4 ) — координаты вектора, одновременно перпендикулярного заданным a → и b → .
Понятие вектора и перпендикулярности векторов
Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Обозначение: $overline$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $overline$ (рис. 1).
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Введем теперь, непосредственно, определение коллинеарных векторов.
Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).
Попробуй обратиться за помощью к преподавателям
Также введем определение скалярного произведения, которое будет нам необходимо далее.
Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
Скалярное произведение также можно найти с помощью координат векторов следующим образом
$overline<α>overline<β>=α_1 β_1+α_2 β_2+α_3 β_3$
Признак перпендикулярности через пропорциональность
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.
Необходимость: Пусть нам даны векторы $overline<α>$ и $overline<β>$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство
Так как векторы $overline<α>$ и $overline<β>$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.
$overline<α>cdot overline<β>=|overline<α>||overline<β>|cos90^circ =|overline<α>||overline<β>|cdot 0=0$
Достаточность: Пусть верно равенство $overline<α>cdot overline<β>=0$. Докажем, что векторы $overline<α>$ и $overline<β>$ будут перпендикулярны друг другу.
По определению 6, будет верно равенство
Следовательно, векторы $overline<α>$ и $overline<β>$ будут перпендикулярны друг другу.
Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.
Найдем скалярное произведение для этих векторов через формулу, данную выше
$overline<α>cdot overline<β>=1cdot 2+(-5)cdot 1+2cdot frac<3><2>=2cdot 5+3=0$
Значит, по теореме 1, эти вектор перпендикулярны.
Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение
Введем вначале понятие векторного произведения.
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Чтобы найти векторное произведение, будем пользоваться формулой
Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.
Найти вектор, перпендикулярный к векторам с координатами $overline<α>=(1,2,3)$ и $overline<β>=(-1,0,3)$
Найдем векторное произведение данных векторов.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Как найти вектор перпендикулярный двум другим. Как найти вектор, перпендикулярный вектору
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Yandex.RTB R-A-339285-1
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
Определение 1
При условии значения угла между двумя ненулевыми векторами равным 90 ° (π 2 радиан) называют перпендикулярными .
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов .
Теорема 1
Скалярное произведение двух ненулевых векторов a → и b → равном нулю для выполнения равенства a → , b → = 0 достаточно для их перпендикулярности.
Доказательство 1
Пусть заданные векторы a → и b → перпендикулярны, тогда выполним доказательство равенства a ⇀ , b → = 0 .
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию a → и b → перпендикулярны, а, значит, исходя из определения, угол между ними 90 ° . Тогда имеем a → , b → = a → · b → · cos (a → , b → ^) = a → · b → · cos 90 ° = 0 .
Вторая часть доказательства
При условии, когда a ⇀ , b → = 0 доказать перпендикулярность a → и b → .
По сути доказательство является обратным предыдущему. Известно, что a → и b → ненулевые, значит, из равенства a ⇀ , b → = a → · b → · cos (a → , b →) ^ найдем косинус. Тогда получим cos (a → , b →) ^ = (a → , b →) a → · b → = 0 a → · b → = 0 . Так как косинус равен нулю, можем сделать вывод, что угол a → , b → ^ векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство (a → , b →) = a x · b x + a y · b y , справедливое для векторов с координатами a → = (a x , a y) и b → = (b x , b y) , на плоскости и (a → , b →) = a x · b x + a y · b y для векторов a → = (a x , a y , a z) и b → = (b x , b y , b z) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .
Применим на практике и рассмотрим на примерах.
Пример 1
Проверить свойство перпендикулярности двух векторов a → = (2 , — 3) , b → = (- 6 , — 4) .
Решение
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
(a → , b →) = a x · b x + a y · b y = 2 · (- 6) + (- 3) · (- 4) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Пример 2
Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → — j → и i → + 2 · j → + 2 · k → быть перпендикулярными.
Решение
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → — j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты (1 , — 1 , 0) и (1 , 2 , 2) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → — j → = 1 · 1 + (- 1) · 2 + 0 · 2 = — 1 .
Выражение не равно нулю, (i → + 2 · j → + 2 · k → , i → — j →) ≠ 0 , а это означает, что векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны.
Пример 3
Даны векторы a → = (1 , 0 , — 2) и b → = (λ , 5 , 1) . Найти значение λ , при котором данные векторы перпендикулярны.
Решение
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + (- 2) · 1 = 0 ⇔ λ = 2
Ответ: векторы перпендикулярны при значении λ = 2 .
И
Вектор перпендикулярный двум другим векторам. Как найти вектор, перпендикулярный вектору
Единичный вектор
находится:
,
где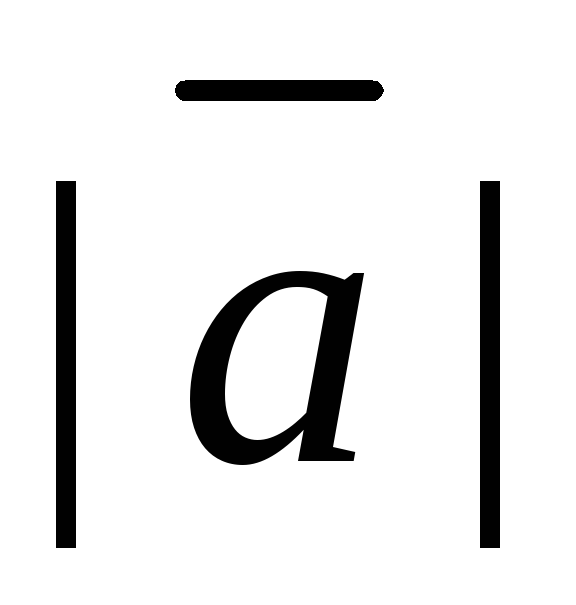 – модуль вектора.
– модуль вектора.
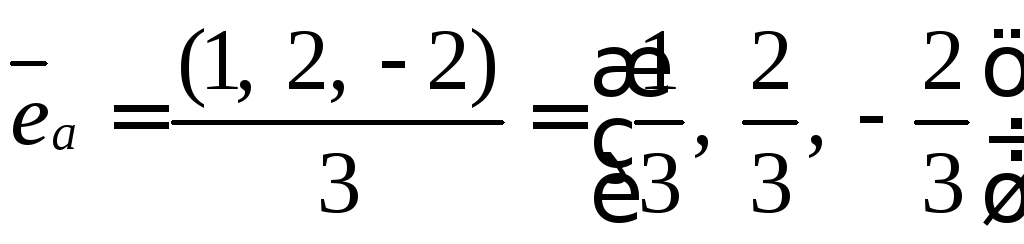
Ответ: 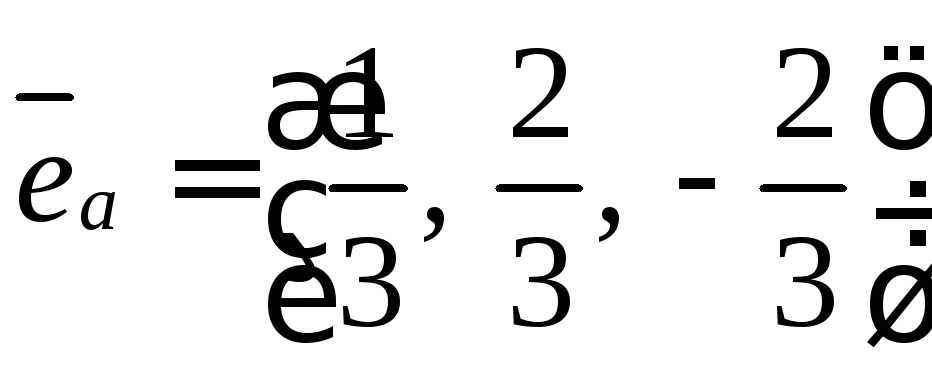 .
.
Примечание. Координаты единичного вектора должны быть не больше единицы.
6.3. Найти длину
и направляющие косинусы вектора  .
Сравните с ответом в предыдущем пункте.
Сделайте выводы.
.
Сравните с ответом в предыдущем пункте.
Сделайте выводы.
Длина вектора – это есть его модуль:
А направляющие косинусы мы можем найти по формуле одного из способов задания векторов:

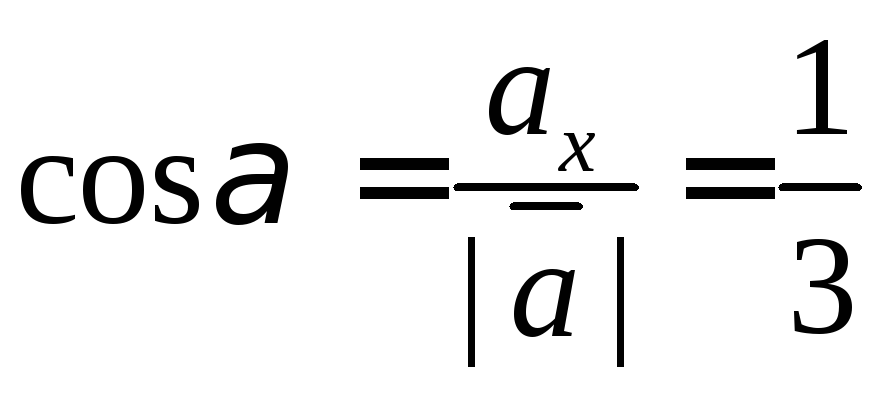
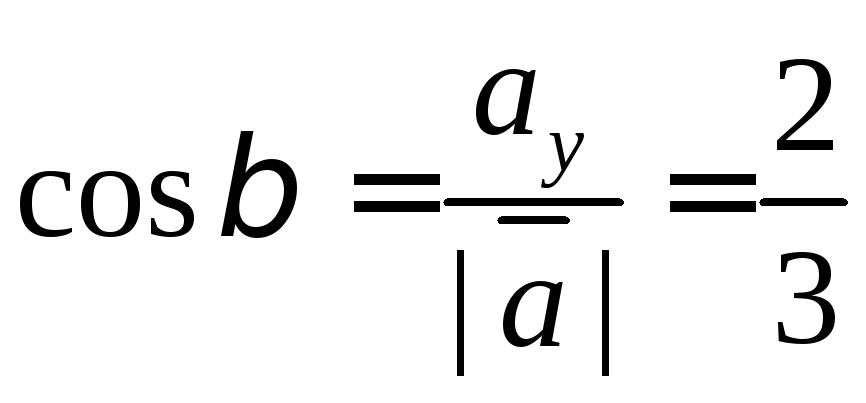
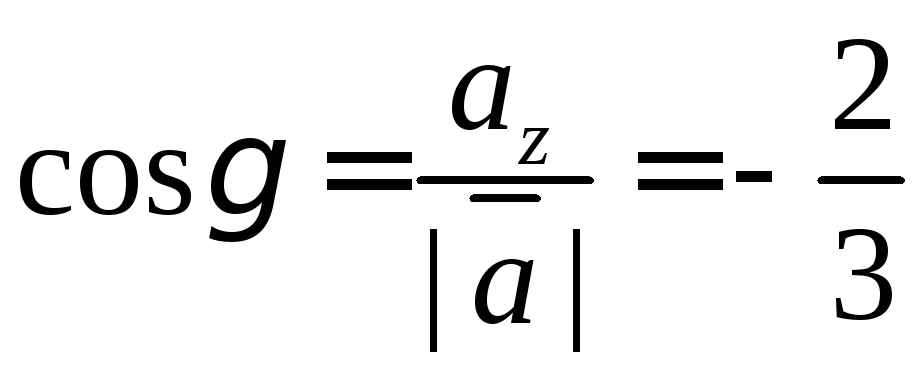
Из полученного мы видим, что направляющие косинусы это и есть координаты единичного вектора.
Ответ: 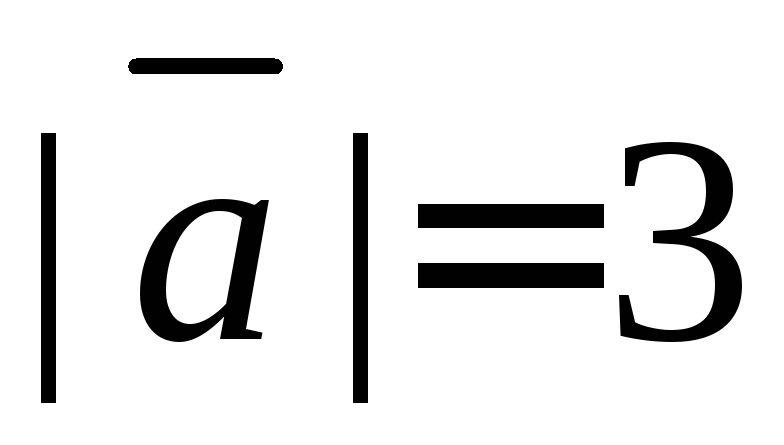 ,
,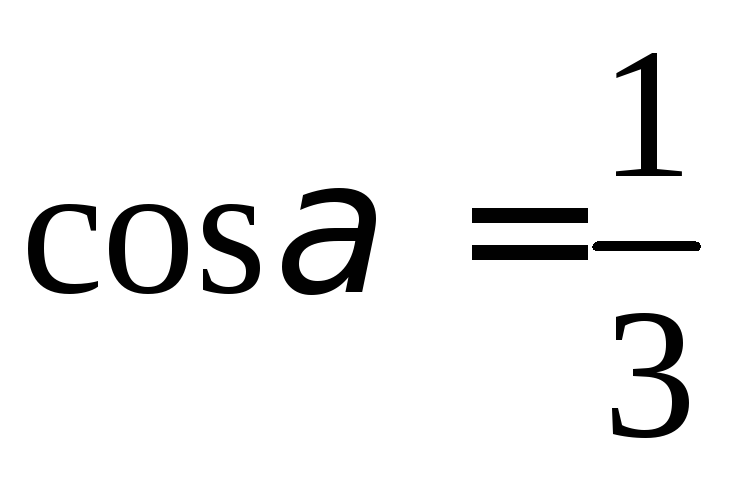 ,
,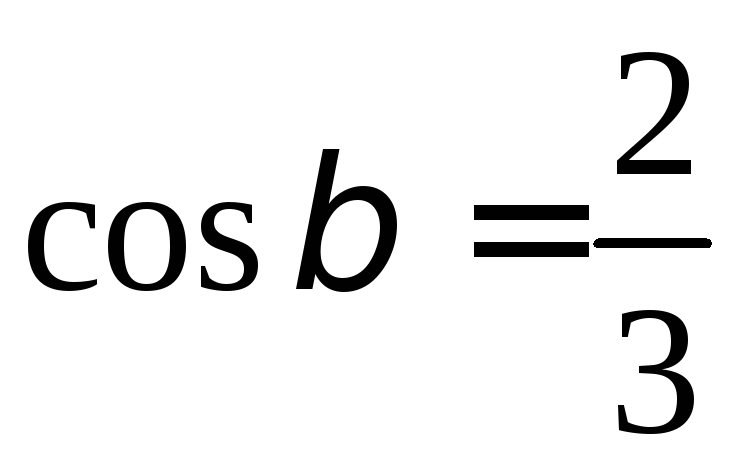 ,
,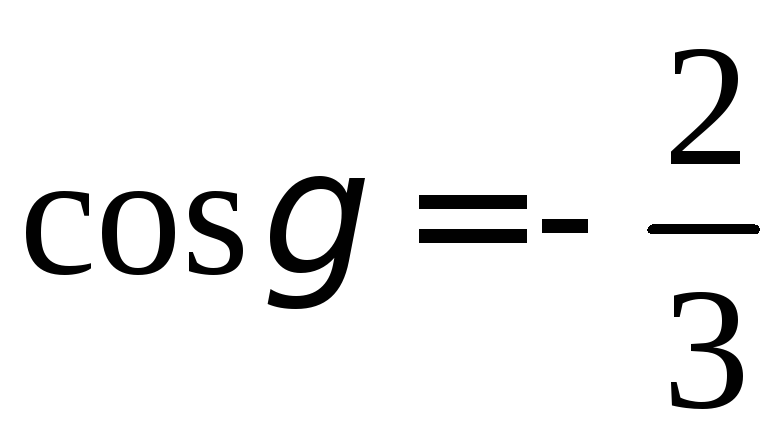 .
.
6.4. Найти 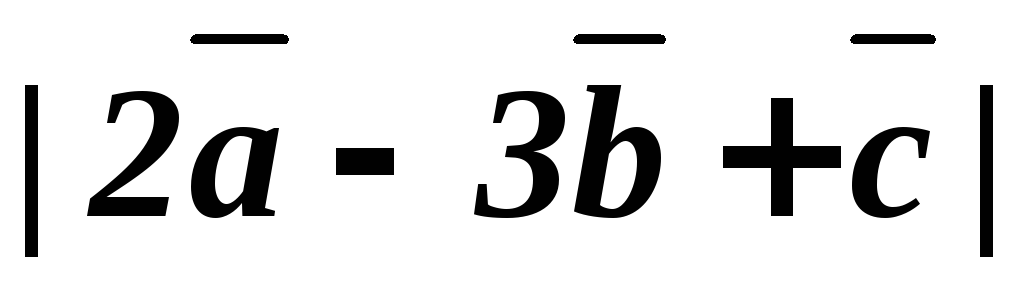 .
.
Необходимо выполнить действия умножения вектора на число, сложения и модуль.
Почленно перемножаем координаты векторов на число.
Почленно складываем координаты векторов.
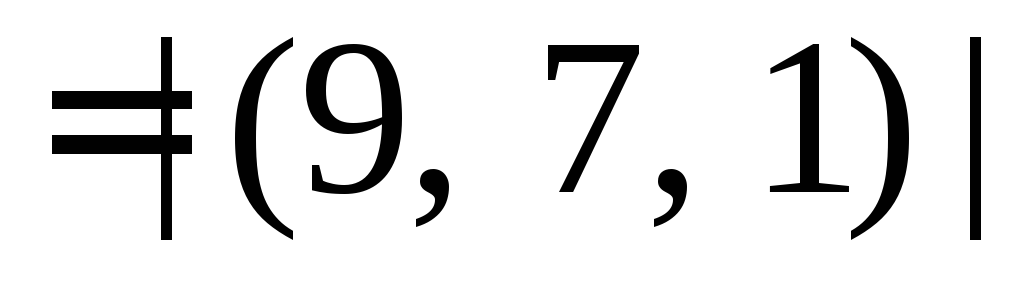
Находим модуль вектора.
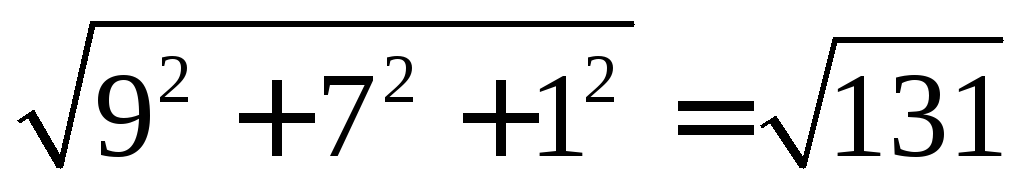
Ответ: 
6.5. Определить
координаты вектора 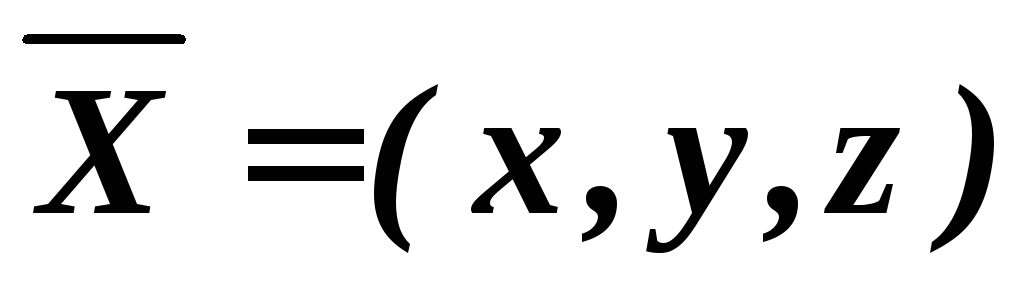 ,
коллинеарного вектору
,
коллинеарного вектору ,
зная, что
,
зная, что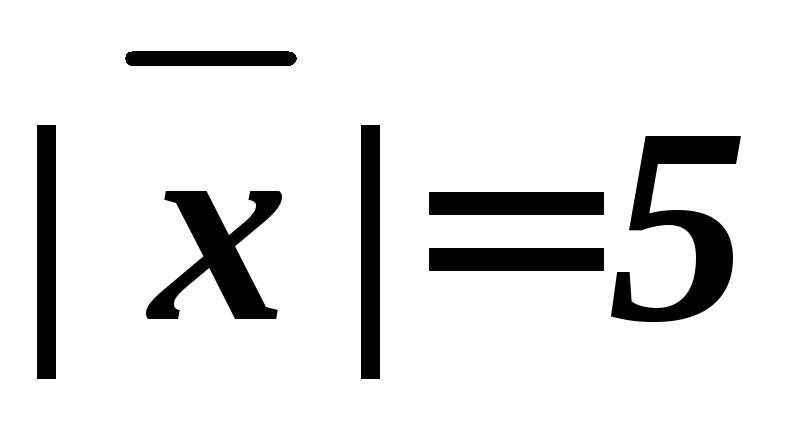 и он направлен в сторону, противоположную
вектору
и он направлен в сторону, противоположную
вектору .
.
Вектор  коллинеарен вектору
коллинеарен вектору ,
значит, его единичный вектор равен
единичному вектору
,
значит, его единичный вектор равен
единичному вектору только со знаком минус, т.к. направлен
в противоположную сторону.
только со знаком минус, т.к. направлен
в противоположную сторону.
Единичный вектор имеет длину равную 1, значит, если его умножить на 5, то его длинна будет равна пяти.
Находим 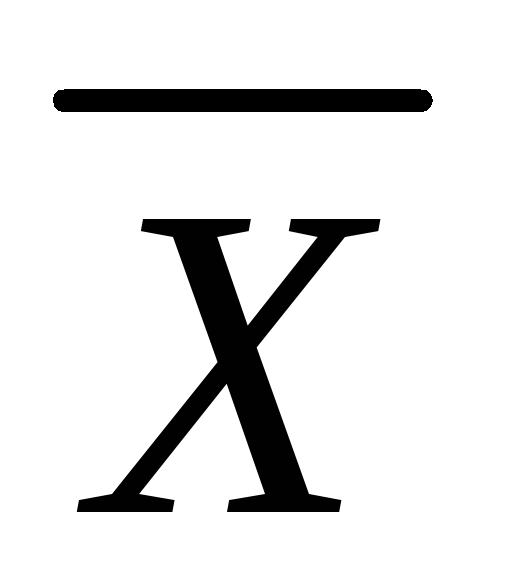
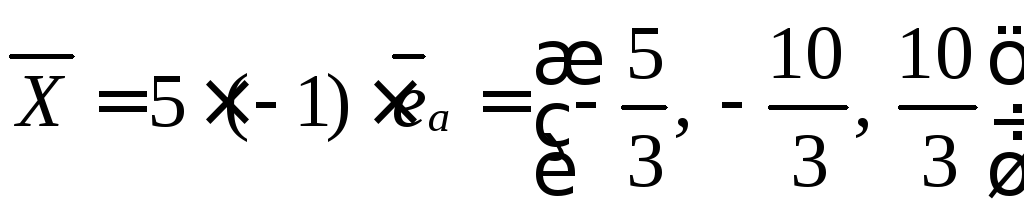
Ответ: 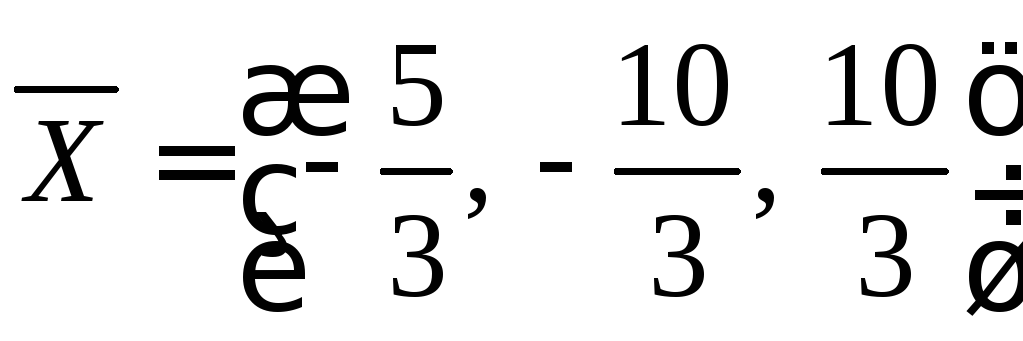
6.6. Вычислить
скалярные произведения 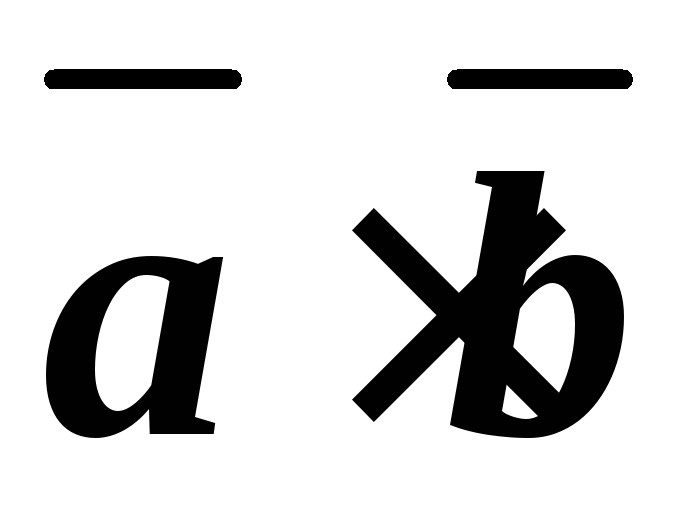 и
и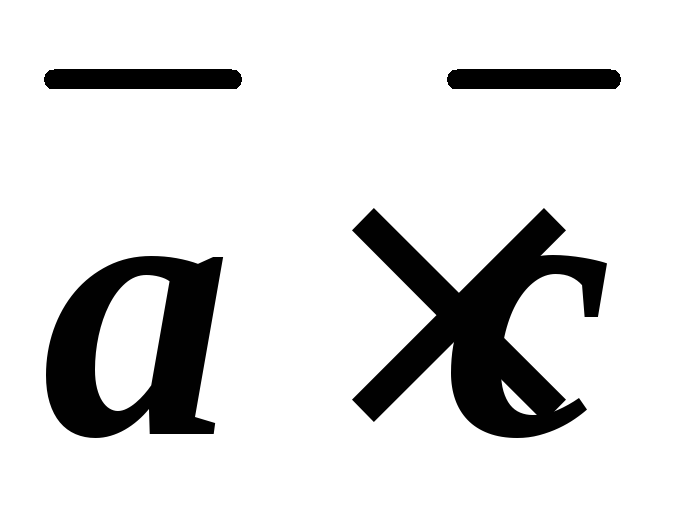 .
Перпендикулярны ли векторы
.
Перпендикулярны ли векторы и
и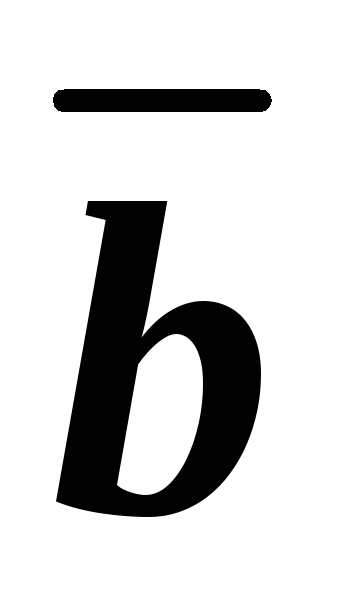 ,
, и
и между собой?
между собой?
Выполним скалярное произведение векторов.
Если вектора перпендикулярны, их скалярное произведение равно нулю.
Мы
видим, что в нашем случае вектора и
и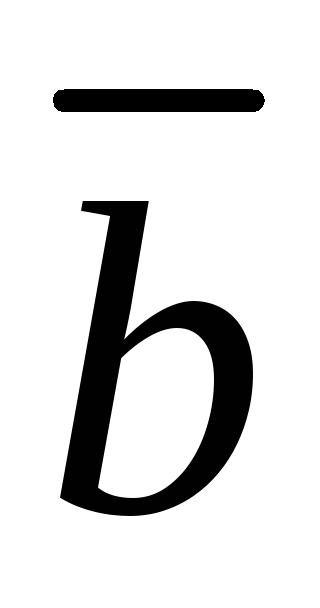 перпендикулярны.
перпендикулярны.
Ответ: 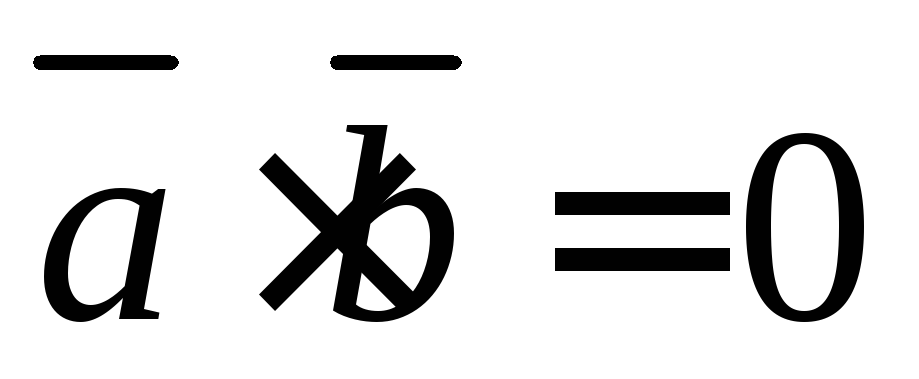 ,
,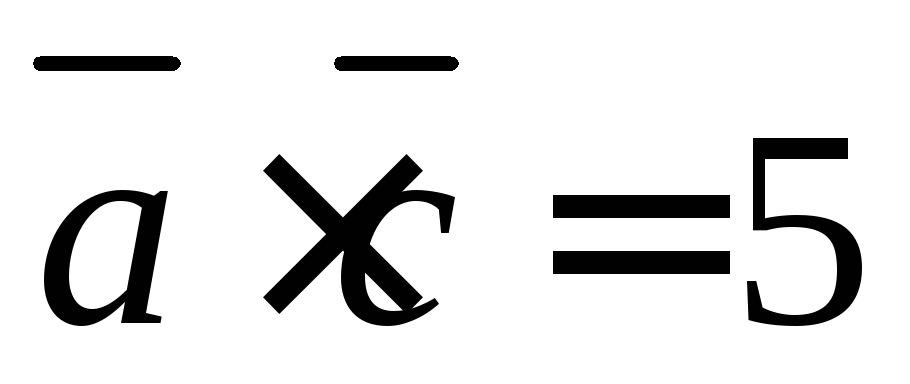 ,
векторы не перпендикулярны.
,
векторы не перпендикулярны.
Примечание. Геометрический смысл скалярного произведения мало
Как найти вектор перпендикулярный вектору — онлайн справочник для студентов
ФОРМУЛА
Чтобы вектор \(\ \overline{a}\) был перпендикулярен вектору \(\ \overline{b}\) , необходимо, чтобы его скалярное произведение было равно нулю, т.е.
\(\ (\overline{a}, \overline{b})=0 \)
Если векторы задаются на плоскости своими координатами \(\ \overline{a}=\left(a_{x} ; a_{y}\right) \) и \(\ \overline{b}=\left(b_{x} ; b_{y}\right) \), то условие их перпендикулярности принимает вид:
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}=0 \)
Если векторы заданы в пространстве и имеют координаты \(\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right) \) и \(\ \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \), то перпендикулярное условие записывается в виде:
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}=0 \)
ПРИМЕРЫ РАСПОЛОЖЕНИЯ ПЕРПЕНДИКУЛЯРНОГО ВЕКТОРА
ПРИМЕР
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}=0 \)
Подставляем координаты указанных векторов в это выражение и из полученного равенства находим \(\ m \):
\(\ 2 \cdot(-3)+(-1) \cdot m=0 \)
\(\ -6-m=0 \)
\(\ m=-6 \)
ПРИМЕР
\(\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}=0 \)
Подставив в него указанные координаты векторов, мы получим:
\(\ 3 \cdot(-1)+(-2) \cdot m+m \cdot 1=0 \)
\(\ 3-2 \cdot m+m=0 \)
Из полученного уравнения находим \(\ m=-6 \):
\(\ 3-m=0 \Rightarrow m=-3 \)
Перпендикулярные векторы и условие перпендикулярности
ОПРЕДЕЛЕНИЕ Два вектора и называются ортогональными (перпендикулярными), если угол между ними прямой.Перпендикулярные векторы и условие перпендикулярности
Условие ортогональности векторов. Векторы и будут ортогональными тогда и только тогда, когда их скалярное произведение равно нулю:
Если векторы заданы своими координатами: и , то условие ортогональности запишется в виде:
Примеры решения задач
ПРИМЕР| Задание | Исследовать векторы и на ортогональность. |
| Решение |
Согласно условию ортогональности, два вектора перпендикулярны, если их скалярное произведение равно нулю. Вычислим скалярное произведение заданных векторов, оно равно сумме произведений соответствующих координат:
Поскольку в результате получили ненулевое значение, то делаем вывод, что векторы не являются ортогональными. |
| Ответ | Векторы и не ортогональны. |
| Задание | При каком значении параметра векторы и будут ортогональными? |
| Решение |
Два вектора ортогональны, если их скалярное произведение равно нулю:
Таким образом, заданные векторы ортогональны при . |
| Ответ |

