Физика Зависимость силы тока от напряжения. Сопротивление. Закон Ома для участка цепи

Материалы к уроку

Конспект урока

Мы продолжаем изучение электрического тока. Вспомним, какая характеристика будет описывать это упорядоченное движение частиц?
Электрический ток в цепи – это упорядоченное движение заряженных частиц в электрическом поле.
Следовательно, заряженные частицы приходят в движение (то есть появляется ток), только при условии, что существует электрическое поле, которое характеризуют еще одной физической величиной – напряжением U Установим зависимость, которая, существует между двумя этими величинами: силой тока и напряжением. Ведь чем больше электрическое поле, тем быстрее будут двигаться заряженные частицы, то есть сила тока будет больше. Проверим этот факт, проведя следующий опыт.  Соберем электрическую цепь, состоящую из источника тока, амперметра, лампочки, вольтметра и ключа. Напомню, что собирая цепь важно соблюдать полярность, клемму со знаком плюс на приборе нужно соединять с положительным полюсом источника тока, клемму со знаком минус с отрицательным полюсом. После того как все элементы цепи соединены, замкнем цепь. Показания приборов занесем в таблицу. Показания вольтметра 1,5В, сила  тока 0,1А. Разомкнем цепь. И увеличим общее напряжение в цепи, присоединив еще одну батарею. Показания увеличились вдвое. Данные так же заносим в таблицу. Напряжение 3В, сила тока 0,2А. И еще раз увеличим напряжение, вцепи, добавив еще одну батарею. Замкнув ключ, получаем напряжение 4,5В, сила тока так же увеличилась и равна 0,3А. Эти данные так же занесем в таблицу. Очевидно, что во сколько раз увеличиваем напряжение, во столько же  раз увеличивается и сила тока. Вам уже известно, что такая зависимость называется прямая зависимость или прямая пропорциональность. Говорят, что сила тока прямо пропорциональна напряжению.

Мы установили вид зависимости между величинами сила тока  и напряжение. Изобразим эту зависимость графически. Воспользуемся данными, которые мы занесли в таблицу. Графиком такой зависимости является прямая. Проведем следующий опыт, в последней цепи вместо лампочки поставим резистор.
Напомню, что последние показания были следующие: напряжение 4,5В, сила тока 0,3А. Замкнув цепь, мы видим, что напряжение осталось прежнее, а вот сила тока стала больше 1,5А.  Как это можно объяснить? Оказывается, что различные тела пропускают ток по-разному. Можно сравнить течение тока с течением воды в трубе.  В трубе, где много засоров, ржавчины на стенках будет слабый напор, так как вода при движение, будет испытывать сопротивление, в гладкой трубе такого сопротивления нет, и поэтому напор будет больше. Так и ток – в одном теле он будет протекать лучше, где сопротивление среды слабое, в другом теле сила тока станет меньше, так как сопротивление среды большое. Физическая величина, которая будет характеризовать способность проводника пропускать электрический ток называется сопротивлением. Обозначают эту величину буквой R. Измеряется она в Омах.
За единицу сопротивления принимают один Ом – это сопротивление такого проводника, в котором при напряжении на концах 1 вольт сила тока равна 1 амперу. Очевидно, что зависимость между силой тока и сопротивлением будет обратная.  То есть, чем большим сопротивлением обладает проводник, тем меньше будет сила тока.  И наоборот, чем меньше сопротивление проводника – тем сила тока будет больше. Говорят, что сила тока обратна пропорциональна сопротивлению. Итак, мы получили зависимость силы тока от двух параметров – напряжения и сопротивления
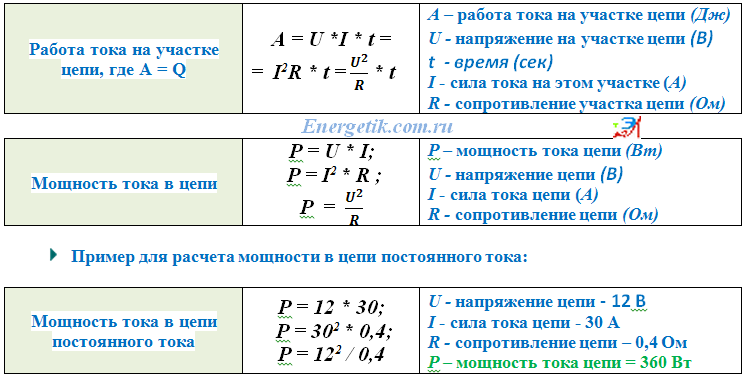
Зависимость силы тока от напряжения на концах проводника и сопротивления самого проводника получила название закона Ома, по имени немецкого ученого, открывшего первым этот закон. Закон Ома для участка цепи: сила тока на участке цепи прямо пропорциональна напряжению  и обратно пропорциональна его сопротивлению.   
Зная силу тока и напряжение на концах проводника, мы сможем найти его сопротивление.
Если известно сопротивление проводника и сила тока, то мы найдем напряжение на концах проводника.
 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

Закон Ома для участка цепи. Последовательное и параллельное соединение проводников. 10 класс. Физика. — Объяснение нового материала.

Комментарии преподавателя

Закон Ома для участка цепи

Сила тока на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению участка.

Закон Ома оказался справедливым не только для металлов, но и для растворов электролитов. Сформулированный закон имеет место для так называемого однородного участка цепи – участка, не содержащего источников тока.

Математическая запись закона Ома проста, как и его формулировка, но экспериментально подтвердить эту зависимость очень трудно. Сила тока, протекающая по участку цепи, мала. Поэтому используют достаточно чувствительные приборы. Г. Ом изготовил чувствительный прибор для измерения силы тока, а в качестве источника тока использовал термопару. Действие амперметра и вольтметра основано на применение закона Ома для участка цепи. Угол поворота стрелки прибора пропорционален силе тока.

Из математической записи закона Ома:

 

можно выразить напряжение :

и сопротивление проводника:

.

Таким образом, закон Ома связывает три параметра, характеризующих постоянный электрический ток, проходящий по проводнику, и позволяет находить любой из них, если известны два других.

Закон Ома имеет границы применимости и выполняется только в том случае, когда при прохождении тока температура заметно не меняется. На вольт–амперной характеристике лампы накаливания видно, что график сильно искривляется при напряжении выше 10В, значит, закон Ома выше этого напряжения применять нельзя.

Также нельзя говорить, что сопротивление проводника зависит от напряжения и силы тока в цепи. Сопротивление участка цепи зависит от свойств проводника: длины, площади поперечного сечения и материала, из которого состоит проводник.

где l-длина проводника, s-его площадь поперечного сечения.

ρ –удельное сопротивление проводника – это физическая величина, характеризующая зависимость сопротивления проводника от материала, из которого он изготовлен.

Удельное сопротивление показывает, каким сопротивлением обладает сделанный из этого вещества проводник длиной 1м и площадью поперечного сечения 1м2 .

Из формулы видно, что единицей измерения в системе СИ является Ом·м. Но так как площадь поперечного сечения проводника достаточно мала, используют единицы измерения

при вычислении площадь поперечного сечения проводника следует выражать в мм2.

В заключении хочется заметить, что Ом начал свои опыты, когда был учителем физики в гимназии. В своих экспериментах Ом брал куски проволоки одинакового диаметра, но разного материала и изменял их длину таким образом, чтобы в цепи сила тока имела одинаковое значение. Находящаяся рядом магнитная стрелка отклонялась при прохождении тока в цепи. Установив связь между напряжением и силой тока, Г. Ом вывел один из основных законов постоянного тока.

Последовательное соединение проводников

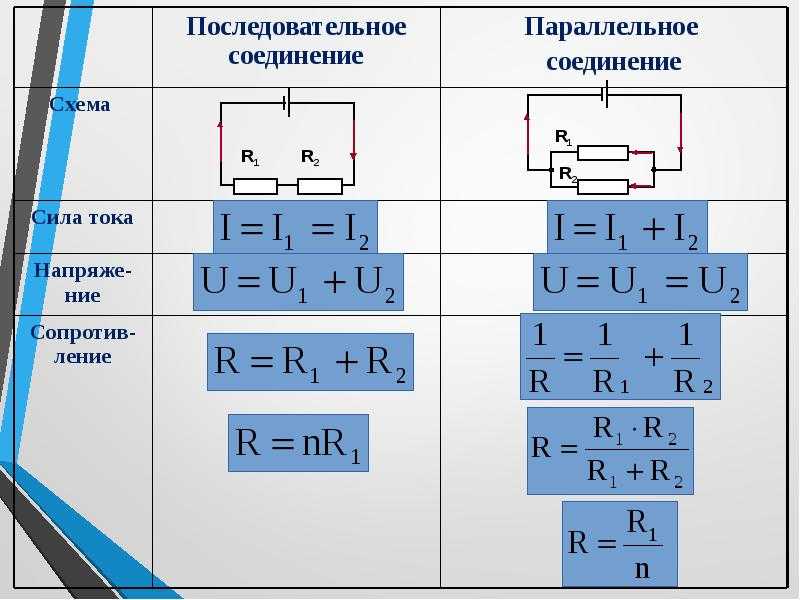
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения. Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.

Рис. Последовательное включение лампочек и источников питания

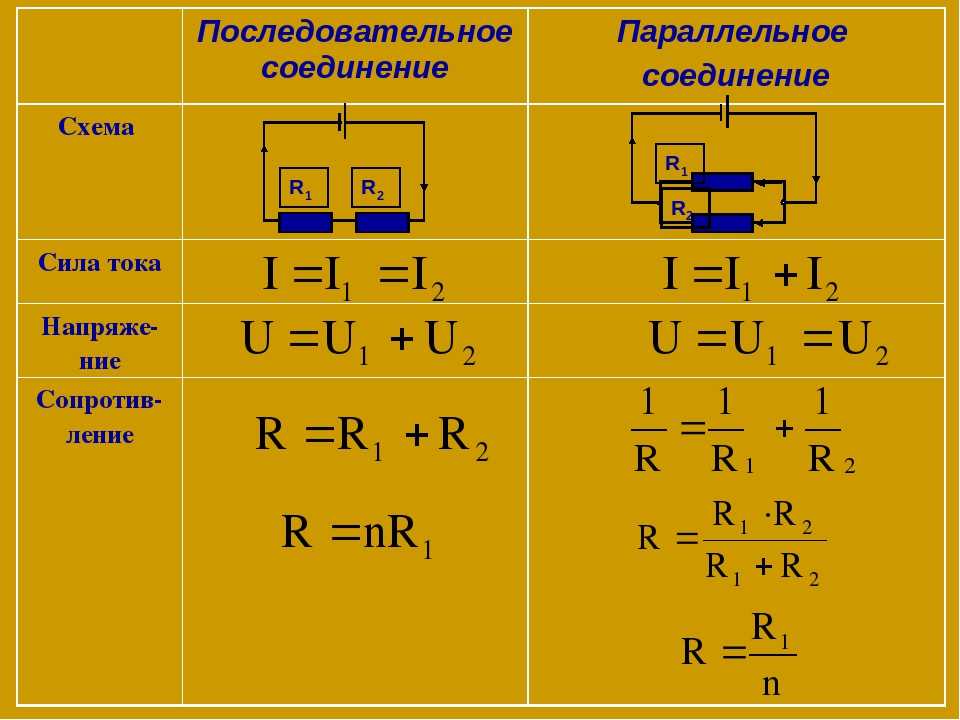
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.

I = I1 = I2

А чему равно сопротивление последовательно соединённых проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.

Последовательное соединение проводников

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

R = R1 + R2

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U1 = IR1, U2 = IR2.

Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:

U = U1 + U2.

Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.

Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.

Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Запишем условие задачи и решим её.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

 

Расчет параметров электрической цепи
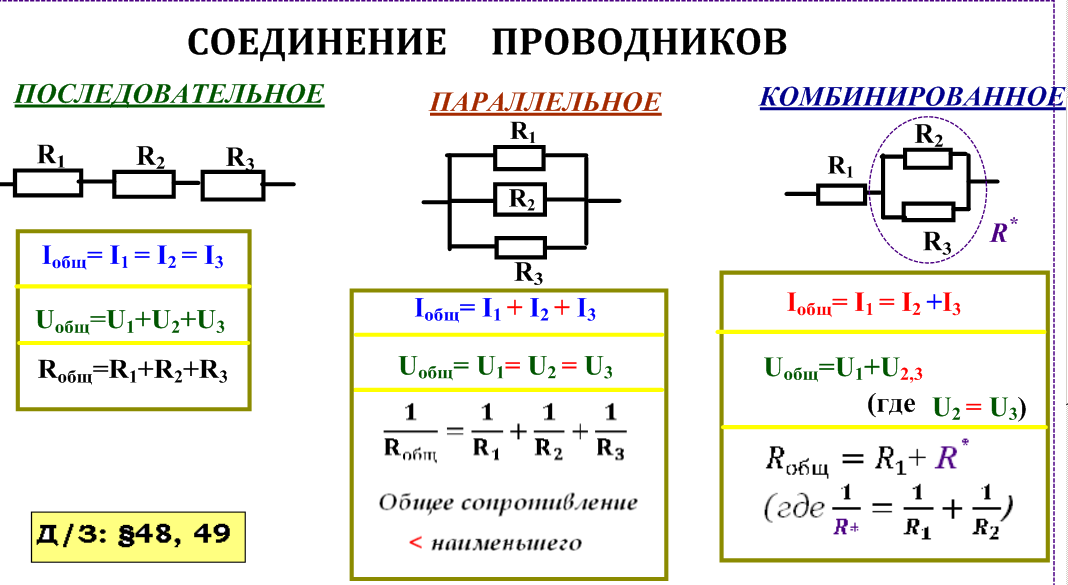
при параллельном соединении сопротивлений:

1. сила тока в неразветвленном участке цепи равна сумме сил токов

во всех параллельно соединенных участках

2. напряжение на всех параллельно соединенных участках цепи одинаково

3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :

( R — сопротивление проводника,
1/R — электрическая проводимость проводника)

Если в цепь включены параллельно только два сопротивления, то:

( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )

4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,

равна сумме работ на отдельных участках:

A=A1+A2

5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:

P=P1+P2

Для двух сопротивлений:

т.е. чем больше сопротивление, тем меньше в нём сила тока.

Домашняя работа.

Задание 1. Ответить на вопросы.

1. Какое соединение проводников называют последовательным? Изобразите его на схеме.
2. Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
3. Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
4. Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?
5. Какое соединение проводников называют параллельным? Изобразите его на схеме.
6. Какая из электрических величин одинакова для всех проводников, соединённых параллельно?
7. Как выражается сила тока в цепи до её разветвления через силы токов в отдельных ветвях разветвления?
8. Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?
9. Какое соединение проводников применяется в жилых помещениях? Какие напряжения используются для бытовых нужд?

Задание 2.Решите задачи.

1. Две лампочки соединены последовательно. Сила тока на первой лампочке 2А. Найдите общее напряжение и напряжение на каждой из ламп, если сопротивление на первой лампе 3Ом, а на второй 4Ом.

2. Две лампочки соединены параллельно. Напряжение на второй лампочке10В. Найдите силу тока в цепи и на каждой из ламп, если сопротивление на первой лампе 1Ом, а на второй 2Ом.

К занятию прикреплен файл  «Это интересно». Вы можете скачать файл в любое удобное для вас время.

Использованные источники:

• http://www.tepka.ru/
• http://class-fizika.narod.ru
• http://www.youtube.com/watch?v=cVKE9NItreo
• http://znaika.ru/catalog/10-klass/physics/
• http://www.youtube.com/watch?v=NB7hOVYe7h0
• https://www.youtube.com/watch?v=cVKE9NItreo
• https://www.youtube.com/watch?v=0hFWeR8ybxs
• http://www.youtube.com/watch?v=EDI8DzWSSWY
• http://www.youtube.com/watch?v=bH_-qGnjJqc
   

 

 

 

Закон

Ом: сопротивление и простые схемы | Физика |

Цели обучения

К концу этого раздела вы сможете:

• Объяснить происхождение закона Ома.
• Расчет напряжения, тока или сопротивления по закону Ома.
• Объясните, что такое омический материал.
• Опишите простую схему.

Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, настенные розетки и т. д., которые необходимы для поддержания тока. Все такие устройства создают разность потенциалов и в широком смысле называются источниками напряжения. Когда источник напряжения подключен к проводнику, он создает разность потенциалов

V , создающий электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.

Закон Ома

Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлическом проводе прямо пропорционален приложенному напряжению :

I∝VI\propto{V}\\I∝V

.

Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, где напряжение является причиной, а ток — следствием. Это эмпирический закон, аналогичный закону трения — экспериментально наблюдаемому явлению. Такая линейная зависимость не всегда имеет место.

Сопротивление и простые схемы

Если напряжение управляет током, что ему препятствует? Электрическое свойство, препятствующее току (грубо похожее на трение и сопротивление воздуха), называется 9.0017 сопротивление R . Столкновения движущихся зарядов с атомами и молекулами в веществе передают энергию веществу и ограничивают ток. Сопротивление определяется как обратно пропорциональное току, или

I∝1RI\propto \frac{1}{R}\\I∝R1​

. Так, например, ток уменьшается вдвое, если сопротивление удваивается. Сочетание отношений тока к напряжению и тока к сопротивлению дает

I=VRI=\frac{V}{R}\\I=RV​

. Эту зависимость также называют законом Ома. Закон Ома в этой форме действительно определяет сопротивление для определенных материалов. Закон Ома (как и закон Гука) не является универсальным. Многие вещества, для которых выполняется закон Ома, называются омический . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление Ом , которое не зависит от напряжения В и тока I . Объект, имеющий простое сопротивление, называется резистором , даже если его сопротивление невелико. Единицей измерения сопротивления является Ом и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V/R дает R = V/I , поэтому единицами сопротивления являются 1 Ом = 1 вольт на ампер:

1Ω=1VA1 \Omega=1\frac{V}{A}\\1Ω= 1АВ​

. На рис.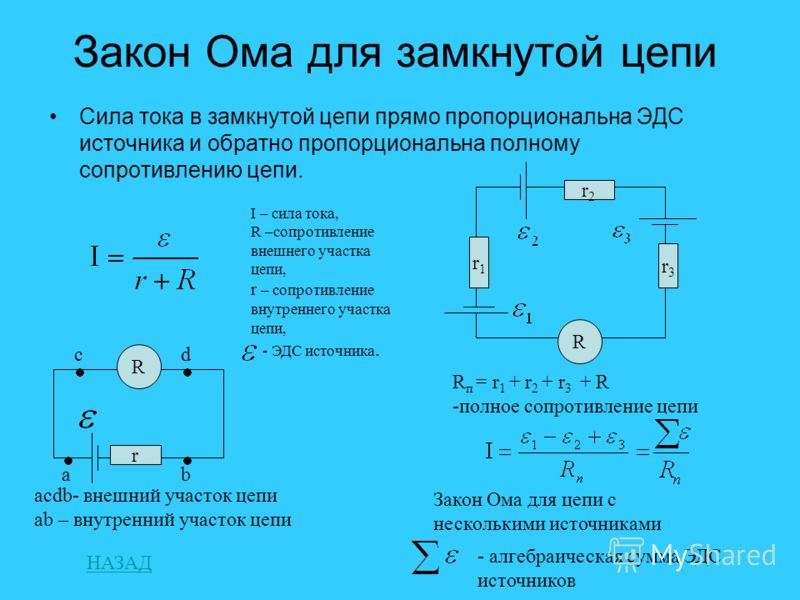  1 показана схема простой цепи. Простая схема имеет один источник напряжения и один резистор. Провода, соединяющие источник напряжения с резистором, можно считать имеющими пренебрежимо малое сопротивление, или их сопротивление можно включить в R .

Рисунок 1. Простая электрическая цепь, в которой замкнутый путь для протекания тока обеспечивается проводниками (обычно металлическими проводами), соединяющими нагрузку с клеммами батареи, представленными красными параллельными линиями. Зигзагообразный символ представляет одиночный резистор и включает любое сопротивление в соединениях с источником напряжения.

Пример 1. Расчет сопротивления: автомобильная фара

Каково сопротивление автомобильной фары, через которую протекает ток 2,50 А при подаче на нее напряжения 12,0 В?

Стратегия

Мы можем преобразовать закон Ома в формулу I = V/R и использовать его для определения сопротивления.

Решение

Преобразование I = V/R и подстановка известных значений дает

R=VI=12,0V2,50A=4,80ΩR=\frac{V}{I}=\frac{12\text{}.{}\text{ }0 В{}}{2\text{}.{}\text{}50 A{}}=\text{}4{}\text{}.{}\text{}80 \Omega {}\\ R=IV​=2.50A12.0V​=4.80Ω

.

Обсуждение

Это относительно небольшое сопротивление, но оно больше холодового сопротивления фары. Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампочка имеет более низкое сопротивление при первом включении и будет потреблять значительно больший ток в течение короткого периода прогрева.

Сопротивления колеблются в пределах многих порядков. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 ¹² Ом или больше. У сухого человека сопротивление между руками и ногами может составлять 10 ⁵ Ом, тогда как сопротивление человеческого сердца составляет около 10 ³ Ом. Метровый отрезок медного провода большого диаметра может иметь сопротивление 10 ⁻⁵ Ом, а сверхпроводники вообще не имеют сопротивления (они неомические). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление». Дополнительную информацию можно получить, решив  I = V/R  для V , что дает

V = IR

Это выражение для V можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I . Для этого напряжения часто используется фраза IR drop . Например, фара в Примере 1 выше имеет падение IR  12,0 В. Если измерить напряжение в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывающему ток — поток заряда. Резистор подобен трубе, которая снижает давление и ограничивает поток из-за своего сопротивления. Сохранение энергии имеет здесь важные последствия. Источник напряжения поставляет энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, в тепловую энергию). В простой цепи (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, поскольку PE = q Δ V , и через каждый протекает тот же самый q . Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны. (См. рис. 2.)

Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.

Соединения: сохранение энергии

В простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму.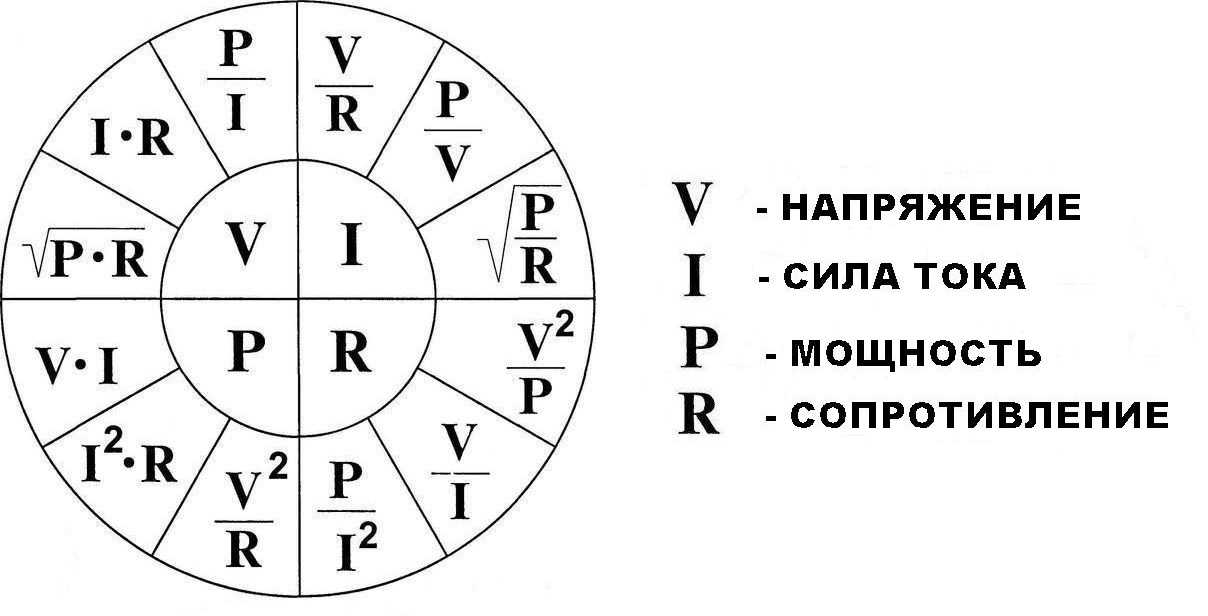 О сохранении энергии здесь свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму одним только резистором. Мы обнаружим, что закон сохранения энергии имеет и другие важные применения в цепях и является мощным инструментом анализа цепей.

Исследования PhET: Закон Ома

Посмотрите, как формула закона Ома соотносится с простой цепью. Отрегулируйте напряжение и сопротивление и посмотрите, как изменится ток в соответствии с законом Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.

Нажмите, чтобы запустить симуляцию.

Резюме раздела

Концептуальные вопросы

1. IR Падение на резисторе означает изменение потенциала или напряжения на резисторе. Изменяется ли ток при прохождении через резистор? Объяснять.
2. Чем падение IR на резисторе похоже на падение давления в жидкости, протекающей по трубе?

Задачи и упражнения

1. Какой ток протекает через лампу фонарика на 3,00 В, если его сопротивление в горячем состоянии равно 3,60 Ом?

2. Рассчитайте эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через который протекает ток 0,200 мА.

3. Каково эффективное сопротивление стартера автомобиля, когда через него протекает ток 150 А, когда автомобильный аккумулятор подает на двигатель напряжение 11,0 В?

4. Сколько вольт подается на световой индикатор DVD-проигрывателя с сопротивлением 140 Ом, если через него проходит 25,0 мА?

5. а) Найдите падение напряжения в удлинителе с сопротивлением 0,0600 Ом, по которому протекает ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0,300 Ом. Каково падение напряжения в нем при протекании 5,00 А? в) Почему напряжение любого используемого электроприбора уменьшается на эту величину? Каково влияние на прибор?

6. Линия электропередачи подвешена к металлическим опорам со стеклянными изоляторами сопротивлением 1,00×10 ⁹ Ом. Какой ток протекает через изолятор, если напряжение равно 200 кВ? (Некоторые высоковольтные линии постоянного тока.)

Глоссарий

Закон Ома:

эмпирическое соотношение, утверждающее, что ток I пропорционален разности потенциалов В , ∝ В ; его часто записывают как I = V/R , где R сопротивление

сопротивление:

электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V/I

ом:

единица сопротивления, определяемая как 1 Ом = 1 В/А

омическое:

тип материала, для которого справедлив закон Ома

простая цепь:

цепь с одним источником напряжения и одним резистором

Избранные решения задач и упражнений

1. 0,833 А

3. 7,33 × 10 ⁻² Ом

5. (a) 0,300 В

(b) 1,50 В

(c) Напряжение, подаваемое на любой используемый прибор, уменьшается, поскольку общее падение напряжения от стены до конечного выхода прибора фиксируется. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на устройстве значительно уменьшается, поэтому выходная мощность устройства может быть значительно снижена, что снижает способность устройства работать должным образом.

Лицензии и авторство

Лицензионный контент CC, совместно используемый ранее

• College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия
• Интерактивное моделирование PhET . Автор: : http://phet.colorado.edu. Лицензия : CC BY: Attribution

Физика! Я могу рассчитать электрический ток, протекающий через сложную цепь, исходя из сопротивления и напряжения.

Физика Физика B Физика C

Кжж М.

спросил 25.03.21

решите это и заполните таблицу ниже, укажите все шаги.

Особенно от того, как вы нашли напряжение, ток. Спасибо

(Всего: 12 В, 3 А, 4 Ом)	Напряжение	Текущий	Сопротивление
Итого	12 В
Р1			4 Ом
Р2			4 Ом
Р3			2 Ом

Подписаться І 1

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: ЛучшиеНовыеСамыеСтарые

Джонатан Д. ответил 25.03.21

Репетитор

4.9 (18)

Репетитор средней школы, специализирующийся на физике.

Смотрите таких репетиторов

Посмотреть таких репетиторов

Закон Ома: V = I*R

Серия:

1. R _s = ∑R _i
2. I постоянная
3. В делится на резисторы так, что V _i = I*R _i , где V = ∑V _i

Параллельно:

1. R _p = (∑(1/R _i )) ^-1
2. В постоянное
3. I делится на резисторы/ветви таким образом, что V = I _i *R _i и I = ∑I _i

У нас есть комбинация параллельного и последовательного соединения. Значения для всей схемы уже указаны в вашей таблице, но давайте пройдемся по расчетам.

R ₁ и R ₂ соединены параллельно, и эта параллельная часть соединена последовательно с R ₃ .

We first substitute the parallel part with a resistance R _p = (1/R ₁ + 1/R ₂ ) ^-1 = 2 Ом

Тогда общее сопротивление или эквивалентное сопротивление цепи равно R = R _p + R ₃ = 4 Ом (последовательно).

Общий ток в цепи равен I = V/R = 3 A .

Давайте вернемся по нашим следам.

Имеем последовательную цепь с R _p и R ₃ с током I и напряжением V.

₃ = I = 3 А

Напряжение делится на оба резистора R _p и R ₃ , которые имеют одинаковое значение,

, поэтому напряжение делится поровну: 3 = 6 В . Если это не так, вы всегда можете рассчитать

В _i = I*R _i (в этом случае оба будут 3 А * 2 Ом = 6 В).

Еще один шаг назад, давайте посмотрим на параллельную часть схемы.

Теперь мы знаем, что напряжение на этой части V _p = 6 В, а ток равен I _p = 3 A.

В чисто параллельной цепи напряжение постоянно на всех резисторах, то есть В ₁ = В ₂ = 6 В.

Ток делится на оба резистора, они снова имеют одинаковое значение, поэтому ток делится поровну, 0 I = I ₂ = 1,5 А.