Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 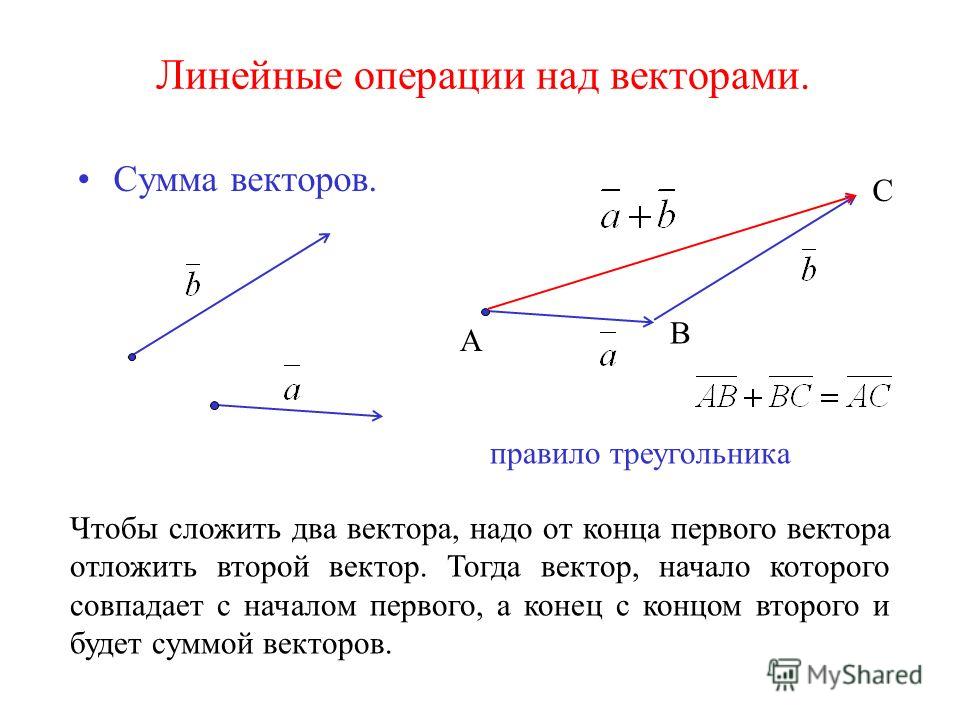 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест.  5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II.  АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ§ 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 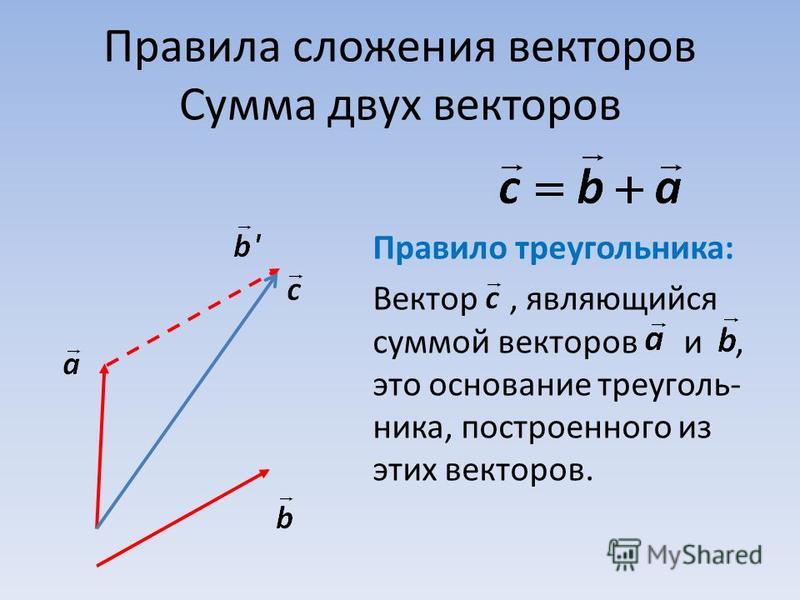 § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов. |
Вычитание векторов и правила вычитания
Оглавление
Время чтения: 4 минуты
1 176
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т.
е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т.
е. соедините начало первого отрезка и конец второго.
е. соедините начало первого отрезка и конец второго.Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Сначала нужно построить сумму,Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Оценить статью (34 оценки):
Поделиться
sum — Как я могу вычислить сумму двух векторов в схеме (Dr Racket)
Я хотел бы реализовать свою функцию sum-of-vectors так, чтобы она принимала два вектора с разными числами в качестве аргументов и возвращала вектор с суммирование соответствующих элементов захваченных векторов .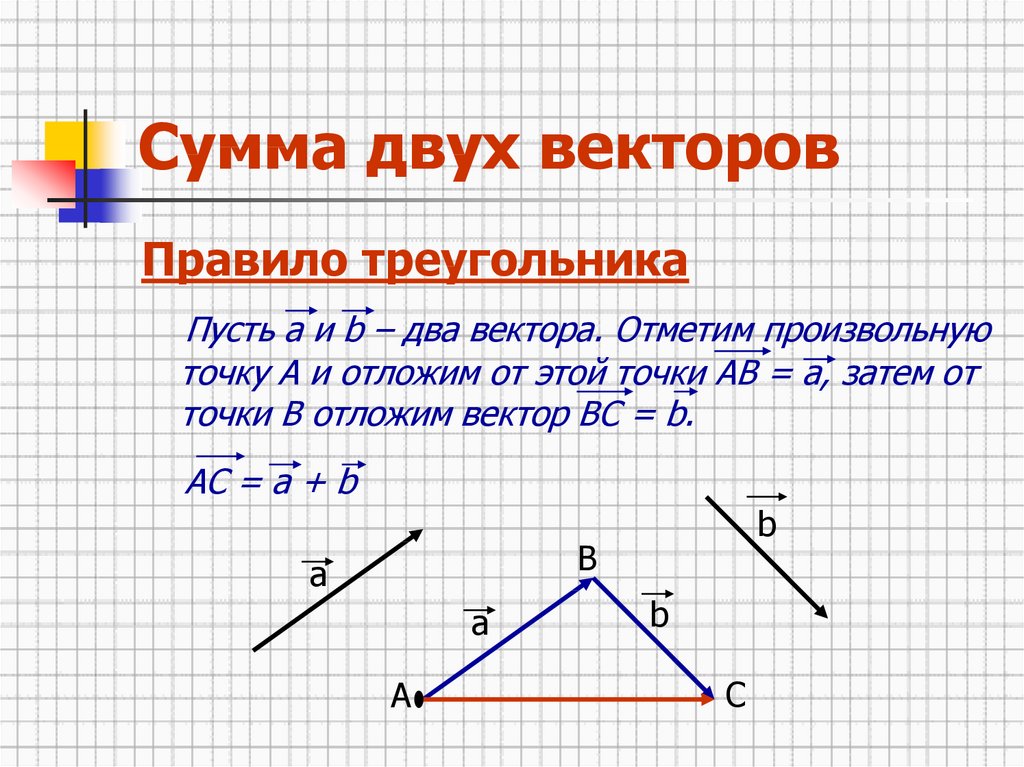
Тестовое выражение: (вектор суммы (вектор 4 6 8 3) (вектор 5 6 7)) => #( 911 15 3)
ПОХОЖИЙ ВОПРОС: Существует близкое решение этого, которое находится на URL, Есть ли способ суммировать два вектора с разной длиной в схеме?
, но разница в том, что он отображает «# (2 4 6 4 5 6) с запятой в начале вопроса, но фактический результат моего требования не должен иметь апостроф (‘) в выходной вектор. должно быть #(9 11 15 3)
- вектор
- сумма
- схема
- ракетка
15
Функция для обработки соответствующих элементов двух списков, которые могут различаться по длине легко записывается: написать заглушку , с подписью и цель , а минимальный пример :
(определить (сумма списков l1 l2) ;; ListOfNumber ListOfNumber -> ListOfNumber ;; составить список сумм соответствующих элементов l1, l2 ;; длина результата больше длин l1, l2 '#()) (проверить-ожидать (сумма списков '() '()) '())
Добавьте следующие примеры и заполните функцию:
(проверка-ожидание (сумма списков '() '(1)) `(1)) (проверить-ожидать (сумма списков '(2) '()) `(2)) (проверить-ожидать (сумма списков '(3) '(4)) `(7)) (определить (сумма-списков l1 l2) ;; ListOfNumber ListOfNumber ->ListOfNumber ;; составить список сумм соответствующих элементов l1, l2 ;; длина результата больше длин l1, l2 (состояние [(и (пусто? l1) (пусто? l2)) пусто] [(пусто? l1) (против (первый l2) (сумма списков l1 (остальные l2))) ] [(пусто? l2) (против (первый l1) (сумма списков (остальные l1) l2)) ] [else (cons (+ (first l1) (first l2)) (sum-of-lists (rest l1) (rest l2))) ]))
(обратите внимание, как 4 плеча cond перекликаются с 4 примерами)
Теперь необходимая сумма векторов равна:
(define (sum-of-vectors von1 von2) ;; VectorOfNumber VectorOfNumber ->ВекторЧисла ;; составить вектор сумм соответствующих элементов von1, von2 ;; длина результата больше длины von1, von2 (список->вектор (сумма-списков (вектор->список фон1) (вектор->список фон2)))) (проверить-ожидать (сумма векторов (вектор 4 6 8 3) (вектор 5 6 7)) (вектор 912 15 3)) Добро пожаловать в DrRacket, версия 8.
4 [cs].
Язык: продвинутый студент.
Все 5 тестов пройдено!
> (сумма векторов '#(1 2 3) '#(1 2 3 4 5 6))
(вектор 2 4 6 4 5 6)
>
Зарегистрируйтесь или войдите в систему
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Найдите сумму векторов А и В, как показано на рисунке, а также найдите направление вектора суммы.
Учитывая A = 4 единицы и B = 3 единицы.Вопрос
Вопрос
DC Pandey Английская база-математика-Execise
14 видеоРеклама
AB Padhai Karo Bina Ads KE
Khareedo DN Pro и Dekho Sari Videos Bina Kisi Adaraavat!
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Стенограмма
Привет всем, поэтому вопрос заключается в том, чтобы найти сумму векторов A и B, показанных на рисунке, а также найти направление некоторого вектора, учитывая, что = 4 единицы и b = 3, поэтому нам нужно найти направление a + b вектора a + b из a + b задается под корнем a квадрат + b квадрат + 2 потому что тета тета это угол между двумя векторами величины a задается равным 43 минуты это может быть записано как под корнем 16 + 9+ 4312 в 24 Коса 60 °, это получится блок маршрута 37. Хорошо, теперь нам нужно найти угол, образованный этим вектором
a + b, чтобы найти направление, поэтому Meenu tan Alpha Alpha — это угол, образованный a + b = b sin theta на небольшой угол между a плюс ближайший + b cos theta нормальное значение этих трех единиц, поэтому 3 sin 60 на 4 + 3 Cos 60 дает нам точку 472, это Tan Alpha 5,47 в Alpha = tan, обратная точка 472, и рассчитывается из калькулятор, мы получим угол 25,3 градуса, сделанный A Plus
хорошо, спасибо
संबंधित वीडियो
3.
Найдите единичный вектор в направлении, параллельном сумме векторов vec a=2hat i+4hat j-5hat k и vec2 khat i+hat i3 также направляющие косинусы этого вектора.
Найдите сумму векторов A и B, как показано на рисунке, а также найдите направление вектора суммы. Учитывая A = 4 единицы и B = 3 единицы.
31087266
Найдите вычитание векторов A и B, как показано на рисунке, а также найдите направление вектора вычитания, учитывая A=4 единицы и b=3 единицы.
31087271
Найдите конинусы направлений вектора (5i+2j+6k). Также запишите значение суммы квадратов направленных косинусов этого вектора.
34887524
Найдите направленные косинусы вектора (5ˆi+2ˆj+6ˆk). Также запишите значение суммы квадратов направленных косинусов этого вектора.
39182758
→ I+2 → J+3 → K, — → I+2 → J+→ K और 3 → I+→ J सदिशों योगफल सदिश कि दिश दिश में औ औ औ → ज ज ज → क योगफल सदिश कि दिश दिश में औ औ सदिश ज जшить क क योगफल सदिश कि
152622103
दो इक|
152622315
Найти единичный вектор в направлении, параллельном сумме векторов →a=2i+4j−5k и →b=i+2j+3k, найти также направляющие косинусы этого вектора.
