Смешанное произведение векторов.

Смешанное произведение векторов.

Навигация по странице:

• Определение смешанного произведения векторов
• Формула вычисления смешанного произведения векторов
• Свойства смешанного произведения векторов
• Примеры задач на вычисления смешанного произведения векторов

Онлайн калькулятор. Смешанное произведение векторов.

Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Формулы вычисления смешанного произведения векторов

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов a = {a_x; a_y; a_z}, b = {b_x; b_y; b_z} и c = {c_x; c_y; c_z} в декартовой системе координат можно вычислить, используя следующую формулу:

a · [b × c] =	ax	ay	az
	bx	by	bz
	cx	cy	cz

Свойства смешанного произведения векторов

• Геометрический смысл смешанного произведения.

  Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:

  V_парал = |a · [b × c]|

• Геометрический смысл смешанного произведения.

  Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:

  Vпир =	1	|a · [b × c]|
  	6

• Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.

• a · [b × c] = b · (a · c) — c · (a · b)

• a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]

• a · [b × c] + b · [c × a] + c · [a × b] = 0 —

  тождество Якоби.

Примеры задач на вычисления смешанного произведения векторов

Пример 1. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.

Решение:

a · [b × с] =	1	2	3	=
	1	1	1
	1	2	1

= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2

Пример 2.

Найти объем пирамиды построенной на векторах a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.

Решение: Найдем смешанное произведение этих векторов:

a · [b × с] =	1	2	3	=
	1	-1	1
	2	0	-1

= 1·(-1)·(-1) + 2·1·2 + 3·1·0 — 3·(-1)·2 — 2·1·(-1) — 1·1·0 =

= 1 + 4 + 0 + 6 + 2 — 0 = 13

Найдем объем пирамиды воспользовавшись свойствами:

Vпир =	1	|a · [b × c]| =	13	= 2	1
	6		6		6

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора.

Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Найти скалярное произведение векторов (3a-2b) и (5a-6b), если модуль в…

Ответы

06. 11.16

Алиса Читать ответы

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет

написать сочинение рассуждение ,раскрывая смысл высказывания известного русского лингвиста Валентины Даниловны Черняк:»в сложном предложении отражаются отношения ,которые говорящий усматривает

В первом и втором букете 14 роз, а во втором и третем 19 роз. В каком букете больше роз в первом или

Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз

Дан вектор m{1;2;2}.Найдите координаты единичного вектора е ,сонаправленного с вектором

Пользуйтесь нашим приложением

1.5: Точечное и перекрестное произведение

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

603

• Ларри Грин
• Общественный колледж Лейк-Тахо

93 \)

Если

\[\textbf{v} = a \hat{\textbf{i}} + b \hat{\textbf{j}} + c \hat{\textbf{k}} \; \;\; \текст{и}\;\;\; \textbf{w}= d \hat{\textbf{i}} + e \hat{\textbf{j}} + f \hat{\textbf{k}} \nonumber \]

, затем

\[ \ textbf{v} \cdot \textbf{w} = объявление + быть + ср. \номер\]

Пример \(\PageIndex{1}\)

Если

\[\textbf{v} = 2\; \ шляпа {\ textbf {я}} + 4 \; \шляпа{\textbf{j}} \;\;\; \текст{и} \;\;\; \textbf{w} = \hat{\textbf{i}} + 5\; \ шляпа {\ textbf {j}} \ не номер \]

, затем

\[ \textbf{v} \cdot \textbf{w} = (2)(1) + (4)(5) = 22. \nonumber \]

Упражнение \(\PageIndex{1}\)

Найдите скалярное произведение \(2 \hat{\textbf{i}}+ \hat{\textbf{j}} — \hat{\textbf{k}} \) и \( \hat{\textbf{i}} + 2 \hat{\textbf{j}} \).

Угол между двумя векторами

Определим угол \(\theta \) между двумя векторами v и w по формуле

\[ \cos q = \dfrac{\textbf{v} \cdot \ textbf{w} }{|| \textbf{v} || || \textbf{ш}|| }\номер \]

, так что

\[ \textbf{v} \cdot \textbf{w} = ||\textbf{v}|| || \textbf{ш} || \cos кв. \nonumber \]

Два вектора называются ортогональными , если их угол прямой. Мы видим, что углы ортогональны тогда и только тогда, когда

\[ \textbf{v} \cdot \textbf{w} = 0. \nonumber \]

угол между

\[ \textbf{v} = 2 \hat{\textbf{i}} + 3 \hat{\textbf{j}} + \hat{\textbf{k}} \nonumber \] 9{-1}\left( \dfrac{13}{\sqrt{14} \sqrt{21}} \right). \nonumber \]

Определение: Направленные косинусы

Пусть

\[\textbf{v} = a \hat{\textbf{i}} + b \hat{\textbf{j}} + c \hat{\ textbf{k}} \nonumber \]

вектор, то мы определяем направляющих косинусов следующим образом:

1.

\[ \cos a = \dfrac{a}{||\textbf {v} ||},\nonumber \]

2.

\[\cos b = \dfrac{b}{ ||\textbf{v} || }, \номер\]

3.

\[ \cos c = \dfrac{c}{||\textbf{v}||}. \nonumber \]

Выступы и компоненты Предположим, что автомобиль остановился на крутом холме, и пусть g будет силой тяжести, действующей на него. Мы можем разделить вектор g на составляющую, толкающую машину по дороге, и составляющую, толкающую машину на дорогу. Определим

Определение: Проекция

Пусть u и v будут векторами. Затем u можно разбить на две составляющие: r и s , так что r параллельно v , а s перпендикулярно v . r называется проекцией u на v и называется компонентой u , перпендикулярной v .

Мы видим, что

\[\begin{align*} \textbf{u} \cdot \textbf{v} = || \textbf{и} || \; || \textbf{v}|| \cos q &= \dfrac{|| \textbf{и} || \; || \textbf{v} || \text{proj}_{\textbf{v}} \textbf{u} }{||\textbf{u}||} \\ &= ||\textbf{v} || \; || \text{proj}_{\textbf{v}} \textbf{u} ||. \end{align*} \nonumber \] 92 } || \textbf{v}|| \nonumber \]

, а правая часть упрощается до приведенной выше формулы. Направление правильное, так как правая часть формулы постоянно кратна v , поэтому вектор проекции имеет направление v , как и требуется.

Чтобы найти вектор s , обратите внимание на диаграмму, что

\[ \text{proj}_{\textbf{v}} \textbf{u} + \textbf{s} = \textbf{u} \ nonumber \]

, так что

\[ \textbf{s} = \textbf{u} — \text{proj}_{ \textbf{v} } \textbf{u}. \номер\]

Работа

Работа, совершенная постоянной силой F вдоль PQ, равна

\[W=\textbf{F}\cdot PQ. \nonumber \]

Пример \(\PageIndex{3}\)

Найдите работу, совершенную против силы тяжести, чтобы переместить 10-килограммового ребенка из точки \((2,3)\) в точку \((5, 7)\)?

Решение

Мы имеем, что вектор силы равен

\[ \textbf{F} = m \textbf{a} = (10 )(-9,8 \hat{\textbf{j}}) = -98 \ шляпа {\ textbf {j}} \ не номер \]

, а вектор смещения равен

\[\textbf{v} = (5-2) \hat{\textbf{i}} + (7-3) \hat{\textbf{j}} = 3 \hat{ \textbf{i}} + 4 \hat{\textbf{j}}.\nonumber \]

Работа представляет собой скалярное произведение

\[\begin{align*} W = \textbf{F} \cdot \ textbf{v} &= (-98 \hat{\textbf{j}} ) \cdot (3 \hat{\textbf{i}} + 4 \hat{\textbf{j}} ) \\ &= (0 )(3) + (-98) (4) \\ &= -392. \end{align*} \nonumber \]

Обратите внимание, что отрицательный знак подтверждает, что работа выполняется против силы тяжести. Следовательно, требуется 392 Дж работы по перемещению ребенка.

Крутящий момент

Предположим, вы катаетесь на лыжах и ужасно падаете. Ваше тело вращается, а лыжи остаются на месте (не пытайтесь делать это дома). При правильном креплении ваши крепления отстегнутся, и лыжа оторвется. Крепления распознают, что была применена сила. Эта сила называется крутящим моментом. Чтобы вычислить его, мы используем перекрестное произведение двух векторов, которое не только дает крутящий момент, но и дает направление, перпендикулярное как силе, так и направлению ноги.

Определение: перекрестное произведение

Пусть \(\textbf{u} = a \hat{\textbf{i}} + b \hat{\textbf{j}} + c \hat{\textbf{k}}\ ) и \(\textbf{v} = d \hat{\textbf{i}} + e \hat{\textbf{j}} + f \hat{\textbf{k}} \) — векторы. Затем мы определяем перекрестное произведение \(\textbf{v} \times \textbf{w} \) определителем матрицы:

\[\begin{pmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} &\hat{\textbf{k}} \\ a & b &c \\ d & e & f \end{pmatrix}. \номер\]

Мы можем вычислить этот определитель как

\[\begin{vmatrix} b & c \\ e & f \end{vmatrix} \hat{\textbf{i}} — \begin{vmatrix} a & c \\ d & f \end{vmatrix} \hat{\textbf{j}} + \begin{vmatrix} a & b \\ d & e \end{vmatrix} \hat{\textbf{k}} \nonumber \]

\[ =(bf — ce) \hat{\textbf{i}} + (cd — af) \hat{\textbf{j}} + (ae — bd)\hat{\textbf{k}}. \nonumber \]

Пример \(\PageIndex{4}\)

Найдите векторное произведение \(\textbf{u} \times \textbf{v} \), если

\[\textbf{u} = 2 \hat{\textbf{i}} + \hat{\textbf{j}} -3 \hat{\textbf{k}}, \;\;\; \textbf{v} = 4 \hat{\textbf{j}} + 5 \hat{\textbf{k}}.\nonumber \]

Решение

Мы вычисляем

\[\begin{align* }\begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 2 & 1 & -3 \\ 0 & 4 & 5 \end{vmatrix} & = \begin{vmatrix} 1 & -3 \\ 4 & 5 \end{vmatrix} \hat{\textbf{i}} — \begin{vmatrix} 2 & -3 \\ 0 & 5 \end{vmatrix} \hat{\textbf{j}} + \begin{vmatrix} 2 & 1 \\ 0 & 4 \end{vmatrix} \hat{\textbf{k}} \\ &= 17 \hat{ \textbf{i}} — 10 \шляпа{\textbf{j}} + 8 \шляпа{\textbf{к}}.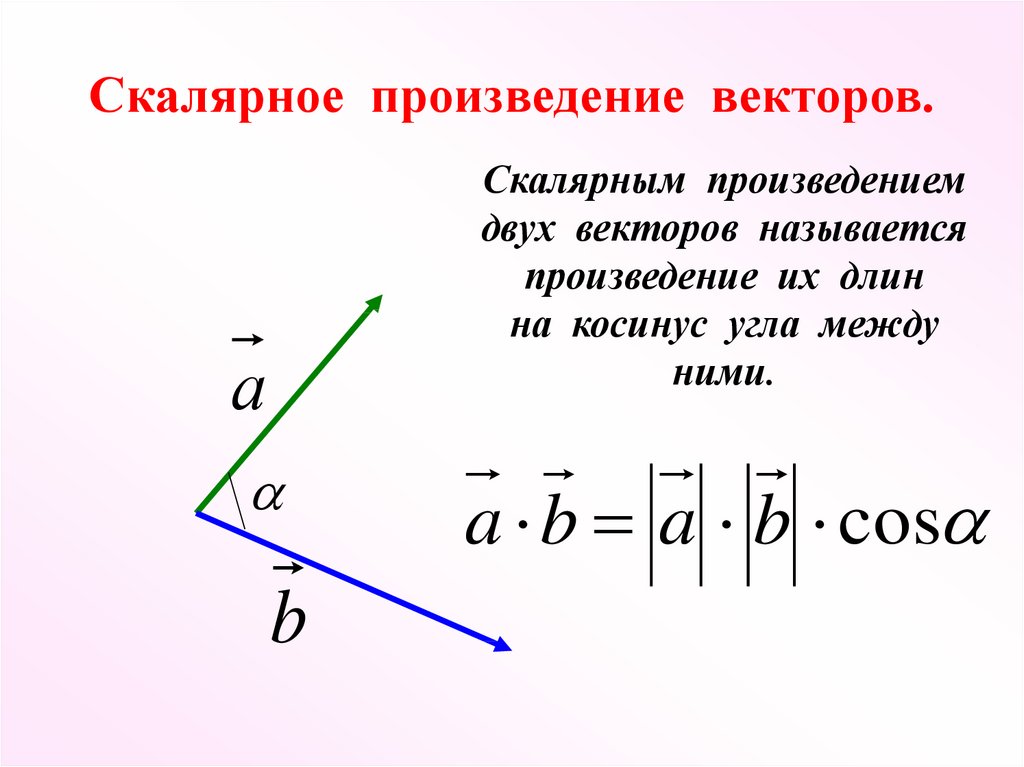 \end{align*} \nonumber \]

Если вам нужна дополнительная помощь, см. конспект лекций по математике 103 B по матрицам.

Упражнения

Найдите \(\textbf{u} \times \textbf{v}\), когда

1. \(\textbf{u} = 3 \hat{\textbf{i}} + \hat{\textbf {j}} — 2 \hat{\textbf{k}}\), \( \textbf{v} = \hat{\textbf{i}} — \hat{\textbf{k}} \),
2. \(\textbf{u} = 2 \hat{\textbf{i}} — 4 \hat{\textbf{j}} — \hat{\textbf{k}} \), \(\textbf{v} = 3 \hat{\textbf{i}} — \hat{\textbf{j}} + 2k \hat{\textbf{k}} \),

Обратите внимание, что поскольку переключение порядка двух строк определителя меняет знак определителя, мы имеем

\[ \textbf{u} \times \textbf{v} = — \textbf{v} \times \textbf{ у}. \nonumber \]

Геометрия и векторное произведение

Пусть u и v — векторы, и рассмотрим параллелограмм, который составляют два вектора.

Затем

\[||\textbf{u} \times \textbf{v} || = \text{Площадь параллелограмма}\nonumber \]

и направление \(\textbf{u} \times \textbf{v}\) является прямым углом к ​​параллелограмму, который следует правилу правой руки.

Примечание. Для \( \hat{\textbf{i}} \times \hat{\textbf{j}}\) величина равна 1, а направление равно \(\hat{\textbf{k}}\) , следовательно, \(\hat{\textbf{i}} \times \hat{\textbf{j}} = \hat{\textbf{k}}\).

Упражнение \(\PageIndex{3}\)

Найдите \(\hat{\textbf{j}} \times \hat{\textbf{k}}\) и \(\hat{\textbf{i} } \times \hat{\textbf{k}}\).

Новый взгляд на крутящий момент

Мы определяем крутящий момент (или момент \(M\) силы \(F\) относительно точки \(Q\)) как

\[M = PQ \times F. \nonumber \]

Пример \(\PageIndex{5}\)

Гаечный ключ на 20 дюймов находится под углом 30 градусов к земле. Сила в 40 фунтов, которая поворачивает ключ под углом 45 градусов к ключу. Найдите крутящий момент.

Решение

Ключ можно записать в виде вектора

\[ 20 \cos 30\; \hat{\textbf{i}} + 20 \sin 30 \; \hat{\textbf{j}} = 17,3 \hat{\textbf{i}} + 10 \hat{\textbf{j}} \nonumber \]

и сила как

\[ -40 \cos 75\; \hat{\textbf{i}} — 40 \sin 75 \; \hat{\textbf{j}} = -10,3 \hat{\textbf{i}} — 38,6 \hat{\textbf{j}}\nonumber \]

, следовательно, крутящий момент представляет собой величину их векторного произведения:

\[\begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 17,3 & 10 & 0 \\ -10,3 & -38,6 & 0 \end{vmatrix}\nonumber \]

\[= -564 \text{дюйм-фунт}. \номер \]

Параллелепипеды

Чтобы найти объем параллелепипеда, натянутого на три вектора u , v и w , находим тройное произведение:

\[\text{Объем}= \textbf{u} \cdot ( \textbf{v} \times \textbf{w}). \nonumber \]

Это можно найти, вычислив определитель трех векторов:

\[\begin{vmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3& v_3 & w_3 \end{vmatrix }.\номер \]

Пример \(\PageIndex{6}\)

Найдите объем параллелепипеда, натянутого на векторы

\[\textbf{u} = <1,0,2>, \;\;\; \textbf{v} = <0,2,3>, \;\;\; \textbf{v} = <0,1,3>.\nonumber \]

Решение

Находим

\[\begin{vmatrix} 1 &0 &2 \\ 0 &2 &3 \\ 0 &1 &3 \end{vmatrix} = 3. \nonumber \]

Авторы и авторство

---

Эта страница под названием 1.5: The Dot and Cross Product распространяется по незаявленной лицензии и была создана, изменена и/или курирована Ларри Грином.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Ларри Грин

   Показать страницу TOC

   нет

2. Теги

   1. компоненты
   2. перекрестное произведение
   3. НАПРАВЛЕННЫЕ КОСИНУСЫ
   4. скалярное произведение
   5. выступ

Как найти угол между двумя векторами — mathsathome.

com

Как найти угол между двумя векторами: видеоурок

Калькулятор угла между двумя векторами

Приведенный ниже калькулятор вычисляет угол между 2D- и 3D-векторами. Просто введите компоненты каждого вектора в форму

Как найти угол между двумя векторами

Чтобы найти угол между двумя векторами:

1. Найдите скалярное произведение двух векторов.
2. Разделите это значение на величину первого вектора.
3. Разделите это значение на величину второго вектора.
4. Возьмите арккосинус этого значения, чтобы получить угол.

Например, найдите угол между и .

Шаг 1. Найдите скалярное произведение двух векторов

Чтобы найти скалярное произведение двух векторов, перемножьте соответствующие компоненты и сложите их.

Скалярное произведение двух двумерных векторов и находится с помощью .

Для векторов и скалярное произведение .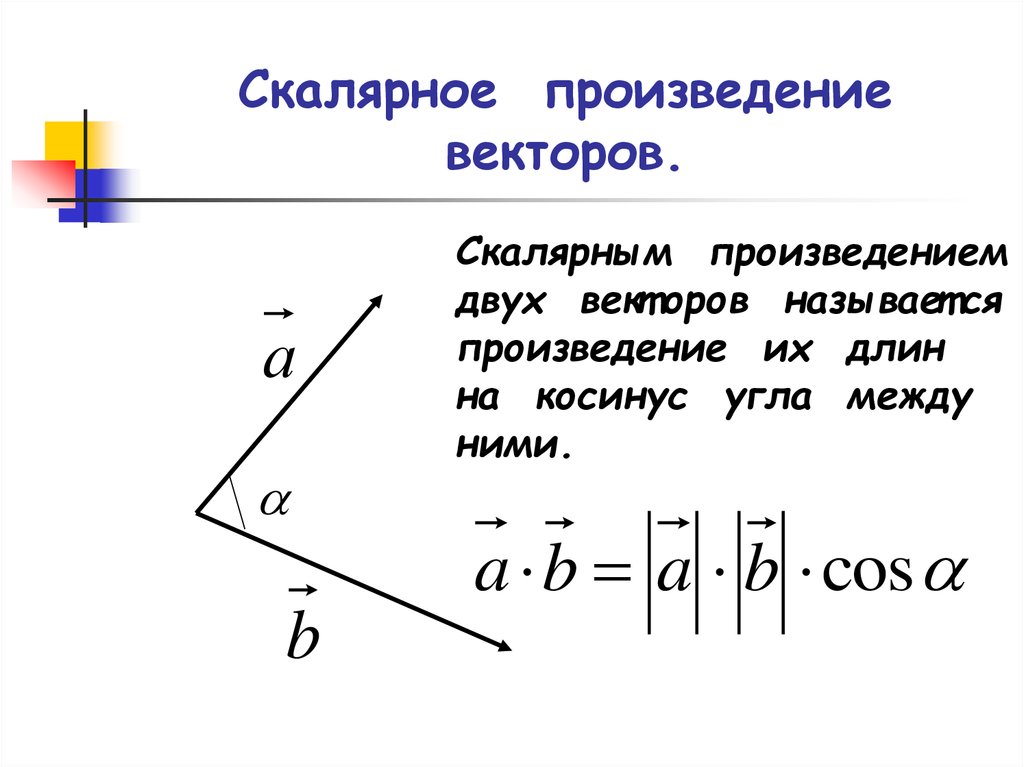

Поэтому

(3\-2)” role=”presentation” style=”font-size: 113%; положение: относительное;»>

Шаг 2. Разделите это на величину первого вектора

Чтобы вычислить величину вектора, используйте теорему Пифагора с компонентами 𝑥 и y вектора.

Величина любого вектора находится следующим образом: .

Следовательно, величина вектора равна .

Это становится который есть .

Величина первого вектора a равна .

Мы делим скалярное произведение, рассчитанное ранее, на эту величину.

Получаем

Шаг 3. Разделим это на величину второго вектора

Величина второго вектора b находится с помощью .

Для вектора величина равна .

Это становится который есть .

Мы делим предыдущий результат на эту величину, чтобы получить

Шаг 4. Возьмем арккосинус этого результата

Формула для нахождения угла между двумя векторами: .

Это можно преобразовать, взяв значение, обратное косинусу в обеих частях уравнения.

Угол между двумя векторами равен .

Как было рассчитано ранее:

Используя калькулятор, мы вводим, .

Это дает нам угол между двумя векторами как .

Формула угла между двумя векторами

Формула для угла между двумя векторами, a и b : . Где вектор a (a _x a _y ) and vector b is (b _x b _y ), the dot product a•b=a _x b _x + a _y б _г . Величина вектора | a | = √ ( A _x ² + A _Y ² ) и магнит ² ) и магнит ² ). б _х ² + б _у ² ).

Наиболее распространенное отображение формулы для угла между двумя векторами показано ниже как .

Эту формулу можно преобразовать в более удобную формулу, взяв арккосинус обеих частей уравнения.

Это дает нам прямую формулу для угла между двумя векторами.

Угол между двумя векторами равен .

Мы можем использовать эту формулу, чтобы найти угол между двумя векторами в 2D.

Найдите угол между векторами и .

В этих двух векторах a _x = 2, a _y = 5, b _x = -4 и b _y = -1.

Скалярное произведение находится с помощью , которое для наших векторов становится и так .

Величина каждого вектора находится с помощью теоремы Пифагора с компонентами 𝑥 и y.

Для этих векторов и так далее. и так .

Теперь можно использовать формулу.

и это можно оценить прямо на калькуляторе, чтобы дать.

Как найти угол между двумя векторами в 3D

Чтобы найти угол между двумя векторами в 3D:

1. Найдите скалярное произведение векторов.
2. Разделите скалярное произведение на величину каждого вектора.
3. Используйте инверсию косинуса к этому результату.

Например, найдите угол между и .

Эти векторы содержат компоненты в трех измерениях: 𝑥, y и z.

Для вектора a _x =2, a _y = -1 и a _z = 3.

Для вектора b _x = 2, b _y = 0 и b _z = 1.

910068 Шаг произведение векторов

Чтобы найти скалярное произведение двух векторов, умножьте соответствующие компоненты каждого вектора и сложите результаты.

Для вектора в 3D .

Для наших векторов это становится .

Это упрощается до .

Шаг 2. Разделите это скалярное произведение на величину двух векторов

Чтобы найти величину вектора в 3D, используйте теорему Пифагора. Например, .

Для вектора , . Это упрощает до .

Для вектора , . Это упрощает до .

Мы делим скалярное произведение, найденное на шаге 1, на обе эти величины.

Получаем .

Шаг 4. Используйте обратный косинус для этого результата

Формула для угла между двумя векторами: . Эту формулу можно использовать для векторов в 2D или 3D.

Чтобы изменить эту формулу для угла, мы берем арккосинус обеих сторон.

Ранее мы рассчитали , и .

Поэтому .

Это можно вычислить на калькуляторе, чтобы получить угол между двумя векторами как .

Что знак cosθ говорит нам о векторах?

Если значение cosθ положительное, угол между векторами острый. Если значение cosθ отрицательно, угол между векторами тупой.

Как определить, перпендикулярны ли два вектора

Два вектора перпендикулярны, если их скалярное произведение равно нулю. Для двух векторов (A _x A _Y ) и (B _x B _Y ), DOT Product дается A • B = A A • B = A

44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444443.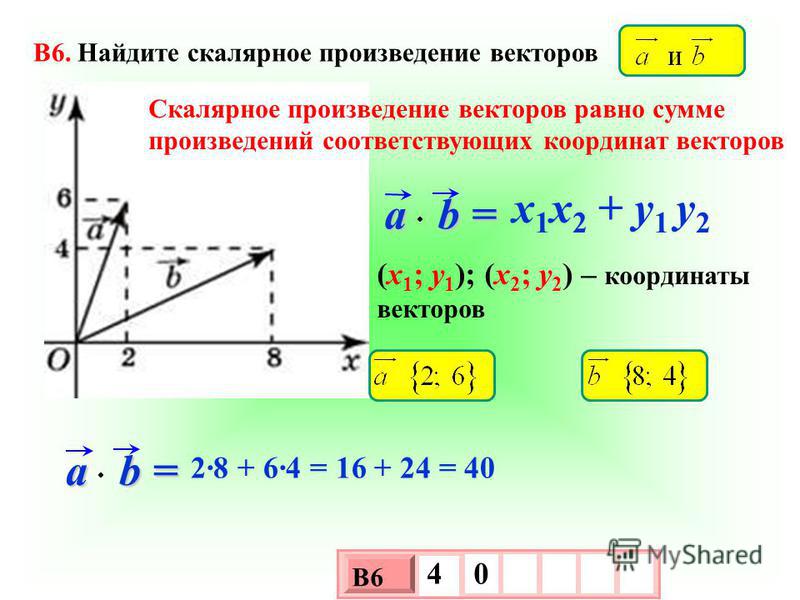 _x + а _у б _у . Если а _х b _x + a _y b _y = 0, два вектора перпендикулярны. Это означает, что они встречаются под прямым углом.

Формула для угла между двумя векторами имеет вид .

Если , то эта формула принимает вид .

Если числитель дроби равен нулю, то вся дробь равна нулю. Поэтому формула становится .

Решая это для угла, мы используем арккосинус нуля, .

Арккосинус нуля равен 90°.

Следовательно, если скалярное произведение двух векторов равно нулю, угол между двумя векторами всегда будет равен 90°.

Например, покажите, что и перпендикулярны.

Если два вектора перпендикулярны, это означает, что они пересекаются под прямым углом.

Чтобы показать, что два вектора перпендикулярны, вычислите скалярное произведение.