{-30} Кл \cdot м$, определить, какую долю от общей поляризуемости (электронной и ориентационной) составляет электронная поляризуемость молекулы. Подробнее

Задача по физике — 9018

Уединенная металлическая сфера электроемкостью $C = 10 пФ$ заряжена до потенциала $\phi = 3 кВ$. Определить энергию $W$ поля, заключенного в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в три раза больше радиуса сферы. Подробнее

Задача по физике — 9019

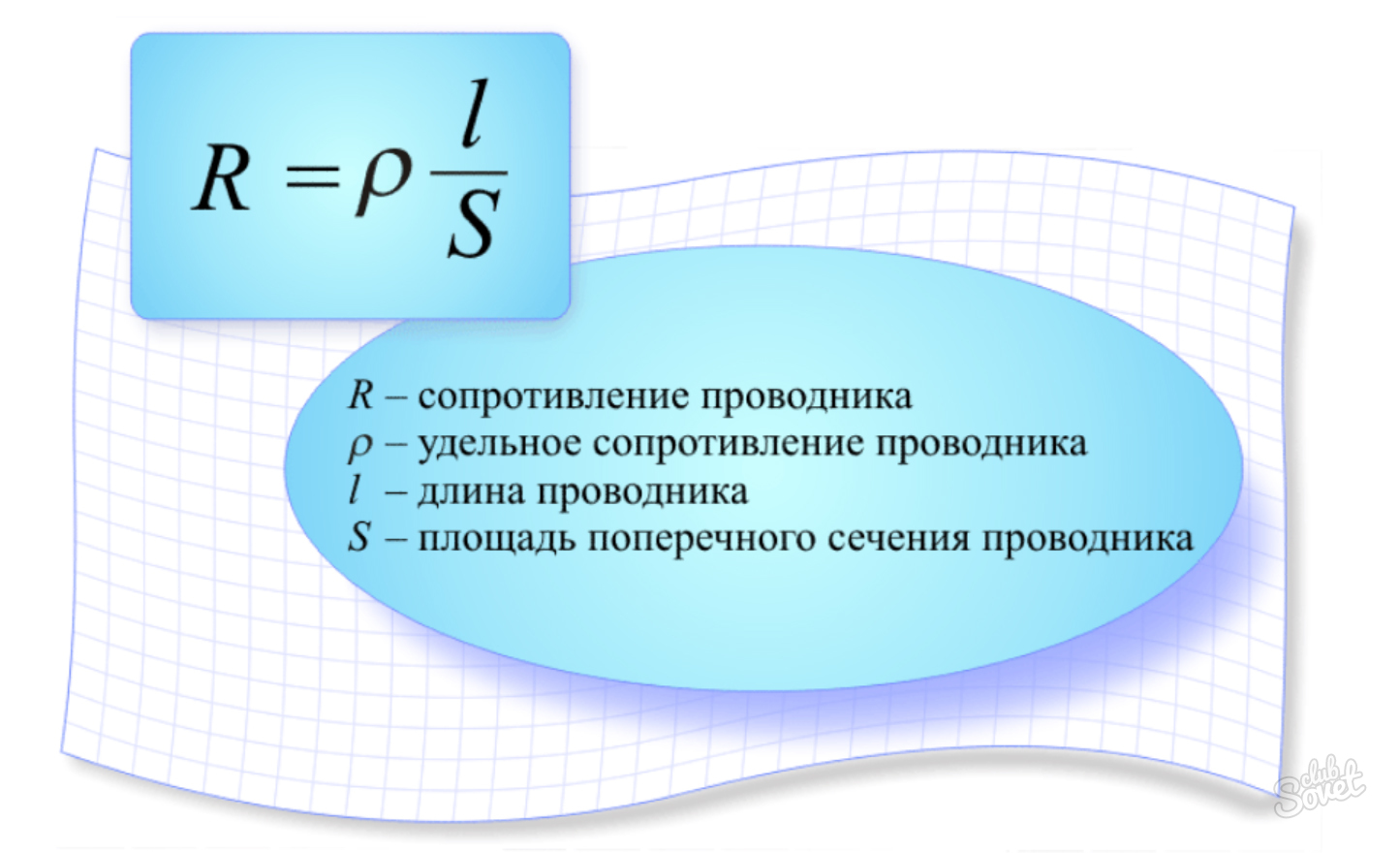
Вычислить сопротивление $R$ графитового проводника, изготовленного в виде прямого кругового усеченного конуса высотой $h = 20 см$ и радиусами оснований $r_{1} = 12 мм$ и $r_{2} =8 мм$. Температура $t$ проводника равна $20^{ \circ} С$. { \circ} С$. Найти сопротивление $R$ проводника, считая градиент температуры вдоль его оси постоянным. Подробнее

Задача по физике — 9021

К источнику тока с ЭДС $\mathcal{E} = 1,5 В$ присоединили катушку с сопротивлением $R = 0,1 Ом$. Амперметр показал силу тока, равную $I_{1} = 0,5 А$. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока $I$ в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления $r_{1}$ и $r_{2}$ первого и второго источников тока. Подробнее

Задача по физике — 9022

Имеется $N$ одинаковых гальванических элементов с ЭДС $\mathcal{E}$ и внутренним сопротивлением $r_{i}$ каждый. Из этих элементов требуется собрать батарею, состоящую из нескольких параллельно соединенных групп, содержащих по $n$ последовательно соединенных элементов. При таком значении $n$ сила тока $I$ во внешней цепи, имеющей сопротивление $R$, будет максимальной? Чему будет равно внутреннее сопротивление $R_{i}$ батареи при этом значении $n$? Подробнее

Задача по физике — 9023

Даны 12 элементов с ЭДС $\mathcal{E} = 1,5 В$ и внутреннем сопротивлением $r = 0,4 Ом$. Как нужно соединить эти элементы, чтобы получить от собранной из них батареи наибольшую силу тока во внешней цепи, имеющей сопротивление $R = 0,3 Ом$? Определить максимальную силу тока $I_{max}$.

Подробнее

Задача по физике — 9024

Два элемента ($\mathcal{E}_{1} =l,2 В, r_{1} = 0,1 Ом; \mathcal{E}_{2} = 0,9 В, r_{2} = 0,3 Ом$) соединены одноименными полюсами. Сопротивление $R$ соединительных проводов равно 0,2 Ом.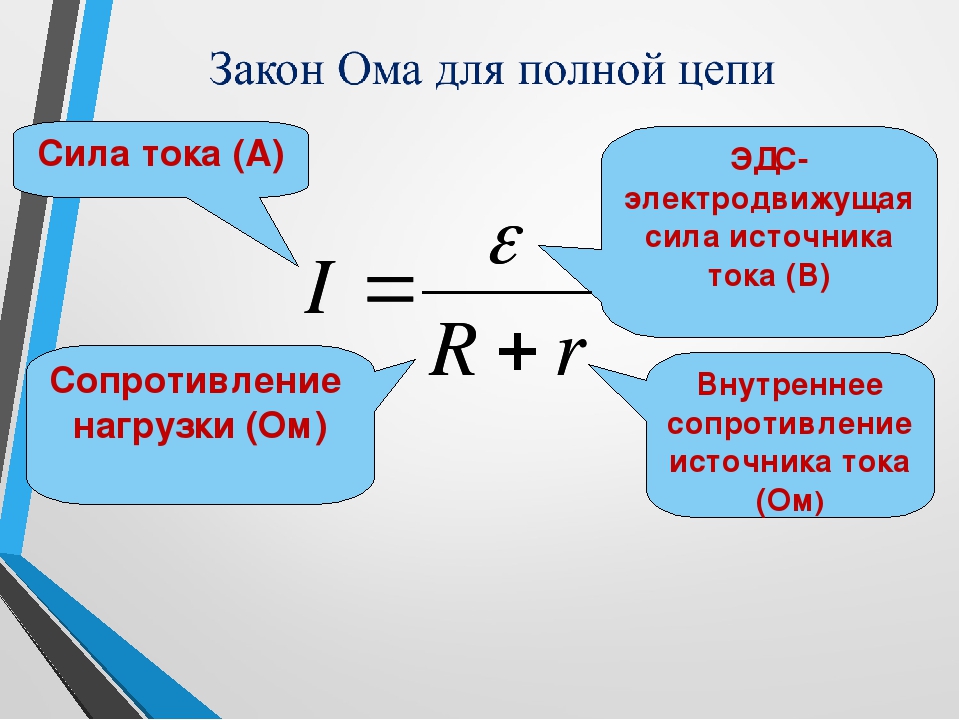 Определить силу тока $I$ в цепи. Подробнее

Задача по физике — 9025

Две батареи аккумуляторов ($\mathcal{E}_{1} = 10 В, r_{1} = 1 Ом; \mathcal{E}_{2} =8 В, r_{2} = 2 Ом$) и реостат ($R = 6 Ом$) соединены, как показано на рис. Найти силу тока в батареях и реостате.
Подробнее

Задача по физике — 9026

Три батареис ЭДС $\mathcal{E}_{1} = 12 В, \mathcal{E}_{2} = 5 В$ и $\mathcal{E} = 10 В$ и одинаковыми внутренними сопротивлениями $r$, равными 1 Ом, соединены между собой одноименными полюсами. Сопротивление соединительных проводов ничтожно мало. Определить силы токов $I$, идущих через каждую батарею. Подробнее

Задача по физике — 9027

ЭДС батареи аккумуляторов $\mathcal{E} = 12 В$, сила тока $I$ короткого замыкания равна 5 А. Какую наибольшую мощность $P_{max}$ можно получить во внешней цепи, соединенной с такой батареей? Подробнее

Задача по физике — 9028

ЭДС $\mathcal{E}$ батареи равна 20 В. Сопротивление $R$ внешней цепи равно 2 Ом, сила тока $I = 4 А$. Найти КПД батареи. При каком значении внешнего сопротивления $R$ КПД будет равен 99%? Подробнее

Задача по физике — 9029

К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС $\mathcal{E}$ батареи равна 24 В, внутреннее сопротивление $r = 1 Ом$. Нагреватель, включенный в цепь, потребляет мощность $P = 80 Вт$. Вычислить силу тока $I$ в цепи и КПД $\eta$ нагревателя. Подробнее

Задача по физике — 9030

Сила тока в проводнике сопротивлением $R = 12 Ом$ равномерно убывает от $I_{0} = 5 А$ до $I=0$ в течение времени $t= 10 с$. Какое количество теплоты $Q$ выделяется в этом проводнике за указанный промежуток времени? Подробнее

Задача по физике — 9031

По проводнику сопротивлением $R=3 Ом$ течет ток, сила которого возрастает. Количество теплоты $Q$, выделившееся в проводнике за время $\tau = 8 с$, равно 200 Дж. Определить количество электричества $q$, протекшее за это время по проводнику. В момент времени, принятый за начальный, сила тока в проводнике равна нулю.

Подробнее

Расчет коэффициента полезного действия: формулы для электрической цепи

Для оценки эффективности расхода энергии на выполнение работы необходимо выяснить, как найти КПД. Полученные сведения пригодятся для оптимизации параметров электрических компонентов цепи, рычагов и других передаточных механизмов. С помощью предварительных вычислений можно увеличить длительность действия автономного источника питания, решить другие практические задачи.

Формула КПД поясняет основные определения

Что такое КПД источника тока

Неподвижный заряд не выполняет работу. Уменьшение энергетического запаса в аккумуляторе происходит за счет химических реакций. Фактически это свидетельство несовершенства конструкции.

После подключения источника к проводникам с подключенной нагрузкой заряды перемещаются по цепи, выполняя определенную работу. Полезная составляющая мощности (Pпол) определяется параметрами внешнего контура. Полная (Pп) – содержит совокупные затраты. Если электротехник пользуется привычными терминами, он быстро установит для коэффициента полезного действия формулу:

КПД = Рпол/Рп = (U*I)/(Е*I) = U/E.

Для чего нужен расчет КПД

Наглядный пример недостаточно эффективного устройства – классическая лампа накаливания. Пропускание тока через вольфрамовую спираль повышает температуру проводника. В рабочем режиме значительное количество потребляемой мощности расходуется на генерацию излучения. Однако к видимой части диапазона относится только небольшая часть спектра. Так как вырабатываемая теплота не выполняет полезного действия, соответствующие энергетические затраты следует узнавать по излишним.

Если выразить КПД через мощность в этом случае, следует одновременно учесть долговечность. Эта методика повышает точность оценки, так как подразумевает необходимость периодической замены испорченного излучателя.

В типовом рабочем режиме лампа накаливания нагревает нить до 2600-2800К. При таком значении срок службы составляет 900-1200 часов, КПД – от 5 до 7%. Увеличить эффективность в 2-5 раз можно повышением температуры до 3400-3600К. Однако в этом варианте долговечность уменьшается до 5-6 часов. Подобные практические характеристики нельзя признать удовлетворительными.

Сравнение эффективности и других параметров разных типов ламп

Эта таблица демонстрирует превосходство экономичных источников света.

Срок службы современных светодиодов измеряется десятками тысяч часов. Даже на завершающих этапах рабочих циклов обеспечиваются высокая яркость и качественное распределение спектральных составляющих.

Нахождение тока в полной цепи

Для изучения эффективности потребления энергии в электротехнике можно использовать базовые формулы. В полной цепи по базовому определению рассматривают источник тока (I) с внутренним сопротивлением (r). Подключенная нагрузка потребляет определенную мощность. Она характеризуется электрическим сопротивлением R.

Прохождение тока по такой цепи обеспечивает энергия источника, которая определена значением электродвижущей силы (ЭДС – E). Ее можно выразить как отношение выполненной сторонними силами работы (A) по передвижению заряда (q) с положительным знаком по соответствующему контуру.

С учетом известной формулы I= q/t несложно определить зависимость между рассматриваемыми величинами:

А = E * I * t,

где t – контрольный временной интервал.

Отдельно можно рассмотреть участки с внутренним и внешним сопротивлением. Каждый из них выделяет определенное законом Джоуля-Ленца количество теплоты Q = I2 * R * t. Так как энергия не пропадает бесследно, можно сделать правильный вывод о равенстве Q = A.

Подставив значения в исходное выражение, получают:

E = I*R + I*r.

ЭДС полной цепи вычисляется сложением двух падений напряжений на внутреннем и внешнем участке. Элементарное преобразование позволяет узнать силу тока в соответствующем проводнике:

I = E/ (R+r).

Расчет КПД электрической цепи

После определения основных параметров можно перейти к изучению эффективности системы. Для вычисления КПД обозначение потребления электроэнергии удобно сделать по стандартным формулам.

Определить мощность можно по следующим соотношениям силы тока, напряжения, электрического сопротивления

Выполняемая работа в цепи определяется количеством перемещенных зарядов, а также скоростью данного процесса. Для объективной оценки последнего параметра измерения выполняют с учетом определенных временных интервалов (Δt). Работу и мощность можно определить следующими формулами:

• A = P * Δt;
• P = A / Δt.

Как и в классической механике, работу можно измерить в джоулях (Дж). Мощность, по стандартам СИ, указывают в ваттах (Вт). Зависимость между отмеченными единицами:

Вт = Дж/ с (для электрических цепей вольт * ампер).

Для обозначения КПД символ «η» применяют в типовых формулах. Базовое определение с учетом приведенных замечаний можно преобразовать следующим образом:

η = A / Q * 100%,

где:

• A – выполненная работа;
• Q – энергия, полученная из источника.

Как найти КПД, формула для полной цепи

Любое подключенное устройство характеризуется определенными потерями. Резистор выделяет тепло. Трансформатор тратит часть энергии на преобразование электромагнитных волн.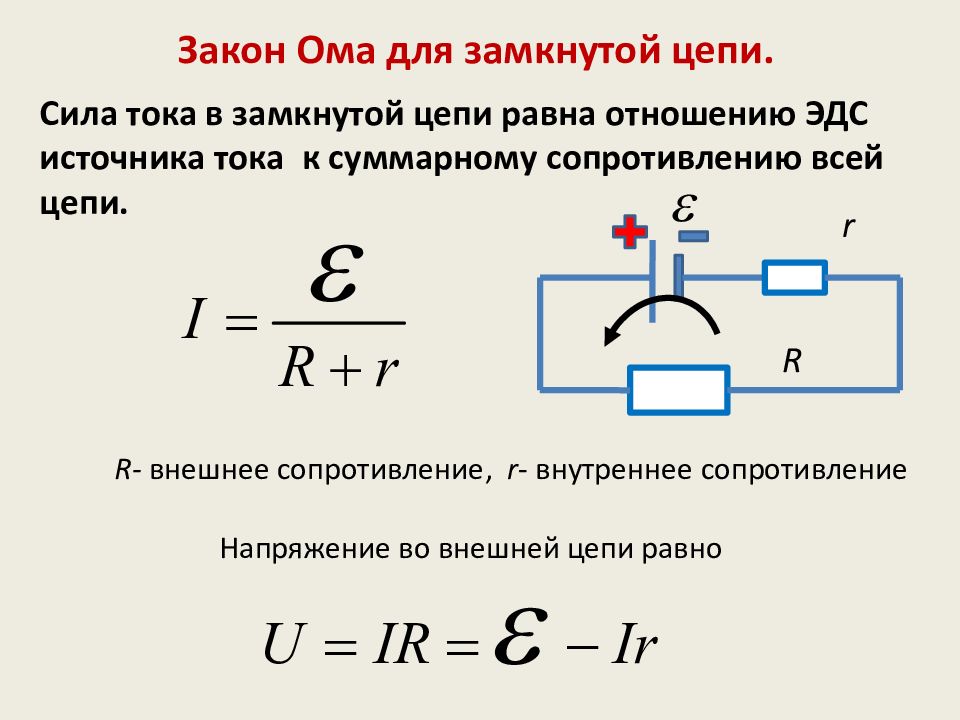 На примере лампы накаливания показана низкая эффективность изделия. С применением КПД увеличивают объективность оценки разных систем, подключаемых потребителей, генераторов. В следующем пункте представлена технология проверки силовых агрегатов.

Методика и порядок измерений

Идеальные условия можно рассматривать только в теории. Для корректной оценки замкнутой системы необходимо учитывать энергетические потери на выполнение необходимой работы. Ниже показано, как определить КПД механических силовых агрегатов с применением разных исходных данных.

Движению поршня в блоке цилиндров двигателя внутреннего сгорания препятствует сила трения. Поступательно-возвратные движения в ходе стандартного цикла преобразуются во вращение вала с дополнительными потерями. Высокая температура не выполняет в данном случае полезные функции. Чтобы не допустить разрушения агрегата, необходимо поддерживать определенный тепловой режим. Приходится обеспечить циркуляцию охлаждающей жидкости с помощью помпы.

Понятно, что в подобном случае сделать общий КПД расчет с учетом каждого компонента конструкции непросто. Однако можно узнать в ходе эксперимента с высокой точностью, какое количество топлива (масса – m) придется затратить на 100 км пробега машины за соответствующее время (t). Далее нужно взять из сопроводительной документации (справочников) следующие данные:

• мощность мотора – Рм;
• удельную теплоту бензина – У.

В этом варианте для расчета КПД двигателя формула преобразуется следующим образом: 

η = (Pм * t) / (У * m).

Для отображения результата в % итоговое значение умножают на 100.

Если мощность силового агрегата не известна, определять эффективность можно по массе авто (Mа). Измерять ее несложно с помощью промышленных весов (на станции техосмотра, элеваторе). В ходе эксперимента разгоняются с места до контрольной скорости (v). Массу топлива вычисляют по объему (переведенному из литров в м кв.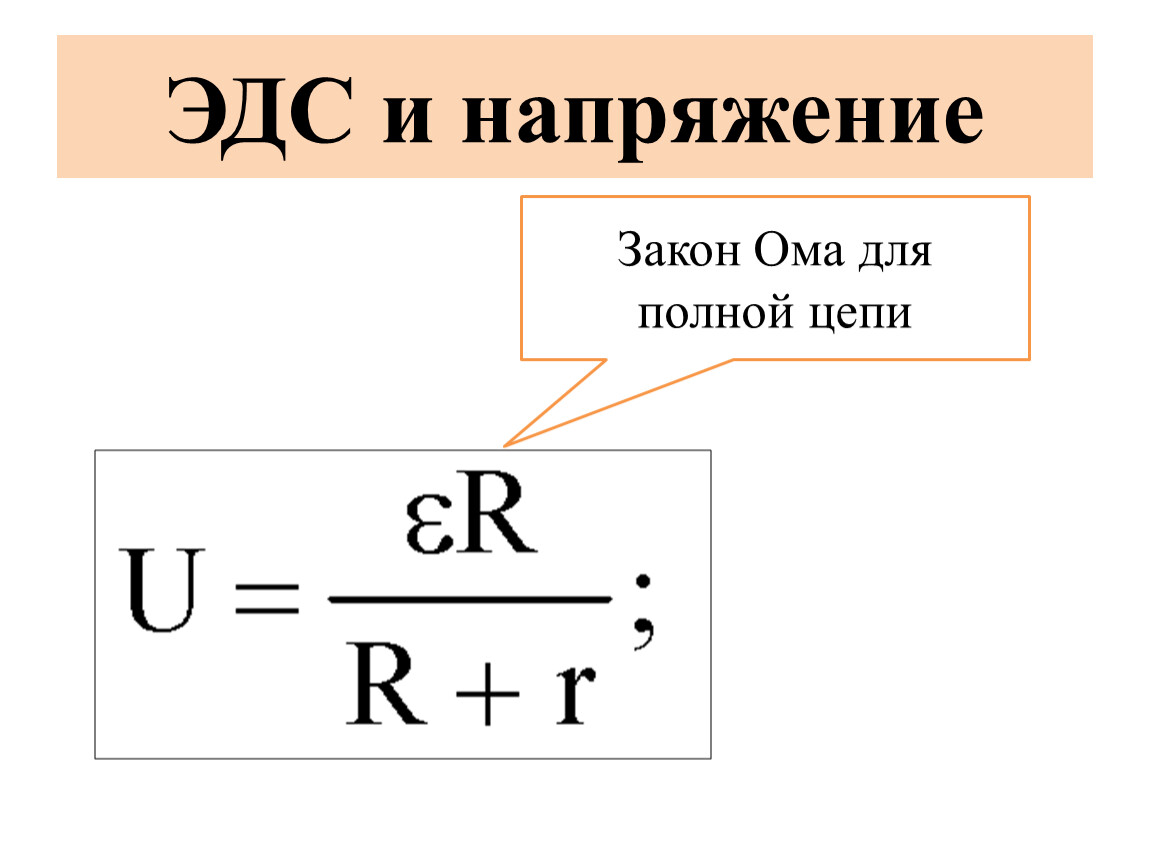 ), который умножают на плотность (справочная величина в кг на куб. м).

В этом случае КПД расчет находят по формуле:

η = (Mа * v2)/(2 * У * m).

Следует перевести предварительно скорость из км/час в м/с.

Проще измеряется эффективность электродвигателя с паспортной мощностью (P). Его подключают к источнику питания с известным напряжением (U). После выхода на стабильную частоту вращения фиксируют значение тока (I) в цепи. Далее применяют классическую формулу:

η = P/ (U * I).

Если сопроводительная документация отсутствует, технические параметры берут с официального сайта производителя. Однако и в этом случае следует понимать ограниченную точность подобных данных. В процессе эксплуатации характеристики могут ухудшиться за счет естественного износа. Погрешность увеличивается после длительной интенсивной эксплуатации, при подключении редуктора или другого переходного устройства.

Значительно улучшить точность можно с применением простой методики:

• устанавливают на вал шкив с закрепленным тросом;
• поднимают на контрольную высоту (h) груз c массой m;
• секундомером фиксируют время (t) на выполнение этой работы;
• мультиметром измеряют напряжение (U) и силу тока (I) на клеммах источника питания и в разрыве цепи, соответственно.

Для нахождения КПД в физике формула выглядит следующим образом:

η = (m * h * g)/(I * U * t),

где g – это гравитационная постоянная (9,80665).

Эффективность любого силового агрегата определяют по соотношению полезной работы к расходованной энергии. Чтобы корректно определять класс техники, пользуются переводом в проценты. Следует подчеркнуть, что значение больше 100% обозначает ошибку в расчетах. Создатель подобного агрегата станет «властелином мира», так как изобретет вечный двигатель.

Видео

как связаны между собой напряжение, ток и сопротивление

Добавлено 30 сентября 2020 в 00:30

Сохранить или поделиться

Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Единицы измерения: вольт, ампер и ом

Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:

Единицы измерения тока, напряжения, сопротивления

Величина	Символ	Единица измерения	Сокращение единицы измерения
Ток	I	Ампер	А
Напряжение	V	Вольт	В
Сопротивление	R	Ом	Ом

«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах.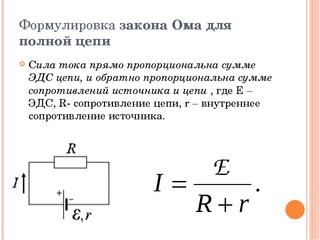 Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.

Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.

Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.

Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.

Кулон и электрический заряд

Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.

Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.

Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.

Формула закона Ома

Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

\[E=IR\]

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:

\[I = \frac{E}{R}\]

\[R = \frac{E}{I}\]

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

Рисунок 1 – Пример простой схемы

В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

Какая величина тока (I) в этой цепи?

\[I = \frac{E}{R} = \frac{12 \ В}{3 \ Ом} = 4 \ А\]

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

Какое сопротивление (R) оказывает лампа?

\[R = \frac{E}{I} = \frac{36 \ В}{4 \ А} = 9 \ Ом\]

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

Какое напряжение обеспечивает батарея?

\[E = IR = (2 \ А)(7 \ Ом) = 14 \ В\]

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Резюме

• Напряжение измеряется в вольтах, обозначается буквами «E» или «V».
• Сила тока измеряется в амперах, обозначается буквой «I».
• Сопротивление измеряется в омах, обозначается буквой «R».
• Закон Ома: E = IR; I = E/R; R = E/I

Оригинал статьи:

Теги

Закон ОмаЗарядКулонОбучениеСила токаСопротивлениеСхемотехникаЭлектрический токЭлектрическое напряжение

Сохранить или поделиться

Сила тока измерение компенсационным методо

    Принцип компенсационного метода измерения э. д. с. гальванических элементов. Электродвижущая сила гальванического элемента может быть измерена компенсационным методом. Непосредственное измерение э. д. с. с помощью чувствительного вольтметра имеет существенные недостатки. Действительно, если обозначим через внутреннее сопротивление элемента, через —сопротивление вольтметра, через Е—истинную электродвижущую силу элемента и через /—силу тока в цепи, то согласно закону Ома  [c.288]
    Для измерения электродвижущих сил пользуются компенсационным методом, преимущество которого состоит в том, что он позволяет измерять э. д. с. элемента, когда в цепи отсутствует ток ( = 0). На рис. 40 приведена принципиальная схема компенсационной у ста и ов к и. [c.153]

    Электродвижущая сила любого гальванического элемента может быть измерена либо включением в цепь чувствительного вольтметра, либо компенсационным методом. В первом случае через цепь обязательно протекает электрический ток, во втором — э.д.с. измеряется при отсутствии тока. В практике методом непосредственного измерения э. д.с. не пользуются. И вот почему. [c.245]

    Прибор состоит из следующих основных узлов потенциометра постоянного тока типа ПП класса 0,2, предназначенного для непосредственных измерений компенсационным методом электродвижущих сил и напряжений [c.84]

    При реакциях осаждений и комплексообразования индикаторным электродом служит электрод, потенциал которого является функцией активности ионов, участвующих в реакциях осаждения или комплексообразования. Например, серебряный электрод используется для определения серебра, а также ионов, дающих с ионами Ад+ малорастворимые соли или прочные комплексные соединения. В качестве электродов сравнения используют каломельный или хлоридсеребряный электрод. Последний, если это допустимо, погружают непосредственно в исследуемый раствор или соединяют при помощи электролитического ключа с титруемым раствором. Измерение возникающей э. д. с. можно проводить по компенсационному и некомпенсационному методам (измерение потенциала электрода, измерение силы тока).  [c.314]

    Разница между э. д. с. и напряжением обусловлена омическим падением напряжения внутри элемента при прохождении тока и другими эффектами. Поэтому измерение э. д. с. обычно проводят компенсационным методом, при котором сила тока, протекающего через элемент, близка к нулю. Для этого к элементу подводят э. д. с. с противоположным знаком от внешнего источника тока, значение которой можно регулировать тем или иным способом. В измерительную цепь включаются также гальванометр для регистрации тока и вольтметр для измерения напряжения. В момент, когда выходное напряжение внешнего источника тока равно э. д. с. гальванического элемента (момент компенсации э. д. с.), сила тока в цепи равна нулю (стрелка гальванометра не отклоняется). Измеренное в этот момент вольтметром напряжение на клеммах гальванического элемента равно его э. д. с. Более простой и менее точный метод измерения э.д. с. заключается в прямом измерении напряжения на клеммах гальванического элемента вольтметром, имеющим высокое омическое сопротивление (высокоомный вольтметр). Вследствие высокого омического сопротивления вольтметра мала сила тока, протекающего через элемент, поэтому невелика разница между э. д. с. и напряжением элемента.  [c.189]

    Измерители тока. Для измерения поляризационных токов пользуются микроамперметрами. Измерители тока включают последовательно в цепь их внутреннее сопротивление небольшое и мало сказывается на общей силе тока. Очень чувствительным и точным методом определения величины силы тока в какой-либо замкнутой цепи является измерение падения напряжения ( ) через прецизионное постоянное известное сопротивление (/ ), включенное последовательно в цепь. Величину V = Я измеряют компенсационным методом с помощью потенциометра. Зная R и V, можно вычислить г с большой точностью. [c.55]

    Сопротивления. Для измерения силы тока в цепи компенсационным методом пользуются набором высокопрецизионных сопротивлений. [c.55]

    Важнейшее место в экспериментальной электрохимии занимает измерение электродвижущих сил. Для измере- > ния э. д. с. электрохимических систем обычно пользуются компенсационным методом, принцип которого состоит в уравновешивании определяемой э. д. с. элемента равным по величине падением напряжения 1г на реохорде или в потенциометре, питаемом от внешнего источника тока (рис. 25). Компенсирующее падение напряжения обычно создается с помощью хорошо заряженного аккумулятора. При этом сопротивление любого отрезка проволоки реохорда пропорционально его длине, а общее сопротивление проволоки равно Кн. В простейшем случае изучаемый гальванический элемент X включается навстречу аккумулятору А (плюс против плюса, минус против минуса). Перемещением движка по реохорду подбирают такое положение его, при котором э.д.с. эле- [c.173]

    При измерении э. д. с. гальванических элементов необходимо, чтобы химическая реакция в гальваническом элементе протекала обратимо, что возможно при небольшом значении силы протекающего тока. Этому требованию удовлетворяет компенсационный метод измерения э. д. с. (метод Поггендорфа), в котором при приближении к компенсации через гальванический элемент проходят токи с силой не более 10 А. [c.554]

    Измерение ЭДС. Для измерения равновесной (обратимой) ЭДС электрохимического элемента необходимо, чтобы процесс совершался бесконечно медленно, т. е. чтобы элемент работал при бесконечно малой силе тока. Это условие выполняется в компенсационном методе измерения, который основан на том, что элемент включается против внешней разности потенциалов, и последняя подбирается так, чтобы ток в цепи отсутствовал. В этом случае внешняя разность потенциалов равна ЭДС изучаемого элемента. Пользуясь компенсационным методом (методом Поггендорфа), можно непосредственно измерить значение равновесной ЭДС элемента. [c.242]

    ЭДС гальванического элемента представляет собой равновесную величину. Поэтому измерение ЭДС необходимо проводить без нарушения электродных равновесий. В равновесном состоянии через поверхность соприкосновения фаз электродов суммарный ток равен нулю. Следовательно, при измерении ЭДС необходимо обеспечить отсутствие тока через гальванический элемент. Этого можно добиться путем компенсации ЭДС противоположно направленным падением напряжения (компенсационный метод). Достоверные результаты получают также с помощью некомпенсационного метода, если сила тока ничтожно мала. [c.268]

    Наиболее точным методом измерения электродвижущих сил (э. д. с.) является компенсационный метод, основанный на том, что падение напряжения, обусловленное исследуемым элементом на проводнике с переменным сопротивлением, компенсируется направленной противоположно электродвижущей силой источника тока с известным напряжением. В момент компенсации (равенства обеих э. д. с.) в проводнике не проходит ток. [c.377]

    Термоэлектродвижущую силу обычно измеряют стрелочным вольтметром хорошего класса точности, по возможности с очень высоким внутренним сопротивлением. Благодаря высокому внутреннему сопротивлению сила тока будет весьма мала и падение напряжения в термопаре и подводящих проводах пренебрежимо мало. При очень точных работах измерения проводят компенсационным методом. [c.51]

    Кроме того, эти потери можно свести к минимуму, применяя компенсационный метод , при котором потери тепла компенсируются электрическим нагревом термопары. Термопара поглощает тепло от пламени, если ее температура ниже температуры пламени, и отдает тепло пламени, если она нагрета до более высокой температуры. Это приводит к отклонению измеренной температуры, определяемой по кривой тепло—сила тока, и полученной при градуировке термопары (обычно в вакууме). Точка пересечения двух кривых (полученных при нагреве термопары в вакууме и пламени) соответствует отсутствию конвективного теплообмена между термопарой и газом, что возможно только при равенстве их температур. Этот принцип может быть применен как к термометрам сопротивления, так и к термопарам. Основное затруднение заключается в создании идентичности условий лучистого теплообмена проволочки с окружающими телами при градуировке и в пламени. Различие этих условий, естественно возникающее в процессе экспериментов, приводит к погрешностям определения температуры газа, часто весьма существенным. [c.38]

    Направление тока определяется соотношением потенциалов двух электродов. Разность потенциалов или электродвижущая сила Е — мера движущей силы реакции. Есл э. д. с. обратимого элемента сбалансирована извне эквивалентной и противоположно направленной э. д. с., то никаких химических изменений в элементе происходить не будет. Однако, если внешнюю э.д.с. затем уменьшить на очень малую величину, от элемента будет течь небольшой ток и пойдет реакция. Если, наоборот, приложенную извне э. д. с. увеличить на очень малую величину, ток начинает течь в противоположном направлении и химическая реакция будет обращена. Измерение э. д. с. гальванического элемента компенсационным методом, когда э. д. с., взятая от потенциометра, сбалансирована почти точно э. д. с. самого элемента, максимально приближается к условиям термодинамической обратимости, поэтому к таким системам могут быть приложимы принципы термодинамического равновесия.  [c.12]

    Чтобы предупредить возникновение поляризации элемента, измерять его э. д. с. следует в тот момент, когда сила тока в системе равна нулю. Такому условию отвечает компенсационный метод измерения э. д. с., который может быть осуществлен с помощью различных приборов, а именно а) реохорда и нормального кадмиевого элемента б) двух движковых реостатов и вольтметра в) двух магазинов сопротивлений и нормального кадмиевого элемента, г) потенциометра. [c.30]

    При записи интегральных полярограмм с сопротивления поляризующее напряжение, плавно изменяющееся в пределах одного вольта. Запись полярограммы начинается с любого заранее заданного напряжения в диапазоне от +0,5 до —2 в. Установка этого напряжения производится переключателями BJ, В2). Измерение силы тока ячейки производится компенсационным методом путем сравнения падения напряжения на одном из сопротивлений с падением напряжения на компенсационном сопротивлении Да. При изменении тока ячейки между точками вид появляется разность напряжений, которая подается на усилитель переменного тока. Усиленный сигнал управляет следящим двигателем (на схеме не показан), перемещающим дви- [c.23]

    Для получения высококачественных полярограмм необходимо обеспечить такие условия, при которых линейность изменения напряжения на ячейке не нарушалась бы при возможных колебаниях силы тока. Решение этой задачи может быть выполнено путем введения компенсации дополнительных падений напряжения на сопротивлениях измерительной цепи и ячейки. В частности, в рассмотренной выше схеме прибора ПЭ-ЗГ2 применен компенсационный метод измерения, обеспечивающий независимость напряжения на ячейке от величины последовательно с ней включенных сопротивлений Для устранения влияния сопротивления раствора в измерительную схему тем или иным способом вводится дополнительное напряжение, равное по величине, но противоположное по знаку падению напряжения в растворе [Л. 10—12]. [c.25]

    Наиболее простым и распространенным методом измерения электродных потенциалов является компенсационный метод. Измерения этим методом не представляют затруднений по указанному выше режиму. При необходимости фиксировать начальные относительно быстрые изменения потенциалов обычную методику приходится усложнять [254]. Компенсационный метод характерен тем, что измерение электродвижущих сил элементов может быть произведено в условиях, когда ток через них не проходит [255, 256]. Его принцип состоит в том, что электродвижущая сила элемента, одним электродом которого является металл [c.153]

    Сущность компенсационного метода измерения состоит в уравновешивании (компенсации) неизвестной электродвижущей силы термопары равной ей разностью потенциалов постороннего источника тока, но противоположной по знаку. Такие приборы называются потенциометрами, или компенса- 1 4 торами. [c.133]

    На рис. 35 показана схема измерения термоэлектродвижущей силы термопар компенсационным методом. Ток строго определенной величины от источника тока Б обтекает цепь, состоящую из последовательно включенных манганиновых сопротивлений — нэ. — рИ -/ доб- Сопротивление Яр, называемое реохордом, изготовляют из однородной манганиновой проволоки [c.133]

    Ток в цепи устанавливают (нормализуют) компенсационным методом при помощи источника с эталонной электродвижущей силой. В качестве такого источника служит нормальный элемент НЭ. Ключ д замыкают с контактом 2 при этом нормальный элемент включается в цепь, состоящую из постоянного сопротивления 7 эИ нуль-гальванометра ЯЯ. Если стрелка нуль-гальванометра показывает отсутствие тока, то разность потенциалов батареи между точками Л и 3 равна электродвижущей силе нормального элемента. При наличии тока в цепи гальванометра движок реостата Яб передвигают до тех пор, пока стрелка нуль-прибора ЯЯ не покажет отсутствие тока. Величину сопротивления / Н9 подбирают такой, чтобы при расчетном токе / в цепи потенциометра разность потенциалов между точками 3 и Л равнялась электродвижущей силе нормального элемента. После установления нормальной величины тока в цепи батареи можно приступить к измерению термоэлектродвижущей силы термопары ключ К замыкают с контактом 1 при этом нуль-прибор подключается к рабочей цепи потенциометра, а нормальный элемент отключается и далее в работе схемы потенциометра, при измерении э. д. с. термопары, участия не принимает. [c.134]

    Измерение электродвижущей силы элемент. С известной степенью точности э. д. с. элемента можно непосредственно измерить вольтметром, имеющим большое внутреннее сопротивление. Сила тока, проходящего через цепь, в этом случае мала, и внутренними потерями в элементе можно пренебречь. При необходимости более точного измерения следует пользоваться компенсационным методом. [c.31]

    Наиболее точным и целесообразным методом измерения является так называемый компенсационный метод, с помощью которого электродвижущие силы элементов могут быть измерены в условиях, когда ток через них не проходит. [c.197]

    Указанные недостатки компенсационного метода заставляют нередко прибегать к измерению э. д. с. при помощи ламповогО электрометра, представляющего собой ламповый вольтметр постоянного тока. Измеряемая э. д. с. подается на вход лампы, вызывая изменение потенциала сетки и, следовательно, силы анодного тока. Чувствительный гальванометр, регистрирующий это изменение, позволяет прочесть величину поданной э. д. с. Высокое входное сопротивление лампового электрометра, достигающее величины 10 °—10 ом, обеспечивает протекание весьма малого тока в элементе. Оно же позволяет измерять э. д. с. элементов с высоким внутренним сопротивлением. Применение лампового электрометра удобно потому, что позволяет непосредственно по шкале прибора прочесть величину э. д. с., не прибегая к компенсации. Однако точность отсчета при этом, конечно, меньше, чем достигаемая при помощи обычного потенциометра. [c.236]

    Большим преимуществом метода компенсации является то, что сопротивление подводящих проводов термометра не оказывает никакого влияния на результат измерения сопротивления чувствительного элемента. В самом деле, в тот момент, когда гальванометр (нуль-индикатор компенсационной схемы) не показывает отклонения, сила тока в потенциометрических подводящих проводах равна нулю. Таким образом, напряжение, измеряемое потенциометром, строго равно напряжению на концах чувствительного элемента термометра.  [c.95]

    Указанных недостатков лишены косвенные методы определения чисел переноса, основанные на измерении электродвижущих сил различных гальванических ячеек, в которых в качестве электролитов используются образцы исследуемых твердых тел. Обычно э. д. с. измеряется компенсационным методом, когда ток через ячейку не проходит и, следовательно, состояние образцов наиболее близко к равновесному. Несомненными достоинствами методов, основанных на измерении э. д. с., являются высокая точность и воспроизводимость измерений и простота экспериментального оформления. [c.207]

    Усилители постоянного или переменного тока, охваченные глубокой (практически близкой к 100%) отрицательной обратной связью, целесообразно выделить в отдельную группу в силу присущих им специфических особенностей. Такие усилители сочетают в себе положительные- свойства компенсационных методов измерения поэтому в качестве регистрирующего прибора можно применять магнито-электрические приборы с непосредственным отсчетом.  [c.130]

    Ячейку питают пониженным напряжением (10—20 мв) промышленной частоты. Последовательно с ячейкой включают сопротивление ограничивающее ток, протекающий через раствор, и эталонное сопротивление по падению напряжения на котором определяют силу тока, протекающего через раствор. Измерение осуществляют компенсационным методом. При помощи переключателя П к компенсатору подключают либо напряжение, [c.242]

    Мерой давления служит величина тока, необходимая для поддерживания пороговой температуры свечения нити. Силу тока целесообразно измерять компенсационным методом, так как при этом можно исключить ток холостого хода и перенести нулевую точку прибора в требуемую область измерений. [c.398]

    Наибольшей точности можно достичь, применяя компенсационный метод измерения напряжения. Он заключается в сравнении измеряемой разности потенциалов с падением напряжения на эталонном сопротивлении. Величина последнего должна быть точно известна. Компенсационным методом можно измерять не только напряжение, но и силу тока и сопротивление. [c.120]

    Измерение электродвижущих сил. Нормальный элемент. При работе гальванического элемента его э. д. с. не сохраняет строго постоянного значения вследствие изменения концентрации растворов и других причин. Поэтому точные измерения 3. д. с. должны производиться при минимальном прохождении тока. Этому отвечает компенсационный метод измерения э. д. с. (метод Поггендор-фа), дающий возможность определить э. д. с. элемента путем измерения разности потенциалов в условиях обратимой работы элемента. Принципиальная схема установки для компенсационного измерения э. д. с. показана на рис. 152. [c.435]

    Метод поляризационных кривых. Для уяснения этого метода разберем простейший случай разряда водородного иона на платиновом катоде в растворе серной кислоты. Будем постепенно увеличивать напряжение злектролизующего тока на электродах, замечая при этом изменения потенциала на катоде, а также силу тока, проходящего через раствор серной кислоты. Измерения напряжения и силы тока ведут с помощью милливольтметра и миллиамперметра, а определение потенциала катода — компенсационным способом. На абсциссе откладывают величины потенциала е, а на ординате — соответствующие силы тока I. Кривая на рис. 94 показывает, что вначале, при постепенном увеличении силы тока, величина е растет довольно быстро и кривая проходит вблизи абсциссы и лишь по достижении некоторого предела дает определенный перегиб, резко поднимаясь вверх. Потенциал электрода, соответствующий началу подъема силы тока, называют потенциалом разряда. Очевидно, что такой резкий подъем силы тока возможен только тогда, когда приложенное внешнее напряжение хотя бы на небольшую величину превышает электродвижущую силу гальванической пары, образующейся в результате электролиза. В рассматриваемом случае такой парой будет платиновый катод, насыщенный водородом, т. е. [c.263]

    Степень поляризации зависит от характера анодных и катодных участков, состава коррозио1шой среды и плотности коррозионного тока. Чем бо,1ьше наклон поляризационных кривых, тем сильнее поляризуется электрод и тем сильнее тормозится анодный или катодный процесс. Для снятия поляризационных кривых могут быть использованы разные схемы установок. Схема любой установки для снятия поляризационных кривых гальваностатическим способом подобна схеме для измерения электродных потенциалов компенсационным методом и отличается от нее по существу только тем, что она предусматривает подвод постоянного тока к исследуемому электроду и измерение его величины, т. е. включает источник постоянного тока, приборы для измерения силы тока и регулирования его величины и вспомогательный поляризующий электрод. Схема установки для снятия поляризационных кривых приведена на рис. 222. [c.342]

    Потенциометр постоянного тока высокоомный ППТВ-1. Потенциометр ППТВ-1 (рис. 29) представляет собой лабораторный переносный прибор, служащий для измерения электродвижущих сил и напряжений постоянного тока компенсационным методом. При этом измеряемая э. д. с. уравновешивается падением напряжения на группе точных сопротивлений, по которым протекает ток строго определенной величиньг. Прибор дает возможность также измерять сопротивления и силу тока при наличии образцовых катушек сопротивления. [c.46]

    Электродвижущую силу гальванических элемент тов измеряют компенсационным методом. Схема ус- тановки для измерения электродвижущей силы компенсационным методом дана на рис. 50. Источник постоянного тока, обычно электрический аккумулятор, подключают к концам реохорда ab. Элемент, эдс которого измеряется, подключают к реохорду в точке а и через гальванометр к подвижному контакту с. Аккумулятор и исследуемый элемент включают таким образом, чтобы их токи протекали навстречу друг другу, т. е. их электродвижущие силы Егкк и компенсируются. Перемещая подвижной контакт с реохорда ab находят такое его положение, при котором гальванометр покажет отсутствие тока. Это оз- начает, что падение потенциала на участке ас точно равно электродвижущей силе исследуемого элемен-. та. Тогда можно записать следующее отношение ExI aKK — ас[аЬ. [c.139]

    Потенциометры. Потенциометрическая усхановка состоит из индикаторного электрода и элёктрода сравнения, погруженных в анализируемый раствор. Потенциал индикаторного электрода финд такой гальванической ячейки измеряют относительно стандартного электрода фст- Если в цепи отсутствует ток, поляризующий электроды, разность потенциалов Аф зависит только от изменения потенциала финд и отличается от него на постоянную величину фс . В практике используют два способа измерения разности потенциалов двух электродов компенсационный и некомпенсационный. Наиболее распространенный и надежный способ измерения э. д. с. потенциометрической ячейки — компенсационный метод. Он основан-на компенсации двух противоположно направленных электродвижущих сил. На электроды ячейки налагают э. д. с внешнего источника постоянного тока, противоположно направленную э. д.,с. гальванической ячейки. При установившейся компенсации в цепи нет тока, э. д. с. ячейки и э. д. с. источника равны. В некомпенсационном методе э.д.с. гальванического элемента измеряют непосредственно гальванометром, последовательно с которым включают большое сопротивление и источник постоянного тока. Такая схема позволяет наблюдать изменение э.д.с. гальванического элемента по изменению силы тока в цепи. [c.121]

    При компенсационном методе измерения потенциалов не исключена возможность поляризации элемента или электрода и получения по этой причине искаженного значения потенциала. В процессе последовательного приближения к точке компенсации мы неизбежно замыкаем измеряемый элемент на чарть сопротивления потенциометра, при этом через измеряемый элемент протекает ток, который его поляризует. По этой причине для измерения электродвижущих сил гальванических элементов употребляются потенциометры с большим внутренним сопротивлением — 10 2 и выше на 1 тУ. Помимо этого, имеется вероятность поляризации элемента даже при достижении компенсации. Момент достижения компенсации устанавливается по отсутствию отклонения нульинструмента. Если в схеме при измерении взят нульинстру-мент с чувстительностью 1-10 А/деление, то тока силой в 10 А мы уже не обнаружим и будем считать, что достигнута полная компенсация. Рассмотрим, какая поляризация может возникнуть в результате протекания тока силою в 10 А. Возьмем элемент с одним практически не поляризующимся электродом (таковым при достаточных размерах [c.214]

    Полярограф предназначен для автоматической записи кривых сила тока — приложенное напряжение . Все полярогра-фы имеют самостоятельный хорошо стабилизированный источник постоянного напряжения, которое подается на реохорд. При движении контакта реохорда разность потенциалов, равномерно возрастающая или убывающая, подается на электрохимическую ячейку. Принимая во внимание, что небольшие изменения потенциала, приложенного к индикаторному электроду, резко влияют на характер и скорость электрохимического процесса, точному измерению потенциалов в полярографии уделяют большое внимание. Для этого обычно используется трехэлектродная ячейка, и потенциал индикаторного электрода имеряется по компенсационному нуль-методу с применением потенциометрического моста. Метод отличается высокой точностью, но недостатком его является длительность измерений и громоздкость установки. [c.161]

    Точнее всего емкость поверхности раздела металл — раствор можно определить по данным переменпоточных измерений импеданса компенсационным методом моста или измерений угла сдвига фаз. Сначала электрод поляризуется током постоянной силы или при постоянном потенциале до установления стационарного состоя- [c.413]

    Принцип компенсационного метода определения электродвижущей силы цепи. Так как не существует надежного и простого способа измерения потенциала отдельного электрода, то всегда его измеряют по отношению к другому стандартному электроду (стандартный полуэле-мент). При соединении обоих электродов создается цепь или элемент, э.д.с. которого можно измерить. Если концы цепи присоединить к гувствительному вольтметру, то нельзя ожидать точных результатов, так как через систему потечет ток от элемента. Этот ток вызовет химические реакции на обоих электродах и, вследствие возникающей поляризации, э. д.с. цепи будет меняться во время измерения. Поэтому обычно применяемым методом является метод Поггендорфа — Дю Буа Реймонда, в котором измеряемая э.д.с. компенсируется известной электродвижущей силой, направленной обратно. Когда неизвестная э.д.с. компенсирована, в цепи отсутствует ток, что можно установить каким-нибудь нулевым инструментом, подобным гальванометру. [c.104]

    Компенсационным методом можно измерять не только напряжение, но также силу тока и сопротивление. На рис. IV.3 приведена схема измерения силы тока. В цепь измеряемого тока включают эталонное сонротивленпе Падение напряжения на сонротивлении измеряют потенциометром и силу тока определяют по формуле [c.121]

    Ячейку питают пониженным напряженпем (10—20 мв) промышленной частоты. Последовательно с ячейкой включают сопротивление ограничивающее ток, протекаюший через ра -«вор, и эталонное сопротивление по паденпю напряжения на котором определяют силу тока, протекающего через раствор. Измерение осуществляют компенсационным методом. При помощи переключателя П к компенсатору подключают либо напряжение, падающее на эталонном сопротивлении i э, либо напряжение, падающее ва ячейке. [c.207]

    В последнее время получили распространение электронные самопишущие полярографы, изготовляемые, как правило, на базе самопишущих электронных потенциометров. Продвижение бумажной ленты синхронизировано в них с движением реохорда, задающего напряжение на ячейку силу поляризационного тока измеряют по падению напряжения на эталонном сопротивлении. Измерение напряжения производят компенсационным методом с помощью само-уравновешивающегося моста самопиш5 щего потенциометра. [c.298]

---

Тест по теме «Закон Ома для полной цепи».

Тест по теме «Закон Ома для полной цепи».

тест по физике 10 класс

Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока.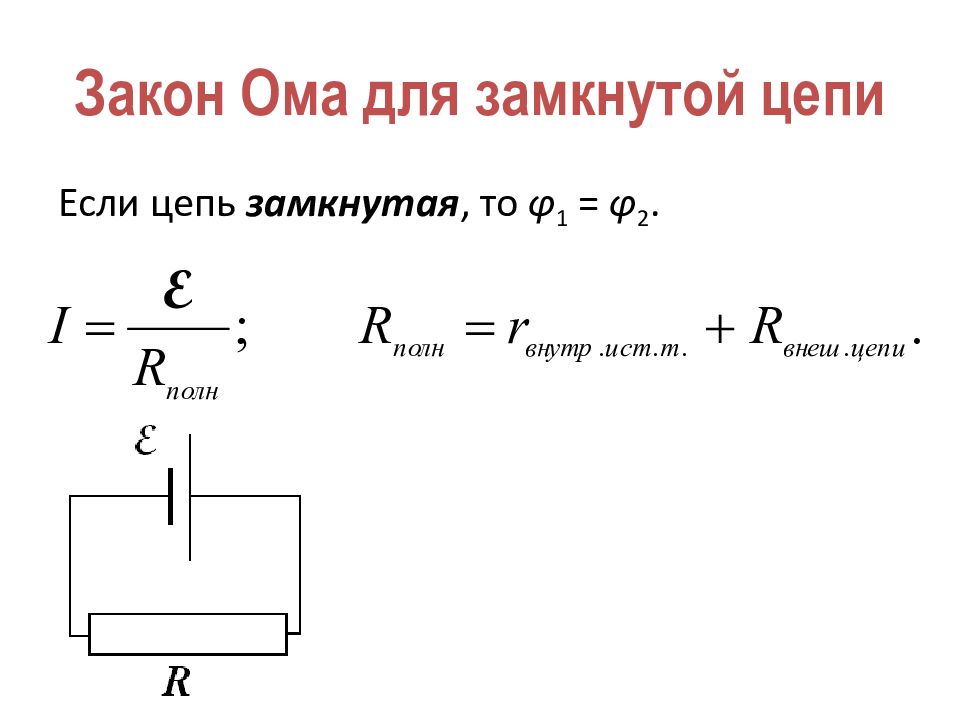 Другое название этого закона — закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно пройдя тест.

Вариант 1.

1. Аккумулятор с ЭДС 35 B и внутренним сопротивлением 2 Ом замкнут на спираль с сопротивлением 5 Ом. Какой ток покажет амперметр, включённый в цепь. (внутренним сопротивлением амперметра пренебречь).

1. 5 А;

2. 7 А;

3. 9 А;

4. 10,5 А;

5. 2 А.

1. Аккумулятор с внутренним сопротивлением 0,4 Ом и ЭДС 4 B замкнут спиралью из проволокой сечением 1 мм² и удельным сопротивлением 0,0000008 Ом•м. Найдите длину спирали, если сила тока в цепи 2 А.

1. 2,3 м;

2. 2 м;

3. 1,5 м;

4. 15 м;

5. 13 м.

1. Если к гальваническому элементу с ЭДС 5 B и внутренним сопротивлением 1 Ом подключить амперметр, то он покажет силу тока 1 A. Определите внутреннее сопротивление амперметра.

1. 2 Ом;

2. 1,5 Ом;

3. 4 Ом;

4. 3,1 Ом;

5. 5,8 Ом;

1. Спираль сопротивлением 4 Ом, подключили к гальваническому элементу с ЭДС 6 B. Амперметр показал ток в спирали 0,6 A. Найдите ток короткого замыкания гальванического элемента. (внутренним сопротивлением амперметра пренебречь).

1. 5,5 А;

2. 6,5 А;

3. 0,3 А;

4. 2,4 А;

5. 1 А.

1. При подключении аккумулятора с ЭДС 10 B к резистору, напряжение на полюсах источника вольтметр показал 8 B, а амперметр показал силу тока в цепи 4 А. Найдите внутреннее сопротивление источника. (внутренним сопротивлением амперметра пренебречь).

1. 5,7 Ом;

2. 1,9 Ом;

3. 3 Ом;

4. 0,3 Ом;

5. 0,5 Ом

1. Внутреннее сопротивление гальванического элемента с ЭДС 3,6 B равно 0,4 Ом. К гальваническому элементу подключены параллельно три спирали сопротивлением по 3 Ом каждая.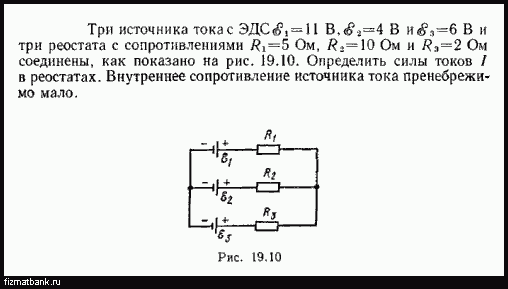 Найдите разность потенциалов на клеммах гальванического элемента?

1. 2,6 В;

2. 4,3 В;

3. 3,9 В;

4. 1,4 В;

5. 0,9 В.

1. В цепи, состоящей из аккумулятора с ЭДС 8 В и внутренним сопротивлением 1 Ом. Подключили проволочный реостат, возник ток в цепи 2 А. Какой будет сила тока в цепи, если сопротивление проволочного реостата уменьшить в 2 раза?

1. 5,1 А;

2. 3,3 А;

3. 1,4 А;

4. 3,2 А;

5. 2,7 А

1. Аккумулятор с ЭДС 12 B и внутренним сопротивлением 2 Ом питает 4 параллельно соединенных лампочки по 8 Ом каждое. Определите напряжение на каждой лампочке.

1. 2,1 В;

2. 6 В;

3. 10,6 В;

4. 8,5 В;

5. 4,7 В.

1. К амперметру, с внутренним сопротивлением 0,1 Ом, подключен шунт (проволочный резистор) сопротивлением 0,0111 Ом. Определите силу тока, протекающего через амперметр, если сила тока в общей цепи 0,27 А.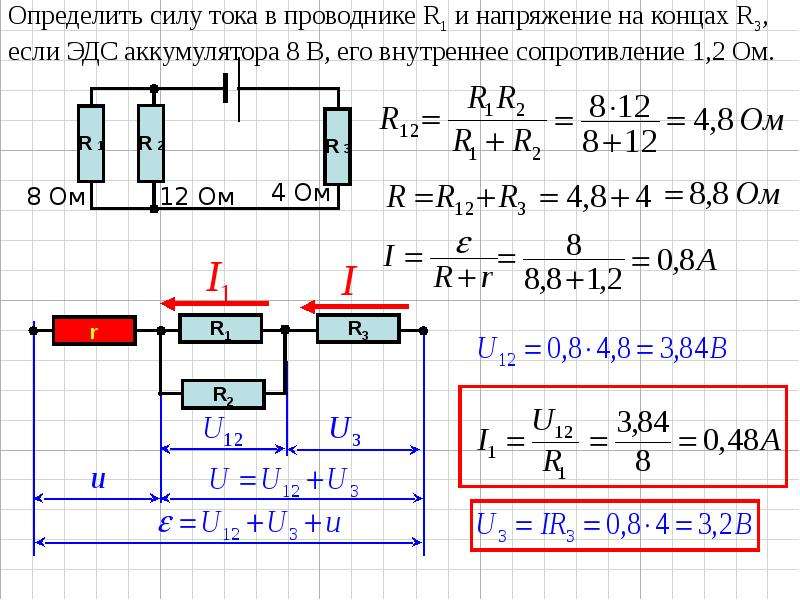

1. 2,7 А;

2. 0,27 А;

3. 0,027 А;

4. 0,0027 А;

5. 0,00027 А.

1. В каких лампах нить накаливания тоньше: в более или менее мощных?

1. В менее мощных нить накаливания тоньше, больше сопротивление нити;

2. В более мощных нить накаливания тоньше, меньше сила тока;

3. В менее мощных нить накаливания толще, больше сила тока;

4. В более мощных нить накаливания тоньше, меньше сопротивление нити;

5. Нет правильного ответа.

Вариант 2.

1. Определите силу тока в цепи, содержащей гальванический элемент с ЭДС, равной 6 В, и внутренним сопротивлением 0,5 Ом при подключении во внешней цепи лампочки с сопротивлением 2,5 Ом.

1. 1 А;

2. 2 А;

3. 0,5 А;

4. 3 А;

5. 10 А;

1. Электрический чайник, включенный в сеть напряжением 220 В, потребляет ток 1,2 А. Определите сопротивление водонагревательного элемента чайника.

1. 183,3 Ом;

2. 100 Ом;

3. 330 Ом;

4. 44,5 Ом;

5. 220,7 Ом;

1. Э ДС гальванического элемента 3 В, его внутреннее сопротивление равно1 Ом, сопротивления резисторов R₁ = R₂ = 1,75 Ом, R₃ = 2 Ом, R₄ = 6 Ом. Чему равна сила тока, протекающего через резистор R₄? (см. рис)

1. 0,5 А;

2. 0,045 А;

3. 2 А;

4. 0,35 А;

5. 0,125 А;

1. Определите сопротивление водонагревательного тэна, если при напряжении 110 В сила тока в нём 2 А.

1. 60 Ом;

2. 35 Ом;

3. 55 Ом;

4. 100 Ом;

5. 135 Ом;

1. Гальванический элемент имеет ЭДС, равный 2,2 В и внутреннее сопротивление r =1 Ом. Он замкнут на лампочку сопротивление, которой равно R=9 Ом. Какой будет при этом сила тока в цепи?

1. 0,22 А;

2. 0,15 А;

3. 0,5 А;

4. 2 А;

5. 1 А;

1. Две лампочки, сопротивления которых R₁=10 Ом и R₂=40 Ом, соединены последовательно и подключены к аккумулятору с ЭДС равным 15 В. Определите внутреннее сопротивление аккумулятора, если сила тока в цепи I=0,29 А.

1. 1,25 А;

2. 0,34 А;

3. 2,15 А;

4. 1,72 А;

5. 3,3 А;

1. Найти силу тока в электрической цепи, если известно, что сопротивление цепи 11 Ом, а источник, подключенный к ней, имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

1. 1 А;

2. 2 А;

3. 3 А;

4. 4 А;

5. 5 А;

1. Аккумулятор подключен к резистору сопротивлением 10 Ом с помощью медной спирали длиной 1 м и площадью поперечного сечения 1 мм². Найти силу тока, зная, что ЭДС аккумулятора равно 12 В, а внутреннее сопротивление 1,9825 Ом.

1. 0,5 А;

2. 0,8 А;

3. 1 А;

4. 1,5 А;

5. 2 А;

1. При внешнем сопротивлении 3,75 Ом в цепи идет ток 0,5 А. Когда в цепь ввели еще сопротивление 1 Ом, сила тока стала равной 0,4 А. Найти ЭДС и внутреннее сопротивление гальванического элемента.

1. 1 В; 0,5 Ом;

2. 2 В; 0,25 Ом;

3. 1 В, 3 Ом;

4. 3 В; 1,5 Ом;

5. 5 В; 4 Ом;

1. Определить ток при коротком замыкании аккумулятора, если при внешнем сопротивлении R₁=50 Ом ток в цепи I₁= 0,2 А, а при сопротивлении R₂= 110 Ом ток I₂= 0,1 А.

1. 1400 мА;

2. 1000 мА;

3. 3000 мА;

4. 1600 мА;

5. 1200 мА;

Ответы: Вариант 1: 1 а; 2 b; 3 с; 4 е; 5 е; 6 а; 7 d; 8 b; 9 с; 10 a.

Вариант 2: 1 b; 2 а; 3 е; 4 с; 5 а; 6 d; 7 а; 8 с; 9 b; 10 е.

Оценка внутреннего сопротивления в цепях | Электрические цепи

Рабочий пример 7: Внутреннее сопротивление в цепи с последовательными резисторами

Для следующей схемы рассчитайте:

1. разности потенциалов \ (V_ \ text {1} \), \ (V_ \ text {2} \) и \ (V_ \ text {3} \) на резисторах \ (R_ \ text {1} \), \ (R_ \ text {2} \) и \ (R_ \ text {3} \)

   .

2. сопротивление \ (R_ \ text {3} \).

3. сопротивление \ (R_ \ text {3} \).

Если внутреннее сопротивление равно \ (\ text {0,1} \) \ (\ text {Ω} \), какова ЭДС батареи и какая мощность рассеивается внутренним сопротивлением батареи?

Примечание

Это очень похожий на то, что вы видели ранее. Это необходимо для того, чтобы выделить Дело в том, что подход к внутреннему сопротивлению строится на том же принципы, с которыми вы уже работали.

Определите, как подойти к проблеме

Нам дана разность потенциалов на ячейке и ток в цепи, а также сопротивления двух из трех резисторов.Мы можем использовать закон Ома для расчета разности потенциалов на известных резисторах. Поскольку резисторы включены в последовательную цепь, разность потенциалов равна \ (V = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \), и мы можем вычислить \ (V_ \ text {3} \). Теперь мы можем использовать эту информацию, чтобы найти разность потенциалов на неизвестном резисторе \ (R_ \ text {3} \).

Вычислить разность потенциалов на \ (R_ \ text {1} \)

Используя закон Ома: \ begin {align *} R_ \ text {1} & = \ frac {V_ \ text {1}} {I} \\ I \ cdot R_ \ text {1} & = I \ cdot \ frac {V_ \ text {1}} {I} \\ V_ \ text {1} & = {I} \ cdot {R_ \ text {1}} \\ & = 2 \ cdot 1 \\ V_ \ текст {1} & = \ текст {2} \ текст {V} \ end {align *}

Вычислить разность потенциалов на \ (R_ \ text {2} \)

Снова используя закон Ома: \ begin {align *} R_ \ text {2} & = \ frac {V_ \ text {2}} {I} \\ I \ cdot R_ \ text {2} & = I \ cdot \ frac {V_ \ text {2}} {I} \\ V_ \ text {2} & = {I} \ cdot {R_ \ text {2}} \\ & = 2 \ cdot 3 \\ V_ \ текст {2} & = \ текст {6} \ текст {V} \ end {align *}

Вычислить разность потенциалов на \ (R_ \ text {3} \)

Поскольку разность потенциалов на всех резисторах вместе взятых должна быть такой же, как разность потенциалов на ячейке в последовательной цепи, мы можем найти \ (V_ \ text {3} \), используя: \ begin {align *} V & = V_ \ text {1} + V_ \ text {2} + V_ \ text {3} \\ V_ \ text {3} & = V — V_ \ text {1} — V_ \ text {2} \\ & = 23-2-6 \\ V_ \ текст {3} & = \ текст {15} \ текст {V} \ end {align *}

Найдите сопротивление \ (R_ \ text {3} \)

Нам известна разность потенциалов на \ (R_ \ text {3} \) и ток через нее, поэтому мы можем использовать закон Ома для вычисления значения сопротивления: \ begin {align *} R_ \ text {3} & = \ frac {V_ \ text {3}} {I} \\ & = \ frac {\ text {15}} {\ text {2}} \\ R_ \ text {3} & = \ text {7,5} ~ ​​\ Omega \ end {align *}

Разница потенциалов внутреннего сопротивления батареи

Значение ЭДС можно рассчитать по разности потенциалов нагрузки и разности потенциалов на внутреннем сопротивлении.2} {R} \), и мы знаем ток в цепи, внутреннее сопротивление и разность потенциалов на нем, поэтому мы можем использовать любую форму уравнения для мощности:

\ begin {align *} P_r & = V_rI_r ​​\\ & = (\ текст {0,2}) (\ текст {2}) \\ & = \ текст {0,4} \ текст {W} \ end {align *}

Напишите окончательный ответ

• \ (V_ \ text {1} = \ text {2,0} \ text {V} \)
• \ (V_ \ text {2} = \ text {6,0} \ text {V} \)
• \ (V_ \ text {3} = \ text {10,0} \ text {V} \)
• \ (R_ \ text {3} = \ text {7,5} \ Omega \)
• \ (\ mathcal {E} = \ text {23,2} \ text {V} \)
• \ (P_r = \ text {0,4} \ text {W} \)

Рабочий пример 8: Внутреннее сопротивление и резисторы параллельно

Разность потенциалов на батарее составляет 18 В, когда она подключена к двум параллельным резисторам \ (\ text {4,00} \) \ (\ Omega \) и \ (\ text {12,00} \) \ ( \ Omega \) соответственно.Рассчитайте ток через ячейку и через каждый из резисторов. Если внутреннее сопротивление батареи \ (\ text {0,375} \) \ (\ text {Ω} \), какова ЭДС батареи?

Сначала нарисуйте схему перед выполнением любых расчетов

Определите, как подойти к проблеме

Нам нужно определить ток через ячейку и каждый из параллельных резисторов. Нам дана разность потенциалов на ячейке и сопротивления резисторов, поэтому мы можем использовать закон Ома для расчета тока.

Рассчитать ток через ячейку

Чтобы рассчитать ток через элемент, нам сначала нужно определить эквивалентное сопротивление остальной части цепи. Резисторы включены параллельно и поэтому: \ begin {align *} \ frac {\ text {1}} {R} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2}} \ \ & = \ frac {\ text {1}} {\ text {4}} + \ frac {\ text {1}} {\ text {12}} \\ & = \ frac {3 + 1} {\ text {12}} \\ & = \ frac {\ text {4}} {\ text {12}} \\ R & = \ frac {\ text {12}} {\ text {4}} = \ text {3,00} \ \ Omega \ end {выровнять *} Теперь, используя закон Ома, чтобы найти ток через ячейку: \ begin {align *} R & = \ frac {V} {I} \\ I & = \ frac {V} {R} \\ & = \ frac {\ text {18}} {\ text {3}} \\ I & = \ text {6,00} \ text {A} \ end {align *}

Теперь определите ток через один из параллельных резисторов

Мы знаем, что для чисто параллельной конфигурации резисторов разность потенциалов на ячейке такая же, как и разность потенциалов на каждом из параллельных резисторов.Для этой схемы: \ begin {align *} V & = V_ \ text {1} = V_ \ text {2} = \ text {18} \ text {V} \ end {выровнять *} Начнем с вычисления тока через \ (R_ \ text {1} \) по закону Ома: \ begin {align *} R_ \ text {1} & = \ frac {V_ \ text {1}} {I_ \ text {1}} \\ I_ \ text {1} & = \ frac {V_ \ text {1}} {R_ \ text {1}} \\ & = \ frac {\ text {18}} {\ text {4}} \\ I_ \ text {1} & = \ text {4,50} \ text {A} \ end {align *}

Рассчитайте ток через другой параллельный резистор

Мы можем снова использовать закон Ома, чтобы найти ток в \ (R_ \ text {2} \): \ begin {align *} R_ \ text {2} & = \ frac {V_ \ text {2}} {I_ \ text {2}} \\ I_ \ text {2} & = \ frac {V_ \ text {2}} {R_ \ text {2}} \\ & = \ frac {\ text {18}} {\ text {12}} \\ I_ \ text {2} & = \ text {1,50} \ text {A} \ end {выровнять *} Альтернативный метод вычисления \ (I_ \ text {2} \) заключался бы в использовании того факта, что токи через каждый из параллельных резисторов должны составлять общий ток через ячейку: \ begin {align *} I & = I_ \ text {1} + I_ \ text {2} \\ I_ \ text {2} & = I — I_ \ text {1} \\ & = 6 — 4.5 \\ I_ \ text {2} & = \ text {1,5} \ text {A} \ end {align *}

Определить ЭДС

Суммарный ток через батарею — это ток через внутреннее сопротивление батареи. Знание силы тока и сопротивления позволяет нам использовать закон Ома для определения разности потенциалов на внутреннем сопротивлении и, следовательно, ЭДС батареи.

Используя закон Ома, мы можем определить разность потенциалов на внутреннем сопротивлении:

\ begin {align *} V & = I \ cdot r \\ & = \ текст {6} \ cdot \ text {0,375} \\ & = \ текст {2,25} \ текст {V} \ end {выровнять *}

Мы знаем, что ЭДС аккумулятора — это разность потенциалов на выводе, суммированная с разностью потенциалов на внутреннем сопротивлении, так:

\ begin {align *} \ mathcal {E} & = V + Ir \\ & = \ text {18} + \ text {2,25} \\ & = \ текст {20,25} \ текст {V} \ end {align *}

Напишите окончательный ответ

Ток через ячейку равен \ (\ text {6,00} \) \ (\ text {A} \).

Ток через резистор \ (\ text {4,00} \) \ (\ Omega \) равен \ (\ text {4,50} \) \ (\ text {A} \).

Ток через резистор \ (\ text {12,00} \) \ (\ Omega \) равен \ (\ text {1,50} \) \ (\ text {A} \).

ЭДС батареи равна \ (\ text {20,25} \) \ (\ text {V} \).

Рабочий пример 9: Мощность в последовательной и параллельной сетях резисторов

Учитывая следующую схему:

Ток, выходящий из батареи, равен \ (\ text {1,07} \) \ (\ text {A} \), общая мощность, рассеиваемая во внешней цепи, равна \ (\ text {6,42} \) \ ( \ text {W} \), отношение полных сопротивлений двух параллельных сетей \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) равно 1: 2, соотношение \ (R_ \ text {1}: R_ \ text {2} \) равно 3: 5 и \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \).

Определите:

1. разность потенциалов АКБ,
2. мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \), и
3. , если батарея имеет ЭДС, равную \ (\ text {6,50} \) \ (\ text {V} \), каково значение сопротивления каждого резистора и мощность, рассеиваемая в каждом из них.

Что требуется

В этом вопросе вам дается различная информация и предлагается определить мощность, рассеиваемую на каждом резисторе и каждой комбинации резисторов.Обратите внимание, что данная информация в основном относится ко всей цепи. Это подсказка, которую вы должны начать с общей схемы и двигаться вниз к более конкретным элементам схемы.

Расчет разности потенциалов аккумулятора

В первую очередь остановимся на аккумуляторе. Нам дана мощность всей цепи, а также ток, покидающий батарею. Мы знаем, что разность потенциалов на клеммах аккумулятора — это разность потенциалов в цепи в целом.

Мы можем использовать соотношение \ (P = VI \) для всей схемы, потому что разность потенциалов такая же, как разность потенциалов на клеммах батареи: \ begin {align *} P & = VI \\ V & = \ frac {P} {I} \\ & = \ frac {\ text {6,42}} {\ text {1,07}} \\ & = \ текст {6,00} \ текст {V} \ end {align *}

Разность потенциалов на батарее равна \ (\ text {6,00} \) \ (\ text {V} \).

Мощность, рассеиваемая в \ (R_ {P \ text {1}} \) и \ (R_ {P \ text {2}} \)

Помните, что мы работаем от общих деталей схемы вниз к деталям отдельных элементов, это противоположно тому, как вы относились к этой схеме ранее.

Мы можем рассматривать параллельные сети как эквивалентные резисторы, поэтому схема, с которой мы сейчас работаем, выглядит так:

Мы знаем, что ток через два элемента схемы будет одинаковым, потому что это последовательная цепь и что сопротивление всей цепи должно быть: \ (R_ {Ext} = R_ {P \ text {1}} + R_ {P \ text {2}} \). Мы можем определить полное сопротивление по закону Ома для цепи в целом: \ begin {align *} V_ {батарея} & = IR_ {Ext} \\ R_ {Ext} & = \ frac {V_ {аккумулятор}} {I} \\ & = \ frac {\ text {6,00}} {\ text {1,07}} \\ & = \ текст {5,61} \ текст {Ω} \ end {align *}

Мы знаем, что соотношение между \ (R_ {P \ text {1}}: R_ {P \ text {2}} \) составляет 1: 2, что означает, что мы знаем: \ begin {align *} R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \ \ \ text {и} \\ R_T & = R_ {P \ text {1}} + R_ {P \ text {2}} \\ & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} + R_ {P \ text {2}} \\ & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\ (\ text {5,61}) & = \ frac {\ text {3}} {\ text {2}} R_ {P \ text {2}} \\ R_ {P \ text {2}} & = \ frac {\ text {2}} {\ text {3}} (\ text {5,61}) \\ R_ {P \ text {2}} & = \ text {3,74} \ text {Ω} \ end {выровнять *} и поэтому: \ begin {align *} R_ {P \ text {1}} & = \ frac {\ text {1}} {\ text {2}} R_ {P \ text {2}} \\ & = \ frac {\ text {1}} {\ text {2}} (3.2 (\ text {3,74}) \\ & = \ текст {4,28} \ текст {W} \ end {выровнять *} Эти значения будут в сумме с исходным значением мощности, которое у нас было для внешней цепи. Если бы они этого не сделали мы бы сделали ошибку в расчетах.

Расчет параллельной сети 1

Теперь мы можем приступить к детальному расчету первого набора параллельных резисторов.

Мы знаем, что соотношение между \ (R _ {\ text {1}}: R _ {\ text {2}} \) составляет 3: 5, что означает, что мы знаем \ (R _ {\ text {1}} = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \).Нам также известно общее сопротивление двух параллельных резисторов в этой сети. это \ (\ text {1,87} \) \ (\ text {Ω} \). Мы можем использовать соотношение между значениями двух резисторов, а также формула для общей сопротивление (\ (\ frac {\ text {1}} {R_PT} = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} {R_ \ text {2) }} \)) чтобы найти номиналы резисторов: \ begin {align *} \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {1}} + \ frac {\ text {1}} { R_ \ text {2}} \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {5}} {3R_ \ text {2}} + \ frac {\ text {1}} { R_ \ text {2}} \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + 1) \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} (\ frac {\ text {5}} { \ text {3}} + \ frac {\ text {3}} {\ text {3}}) \\ \ frac {\ text {1}} {R_ {P \ text {1}}} & = \ frac {\ text {1}} {R_ \ text {2}} \ frac {\ text {8}} {\ текст {3}} \\ R_ \ text {2} & = R_ {P \ text {1}} \ frac {\ text {8}} {\ text {3}} \\ & = (\ text {1,87}) \ frac {\ text {8}} {\ text {3}} \\ & = \ текст {4,99} \ текст {Ω} \ end {выровнять *} Мы также можем вычислить \ (R _ {\ text {1}} \): \ begin {align *} R _ {\ text {1}} & = \ frac {\ text {3}} {\ text {5}} R _ {\ text {2}} \\ & = \ frac {\ text {3}} {\ text {5}} (\ text {4,99}) \\ & = \ текст {2,99} \ текст {Ω} \ end {align *}

Для определения мощности нам нужно рассчитанное нами сопротивление и либо разность потенциалов, либо ток. 2} {\ text {4,99}} \\ & = \ текст {0,80} \ текст {W} \ end {align *}

Параллельная сеть 2 вычисления

Теперь мы можем приступить к детальному расчету второго набора параллельных резисторов.

Нам дано \ (R_ \ text {3} = \ text {7,00} \ text {Ω} \), и мы знаем \ (R_ {P \ text {2}} \), поэтому мы можем вычислить \ (R_ \ text {4} \) из: \ begin {align *} \ frac {\ text {1}} {R_ {P \ text {2}}} & = \ frac {\ text {1}} {R_ \ text {3}} + \ frac {\ text {1}} { R_ \ text {4}} \\ \ frac {\ text {1}} {\ text {3,74}} & = \ frac {\ text {1}} {\ text {7,00}} + \ frac {\ text {1}} {R_ \ текст {4}} \\ R_ \ text {4} & = \ text {8,03} \ text {Ω} \ end {align *}

Мы можем вычислить разность потенциалов во второй параллельной сети, вычтя разность потенциалов первой параллельной сети из разности потенциалов батареи, \ (V_ {P \ text {2}} = \ text {6,00} — \ text {2,00} = \ text {4,00} \ text {V} \).2} {\ text {8,03}} \\ & = \ текст {1,99} \ текст {W} \ end {align *}

Внутреннее сопротивление

Мы знаем, что ЭДС батареи равна \ (\ text {6,5} \) \ (\ text {V} \), но что разность потенциалов, измеренная на клеммах, составляет всего \ (\ text {6} \) \ (\ текст {V} \). Разница — это разность потенциалов на внутреннем сопротивлении батареи, и мы можем использовать известный ток и закон Ома для определения внутреннего сопротивления:

\ begin {align *} V & = I \ cdot R \\ R & = \ frac {V} {I} \\ & = \ frac {\ text {0,5}} {\ text {1,07}} \\ & = \ text {0,4672897} \\ & = \ текст {0,47} \ текст {Ω} \ end {выровнять *}

Мощность, рассеиваемая внутренним сопротивлением батареи:

\ begin {align *} P & = VI \\ & = \ текст {0,5} \ cdot \ text {1,07} \\ & = \ текст {0,535} \ текст {W} \ end {align *}

Рабочий пример 10: Внутреннее сопротивление и фары [NSC 2011 Paper 1]

Фара и два ИДЕНТИЧНЫХ задних фонаря скутера подключены параллельно к батарее с неизвестным внутренним сопротивлением, как показано на упрощенной принципиальной схеме ниже.Фара имеет сопротивление \ (\ text {2,4} \) \ (\ text {Ω} \) и управляется переключателем \ (\ textbf {S} _1 \). Задние фонари управляются переключателем \ (\ textbf {S} _2 \). Сопротивлением соединительных проводов можно пренебречь.

На приведенном рядом графике показана разность потенциалов на клеммах батареи до и после включения переключателя \ (\ textbf {S} _1 \) (пока переключатель \ (\ textbf {S} _2 \) открыт). Переключатель \ (\ textbf {S} _1 \) закрывается в момент \ (\ textbf {t} _1 \).

1. Используйте график, чтобы определить ЭДС аккумулятора.

   (1 балл)

2. ПРИ ТОЛЬКО ПЕРЕКЛЮЧАТЕЛЬ \ (\ textbf {S} _1 \) ЗАКРЫТО, рассчитайте следующее:

   1. Ток через фару

      (3 балла)

   2. Внутреннее сопротивление \ (r \) батареи

      (3 балла)

3. ОБЕ ПЕРЕКЛЮЧАТЕЛИ \ (\ textbf {S} _1 \) И \ (\ textbf {S} _2 \) ТЕПЕРЬ ЗАКРЫТЫ.Батарея выдает ток \ (\ text {6} \) \ (\ text {A} \) в течение этого периода.

   Рассчитайте сопротивление каждого заднего фонаря.

   (5 баллов)

4. Как повлияет на показания вольтметра, если фара перегорит? (Оба переключателя \ (\ textbf {S} _1 \) и \ (\ textbf {S} _2 \) все еще закрыты.)

   Запишите только УВЕЛИЧИВАЕТ, УМЕНЬШАЕТСЯ или ОСТАЕТСЯ ОДИН ТО ЖЕ.

   Дайте объяснение.

   (3 балла)

Вопрос 1

\ (\ text {12} \) \ (\ text {V} \)

(1 балл)

Вопрос 2.1

Вариант 1:

\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {\ text {9,6}} {\ text {2,4}} \\ & = \ текст {4 A} \ end {выровнять *}

Вариант 2:

\ begin {align *} \ text {emf} & = IR + Ir \\ 12 & = I (\ text {2,4}) + \ text {2,4} \\ \ поэтому I & = \ text {4 A} \ end {выровнять *}

(3 балла)

Вопрос 2.2

Вариант 1:

\ begin {align *} \ text {emf} & = IR + Ir \\ 12 & = \ text {9,4} + 4r \\ r & = \ текст {0,6} \ \ Omega \ end {выровнять *}

Вариант 2:

\ begin {align *} V_ {потеряно} & = Ir \\ \ text {2,4} & = \ text {4} r \\ \ поэтому r & = \ text {0,6} \ \ Omega \ end {выровнять *}

Вариант 3:

\ begin {align *} \ text {emf} & = I (R + r) \\ \ text {12} & = \ text {4} (\ text {2,4} + r) \\ \ поэтому r & = \ text {0,6} \ \ Omega \ end {выровнять *}

(3 балла)

Вопрос 3

Вариант 1:

\ begin {align *} \ text {emf} & = IR + Ir \\ \ text {12} & = \ text {6} (R + \ text {0,6}) \\ R _ {\ text {ext}} & = \ text {1,4} \ \ Omega \ конец {выравнивание *} \ begin {выравнивание *} \ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\ R & = \ текст {3,36} \ \ Omega \ end {выровнять *}

Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)

Вариант 2:

\ begin {align *} \ text {Emf} & = V _ {\ text {terminal}} + Ir \\ 12 & = V _ {\ text {терминал}} + 6 (\ text {0,6}) \\ \ поэтому V _ {\ text {terminal}} & = \ text {8,4} \ text {V} \ конец {выравнивание *} \ begin {выравнивание *} I _ {\ text {2,4} \ \ Omega} & = \ frac {V} {R} \\ & = \ frac {\ text {8,4}} {\ text {2,4}} \\ & = \ text {3,5 A} \ конец {выравнивание *} \ begin {выравнивание *} I _ {\ text {задние фонари}} & = 6 — \ text {3,5} \\ & = \ текст {2,5} \ текст {A} \\ R _ {\ text {задние фонари}} & = \ frac {V} {I} \\ & = \ frac {\ text {8,4}} {\ text {2,5}} \\ & = \ текст {3,36} \ \ Omega \\ R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega \ end {выровнять *}

Вариант 3:

\ begin {align *} V & = IR \\ \ text {12} & = \ text {6} (R) \\ R _ {\ text {ext}} & = 2 \ \ Omega \ конец {выравнивание *} \ begin {выравнивание *} R _ {\ text {parallel}} & = 2 — \ text {0,6} \\ & = \ текст {1,4} \ \ Omega \\ \ frac {1} {R} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} \\ \ frac {1} {\ text {1,4}} & = \ frac {1} {\ text {2,4}} + \ frac {1} {R} \\ R & = \ текст {3,36} \ \ Omega \ end {выровнять *}

Каждый задний фонарь: \ (R = \ text {1,68} \ \ Omega \)

Вариант 4:

Для параллельной комбинации: \ (I_ {1} + I_ {2} = 6 \ text {A} \)

\ begin {align *} \ поэтому \ frac {V} {\ text {2,4}} + \ frac {V} {R _ {\ text {задние фонари}}} & = \ text {6} \\ \ text {8,4} \ left (\ frac {1} {\ text {2,4}} + \ frac {1} {R _ {\ text {задние фонари}}} \ right) & = \ text {6 } \\ \ поэтому R _ {\ text {задние фонари}} & = \ text {3,36} \ \ Omega \\ R _ {\ text {задний фонарь}} & = \ text {1,68} \ \ Omega \ end {выровнять *}

(5 баллов)

Вопрос 4

Увеличивает

Сопротивление увеличивается, а ток уменьшается.В.

Данные можно ввести в любое из полей. Когда вы закончили ввод данных, щелкните количество, которое вы хотите рассчитать, в активной формуле выше. Количество не будет принудительно согласованным, пока вы не нажмете на выбор. Для неопределенных параметров будут введены значения по умолчанию, но все значения могут быть изменены.

После того, как вы рассчитали генерируемое напряжение, разумным последующим вопросом будет «Какой ток и мощность я могу получить от генератора?».Несмотря на то, что это не будет практичной геометрией генератора, она может служить идеализация для обсуждения принципов генерации напряжения при взаимодействии с магнитным полем. Принимая это простая геометрия, электрический ток в амперах, возникающий при перемещении провода через магнитное поле будет определяться сопротивлением цепи, к которой он подключен. связаны, используя закон Ома, I = V / R. Если вы сгенерировали 10 вольт и были подключены к цепи сопротивление 1 Ом, результирующий ток будет 10 ампер, а передаваемая мощность P = VI = 10 вольт x 10 амперы = 100 Вт (см. соотношение мощности).Но бесплатного обеда не существует, и вам придется приложить больше усилий, чтобы двигаться. провод через магнитное поле с такой скоростью — вы, по сути, торгуете механической энергией толкания для выработки электроэнергии, всегда ограничиваясь принципом сохранения энергии. Вам придется приложите (по крайней мере) 100 Вт механической мощности толкания, чтобы получить 100 Вт электроэнергии. Практические генераторы почти всегда используют геометрию вращающейся катушки, а крупномасштабные генераторы энергии используют что-то вроде паровой турбины или водяной турбины, чтобы повернуть катушку с проволокой в магнитное поле, получающее напряжение, генерируемое с обеих сторон вращающейся катушки.

Если указанный выше генератор был подключен к цепи с сопротивлением R = Ом,

электрический ток будет I = V / R = амперы для скорости, перпендикулярной B.

Мощность, подаваемая в схему, будет P = VI = Вт.

В идеальном случае, когда не было потерь, механическая мощность P = Fv, необходимая для проталкивания провода через магнитное поле, была бы равна электрической мощности. Для указанной выше скорости требуемая сила равна

.

Идеальная минимально необходимая сила:

F = P / v = ньютоны = фунты.

Электрический ток | Безграничная физика

Аккумулятор

Аккумулятор — это устройство, преобразующее химическую энергию непосредственно в электрическую.

Цели обучения

Опишите функции и определите основные компоненты батареи

Основные выводы

Ключевые моменты

• Батарея накапливает электрический потенциал химической реакции. Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию по мере прохождения электронов по цепи.
• Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q, перемещенного из точки 1 в точку 2, деленное на заряд.
• Напряжение батареи является синонимом ее электродвижущей силы или ЭДС. Эта сила отвечает за прохождение заряда через цепь, известную как электрический ток.

Ключевые термины

• аккумулятор : устройство, вырабатывающее электричество в результате химической реакции между двумя веществами.
• ток : временная скорость протекания электрического заряда.
• напряжение : величина электростатического потенциала между двумя точками в пространстве.

Обозначение батареи на принципиальной схеме : Это символ батареи на принципиальной схеме. Он возник как схематический рисунок батареи самого раннего типа — гальванической батареи. Обратите внимание на положительный катод и отрицательный анод. Эта ориентация важна при рисовании принципиальных схем, чтобы изобразить правильный поток электронов.

Аккумулятор — это устройство, преобразующее химическую энергию непосредственно в электрическую. Он состоит из ряда гальванических элементов, последовательно соединенных проводящим электролитом, содержащим анионы и катионы. Одна полуячейка включает электролит и анод или отрицательный электрод; другая полуячейка включает электролит и катод или положительный электрод. В окислительно-восстановительной реакции, которая приводит в действие аккумулятор, катионы восстанавливаются (добавляются электроны) на катоде, а анионы окисляются (электроны удаляются) на аноде.Электроды не касаются друг друга, но электрически связаны электролитом. В некоторых элементах используются два полуэлемента с разными электролитами. Разделитель между полуэлементами позволяет ионам течь, но предотвращает смешивание электролитов.

Каждая полуячейка имеет электродвижущую силу (или ЭДС), определяемую ее способностью передавать электрический ток изнутри во внешнюю часть ячейки. Чистая ЭДС клетки — это разность между ЭДС ее полуэлементов или разность восстановительных потенциалов полуреакций.

Электрическая движущая сила на выводах элемента известна как напряжение на выводах (разность) и измеряется в вольтах. Когда батарея подключена к цепи, электроны от анода проходят через цепь к катоду по прямой цепи. Напряжение батареи является синонимом ее электродвижущей силы или ЭДС. Эта сила отвечает за прохождение заряда через цепь, известную как электрический ток.

Аккумулятор накапливает электрический потенциал в результате химической реакции.Когда он подключен к цепи, этот электрический потенциал преобразуется в кинетическую энергию по мере прохождения электронов по цепи. Электрический потенциал определяется как потенциальная энергия на единицу заряда ( q ). Напряжение или разность потенциалов между двумя точками определяется как изменение потенциальной энергии заряда q , перемещенного из точки 1 в точку 2, деленное на заряд. В перестроенном виде это математическое соотношение можно описать как:

[латекс] \ Delta \ text {PE} = \ text {q} \ Delta \ text {V} [/ latex]

Напряжение — это не то же самое, что энергия.Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но при этом один хранит гораздо больше энергии, чем другой. Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора 12 В.

Идеальные и настоящие батареи : Краткое введение в идеальные и настоящие батареи для студентов, изучающих электрические схемы.

Измерения тока и напряжения в цепях

Электрический ток прямо пропорционален приложенному напряжению и обратно пропорционален сопротивлению в цепи.

Цели обучения

Опишите взаимосвязь между электрическим током, напряжением и сопротивлением в цепи

Основные выводы

Ключевые моменты

• Простая схема состоит из источника напряжения и резистора.
Закон
• Ома дает соотношение между током I , напряжением В и сопротивлением R в простой цепи: I = В / R .
• Единицей измерения скорости протекания электрического заряда в системе СИ является ампер, который равен заряду, протекающему через некоторую поверхность со скоростью один кулон в секунду.

Ключевые термины

• электрический ток : движение заряда по цепи
• Ом : в Международной системе единиц производная единица электрического сопротивления; электрическое сопротивление устройства, на котором разность потенциалов в один вольт вызывает ток в один ампер; символ: Ω
• ампер : единица электрического тока; стандартная базовая единица в Международной системе единиц.Аббревиатура: amp. Символ: A.

Чтобы понять, как измерять ток и напряжение в цепи, вы также должны иметь общее представление о том, как работает схема и как связаны ее электрические измерения.

Что такое напряжение? : Это видео помогает с концептуальным пониманием напряжения.

Электрическая цепь — это тип сети с замкнутым контуром, который обеспечивает обратный путь для тока. Простая схема состоит из источника напряжения и резистора и схематически может быть представлена ​​как на рис.

Простая схема : Простая электрическая цепь, состоящая из источника напряжения и резистора

Согласно закону Ома, электрический ток I , или движение заряда, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В . Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R . Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток.Сопротивление обратно пропорционально току. Следовательно, закон Ома можно записать следующим образом:

[латекс] \ text {I} = \ text {V} / \ text {R} [/ latex]

, где I — ток через проводник в амперах, В, — разность потенциалов, измеренная на проводнике в вольтах, а R — сопротивление проводника в омах (Ом). Более конкретно, закон Ома гласит, что R в этом отношении является постоянным, не зависящим от тока.Используя это уравнение, мы можем рассчитать ток, напряжение или сопротивление в данной цепи.

Например, если у нас есть батарея на 1,5 В, которая была подключена по замкнутой цепи к лампочке с сопротивлением 5 Ом, какой ток течет по цепи? Чтобы решить эту проблему, мы просто подставим указанные значения в закон Ома: I = 1,5 В / 5 Ом; I = 0,3 ампера. Зная ток и сопротивление, мы можем изменить уравнение закона Ома и найти напряжение В :

[латекс] \ text {V} = \ text {IR} [/ латекс]

Вид под микроскопом: скорость дрейфа

Скорость дрейфа — это средняя скорость, которую достигает частица под действием электрического поля.

Цели обучения

Свяжите скорость дрейфа со скоростью свободных зарядов в проводниках

Основные выводы

Ключевые моменты

• В проводниках есть электрическое поле, которое заставляет электроны дрейфовать в направлении, противоположном полю. Скорость дрейфа — это средняя скорость этих свободных зарядов.
• Выражение для связи между током и скоростью дрейфа можно получить, рассматривая количество свободных зарядов в отрезке провода.
• I = qnAv связывает скорость дрейфа с током, где I — ток через провод с площадью поперечного сечения A , сделанный из материала с плотностью свободного заряда n . Каждый из носителей тока имеет заряд q и движется со скоростью дрейфа величиной v .

Ключевые термины

• скорость дрейфа : средняя скорость свободных зарядов в проводнике.

Скорость дрейфа

Известно, что электрические сигналы движутся очень быстро.Телефонные разговоры по проводам проходят на большие расстояния без заметных задержек. Свет загорается при нажатии переключателя. Большинство электрических сигналов, переносимых токами, передаются со скоростью порядка 10 ⁸ м / с, что составляет значительную часть скорости света. Интересно, что отдельные заряды, составляющие ток, в среднем движутся намного медленнее, обычно дрейфуя со скоростью порядка 10 ^-4 м / с.

Высокая скорость электрических сигналов является результатом того факта, что сила между зарядами действует быстро на расстоянии.Таким образом, когда бесплатный заряд вводится в провод, входящий заряд выталкивает другие заряды впереди себя, которые, в свою очередь, проталкивают заряды дальше по линии. Возникающая в результате электрическая ударная волна движется по системе почти со скоростью света. Если быть точным, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.

Электроны, движущиеся через проводник : Когда заряженные частицы выталкиваются в этот объем проводника, такое же количество быстро вынуждено покинуть его.Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только один заряд входит, другой почти сразу уходит, быстро передавая сигнал вперед.

Скорость дрейфа

У хороших проводников много бесплатных зарядов. В металлах свободными зарядами являются свободные электроны. Расстояние, на которое может перемещаться отдельный электрон между столкновениями с атомами или другими электронами, довольно мало. Таким образом, пути электронов кажутся почти случайными, как движение атомов в газе.Однако в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). Скорость дрейфа v _d — это средняя скорость свободных зарядов после приложения поля. Скорость дрейфа довольно мала, так как свободных зарядов очень много. Имея оценку плотности свободных электронов в проводнике (количество электронов в единице объема), можно вычислить скорость дрейфа для заданного тока.Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Скорость дрейфа : Свободные электроны, движущиеся в проводнике, совершают множество столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется дрейфовой скоростью и направлена ​​в направлении, противоположном электрическому полю электронов. Столкновения обычно передают энергию проводнику, требуя постоянного подвода энергии для поддержания постоянного тока.

Можно получить выражение для связи между током и скоростью дрейфа, учитывая количество свободных зарядов в отрезке провода. Количество бесплатных зарядов на единицу объема обозначается символом n и зависит от материала. Ax — это объем сегмента, поэтому количество свободных зарядов в нем составляет nAx . Заряд ΔQ в этом сегменте, таким образом, равен qnAx , где q — это количество заряда на каждом носителе.(Напомним, что для электронов q равно 1,60 × 10−19C.) Ток — это заряд, перемещаемый за единицу времени. Таким образом, если все первоначальные заряды покидают этот сегмент за время t, ток равен:

[латекс] \ text {I} = \ Delta \ text {Q} / \ Delta \ text {t} = \ text {qnAx} / \ Delta \ text {t} [/ latex]

Примечательно, что x / Δt — это величина скорости дрейфа v _d , поскольку заряды перемещаются на среднее расстояние x за время t. Перестановка членов дает: I = qnAv _d , где I — ток через провод с площадью поперечного сечения A , изготовленный из материала с плотностью свободного заряда n .Каждый носитель тока имеет заряд q и движется со скоростью дрейфа величиной v _d .

Плотность тока — это электрический ток на единицу площади поперечного сечения. Он имеет единицы ампер на квадратный метр.

Страница не найдена | MIT

Перейти к содержанию ↓

• Образование
• Исследовать
• Инновации
• Прием + помощь
• Студенческая жизнь
• Новости
• Выпускников
• О Массачусетском технологическом институте
• Подробнее ↓
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О Массачусетском технологическом институте

Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

САМАЯ ПРОСТАЯ ЦЕПЬ:

САМАЯ ПРОСТАЯ ЦЕПЬ:

ЗАКОН ОМА

САМАЯ ПРОСТАЯ ЦЕПЬ:

Мы можем заставить ток течь по кругу (цепи) соединяя клеммы аккумулятора вместе.Это растопит провод, разжигай искры и, возможно, разжигай огонь, так что не делай этого. Вместо этого подключите что-нибудь для управления током. Способность к управляющий ток называется сопротивлением, и все материалы имеют его в некоторой степени — на самом деле мы классифицируем материалы в соответствии с их сопротивление: с очень низким сопротивлением — проводники, с много сопротивления — изоляторы. Есть устройства, называемые резисторами которые используются в электронных гаджетах — у них есть сопротивление, которое что-то среднее между проводимостью и изоляцией и предсказуемо.Так вот безопасная цепь:

Батарея имеет определенное нажатие, называется электродвижущей силой или ЭДС. Это измеряется в единицах, называемых вольт . Обозначаем ЭДС (часто называемую напряжением) в формулах буквой E ​​. Напряжение необходимо измерять между двумя точками цепи в таким же образом измеряется высота между двумя точками на сторона горы. Нет такого понятия, как «0 вольт», за исключением того, что напряжение между двумя точками равно 0, если они соединены все вместе.

Резистор имеет определенную величину Сопротивление, измеренное в единицах, называется Ом . Мы указываем сопротивление в формулах с буквой R .

Когда ток течет, мы измеряем его в единицы называют ампер , и обозначают его буквой I .

Эти три связаны простой формулой называется законом Ома:

I = E / R

Также написано E ​​= IR или R = E / I.

Это говорит нам о токе, если мы знаем напряжение и сопротивление, или напряжение, если мы знаем ток и сопротивление или сопротивление, если нам известны ток и напряжение. Если вам это кажется немного замкнутым, вы правы. Мы можем измерить ток силой магнитного поля, которое он будет генерировать, но там не является критерием для измерения напряжения, кроме как увидеть, сколько тока течет через известное сопротивление. А как узнать сопротивление? Мы применяем известное напряжение и посмотрите, сколько тока течет.

Определение единиц также круглое: 1 ампер — это количество тока, протекающего через резистор сопротивлением 1 Ом. если приложено 1 вольт.

---

Два резистора последовательно:

Будет немного сложнее, если есть два резистора:

Какой бы ни был ток, он такой же в A, B и C. (Больше некуда течь ток).

Напряжение между A и C равно этому между A и B добавляется к тому, что между B и C.

E ​​ AC = E ​​ AB + E ​​ BC

Напряжения складываются, как и высота Дом — это сумма высот его этажей.

Напряжение на каждом резисторе равно пропорционально сопротивлению каждого резистора.

E ​​ AB / R 1 = E ​​ BC / R 2

Видите ли, закон Ома верен для каждой части схема, а также схема в целом.Какой бы ток ни тек, это то же самое в каждом резисторе, поэтому напряжения будут регулироваться сами себя.

Суммарное сопротивление R 1 + R 2

---

Два параллельных резистора

Ток через А равен току через B плюс ток через C. Ток разделяется и идет вместе, как вода, текущая вокруг острова.

Напряжение на R 1 такое же, как и на напряжение на R 2.

E ​​ AB = E ​​ AC, так I B R 1 = I C R 2 и I B / R 2 = I C / R 1

Другими словами, ток через каждый резистор обратно пропорционален номиналам резисторов. Также важно помнить резистор высокого номинала проходит через небольшой Текущий.

Мы можем решить вышеуказанную проблему для полного тока ( I B + I C) и получите эквивалент сопротивление для двух резисторов:

В частном случае, когда резисторы То же, эквивалентное сопротивление составляет R 1 /2. Это появляется чаще, чем вы можно было ожидать.

В другом особом случае, когда R2 больше, чем 100-кратное значение R1, R2 составляет такую ​​небольшую часть ток, который мы не удосужились включать в расчеты. Тогда мы говорим, что R2 не загружает схему.

---

Вот более сложный пример:

R1 — резистор особого типа. с регулируемым краном посередине.Это действительно заставляет R1 вести себя как два последовательно включенных резистора. Если мы скажем, что R2 в 100 раз больше R1, мы можем оставьте это в расчетах и ​​обнаружите, что напряжение E2 будет напрямую зависит от положения крана.

Если бы R2 было сопоставимо с R1 по стоимости, мы бы нужно вычислить, сначала решив R2 и нижнюю часть R1 как два резистора параллельно, и используя результат этого последовательно расчет, чтобы найти напряжение E2 и полный ток. В результирующая кривая напряжения (то, что вы получили бы, если бы построили E2 для различных положения крана) довольно беспорядочно, поэтому мы действительно предпочитаем R2, который не нагружает цепь.

Вернуться к темам Mu126

Закон

Ома: определение и взаимосвязь между напряжением, током и сопротивлением — Видео и стенограмма урока

Закон Ома

Взаимосвязь между напряжением, током и сопротивлением описывается законом Ома . Это уравнение, i = v / r , говорит нам, что ток, i , протекающий по цепи, прямо пропорционален напряжению, v , и обратно пропорционален сопротивлению, r .Другими словами, если мы увеличим напряжение, то увеличится и ток. Но, если увеличить сопротивление, то ток уменьшится. Мы увидели эти концепции в действии с садовым шлангом. Увеличение давления привело к увеличению потока, но изгиб шланга увеличил сопротивление, что привело к уменьшению потока.

Эта диаграмма — простой способ решать уравнения.

Как написано здесь уравнение, было бы легко использовать закон Ома, чтобы вычислить ток, если бы мы знали напряжение и сопротивление.Но что, если бы мы вместо этого захотели вычислить напряжение или сопротивление? Один из способов сделать это — переставить члены уравнения для решения других параметров, но есть более простой способ. Приведенная выше диаграмма даст нам соответствующее уравнение для решения любого неизвестного параметра без использования алгебры. Чтобы использовать эту диаграмму, мы просто закрываем параметр, который пытаемся найти, чтобы получить правильное уравнение. Это станет более понятным, когда мы начнем его использовать, поэтому давайте рассмотрим несколько примеров.

Закон Ома в действии

Ниже представлена ​​простая электрическая схема, которую мы будем использовать для выполнения наших примеров. Наш источник напряжения — это аккумулятор, подключенный к лампочке, которая обеспечивает сопротивление электрическому току. Для начала предположим, что наша батарея имеет напряжение 10 вольт, электрическая лампочка имеет сопротивление 20 Ом, и нам нужно вычислить ток, протекающий по цепи. Используя нашу диаграмму, мы закрываем параметр, который мы пытаемся найти, то есть ток, или i , и это оставляет нам напряжение v над сопротивлением r .Другими словами, чтобы найти ток, нам нужно разделить напряжение на сопротивление. Делая математические вычисления, 10 вольт, разделенные на 20 Ом, дают половину ампера тока, протекающего в цепи.

Чтобы найти ток, разделите напряжение (20 вольт) на сопротивление (20 Ом).

Теперь давайте увеличим напряжение, чтобы посмотреть, что происходит с током. Мы будем использовать ту же лампочку, но перейдем на 20-вольтовую батарею.Используя то же уравнение, что и раньше, мы разделим 20 вольт на 20 Ом, и мы получим 1 ампер тока. Как мы видим, удвоение напряжения привело к удвоению тока. Это имеет смысл, когда мы думаем о садовом шланге. Если бы мы увеличили давление в шланге, можно было бы ожидать, что поток воды также увеличится. Всегда полезно перепроверить свою работу, спросив, соответствуют ли результаты тому, что вы ожидали.

Если бы мы увеличили сопротивление лампочки, что бы вы ожидали, что произойдет с током? Чтобы выяснить это, давайте заменим нашу существующую лампочку на другую с сопротивлением 40 Ом.Поскольку мы все еще ищем ток, мы используем то же уравнение, что и раньше. Разделив 20 вольт на 40 Ом, мы получим половину ампера тока. Этот результат говорит нам, что удвоение сопротивления уменьшило ток вдвое. Вы этого ожидали? Если вспомнить наш шланг, логично предположить, что перегиб в шланге уменьшит поток воды, точно так же, как увеличение сопротивления в цепи уменьшит ток.

До сих пор мы только рассчитали ток в цепи, но что, если бы кто-то поменял нашу лампочку, когда мы не смотрели, и нам нужно было вычислить сопротивление новой? Что ж, мы знаем, что напряжение нашей батареи составляет 20 вольт, и мы можем измерить ток в цепи с помощью инструмента, называемого амперметром, поэтому все, что осталось, — это выполнить некоторые вычисления.Используя нашу диаграмму, мы закрываем параметр, который мы пытаемся найти, а именно сопротивление, r . Схема теперь показывает нам, что нам нужно разделить напряжение на ток. Если наш амперметр измерил ток в 5 ампер, протекающий по цепи, то сопротивление будет равно 20 вольт, разделенным на 5 ампер, что составляет 4 Ом

Чтобы определить напряжение, умножьте силу тока (3 ампера) на сопротивление (4 Ом).

Наконец, представьте, что кто-то заменил нашу батарею, и нам нужно выяснить ее напряжение.Процесс почти такой же. Мы знаем, что наша новая лампочка имеет сопротивление 4 Ом, и мы можем измерить ток в цепи с помощью амперметра. Используя диаграмму, мы покрываем напряжение v , которое говорит нам, что нам нужно умножить ток на сопротивление. Если бы амперметр измерял ток в 3 ампера, тогда напряжение было бы 3 ампера, умноженным на 4 Ом, что составляет 12 вольт. Вот и все. Зная любые два из трех параметров, мы всегда можем вычислить третий, используя закон Ома.

Резюме урока

Закон Ома определяет соотношение между напряжением, током и сопротивлением в электрической цепи: i = v / r . Ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Это означает, что увеличение напряжения приведет к увеличению тока, а увеличение сопротивления приведет к уменьшению тока. Зная любые два из трех параметров, мы можем вычислить третий, неизвестный параметр.Мы можем сделать это, переставив члены в уравнении закона Ома или используя диаграмму, приведенную выше в уроке. Скрытие параметра, который мы пытаемся найти, показывает нам соответствующее уравнение с использованием двух известных параметров.

Результаты обучения

По завершении этого урока вы сможете:

• Описывать взаимосвязь между напряжением, током и сопротивлением, используя закон Ома
• Напишите уравнение закона Ома
• Объясните, как можно найти любую из трех переменных в уравнении закона Ома, если вам известны две другие.
• Рассчитайте любую из трех переменных, используя уравнение закона Ома

Электричество и магнетизм — IB Physics

См. Руководство по этой теме.-19С.

Электрический заряд всегда сохраняется. Хотя заряды могут переходить от одного тела к другому, общий заряд остается прежним.

FYI

Проводники — это материалы, пропускающие электрический заряд. Это связано с наличием свободных электронов в твердых проводниках.

• Примеры проводников включают все металлы, графит, людей.

Изоляторы — это материалы, не пропускающие электрический заряд.

• Примеры изоляторов: деревянные, стеклянные и пластиковые ведра.

Электрические поля могут быть графически представлены в виде линий электрического поля.

• Направление поля в точке равно направлению силовой линии, проходящей через эту точку (стрелки от положительного полюса к отрицательному).
• Величина поля в точке соответствует плотности силовых линий вокруг этой точки. Для однородного электрического поля силовые линии прямые, параллельные и равномерно разнесенные.

Неоднородное электрическое поле

Однородное электрическое поле

Линии электрического поля изгибаются наружу около края пластин. Это известно как «краевой эффект».

Напряженность электрического поля (E) — это сила на единицу заряда, испытываемая при положительном тестовом изменении, помещенном в поле.

Согласно закону Кулона

где F — сила, q1 и q2 — заряд двух объектов (обычно одинаковый при рассмотрении двух электронов), а r — радиус / расстояние между двумя зарядами.2, мы можем сделать вывод, что для неоднородных электрических полей напряженность электрического поля может быть рассчитана по

, отменив q (заряд) с обеих сторон.

Для однородных электрических полей напряженность электрического поля можно рассчитать по

См. Предыдущий раздел (Электрическое поле).

Наличие разности электрических потенциалов (см. Последний раздел 5.1) на объекте заставляет заряды течь через объект.

Электрический ток (I) относится к скорости потока электрического заряда и может быть задан уравнением

Направление (обычного) электрического тока противоположно направлению потока электронов.

Постоянный ток (dc) — это равномерный ток, текущий в одном фиксированном направлении в цепи.

Постоянный ток обычно подается от кислотных батарей или сухих элементов.

Разность электрических потенциалов (pd) между двумя точками равна проделанной работе (энергии), необходимой на единицу заряда для перемещения из одной точки в другую. Он также известен как напряжение (В).

Напряжение аналогично разнице между входами и выходами, где поток воды в потоке — это поток электронов внутри цепи.

5.2 — Нагревательное действие электрических токов

Электрическая цепь — это соединение электрических компонентов в замкнутом контуре.

Резисторы

Резистор — это электрический компонент, который реализует определенное сопротивление в электрической цепи.

Резистор с регулируемым сопротивлением называется переменным резистором.

Резисторы можно подключать последовательно или параллельно.

FYI

Вольтметры

Вольтметр используется для измерения разности потенциалов между двумя точками.

Вольтметр должен быть подключен параллельно измеряемым компонентам.

Идеальный вольтметр имеет бесконечное сопротивление.

Амперметр

Амперметр используется для измерения тока, проходящего через точку.

Амперметр должен быть подключен последовательно в точке измерения.

Идеальный амперметр имеет нулевое сопротивление.

• Окружные законы Кирхгофа

Правило соединения Кирхгофа — это утверждение о сохранении потока заряда во времени. Сумма всех токов, текущих в переход, должна равняться сумме всех текущих токов.

Правило петли Кирхгофа — это утверждение о сохранении электрической потенциальной энергии на заряд. Для полного цикла электрической цепи все повышения электрического потенциала, сложенные вместе, должны равняться всем падениям электрического потенциала, сложенным вместе.

• Сопротивление выражается как R = V / I

Сопротивление (R) объекта можно рассматривать как меру противодействия электрическому току, протекающему через объект.

Дается соотношением между разностью электрических потенциалов (V) и индуцированным током (I).

Закон

Ома гласит, что ток, протекающий по проводнику, пропорционален разности электрических потенциалов на проводнике.

• Если мы построим график зависимости тока от разности потенциалов, наклон полученного графика будет постоянным.

Закон Ома не всегда соблюдается. Проводник, подчиняющийся закону Ома, имеет постоянное сопротивление и называется омическим проводником.

Неомический проводник изображает график, который не имеет постоянного градиента (нелинейный).

Сопротивление объекта пропорционально его длине (L) и обратно пропорционально его площади поперечного сечения (A).

На сопротивление влияет постоянная удельного сопротивления объекта (определяется материалом, из которого он сделан).

Мощность (P), рассеиваемая на резисторе, может быть равна

.

FYI

Это означает, что электрическая энергия «теряется» в виде тепловой энергии или других форм энергии, которые не считаются полезными с течением времени.

5.3 — Электроэлементы

Ячейка в цепи действует как источник электрической энергии и создает разность электрических потенциалов на своих выводах.

Батарея состоит из двух соединенных ячеек.

Внутреннее сопротивление — это сопротивление источника, определяемое материалом, из которого он сделан.

Внутреннее сопротивление можно использовать для расчета ЭДС. (см. последний раздел 5.3)

Вторичный элемент или аккумулятор можно перезарядить после использования, пропуская ток через цепь в направлении, противоположном току во время разряда.

• Разность потенциалов клемм

Разность потенциалов на выводах источника меньше ЭДС источника из-за внутреннего сопротивления.(см. последний раздел 5.3)

• Электродвижущая сила (ЭДС)

Электродвижущая сила (ЭДС) источника определяется как энергия на единицу заряда, поставляемая источником.

Единица измерения ЭДС — вольт (В).

5.4 — Магнитные эффекты электрических токов

Магнитные поля возникают из-за наличия магнитов или движущихся зарядов.

Подобно тому, как электрический заряд испытывает силу в электрическом поле, магнит или электрический ток испытывают силу в магнитном поле.

Единица магнитного поля — Тесла (Тл).

Диаграммы магнитного поля

Магнитные поля могут быть графически представлены с помощью силовых линий магнитного поля.

• Направление поля в точке равно направлению силовой линии, проходящей через эту точку.
• Величина поля в точке соответствует плотности силовых линий вокруг этой точки.

Магниты

Провод с током

Соленоид с током

FYI

При просмотре магнитного поля в трехмерном формате точки представляют собой магнитные поля, исходящие из страницы (как острие стрелки), а крестики представляют собой магнитные поля, входящие в страницу (как острие стрелки).

Величину силы, действующей на провод с током из-за магнитного поля, можно определить как

.

Уравнение можно умножить на sinθ, где θ — угол между направлением поля и током. Это можно игнорировать, если θ = 90 градусов, потому что sin90 градусов равно 1.

Магнитная сила на движущемся заряде

Величину силы, действующей на движущийся заряд из-за магнитного поля, можно определить как

.

где F — сила, действующая на провод, B — магнитное поле, q — количество заряда, v — скорость заряда, а θ — угол между направлением поля и скоростью.

Помните, что направление (обычного) тока на противоположно направлению потока электронов на .

Поскольку магнитная сила всегда перпендикулярна скорости заряда, она действует как центростремительная сила (см. Раздел 6), и заряд движется по круговой траектории. Магнитное поле не производит никакой работы с зарядом.

Нравится:

Нравится Загрузка .