Электротехника

Электротехника

Ломоносов В. Ю. и др. Электротехника/В. Ю. Ломоносов, К. М. Поливанов, О. П. Михайлов. — М.: Энергоатомиздат, 1990. — 400 с. Приводятся основные понятия об элементах электрической цепи, методах расчета простых цепей постоянного и переменного тока. Дается общее описание физических процессов, происходящих в электрическом и магнитном полях. Излагается принцип действия полупроводниковых приборов, электрических машин и аппаратов, электроизмерительных приборов. Приводятся сведения о применении электронных вычислительных устройств в электротехнике. Для читателей, интересующихся основами электротехники и электроники. Оглавление ПРЕДИСЛОВИЕ ИЗ ПРЕДИСЛОВИЯ КО ВТОРОМУ ИЗДАНИЮ ГЛАВА ПЕРВАЯ. ТОК И НАПРЯЖЕНИЕ 1.2. ПРОСТЕЙШАЯ ЭЛЕКТРОТЕХНИЧЕСКАЯ УСТАНОВКА 1.3. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ 1.4. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ 1.5. ВКЛЮЧЕНИЕ АМПЕРМЕТРА И ВОЛЬТМЕТРА 1.6. МОЩНОСТЬ 1.7. СОПРОТИВЛЕНИЕ ЦЕПИ И ЗАКОН ОМА 1.8. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ 1.9. ПОЧЕМУ ЦЕПИ, ПОДЧИНЯЮЩИЕСЯ ЗАКОНУ ОМА, НАЗЫВАЮТ ЛИНЕЙНЫМИ 1.10. НЕЛИНЕЙНЫЕ ЦЕПИ 1.11. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ 1.12. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА И ЗАКОН ДЖОУЛЯ — ЛЕНЦА 1.13. НАПРАВЛЕНИЕ ТОКА И ЕГО ХИМИЧЕСКОЕ ДЕЙСТВИЕ 1.14. НАПРАВЛЕНИЕ ТОКА И ВЫПРЯМЛЯЮЩИЕ УСТРОЙСТВА 1.15. АККУМУЛЯТОРЫ И ГАЛЬВАНИЧЕСКИЕ ЭЛЕМЕНТЫ 1.16. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ 1.17. ТОК В СЛОЖНЫХ ЦЕПЯХ 1.18. ЭЛЕКТРОДВИЖУЩАЯ СИЛА И ПОТЕРЯ НАПРЯЖЕНИЯ 1.19. ЗАЗЕМЛЕНИЕ И ПОТЕНЦИАЛ 1.20. ЗАКОНЫ КИРХГОФА ГЛАВА ВТОРАЯ. МАГНИТЫ. МАГНИТНОЕ ПОЛЕ. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА 2.1. МАГНИТЫ И МАГНИТНОЕ ПОЛЕ 2.2. МАГНИТНОЕ ДЕЙСТВИЕ ТОКА 2.3. МАГНИТНОЕ ПОЛЕ ДЕЙСТВУЕТ НА ПРОВОДНИК С ТОКОМ 2. 4. МАГНИТНАЯ ИНДУКЦИЯ 2.6. НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ МАГНИТНЫХ ПОЛЕЙ 2.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ 2.8. ИЗМЕНЕНИЕ МАГНИТНОГО ПОЛЯ СОЗДАЕТ ЭЛЕКТРОДВИЖУЩУЮ СИЛУ 2.9. ПРАВИЛО ЛЕНЦА 2.10. МАГНИТНЫЙ ПОТОК 2.11. ЗАКОН НАВЕДЕНИЯ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ 2.12. НАВЕДЕНИЕ ЭДС В ПРЯМОЛИНЕЙНОМ ПРОВОДНИКЕ, ДВИЖУЩЕМСЯ В ПОЛЕ 2.13. ВЗАИМНАЯ ИНДУКДИЯ 2.14. САМОИНДУКЦИЯ 2.15. ВЛИЯНИЕ САМОИНДУКЦИИ НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ 2.16. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ ГЛАВА ТРЕТЬЯ. ЖЕЛЕЗО В МАГНИТНОМ ПОЛЕ. МАГНИТНЫЕ ЦЕПИ. ПОСТОЯННЫЕ МАГНИТЫ 3.1. ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОЙ ИНДУКЦИИ ПРИ ОТСУТСТВИИ ЖЕЛЕЗА 3.2. НАМАГНИЧИВАНИЕ ЖЕЛЕЗНОГО КОЛЬЦА 3.3. ОТНОСИТЕЛЬНАЯ МАГНИТНАЯ ПРОНИЦАЕМОСТЬ 3.4. РАСЧЕТ ПОЛЯ В КОЛЬЦЕВОЙ КАТУШКЕ СО СПЛОШНЫМ СЕРДЕЧНИКОМ ПО МАГНИТНЫМ ХАРАКТЕРИСТИКАМ 3.5. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ОДНОРОДНОГО ПОЛЯ В ФЕРРОМАГНИТНОЙ СРЕДЕ 3.6. ЗАКОН ПОЛНОГО ТОКА ДЛЯ ПОЛЯ В НЕОДНОРОДНОЙ СРЕДЕ 3.7. СТАЛЬНОЕ КОЛЬЦО С РАЗРЕЗОМ 3.8. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ, РАСЧЕТ МАГНИТНОЙ 3. 9. НАМАГНИЧЕННОСТЬ ГЛАВА ЧЕТВЕРТАЯ. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ И ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 4.1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ 4.2. ИЗОЛЯТОРЫ И ПРОВОДНИКИ 4.3. ПРОСТЕЙШИЕ ОПЫТЫ С НЕПОДВИЖНЫМИ ЭЛЕКТРИЧЕСКИМИ ЗАРЯДАМИ (ЭЛЕКТРОСТАТИКА) 4.4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 4.5. НАПРЯЖЕНИЕ (РАЗНОСТЬ ПОТЕНЦИАЛОВ) 4.6. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ 4.7. КОНДЕНСАТОР В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ 4.8. ДВИЖЕНИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ В МАГНИТНОМ ПОЛЕ ГЛАВА ПЯТАЯ. ПЕРЕМЕННЫЙ ТОК 5.1. ЗАЧЕМ НУЖЕН ПЕРЕМЕННЫЙ ТОК? 5.2. ПОЛУЧЕНИЕ ПЕРЕМЕННОГО ТОКА 5.3. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА 5.4. СИНУСОИДА 5.5. ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА ГЛАВА ШЕСТАЯ. ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.1. КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.2. ФАЗОВЫЙ СДВИГ В ИНДУКТИВНОЙ ЦЕПИ 6.3. КОЭФФИЦИЕНТ МОЩНОСТИ 6.4. КОНДЕНСАТОВ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 6.5. КОМПЕНСАЦИЯ СДВИГА ФАЗ 6.6. РАСЧЕТ ПРОСТЕЙШИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА 6.7. РЕЗОНАНС ТОКОВ 6.8. РЕЗОНАНС НАПРЯЖЕНИЙ ГЛАВА СЕДЬМАЯ. ТРЕХФАЗНЫЙ ТОК 7.1. ТРЕХФАЗНАЯ СИСТЕМА 7.2. РАЗМЕТКА КОНЦОВ ТРЕХФАЗНОЙ СИСТЕМЫ 7.3. СЛОЖЕНИЕ ФАЗНЫХ ЭДС 7.4. СОЕДИНЕНИЕ В ЗВЕЗДУ 7.5. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ 7.6. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА 7.7. ПОТЕРИ МОЩНОСТИ В ТРЕХФАЗНОЙ ЛИНИИ ГЛАВА ВОСЬМАЯ. ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ НА МИКРОКАЛЬКУЛЯТОРАХ 8.1. КАК РАБОТАЕТ МИКРОКАЛЬКУЛЯТОР 8.2. ПРОСТЕЙШИЕ ЭЛЕКТРОТЕХНИЧЕСКИЕ РАСЧЕТЫ 8.3. О ТОЧНОСТИ ВЫЧИСЛЕНИЙ 8.4. ПРОГРАММИРУЕМЫЕ МИКРОКАЛЬКУЛЯТОРЫ 8.5. РАСЧЕТЫ НА ПРОГРАММИРУЕМЫХ МИКРОКАЛЬКУЛЯТОРАХ ГЛАВА ДЕВЯТАЯ. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ 9.1. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 9.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ. ВЫПРЯМИТЕЛИ 9.3. ТРАНЗИСТОРЫ. УСИЛИТЕЛИ ЭЕКТРИЧЕСКИХ СИГНАЛОВ 9.4. ОБРАТНАЯ СВЯЗЬ В УСИЛИТЕЛЯХ 9.5. ГЕНЕРАТОРУ СИНУСОИДАЛЬНЫХ КОЛЕБАНИЙ 9.6. ТИРИСТОРЫ, УПРАВЛЯЕМЫЕ ВЫПРЯМИТЕЛИ 9.7. КЛЮЧИ 9.8. НЕИЗБЕЖНОСТЬ МИКРОЭЛЕКТРОНИКИ 9.9. ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ ГЛАВА ДЕСЯТАЯ. МАШИНЫ ПОСТОЯННОГО ТОКА 10.1. НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН 10. 2. МАГНИТНАЯ СИСТЕМА МАШИН ПОСТОЯННОГО ТОМА 10.3. КОЛЛЕКТОР 10.4. ЯКОРНЫЕ ОБМОТКИ 10.5. РАБОЧИЙ РЕЖИМ МАШИН ПОСТОЯННОГО ТОКА 10.6. СПОСОБЫ ВОЗБУЖДЕНИЯ МАШИН 10.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. РАБОТА ДВИГАТЕЛЯ 10.8. ДВИГАТЕЛИ С ПАРАЛЛЕЛЬНЫМ И ПОСЛЕДОВАТЕЛЬНЫМ ВОЗБУЖДЕНИЕМ ГЛАВА ОДИННАДЦАТАЯ. ТРАНСФОРМАТОРЫ 11.1. УСТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ ТРАНСФОРМАТОРА 11.2. РАБОТА ТРАНСФОРМАТОРА 11.3. ТРАНСФОРМАТОР ТРЕХФАЗНОГО ТОКА 11.4. ПОТЕРИ В ТРАНСФОРМАТОРЕ 11.1. АВТОТРАНСФОРМАТОРЫ ГЛАВА ДВЕНАДЦАТАЯ. МАШИНЫ ПЕРЕМЕННОГО ТОКА 12.1. ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА 12.2. СИНХРОННЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА 12.3. ТРЕХФАЗНЫЕ МАШИНЫ ПЕРЕМЕННОГО ТОКА 12.4. РАБОТА СИНХРОННЫХ МАШИН 12.5. ПАРАЛЛЕЛЬНАЯ РАБОТА СИНХРОННЫХ ГЕНЕРАТОРОВ 12.6. ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ 12.7. АСИНХРОННЫЕ ДВИГАТЕЛИ 12.8. КПД ЭЛЕКТРИЧЕСКИХ МАШИН ГЛАВА ТРИНАДЦАТАЯ. ЭЛЕКТРИЧЕСКИЕ АППАРАТЫ 13.1. ВЫКЛЮЧАТЕЛИ, КНОПКИ И КЛАВИШИ 13.2. РАБОТА ЭЛЕКТРИЧЕСКИХ КОНТАКТОВ 13. 3. ЭЛЕКТРОМАГНИТЫ 13.4. КОНТАКТОРЫ 13.5. ЭЛЕКТРОМАГНИТНЫЕ РЕЛЕ 13.6. ПРЕДОХРАНИТЕЛИ, РЕЛЕ ТОКА И ТЕПЛОВЫЕ РЕЛЕ 13.7. ПУТЕВЫЕ ВЫКЛЮЧАТЕЛИ ГЛАВА ЧЕТЫРНАДЦАТАЯ. УПРАВЛЕНИЕ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ 14.1. КАК СОСТАВЛЯЮТСЯ ЭЛЕКТРИЧЕСКИЕ СХЕМЫ 14.2. ДВА ТИПА ЭЛЕКТРИЧЕСКИХ СХЕМ 14.3. КАК ВКЛЮЧИТЬ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ 14.4. СХЕМЫ ТОРМОЖЕНИЯ 14.5. ЗАЩИТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 14.6. КАК ОПИСАТЬ ЭЛЕКТРИЧЕСКУЮ СХЕМУ ГЛАВА ПЯТНАДЦАТАЯ. ИЗМЕРЕНИЯ В ЭЛЕКТРОТЕХНИКЕ 15.1. РОЛЬ ИЗМЕРЕНИЙ В ЭЛЕКТРОТЕХНИКЕ 15.2. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ПОСТОЯННОГО ТОКА 15.3. ШУНТЫ И ДОБАВОЧНЫЕ СОПРОТИВЛЕНИЯ 15.4. ИЗМЕРЕНИЕ ОЧЕНЬ МАЛЫХ ТОКОВ. ГАЛЬВАНОМЕТРЫ 15.5. ПРИБОРЫ ПЕРЕМЕННОГО ТОКА 15.6. КАК ИЗМЕРИТЬ МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА 15.7. ЭЛЕКТРИЧЕСКИЙ СЧЕТЧИК ПЕРЕМЕННОГО ТОКА 15.8. ИЗМЕРЕНИЕ МОЩНОСТИ И ЭНЕРГИИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА 15.9. САМОПИСЦЫ И ОСЦИЛЛОГРАФЫ 15.10. ЦИФРОВЫЕ ПРИБОРЫ 15.11. ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ЦЕПИ

Лр 1.

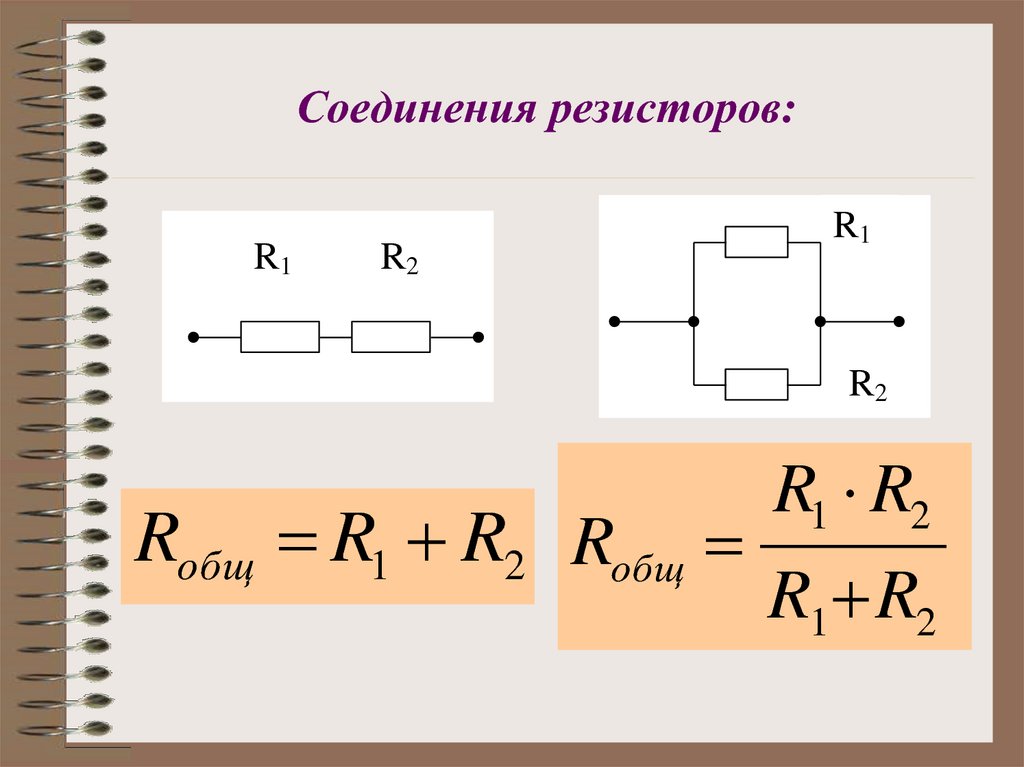1. Виды соединений резисторов.

1. Назвать основные свойства последовательного соединения резисторов.

1. Токи во всех последовательно соединенных резисторах одинаковы и равны общему току цепи

I=I₁=I₂=I₃.

2. Падения напряжений на отдельных резисторах пропорциональны их сопротивлению U_n~R_n.

3. Сумма напряжений на отдельных резисторах равна общему напряжению на зажимах цепи

U=U₁+U₂+U₃.

4. Эквивалентное сопротивление цепи равно сумме сопротивлений всех последовательно соединенных резисторов

R=R₁+R₂+R₃.

2. Назвать основные свойства параллельного соединения резисторов.

1. Напряжения на всех параллельно соединенных резисторах одинаковы и равны общему напряжению цепи U=U₁=U₂=U₃.

2. Токи в отдельных резисторах обратно пропорциональны их сопротивлению I

~.

3. Сумма токов в отдельных резисторах равна общему току I=I₁+I₂+I₃.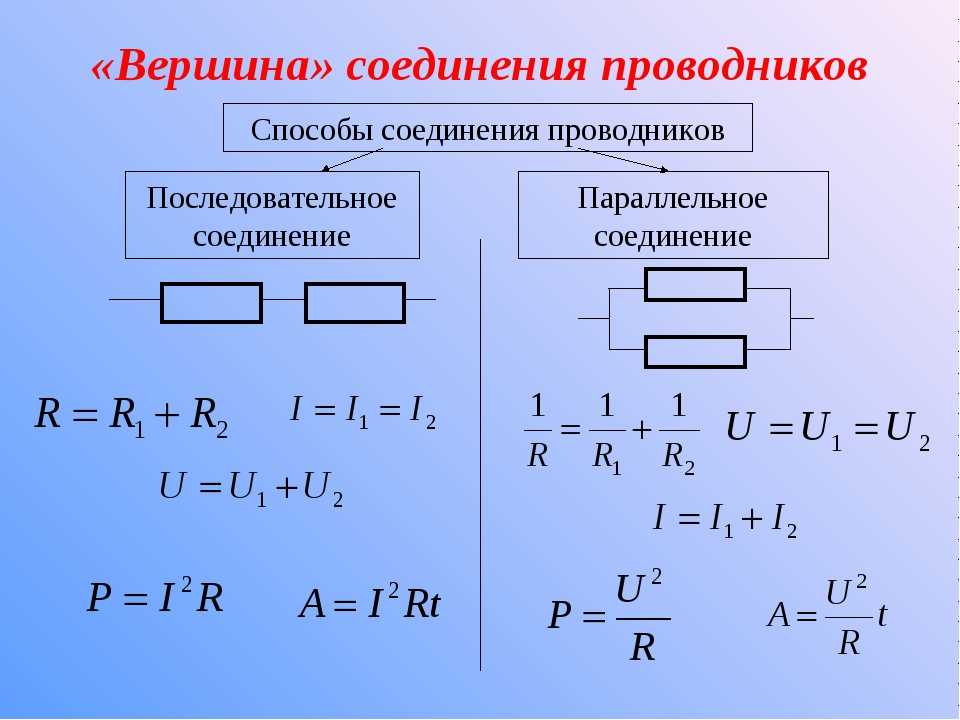

3. Как изменятся параметры цепи, если при последовательном соединении увеличить в два раза сопротивление резистора R₁?

Если при последовательном соединении увеличить в два раза сопротивление резистора R₁, то R_экв цепи увеличится, ток в цепи уменьшится, падение напряжения на резисторах R₂ и R₃ уменьшатся, а на резисторе R₁ увеличится.

4. Как изменятся параметры цепи, если при последовательном соединении уменьшить в два раза сопротивление резистора R₃?

Если при последовательном соединении уменьшить в два раза сопротивление резистора R₃, то R_экв цепи уменьшится, ток в цепи увеличится, падение напряжения на резисторах R₁ и R₂ увеличатся, а на резисторе R₃ уменьшится.

5. Как изменятся параметры цепи, если при параллельном соединении увеличить в два раза сопротивление резистора R₁?

Если при параллельном соединении увеличить в два раза сопротивление резистора R₁, то напряжения на параллельных ветвях останутся прежними, токи I₂, I₃ останутся прежними, ток I₁ уменьшится в 2 раза, а, следовательно, общий ток I тоже уменьшится.

6. Как изменятся параметры цепи, если при параллельном соединении уменьшить в два раза сопротивление резистора R₂?

Если при параллельном соединении уменьшить в два раза сопротивление резистора R₂, то напряжения на параллельных ветвях останутся проежними, токи I₂, I₃ останутся прежними, ток I₂ увеличится в 2 раза, а, следовательно, общий ток I тоже увеличится.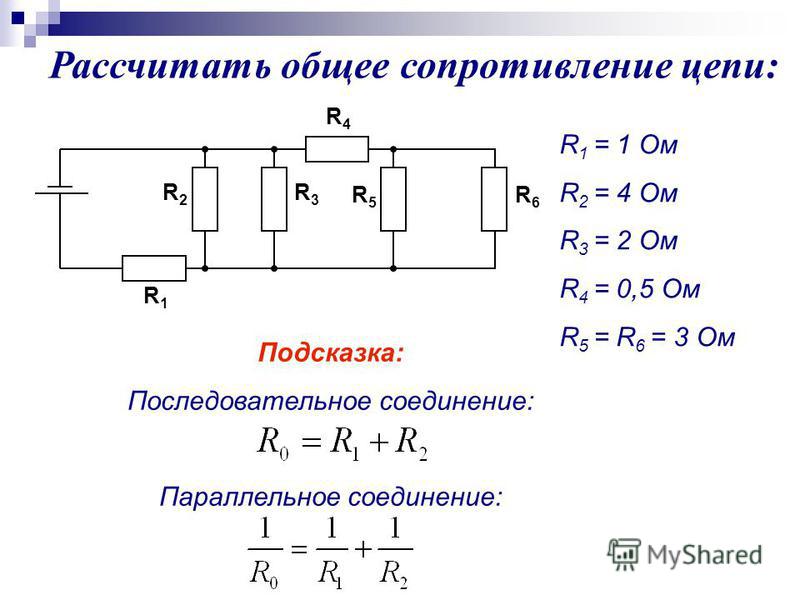

7. Как изменятся параметры цепи, если при параллельном соединении уменьшить в два раза напряжение сети?

Если при параллельном соединении уменьшить в два раза напряжение сети, то напряжения на всех параллельных ветвях уменьшатся в 2раза, а, следовательно, токи в параллельных ветвях и общий ток тоже уменьшатся в 2 раза.

Лр 2 Параллельное соединение катушки индуктивности и конденсатора.

1. Как определить опытным путём величину активного сопротивления катушки?

Активное сопротивление катушки определяется: R= P/I² (1)

Следовательно, для определения опытным путем активного сопротивления, необходимо включить два измерительных прибора: ваттметр и амперметр. Измерив мощность Р, с помощью ваттметра и силу тока I₁ с помощью амперметра активное сопротивление определим по формуле (1).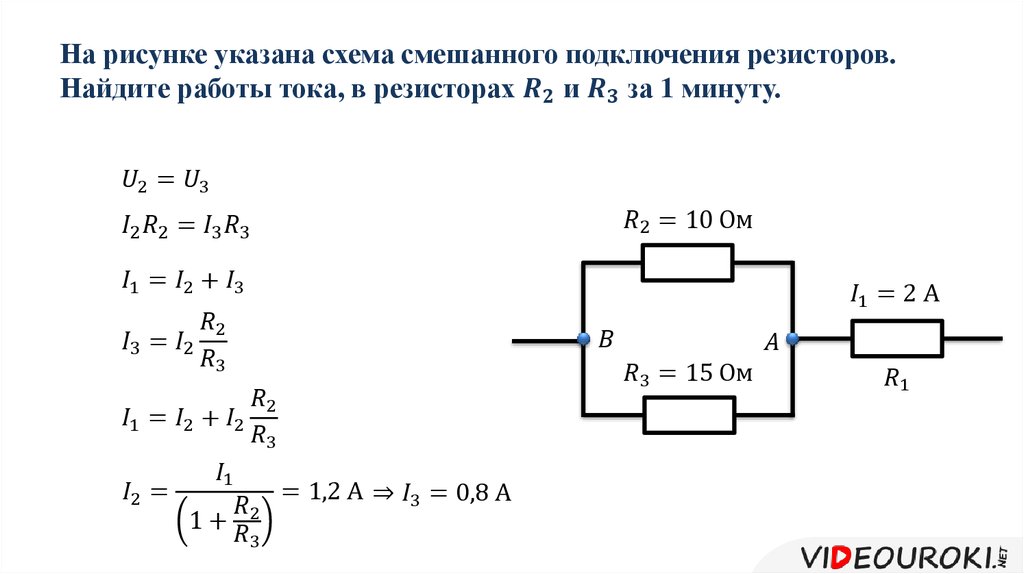

2.Как определить опытным путём величину индуктивного сопротивления катушки?

Индуктивное сопротивление катушки определяется: (2), где: Z = U/I (3), R =P/I² (1).

Следовательно, для определения опытным путем индуктивного сопротивления катушки, необходимо включить три измерительных прибора: вольтметр, амперметр и ваттметр. Измерив, напряжение U с помощью вольтметра и силу тока I₁ с помощью амперметра, определим полное сопротивление катушки Z по формуле (3). Измерив, мощность Р с помощью ваттметра и силу тока I₁ с помощью амперметра, определим активное сопротивление R по формуле (1).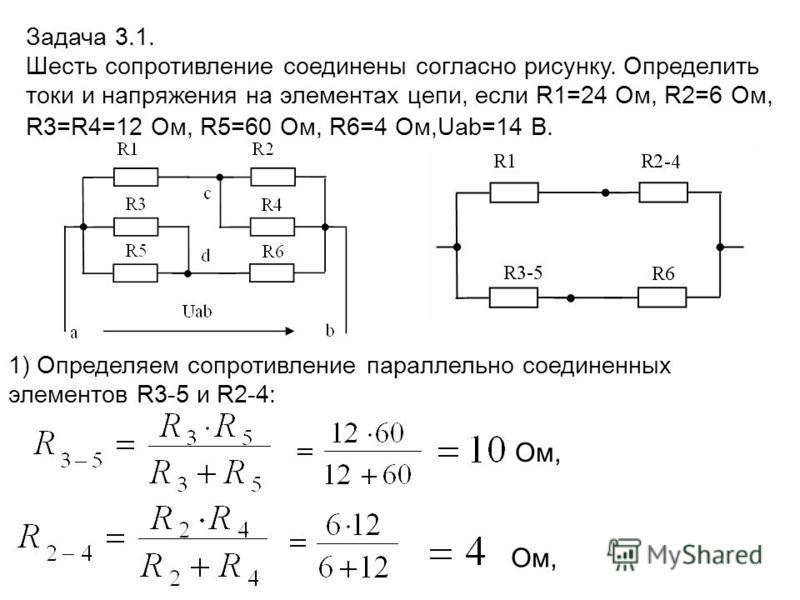 Подставив значения Z и R в формулу (2) определим индуктивное сопротивление катушки Х_L.

как определить ток в этой цепи

\$\начало группы\$

После расчета общего сопротивления и полного тока я применяю деление тока и получаю (6/6+6)*1А = 1/2 А. Но в ключе ответа это представлено как 1/3 А.

Что я делаю не так?

• текущий

\$\конечная группа\$

7

\$\начало группы\$

Простой подход к этой проблеме следующий (подробности расчетов я оставлю вам): Найдите эквивалентное сопротивление резисторов 3 и 6 Ом. Рассмотрим это сопротивление с резистором 4 Ом в качестве делителя напряжения. Это даст вам напряжение на резисторе 6 Ом. Затем закон Ома даст вам ток через резистор 6 Ом. Если вы сделаете эти расчеты правильно, вы обнаружите, что ток в резисторе 6 Ом действительно равен 1/3 ампера.

\$\конечная группа\$

\$\начало группы\$

Вы, кажется, неправильно применяете концепцию текущего деления. В этой схеме ток через резистор 4 Ом делится между резисторами 3 Ом и 6 Ом на обратном пути к источнику. Текущая формула делителя

\$ I_1 = I \frac{G_1}{G_1+G_2} \$

где \$G_1\$ и \$G_2\$ в данном случае проводимости резисторов 6 Ом и 3 Ом соответственно, \$I\$ это полный ток и \$I_1\$ ток через \$G_1\$

Вы обнаружили, что общий ток равен 1 А. Поскольку проводимость \$G\$ обратно пропорциональна сопротивлению, \$G = \frac{1}{R}\$, ток в резисторе 6 Ом равен

\$ I_1 = 1 \cdot \ frac {\ frac {1} {6}} {\ frac {1} {6} + \ frac {1} {3}} = \ frac {1} {3} \$

\$\конечная группа\$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Как использовать теорему Тевенина | EAGLE

Узнайте, как использовать теорему Тевенина для расчета тока и напряжения на нагрузочном резисторе в линейной цепи.

Как рассчитать ток и напряжение нагрузки с помощью теоремы Тевенина — не усложняйте задачу

Существует множество методов анализа сложных электрических цепей. К ним относятся сеточный анализ, узловой анализ или законы цепей Кирхгофа. Проблема заключается в том, что при проектировании сети питания постоянного тока у вас будет нагрузка, значение которой будет меняться по мере развертывания процесса проектирования. Вместо того, чтобы пересчитывать ток и напряжение всей цепи каждый раз при изменении нагрузки, вы можете упростить этот процесс с помощью теоремы Тевенина. В этом блоге мы рассмотрим, как упростить любую сложную линейную схему до единого источника напряжения и последовательного сопротивления. Оттуда мы можем использовать нашу эквивалентную схему Thevenin для быстрого расчета тока и напряжения. Давай начнем.

Что такое Теорема Тевенина?

Как и все другие математические и научные теории/законы, Теорема Тевенина была изобретена самим человеком, Леоном Шарлем Тевенином. Тевенен был французским инженером-телеграфистом, родившимся в Мо, Франция. После службы в корпусе телеграфных инженеров в 1882 году он был назначен преподавателем-инспектором в Высшей школе телеграфии. Именно здесь он заинтересовался измерением электрических цепей. В то время он использовал два доступных метода — законы Кирхгофа и закон Ома.

Léon Charles Thévenin (Источник изображения)

Пытаясь упростить анализ сложных схем для каждого инженера, Тевенин разработал свою знаменитую теорему Тевенина. Эта теорема сводит сложные схемы к упрощенным эквивалентным схемам Тевенина.

Теорема

Th e гласит, что можно взять любую линейную цепь, которая может содержать несколько ЭДС и резистивных составляющих, и упростить схему до одного источника напряжения и последовательного сопротивления, подключенного к нагрузке.

Упрощенная эквивалентная схема Thevenin с одним источником напряжения и сопротивлением. (Источник изображения)

Зачем использовать теорему Тевенина?

В этом случае линейная цепь включает пассивные компоненты, такие как резисторы, катушки индуктивности и конденсаторы. Однако если вы работаете со схемой, включающей газоразрядные или полупроводниковые компоненты, то у вас нелинейная схема. Теорема Тевенина подходила не для этого. Так зачем же использовать эту теорему для анализа линейных цепей?

• Эффективность . Теорема Тевенина обеспечивает простой метод анализа силовых цепей, которые обычно имеют нагрузку, значение которой изменяется в процессе анализа. Эта теорема обеспечивает эффективный способ расчета напряжения и тока, протекающих через нагрузку, без необходимости заново пересчитывать всю схему.
• Фокус . Теорема Тевенина также предоставляет эффективный способ сосредоточить анализ на определенной части схемы. Это позволяет вам рассчитать напряжение и ток на конкретной клемме, упростив остальную часть схемы с помощью эквивалента Thevenin.

Например, посмотрите на схему ниже. Здесь у нас есть резистор R2 в качестве нагрузки. Мы хотим рассчитать напряжение и ток, протекающие через этот резистор, без необходимости использовать трудоемкий метод анализа, такой как ток ответвления, ток сетки и т. д., каждый раз, когда значение нагрузочного резистора изменяется.

(Источник изображения)

Чтобы упростить задачу, мы можем использовать теорему Тевенина для удаления сопротивления нагрузки и напряжения. Затем мы упрощаем остальную часть схемы, используя один источник напряжения и последовательное сопротивление. В этой упрощенной схеме Thevenin два резистора R1 и R3 вместе с вторичным напряжением B2 упрощены до единого источника напряжения и последовательного сопротивления. Что касается нагрузочного резистора, то упрощенное напряжение и сопротивление будут работать так же, как наша исходная схема. Теперь у нас есть только две простые переменные для расчетов.

(Источник изображения)

Теорема Тевенина в действии

Давайте рассмотрим пример схемы и рассчитаем ток, протекающий через нагрузочный резистор между двумя выводами. Процесс анализа цепи постоянного тока с использованием теоремы Тевенина требует следующих шагов:

1. Найдите сопротивление Thevenin, удалив все источники напряжения и нагрузочный резистор.
2. Найдите напряжение Thevenin, подключив напряжения.
3. Используйте сопротивление и напряжение Thevenin, чтобы найти ток, протекающий через нагрузку.

Вот пример схемы, с которой мы будем работать:

(Источник изображения)

Шаг 1. Сопротивление тевенину

Сначала нам нужно снять нагрузочный резистор 40 Ом, соединяющий клеммы A и B, вместе со всеми источниками напряжения. Это даст нам разомкнутую цепь при нулевом напряжении, в результате чего останутся только два резистора, соединенных последовательно.

(Источник изображения)

Чтобы рассчитать общую устойчивость к тевенину, мы можем использовать следующий процесс:

Шаг 2 – Напряжение Thevenin

Затем мы можем использовать закон Ома для расчета полного тока, протекающего через цепь, следующим образом:

Поскольку эти резисторы соединены последовательно, они будут иметь одинаковые 0,33 ампера. Мы можем использовать эти значения резисторов и наш ток для расчета падения напряжения, которое составляет:

Шаг 3 — Ток нагрузки

Теперь, когда у нас есть сопротивление и напряжение Thevenin, мы можем соединить нашу эквивалентную схему Thevenin с нашим исходным нагрузочным резистором, как показано ниже.

Отсюда мы можем использовать закон Ома для расчета полного тока, протекающего через нагрузочный резистор, следующим образом:

Готовы проверить свои навыки? Используйте теорему Тевенина, чтобы найти iload и vload для схемы ниже!

Запомните трехэтапный процесс:

1. Найдите сопротивление Thevenin, удалив все источники напряжения и нагрузку.
2. Найдите напряжение Тевенина, повторно подключив источники напряжения.
3. Используйте сопротивление и напряжение Thevenin, чтобы найти полный ток, протекающий через нагрузку.

Будь проще

Планируете спроектировать силовую цепь постоянного тока? Скорее всего, вы будете включать нагрузку, значение которой изменится во время анализа схемы.