Урок решения задач по теме «Закон Ома для участка цепи, последовательное и параллельное соединения»
Цель урока: Закрепить изученный материал путем решения задач.
Задачи:
Образовательные:
- Научить учащихся решать задачи на последовательное и параллельное соединение проводников;
- Углубить и расширить знания о данных видах соединения проводников;
- Научить определять силу тока, напряжение, сопротивление при последовательном и параллельном соедини проводников;
- Научить решать задачи на смешанное соединение проводников;
- Научить учащихся разбираться в схемах электрических цепей.
Воспитательные:
- Развить личные качества учащихся: аккуратность, внимание, усидчивость;
- Воспитывать культуру общения при работе в
группах.
Развивающие:
- Продолжить развитие навыков решения задач на данную тему;
- Продолжить развитие умений анализировать условия задач и ответов, умений делать выводы, обобщения;
- Продолжить развитие памяти, творческих способностей.
План урока
| № | Этап | Время | |
| Организационный момент | 2 мин | Словесный | |
| I | Актуализация знаний | 5 мин | Письменная работа в парах |
| II | Вводная часть | 2 мин | Слово учителя, опрос учащихся |
| III | Решение задач | 45-50 мин | Работа учителя, учащихся у доски |
| IV | Работа учащихся в группах | 20 мин | Групповой работы, устный, письменный |
| V | Итог урока | 1-2 мин | Словесный метод |
Оформление класса: Проектор с экраном, доска с
мелом.
Слайд 1 включен в начале урока. Урок начинается с физического диктанта.
I. Актуализация знаний.
На слайде физический диктант. (Слайд 2). Учащимся выдается таблица для заполнения.
1. Заполнить двенадцать ячеек таблицы на карточке:
| Ученый | Физическая величина | Формула | |
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| Выполнил ______________ Проверил __________ Оценка__________ | |||
2.
| Кол-во ошибок | 1 | 2-3 | 4-6 | 7 и более |
| Оценка | 5 | 4 | 3 | 2 |
II. Вводное слово.
Сегодня на уроке мы с вами будем решать задачи на закон Ома, на последовательное и параллельное соединение проводников. (Слайд 3).
Запишите тему урока. (Слайд 4).
Для этого вспомним формулы и законы, которые нам пригодятся при решении задач.
III. Решение задач.
(3 ученика выходят к доске и записывают:
первый закон Ома и выражает и него напряжение и
сопротивление; второй – формулы справедливые
для последовательного соединения; третий –
формулы справедливые для последовательного
соединения).
Задача 1. Для начала решим устную задачу на запоминание закона Ома. (Слайд 5)
a) U = 20B,R=10Om,I-?
б) I=10A,R = 5Om, R-?
Ответ: а) I = 2А; б) U= 50 Ом; в) R = 3 Ом.
Задача 2. (Решает учитель с использованием презентации) Слайд 6.
Рассчитать силу тока, проходящую по медному проводу длиной 100м, площадью поперечного сечения 0,5мм2, если к концам провода приложено напряжение 6,8B.
Дано:
I=100м
S=0,5мм2
U=6,8В
I-?
Решение:
Ответ: Сила тока равна 2А.
Вопросы: Что известно из условия
задачи? Какую величину необходимо определить? По
какому закону будем определять силу тока? Какие
величины нам неизвестны для нахождения силы тока
и как их найти? 
Теперь найдем
R и полученное значение подставим в формулу
для нахождения силы тока. (Перевод S в м2
не нужно делать, т.к. в единицах измерения
плотности тоже присутствуют тоже мм2)
Задача 3. (Решает у доски сильный ученик) Условия задачи Слайд 7.
В электрическую цепь включены последовательно резистор сопротивлением 5 Ом и две электрические лампы сопротивлением 500 Ом. Определите общее сопротивление проводника.
Дано:
RAB=5 Ом
RBC=500 Ом
RCD=500 Ом
RAD-?
Решение:
Ответ: Общее сопротивление проводника равно 1005 Ом.
Вопросы: Какие элементы цепи нам даны? Как найти общее сопротивление?
Задача 4. (Класс делится на 2
группы, каждая из которой решает задачу своим
способом (одни находя силу тока используя закон
Ома, вторые используя формулу параллельного
соединения).
Два резистора сопротивлением r 1 = 5 Ом и r2= 30 Ом включены, как показано на рисунке, к зажимам источника тока напряжением 6В. Найдите силу тока на всех участках цепи.
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ:
Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? Как найти I0? Что для этого неизвестно? Как найти I 1 и I2?
Второй способ решения данной задачи:
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех
участках цепи равна 1,4А.
Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? По какой формуле будем находить общий ток в цепи? Какая величина нам неизвестна при нахождении силы тока и как ее найти?
Задача 5. (Решает ученик, можно вызвать два ученика по очереди). Определите полное сопротивление цепи и токи в каждом проводнике, если проводники соединены так, как показано на рисунке, а r1=1 Ом, r2=2 Ом, r3= 3 Ом, UAC = 11В. Условие задачи Слайд 9.
Дано:
r1=1 Ом
r2=2 Ом
r3=3 Ом
UAB=11B
RAC-?
I1-?
I2-?
I3-?
Решение:
Ответ: RАС =2,2 Ом, I1=2A, I2=3
А, I3=2A.
Вопросы: Какие типы соединения изображены на рисунке? Что нужно определить? Как найти полное сопротивление и величины в него входящие? Как найти силу тока в цепи? Как определить I1 и 12? Как определить UBC?
Задача 6. Условия задачи Слайд 10. (Вопросы 1,2,5 решаются устно. 3,4 – два ученика).
- Какому значению силы тока и напряжения соответствует точка А?
- Какому значению силы тока и напряжения соответствует точка В?
- Найдите сопротивление в точке А и в точке В.
- Найдите по графику силу тока в проводнике при напряжении 8 В и вычислите сопротивление в этом случае.
- Какой вывод можно проделать по результатам задачи?
Ответ:
- Сила тока = 0,4 А, напряжение – 4В.
- Сила тока = 0,6 А, напряжение – 6В.
- Сопротивление в т.А – 10 Ом, в т.В – 10 Ом.
- Сила тока = 0,8А, сопротивление – 10 Ом.
- При изменении силы тока и напряжения на одинаковую величину, сопротивление остается постоянным.
IV. Самостоятельная работа в группах.
Учащиеся делятся на 4 группы и каждой группе дается карточка с заданием.
Учитель объясняет критерии выставления оценок:
Во время работы в группах ведется наблюдение за более и менее активными участниками группы. Соответственно это будет влиять на более или менее высокую оценку при проверке записей в тетради, также будет учитываться уровень сложности решенных задач. Тетради с записями сдаются в конце урока. Время для решения задач ограниченное.
Задание 1. Слайд 11. (8 мин.)
Вопросы к карточкам:
- Перечислите все элементы цепи.
- Какие виды соединения используются?
- Рассчитайте напряжение на лампе.
- Рассчитайте напряжение на реостате.
- Рассчитайте силу тока на всем участке цепи.
Задание 2. Слайд 12. (4 мин.)
Определить общее сопротивление в цепи.
R1 = 2 Ом, R2 = 102 Ом, R 3 = 15 Ом, R4 = 4 Ом.
Задание 3. Слайд 13. (3 мин.)
Определите силу тока I при заданных U и R.
| Группа | R, Ом | U, В | I, А |
| I | 2 | 55 | ? |
| II | 14,2 | 87,4 | ? |
| III | 21 | 100 | ? |
| IV | 0,16 | 0,28 | ? |
Задание 4.
Слайд 14. (5 мин)
Моток проволоки имеет сопротивление R и длину l .
Вычислить площадь поперечного сечения S.
| Группа | Материал | Параметры | ||
| Сопротивление | Длина проводника | Удельное сопротивление | ||
| R, Ом | l, мм2 | p, Ом·мм2/м | ||
| I | Медь | 0,83 | 33,9 | 1,7·10-2 |
| II | Алюминий | 16,1 | 83,1 | 2,8·10-2 |
| III | Серебро | 0,39 | 0,234 | 1,6·10-2 |
| IV | Сталь | 23,2 | 3,06 | 12·10-2 |
После выполнения заданий группами, тетради
сдаются учителю.
V. Итог урока.
На сегодня все. Мы с вами научились решать задачи на последовательное и параллельное соединение проводников, закрепили знания о законе Ома для участка цепи.
Домашнее задание. Повторить все формулы и физические величины.
Закон Кирхгофа для сложных цепей | ОРЕЛ
Закон Ома — ваш золотой билет для расчета напряжения, тока или сопротивления в простой последовательной или параллельной цепи, но что происходит, когда ваша цепь более сложная? Вы можете проектировать электронику, которая имеет как параллельное, так и последовательное сопротивление, и закон Ома начинает нарушаться. Или что, если у вас нет источника постоянного тока? В этих ситуациях, когда вы не можете использовать только V = IR, пришло время встать на плечи Ома и использовать закон Кирхгофа. Здесь мы рассмотрим, что такое закон Кирхгофа о цепях и как его использовать для анализа напряжения и тока в сложных электрических цепях.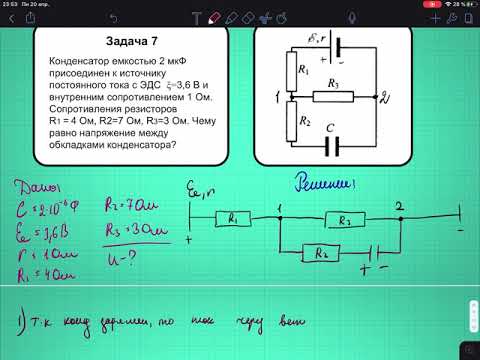
Что такое закон Кирхгофа?
Когда вы строите сложную схему, включающую мосты или тройники, вы не можете полагаться исключительно на закон Ома для определения напряжения или тока. Здесь пригодится закон Кирхгофа о цепях, который позволяет рассчитать как ток, так и напряжение для сложных цепей с помощью системы линейных уравнений. Есть два варианта закона Кирхгофа, в том числе:
- Закон тока Кирхгофа: Для анализа полного тока сложной цепи
- Закон Кирхгофа о напряжении : Для анализа полного напряжения сложной цепи
- Если объединить эти два закона, получится Закон Кирхгофа о цепях
Как и любой другой научный или математический закон, названный в честь его создателя, Закон Кирхгофа был изобретен немецким физиком Густавом Кирхгофом. Густав был известен многими достижениями при жизни, в том числе теорией спектрального анализа, которая доказала, что элементы излучают уникальный световой узор при нагревании.
Когда Кирхгоф и химик Роберт Бунзен проанализировали эти световые узоры через призму, они обнаружили, что каждый элемент в периодической таблице имеет свою уникальную длину волны. Открытие этой закономерности позволило дуэту открыть два новых элемента, цезий и рубидий.
Густав Кирхгоф (слева) и Роберт Бунзен (справа)
Позже Кирхгоф применил свою теорию спектрального анализа для изучения состава Солнца, где он обнаружил много темных линий в солнечном спектре длин волн. Это было вызвано тем, что солнечный газ поглощал световые волны определенной длины, и это открытие ознаменовало начало новой эры исследований и исследований в области астрономии.
Чуть ближе к дому в мире электроники Кирхгоф объявил свой свод законов для анализа тока и напряжения для электрических цепей в 1845 году, известный сегодня как Закон Кирхгофа о цепях. Эта работа основана на фундаменте, изложенном в законе Ома, и помогла проложить путь для анализа сложных цепей, на который мы полагаемся сегодня.
Первый закон – Текущий закон Кирхгофа
Закон тока Кирхгофа гласит, что количество тока, входящего в узел, равно количеству тока, выходящего из узла. Почему? Потому что, когда ток входит в узел, ему некуда идти, кроме выхода. То, что входит, должно выйти. Вы можете определить узел, в котором два или более пути соединены через общую точку. На схеме это будет точка соединения, соединяющая два пересекающихся сетевых соединения.
Взгляните на изображение ниже, чтобы наглядно понять этот Закон. Здесь у нас есть два тока, входящие в узел, и три тока, выходящие из узла. Согласно закону токов Кирхгофа отношение между этими токами, входящими в узел и выходящими из узла, можно представить как I 1 + I 2 = I 3 + I 4 + I 1 1 9.0101 90
Закон тока Кирхгофа, ток на входе должен равняться току на выходе. (Источник изображения)
Если сбалансировать это уравнение как алгебраическое выражение, то можно сделать вывод, что ток входа и выхода из узла всегда будет равен 0, или0010 3 + -I 4 + -I 5 ) = 0 Все должно уравновеситься, и Кирхгоф назвал этот принцип Сохранение заряда .
Давайте посмотрим на пример схемы, чтобы увидеть, как это работает. Ниже у нас есть схема с четырьмя узлами: A, C, E и F. Ток сначала течет от источника напряжения и разделяется в узле A, который затем течет через резисторы R1 и R2. Оттуда ток рекомбинирует в узле C и снова разделяется, чтобы течь через резисторы R3, R4 и R5 , где он встречается с узлом E и узлом F.
(Источник изображения)
Чтобы подтвердить действие закона тока Кирхгофа в этой цепи, нам необходимо предпринять следующие шаги:
- Расчет полного тока цепи
- Рассчитать ток, протекающий через каждый узел
- Сравните входной и выходной токи в определенных узлах, чтобы подтвердить закон Кирхгофа о токе.
1. Расчет общего тока
Здесь мы используем закон Ома, чтобы получить общий ток нашей цепи с I = В/Р . У нас уже есть общее напряжение 132 В, и теперь нам просто нужно найти общее сопротивление во всех наших узлах. Для этого требуется простой метод расчета общего сопротивления резисторов, соединенных параллельно, которое составляет:
Начиная с узла AC, мы получаем следующее сопротивление для параллельных резисторов R1 и R2:
И переходя к Node CEF, мы получаем следующее сопротивление для параллельных резисторов R3, R4 и R5:
Теперь у нас есть общее сопротивление 11 Ом для всей цепи, которое мы затем можем подставить в закон Ома I = V/R , чтобы получить полный ток в нашей цепи:
2.
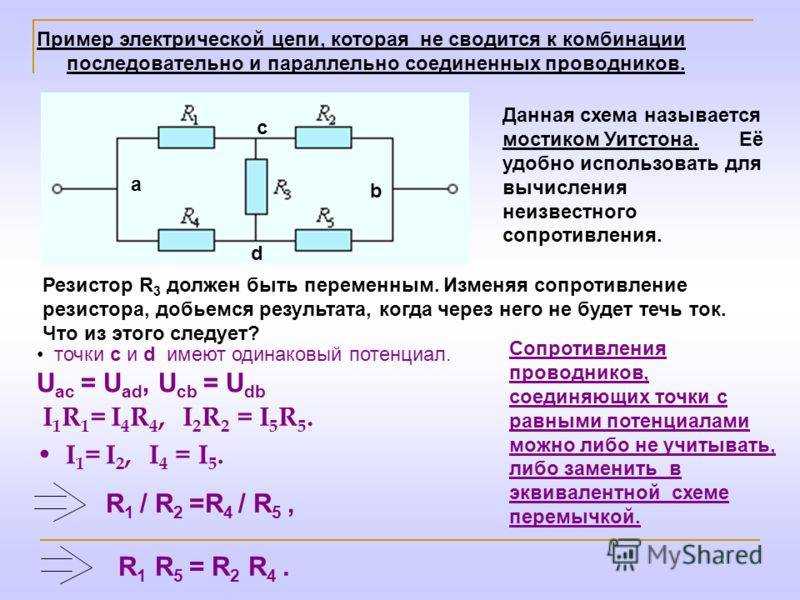Расчет узловых токовТеперь, когда мы знаем, что из нашей цепи вытекает 12 ампер, мы можем рассчитать ток в каждом наборе узлов. Мы снова воспользуемся законом Ома в виде I = V/R , чтобы получить ток для каждой ветви узла.
Во-первых, нам нужны напряжения для узловых ветвей AC и CF:
Затем мы можем рассчитать ток для каждой ветки узла:
3. Подтвердить действующий закон Кирхгофа
После расчета тока для каждой ветви узла у нас теперь есть две различные точки отсчета, которые мы можем использовать для сравнения наших входных и выходных токов. Это позволит нам проанализировать нашу схему и подтвердить закон тока Кирхгофа следующим образом:
Второй закон – закон напряжения Кирхгофа
Закон Кирхгофа о напряжении гласит, что в любой цепи с замкнутым контуром общее напряжение всегда будет равно сумме всех падений напряжения в контуре. Падение напряжения происходит всякий раз, когда ток протекает через пассивный компонент, такой как резистор, и Кирхгоф назвал этот закон Законом сохранения энергии .
Опять же, то, что входит, должно выйти.
Взгляните на изображение ниже, чтобы понять это визуально. В этой схеме у нас есть источник напряжения и четыре области в цепи, где напряжение будет встречаться с пассивной составляющей, что вызовет отчетливое падение напряжения.
Поскольку эти пассивные компоненты соединены последовательно, вы можете просто сложить общее падение напряжения и сравнить его с общим напряжением, чтобы получить соотношение, которое выглядит следующим образом:
Давайте начнем с простой схемы, чтобы продемонстрировать, как это работает. В приведенном ниже примере у нас есть две известные переменные: общее напряжение и падение напряжения на резисторе R1.
(Источник изображения)
Что нам нужно вычислить, так это падение напряжения на резисторе R2, и мы можем использовать закон Кирхгофа о напряжении, чтобы вычислить это со следующим соотношением:
Поскольку общее падение напряжения в цепи должно равняться общему напряжению источника, это обеспечивает простой способ вычисления отсутствующей переменной.
Если бы вы хотели выразить это соотношение в виде правильного алгебраического выражения, вы бы получили сумму всех падений напряжения и общее напряжение, равное нулю, как показано здесь:
Давайте посмотрим на другой пример. В схеме ниже у нас есть три резистора, соединенных последовательно с 12-вольтовой батареей.
Чтобы подтвердить закон Кирхгофа о напряжении в этой схеме, нам нужно предпринять следующие шаги:
- Рассчитать полное сопротивление цепи
- Рассчитать полный ток цепи
- Рассчитать ток через каждый резистор
- Рассчитайте падение напряжения на каждом резисторе .
Сравните источник напряжения с полным падением напряжения , чтобы подтвердить закон Кирхгофа о напряжении
1. Рассчитать общее сопротивление
Поскольку все наши резисторы соединены последовательно, мы можем легко найти общее сопротивление, просто сложив все значения сопротивления вместе:
2.
Рассчитать общий токТеперь, когда мы знаем наше общее сопротивление, мы можем снова использовать закон Ома, чтобы получить полный ток нашей цепи в виде I = V/R, , что выглядит так:
3. Рассчитайте ток через каждый резистор
Поскольку все наши резисторы соединены последовательно, через них будет протекать одинаковая величина тока, которую можно выразить как:
4. Рассчитайте падение напряжения на каждом резисторе
Наш окончательный расчет снова будет использовать закон Ома, чтобы получить общее падение напряжения для каждого резистора в виде В = IR , что выглядит следующим образом:
5. Проверка закона Кирхгофа о напряжении
Теперь у нас есть все необходимые данные, включая общее напряжение нашей схемы, а также каждое падение напряжения на каждом из наших резисторов. Собрав все это вместе, мы можем легко подтвердить закон Кирхгофа о напряжении с помощью этого соотношения:
Это также может быть выражено как:
Как видите, общее напряжение равно общему падению напряжения в нашей схеме.
То, что входит, должно выйти наружу, и закон Кирхгофа снова работает!
Процесс использования закона Кирхгофа о цепях
Теперь, когда вы понимаете, как работает закон Кирхгофа о цепях, у вас есть новый инструмент для анализа напряжения и тока в полных цепях. При использовании этих законов в дикой природе рассмотрите возможность использования следующего пошагового процесса:
- Во-первых, начните с маркировки всех известных напряжений и сопротивлений в вашей цепи.
- Затем назовите каждую ветвь вашей цепи текущей меткой, например I1, I2, I3 и т. д. Ветвь – это один или группа компонентов, соединенных между двумя узлами.
- Затем найдите закон тока Кирхгофа для каждого узла в вашей цепи.
- Затем найдите закон Кирхгофа для напряжения для каждого из независимых контуров вашей цепи.
После того, как вы рассчитали законы тока и напряжения Кирхгофа, вы можете использовать ваши уравнения, чтобы найти недостающие токи. Готовы попробовать сами? Взгляните на схему ниже и посмотрите, сможете ли вы проверить закон Кирхгофа для тока и закон напряжения с небольшой помощью Ома!
Дайте свои ответы в комментариях ниже!Стоя на плечах Ома
Имея в руках закон Кирхгофа о цепях, у вас теперь есть все инструменты, необходимые для анализа напряжения и тока в сложных цепях.
Как и многие другие научные и математические принципы, закон Кирхгофа стоит на плечах того, что было до него — закона Ома. Вы обнаружите, что используете закон Ома для расчета отдельных сопротивлений, напряжений или токов, а затем опираетесь на эти расчеты с помощью закона Кирхгофа, чтобы увидеть, соответствует ли ваша схема этим принципам тока и напряжения.
Готовы применить закон Кирхгофа в своем собственном проекте по разработке электроники? Попробуйте Autodesk EAGLE бесплатно уже сегодня!
Физика! Я могу рассчитать электрический ток, протекающий через сложную цепь, исходя из сопротивления и напряжения.
Физика Физика B Физика C
Кжж М.
спросил 25.03.21решите это и заполните таблицу ниже, укажите все шаги.
Особенно от того, как вы нашли напряжение, ток. Спасибо
| (Всего: 12 В, 3 А, 4 Ом) | Напряжение | Текущий | Сопротивление |
| Итого | 12 В | | |
| Р1 | | | 4 Ом |
| Р2 | | | 4 Ом |
| Р3 | | | 2 Ом |
Подписаться І 1
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Джонатан Д.
ответил 25.03.21
Репетитор
4.9 (18)
Репетитор средней школы по физике.
Смотрите таких репетиторов
Смотрите таких репетиторов
Закон Ома: V = I*R
Серия:
- R s = ∑R i
- I постоянная
- В делится на резисторы так, что V i = I*R i , где V = ∑V i
Параллельно:
- R p = (∑(1/R i )) -1
- В постоянное
- I делится на резисторы/ветви таким образом, что V = I i *R i и I = ∑I i
У нас есть комбинация параллельного и последовательного соединения. Значения для всей схемы уже указаны в вашей таблице, но давайте пройдемся по расчетам.
R 1 и R 2 соединены параллельно, и эта параллельная часть соединена последовательно с R 3 .
We first substitute the parallel part with a resistance R p = (1/R 1 + 1/R 2 ) -1 = 2 Ом
Общее сопротивление или эквивалентное сопротивление цепи тогда равно R = R p + R 3 = 4 Ом (последовательно).
Полный ток в цепи равен I = V/R = 3 A .
Давайте вернемся по нашим следам.
Имеем последовательную цепь с R p и R 3 с током I и напряжением V.
3 = I = 3 А
Напряжение делится на оба резистора R p и R 3 , которые имеют одинаковое значение,
, поэтому напряжение делится поровну: 3 = 6 В .
Если это не так, вы всегда можете рассчитать
В i = I*R i (в этом случае оба будут 3 А * 2 Ом = 6 В).
Еще один шаг назад, давайте посмотрим на параллельную часть схемы.
Теперь мы знаем, что напряжение на этой части V p = 6 В, а ток равен I p = 3 A.
В чисто параллельной цепи напряжение постоянно на всех резисторах, то есть В 1 = В 2 = 6 В. = I 2 = 1,5 А.
Опять же, если бы это было не так, вы всегда могли бы вычислить, используя закон Ома, I i = V p /R i для обоих это 6 В / 4 Ом = 1,5 А).
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
