подробный анализ и задачи —

Чтобы найти коэффициент при трение, нормальная реакция и трение участвуют в необходимых количествах. Но как найти коэффициент трения с учетом скорость и расстояние? 

Компания скорость расстояние способствуют возникновению трения между поверхностями. Влияние этих двух величин можно устранить. Зная скорость и расстояние, на которое перемещается объект, можно рассчитать коэффициент трения.

Как найти коэффициент трения с учетом скорости и расстояния, пройденного объектом

Чтобы найти коэффициент трения, указанный скорость и расстояние, рассмотрим объект массы m, движущийся со скоростью v на расстоянии d от исходного положения. Сила трения F_f замедляет движение объекта в направлении, противоположном движению. Нормальная реакция F_n действует перпендикулярно движению объекта. На движение объекта влияет сила тяжести g, что приводит к нормальной реакции.

Чтобы найти коэффициент трения с учетом скорости и расстояния

Мы можем найти коэффициент трения с учетом скорости и расстояния двумя способами. Давайте обсудим это по очереди.

Метод 1: учитывая работу, проделанную трением

Работа, проделанная трение по объекту дается

W = PE + KE + E_от 

Поскольку объект движется, запасенная потенциальная энергия равна нулю, а потеря энергии в процессе незначительна. Таким образом, проделанную работу можно переписать в виде

Где m — масса объекта, а v — скорость, с которой объект движется.

Эта медитация совершаемая работа равна силе трения сила, умноженная на расстояние, поэтому мы можем записать уравнение как

Сила трения, действующая на объект, определяется выражением

F_f = мкФ_n

Где µ — коэффициент трения, а F_n это нормальная реакция.

Нормальная реакция равна весу нетто объекта, определяемому F_n= мг

Таким образом, трение определяется уравнением

F_f = мкг… . . (2)

Поскольку два приведенных выше уравнения трения одинаковы, мы можем приравнять их

Переставляя уравнение, мы получаем,

Теперь рассмотрим, что изначально объект движется со скоростью v₀, со временем его скорость изменяется и, наконец, он движется со скоростью v_f пройдя расстояние d, коэффициент трения определяется выражением

Метод 2: Используя кинематику

Кинематическое уравнение движения для заданной скорости и расстояния:

v_f² = V₀² + 2 объявления

Где, v_f² — конечная скорость движущегося объекта.

v₀² — начальная скорость движущегося объекта.

a — ускорение, d — расстояние, пройденное объектом.

Здесь мы считаем, что объект движется с постоянная скорость так что конечная скорость vf2 становится равной нулю. Следовательно, мы можем изменить уравнение как

0 = в₀² + 2 объявления

-v₀² = 2 объявления

Согласно второму закону движения Ньютона, связь между ускорением и силой определяется выражением

F = m * a

Подставляя в приведенное выше уравнение, получаем

Сила, действующая на объект, не может иметь отрицательного значения. Мы можем принять величину уравнения как

Поскольку в данном случае мы рассмотрели силу, действующую на объект, равную сила трения так что подставляя формулу трения, мы получаем уравнение в виде

В общем случае уравнение можно записать как

При перестановке терминов получаем коэффициент трения в виде,

Понятно, что коэффициенты трения, полученные обоими методами, одинаковы. Используя приведенную выше формулу, мы можем найти коэффициент трения с учетом скорости и расстояния.

Решенные задачи о коэффициенте трения

Объект массой 2 кг движется со скоростью 12 мс.^-2сила трения, действующая на тело, заставляет объект остановиться на расстоянии 22 м. Найдите коэффициент трения и рассчитайте силу трения. Ускорение свободного падения g равно 10 мс.^-2.

Решение:

               Дано: Масса объекта m = 2 кг.

                            Скорость v = 13 мс^-2

                            Расстояние, пройденное объектом d = 22м

                            Ускорение свободного падения g = 10 мс^-2

Формула для определения коэффициента трения с учетом скорости и расстояния:

Подставляя значения данных членов в приведенное выше уравнение

µ = 0. 38

Формула для расчета трения:

F_f = мкг

F_f = 0.38 × 10 × 2

F_f = 7.68 н.

Найдите коэффициент трения при заданной скорости и расстоянии как 28 мс.^-2 и 34m соответственно и, следовательно, найти нормальную реакцию и силу трения. (Дано: масса объекта 4 кг. и ускорение свободного падения 10 мс.^-2).

Решение:

Скорость 17 мс.^-2

Расстояние, пройденное объектом, составляет 34 метра. 

Коэффициент трения для данной скорости и расстояния определяется формулой

Подставляя значения в выражение,

µ = 0.425

Нормальная реакция представлена ​​F_N = м * г

F_N = 4 × 10

F_N = 40 Н.

Сила трения, действующая на объект, равна F_f = мкФ_N

F_f = 0.425 × 40

F_f = 17 Н.

Тело массой 12 кг движется по шероховатой поверхности. Он прошел расстояние 72 метра, а затем его движению препятствовала сила трения 45 Н. Рассчитайте коэффициент трения и, следовательно, найдите скорость, с которой движется тело.

Решение:

Масса корпуса m = 12кг

Расстояние, пройденное телом d = 72м.

Сила трения, действующая на тело F_f = 45 Н

Ускорение свободного падения g = 9.8 мс^-2.

Коэффициент трения для данного трения определяется формулой

Подставляя значения в приведенное выше уравнение

µ = 0.382

Чтобы найти скорость, рассмотрим уравнение

Переставляя члены, мы получаем уравнение для скорости как,

v² = 2 мкгд

Подставляя значения

v² = 2 × 0.382 × 9.8 × 72

v² = 539.07

Извлекая квадратный корень, получаем

Скорость движения тела v = 23.21 мс.^-2.

Коэффициент трения 0.46, масса объекта 7 кг. Объект движется с постоянной скоростью 46 мс.^-2. Вычислите расстояние, пройденное объектом после того, как трение замедлит движение объекта.

Решение:

Коэффициент трения µ = 0.46

Масса объекта m = 7кг

Скорость объекта v = 16 мс^-2

Ускорение свободного падения g = 9.8 мс^-2

Изменение выражения

d = 28.39м.

Объект преодолевает расстояние 28.39 м, прежде чем прекращает движение.

Блок массой 5 ​​кг движется с начальной скоростью 12 мс.^-2. Через время t его скорость увеличивается на 19 мс.^-2 и преодолевает расстояние 33 м, затем его движение останавливается за счет трения. Найдите коэффициент трения с учетом скорости и расстояния и, следовательно, найдите трение, необходимое для остановки движения объекта.

Решение:

Начальная скорость объекта v₀ = 12 мс^-2

Конечная скорость объекта v_f = 19ms^-2

Расстояние, пройденное объектом d = 33м.

Масса объекта m = 5кг

Коэффициент трения для заданной начальной и конечной скорости определяется выражением

µ = 0.33

Трение, необходимое для остановки движения объекта, равно

F_f = мкг

F_f = 0.33 × 5 × 9.8

F_f = 16.17 Н.

Узнаем как найти коэффициент трения для разных видов трения?

Явление трения в жизни человека играет как положительную, так и отрицательную роль. С одной стороны, без его присутствия было бы невозможным движение, с другой же стороны, из-за трения происходят огромные потери энергии и рабочих материалов. В статье рассмотрим с точки зрения физики, что собой представляет трение, а также как найти коэффициент трения.

Явление трения

Трение — это контактное явление, которое возникает в зоне соприкосновения различных тел, и которое оказывает противодействие любому их взаимному движению.

В механике движения твердых тел выделяют три вида трения:

• действующее в покое;
• действующее во время скольжения поверхностей друг по другу;
• возникающее при качении тел.

Трение покоя возникает, когда мы прикладываем внешнюю касательную к поверхности силу к телу, чтобы сдвинуть его с места. Яркими примерами трения скольжения является скольжение лыж по снегу. Наконец, трение во время качения проявляет себя, когда колесо транспортного средства катится по дороге.

Формула для определения силы трения

В физике перечисленные виды трения описываются одной и той же формулой при расчете действующих сил. Эта формула имеет следующий вид:

Узнаем как находить коэффициент трения: экспериментальные…

Трение является тем физическим процессом, без которого не могло бы существовать само движение в…

F_t = µ * N.

Сила трения F_t равна произведению коэффицента трения µ на реакцию опоры N. При рассмотрении соответствующего вида трения меняется только значение коэффициента µ, который является величиной безразмерной.

В случае сил трения покоя и скольжения величина µ составляет порядка десятых долей единицы. Зависит µ от контактирующих материалов, от шероховатости их поверхности, и не зависит от площади контакта или скорости скольжения.

Для трения качения коэффициент µ (его принято обозначать C_R) зависит от характеристик упругости катящегося тела, от его твердости, от радиуса качения и некоторых других факторов. Для большинства материалов величина этого коэффициента для качения составляет сотые и тысячные доли от единицы.

Поскольку влияющих на величину µ факторов много, то определенной математической формулы для его расчета не существует. Отвечая на вопрос, как найти трения коэффициент, следует сказать, что его измеряют экспериментально.

Определение коэффициента µ

В этом пункте рассмотрим два способа практического определения величины µ на примере трения скольжения и покоя.

Первый способ, дающий ответ на вопрос, как найти коэффициент трения, заключается в помещении на горизонтальную плоскость бруска, к которому прикреплен динамометр. Брусок и плоскость изготовлены из исследуемой пары материалов, например, из стекла и дерева. Перемещая равномерно брусок, взявшись за динамометр, можно определить силу скольжения F_t. Зная массу m бруска, коэффициент µ рассчитывают так:

µ = F_t / (m * g).

Второй способ удобен для определения µ для трения покоя. Для этого необходимо поместить на горизонтальную плоскость брусок. Затем, следует медленно поднимать один конец плоскости, наклоняя ее на некоторый угол к горизонту. При определенном угле θ брусок начнет соскальзывать с поверхности. Измерив этот угол, коэффициент трения µ можно определить из равенства:

µ = tg(θ).

Измерение µ для трения качения предполагает использование более сложной установки, которая называется наклонным маятником. Расчет µ в этом случае выполняется при помощи исследования уравнений динамики движения.

Нахождение коэффициента трения покоя на склоне

спросил 6 лет, 10 месяцев назад

Изменено 4 года, 5 месяцев назад

Просмотрено 32к раз

$\begingroup$

Моя проблема

Блок массой 1,0 кг лежит на горизонтальной наклонной плоскости. Самолет наклоняется в блок и начинает скользить. Вы замечаете, что плоскость наклонена под углом 32 градуса над горизонталью, когда блок начинает скользить. Вычислите коэффициент статического трения, действующего между бруском и плоскостью.

Мое решение

Я попытался решить эту проблему, выполнив FgSinθ=μCosθ и преобразовав его в Sinθ/Cosθ=μ, что равно Tanθ=μ. Получается, что Tan(32)=0,62

Мой вопрос к вам

Но мой вопрос в том, что он уже движется под углом 32 градуса, поэтому я нахожу коэффициент КИНЕТИЧЕСКОГО трения так, как я это делал. Если да, то как мне найти коэффициент СТАТИЧЕСКОГО трения с учетом имеющейся у меня информации.

• трение

$\endgroup$

$\begingroup$

Вы нашли критический угол $\theta_c$, при котором блок начинает скользить. Это дает вам коэффициент статического трения $\mu_s = \tan\theta_c$. Кинетическое трение учитывается, когда блок действительно движется.

Прежде чем блок сможет двигаться, сила $mg\sin\theta$, действующая вниз по склону, должна быть как минимум равна максимально возможному значению силы трения покоя, которая равна $\mu_s mg\cos\theta$, действующей вверх по самолету. Когда блок только начинает двигаться под углом $\theta_c$, эти две силы равны:
$mg\sin\theta_c = \mu_s mg\cos\theta_c$
$\mu_s = \tan\theta_c$.

При движении скользящий блок может — и обычно делает — ускоряться вниз по склону, потому что кинетическое трение $\mu_k$ часто меньше статического трения $\mu_s = \tan\theta_c$. Скорость ускорения $a$ определяется как
$a = g\sin\theta_c — \mu_k g\cos\theta_c = (\tan\theta_c — \mu_k)g\cos\theta_c = (\mu_s — \mu_k) g\cos\theta_c.$

Если блок не ускоряется вниз по склону ($a=0$), а движется с постоянной скоростью, то $\mu_k = \mu_s = \tan\theta_c$. Если блок действительно ускоряется ($a\ne 0$), вы можете изменить это отношение, чтобы найти $\mu_k$.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

Коэффициент трения – Maths A-Level Revision

Трение – это «сопротивление, с которым объект сталкивается при движении по другому» (OED).

Проводить предметом по стеклу легче, чем наждачной бумагой. Причина этого в том, что наждачная бумага оказывает большее сопротивление трению. Во многих задачах предполагается, что поверхность «гладкая», то есть на нее не действует сила трения. Однако в реальной жизни это было бы не так. Шероховатая поверхность — это та, которая оказывает некоторое сопротивление трению.

Предельное равновесие

Представьте, что вы пытаетесь толкнуть пальцем книгу по столу. Если приложить очень маленькое усилие, книга не сдвинется. Это должно означать, что сила трения равна силе, с которой вы толкаете книгу. Если бы сила трения была меньше силы, создаваемой вашим пальцем, книга скользила бы вперед. Если бы он был больше, книга скользила бы назад.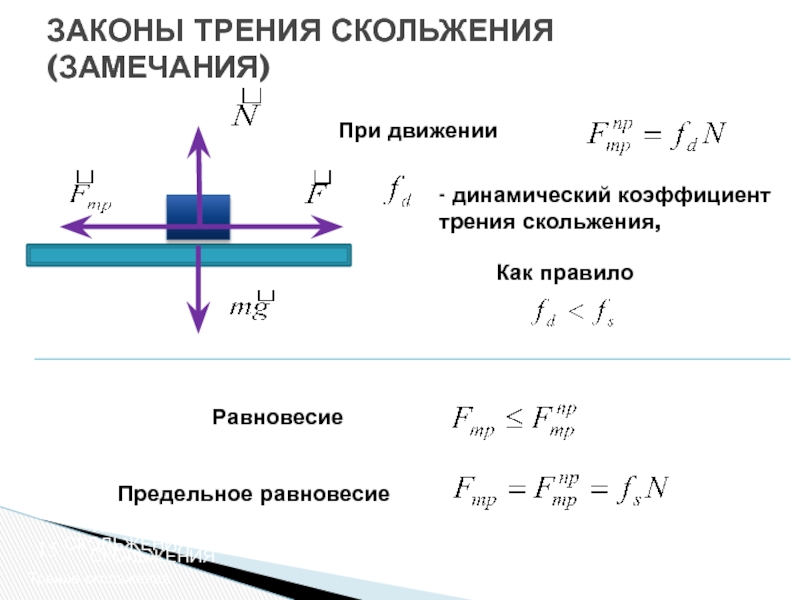

Если вы нажмете на книгу немного сильнее, она все равно останется неподвижной. Следовательно, сила трения должна была увеличиться, иначе книга сдвинулась бы. Если вы продолжите давить сильнее, в конце концов будет достигнута точка, когда сила трения перестанет увеличиваться. Когда сила трения достигает максимально возможного значения, говорят, что трение равно ограничение . Если трение ограничивает, но книга все еще неподвижна, говорят, что она находится в

предельном равновесии. Если вы нажмете немного сильнее, книга начнет двигаться. Если тело движется, трение будет принимать предельное значение.

Итого:

Сила трения между двумя объектами не постоянна, а увеличивается, пока не достигнет максимального значения. Когда сила трения максимальна, рассматриваемое тело либо движется, либо находится на грани движения.

Коэффициент трения

Коэффициент трения — это число, представляющее трение между двумя поверхностями.