Подробно расскажем как определить фазу и ноль индикаторной отверткой
При работе с бытовыми электросетями необходимо знать, как найти фазу и ноль. Привычные нам 220 вольт возникают не из ниоткуда.
Вся низковольтная сеть (имеется ввиду величина, для потребителей), является трехфазной. Напряжение между фазами переменное, 380 вольт.
Для бытовых нужд, используется напряжение 220 вольт. Чтобы не вдаваться в тригонометрические подробности построения трех фаз, достаточно знать формулу: напряжение между фазой и нулем равно напряжению между фазами, разделенное на квадратный корень числа Пи. То есть если между фазами 380 вольт, то напряжение между фазой и нулем будет 380/1,73 = 220 вольт.
Для чего необходимо знать, где ноль, а где фаза?
Многие пользователи бытовых приборов полагают, что нет разницы, как подключать электроприборы к переменной сети 220 вольт. Полярности нет, напряжение не меняется при смене контактов. Это верно с точки зрения простого включения в розетку.
А если вы самостоятельно делаете разводку или ремонт электросети в своем доме, необходимо точно знать, где ноль, а где фаза.
- При проектировании электрощитов, автоматы применяются одноконтактные. На них заводится только фаза. Нулевая линейка остается не размыкаемой. Каждая линия подключается одним проводом к фазе через выключатель, и к нулевой линейке напрямую;
- Приборы освещения питаются стандартным способом, при помощи однофазных выключателей. Размыкается только фазный провод, нулевой всегда подключен к световому прибору. Если перепутать ноль и фазу, простая замена лампочки может привести к поражению электрическим током.
Важно! Если перепутать ноль и фазу при таком подключении – пользоваться сетью будет опасно для жизни.
Поэтому необходимо отслеживать фазный и нулевой провод по цепочке от счетчика до каждого потребителя.
Несколько способов как определить фазу и ноль
Способ №1, при помощи тестера способного измерять напряжение до 1000 вольт.
Это надежный способ, но для проверки необходимо иметь качественно подключенный провод заземления. В квартирах старой проектировки его нет.
При наличии такой точки подключения, просто производится замер напряжения между гарантированной «землей» и тестируемым контактом. Там, где прибор покажет 220 вольт – находится фаза.
Способ №2.
Если подключить к фазному контакту измерительный провод, соединенный с мультиметром (разъем – измерение напряжения), на цифровом табло появится значение 8-15 вольт.
Важно! Второй измерительный кабель должен быть подключен к разъему COM, предел измерений 500 или 1000 вольт. Нулевой контакт не покажет никакого значения.
Индикаторной отверткой.
Для проверки не требуется наличие внешней «земли». Отвертка тестер показывает фазу автономно, при касании одного провода.
Первые два способа не гарантируют точного измерения, поэтому пользоваться ими можно лишь когда иные способы недоступны. На третьем (надежном) способе остановимся подробнее.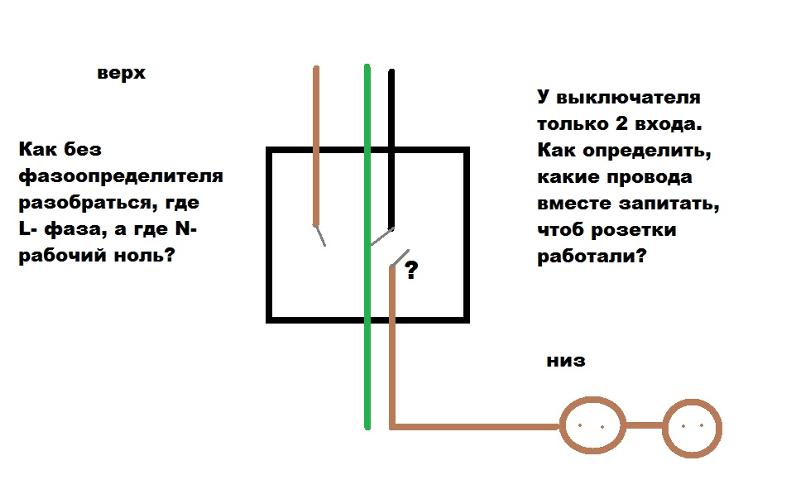
Как работает отвертка индикатор
В любом магазине электротоваров можно приобрести тестер фазы. Однако не все знают, как пользоваться индикаторной отверткой.
Существует несколько видов индикаторов. Есть отличия по форме исполнения, по принципу действия, но все они предназначены для определения фазного провода при подключении к одному контакту. Разберем устройство индикаторной отвертки:
Отвертка индикатор с неоновой лампой.
Самая распространенная конструкция. Состоит из токопроводящего металлического стержня, оканчивающегося плоским жалом (как обычная отвертка), резистора для безопасности оператора и неоновой лампы. Лампа прижимается к резистору с помощью пружины.
Для работы необходимо создать разомкнутую цепь: фазный провод (контакт), внутренняя схема отвертки, тело человека, которое обладает определенным сопротивлением.
При касании одновременно рабочим жалом фазного контакта и пальцем контакта на рукоятке, неоновая лампа начинает устойчиво светиться.
При отсутствии фазного напряжения лампа гаснет.
Преимущество такой схемы – простота изготовления и дешевизна. Недостаток – диапазон напряжения, с которым работает индикатор, от 90 до 380 вольт. К тому же, определить фазный провод можно только при непосредственном электрическом контакте.
Многофункциональная индикаторная отвертка со светодиодным сигнализатором.
Для питания светодиода напрямую, силы тока, которую может сгенерировать традиционная схема недостаточно. Поэтому в рассматриваемом индикаторе применен так называемый «трансформатор времени». Светодиод работает в импульсном режиме. Во сколько раз уменьшается время непрерывного свечения, во столько же раз увеличивается сила тока, протекающая через диод.
Через ограничительный резистор, рабочий щуп подключен к разнополярному контакту диодного моста-выпрямителя. Второй контакт выведен на рукоятку индикатора для касания пальцем. Возникший на полярных контактах выпрямителя небольшой постоянный ток, подается на накопительный конденсатор.
Далее вступает в работу лавинный транзистор К101КТ1, включенный по инверсной схеме. В результате на светодиод подается пульсирующий ток. Мерцание не влияет на восприятие органами зрения человека.
Отвертка с индикатором напряжения, выполненная по такой схеме, может определить фазу уже при напряжении 45 вольт. К тому же, если вместо щупа подключить небольшую антенну – можно бесконтактно обнаружить переменное электрическое поле.
Полезная информация! Как найти проводку в стене индикаторной отверткой? Используя подобное устройство, вы без труда обнаружите фазный провод под слоем штукатурки.
В качестве антенны для поиска используется длинное жало отвертки. Обнаружить рассеянное поле таким способом не удастся, а наводку вокруг электрокабеля в стене – запросто!
Недостаток такой схемы – иногда паразитные наводки мешают основной работе – контактному поиску фазы.
Рассмотренная выше схема эффективна, но сложна в изготовлении.
Поэтому стоимость ее достаточно высока. Если не нужна функция поиска скрытой проводки – рассмотрим, как работает индикаторная отвертка на светодиоде, собранная по упрощенной схеме.
Тело человека является достаточно емким конденсатором. При касании пальцем сенсора, в цепи возникает электрический ток порядка 0,5 мкА. Если одновременно коснуться жалом отвертки фазного провода – сила тока увеличится до величины, способной открыть транзистор. Питающий элемент подключается к светодиоду, он начинает светиться.
Такая отвертка имеет низкую стоимость и хорошую надежность. Напряжение срабатывания – порядка 50 вольт. Наличие элементов питания позволяет снизить чувствительность. Поэтому ложных срабатываний от наводок электрическим полем у этого индикатора не бывает. Недостаток – индикатор такого типа не в состоянии обнаружить скрытую проводку.
Важно! Мы рассмотрели технологию, как определить фазу и ноль индикаторной отверткой. Поскольку работы проводятся с высоким напряжением, надо знать, как безопасно пользоваться пробником.
Главные правила:
- ваша обувь должна быть с резиновой подошвой;
- руки должны быть сухими;
- пробник удерживается одной рукой.
Как определить фазу и ноль
Задача монтажа для профессионалов является легкой, но для обычных людей она может быть сложной. Несмотря на это, поиск нуля и фазы не является сложным процессом и имеет несколько методов определения.
Проведение ремонтных работ в любом помещении, важным моментом является оснащение этого помещения электричеством. Помимо электропроводки, не стоит забывать о необходимости установки розеток и выключателей, при помощи которых будет происходить регулирование освещения. Тут достаточно важным моментом будет определение фазы, нуля и заземляющего проводника системы.
Следует понимать, что проводка в квартире обычно имеет напряжение в 220В, поскольку она предусматривает подключение к нулевому проводнику и к одной из фаз. При этом обязательным является заземление, что делает электрификацию помещения безопасной для обитателей.
Чтобы уловить принцип нахождения фазы и нуля в сети, следует для начала определить для себя, что означают данные термины, которые для простого обывателя могут звучать как совершенно непонятные понятия. Любая система, независимо от ее протяженности, состоит из трех фаз, причем касается также и низковольтных линей, задачей которых является питание жилых домов.
Между двумя любыми фазами возникает линейное напряжение, составляющее 380В. Однако напряжение бытовой сети составляет 220В, главной задачей является появление требуемого для сети напряжения. Для этой цели в любой сети присутствует нулевой провод, которой в сочетании с любой фазой образует разность потенциалов в 200В, которая и будет представлять собой фазное напряжение.
Нулем в электрической цепи называется проводник, который соединяется с контуром земли и используется для создания нагрузки от фазы. Фаза эта подключена к противоположному концу обмотки на ТП. Таким образом, в стандартной розетке, для наглядности, один вход принимается за фазу, а второй за ноль.
Если говорить более простым языком, то фаза представляет собой провод, по которому поступает ток. По нулевому проводу ток возвращается обратно к источнику. В зависимости от количества фаз, система имеет несколько проводов. Допустим, в трехфазовой цепи имеются три фазовых провода и один обратный, нулевой.
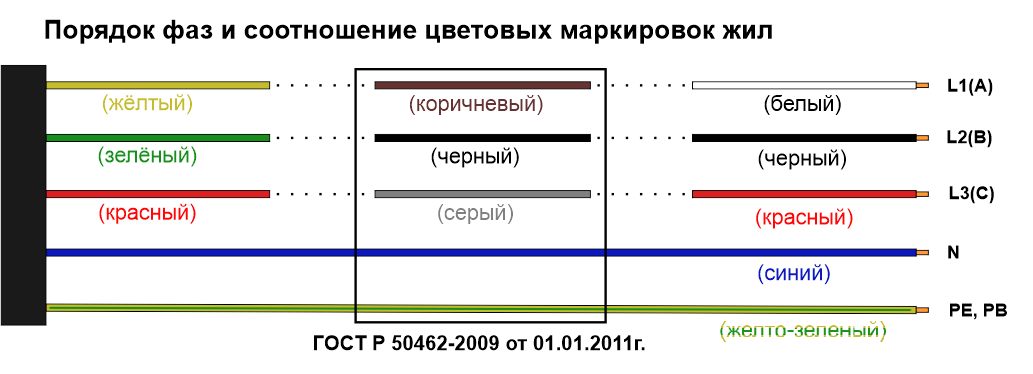
Цветовое обозначение. Не редко многих интересует вопрос, какого цвета провода фаза ноль земля, как определить, где какой провод, часто предоставляется возможным при помощи используемых в электрике цветовых разграничений. Однако сработает данный метод только в случае, если проводка действительно выполнена по всем правилам. Изоляция нулевого провода обычно обозначается синим или голубым цветом, земля сочетает в себе сразу две окраски – зеленую и желтую. Провод фазы по правилам обозначается в коричневый, белый или черный цвет.
Обозначение фазы и нуля буквы
Кроме того, свое обозначение имеет и заземление, обозначать которое принято буквой “G”.Для нахождение фазы и нуля в сети можно использовать различные инструменты. Наиболее удачным изобретением в помощь начинающим электрикам считается индикаторная отвертка, имеющая специальные чувствительные элементы и индикатор-отражатель.
Осуществлять проверку фазу и нуля в сети при помощи отвертки проще простого. Отвертку следует зажать между большим и средним пальцем. Касаться неизолированной части жала отвертки не разрешается. Палец указательный следует поставить на металлический круглый выступ в конце рукоятки.
Далее жало прикладывают к оголенным концам проводов. В том случае, если произошло касание с фазным проводником, в отвертке загорается соответствующий светодиод.
Определить принцип действия индикаторной отвертки нетрудно, внутри нее расположена специальная лампа, а также резистор, представляющий собой сопротивление. Лампа загорается, если замыкается цепь. Благодаря сопротивлению, можно не бояться поражения током во время проверки, поскольку оно снимает его значение до минимального показателя.
Найти ноль такой отверткой, соответственно, не получится. Кроме того, подобный способ нередко дает сбой из-за не слишком хорошей чувствительности. В итоге индикаторная отвертка, реагируя на наводки, может выдать напряжение там, где его совершенно нет.
Помимо применения индикаторной отвертки, возможным является использование мультиметра, который также позволит определить токонесущие провода в сети. Обязательным условием для его использования является предварительная зачистка проводов.
На приборе перед использованием требуется установить значение предела измерения переменного тока, величина которого должна превышать 220В. Ориентироваться также следует по маркировке гнезд, куда включены щупы прибора. Для данного типа проверки потребуется щуп, включенный в гнездо с маркировкой «V».
Сама проверка заключается в прикосновении щупа к одному из проводов, следя при этом за показаниями прибора.
Если мультиметр идентифицирует какое либо напряжение, то данный провод является фазным. Если другой провод покажет нулевое значение, то это, соответственно, нулевой провод.
Прибор для работы может использоваться любого типа – стрелочный или с цифровым индикатором. В любом случае, важным моментом будет соблюдение мер безопасности, а также правильная индикация прибором показаний с проводов. Точность этого прибора обычно выше индикаторной отвертки.
Главным правилом при использовании мультиметра является запрет на одновременное касание фазного провода и заземляющего контура. Такая халатность может привести к короткому замыканию и, как следствие, к травматическим ожогам.
Несмотря на столь широкое распространение приборных способов определения фазы и нуля в сети, далеко не всегда под рукой может оказаться нужное устройство, которое позволит сделать верное заключение. При этом неправильное выявление проводов в сети «на глаз» может привести к достаточно опасным последствиям.
Первый метод, позволяющий справиться с данной задачей, был описан в одном из разделов выше.
Заключается он в нахождении проводов, в зависимости от цвета их изоляции, а также от маркировки. Однако это окажется верным только в том случае, если проводка была выполнена по всем правилам.
Второй способ определить их – это сделать так называемую контрольную лампочку, применяя при этом подручные средства. Для этого потребуется простая лампа накаливания и два отрезка провода, длиной примерно 50 сантиметров. Жилы проводов следует присоединить к лампочке, при этом вторым концом одного из проводов следует прикоснуться к трубам отопления (зачищенным), а вторым прикоснуться к «прозваниваемым» проводам. Тот провод, при прикосновении к которому загорается лампочка, является фазным.
Стоит обратить внимание, что описанный способ является очень опасным и может привести к поражению током во время его использования. Ни в коем случае не рекомендуется применять его в случае наличия предельного напряжения в сети, а также нельзя касаться оголенных проводов.
Альтернативной лампочки накаливания может стать лампочка неоновая, которая позволит найти полярность системы.
В заключении следует отметить, что ответ на вопрос «как определить фазу и ноль» имеет несколько решений. А именно: индикаторной отверткой, мультиметром, а также можно без приборов. Все зависит от возможностей и наличия приборов под рукой. Обязательным является соблюдение всех мер безопасности при работе с электричеством.
Амплитуда, период и фазовый сдвиг
Вы должны знать, что
три слагаемых: амплитуда, период и
среднее значение фазового сдвига,
в контексте обобщенных синусоидальных и косинусоидальных кривых, показанных ниже:
Как обсуждается ниже,
учитывая любую обобщенную кривую синуса или косинуса,
, вы должны быть в состоянии
определить его амплитуду, период и фазовый сдвиг.
Пример вопроса:
Укажите амплитуду, период и фазовый сдвиг $\,y = 5\sin(3x-1)\,.$
В следующем разделе вы напишете
уравнение кривой с заданными амплитудой, периодом и фазовым сдвигом.
Пример вопроса:
Напишите уравнение синусоиды с амплитудой $\,5\,$, периодом $\,3\,$ и фазовым сдвигом $\,2\,.$
Краткое изложение основных понятий
АМПЛИТУД:
| |
ПЕРИОД:
| |
ФАЗОВЫЙ СДВИГ:
|
) 
$
Если $\,а
Периодические функции и
Период периодической функции.
$
Затем применяется горизонтальное растяжение/сжатие, которое снова перемещает точку.
В этом случае в формулу фазового сдвига входят как $\,B\,$, так и $\,k\,.$
$
Учитывая обобщенную синусоидальную/косинусную кривую:
найти амплитуду, период и фазовый сдвиг
ПРИМЕР:
Укажите амплитуду, период и фазовый сдвиг $\,y = 5\sin(3x-1)\,.$
РЕШЕНИЕ:
| Аргумент имеет вид $\,kx + B\,.$ Выражение имеет вид $\,a\sin(kx+B)\,.$ Здесь $\,a = 5\,$ $\,k = 3\,$ и $\,B = -1\,.$ Амплитуда $\,|a| = |5| = 5\,.$ Период $\,\displaystyle\frac{2\pi}{|k|} = \frac{2\pi}{3}\,.$ Установка $\,3x-1 = 0\,$ дает $\,\displaystyle x = \frac{1}{3}\,$;
фазовый сдвиг равен $\,\displaystyle\frac{1}{3}\,. Альтернативный фазовый сдвиг: $\,\displaystyle\frac{-B}{k} = \frac{-(-1)}3 = \frac{1}{3}\,$ |
$ ПРИМЕР:
Укажите амплитуду, период и фазовый сдвиг $\displaystyle\,y = -3\cos 2(x+\frac{\pi}{5})\,.$
РЕШЕНИЕ:
| Аргумент имеет вид $\,k(x + b)\,.$ Выражение имеет вид $\,a\cos k(x + b)\,.$ Здесь $\,a = -3\,$ $\,k = 2\,$ и $\displaystyle\,b = \frac{\pi}{5}\,.$ Амплитуда $\,|a| = |-3| = 3\,.$ Период $\,\displaystyle\frac{2\pi}{|k|} = \frac{2\pi}{2} = \pi\,.$ Установка $\displaystyle\,2(x+\frac{\pi}{5}) = 0\,$ дает $\,\displaystyle x = -\frac{\pi}{5}\,$;
фазовый сдвиг равен $\,\displaystyle -\frac{\pi}{5}\,. Альтернативный фазовый сдвиг: $\displaystyle\,-b = -\frac{\pi}{5}\,$ |
$Фазовый угол: определение, формула и символ
Знаете ли вы, что могут быть две точные волны, разница между которыми лишь в том, что одна из них смещена от определенной точки отсчета? Волна — это пространственный и временной процесс, в котором переносится энергия. Периодическая волна — это волна, которая повторяется в зависимости от положения и времени. Математически периодические волны используются для описания колебаний и простого гармонического движения, которое описывает движение систем пружина-масса. Этот тип волны описывается двумя характеристиками: величиной и фазой. В этой статье мы обсудим понятие фазового угла в периодической волне.
Фазовый угол
В предыдущих статьях мы обсуждали дифференциальное уравнение, описывающее колебательное движение, особенно простое гармоническое движение.
Мы знаем, что решение, удовлетворяющее уравнению, выражается как
$$x=A\sin\left(\omega t+\phi_0\right).$$
Где \(A\) — амплитуда в метрах \(( \mathrm m)\), \(\omega\) — угловая частота в радианах в секунду \((\frac{\mathrm{rad}}{\mathrm s})\), а \(\phi_0\) — начальная фаза в радианах \((\mathrm{rad})\).
Фазовый угол — это угловая составляющая периодической волны, которая определяется как аргумент синусоидальной функции \(\omega t+\phi_0\). Выбирая \(\phi_0\), мы указываем начальную позицию колеблющегося объекта , чтобы убедиться, что у нас есть правильное уравнение с позицией осциллятора, независимо от того, где он мог быть расположен в точке \(t=0\). Мы можем переформулировать приведенное выше уравнение в терминах символа \(\phi\) для фазового угла.
$$\begin{align*}\phi&=\omega t+\phi_0,\\x&=A\sin\left(\phi\right).\end{align*}$$ 9{-1}\left(\frac{x_0}A\right),$$
где \(A\) — амплитуда в метрах, \((\mathrm m)\) и \(x_0\) — начальная положение объекта в точке \(t=0\) в метрах \((\mathrm m)\).
Простой гармонический осциллятор имеет амплитуду \(3,0\;\mathrm{см}\) и частоту \(4,0\;\mathrm{Гц}\). В момент времени \(t=0\) его положение равно \(y=3.0\;\mathrm{см}\). Где он находится в момент времени \(t=0.3\;\mathrm s\)?
Амплитуда равна \(A=0,03\;\mathrm м\), а угловая частота равна \(\omega=2\pi f=2\pi(4,0\;\mathrm{Гц})=8\pi\ {\ textstyle \ frac {\ mathrm {rad}} {\ mathrm s}} \). Теперь мы можем определить начальную фазу, 9{-1}\left(\frac{0.03\;\mathrm m}{0.03\;\mathrm m}\right),\\\phi_0&=\frac\pi2.\end{align*}
Теперь мы знаем положение осциллятора в любой момент времени,
$$y(t)=0.03\sin\left(8\pi t+\frac\pi2\right).$$
Мы можем найти положение осциллятора во время \(t=0,3\;\mathrm s\),
\begin{align*}y(0,3\;\mathrm s)&=(0,03\;\mathrm m)\sin\left((8\ пи \; {\ textstyle \ frac {\ mathrm {rad}} {\ mathrm s}}) (0,3 \; \ mathrm s) \; + \; \ frac \ pi2 \; \ mathrm {rad} \ right), \\y(0,3\;\mathrm с)&=0,0093\;m.\end{align*}
Положение осциллятора задается уравнением:
$$y=(0.
04\;\mathrm m)\sin\left((6\pi\;{ \textstyle\frac{\mathrm{rad}}{\mathrm s}})t-\frac\pi2\;\mathrm{rad}\;\right).$$
Где находится осциллятор в момент времени \(t =0\)?
\begin{align*}y(0\;\mathrm s)&=(0,04\;\mathrm m)\sin\left((6\pi\;{\textstyle\frac{\mathrm{rad}} {\mathrm s}})(0\;\mathrm s)-\frac\pi2\;\mathrm{rad}\;\right),\\y(0\;\mathrm s)&=-0,04\; \mathrm m.\end{align*}
Начальная фаза определяет, используется ли функция синуса или косинуса для описания положения колеблющегося объекта. Например, если \(\phi_0=\frac\pi2\) мы можем использовать функцию косинуса вместо функции синуса с начальной фазой. Это связано с тригонометрическим тождеством \(\sin\left(\frac\pi2+\theta\right)=\cos\left(\theta\right)\). В приведенной ниже таблице поясняется, как два выражения дают одинаковые результаты в любое время.
Уравнение | \(t=0\) | \(t=\frac\pi{2\omega}\) |
\(\sin\left(\omega t+\;\frac\pi2 \ справа) \) | 1 | |
\ (\ cos \ lef (\ omega t \ rugh фазовый угол играет очень важную роль в экспериментальной физике, особенно в электронике, где существует прямая связь между напряжением и синусоидальными функциями. Понимание начальной фазы на графикеМы рассмотрели теоретическое определение фазового угла и начальной фазы. Как мы понимаем влияние изменения начальной фазы синусоидальной функции? Легче понять, если мы на самом деле представляем синусоидальные функции на графике. Рис. 1. Различные примеры начальных фаз для визуализации влияния регулировки начальной фазы на синусоидальную функцию. На изображении выше мы видим, что при начальном значении \(x=0\), \(f(0)=\sin\left(0\right)=0\). Для той же синусоидальной функции с начальной фазой \(\phi_0=\frac{-\pi}4\), \(f(0)=\sin\left(0-\frac\pi4\right)=-\frac {\sqrt2}2\) и \(f(\frac\pi4)=\sin\left(\frac\pi4-\frac\pi4\right)=0\). Мы замечаем, что функция синуса сместилась по горизонтали вправо на величину \(\frac\pi4\). Если мы изменим начальную фазу на \(\phi_0=-\pi\), мы заметим, что функция синуса сдвинется вправо на величину \(\pi\). Рис. 2 — Синусоидальная функция: случай, когда начальная фаза равна нулю. Рис. 3 – Влияние положительной начальной фазы на синусоидальную функцию. Рис. 4 – Влияние отрицательной начальной фазы на синусоидальную функцию. Фазовый угол — основные выводы
|
В электронике фазовый угол относится к угловому смещению между формами сигналов напряжения и тока в цепи переменного тока.
Здесь мы замечаем закономерность: отрицательная начальная фаза сдвинет функцию по горизонтали вправо, а положительная начальная фаза сдвинет функцию по горизонтали влево. Наглядно это представлено на рисунке ниже.
