Формула емкостного сопротивления конденсатора в цепи переменного тока
Содержание
- Емкостное сопротивление конденсатора
- Емкостное сопротивление конденсатора
- Характеристики прибора
- Фазор
- Примеры решения задач
- Сопротивление конденсатора переменному напряжению
- Векторная диаграмма токов в цепи с конденсатором
- О заряде конденсатора.
- До какого напряжения заряжается конденсатор?
- О заряде конденсатора.
- До какого напряжения заряжается конденсатор?
- О реальном конденсаторе
- Емкостное сопротивление в цепи переменного тока
- Емкость в цепи переменного тока
- Сопротивление конденсатора.
- Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?
- О реальном конденсаторе
- Соединение конденсаторов
- Последовательное соединение ёмкостей
- Параллельное соединение
Емкостное сопротивление конденсатора
Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
Емкостное сопротивление можно отнести к реактивному, не вызывающему безвозвратных энергетических потерь. Зарядка конденсатора происходит до того уровня напряжения, которое отдается источником питания.
Совершенно по-другому на конденсатор воздействует переменный ток, вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.
В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех. Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Емкостное сопротивление конденсатора
Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
Существуют качества, присущие только конденсаторам. Например, они совершенно не пропускают через себя постоянный ток, хотя и заряжаются от него. После полной зарядки емкости, течение тока полностью прекращается, а внутреннее сопротивление устройства принимает бесконечно высокое значение.
Совершенно по-другому на конденсатор воздействует , вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.
В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех.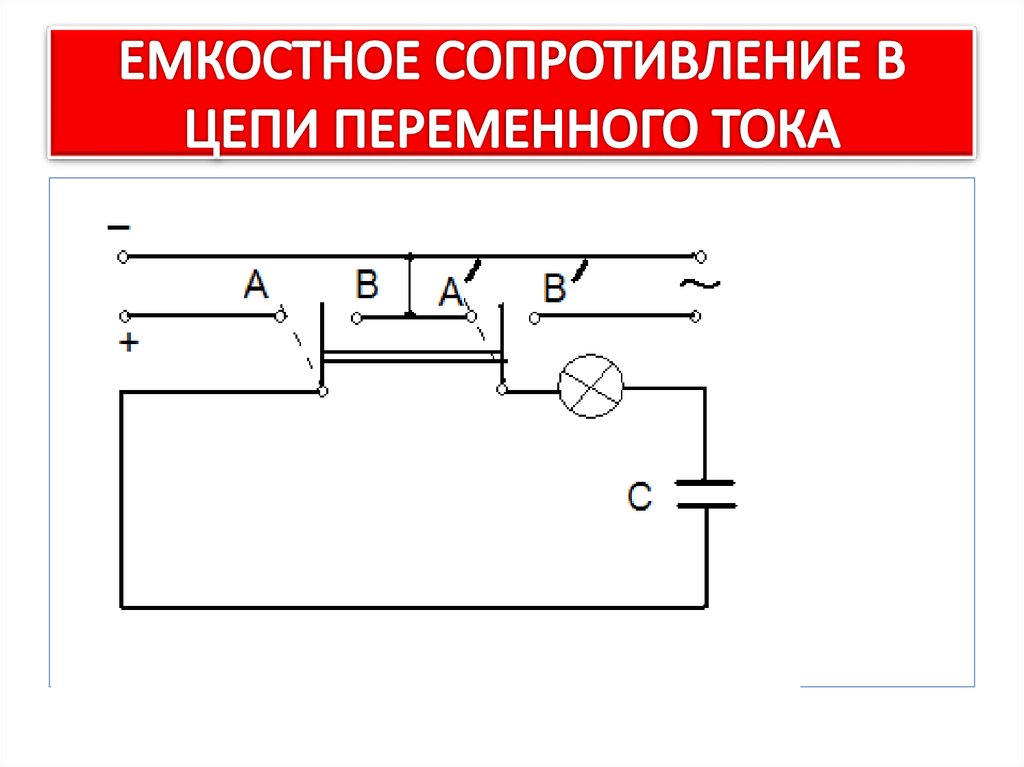 Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Фазор
Благодаря фазовым векторам сложный и меняющийся во времени сигнал можно представить в виде комплексного числа (не зависит от времени) и сложного сигнала (зависит от времени). Фазоры делятся на основе А (амплитуды), v (частоты) и θ (фазы). Это приносит большую пользу, ведь частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В подобных ситуациях факторы исключают факультативную характеристику и основываются лишь на A и θ.
К примеру, можно представить A⋅cos (2πνt + θ) просто как комплексную постоянную Aeiθ. Из-за того, что фазовые векторы передаются величиной и углом, наглядно изображаются вектором в плоскости x-y.
Фазор можно рассматривать с позиции вектора, вращающегося вокруг начала координат. Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0
Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0
Примеры решения задач
ПРИМЕР 1
| Задание | Колебательный контур имеет сопротивление (R), катушку индуктивности (L) и конденсатор емкости C (рис.1). К нему подключено внешнее напряжение, амплитуда которого равна , а частота составляет . Какова амплитуда силы тока в цепи? |
| Решение | Сопротивление контура рис.1 складывается из активного сопротивления R, емкостного сопротивления конденсатора и сопротивления катушки индуктивности . Полное сопротивление цепи (Z), которая содержит названные выше элементы, находят как: Закон Ома для нашего участка цепи можно записать как: Выразим искомую амплитуду силы тока из (1.2), подставим вместо Z правую часть формулы (1.1), имеем: |
| Ответ |
Сопротивление конденсатора переменному напряжению
При включении конденсатора в цепь с переменным током, ток свободно проходит через конденсатор. Это объясняется очень просто: происходит процесс постоянной зарядки и разрядки конденсатора. При этом говорят, что в цепи присутствует емкостное сопротивление конденсатора, помимо активного сопротивления.
Это объясняется очень просто: происходит процесс постоянной зарядки и разрядки конденсатора. При этом говорят, что в цепи присутствует емкостное сопротивление конденсатора, помимо активного сопротивления.
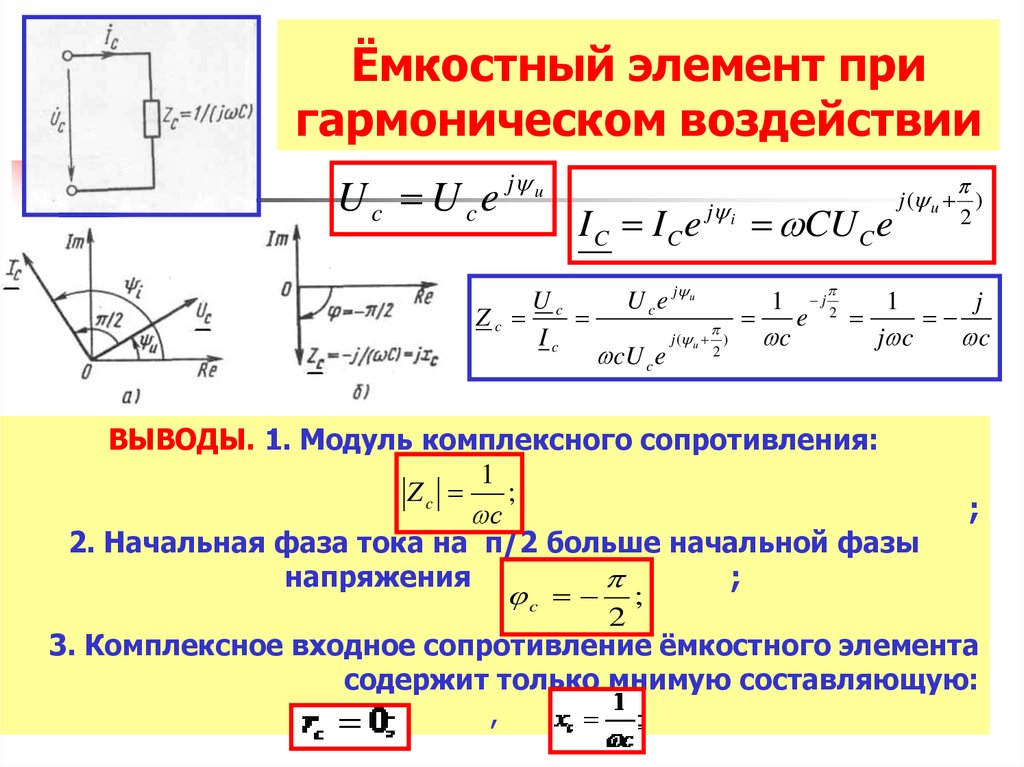
И так, конденсатор, который включен в цепь переменного тока, ведет себя как сопротивление, то есть оказывает влияние на силу тока, текущую в цепи. Величину емкостного сопротивления обозначим как , его величина связана с частотой тока и определена формулой:
где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.
Если конденсатор включен в цепь переменного тока, то в нем не затрачивается мощность, потому что фаза тока сдвинута по отношению к напряжению на . Если рассмотреть один период колебания тока в цепи (T), то происходит следующее: при заряде конденсатора (это составляет ) энергия в поле конденсатора запасается; на следующем отрезке времени () конденсатор разряжается и отдает энергию в цепь. Поэтому ёмкостное сопротивление называют реактивным (безваттным).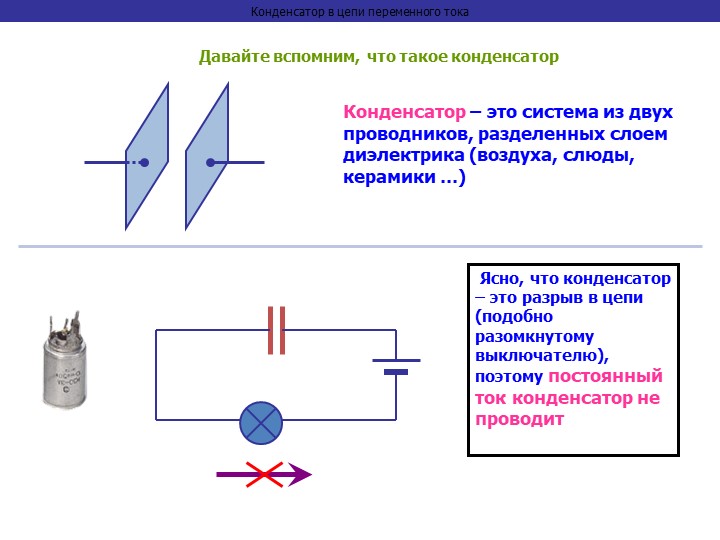
Следует заметить, что в каждом реальном конденсаторе реальная мощность (мощность потерь) все же тратится, при течении через него переменного тока. Это вызвано тем, что происходят изменения в состоянии диэлектрика конденсатора. Помимо этого существует некоторая утечка в изоляции обкладок конденсатора, поэтому появляется небольшое активное сопротивление, которое как бы включено параллельно конденсатору.
Векторная диаграмма токов в цепи с конденсатором
Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению
I = IG + IC
Действующие величины составляющих тока:
IG = GU (13.31)
IC = BCU (13.32)
Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φa =0). Вектор IG совпадает по направлению с вектором U, а вектор I
Вектор IG совпадает по направлению с вектором U, а вектор I
При напряжении u = Umsinωt соответствии с векторной диаграммой уравнение тока
i = Imsin(ωt + φ)
О заряде конденсатора.
Замкнем цепь. В цепи пойдет ток заряда конденсатора. Это значит что с левой обкладки конденсатора часть электронов уйдет в провод, а из провода на правую обкладку зайдет такое же количество электронов. Обе обкладки будут заряжены разноименными зарядами одинаковой величины.
Между обкладками в диэлектрике будет электрическое поле.
А теперь разомкнем цепь. Конденсатор останется заряженным. Закоротим куском провода его обкладки. Конденсатор мгновенно разрядится. Это значит что с правой обкладки уйдет в провод избыток электронов, а из провода на левую обкладку войдет недостаток электронов. На обоих обкладках электронов будет одинаково, конденсатор разрядится.
Конденсатор останется заряженным. Закоротим куском провода его обкладки. Конденсатор мгновенно разрядится. Это значит что с правой обкладки уйдет в провод избыток электронов, а из провода на левую обкладку войдет недостаток электронов. На обоих обкладках электронов будет одинаково, конденсатор разрядится.
До какого напряжения заряжается конденсатор?
О заряде конденсатора.
Замкнем цепь. В цепи пойдет ток заряда конденсатора. Это значит что с левой обкладки конденсатора часть электронов уйдет в провод, а из провода на правую обкладку зайдет такое же количество электронов. Обе обкладки будут заряжены разноименными зарядами одинаковой величины.
Между обкладками в диэлектрике будет электрическое поле.
А теперь разомкнем цепь. Конденсатор останется заряженным. Закоротим куском провода его обкладки. Конденсатор мгновенно разрядится. Это значит что с правой обкладки уйдет в провод избыток электронов, а из провода на левую обкладку войдет недостаток электронов.
До какого напряжения заряжается конденсатор?
О реальном конденсаторе
Реальный конденсатор имеет одновременно два сопротивления: активное и емкостное. Их следует считать включенными последовательно.
Напряжение приложенное генератором к активному сопротивлению и ток идущий по активному сопротивлению совпадают по фазе.
Напряжение приложенное генератором к емкостному сопротивлению и ток идущий по емкостному сопротивлению сдвинуты по фазе на 90 . Результирующее напряжение приложенное генератором к конденсатору можно определить по правилу параллелограмма.
На активном сопротивлении напряжение Uакт и ток I совпадают по фазе. На емкостном сопротивлении напряжение Uc отстает от тока I на 90 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 .
Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 .
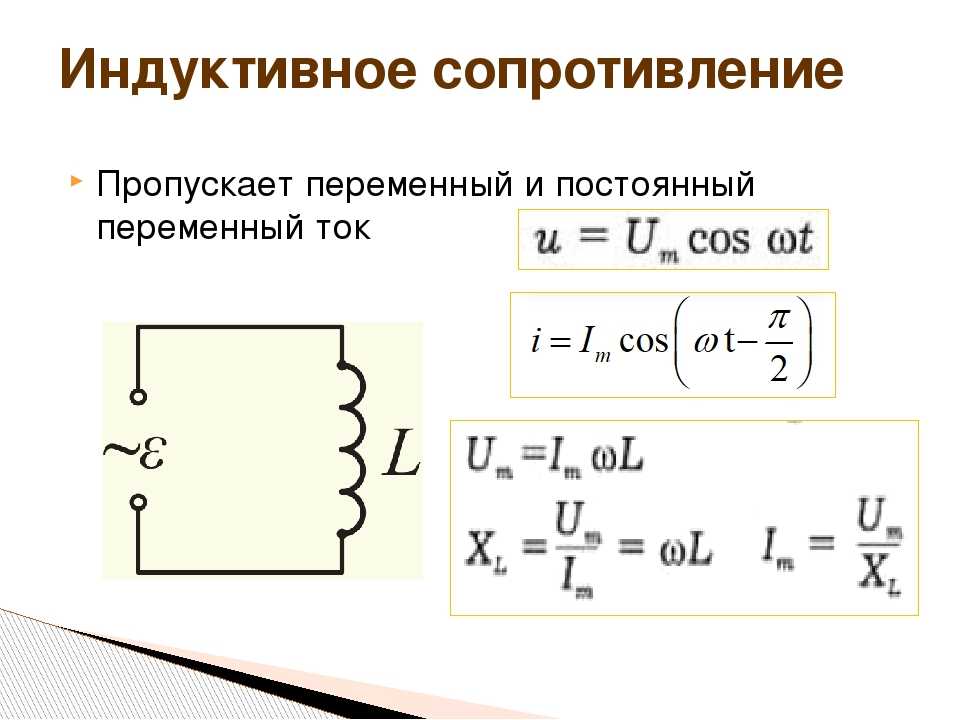
Емкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q является количеством электричества, протекающим по цепи в течение промежутка времени t. В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U – напряжением сети, Uc – напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).
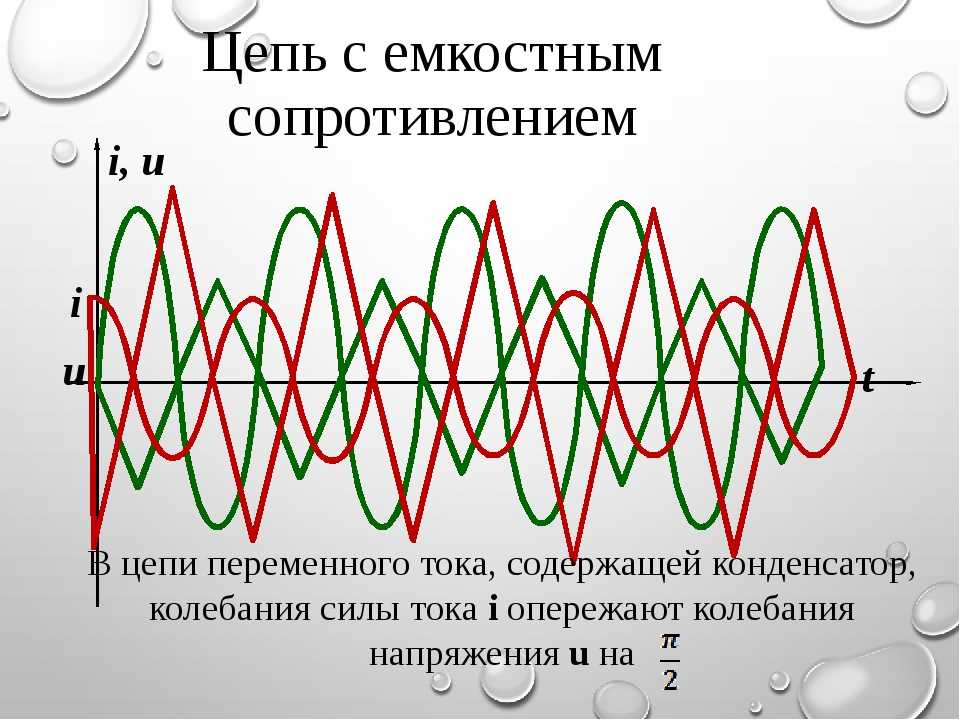
При наступлении второй четверти периода произойдет уменьшение сетевого напряжения и начнется разрядка конденсатора. Ток в цепи изменит свое направление и будет течь в обратную сторону. В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
Установлено что изменения тока конденсатора происходят со скоростью, находящейся в пропорциональной зависимости с угловой частотой ω. Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.
Далее уже совсем несложно установить значение емкостного сопротивления или реактивного сопротивления емкости: xc = 1/2π x f x C = 1/ ω x C. Данный параметр вычисляется, когда конденсаторная емкость включается в цепь переменного тока. Поэтому в соответствии с законом Ома в цепи переменного тока с включенным конденсатором, значение силы тока будет следующим: I = U/xc, а напряжение на обкладках составит: Uc = Ic x xc.
Часть сетевого напряжения, приходящаяся на конденсатор, получила название емкостного падения напряжения. Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.
Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.
ОПРЕДЕЛЕНИЕ
Конденсатор
, в простейшем случае состоит из двух металлических проводников (обкладок), которые разделяет слой диэлектрика. Каждая из обкладок конденсатора имеет свой вывод и может быть подключена к электрической цепи.
Конденсатор характеризуют при помощи ряда параметров (емкость, рабочее напряжение и т. д), одной из таких характеристик является сопротивление. Конденсатор практически не пропускает постоянный электрический ток. То есть сопротивление конденсатора является бесконечно большим для постоянного тока, но это идеальный случай. Через реальный диэлектрик очень малый ток протекать может. Этот ток называют током утечки. Ток утечки является показателем качества диэлектрика, который применяется при изготовлении конденсатора. У современных конденсаторов ток утечки составляет некоторые доли микроампера. Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.
Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
Косвенное измерение
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Сопротивление конденсатора.
Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.
Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.
Вся энергия затрачиваемая источником тока на преодоление емкостного
сопротивления превращается в энергию электрического поля конденсатора.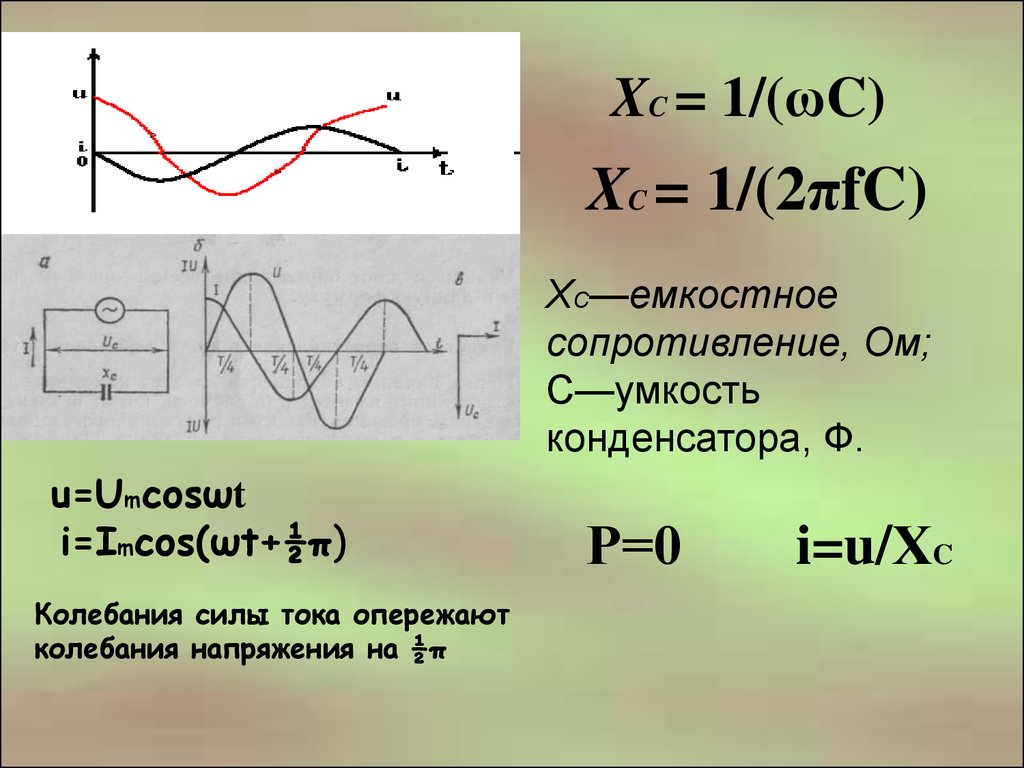
Когда конденсатор будет разряжаться вся энергия электрического поля
вернется обратно в цепь в виде энергии электрического тока. Таким
образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.
Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?
Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.
А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.
В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора.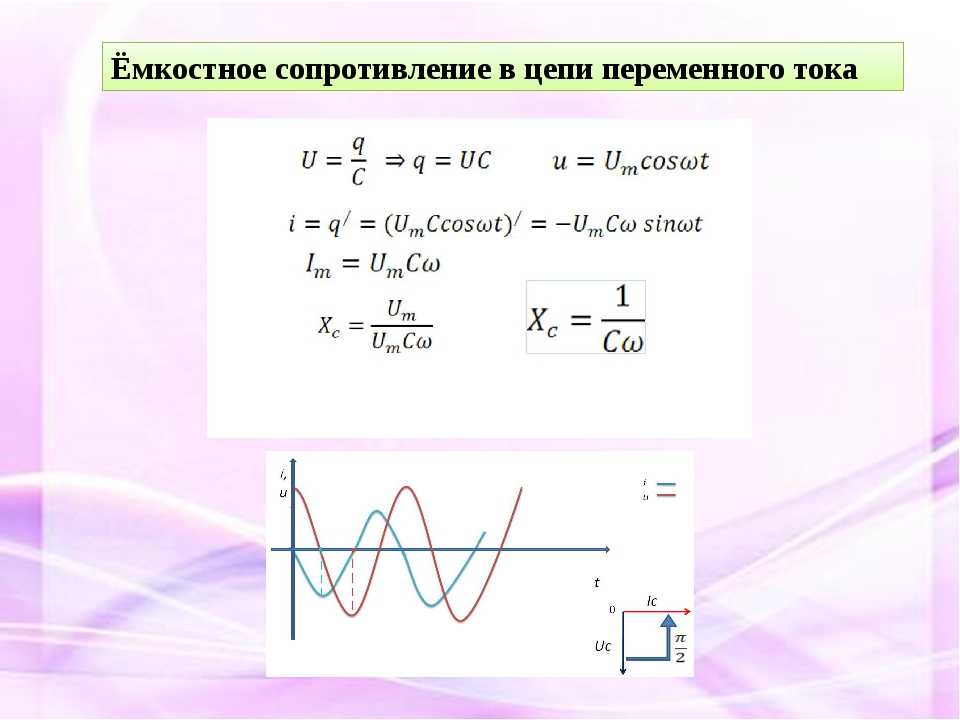 В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.
В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.
Одновременная поляризация огромного количества атомов образует ток, называемый током смещения.
Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.
конденсатора определяется по формуле
На активном сопротивлении напряжение U акт и ток I совпадают по фазе. На емкостном сопротивлении напряжение U c отстает от тока I на 90 0 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 0 .
О реальном конденсаторе
Реальный конденсатор имеет одновременно два сопротивления: активное и емкостное. Их следует считать включенными последовательно.
Напряжение приложенное генератором к активному сопротивлению и ток идущий по активному сопротивлению совпадают по фазе.
Напряжение приложенное генератором к емкостному сопротивлению и ток идущий по емкостному сопротивлению сдвинуты по фазе на 90 . Результирующее напряжение приложенное генератором к конденсатору можно определить по правилу параллелограмма.
На активном сопротивлении напряжение Uакт и ток I совпадают по фазе. На емкостном сопротивлении напряжение Uc отстает от тока I на 90 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 .
Соединение конденсаторов
Часто самого по себе конденсатора недостаточно. Поэтому такие электронные компоненты приходится объединять в группы, так называемые батареи. При таком подключении множество ёмкостей соединяются друг с другом для получения новой, обладающей другими характеристиками.
Выделяют 2 основных способа соединения деталей:
- последовательный;
- параллельный.

Последовательное соединение ёмкостей
При этом виде соединения множество деталей выстраивается в длинную цепь (от двух штук и более). Чаще всего на практике применяются комбинации из 2-5 деталей. Каждая предшествующая соединяется с последующей. В результате получается длинная цепочка, напоминающая вагоны в железнодорожном составе.
Последовательное включение
Последовательное соединение конденсаторов снижает их общую ёмкость. Вызвано это тем, что увеличивается толщина диэлектрика между обкладками прибора, а площадь их пересечения при этом остаётся неизменной (см. формулу выше). Как рассчитать суммарную ёмкость конденсатора при последовательном подключении, можно узнать из формулы ниже.
Ёмкость последовательно включенных конденсаторов
На деле такое подключение используется для получения нового значения ёмкости, но такой конденсатор просто не выпускается промышленностью. Например, имея два элемента номиналом 10 uF каждый и соединив их последовательно, можно получить общую ёмкость в 5 uF.
Пример последовательного расчёта
Другая особенность последовательного соединения – это увеличение общего напряжения. Если взять 2 ёмкости на 200 В каждую и подключить их описываемым способом, то итоговое напряжение батареи составит 200 + 200 = 400 вольт.
Параллельное соединение
При параллельном соединении деталей все левые (условно) выводы ёмкостей объединяются в один. С правыми – так же. Если конденсаторы электролитические, то все плюсы подключаются вместе, так же, как и все минусы. В итоге получается большая сборка деталей, имеющая всего два вывода.
Параллельное включение конденсаторов
Данное соединение подразумевает уже сложение ёмкостей, так как увеличивается общая площадь взаимодействующих обкладок. При этом максимальное напряжение, которое можно приложить к этой батареи, не превышает значения самого низковольтного элемента. Расчёт конденсатора, а именно его ёмкости, в таком случае производится по следующему выражению.
Ёмкость параллельно подключенных конденсаторов
Метод применяется, когда из множества элементов с низкой ёмкостью нужно получить один, но с большой.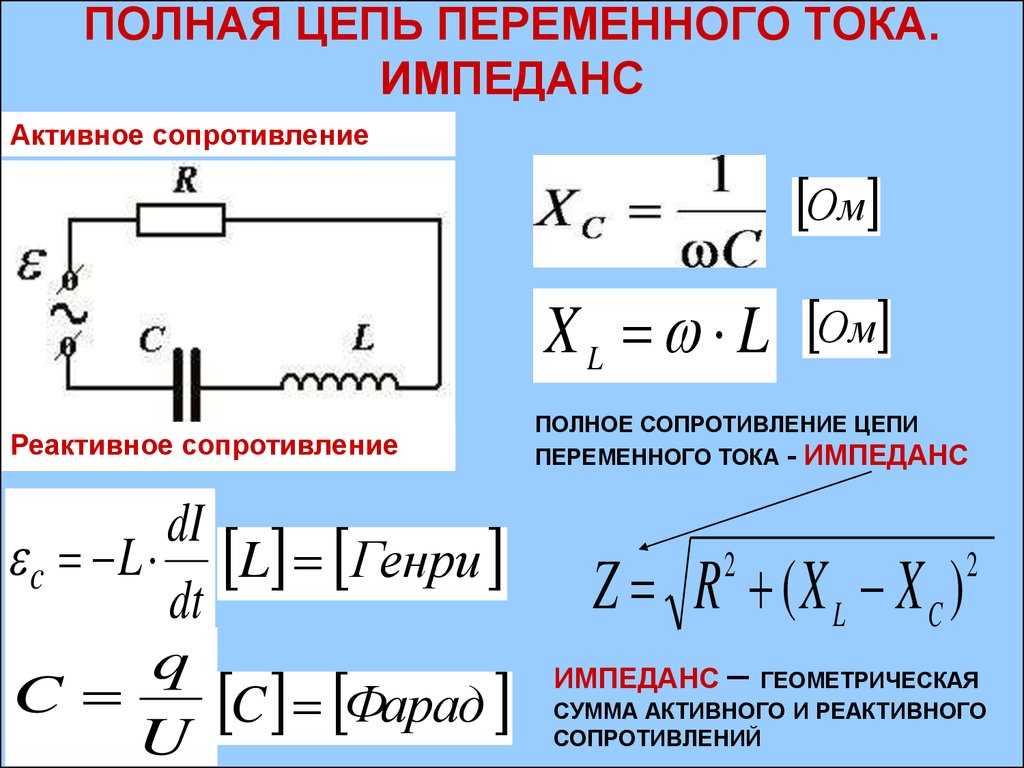 Пример использования такого подключения можно найти во фрагменте схемы одного из популярных сварочных инверторов. Она приведена ниже. Из изображения видно, что параллельно применяются 6 электролитических конденсаторов, которые стоят сразу после диодного выпрямителя. Каждый из них на 400 В 470 uF. В результате суммарная ёмкость полученной батареи составляет 470 * 6 = 2820 микрофарад. Приведённое вычисление всегда можно выполнить в специализированном интернет калькуляторе. Пиковое напряжение, которое приложено к этой сборке, не должно превышать 400 вольт. Это значение взято с запасом примерно в 30 %, ведь на деле в данном узле сварочного аппарата действующий вольтаж составляет 300 В.
Пример использования такого подключения можно найти во фрагменте схемы одного из популярных сварочных инверторов. Она приведена ниже. Из изображения видно, что параллельно применяются 6 электролитических конденсаторов, которые стоят сразу после диодного выпрямителя. Каждый из них на 400 В 470 uF. В результате суммарная ёмкость полученной батареи составляет 470 * 6 = 2820 микрофарад. Приведённое вычисление всегда можно выполнить в специализированном интернет калькуляторе. Пиковое напряжение, которое приложено к этой сборке, не должно превышать 400 вольт. Это значение взято с запасом примерно в 30 %, ведь на деле в данном узле сварочного аппарата действующий вольтаж составляет 300 В.
Фрагмент схемы сварочного аппарата
Дополнительная информация. Конденсаторы на входе мощных устройств часто используются в роли фильтров от помех и узлов для компенсации реактивной мощности. Подобные меры позволяют повысить качество напряжения сети и защитить оборудование от кратковременных скачков напряжения.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
-
3.
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Видео-вопрос: нахождение неизвестной емкости из комбинации последовательностей
Стенограмма видео
Цепь на схеме содержит два последовательно соединенных конденсатора.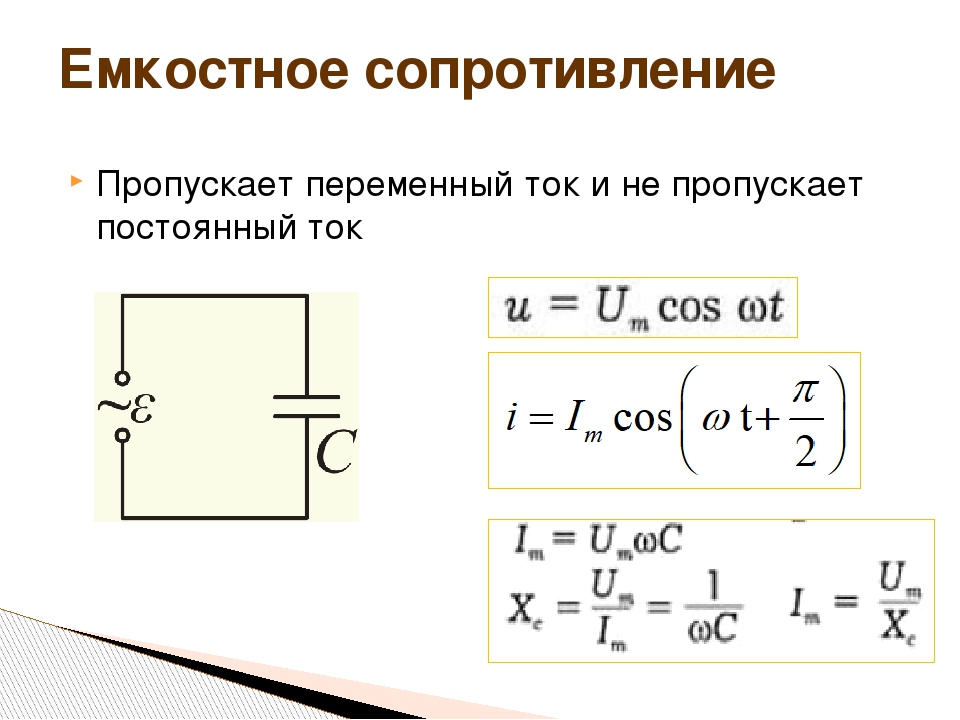 Суммарная емкость цепи 12 мкФ. Какая емкость 𝐶?
Суммарная емкость цепи 12 мкФ. Какая емкость 𝐶?
Мы видим, что у нас есть диаграмма, на которой показана цепь, в которой ячейка соединена последовательно с двумя конденсаторами. Этот конденсатор слева имеет маркировку емкостью 45 мкФ. И этот здесь помечен емкостью 𝐶. Значение 𝐶 — это то, что нас просят найти. Вопрос говорит нам, что общая емкость цепи, которую мы обозначили 𝐶 нижним индексом T, равна 12 микрофарад. Чтобы ответить на этот вопрос, нам нужно вспомнить формулу, которая говорит нам, как последовательно соединять конденсаторы.
Если у нас есть несколько конденсаторов, соединенных последовательно, то, если мы прибавим обратную величину их отдельных емкостей, мы получим единицу сверх общей емкости цепи. То есть, если у нас есть конденсаторы ёмкостью 𝐶 один, 𝐶 два, 𝐶 три и так далее, то при их последовательном соединении единица над общей ёмкостью 𝐶 индекс Т будет равна единице над 𝐶 единица плюс единица над 𝐶 два плюс один на 𝐶 три и так далее для всех конденсаторов, соединенных последовательно.
В схеме из этого вопроса у нас всего два конденсатора. Итак, нам нужны только первые два члена в правой части этого уравнения. Это уравнение связывает общую емкость цепи со значениями двух отдельных емкостей. В нашем случае мы знаем значение общей емкости 𝐶 с индексом T. Мы пытаемся найти эту величину 𝐶, которая будет одной из этих двух емкостей в правой части. Для ясности скажем, что 𝐶 — это наше количество 𝐶 два. И затем, это делает нашу другую емкость 45 микрофарад нашей ценностью за 𝐶 единицу. Это означает, что мы хотим взять это уравнение и изменить его, чтобы сделать 𝐶 два предметом.
Первый шаг — вычесть единицу на 𝐶 единицу из обеих частей уравнения. Затем в правой части у нас есть единица на 𝐶 единицу и отрицательная единица на 𝐶 единицу. Таким образом, эти два термина сокращаются. Это дает нам, что единица на 𝐶 нижнего индекса T минус единица на 𝐶 один равна единице на 𝐶 два. В левой части мы можем переписать первую дробь, умножив числитель и знаменатель на 𝐶 единицу. И мы можем переписать вторую дробь, умножив числитель и знаменатель на 𝐶 нижний индекс T. Затем, поскольку обе дроби слева теперь имеют одинаковый знаменатель, мы можем переписать левую часть как одну дробь. Когда мы это делаем, левая часть становится равной 𝐶 единице минус 𝐶 индексу T, деленной на 𝐶 единицу, умноженной на 𝐶 индексу T.
И мы можем переписать вторую дробь, умножив числитель и знаменатель на 𝐶 нижний индекс T. Затем, поскольку обе дроби слева теперь имеют одинаковый знаменатель, мы можем переписать левую часть как одну дробь. Когда мы это делаем, левая часть становится равной 𝐶 единице минус 𝐶 индексу T, деленной на 𝐶 единицу, умноженной на 𝐶 индексу T.
Затем мы можем умножить обе части уравнения на 𝐶 один, 𝐶 нижний индекс T и 𝐶 два. Слева 𝐶 в числителе и знаменателе сокращаются, как и нижний индекс 𝐶 Ts. Между тем справа двойка 𝐶 в числителе сокращается с двойкой 𝐶 в знаменателе. После того, как мы избавились от членов, которые сокращаются, мы остаемся с тем, что 𝐶 два, умноженные на 𝐶 один минус 𝐶 нижний индекс T, равно 𝐶 один раз 𝐶 нижний индекс T. Наконец, мы можем разделить обе части уравнение на 𝐶 один минус 𝐶 нижний индекс T. Слева у нас тогда 𝐶 один минус 𝐶 нижний индекс T как в числителе, так и в знаменателе. Так что это отменяется.
В итоге мы получаем уравнение, где 𝐶 два — подлежащее. И у нас есть 𝐶 два равно 𝐶 один раз 𝐶 индекс T разделить на 𝐶 один минус 𝐶 индекс T. В этом вопросе мы знаем значения величин 𝐶 один и 𝐶 индекс T. А количество 𝐶 два является значением 𝐶 что мы пытаемся найти. Подставляя эти значения в это уравнение, мы получаем, что 𝐶 равно 45 мкФ, умноженным на 12 мкФ, деленным на 45 мкФ минус 12 мкФ. В числителе 45 мкФ, умноженные на 12 мкФ, дают 540 мкФ в квадрате. В знаменателе имеем 45 мкФ минус 12 мкФ, что равно 33 мкФ.
И у нас есть 𝐶 два равно 𝐶 один раз 𝐶 индекс T разделить на 𝐶 один минус 𝐶 индекс T. В этом вопросе мы знаем значения величин 𝐶 один и 𝐶 индекс T. А количество 𝐶 два является значением 𝐶 что мы пытаемся найти. Подставляя эти значения в это уравнение, мы получаем, что 𝐶 равно 45 мкФ, умноженным на 12 мкФ, деленным на 45 мкФ минус 12 мкФ. В числителе 45 мкФ, умноженные на 12 мкФ, дают 540 мкФ в квадрате. В знаменателе имеем 45 мкФ минус 12 мкФ, что равно 33 мкФ.
Таким образом, в этом выражении в единицах измерения мы теперь можем исключить один множитель микрофарад из числителя и знаменателя. Это оставляет нам единицы микрофарад для емкости 𝐶. Вычисление выражения дает результат 16,36 повторяющихся микрофарад. Поскольку значения емкостей, которые нам дали в вопросе, были даны с двумя значащими цифрами, то мы должны процитировать наш ответ с одинаковым уровнем точности. Округление до двух значащих цифр дает нам ответ для емкости 𝐶 16 микрофарад.
домашнее задание и упражнения — Найти емкость конденсатора
$\begingroup$
Дано: Рассмотрим конденсатор, подключенный к батарее напряжением V .
Пусть конденсатор имеет площадь А и расстояние между пластинами L. Предположим, что конденсатор имеет слой линейного диэлектрика (с диэлектрической проницаемостью κ, так что ε = κε0) толщиной L/2 на нижней пластине.
Я обнаружил, что емкость равна $C=\frac{2\kappa\epsilon_0 A}{L}$. Я был прав насчет разделительного расстояния? В более распространенных примерах конденсатора они утверждают, что пластины плоские, между ними ничего нет. В этом случае высота линейного диэлектрика равна половине общего расстояния между пластинами. Правильно ли я использую оставшееся свободное пространство, а именно $L/2$, в качестве разделительного расстояния в уравнении? Для справки, уравнение:
$$C=\frac{\kappa \epsilon_0 A}{d}$$
- домашние задания и упражнения
- емкость
- напряжение
$\endgroup$
$\begingroup$
Мгновенная проверка, которая показывает, что ваш ответ неверен: установите $\kappa = 1$, как если бы диэлектрика не было, и вы не восстановите формулу для параллельных пластин для зазора $L$.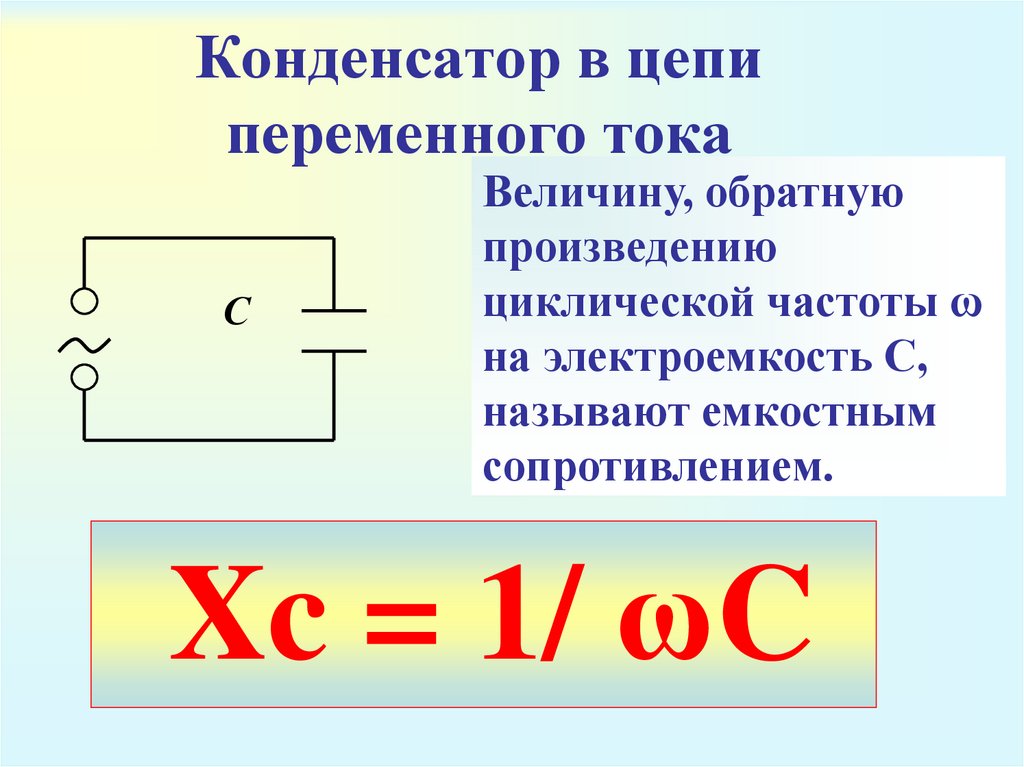
Как решить эту задачу:
Пусть напряжение на конденсаторе равно $V$, а напряжение сверху и снизу равно $V_t$ и $V_b$ соответственно, тогда $$V=V_t+V_b,$$ что подразумевает, что $$1/C=1/C_t+1/C_b$$, поскольку $V=Q/C$.
Таким образом, эта система состоит из двух последовательных конденсаторов. Один конденсатор — это верхний зазор, а другой — нижняя часть. Используйте формулу для пластинчатых конденсаторов дважды, с расстоянием $L/2$ в обоих случаях, затем получите общую емкость, используя формулу для двух последовательно соединенных конденсаторов. Задействована некоторая алгебра.
Вы можете снова проверить полученный ответ, установив $\kappa=1$ и посмотрев, восстанавливаете ли вы обычную формулу тарелки.
$\endgroup$
5
$\begingroup$
Поле $\mathbf{D}$ между пластинами (как обычно, без учета эффекта интерференции) однородно и нормально к плоскости пластин (для простоты предположим, что в направлении z) и определяется выражением
$$\ mathbf{D} = \frac{Q}{A}\hat{\mathbf{z}}$$
, где пластины имеют заряд $Q$ и $-Q$ соответственно.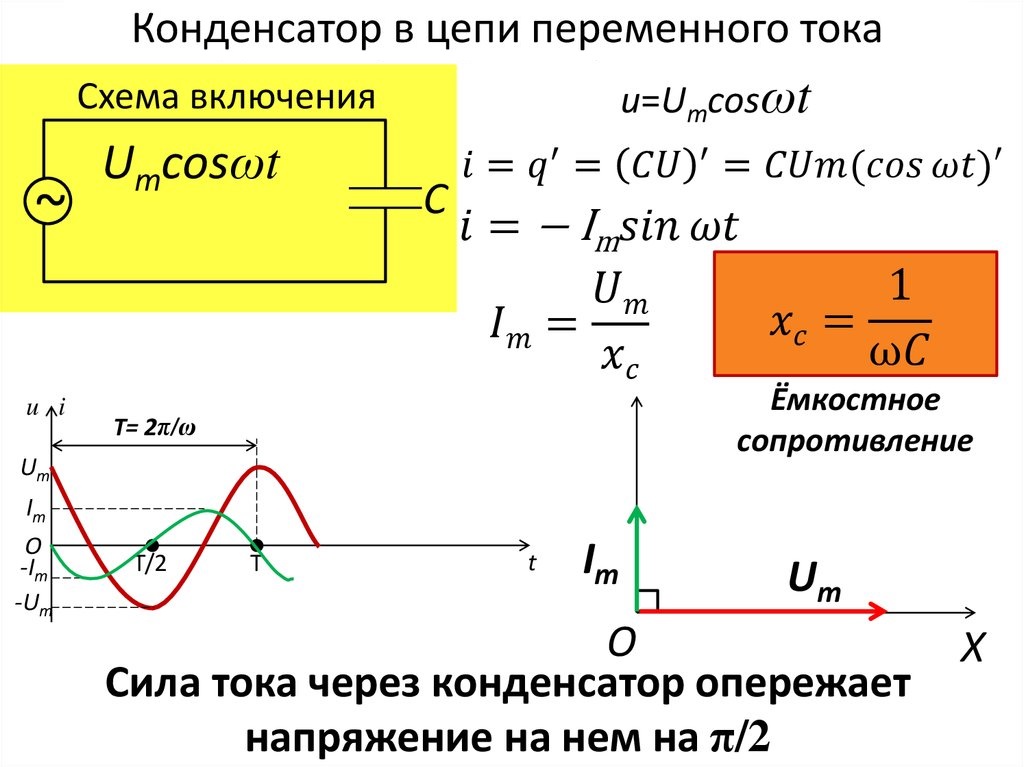



 2 Термодинамика
2 Термодинамика
 3 Фотометрия
3 Фотометрия
 Пусть конденсатор имеет площадь А и расстояние между пластинами L. Предположим, что
конденсатор имеет слой линейного диэлектрика (с диэлектрической проницаемостью κ, так что
ε = κε0) толщиной L/2 на нижней пластине.
Пусть конденсатор имеет площадь А и расстояние между пластинами L. Предположим, что
конденсатор имеет слой линейного диэлектрика (с диэлектрической проницаемостью κ, так что
ε = κε0) толщиной L/2 на нижней пластине.