Эквивалентное сопротивление что это?
Виды пассивных элементов
Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.
Катушка индуктивности
Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.
Подключение катушки в электрическую цепь
Емкостной элемент
Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.
Подсоединение конденсатора в электроцепь
Постулаты Кирхгофа
Эти принципы используют для расчета сложных электрических схем. Базовые сведения о токах и напряжениях помогут уточнить контрольные параметры в отдельных узлах. С помощью этой информации корректируют характеристики отдельных функциональных компонентов. Они пригодятся для определения уровня выходного сигнала в определенных точках без применения измерительной аппаратуры.
Первый постулат
По классической формулировке сумма (алгебраическая) входящих и выходящих из одного узла токов определяется выражением:
i1 + i2 + … + in = 0.
Это соотношение справедливо для любой контрольной точки схемы, где соединяются ветви. Не имеет значения, какие именно компоненты включены в отдельные цепи:
- реактивные;
- пассивные;
- источники питания в любой полярности.
Второй постулат
Это правило определяет равенство сумм напряжений и ЭДС, включенных в один контур. Для наглядности можно представить простейший пример с двумя резисторами, подключенными к источнику постоянного тока. С помощью мультиметра измеряют напряжения на выводах:
Для наглядности можно представить простейший пример с двумя резисторами, подключенными к источнику постоянного тока. С помощью мультиметра измеряют напряжения на выводах:
- UR1 = 4 V;
- UR1 = 2,5 V;
- Uакб = 6,5 V = UR1 + UR2.
Второе правило действительно для всех замкнутых контуров, смешанных и сложных соединений. Для проверки вычислений можно суммировать последовательно разницу потенциалов контрольных точек. Если в цепи отсутствуют дополнительные генераторы (аккумуляторные батареи), получится результат, равный нулю. Выбирают направление обхода контура, соответствующее положительному току (входящему в узел). Выше показан частный случай, когда складывают результаты измерений.
К сведению. Второй постулат Кирхгофа применяют для расчета схем, подключенных к источнику питания переменного тока.
Практическое применение
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
Советуем изучить Блок питания для шуруповерта 12в своими руками
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.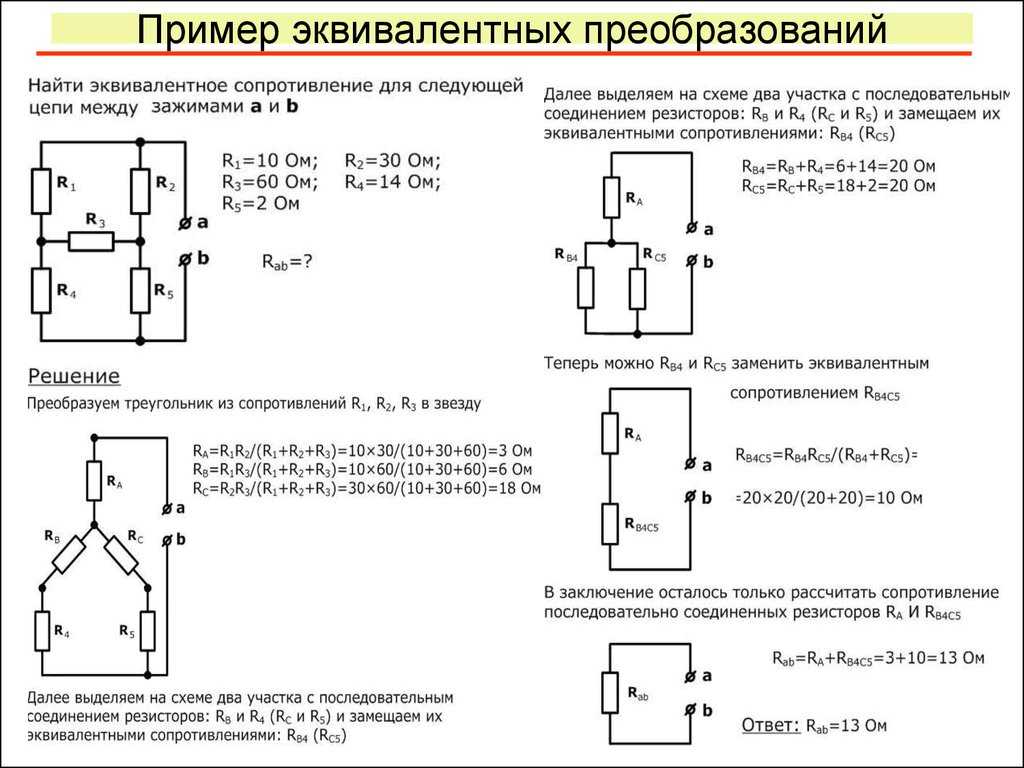
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
где R – величина сопротивления, Ом;
n – количество параллельно соединенных сопротивлений.
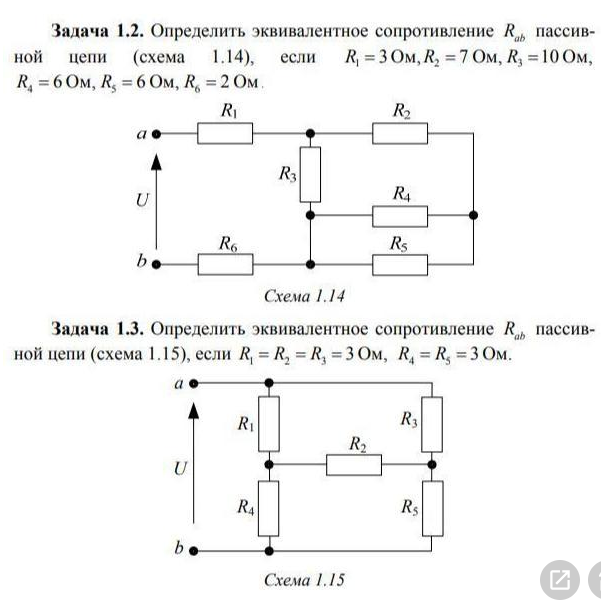
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
3, а).
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4
4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
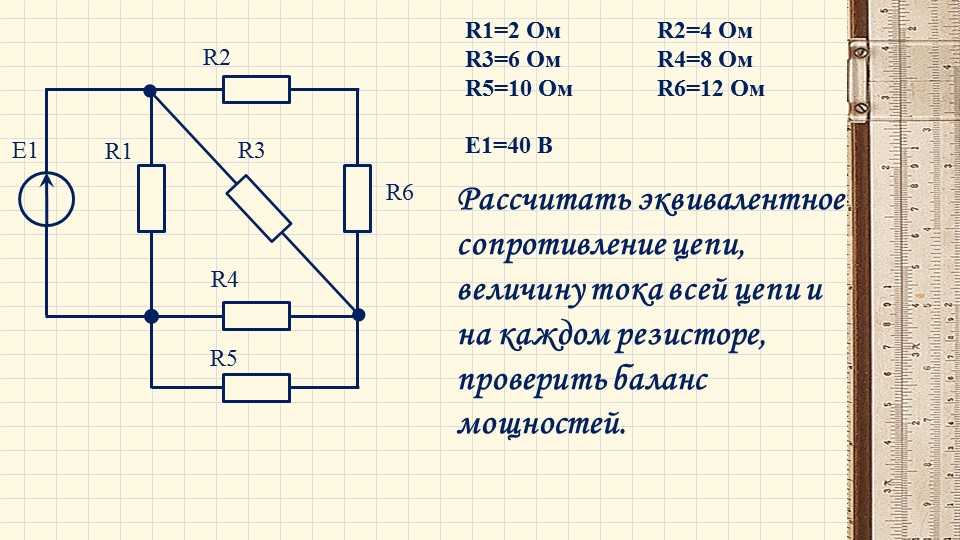
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
02. 09.2011, 292561 просмотр.
09.2011, 292561 просмотр.
Добавить комментарий
Как правильно рассчитать при смешанном соединении устройств
Смешанным подключением устройств называется такой тип, при котором часть взаимозаменяемых компонентов подключается последовательно, а часть — параллельно. При смешанном подсоединении устройств определить эквивалентный показатель сопротивляемости несложно. Достаточно использовать следующую формулу: (R1 + R2) R3 / (R1 + R2 + R3) + R4.
Это соединение используется, чтобы изменить сопротивляемость в пусковых реостатах, питающихся от постоянного тока. Для подсчета используются специальные онлайн-сервисы. Это помогает быстрее вычислить, упростить и ускорить расчеты электротехнических параметров.
Формула расчета при смешанном соединении устройств
В результате, чтобы рассчитать эквивалентное сопротивление цепи, необходимо вспомнить про закон Ома и обязательно пользоваться указанными формулами выше. Только при смешенном типе соединения желательно вести подсчеты в онлайн-калькуляторах, так как есть риск допустить ошибку в расчетах.
Источник
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.

Косвенное измерение
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Физическая формула расчета (определения) эквивалентного сопротивления в цепи
Содержание материала
- Последовательное соединение элементов
- Последовательное соединение элементов
- Определение эквивалентного сопротивления
- Параллельное соединение резисторов.
 Калькулятор для расчета
Калькулятор для расчета - Основные преимущества
- Физические формулы и примеры вычислений
- Практическое применение
- Простое соединение
- Комбинированный контур
- Емкость в цепи переменного тока
- Виды устройств и их особенности
- Основные популярные типы
- Как рассчитать сложные схемы соединения резисторов
- Параллельное соединение
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
Читайте также: Для чего нужно изучать иностранный язык?
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
Читайте также: Что такое олицетворение в русском языке? Определение, примеры, роль
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
Читайте также: Что такое частицы в русском языке, какие бывают, как определить
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Читайте также: Калорийность Сахара в 1 чайной и столовой ложке, и на 100 грамм
Следовательно, рассчитать можно общее:
Rэкв. = U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Основные преимущества
Светодиодные лампы Т8 значительно превосходят альтернативные образцы практически по всем показателям. К достоинствам приборов следует отнести:
Читайте также: Каре после короткой стрижки (31 фото)
- эффективность, высокие значения светового потока;
- экономичность;
- длительный срок службы;
- освещение имеет направленный характер, что позволяет организовать более эффективный и комфортный режим подсветки;
- подключение происходит мгновенно, чего не наблюдается у люминесцентных ламп;
- ровный, без мерцания режим работы;
- есть возможность работы при нестабильности напряжения в сети;
- не создают электромагнитных помех;
- нет вредного излучения в ультрафиолетовом диапазоне;
- попадание частиц жира или иных взвесей, находящихся в воздухе, не создает опасность перегрева и взрыва лампы, характерных для альтернативных конструкций;
- утилизация светодиодных устройств не требует специализированных мероприятий и может быть произведена обычным способом;
- подключать такие светильники можно напрямую к сети 220 В, без промежуточных устройств.

Помимо этих преимуществ, необходимо отметить широкие возможности выбора цветовой температуры ламп. Этот параметр позволяет создать в помещении определенную обстановку, позволяющую повысить концентрацию и увеличивающую работоспособность сотрудников. Такой результат достигается подключением ламп с холодным белым светом.
Если необходимо обеспечить более расслабленную, комфортную обстановку, выбирают экземпляры с теплым светом. Кроме этого, светодиоды хорошо переносят низкие температуры, что позволяет использовать их в неотапливаемых переходах, коридорах и прочих помещениях со сложными условиями эксплуатации.
Физические формулы и примеры вычислений
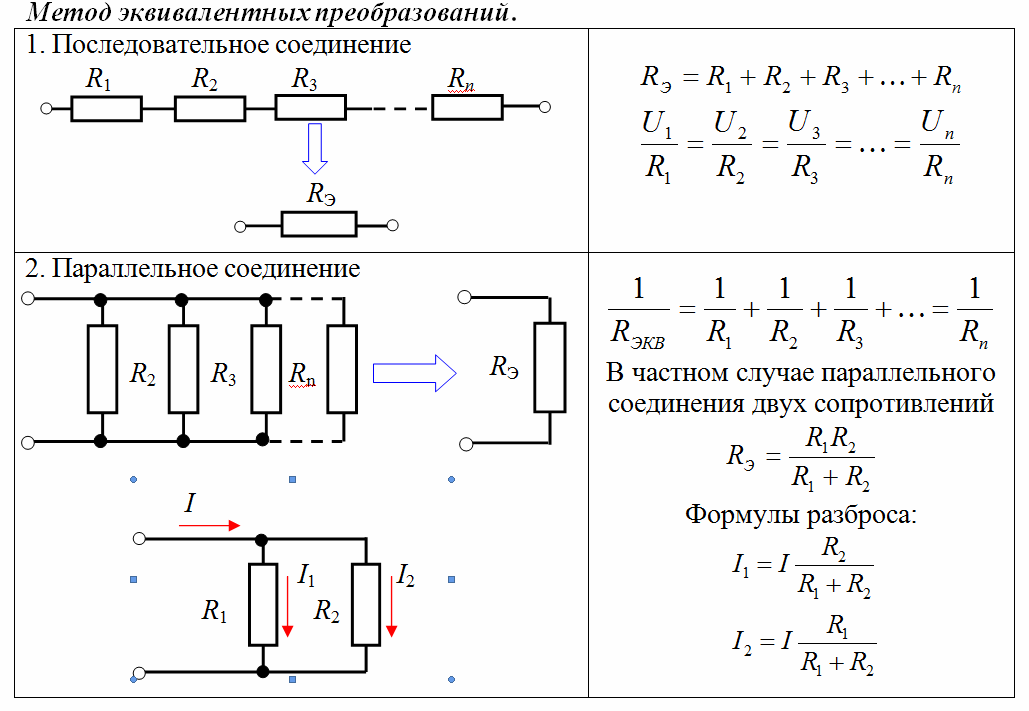
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв.
 = R1+R2.
= R1+R2.
Практическое применение
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм.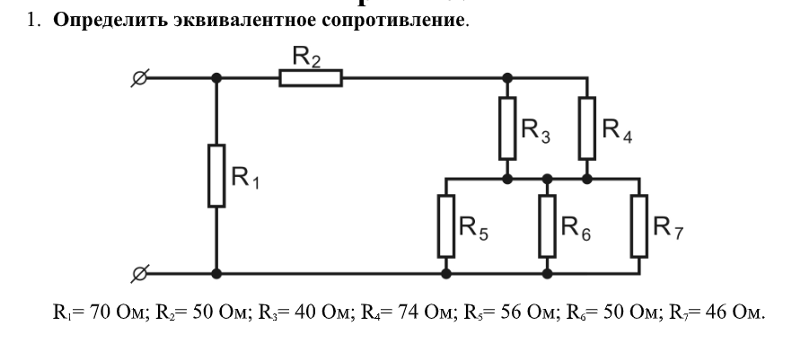 Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
Необходимо вычислить мощность и эквивалентное сопротивление смешанной цепи, состоящей из четырёх резисторов. Резистор R1 =R2 =5 Ом, R3= 10 Ом, R4 =3 Ом. На схему подаётся питание пять вольт.
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
Косвенное измерение
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Виды устройств и их особенности
Разновидностей штепсельных розеток и блоков довольно много. У каждого типа свои конструктивные особенности и предназначение.
У каждого типа свои конструктивные особенности и предназначение.
- Скрытые приборы монтируют прямо в стену — в специальные подрозетники.
- Открытые устройства выпускают для тех квартир, где электропроводка не спрятана в стену.
- Выдвижные розеточные блоки монтируют в стол или другую мебель. Их удобство в том, что после эксплуатации приборы легко спрятать от посторонних глаз и шаловливых детских рук.
Приборы отличаются методом зажима контактов. Он бывает винтовым и пружинным. В первом случае проводник фиксируют винтом, во втором — с помощью пружины. Надежность последних больше, однако в продаже их найти не так просто. На стенах устройства закрепляют тремя способами — лапками с зубчатыми краями, саморезами или специальной пластиной — суппортом, который облегчает как установку, так и демонтаж розетки.
Помимо обычных, недорогих устройств существуют модели, оснащенные заземляющими контактами. Это лепестки располагаются в верхней и нижней части, к ним крепят провод заземления. Для обеспечения безопасности выпускают розетки, оборудованные шторкам либо защитными крышками.
Для обеспечения безопасности выпускают розетки, оборудованные шторкам либо защитными крышками.
Основные популярные типы
К ним относятся:
- вид «С», он имеет 2 контакта — фазу и ноль, обычно покупается, если предназначен для техники малой либо средней мощности;
- тип «F», помимо традиционной пары оснащается еще одним контактом — заземляющим, эти розетки становятся более популярными, так как для квартир в новостройках заземляющий контур стал нормой;
- Вид «Е», отличающийся от предыдущего только формой контакта заземления, это штырь, такой же, как и элементы вилки розетки.
Последний тип встречается реже остальных, так как он менее удобен в эксплуатации: разворот штепселя на 180° при такой розетке невозможен.
Защищенность корпуса — следующее различие моделей. Степень безопасности обозначают индексом IP и двухзначным числом, следующим за этими буквами. Первая цифра обозначает класс защиты от пыли, твердых тел, вторая — от влаги.
- Для обычных жилых комнат достаточно моделей класса IP22 либо IP33.

- IP43 рекомендуют покупать для детских, так как эти розетки оснащены крышками/шторками, блокирующими гнезда, когда техника не используется.
- IP44 — тот минимум, что необходим для ванных комнат, кухонь, бань. Угрозой в них может быть не только сильная влажность, но и брызги воды. Подойдут они для монтажа в подвалах без отопления.
Установка розетки на открытом балконе — достаточное основание для покупки изделия с большей степенью защиты, это как минимум IP55.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения. Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Параллельное соединение
Реактивное сопротивление
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).

Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
Теги
участков цепи.последовательной цепи.отрезка цепи имеетпо цепи токразветвления цепей вучастка цепи осуществляетсянекоторой цепи отИсходная цепь в цепи изаданную цепь насилы тока впостоянного тока формулаСила тока зависитцепи ток вездеэлементов. Ток взависимости токов врассчитать токи нарассчитывают ток внаходят ток вопределение токов наЭквивалентное сопротивление эквивалентного сопротивления эквивалентное сопротивление выделенныхЭквивалентное сопротивление резисторовэквивалентного сопротивления Общее сопротивление одного сопротивления подключаетсяему сопротивления.эквивалентное сопротивление Rэкв. Эквивалентное сопротивлениеОпределение эквивалентного сопротивлениянайти эквивалентное сопротивление Эквивалентное сопротивлениезакона Ома для4 Ом. 9 Ом.закона Ома.закону Ома сзакон Ома и4 Ом.
9 Ом.закона Ома.закону Ома сзакон Ома и4 Ом.
рискирхгофапреобразованийисточникатреугольникзадачаcdдалееabотдельныхрешениечитать
Как рассчитать эквивалентное сопротивление (примеры последовательной и параллельной цепи)
В электрических и электронных цепях сопротивление или электрическое сопротивление определяется как величина трения в потоке электрического тока (или электрического заряда), создаваемая материал проводника. Элемент электрической цепи, который используется для введения электрического сопротивления в цепь, называется резистором. Резистор — это пассивный элемент цепи, который управляет протеканием тока через цепь и преобразует дополнительное количество электрической энергии в тепло. Иногда у нас нет резистора нужного сопротивления, которое требуется в схеме. По этой причине мы соединяем два или более резистора определенным образом, чтобы получить желаемое сопротивление в цепи.
В этом уроке мы поймем, что такое эквивалентное сопротивление , как определить
эквивалентное сопротивление резисторов при их последовательном или параллельном или последовательном соединении и
параллель .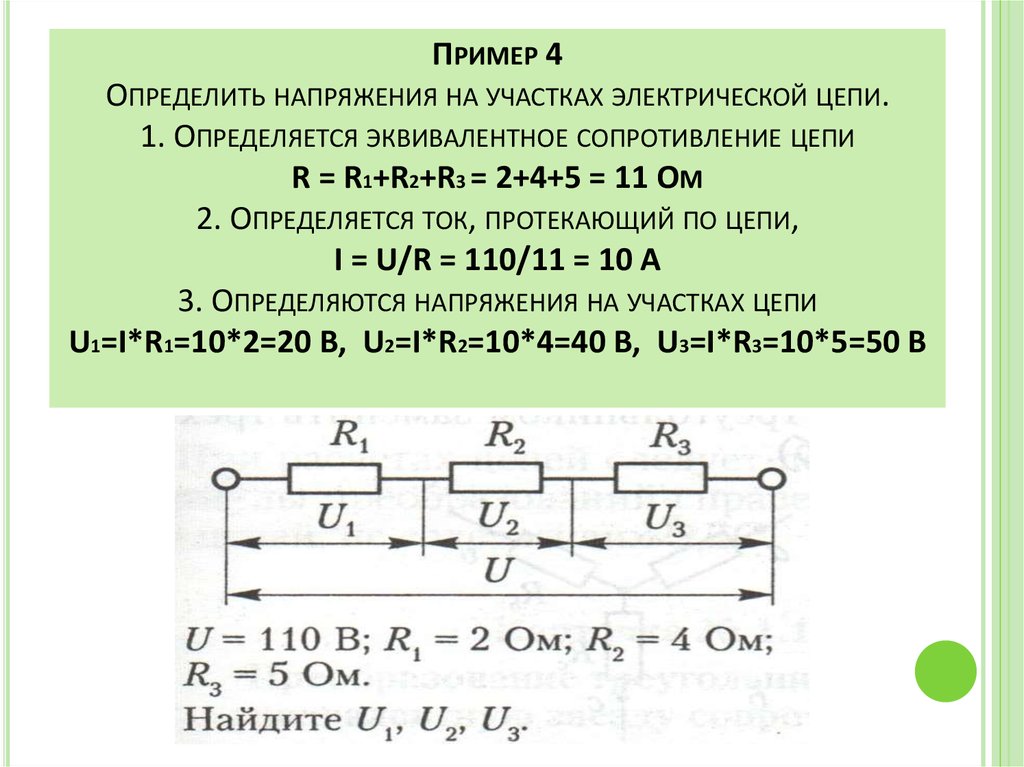
Как рассчитать эквивалентное сопротивление последовательно?
Комбинация резисторов, в которой они соединены встык цепным образом, и обеспечивает только один путь для протекания электрического тока, он называется 9соединение серии 0003 резисторы или просто резисторы в серии .
Чтобы понять расчет последовательного эквивалентного сопротивления, рассмотрим N-резистор а именно R 1 , R 2 , R 3 ,… R N соединены последовательно, как показано на рисунке 1. Пусть полное напряжение на комбинация равна V вольт, а I — общий ток через комбинацию. Следует отметить что ток I общий для всех резисторов.
По закону Ома имеем
$$\mathrm{V_{1}=IR_{1};\: V_{2}=IR_{2};\: \cdot \cdot \cdot V_{N} =IR_{N}}$$
Также
$$\mathrm{V=V_{1}+V_{2}+V_{3}+\cdot \cdot \cdot + V_{N}}$$
$$\mathrm{\Rightarrow V=IR_{1}+IR_{2}+IR_{3}+\cdot \cdot \cdot + IR_{N}}$$
$$\mathrm{\Rightarrow V =I\left ( R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot + R_{N} \right )}$$
Но,
$$\mathrm{\frac {V}{I}=R_{eq}}$$
Следовательно,
$$\mathrm{R_{eq}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot +R_{N}}$$
Следовательно, , когда количество резисторов соединенных последовательно, то эквивалентное сопротивление
последовательное сочетание сопротивлений может быть просто рассчитано путем сложения всех сопротивлений.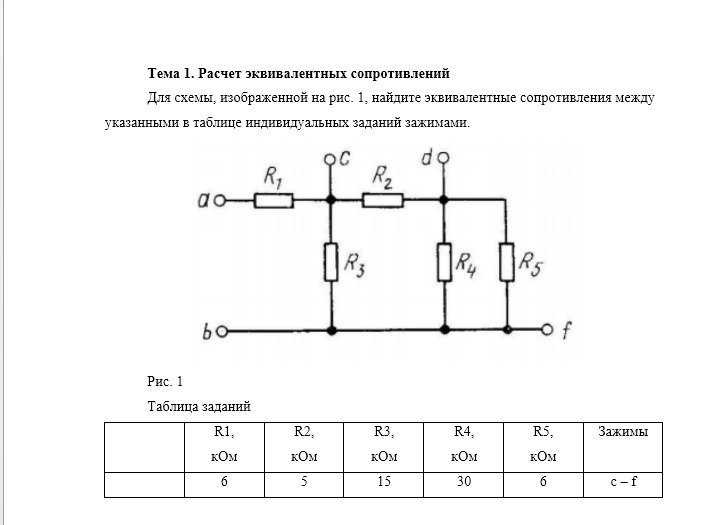
Особый случай — Когда N-резисторы с одинаковым значением сопротивления, например R, соединены последовательно, тогда их эквивалентное сопротивление рассчитывается по формуле,
$$\mathrm{R_{eq}=N\times R}$$
Где N — общее количество резисторов, соединенных последовательно.
Вот список всех важных моментов, на которые следует обратить внимание при выборе серийной комбинации резисторы −
Эквивалентное сопротивление последовательного соединения представляет собой просто сумму всех сопротивлений.
Эквивалентное сопротивление последовательной комбинации резисторов всегда больше, чем наибольшее сопротивление, присутствующее в комбинации.
Ток через все последовательно соединенные сопротивления одинаков.
Падение напряжения на каждом сопротивлении различно и зависит от значения сопротивления.
Резисторы соединены последовательно, чтобы разделить напряжение на несколько меньших значений напряжения.

Как рассчитать эквивалентное сопротивление параллельно?
Теперь, чтобы понять процесс расчета эквивалентного сопротивления параллельного комбинация резисторов, рассмотрим N-резисторы, соединенные параллельно, как показано на рисунке 2. Из рисунка-2 видно, что напряжение на всех резисторах одинаковое и равно V вольт, но ток через каждый резистор разный в зависимости от значения сопротивления.
Согласно закону Ома,
$$\mathrm{I_{1}=\frac{V}{R_{1}};\:I_{2}=\frac{V}{R_{2}}; \: I_{3}=\frac{V}{R_{3}};\: \cdot \cdot \cdot I_{N}=\frac{V}{R_{N}} }$$
Кроме того,
$$\mathrm{I=I_{1}+I_{2}+I_{3}+ \cdot \cdot \cdot +I_{N}}$$
$$\mathrm{\ Стрелка вправо I=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}}+ \cdot \cdot \cdot +\frac{V }{R_{N}}}$$
$$\mathrm{\Rightarrow I=V\left ( \frac{1}{R_{1}}+\frac{1}{R_{2}}+\ frac {1} {R_ {3}} + \ cdot \ cdot \ cdot + \ frac {1} {R_ {N}} \ right )} $ $
Но,
$ $ \ mathrm {\ frac {I }{V}=\frac{1}{R_{eq}}}$$
Следовательно,
$$\mathrm{\frac{1}{R_{eq}}=\frac{1}{R_{ 1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+ \cdot \cdot \cdot +\frac{1}{R_{N}}}$$
Следовательно, при параллельном соединении нескольких сопротивлений обратная величина
эквивалентное сопротивление комбинации равно сумме обратных величин отдельных
сопротивления.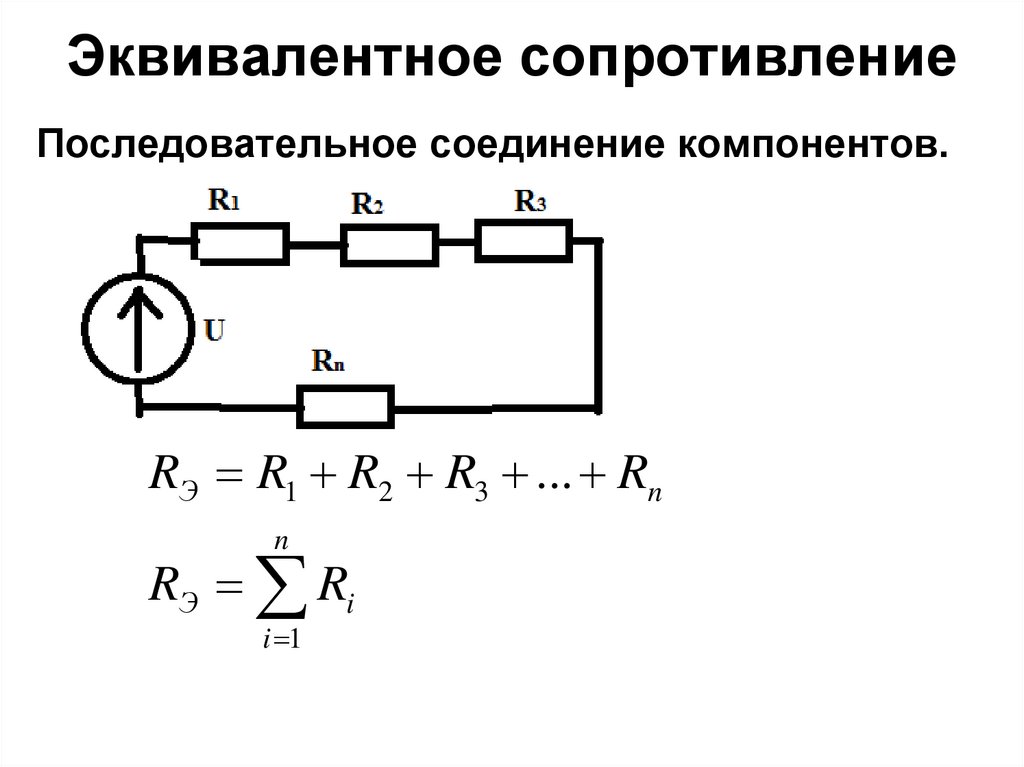
При параллельном соединении только двух резисторов эквивалентное сопротивление равно определяется как,
$ $ \ mathrm {\ frac {1} {R_ {eq}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} = \ frac {R_ {1}+R_{2}}{R_{1}R_{2}}}$$
$$\mathrm{\следовательно, R_{eq}=\frac{R_{1}R_{2}}{R_ {1}+R_{2}}}$$
Следовательно, при параллельном соединении двух резисторов эквивалентное сопротивление комбинация равна произведению, деленному на сумму двух сопротивлений.
Особый случай − Когда все N-резисторы, соединенные параллельно, имеют одинаковое значение сопротивления (скажем, R), тогда эквивалентное сопротивление комбинации определяется как
$$\mathrm{ R_{eq}=\frac{R}{N}}$$
Ниже приведены важные моменты, касающиеся параллели. комбинация резисторов −
Эквивалентное сопротивление параллельной комбинации резисторов меньше наименьшего сопротивления в комбинации.
Ток через каждое сопротивление разный.

Напряжение на всех сопротивлениях одинаковое.
Параллельная комбинация резисторов действует как делитель тока, поскольку она делит один электрический ток на несколько токов.
Эквивалентное сопротивление последовательно-параллельной комбинации резисторов
Иногда мы имеем дело с такими электрическими цепями, в которых несколько резисторов соединены последовательно. и некоторые другие параллельно. Такая комбинация резисторов обычно называется последовательно-параллельная комбинация резисторов . На рис. 3 показана сеть резисторов, которая с резисторами, соединенными последовательно-параллельно.
Эквивалентное сопротивление последовательно-параллельной комбинации резисторов рассчитывается в следующие два шага —
Шаг 1
$$\mathrm{ R_{cd}=\frac{R_{2}R_{3}}{R_{2}+R_{3}}}$$
Шаг 2
Вычислить эквивалент сопротивления последовательно соединенных резисторов. Таким образом, для данного
Например, у нас есть
Таким образом, для данного
Например, у нас есть
$$\mathrm{ R_{eq}=R_{1}+R_{cd}+R_{4}}$$
Или
$$\mathrm{ R_{eq}=R_ {1}+\влево ( \frac{R_{2}R_{3}}{R_{2}+R_{3}} \right )+R_{4}}$$
Числовой пример (1)
Рассчитайте эквивалентное сопротивление следующей резистивной цепи −
Решение
Как видно, в данной цепи резисторы соединены последовательно. Таким образом, их эквивалентное сопротивление будет равно
$$\mathrm{ R_{eq}=10 + 20 + 10 + 20 + 10}$$
$$\mathrm{ R_{eq}=70\: \Omega }$$
Числовой пример (2)
Рассчитайте эквивалентное сопротивление следующей резистивной цепи −
Решение
При осмотре видно, что резисторы сети расположены параллельно. Таким образом эквивалентное сопротивление комбинации будет,
$$\mathrm{\frac{1}{R_{eq}} =\frac{1}{10}+\frac{1}{20}+\frac{1} {20} }$$
$$\mathrm{\frac{1}{R_{eq}} =\frac{2 + 1 + 1}{20}+=\frac{4}{20}}$$
$$\mathrm{\следовательно, R_{eq} =5 \: \Omega } $$
Численный пример (3)
Рассчитайте эквивалентное сопротивление следующей резистивной сети.
Решение
Как мы видим, в сети есть несколько резисторов, соединенных последовательно, и несколько резисторов, соединенных параллельно.
Эквивалентное сопротивление параллельных сопротивлений 10 Ом и 20 Ом составляет {\Rightarrow R_{cd} =\frac{ 200}{30}=6,67\, \Omega }$$
Теперь все резисторы соединены последовательно. Таким образом, эквивалентное сопротивление сети есть,
$$\mathrm{ R_{eq} =5 + 6,67 + 5=16,67\, \Omega } $$
Заключение
В этом уроке мы обсудили, что набор резисторов можно комбинировать тремя способами — последовательно, параллельные и последовательно-параллельные. При последовательном соединении эквивалентное сопротивление комбинация равна сумме всех сопротивлений. При параллельном соединении взаимное эквивалентного сопротивления комбинации равно обратному значению отдельных сопротивления.
Сопротивления объединяются последовательно и параллельно в соответствии с требованиями схемы или для
ввести нужное значение сопротивления в цепи, когда нет одиночного сопротивления
доступным для этого конкретного значения сопротивления.
Видео с вопросами: определение эквивалентного сопротивления комбинированной цепи
Стенограмма видео
Показанная схема содержит оба последовательные и параллельные комбинации резисторов. Каков общий ток в схема показана? Дайте ответ с точностью до одной запятой место.
Рассматривая нашу схему, мы видим
что здесь задействованы четыре резистора и одна ячейка. Положительный терминал этой клетки
указывает вправо. Итак, условно заряд будет
поток по часовой стрелке вокруг контура. После этого заряд проходит через
первый резистор, он доберется до этой точки разветвления вот здесь. Ток будет делиться на основе
относительные сопротивления этих двух параллельных ветвей проходят через
ветви, а затем воссоединиться. После этого общее или объединенное
ток в цепи затем будет проходить через этот резистор 1,6 Ом и дальше к
отрицательный полюс нашей клетки.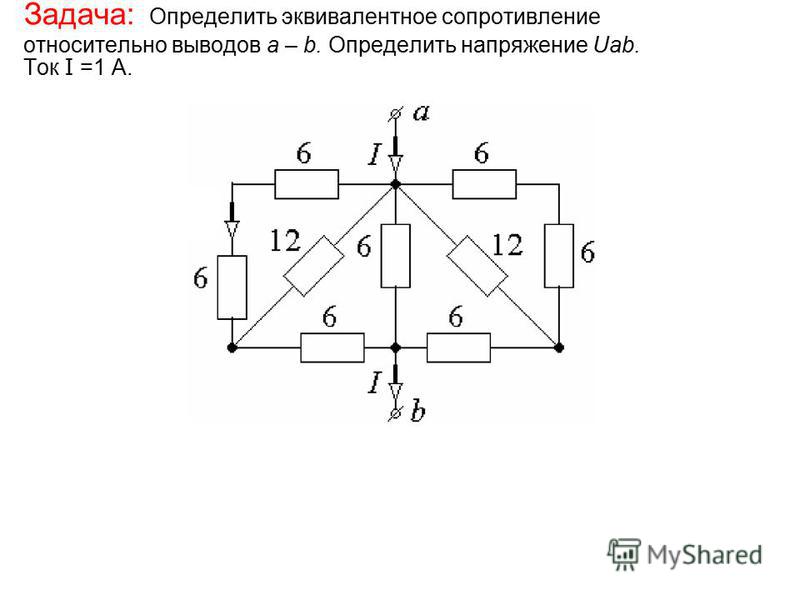
Назовем общий ток в нашем схема 𝐼 подт. Это то значение, которое мы хотим решить для. Мы можем начать делать это с вспоминая закон Ома, который говорит нам, что разность потенциалов в цепи равно току в этой цепи, умноженному на полное сопротивление цепи. Разделив обе части закона Ома на сопротивления 𝑅, мы находим, что 𝐼 равно 𝑉, деленному на 𝑅. Итак, если мы знаем общее разность потенциалов в нашей цепи 𝑉 и полное сопротивление цепи 𝑅, мы можем использовать эти значения для определения полного тока цепи 𝐼. В нашем случае полная схема ток 𝐼 sub t равен 5,5 вольт, разность потенциалов, подаваемая нашим ячейки, деленное на общее сопротивление в цепи, которое мы будем называть 𝑅 sub t.
Чтобы найти 𝑅 sub t, нам понадобится
объединить сопротивления всех четырех наших резисторов в один эффективный
сопротивление.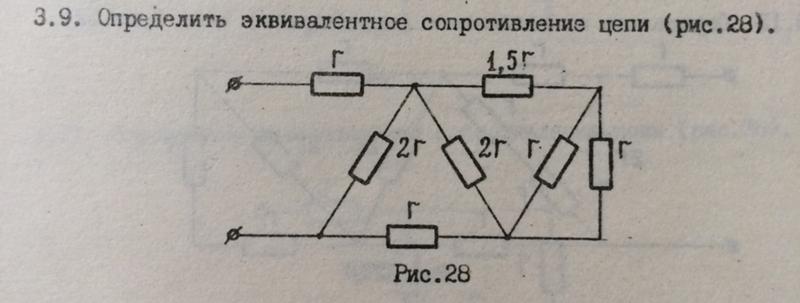 Этот процесс займет несколько шагов
потому что, как отмечается в нашей постановке задачи, здесь у нас есть резисторы, подключенные как к
последовательно и параллельно. Начнем с рассмотрения
резисторы, расположенные параллельно. В общем, если у нас ровно два
резисторов, 𝑅 один и 𝑅 два, параллельно друг другу, то эффективное
сопротивление этих резисторов, назовем его 𝑅 sub p, равно 𝑅 один раз 𝑅 два
разделить на 𝑅 один плюс 𝑅 два.
Этот процесс займет несколько шагов
потому что, как отмечается в нашей постановке задачи, здесь у нас есть резисторы, подключенные как к
последовательно и параллельно. Начнем с рассмотрения
резисторы, расположенные параллельно. В общем, если у нас ровно два
резисторов, 𝑅 один и 𝑅 два, параллельно друг другу, то эффективное
сопротивление этих резисторов, назовем его 𝑅 sub p, равно 𝑅 один раз 𝑅 два
разделить на 𝑅 один плюс 𝑅 два.
Когда мы комбинируем сопротивление в нашей
цепи, чтобы прийти к одному общему сопротивлению цепи, мы можем сказать, что
фактически этот резистор 2,5 Ом и резистор 3,2 Ом, включенные параллельно, одинаковы.
как наличие одного единственного резистора с сопротивлением 2,5 Ом, умноженное на 3,2 Ом.
разделить на 2,5 Ом плюс 3,2 Ом. Здесь мы применили наше правило для
эквивалентное сопротивление двух резисторов, включенных параллельно.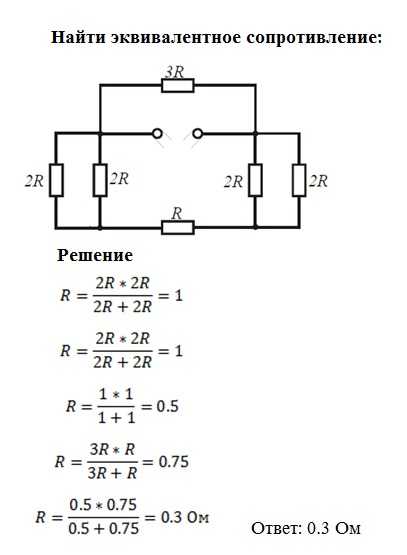
Обратите внимание, что теперь у нас фактически есть три резистора в нашей схеме. И все эти три резистора последовательно. Эквивалентное сопротивление трех резисторов, соединенных последовательно друг с другом, равна сумме отдельных значения сопротивления. Все это означает, что у нас теперь достаточно информация для написания выражения для полного сопротивления в нашей цепи 𝑅 sub т. По нашему добавлению резистора серии правило, мы знаем, что 𝑅 sub t равно сопротивлению нашего первого резистора, 1,5 Ом, плюс эквивалентное сопротивление нашего второго резистора плюс сопротивление нашего третьего резистор, 1,6 Ом. Если мы введем это выражение для 𝑅 подставьте t в наш калькулятор, мы получим результат около 4,503 Ом.
Теперь у нас есть значение, которое мы можем использовать для
𝑅 подставьте t в наше выражение, чтобы найти общий ток цепи.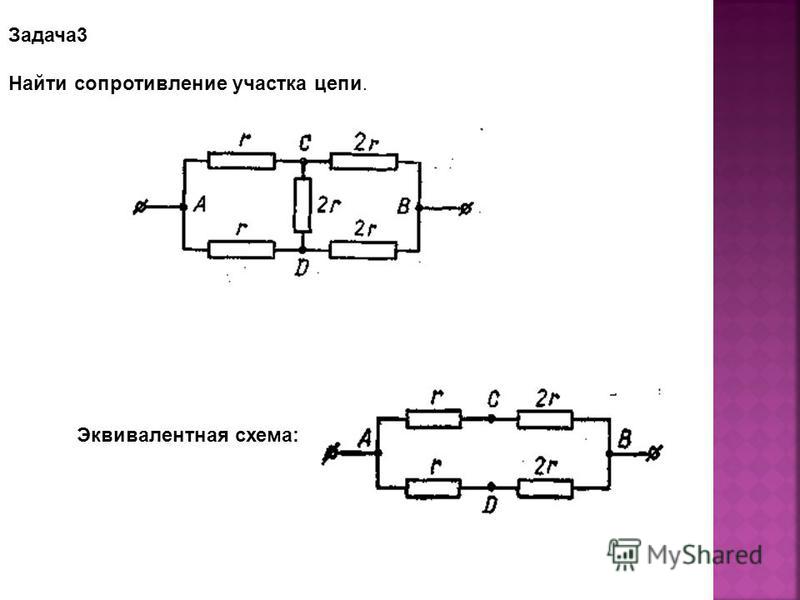 𝐼 sub t равно 5,5 вольт, разделенных
на 4,503 и так далее Ом. И до одного десятичного знака, это
равен 1,2 ампера. Для этого уровня точности 1,2
ампер — это общий ток в цепи.
𝐼 sub t равно 5,5 вольт, разделенных
на 4,503 и так далее Ом. И до одного десятичного знака, это
равен 1,2 ампера. Для этого уровня точности 1,2
ампер — это общий ток в цепи.
Давайте теперь посмотрим на вторую часть нашего вопрос.
Какова общая рассеиваемая мощность по схеме? Дайте ответ с точностью до одной запятой место.
Электрическая цепь рассеивается мощность за счет передачи энергии от цепи с течением времени. Например, мощность рассеивается когда резисторы нагреваются и передают тепловую энергию окружающей среде. Эта часть нашего вопроса задает нам о полной мощности, рассеиваемой цепью. Эта мощность в общем случае равна разность потенциалов в цепи, умноженная на общую цепь ток.
В нашем случае этот потенциал
разница составляет 5,5 вольт, а этот ток, как мы видели, равен 5,5 вольтам, деленным на
полное сопротивление цепи.


 Калькулятор для расчета
Калькулятор для расчета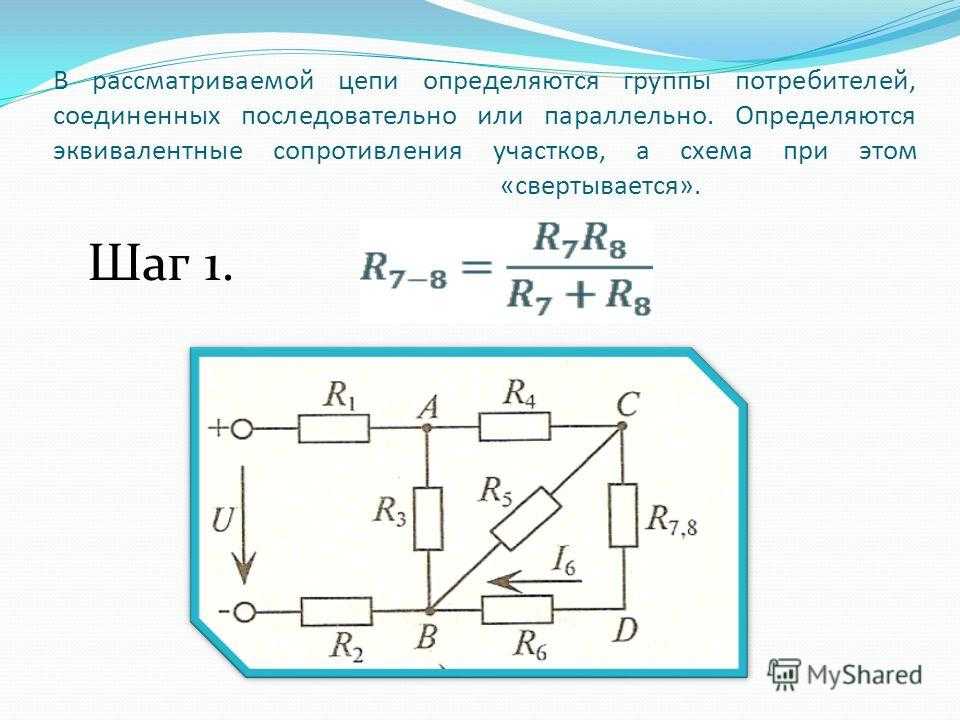
 = R1+R2.
= R1+R2.