v, который находится в том же направлении, что и v.

Каковы единицы единичного вектора? Единичные векторы — это векторы, величина ровно 1 единица.

Что такое единичный вектор в математике? В математике единичный вектор в стандартизированном векторном пространстве — это вектор (часто пространственный вектор) длины 1. Единичный вектор часто обозначается строчной буквой с циркумфлексом или «шляпой», например. (произносится как «в-шляпа»).

Во-вторых, может ли единичный вектор иметь единицу? Единичный вектор имеет только направление и никаких единиц или размеров.

Что такое класс единичных векторов 11?

Единичные векторы

Единичный вектор вектор единичной величины и определенного направления. Они задают только направление. Они не имеют никакого измерения и единицы. В прямоугольной системе координат оси x, y и z представлены единичными векторами î, ĵ и k̂. Эти единичные векторы перпендикулярны друг другу.

тогда Что такое единичный вектор в исчислении? Единичный вектор вектор, который имеет величину в одну единицу и может иметь любое направление. … Единичные векторы несут значение направления вектора в каждом из координатных направлений. Число перед единичным вектором показывает его величину или длину.

Что такое значение единичного вектора? Единичный вектор — это вектор, который имеет Величина 1. Они помечены знаком » «, например: . Любой вектор может стать единичным вектором, если его разделить на величину вектора.

Как найти длину единичного вектора?

Всегда ли единичный вектор равен 1? Единственная цель единичного вектора — указать направление вектора силы вдоль линии относительно начала координат, поэтому его величина только одна. ‘) рядом с ней. Вектор может быть представлен в пространстве с помощью единичных векторов.

Что называется единичным вектором?

Единичный вектор вектор длины 1, иногда также называемый вектором направления (Джеффрис и Джеффрис, 1988). Единичный вектор, имеющий то же направление, что и заданный (ненулевой) вектор, определяется как. где обозначает норму , является единичным вектором в том же направлении, что и (конечный) вектор .

Что такое физика единичных векторов? Единичный вектор в физике вектор единичной величины и определенного направления. Единичный вектор определяет единственное направление. У них нет размеров и единиц измерения. В прямоугольной системе координат представлены оси x, y и z.

Как найти единичный вектор в трех измерениях?

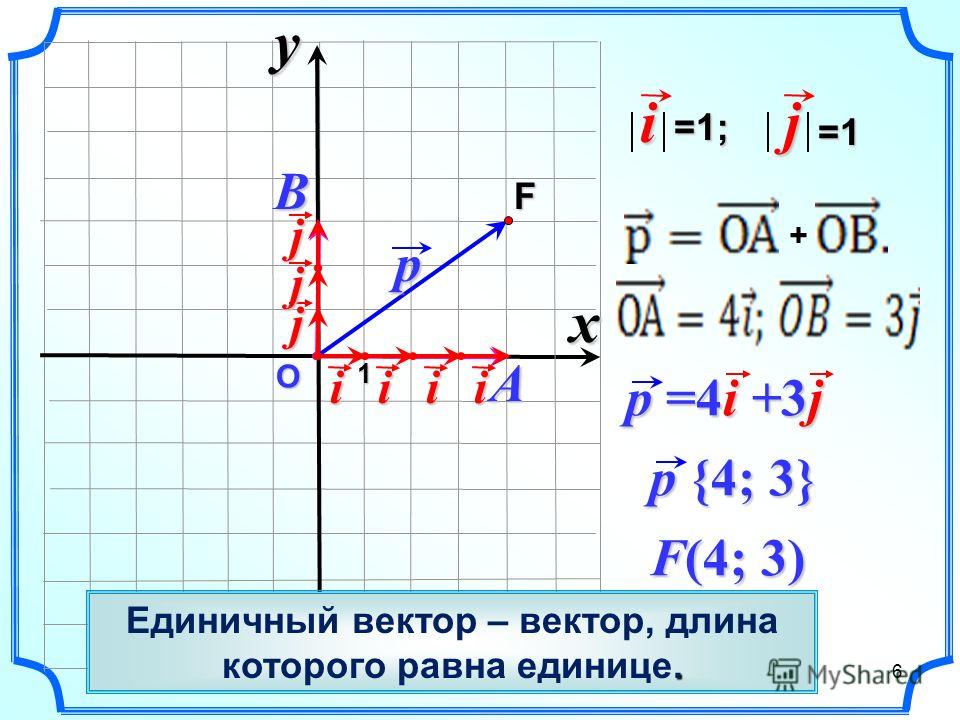
Что такое единичные векторы IJ и K? Единичный вектор — это вектор, величина которого равна 1.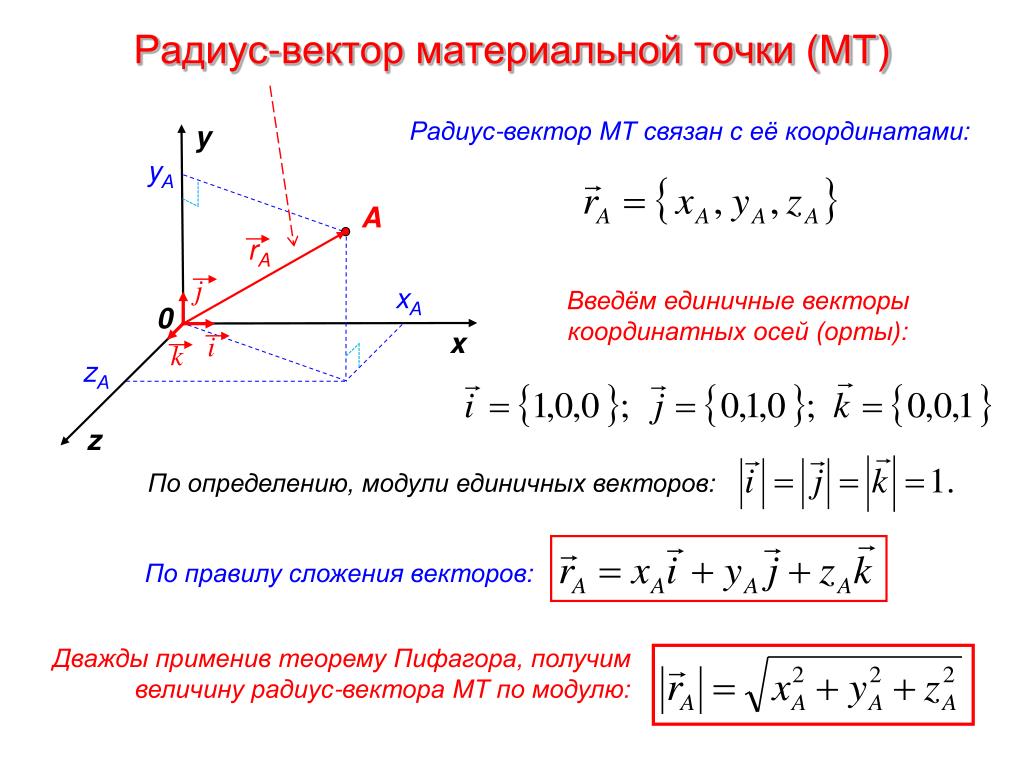 … единичный вектор в направлении оси x равен i, единичный вектор в направлении оси y равен j, а единичный вектор в направлении оси z равен k.

Сколько существует единичных векторов?

Единичный вектор для данного вектора указывает в том же направлении, что и этот вектор. Здесь есть только один единичный вектор в заданном направлении.

Является ли вектор безразмерным? Нет, единичные векторы не безразмерны. Они имеют ту же единицу измерения, что и родительский вектор. Величина единичного вектора равна 1, а направление такое же, как у родительского вектора.

Как вы пишете обозначение единичного вектора?

Теперь можно определить следующие три вектора в трех координатных направлениях. Vx = Vxi, Vy = Vyj, Vz = Vz k. Используя правило треугольника для сложения векторов дважды, это дает V = Vx + Vy + Vz = Vxi+ Vyj+ Vz k. Это известно как единичное векторное обозначение вектора.

6.2. Найти единичный вектор того же направления что и .

Единичный вектор находится: , где– модуль вектора.

Находим

тогда

Ответ: .

Примечание. Координаты единичного вектора должны быть не больше единицы.

6.3. Найти длину и направляющие косинусы вектора . Сравните с ответом в предыдущем пункте. Сделайте выводы.

Длина вектора – это есть его модуль:

, а направляющие косинусы мы можем найти по формуле одного из способов задания векторов:

Из полученного мы видим, что направляющие косинусы это и есть координаты единичного вектора.

Ответ: ,,,.

6.4. Найти .

Необходимо выполнить действия умножения вектора на число, сложения и модуль.

Почленно перемножаем координаты векторов на число.

Почленно складываем координаты векторов.

Находим модуль вектора.

Ответ:

6.5. Определить координаты вектора , коллинеарного вектору, зная, чтои он направлен в сторону, противоположную вектору.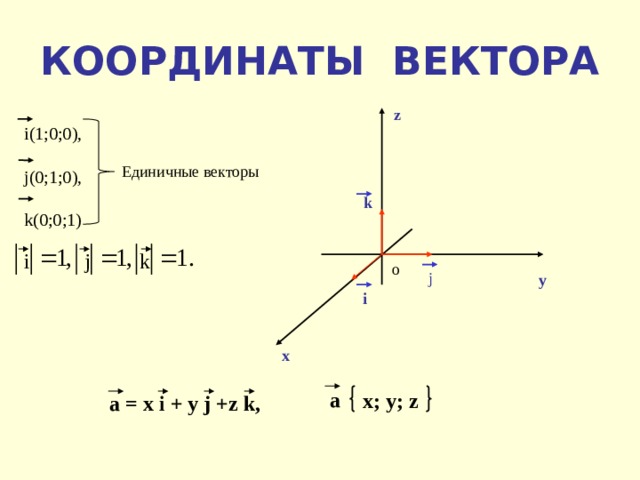

Вектор коллинеарен вектору, значит, его единичный вектор равен единичному векторутолько со знаком минус, т.к. направлен в противоположную сторону.

Единичный вектор имеет длину равную 1, значит, если его умножить на 5, то его длинна будет равна пяти.

Находим

Ответ:

6.6. Вычислить скалярные произведения и. Перпендикулярны ли векторыи,имежду собой?

Выполним скалярное произведение векторов.

Если вектора перпендикулярны, их скалярное произведение равно нулю.

Мы видим, что в нашем случае вектораиперпендикулярны.

Ответ: ,, векторы не перпендикулярны.

Примечание. Геометрический смысл скалярного произведения малоприменим на практике, но все-таки существует. Результат такого действия можно изобразить и вычислить геометрически.

6.7. Найти работу, совершённую материальной точкой к которой приложена сила , при перемещении её из точки B в точку С.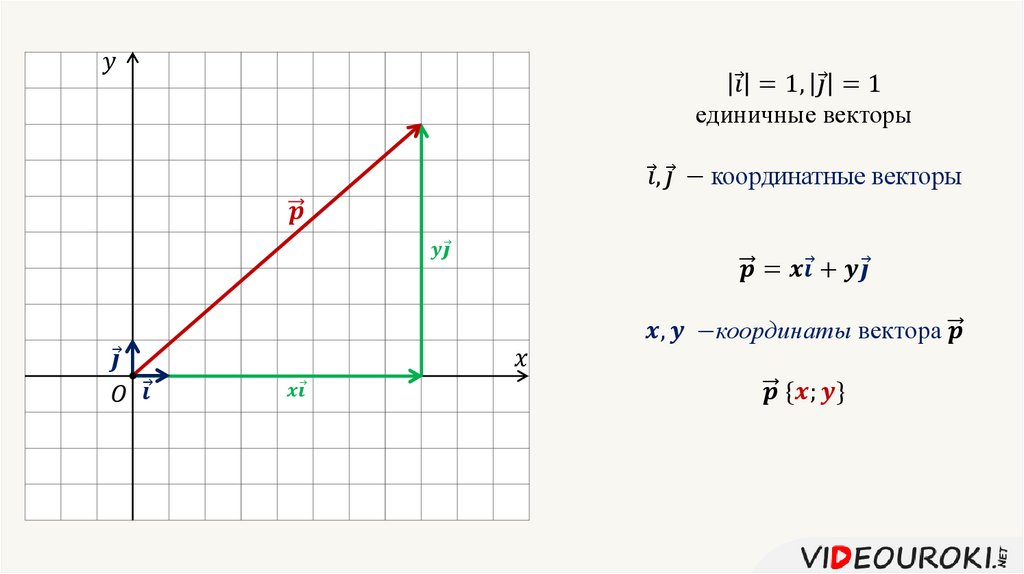

Физический смысл скалярного произведения – это работа. Вектор силы здесь , вектор перемещения – это. А произведение этих векторов и будет искомой работой.

Находим работу

Ответ: -3.

6.8. Найти внутренний угол при вершине A и внешний угол при вершине C треугольника ABC.

Из определения, скалярного произведения векторов получим формулу нахождения угла: .

Далее, нам нужно определить вектора, между которыми будем искать угол.

Внутренний угол будем искать как угол между векторами, выходящими из одной точки.

Для нахождения внешнего угла нужно совмещать вектора, таким образом, чтоб они выходили из одной точки. Рисунок это поясняет.

Стоит заметить, что , только имеют разные начальные координаты.

Находим необходимые вектора и углы

Ответ: внутренний угол при вершине А = , внешний угол при вершине В =.

Вспомним вектора-орты: ,,.

Проекция находится также из скалярного произведения

–проекция b на a.

Ранее полученные нами вектора

, ,

Находим проекцию

Находим вторую проекцию

Ответ: ,

Примечание. Знак минуса при нахождении проекции означает то, что проекция опускается не на сам вектор, а в противоположную сторону, на линию на которой лежит этот вектор.

6.10. Вычислить .

Выполним векторное произведение векторов

Найдем модуль

Синус угла между векторами найдём из определения векторного произведения векторов

Ответ: ,,.

6.11. Найти площадь треугольника ABC и длину высоты, опушенной из точки С.

Геометрический смысл модуля векторного произведения состоит в том, что это площадь параллелограмма, образованного этими векторами. А площадь треугольника равна половине площади параллелограмма.

Площадь треугольника также можно найти как произведение высоты, на основание, делённое на два, из этого можно вывести формулу нахождения высоты.

Таким образом, найдём высоту

Ответ: ,.

6.12. Найти единичный вектор, перпендикулярный векторам и.

Результатом скалярного произведения есть вектор, который перпендикулярный двум исходным. А единичный вектор – это вектор, делённый на его длину.

Ранее, нами было найдено:

,

Ответ: .

6.13. Определить величину и направляющие косинусы момента силы , приложенной к А относительно точки С.

Физический смысл векторного произведения – это момент силы. Приведём иллюстрацию к данному заданию.

Находим момент силы

Ответ: .

6. 14. Лежат ли векторы ,ив одной плоскости? Могут ли эти векторы образовывать базис пространства? Почему? Если могут, разложите по этому базису вектор.

Чтобы проверить лежат ли вектора в одной плоскости необходимо выполнить смешанное произведение этих векторов.

Смешанное произведение не равно нулю, следовательно, вектора не лежат в одной плоскости (не компланарные) и могут образовывать базис. Разложим по этому базису.

Разложим по базису, решив уравнение

Ответ: Векторы ,ине лежат в одной плоскости..

6.15. Найти . Чему равен объём пирамиды с вершинами A, B, C, D и её высота, опущенная из точки A на основание BCD.

Геометрический смысл смешанного произведения в том, что это объём параллелепипеда образованного этими векторами.

Объём же пирамиды в шесть раз меньше объёма параллелепипеда.

Объём пирамиды, ещё можно найти так:

Получим формулу нахождения высоты

Находим

Находим высоту

Ответ: объём = 2.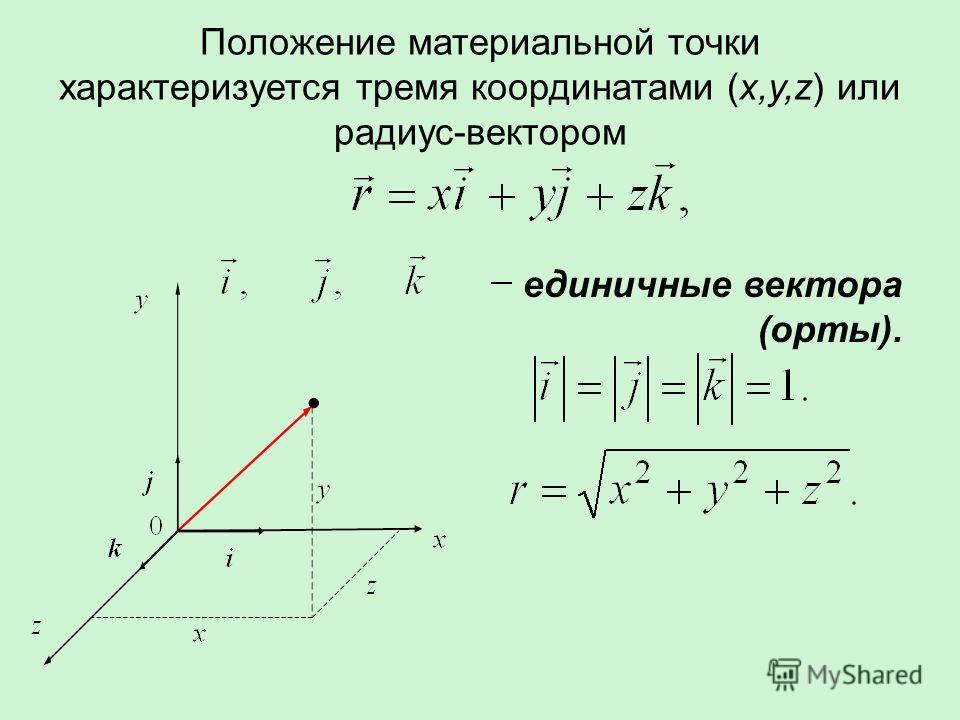

5, высота =.

6.16. Вычислить и.

–над этим заданием предлагаем вам подумать самим.

–выполним произведение.

Ранее было получено

Ответ: .

6.17. Вычислить

Выполним действия по частям

1)

2)

3)

4)

5)

Суммируем полученные значения

Ответ: .

6.18. Найти вектор , зная, что он перпендикулярен векторами, а его проекция на векторравна 5.

Разобьем данную задачу на две подзадачи

1) Найдём вектор, перпендикулярный векторам ипроизвольной длинны.

Перпендикулярный вектор мы получим в результате векторного произведения

Ранее, нами было найдено:

Искомый вектор отличается лишь длинной, от полученного

2) Найдем через уравнение

Ответ:

6.19. Найти вектор , удовлетворяющий условиям,,.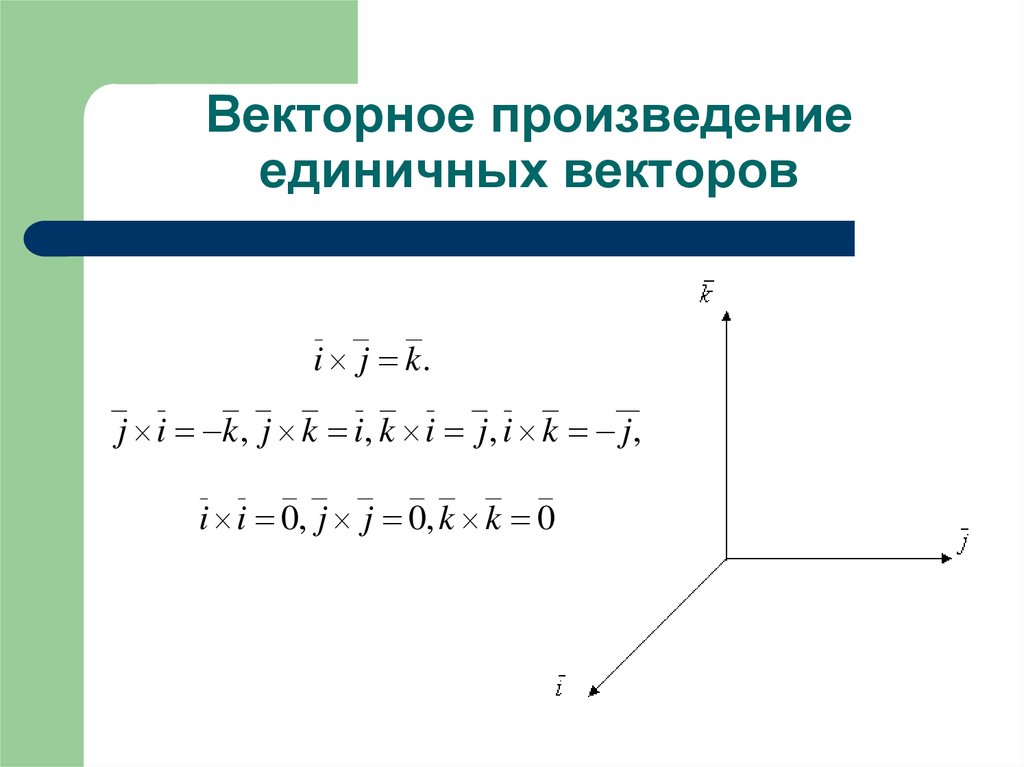

Рассмотрим более детально данные условия.

Это система линейных уравнений. Составим и решим данную систему.

Ответ:

6.20. Определить координаты какого-либо вектора , компланарного с векторамии, и перпендикулярного вектору.

В данном задании два условия: компланарность векторов и перпендикулярность, выполним сначала первое условие, а потом второе.

1) Если вектора компланарны, значит их смешанное произведение равно нулю.

Отсюда получим некоторую зависимость координат вектора

Найдем вектор .

2) Если вектора перпендикулярны, значит их скалярное произведение равно нулю

Мы получили вторую зависимость координат искомого вектора

Для любого значения вектор будет удовлетворять условиям. Подставим.

Ответ: .

Аналитическая геометрия

Как рассчитать единичный вектор?

Физические величины делятся на два типа: «векторные» и «скалярные».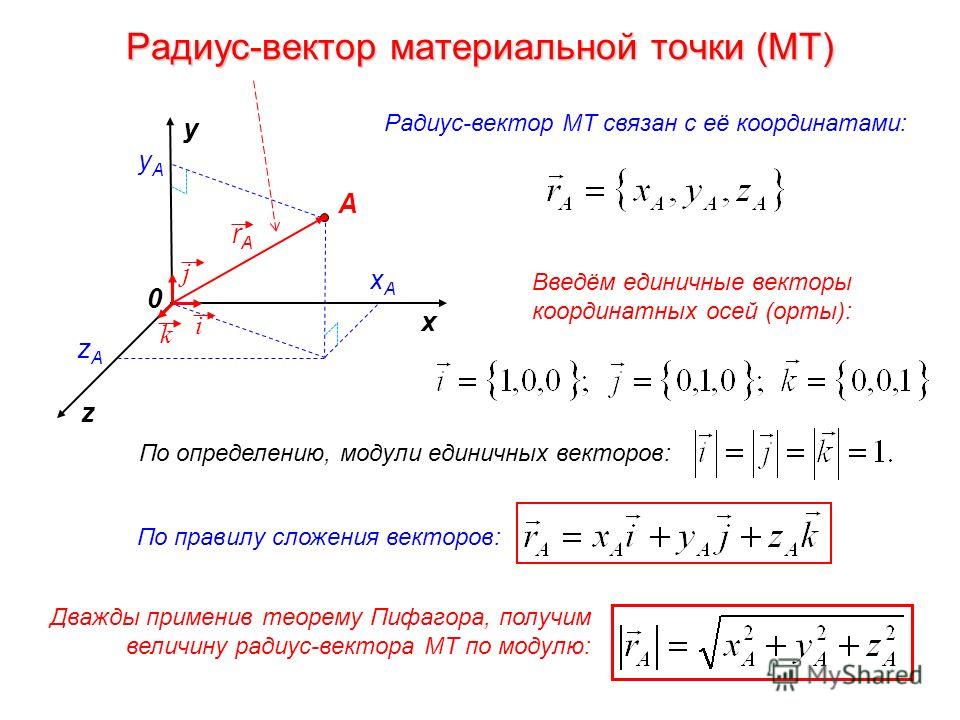 Термин «вектор» относится к физической величине, которая имеет как величину, так и направление. Это физические величины, которые подчиняются треугольному закону сложения векторов. Некоторыми примерами векторных величин являются электрическое поле, смещение, импульс, скорость, сила и ускорение. Все эти величины имеют как величину, так и направление. С другой стороны, «скалярные» величины имеют только величину. Некоторыми примерами скалярных величин являются расстояние, длина, объем, температура и площадь.

Типы векторов

• Равные векторы: Векторы, имеющие одинаковую величину и одинаковое направление, называются равными векторами.
• Коллинеарные векторы: Векторы, направленные либо в одном, либо в противоположном направлении друг другу, называются коллинеарными векторами.
• Параллельные векторы: Параллельные векторы также известны как подобные векторы . Коллинеарные векторы с одинаковыми направлениями называются параллельными векторами. Угол между этими векторами равен нулю.
• Антипараллельные векторы: Антипараллельные векторы также известны как непохожие векторы. Коллинеарные векторы с противоположными направлениями называются антипараллельными векторами. Угол между этими векторами 180°.
• Копланарные векторы: Все векторы, лежащие в одной плоскости, называются копланарными векторами.
• Нулевые векторы: Вектор с одинаковыми начальной и конечной точками называется нулевым вектором. Его также называют Null vector 9.0009 . Величина такого вектора равна 0, а его направление неопределенно.

Вычисление единичного вектора

Единичный вектор — это вектор величины 1, направленный вдоль заданного вектора. Он представляет направление данного вектора. Единичный вектор вектора находится путем деления вектора на его модуль. Модуль вектора — это величина вектора.

Он представлен символом ‘  ‘(шляпа или кепка) над переменной как  и определяется как,

Где |А| — модуль вектора A, а для вектора |A| определяется как,

Таким образом, для вектора единичный вектор определяется как,

Примеры задач

Задача 1: задано . Найдите .

Решение:

Модуль вектора,

= = √9

= 3

Единый вектор,

=

=

=

=

Проблема 2: Является ли вектор, заданный , также единичным вектором?

Решение:

Модуль вектора, 

=  = √3

Величина этого вектора не равна 1. Следовательно, это не единичный вектор.

Задача 3. Найдите единичный вектор в направлении .

Решение:

Модуль вектора, 

=  = √3

Единичный вектор, 

= 

=

Задача 4. Если — единичный вектор, найдите значение z.

Решение:

Магнитуда единичного вектора составляет 1, а это означает:

, что означает,

Квадрат с обеих сторон,

Вопрос 5: Find

. единичный вектор .

Решение:

Модуль вектора,

=

Единичный вектор,

=

=

Вопрос 6. Найдите единичный вектор вдоль .

Решение:

Модуль вектора,

=

Единый вектор,

=

=

Вопрос 7: ЕДИНИРОВАНСКИЙ ВЕКТОР НА ГЛАВНА 2 ?2. Находить .

Решение:

Единичный вектор,

Что означает

Таким образом, 

электростатика — Учитывая единичный вектор и Силу, как я могу рассчитать ее компоненты?

спросил 1 год, 3 месяца назад

Изменено 1 год, 3 месяца назад

Просмотрено 559 раз

$\begingroup$ 9{2}$ и вектор направления $(x, y, z). $ Как найти составляющие силы $F_{x}$, $F_{y}$ и $F_{z}$?

• силы
• электростатика
• векторы

$\endgroup$

$\begingroup$

Чтобы найти компоненты любого вектора $\bf F$ с помощью единичных векторов, вы можете использовать скалярное произведение между вектором и каждым единичным вектором.

Таким образом, x-компонента $\bf F$ равна $\bf F\cdot \hat i$, y-компонента равна $\bf F\cdot \hat j$, а z-компонента равна $\bf F\ cdot\hat k$

Если у вас есть «вектор направления» $\bf u=(x,y,z)$, то его единичный вектор будет $$\bf \hat u=\frac{u}{\mid u\mid}$ $ так, что $$\bf F\cdot \hat u$$ является проекцией $\bf F$ в направлении единичного вектора $\bf \hat u$ или компоненты $\bf F$ вдоль $\бф и$.

$\endgroup$

$\begingroup$

Из вашего вопроса несколько неясно, но я интерпретировал $F$ просто как величину силы (скаляр), и вы хотите построить силу этой величины, указывающую вдоль заданного вектора направления.