Найти полное сопротивление участка цепи,… — Учеба и наука

Лучший ответ по мнению автора

Андрей Андреевич 08. 04.13 Лучший ответ по мнению автора

Другие ответы

R=((((R1*R2/R1+R2)+R3))*R4 )/(((R1*R2/(R1+R2))+R3)+R4 ) =2 Ома 08. 04.13

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Владимир Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Похожие вопросы

в момент, когда опоздавший пассажир вбежал на платформу, мимо него за 10 с проехал предпоследний вагон, последний проехал за 8с на сколько времени опоздал пассажир

Молекулярная физика

Колебательный контур состоит из конденсатора емкостью С=2.

5 мкФ

Решено

Чему равна энергия теплового движения…

Решено

интенсивность света

Пользуйтесь нашим приложением

Расчёт сопротивления электрических цепей с использованием законов последовательного и параллельного соединений

• Волкова Вера Васильевна, учитель математики
• Швейкина Юлия Сергеевна, учитель физики

Разделы: Физика

---

Цели:

Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.

Развивающая: развить мышление учащихся, активизировать познавательную деятельность через решение задач на расчет электрических цепей, развить умение рассчитывать параметры электрических цепей и совершенствовать полученные на уроке навыки.

Воспитательная: формирование интереса к изучаемому предмету, продолжить формирование коммуникативных умений.

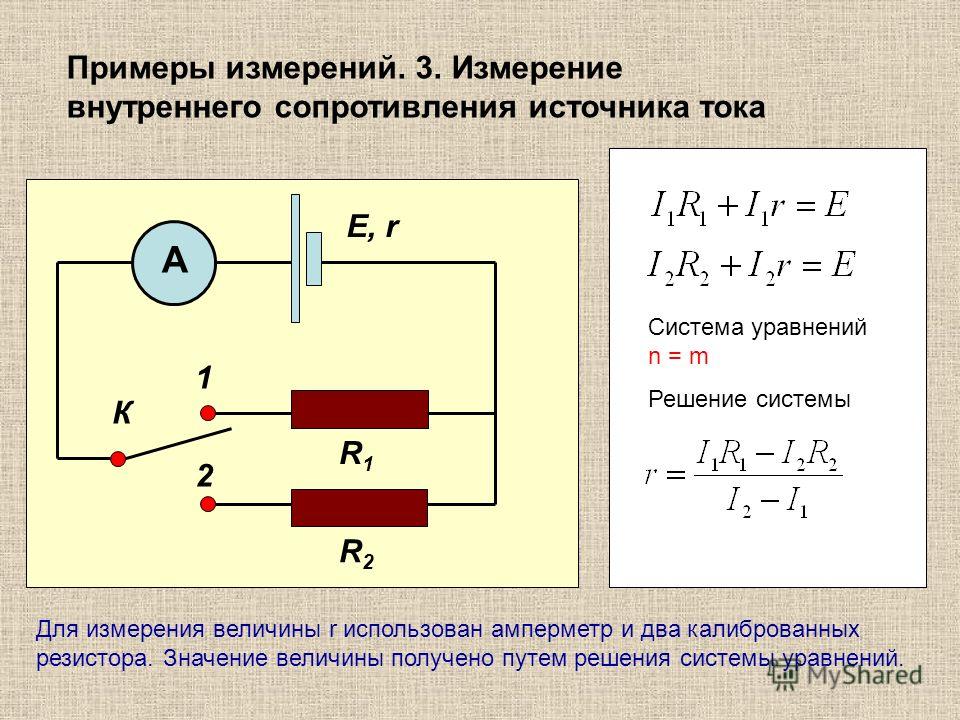
Тип урока: урок проверки и закрепления новых знаний по физике и математике.

Метод проведения урока: практический

Оборудование:

• Громов С.В. Учебник “Физики-9”;
• план урока;
• методика расчета участка электрической цепи постоянного тока;
• карточки-задания.

Приложение 1

Ход урока

Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.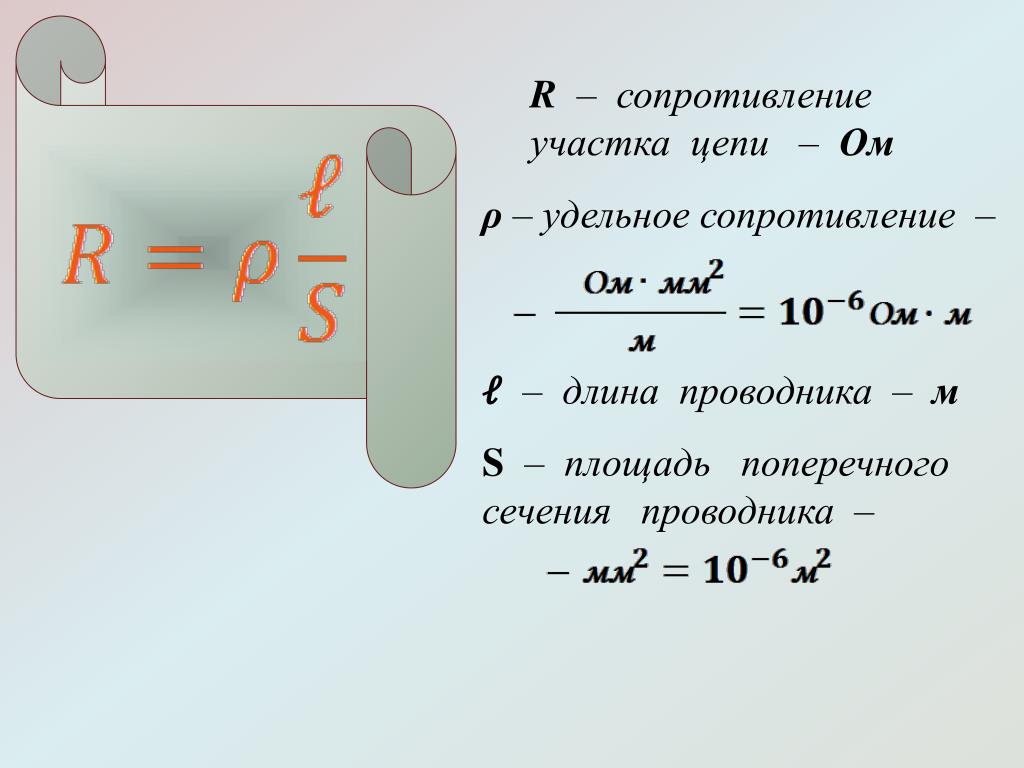

Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:

1) Какие виды соединений бывают и как они изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного соединения?

Рассмотрим расчёт участка электрической цепи на примере следующих задач:

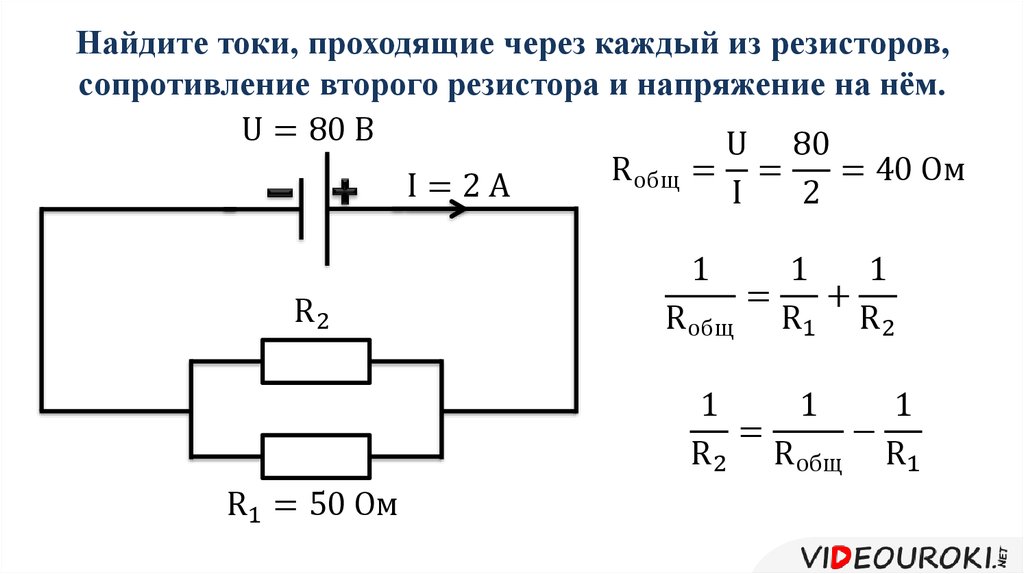
1. Рассчитайте общее электрическое сопротивление участка цепи?

1) Наиболее удалённые от источника элементы – это резисторы R₂ и R₃.

2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R₂ и R₃ подключены параллельно, т.к образуют в соединении два узла, следовательно:

Ом

3) Изображаем получившуюся в результате свёртывания резисторы R₂ и R₃ электрическую схему:

4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R₁ и R_об.1 соединены последовательно, значит:

R_об = R₁ + R_об.1 = 4 Ом + 2 Ом = 6 Ом

Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.

2. Рассчитайте общее электрическое сопротивление участка цепи?

1) Резисторы R₁ и R₂ соединены между собой последовательно:

R_об.1 = R₁ + R₂ = 1 Ом + 2 Ом = 3 Ом

Изобразим полученный электрический участок цепи:

2) Резисторы R₃ и R₄ соединены между собой последовательно:

R_об.2 = R₃ + R₄ = 3 Ом + 4 Ом = 7 Ом

Изобразим полученный электрический участок цепи:

3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление. Так как резисторы R_об.1 и R_об.2 соединены параллельно, значит:

Ом

Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.

3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:

а) Рассчитайте общее электрическое сопротивление участка цепи?

б) Рассчитайте общее электрическое сопротивление участка цепи?

в) Рассчитайте общее электрическое сопротивление участка цепи?

Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.

17. 06.2013

сопротивление и удельное сопротивление | Физика |

Цели обучения

К концу этого раздела вы сможете:

• Объяснить понятие удельного сопротивления.
• Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.
• Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.

Зависимость сопротивления от материала и формы

Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорциональна его длине L , подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет.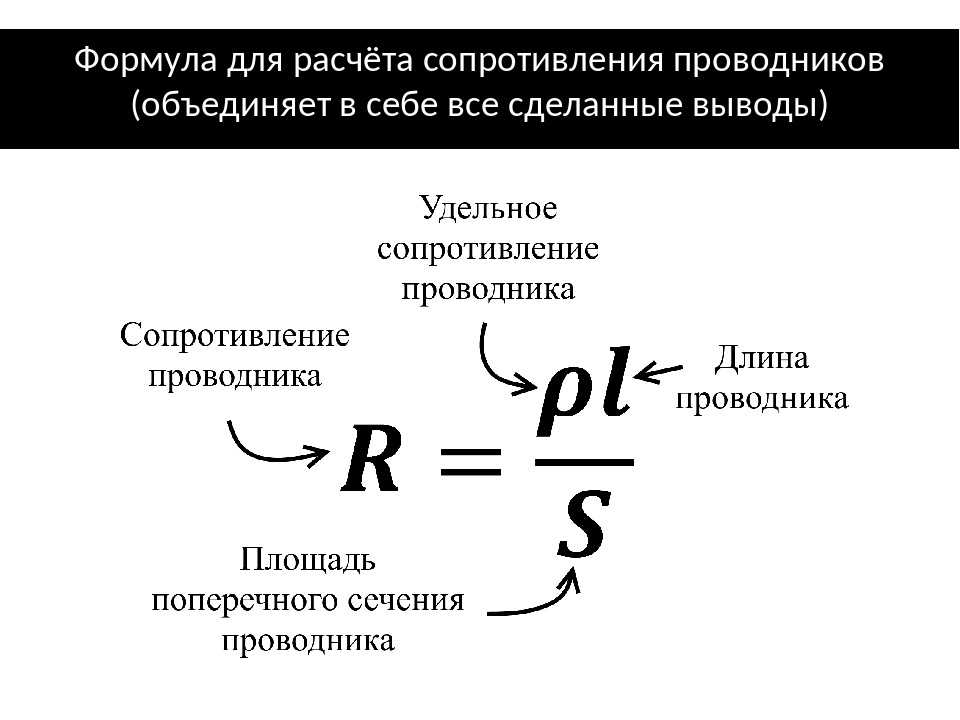 Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле R обратно пропорционально площади поперечного сечения цилиндра A .

Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.

Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Определим удельное сопротивление ρ вещества так, что сопротивление R объекта прямо пропорционально ρ . Удельное сопротивление ρ является внутренним свойством материала, не зависящим от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , равно

R=ρLAR=\frac{\rho L}{A} \\R=AρL​

.

В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах.

Таблица 1. Удельные сопротивления ρ различных материалов при 20ºC

Материал	Удельное сопротивление ρ ( Ом ⋅ м )
Проводники
Серебро	1. 59 × 10 −8
Медь	1. 72 × 10 −8
Золото	2. 44 × 10 −8
Алюминий	2. 65 × 10 −8
Вольфрам	5. 6 × 10 −8
Железо	9. 71 × 10 −8
Платина	10. 6 × 10 −8
Сталь	20 × 10 −8
Свинец	22 × 10 −8
Манганин (сплав меди, марганца, никеля)	44 × 10 −8
Константан (сплав Cu, Ni)	49 × 10 −8
Меркурий	96 × 10 −8
Нихром (сплав Ni, Fe, Cr)	100 × 10 −8
Полупроводники [3]
Углерод (чистый)	3,5 × 10 5
Углерод	(3,5 − 60) × 10 5
Германий (чистый)	600 × 10 −3
Германий	(1−600) × 10 −3
Кремний (чистый)	2300
Кремний	0,1–2300
Изоляторы
Янтарный	5 × 10 14
Стекло	10 9 − 10 14
Люцит	>10 13
Слюда	10 11 − 10 15
Кварц (плавленый)	75 × 10 16
Резина (твердая)	10 13 − 10 16
Сера	10 15
Тефлон	>10 13
Дерево	10 8 − 10 11

Пример 1.

Расчет диаметра резистора: нить накала фары

Нить накала автомобильной фары изготовлена ​​из вольфрама и имеет холодное сопротивление 0,350 Ом. Если нить представляет собой цилиндр длиной 4,00 см (можно свернуть в спираль для экономии места), то каков ее диаметр?

Стратегия

Мы можем изменить уравнение

R=ρLAR=\frac{\rho L}{A}\\R=AρL​

 найти площадь поперечного сечения A нити накала по данной информации. Тогда его диаметр можно найти, предполагая, что он имеет круглое поперечное сечение.

Раствор

Площадь поперечного сечения, найденная перестановкой выражения для сопротивления цилиндра, приведенного в

R=ρLAR=\frac{\rho L}{A}\\R=AρL​

, равна

A=ρLRA =\frac{\rho L}{R}\\A=RρL​

. Подставляя данные значения и принимая 9{-5}\text{м}\end{массив}\\D​==​2(pA​)21​=2(3.146.40×10−9м2​)21​9.0×10−5м​

.

Обсуждение

Диаметр чуть меньше десятой доли миллиметра. Оно приводится только с двумя цифрами, потому что ρ известно только с двумя цифрами.

Изменение сопротивления в зависимости от температуры

Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.)

Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем увеличивается почти линейно с температурой.

И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC и менее) удельное сопротивление ρ изменяется с изменением температуры Δ T , что выражается в следующем уравнении где ρ ₀ — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления . (См. значения α в Таблице 2 ниже.) Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение, чтобы найти р . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет α , близкое к нулю (трем цифрам на шкале в таблице 2), и поэтому его удельное сопротивление лишь незначительно зависит от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Таблица 2. Температурные коэффициенты сопротивления α

Материал	Коэффициент (1/°C) [4]
Проводники
Серебро	3,8 × 10 −3
Медь	3,9 × 10 −3
Золото	3,4 × 10 −3
Алюминий	3,9 × 10 −3
Вольфрам	4,5 × 10 −3
Железо	5,0 × 10 −3
Платина	3,93 × 10 −3
Свинец	3,9 × 10 −3
Манганин (сплав Cu, Mn, Ni)	0,000 × 10 −3
Константан (сплав Cu, Ni)	0,002 × 10 −3
Меркурий	0,89 × 10 −3
Нихром (сплав Ni, Fe, Cr)	0,4 × 10 −3
Полупроводники
Углерод (чистый)	−0,5 × 10 −3
Германий (чистый)	−50 × 10 −3
Кремний (чистый)	−70 × 10 −3

Отметим также, что α является отрицательным для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры.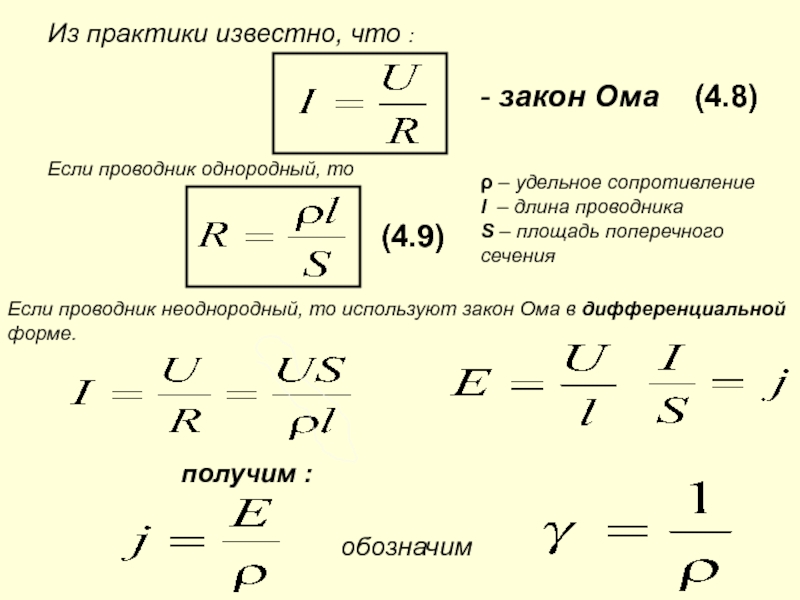 Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R ₀ прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно меняются с температурой, то R будет иметь такую ​​же зависимость от температуры, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A составляет примерно два порядка меньше, чем на ρ .) Таким образом,

R = R ₀ (1 + α or T )

9 – температурная зависимость сопротивления объекта, где R ₀ – исходное сопротивление, а R – сопротивление после изменения температуры Δ T . Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)

Пример 2. Расчет сопротивления: сопротивление горячей нити

Хотя предупреждение должно использоваться при применении ρ = ρ ₀ (1 + α Δ T ) и R = R ₀ (1 + α 2020202020202020202020202020202019 ₀ (1 + α 20202020202020202020202020202020202020 ₀ (1 + α 20202020202020202020202010 ₀ (1 + . {-3}/º\текст{C}\вправо)\влево(2830°\текст{C}\вправо)\вправо]\\ & =& {4,8\Omega }\end{массив}\\R​===​R0​(1+αΔT)(0.350Ω)[1+(4.5×10−3/ºC)(2830ºC)]4.8Ω​

.

Обсуждение

Это значение согласуется с примером сопротивления фары в Законе Ома: сопротивление и простые схемы.

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

Нажмите, чтобы запустить симуляцию.

Резюме сечения

• Сопротивление R цилиндра длиной L и площадью поперечного сечения A равно

  R=ρLAR=\frac{\rho L}{A}\\R=AρL​

  , где ρ — удельное сопротивление материала.
• Значения ρ в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .
• Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление

  ρ=ρ0(1+αΔT)\rho ={\rho }_{0}\left(\text{1}+\alpha \Delta T\right)\\ρ=ρ0​( 1+αΔT)

  , где ρ ₀  – исходное удельное сопротивление, а

  α\alpha α

  – температурный коэффициент удельного сопротивления.
• В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
• Сопротивление R объекта также зависит от температуры:

  R=R0(1+αΔT)R={R}_{0}\left(\text{1}+\alpha \Delta T\right)\ \R=R0​(1+αΔT)

  , где R ₀ — исходное сопротивление, а R — сопротивление после изменения температуры.

Концептуальные вопросы

1. В каком из трех полупроводниковых материалов, перечисленных в таблице 1, примеси создают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого и определите, имеет ли чистый полупроводник более высокую или более низкую проводимость.)

2. Зависит ли сопротивление объекта от пути прохождения тока через него? Рассмотрим, например, прямоугольный стержень — одинаково ли его сопротивление по длине и по ширине? (См. рис. 5.)

Рис. 5. Встречает ли ток, проходящий двумя разными путями через один и тот же объект, разное сопротивление?

3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?

4. Объясните, почему

R=R0(1+αΔT)R={R}_{0}\left(1+\alpha\Delta T\right)\\R=R0​(1+αΔT)

для температурное изменение сопротивления R  объекта не так точно, как

ρ=ρ0(1+αΔT)\rho ={\rho }_{0}\left({1}+\alpha \Delta T \справа)\\ρ=ρ0​(1+αΔT)

, что дает температурное изменение удельного сопротивления ρ .

Задачи и упражнения

1. Чему равно сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?

2. Диаметр медной проволоки нулевого калибра составляет 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.

3. Если вольфрамовая нить накаливания диаметром 0,100 мм в электрической лампочке должна иметь сопротивление 0,200 Ом при 20°С, какой длины она должна быть?

4. Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как это могло бы быть в бытовой электропроводке).

5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см, если к нему приложено напряжение 1,00 × 10 ³ В? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц. )

6. (а) До какой температуры вы должны нагреть медный провод, первоначально равный 20,0 °С, чтобы удвоить его сопротивление, не принимая во внимание изменение размеров? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?

7. Резистор из нихромовой проволоки используется в приложениях, где его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?

8. Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?

9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит чисто углеродные резисторы. Во сколько раз увеличивается их сопротивление в этом диапазоне?

10. а) Из какого материала сделан провод, если он имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77,7 Ом при 20,0°С? б) Каково его сопротивление при 150°С?

11. Предполагая постоянный температурный коэффициент удельного сопротивления, каково максимальное процентное уменьшение сопротивления константановой проволоки, начиная с 20,0ºC?

12. Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?

13. Медный провод имеет сопротивление 0,500 Ом при 20,0°С, а железный провод имеет сопротивление 0,525 Ом при той же температуре. При какой температуре их сопротивления равны?

14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (которое имеет α  = –0,0600/ºC), когда оно имеет ту же температуру, что и пациент. Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (б) Отрицательное значение для α нельзя эксплуатировать при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)

15. Интегрированные концепции  (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения равным 12 × 10 ⁻⁶ /ºC. б) На сколько процентов ваш ответ отличается от ответа в примере?

16. Необоснованные результаты  (a) До какой температуры вы должны нагреть резистор, сделанный из константана, чтобы удвоить его сопротивление, предполагая постоянный температурный коэффициент удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?

Сноски

1. 1 Значения сильно зависят от количества и типов примесей
2. 2 Значения при 20°C.

Глоссарий

удельное сопротивление:

внутреннее свойство материала, не зависящее от его формы или размера, прямо пропорциональное сопротивлению, обозначаемое ρ

температурный коэффициент удельного сопротивления:

обозначается α , что описывает изменение сопротивления или удельного сопротивления материала при температуре

Избранные решения задач и упражнений

1. 0,104 Ом

3. 2,8 × 10 ⁻² м

5. 1,10 × 10 ⁻³ А 7. -5ºC до 45ºC

9. 1.03

11. 0.06%

13. -17ºC

15. (a) 4,7 Ом (всего) (b) 3,0% уменьшение

5

5 Ценности «сильно зависят от количества и типов примесей» ↵

Ценности «при 20°С». ↵

Ценности «сильно зависят от количества и типов примесей» ↵

Ценности «при 20°С». ↵

Лицензии и ссылки

Контент по лицензии CC, совместно используемый ранее

• College Physics. Автор: : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия
• Интерактивное моделирование PhET . Предоставлено : Университет Колорадо в Боулдере. Расположен по адресу : https://phet.colorado.edu/. Лицензия : CC BY: Attribution

Как рассчитать водонепроницаемость? |

Автор: gatewaycable, 7 сентября 2021 г., Wire

Здесь, в Gateway Cable Company, мы гордимся тем, что продаем широкий спектр продуктов для использования в военной, сельскохозяйственной и автомобильной промышленности. Возможно, у нас нет калькулятора водонепроницаемости, но мы понимаем, что некоторые могут спросить: «Как рассчитать водонепроницаемость?» Мы написали руководство ниже, чтобы показать вам и другим жителям, как это сделать.

Что такое водонепроницаемость?

Прежде чем мы объясним, как вы можете измерить водостойкость, полезно установить базовое понимание, ответив на вопрос: «Что представляет собой водонепроницаемость ?» Водонепроницаемость, или удельное сопротивление воды, — это способность воды сопротивляться электрическому току. Водонепроницаемость коррелирует с уровнем растворенной соли в воде. Помните об этом: более высокая концентрация растворенной соли в воде коррелирует с низким сопротивлением электрическому току, а более низкая концентрация растворенной соли в воде коррелирует с высоким сопротивлением электрическому току.

Когда мне нужно рассчитывать водонепроницаемость

Понимание того, когда нужно рассчитывать водонепроницаемость, зависит от области применения. Например, для некоторых промышленных процессов требуется сверхчистая вода. Измерение сопротивления воды может сообщить вам о концентрации растворенной соли и потенциальных загрязнителей в воде. Если вы произведете расчет на водонепроницаемость и обнаружите высокое сопротивление электрическому току, это будет означать более чистую воду, и наоборот.

Какие инструменты мне нужны для расчета водонепроницаемости?

Чтобы рассчитать сопротивление воды в вашей системе, вам необходимо использовать закон Лома для потока жидкости.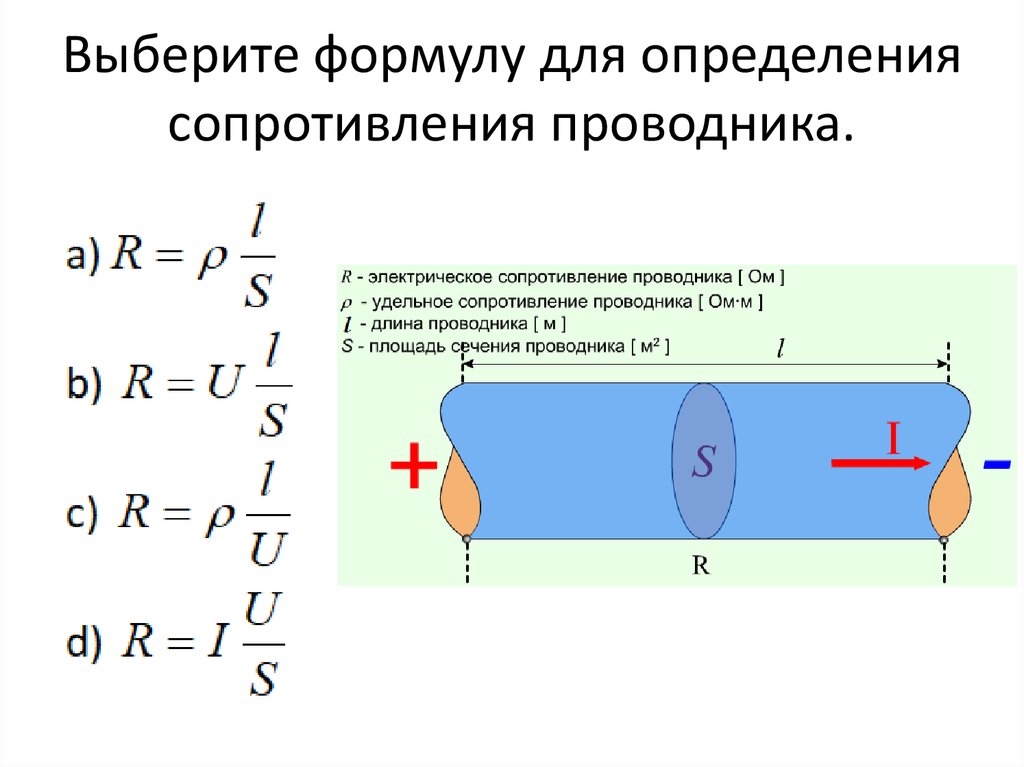 Пока вы измеряете воду и используете единицы измерения давления в фунтах на квадратный дюйм и расхода в галлонах в минуту, это довольно простой расчет, но вы все еще можете спросить: «Какие инструменты мне нужны для расчета водонепроницаемости?» Вам понадобится всего три: 

• Измеритель перепада давления
• Измеритель расхода воды
• Калькулятор

Вы сможете найти все три или заказать их доставку прямо на дом. Посмотрите ниже наше объяснение закона Лома для потока жидкости и то, как вы будете использовать эти инструменты для расчета сопротивления воды. Как только вы научитесь делать это самостоятельно, вам не понадобится калькулятор водонепроницаемости.

Как рассчитать водонепроницаемость

Если у вас есть соответствующие инструменты, вам нужно найти переменные, необходимые для выполнения расчета. Переменные закона сопротивления жидкости Лома: 

• I = расход
• H = перепад давления
• V = поправочный коэффициент вязкости (зависит от устройства, так как определяется взаимодействием между вязкостью и геометрией устройства. Используйте 1,0 для воды при температуре 80 градусов по Фаренгейту) 
• S = Удельный вес (Используйте 1,0 для воды при температуре 80 градусов по Фаренгейту)
• K = Постоянная (Это значение учитывает единицы измерения. Используйте 20 для фунтов на квадратный дюйм и галлонов в минуту)

Поскольку вы рассчитываете сопротивление воды, вы Мне нужно найти только две из этих переменных: I и H. Однако, для понимания, вот полное уравнение для расчета сопротивления жидкости, также известное как Ломс.

Как мы уже говорили, вы рассчитываете сопротивление воды. Это позволяет вам использовать значение 1 для переменных V и S, и пока вы используете единицы измерения psi и gpm, K будет равно 20. Это оставляет уравнение.

Теперь вам нужно измерить только дифференциальное давление и скорость потока. Чтобы рассчитать водонепроницаемость, выполните следующие действия:

1. Используйте измеритель перепада давления для измерения перепада давления в вашей системе.