Электромагнитные колебания и волны — Технарь

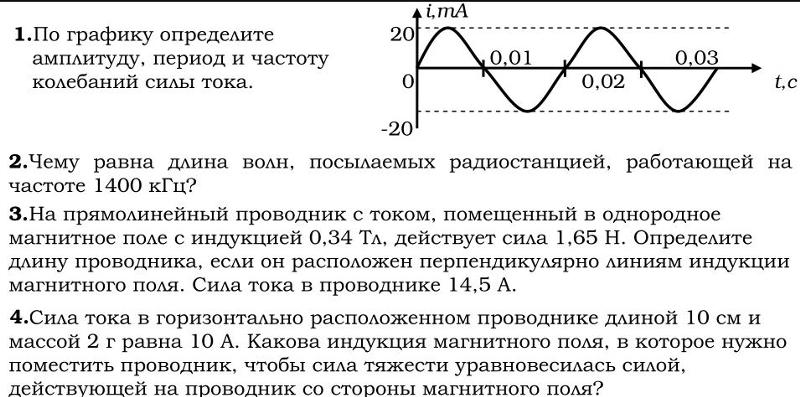
Колебательный контур состоит из конденсатора с емкостью 48 мкФ и катушки с индуктивностью 24 МГн и активным со­противлением 20 Ом. Определить частоту свободных электромагнит­ных колебаний в этом контуре. Насколько изменится частота элек­тромагнитных колебаний в контуре, если пренебречь активным со­противлением катушки?

Дано: С=4,8*10^-5 Ф — электроемкость конденсатора, L=2,4*10^-2 Гн — индуктивность катушки, R=20 Ом — активное сопротивление катушки.

Найти: v₁— частоту свободных электромагнитных колебаний в контуре; ∆v=(v₁—v₂) — насколько изменится частота колебаний в контуре, если его активное сопротивление будет равно нулю.

Решение. Частоту колебаний можно найти из соотношения:

Находим частоту v₁:

Если сопротивление R равно нулю, то формула для периода колебаний примет вид:

Отсюда найдем период колебаний при R=0 и частоту колебаний v₂, а затем ∆v.

Определяем частоту v₂:

Вычисляем изменение частоты:

Ответ. Частота свободных колебаний в контуре 132 Гц; в идеальном случае, когда R=0, частота собственных колебаний в кон­туре на 16 Гц больше.

Определить длину электромагнитной волны в ваку­уме, на которую настроен колебательный контур, если максималь­ный заряд конденсатора 2,0*10^-8 Кл, а максимальный ток в контуре 1,0 А. Какова емкость конденсатора, если индуктивность контура 2,0*10^-7 Гн? Какова энергия электрического поля конденсатора в тот момент, когда энергия магнитного поля составляет 3/4 от ее максимального значения? Определить напряжение на конденсаторе в этот момент. Активным сопротивлением контура пренебречь.

Дано: q_м=2,0*10^-8 Кл — максимальный заряд конденсатора, I_м=1,0 А — максимальный ток в контуре, L=2,0*10^-7 Гн — индуктивность контура, R=0 — активное сопротивление контура, с =3*10⁸ м/с — скорость распространения электромагнитных волн и вакууме.

Найти: λ — длину электромагнитной волны, на которую настроен колебательный контур; С — емкость конденсатора; W_эл — энергию электрического поля в тот момент, когда энергия магнит­ного поля составляет 3/4 от ее максимального значения; U— на­пряжение на конденсаторе в тот же момент времени.

Решение. Длина волны определяется по формуле:

λ=cT

где T = 2π√(LС). Для нахождения периода колебаний используем закон сохранения и превращения энергии. При незатухающих ко­лебаниях максимальная энергия магнитного поля равна максималь­ной энергии электрического поля и равна полной энергии электро­магнитных колебаний в контуре, т. е.

W_эл.м=W_маг.м=W;

отсюда

q_м²/2С=LI_м²/2 и LC=q _м²/ I_м²  

Тогда Т =2π(q _м/ I_м)

Находим длину электромагнитной волны:

Зная индуктивность контура, находим емкость конденсатора:

Полная энергия электромагнитных колебаний в контуре равна сумме мгновенных значений энергии электрического и магнитного полей и, при отсутствии затухания колебаний, есть величина постоянная:

где

Следовательно,

Подставляя числовые значения, находим энергию электрического поля для данного момента времени:

Энергия электрического поля определяется по формуле W_эл=CU²/2. Получаем

откуда находим мгновенное зна­чение напряжения U на конденсаторе:

Ответ. Длина электромагнитной волны 38 м; емкость конденса­тора 2,0*10^-9 Ф; мгновенное значение энергии электрического поля 2,5*10^-7 Дж; мгновенное напряжение 5,0 В.

Определить длину электромагнитной волны в ваку­уме, если частота колебаний в ней 4,5*10¹¹ Гц. Чему равна скорость распространения и длина этой же волны в бензоле, если его отно­сительная диэлектрическая проницаемость 2,28? При решении ис­пользовать теорию Максвелла.

Дано: v=4,5*10¹¹ Гц — частота колебаний в волне, ε=2,28 — диэлектрическая проницаемость бензола, ε₀=8,85*10^-12 Ф/м — элек­трическая постоянная, μ₀=4π*10^-7 Гн/м — магнитная постоянная.

Найти: λ₀— длину электромагнитной волны в вакууме; υ — скорость распространения волны в бензоле; λ— длину этой же волны в бензоле.

Решение. Вычисляем скорость распространения электро­магнитных волн в вакууме:

Определяем длину волны в вакууме:

Находим скорость распространения электромагнитной волны в бензоле *) и вычисляем ее длину:

*) Прозрачными веществами для электромагнитных волн являются диэлект­рики, у которых магнитные свойства очень слабо зависят от их рода, поэтому их относительную магнитную проницаемость можно принять равной единице. По-скольку

Ответ. Длина волны электромагнитных волн в вакууме 0,67 мм; скорость распространения волны в бензоле 2*10⁸ м/с; длина этой же волны в бензоле 0,44 мм.

Метки: бензолдиэлектрическая проницаемостьдлина волныкатушка с индуктивностьюколебания в контуреколебательный контурмагнитное полеполная энергиячастота колебанияэлектроемкость конденсатораЭлектромагнитные волныЭлектромагнитные колебанияэнергия магнитного поляэнергия электрического поля

Задачи на колебания и волны с подробными решениями

Механические гармонические колебания

9. 1.1 Уравнение гармонических колебаний имеет вид x=4*sin(2*pi*t) (м). Определить
9.1.2 Материальная точка совершает гармонические колебания. Период колебаний 0,5 с
9.1.3 За какое время от начала движения точка, колеблющаяся по закону x=7*sin(0,5*pi*t) (м)
9.1.4 Две точки совершают гармонические колебания. Максимальная скорость первой точки
9.1.5 За какой промежуток времени маятник, совершающий гармонические колебания
9.1.6 Тело совершает гармонические колебания. Период колебаний 0,15 с, максимальная
9.1.7 Определите смещение от положения равновесия материальной точки, совершающей
9.1.8 За равные промежутки времени первое тело совершило 100, а второе – 400 колебаний
9.1.9 Материальная точка совершает гармонические колебания с периодом 0,8 с
9.1.10 При гармонических колебаниях вдоль оси ox координата тела изменяется по закону
9.1.11 Уравнение движения колеблющейся точки имеет вид x=0,05*cos(2*pi*t/3) (м)
9.1.12 Уравнение движения точки x=0,05*cos(3*pi*t) (м). Чему равна амплитуда
9.1.13 Найти максимальное значение скорости точки, уравнение движения которой
9.1.14 Во сколько раз изменится амплитуда колебаний ускорения гармонически колеблющейся
9.1.15 Материальная точка совершает гармонические колебания по закону
9.1.16 Найти период гармонического колебания, фаза которого увеличивается
9.1.17 При фазе pi/3 смещение частицы, колеблющейся по закону косинуса, было равно 1 см
9.1.18 Материальная точка совершает гармонические колебания с периодом 0,5 с. Амплитуда
9.1.19 Уравнение колебаний материальной точки имеет вид x=0,02*sin(pi*t/2+pi/4)
9.1.20 Маятник массой 5 кг и длиной 0,8 м совершает колебательное движение с амплитудой
9.1.21 Тело совершает гармонические синусоидальные колебания с нулевой начальной фазой
9.1.22 Материальная точка совершает синусоидальные колебания с амплитудой 8 см
9.1.23 Найти период гармонического колебания, изображенного на рисунке
9.1.24 T=0,2 с – период гармонического колебания с амплитудой 10 см. Найти смещение тела
9.1.25 Материальная точка совершает гармонические колебания. Если при неизменной
9.1.26 Материальная точка совершает гармонические колебания. Если при неизменной амплитуде

Математический маятник

9.2.1 Во сколько раз изменится частота колебаний математического маятника
9.2.2 Амплитуда колебаний математического маятника 10 см. Наибольшая скорость 0,5 м/с
9.2.3 Частота гармонических колебаний математического маятника возрастает в 2 раза
9.2.4 Период колебаний маятника на Земле равен 1 с. Каким он будет на Луне, если ускорение
9.2.5 Какова длина математического маятника, совершающего колебания по закону
9.2.6 Два математических маятника с периодами колебаний 6 и 5 с соответственно одновременно
9.2.7 Два маятника начинают одновременно совершать колебания. За время первых
9.2.8 При опытном определении ускорения свободного падения учащийся за 5 мин насчитал
9.2.9 Маятник установлен в кабине автомобиля, движущегося прямолинейно со скоростью
9. 2.10 Один математический маятник имеет период 3 с, а другой – 4 с. Каков период
9.2.11 Математический маятник длиной 0,01 м имеет ту же частоту колебаний, что и шарик
9.2.12 Математический маятник длиной 2,45 м совершает 100 колебаний за 314 с. Определите
9.2.13 Какова длина математического маятника, совершающего колебания по закону
9.2.14 Маятник состоит из металлического шарика массой 1 г и нити. На шарик поместили
9.2.15 Определите длину математического маятника, который за 10 с совершает на 4 полных
9.2.16 Математический маятник длиной 1 м совершает гармонические колебания
9.2.17 Во сколько раз время прохождения колеблющейся точки первой половины амплитуды
9.2.18 К потолку подвешены два маятника. За одинаковое время первый маятник совершил
9.2.19 Первый шарик, подвешенный на нити длиной 1 м, отклонили от положения равновесия
9.2.20 Математический маятник совершает колебания. В положении наибольшего отклонения
9.2.21 Кубик совершает малые колебания в вертикальной плоскости, двигаясь без трения
9. 2.22 Небольшой металлический шарик массой 10 г, подвешенный на нити длиной 0,1 м
9.2.23 Математический маятник с длиной нити L совершает свободные колебания вблизи стены
9.2.24 В неподвижном лифте период собственных колебаний математического маятника

Пружинный маятник

9.3.1 Шарик массой 5 г колеблется по закону x=0,04*sin(2*pi*(t/T+0,5))
9.3.2 Шарик на пружине сместили на 1 см от положения равновесия и отпустили
9.3.3 Определить амплитуду колебаний, если для фазы 45 градусов смещение частицы
9.3.4 Частота колебаний шарика, прикрепленного к вертикальной пружине, равна 2,8 Гц
9.3.5 Найти массу груза, который на пружине жесткостью 25 Н/см делает 20 колебаний
9.3.6 Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период
9.3.7 Груз, подвешенный к пружине, совершает 10 колебаний в минуту. Определите жесткость
9.3.8 Пружина под действием груза массой 10 кг совершает 50 колебаний в минуту
9.3.9 Уравнение колебаний пружинного маятника массой 200 г имеет вид
9. 3.10 Груз, подвешенный к пружине, вызвал её удлинение на 4 см. Найти период собственных
9.3.11 Автомобильные рессоры имеют жесткость 20 кН/м. Каким будет период колебаний
9.3.12 Длина пружинного маятника увеличилась в 4 раза. Во сколько раз изменится период
9.3.13 Висящий на пружине груз массой 0,1 кг совершает вертикальные колебания
9.3.14 Тело совершает гармонические колебания в горизонтальной плоскости на пружине
9.3.15 Найти массу груза, который на пружине с жесткостью 250 Н/м совершает 100 полных
9.3.16 Невесомая пружина жесткостью 100 Н/м подвешена за один из концов так
9.3.17 На пружине подвешена чаша весов с гирями. При этом период вертикальных колебаний
9.3.18 Грузы массы 200 г, подвешенный к пружине, колеблется с такой же частотой
9.3.19 Как изменится период вертикальных колебаний груза, подвешенного на двух

Энергия механических колебаний

9.4.1 Груз, подвешенный на пружине, жесткость которой 1 кН/м, совершает косинусоидальные
9. 4.2 Во сколько раз изменится полная механическая энергия колеблющегося маятника
9.4.3 Найти потенциальную энергию математического маятника массой 200 г в положении
9.4.4 Груз массой 0,2 кг колеблется на пружине жесткостью 500 Н/м. Чему равна полная
9.4.5 Смещение груза, подвешенного на пружине, в зависимости от времени задается законом
9.4.6 Найти кинетическую энергию груза, совершающего косинусоидальные колебания
9.4.7 Груз массой 0,2 кг, подвешенный на пружине, совершает 30 колебаний за 1 минуту
9.4.8 Пружинный маятник вывели из положения равновесия и отпустили. Через какое время
9.4.9 Пружинный маятник совершает косинусоидальные колебания, после того как его вывели
9.4.10 Материальная точка совершает гармонические колебания. Как изменится кинетическая
9.4.11 Максимальная кинетическая энергия материальной точки массы 10 г, совершающей
9.4.12 Тело массы 5 кг совершает гармонические колебания с амплитудой 10 см
9.4.13 Тело массы 5 кг совершает гармонические колебания с частотой 2,5 Гц

Механический резонанс

9. 5.1 При какой скорости поезда маятник длиной 10 см, подвешенный в вагоне, особенно
9.5.2 Ведра с водой на коромысле имеют частоту собственных колебаний 0,625 Гц. При какой
9.5.3 Автомобиль движется по неровной дороге, на которой расстояние между буграми
9.5.4 Трактор оставил на грунтовой дороге следы в виде углублений на расстоянии 0,3 м

Механические волны

9.6.1 Точки, находящиеся на одном луче и удаленные от источника колебаний на 12 и 14,7 м
9.6.2 Какую разность фаз будут иметь колебания двух точек, находящихся на расстоянии
9.6.3 Эхо от оружейного выстрела дошло до стрелка через 6 с после выстрела. На каком
9.6.4 Скорость распространения волн, качающих лодку, 1,5 м/с. Расстояние между
9.6.5 Во сколько раз изменится длина звуковой волны при переходе из воздуха в воду
9.6.6 Плоская волна, возбуждаемая источником, колеблющимся по закону x=0,2sin(62,8t) (м)
9.6.7 В струне, закрепленной с двух концов, возбуждены колебания. На рисунке показаны
9. 6.8 Волна с частотой 5 Гц распространяется в пространстве со скоростью 3 м/с
9.6.9 Волны распространяются в упругой среде со скоростью 100 м/с. Наименьшее расстояние
9.6.10 На озере в безветренную погоду с лодки бросили тяжелый якорь. От места бросания
9.6.11 Рассчитать длину звуковой волны в воде, если частота колебаний 440 Гц
9.6.12 Определить расстояние между двумя ближайшими точками бегущей волны
9.6.13 Найти разность фаз колебаний между двумя точками звуковой волны, отстоящими
9.6.14 Длина волны 60 см. На каком расстоянии друг от друга находятся точки волны
9.6.15 Вдоль резинового шнура распространяется волны со скоростью 3 м/с при частоте 2 Гц
9.6.16 Скорость звука в воздухе 330 м/с. Какова частота звуковых колебаний, если длина
9.6.17 Рыболов заметил, что за 10 с поплавок совершил на волнах 20 колебаний
9.6.18 На рисунке приведена “мгновенная фотография” участка струны, по которой
9.6.19 У звуковой волны частоты 2 кГц при переходе из стали в воздух длина волны
9. 6.20 Звуковая волна с частотой колебаний 500 Гц распространяется в стальном стержне
9.6.21 Стальную деталь проверяют ультразвуковым дефектоскопом с частотой 1 МГц
9.6.22 Сигнал ультразвукового эхолота возвратился на корабль через 0,4 с после излучения
9.6.23 Какова длина волны ультразвукового сигнала, посланного корабельным гидролокатором
9.6.24 Толщина стального листа контролируется генератором, излучающим ультразвуковые

Колебательный контур

9.7.1 Собственные колебания тока в контуре протекают по закону I=0,01*cos(1000*pi*t) (А)
9.7.2 Изменение заряда конденсатора в колебательном контуре происходит по закону
9.7.3 Индуктивность колебательного контура 500 мкГн. Какую емкость следует выбрать
9.7.4 Необходимо изготовить колебательный контур, собственная частота которого 15 кГц
9.7.5 Мгновенное значение силы синусоидального тока через 1/3 периода равно 2,6 А
9.7.6 Колебательный контур состоит из катушки индуктивности и плоского воздушного
9. 7.7 В колебательном контуре к конденсатору подсоединили параллельно другой конденсатор
9.7.8 Колебательный контур состоит из катушки индуктивности и двух одинаковых конденсаторов
9.7.9 Напряжение на конденсаторе в идеальном колебательном контуре изменяется
9.7.10 К конденсатору с зарядом 0,25 нКл подключена катушка индуктивности. Каков
9.7.11 Частота собственных колебаний в колебательном контуре увеличилась в 3 раза
9.7.12 Чему равен период собственных колебаний в колебательном контуре, индуктивность
9.7.13 Во сколько раз изменится период свободных электрических колебаний
9.7.14 Заряд на обкладках конденсатора колебательного контура изменяется по закону
9.7.15 Во сколько раз изменится амплитуда колебаний силы тока, протекающего
9.7.16 Во сколько раз изменится частота колебаний в колебательном контуре, при увеличении
9.7.17 Сила тока изменяется со временем по закону I=2*cos(10*t) (А). Чему равен
9.7.18 В колебательном контуре конденсатор емкостью 50 нФ заряжен до максимального
9. 7.19 Батарею из двух одинаковых конденсаторов емкостью 10 нФ каждый, заряженную
9.7.20 Колебательный контур составлен из индуктивности 0,1 Гн и конденсатора емкостью 10 мкФ
9.7.21 Колебательный контур составлен из дросселя с индуктивностью 0,2 Гн и конденсатора
9.7.22 В колебательном контуре совершаются незатухающие электромагнитные колебания
9.7.23 Электрический колебательный контур содержит катушку индуктивности 10 мГн
9.7.24 Ток в идеальном колебательном контуре изменяется по закону I=0,01cos(1000t) (А)
9.7.25 Как изменится частота колебаний в идеальном колебательном контуре

Затухающие колебания

9.8.1 Сила тока в сети изменяется по закону I=4,2sin(omega*t) (А). Какое количество теплоты
9.8.2 В колебательном контуре происходят затухающие электромагнитные колебания
9.8.3 Конденсатор емкостью 10 мкФ зарядили до напряжения 400 В и подключили к катушке

Энергия электромагнитных колебаний

9.9.1 Определить силу тока в колебательном контуре в момент полной разрядки конденсатора
9. 9.2 Полная энергия колебаний в контуре равна 5 Дж. Найти максимальную силу тока
9.9.3 Уравнение колебаний электрического заряда в колебательном контуре (L=2 Гн)
9.9.4 Через поперечное сечение катушки индуктивностью 12 мГн проходит заряд 60 мКл
9.9.5 В колебательном контуре сила тока изменяется по закону I=-0,02*sin(400*pi*t) (А)
9.9.6 В колебательном контуре индуктивность катушки равна 0,2 Гн. Амплитуда силы тока
9.9.7 Заряженный конденсатор замкнули на катушку индуктивности. Через какое время
9.9.8 В электрическом колебательном контуре индуктивность катушки 4 мГн, а максимальный

Переменный ток

9.10.1 Сила тока изменяется по формуле I=8,5*sin(314t+0,651) (А). Определить
9.10.2 Катушка индуктивностью 20 мГн включена в сеть промышленного переменного тока
9.10.3 Мгновенное значение ЭДС синусоидального тока 120 В для фазы 45 градусов
9.10.4 Напряжение на концах участка цепи, по которой течет переменный ток, изменяется
9.10.5 В цепь переменного тока включены последовательно конденсатор емкостью 1 мкФ
9. 10.6 Вольтметр, включенный в цепь переменного тока, показывает 220 В. На какое
9.10.7 Максимальное напряжение в колебательном контуре, состоящем из катушки
9.10.8 При включении конденсатора на синусоидальное напряжение 220 В с частотой 50 Гц
9.10.9 Определить емкость конденсатора фильтра выпрямителя, если частота тока 50 Гц
9.10.10 Конденсатор емкостью 10 мкФ включен в цепь, в которой мгновенное значение
9.10.11 Емкостное сопротивление конденсатора на частоте 50 Гц равно 100 Ом. Каким оно
9.10.12 К зажимам генератора присоединен конденсатор с емкостью 0,1 мкФ. Найти
9.10.13 В сеть переменного тока напряжением 220 В и частотой 50 Гц включен конденсатор
9.10.14 ЭДС в цепи переменного тока выражается формулой E=120*sin(628*t) (В). Определить
9.10.15 Длина воздушной линии передачи равна 300 км, частота тока 50 Гц. Найдите сдвиг
9.10.16 В цепь переменного тока включены последовательно сопротивление 100 Ом

Трансформаторы

9.11.1 Трансформатор включен в сеть с напряжением 120 В. Первичная обмотка его
9.11.2 Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на её концах 220 В
9.11.3 ЭДС первичной и вторичной обмоток трансформатора соответственно равны 220 и 20 В
9.11.4 Понижающий трансформатор с коэффициентом трансформации 10 включен в сеть
9.11.5 Сила тока в первичной обмотке трансформатора 0,6 А, напряжение на её концах 120 В
9.11.6 Трансформатор повышает напряжение с 220 до 660 В и содержит в первичной
9.11.7 Обмотка трансформатора со стальным сердечником имеет индуктивность 0,6 Гн
9.11.8 Первичная обмотка трансформатора, включенного в сеть 380 В, имеет 2400 витков
9.11.9 На первичную обмотку понижающего трансформатора с коэффициентом трансформации
9.11.10 В сердечнике трансформатора, включенного в сеть переменного тока частотой 50 Гц
9.11.11 Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть

Резонанс в колебательном контуре

9.12.1 В катушке индуктивности сила тока линейно увеличивается со скоростью 10 А/с
9. 12.2 В цепь включены конденсатор 2 мкФ и индуктивность 0,05 Гн. Какой частоты ток надо
9.12.3 Параметры контуров таковы: C1=120 пФ, L1=3,5 мГн, C2=150 пФ, L2=5 мГн. На сколько
9.12.4 Резонанс в колебательном контуре с конденсатором 1 мкФ наступает при частоте
9.12.5 При изменении емкости конденсатора на 100 пФ резонансная частота

Электромагнитные волны

9.13.1 Колебательный контур имеет емкость 2,6 пФ и индуктивность 0,012 мГн. Какой длины
9.13.2 Найти емкость конденсатора колебательного контура, если при индуктивности
9.13.3 При изменении тока в катушке индуктивности на 1 А за 0,6 с в ней индуцируется ЭДС
9.13.4 Определите максимальный ток в контуре, если длина электромагнитной волны
9.13.5 В каком диапазоне длин волн можно улавливать радиопередачи приемником
9.13.6 Радиопередатчик искусственного спутника Земли работает на частоте 20 МГц
9.13.7 Максимальная величина заряда на конденсаторе колебательного контура 1 мкКл
9.13.8 Колебательный контур создает в воздухе электромагнитные волны длиной 150 м
9. 13.9 Если конденсатор с расстоянием между пластинами 1 см определенным образом
9.13.10 Как нужно изменить емкость конденсатора в колебательном контуре радиоприемника
9.13.11 Индуктивность катушки пропорциональна квадрату числа ее витков. Как следует
9.13.12 Электрический колебательный контур радиоприемника содержит катушку индуктивности
9.13.13 Колебательный контур радиоприемника содержит конденсатор емкости 1 нФ

Пожалуйста, поставьте оценку

( 30 оценок, среднее 4.9 из 5 )

Вы можете поделиться с помощью этих кнопок:

Резонанс: Значение, Частота, Формула, Магнитный

Резонанс может возникнуть, когда есть периодическая внешняя движущая сила, вызывающая колебания системы. Когда частота движущей силы приближается к собственной частоте системы, она начинает вибрировать с гораздо большей амплитудой, которая продолжает увеличиваться до максимума, когда две частоты равны.

Факторы, ведущие к резонансу

Есть несколько факторов, которые приводят к резонансу, как мы рассмотрим ниже.

Собственная частота

Собственная частота объекта — это частота, с которой он колеблется во время свободных колебаний, то есть когда нет внешних сил, влияющих на его движение, и, следовательно, нет передачи энергии между объектом и его окружением.

В качестве примера рассмотрим систему масса-пружина. Если бы вы удержали массу вдали от положения равновесия, чтобы пружина растянулась, а затем отпустили бы массу, система колебалась бы с собственной частотой. Если никакая энергия не передается в окружающую среду, масса продолжает колебаться на этой частоте вечно. В действительности, однако, масса в конечном итоге замедляется силами трения, такими как сопротивление воздуха.

Рис. 1. Система масса-пружина, колеблющаяся с собственной частотой. Источник: Physics LibreTexts (CC BY-SA 4.0).

Вынужденные колебания

Периодическая внешняя движущая сила, действующая на систему, вызывает вынужденные колебания. Частота силы называется движущей частотой. Если она равна собственной частоте системы, это вызывает очень большие колебания, и в этот момент система находится в резонансе.

Примером системы, которая может быть вызвана в резонанс движущей силой, являются качели на игровой площадке. Если кто-то толкает ее через промежутки времени, правильно совпадающие с ее возвратно-поступательным движением, т. е. если частоты толчков и раскачивания одинаковы, система резонирует, и колебания становятся намного выше.

Родитель толкает ребенка на качелях каждые 2 секунды, так что качели заканчиваются очень высоко – система резонирует.

Какова частота движущей силы (родительского толчка)? И каков временной интервал t между приложением родителем максимальной силы и моментом, когда ребенок достигает вершины качелей?

Частота связана с периодом периодического движения соотношением:

f =

f = 0,5 Гц

Родитель должен толкать, когда качели проходят положение равновесия. Это четверть периода движения качелей.

t =

t = 0,5 с

Разность фаз

Из предыдущего примера видно, что если человек толкает качели в неподходящее время, например, когда качели движутся к нему, система не будет резонировать. Чтобы увеличить высоту колебаний, наибольшую силу следует прикладывать, когда качели удаляются от человека, толкающего их, и проходят через положение равновесия, когда их скорость наибольшая. Время, затрачиваемое на то, чтобы качели переместились между высшей точкой и положением равновесия, равно четверти всего периода времени, и, следовательно, это должна быть разница во времени между моментом, когда качание находится в максимальном смещении, и моментом, когда сила равна применяемый.

При более высоких и более низких значениях частоты возбуждения, по сравнению с собственной частотой воздействующего объекта, передача энергии в систему значительно менее эффективна, а амплитуда значительно ниже.

• При низких частотах движения сила колеблется намного медленнее, чем объект, и между ними существует разность фаз, равная 0.
• При резонансе разность фаз равна , что вызывает наибольшую передачу энергии, так как сила всегда действует в том же направлении, что и движение, и сила наибольшая, когда объект проходит через состояние равновесия с максимальной скоростью. Это также называется резонансом скоростей — графики движущей силы и скорости осциллятора имеют одинаковую форму.
• Когда частота возбуждения продолжает увеличиваться после точки резонанса, разность фаз увеличивается до π, и сила полностью не совпадает по фазе с генератором. В этот момент осциллятор не может угнаться за движущей силой.

Рис. 2. Разность фаз между драйвером и генератором в зависимости от отношения их частот. Источник: Physics LibreTexts (CC BY-NC-SA 4.0).

Демпфирование

Настоящие колебательные системы не вибрируют вечно, так как они отдают энергию окружающей среде. Обычно это происходит из-за демпфирующих сил, которые представляют собой силы трения, такие как сопротивление воздуха или трение между движущимися частями системы. Они уменьшают амплитуду колебаний и тем самым минимизируют эффект резонанса.

Влияние различных типов демпфирования на амплитуду

Световое демпфирование : объект останавливается долго. Примером этого является сопротивление воздуха, действующее на качающийся маятник, медленно уменьшающее амплитуду колебаний.

Рис. 3. Система со слабым демпфированием. Источник: Wikibooks IB Physics/Oscillations and Waves (CC BY-SA 3.0).

Сильное демпфирование : большая сила прикладывается к движению вибрирующего объекта. В этом случае для прекращения колебаний требуется гораздо меньше времени. Амплитуда сильно уменьшается в течение каждого периода. График зависимости смещения от времени будет иметь форму, аналогичную графику затухания света, но будет уменьшаться до нуля гораздо быстрее. Примером сильного демпфирования может быть использование объекта с очень большой площадью поверхности вместо груза на простом маятнике. Сопротивление воздуха будет намного больше, и амплитуда уменьшится быстрее.

Критическое демпфирование : это точная величина силы сопротивления, необходимая для прекращения колебаний системы в кратчайшие сроки.

Передемпфирование : системы с передозировкой имеют большую силу сопротивления, действующую на них, чем системы с критическим демпфированием, но им требуется больше времени, чтобы вернуться в состояние равновесия. Передемпфирование используется для очень больших и тяжелых дверей, чтобы заставить их закрываться медленно, а не захлопываться.

Рис. 4. Смещение во времени в системе с критическим демпфированием (A) и системе с избыточным демпфированием (B). Источник: Lumen Physics Damped Harmonic Motion (CC BY 4.0).

Влияние демпфирования на резонанс

Увеличение амплитуды, вызванное резонансом, зависит от демпфирования в колебательной системе. Слегка демпфированные системы имеют очень резкий пик амплитуды при резонансе: система очень чувствительна к моменту достижения резонансной частоты. По мере увеличения демпфирующих сил пик резонансных кривых становится более пологим, и пик начинает возникать немного раньше резонанса – резонансная частота уменьшается.

Рисунок 5. Кривые резонанса для систем с различной степенью демпфирования. Амплитуда колебательных систем отложена по оси y, B — константа, представляющая степень демпфирования, а w ₀ — резонансная частота объекта. Источник: Дэниел А. Рассел, «Акустика и вибрационная анимация» (CC BY-NC-ND 4.0).

Эффект демпфирования может быть очень полезен в некоторых случаях, поскольку резонанс может вызвать проблемы в больших конструкциях, таких как мосты. Люди и объекты, движущиеся по мосту, могут вызвать легкую вибрацию моста, и если частота совпадает с собственной частотой моста, он может сильно колебаться и даже разрушиться. Этого можно избежать, сконструировав мост таким образом, чтобы было больше трения между движущимися частями, чтобы уменьшить амплитуду колебаний.

Применение резонанса

Хотя резонанс может быть источником опасности, он также играет важную роль во многих полезных применениях, включая, например, МРТ и музыкальные инструменты.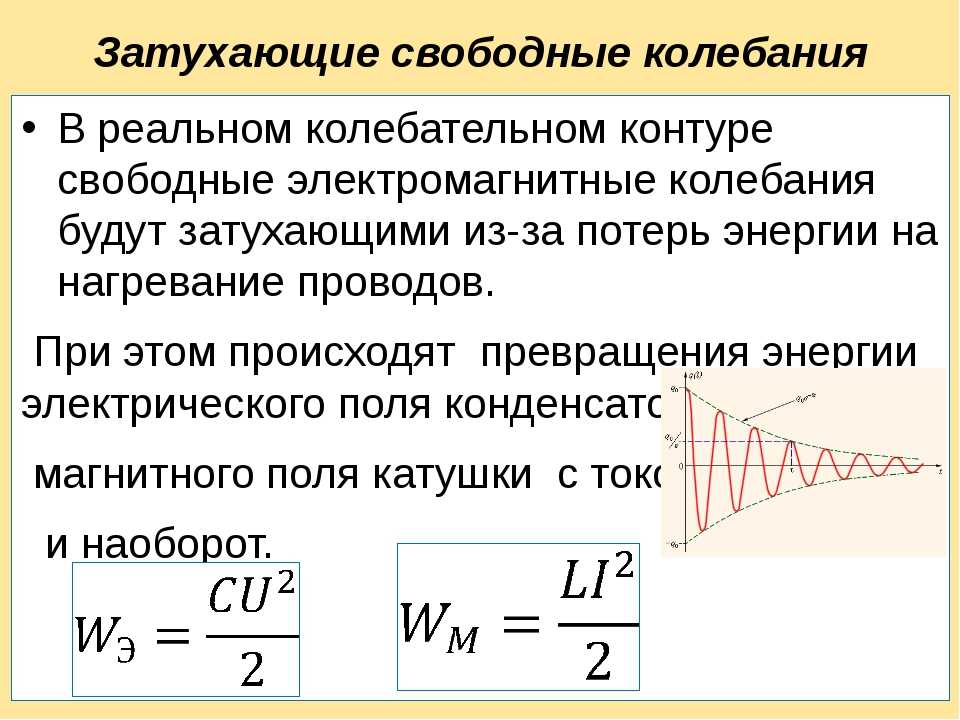

МРТ

МРТ основаны на эффекте ядерного магнитного резонанса (ЯМР). Ядра водорода имеют собственную частоту, и если к одному из них приложить очень сильное магнитное поле, оно может поглощать энергию электромагнитного излучения (в диапазоне радиочастот), равную этой частоте. Контролируемая девозбуждение ядер водорода позволяет определять их местонахождение на основе испускаемого ими излучения, что позволяет картировать ткани тела.

Музыкальные инструменты

Музыкальные инструменты также зависят от резонанса. Например, когда дергают за гитарную струну, возникает волна, и суперпозиции этой волны образуют стационарную волну на струне (частота стационарной волны определяет высоту тона). Сами струны будут издавать только тихий звук, поскольку они легко перемещаются по воздуху, вызывая тем самым небольшую вибрацию молекул воздуха. Вибрации струн передаются на весь корпус гитары мостом на конце струн. Корпус рассчитан на те же резонансные частоты, что и частоты стоячих волн на струнах.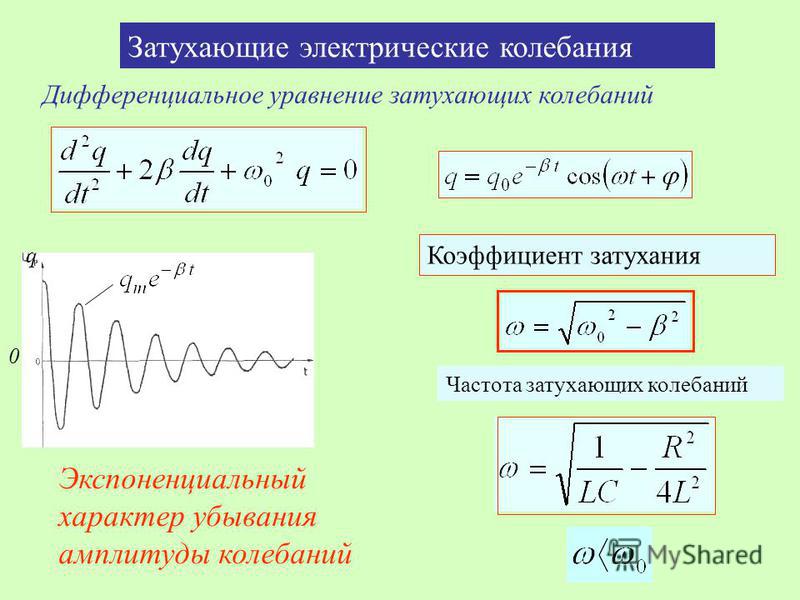 Это означает, что гитара резонирует, когда на нее нажимают, заставляя окружающие молекулы воздуха вибрировать достаточно, чтобы производить более громкий звук.

Резонанс — основные выводы

• Резонанс описывает колебания очень большой амплитуды, которые происходят, когда система приводится в действие периодической силой с собственной частотой системы.
• Разность фаз между драйвером и генератором при резонансе составляет .
• Демпфирование уменьшает максимальную амплитуду резонанса и приводит к уменьшению резонансной частоты.

16.8 Вынужденные колебания и резонанс — Физика колледжа 2e

Цели обучения

К концу этого раздела вы сможете:

• Наблюдайте за резонансом гребного шарика на струне.
• Измерьте амплитуду затухающего гармонического осциллятора.

Рисунок 16.23 Вы можете заставить струны фортепиано вибрировать, просто производя звуковые волны своим голосом.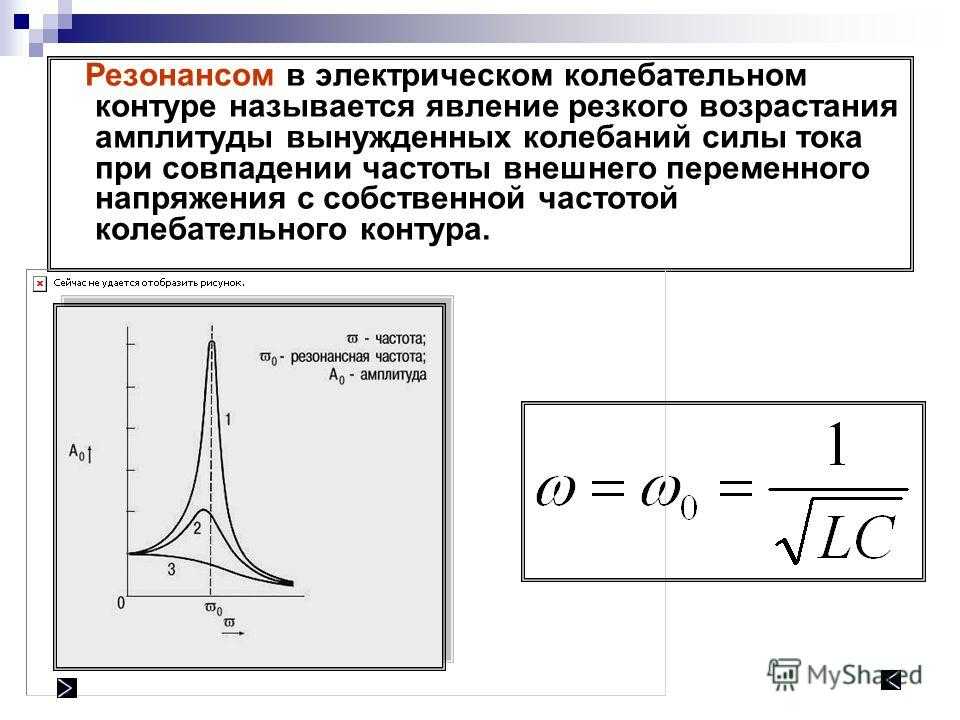 (Фото: Мэтт Биллингс, Flickr)

Сядьте как-нибудь перед пианино и спойте громко короткую ноту, сняв демпферы со струн. Он пропоет вам ту же ноту — струны, имеющие ту же частоту, что и ваш голос, резонируют в ответ на силы звуковых волн, которые вы им послали. Ваш голос и струны фортепиано — хороший пример того, что объекты — в данном случае струны фортепиано — можно заставить колебаться, но лучше всего колебаться на своей собственной частоте. В этом разделе мы кратко рассмотрим применение периодическая движущая сила

Рисунок 16.26 В 1940 году рухнул мост Такома-Нарроуз в штате Вашингтон. Сильный боковой ветер приводил мост в колебания на резонансной частоте. Демпфирование уменьшилось, когда опорные тросы ослабли и начали скользить по башням, что позволяло увеличивать амплитуду до тех пор, пока конструкция не разрушилась (кредит: PRI’s 9).0143 Studio 360 , через Flickr)

Проверьте свое понимание

Известный фокус состоит в том, что исполнитель поет ноту в сторону хрустального стекла, пока стекло не разбивается.