НОУ ИНТУИТ | Лекция | Задачи линейной алгебры
< Лекция 12 || Лекция 5: 123456789
Аннотация: Познакомимся с инструментами Octave, предназначенными для работы с векторами и матрицами, а также с возможностями, которые предоставляет пакет при непосредственном решении задач линейной алгебры.
5.1 Ввод и формирование векторов и матриц
Векторы и матрицы в Octave задаются путём ввода их элементов. Элементы вектора-строки отделяют пробелами или запятыми, а всю конструкцию заключают в квадратные скобки:
>>> a =[2 -3 5 6 -1 0 7 -9] a = 2 -3 5 6 -1 0 7 -9 >>> b =[ -1,0,1] b = -1 0 1
Вектор-столбец можно задать, если элементы отделять друг от друга точкой с запятой:
>>> c=[-pi; -pi / 2; 0; pi / 2; pi ] c = -3.14159 -1.57080 0.00000 1.57080 3.14159
Обратиться к элементу вектора можно указав имя вектора, а в круглых скобках — номер элемента, под которым он хранится в этом векторе:
>>> a( 1 ) ans = 2 >>> b( 3 ) ans = 1 >>> c( 5 ) ans = 3.1416
Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:
>>> Matr=[0 1 2 3; 4 5 6 7 ] Matr = 0 1 2 3 4 5 6 7
Обратиться к элементу матрицы можно указав после имени матрицы, в круглых скобках, через запятую, номер строки и номер столбца, на пересечении которых элемент расположен:
>>> Matr ( 2, 3 ) ans = 6 >>> Matr ( 1, 1 ) ans = 0 >>> Matr ( 1, 1 )=pi; Matr ( 2, 4 )= _pi; >>> Matr Matr = 3.1416 1.0000 2.0000 3.0000 4.0000 5.0000 6.0000 -3.1416
Матрицы и векторы можно формировать, составляя их из ранее заданных матриц и векторов:
>>> a=[-3 0 2 ]; b=[3 2 -1]; c =[5 -2 0 ]; >>> M=[a b c ] % Горизонтальная конкатенация векторов–строк M = -3 0 2 3 2 -1 5 -2 0 % результат — вектор–строка >>> N=[a; b; c ] % Вертикальная конкатенация векторов–строк, % результат — матрица N = -3 0 2 3 2 -1 5 -2 0 >>> Matrica =[N N N] % Горизонтальная конкатенация матриц Matrica = -3 0 2 -3 0 2 -3 0 2 3 2 -1 3 2 -1 3 2 -1 5 -2 0 5 -2 0 5 -2 0 >>> Tablica =[M;M;M] % Вертикальная конкатенация матриц Tablica = -3 0 2 3 2 -1 5 -2 0 -3 0 2 3 2 -1 5 -2 0 -3 0 2 3 2 -1 5 -2 0
>>> Tabl =[ -1.2 3.4 0.8; 0.9 -0.1 1.1; 7.6 -4.5 5.6; 9.0 1.3 -8.5] Tabl = -1.20000 3.40000 0.80000 0.90000 -0.10000 1.10000 7.60000 -4.50000 5.60000 9.00000 1.30000 -8.50000 >>> Tabl( :, 3 ) % Выделить из матрицы 3-й столбец ans = 0.80000 1.10000 5.60000 -8.50000 >>> Tabl( 1, : ) % Выделить из матрицы 1-ю строку ans = -1.20000 3.40000 0.80000 >>> Matr=Tabl( 2 : 3, 1 : 2 ) % Выделить из матрицы подматрицу Matr = 0.90000 -0.10000 7.60000 -4.50000 % Вставить подматрицу в правый нижний угол исходной матрицы >>> Tabl( 3 : 4, 2 : 3 )=Matr Tabl = -1.20000 3.40000 0.80000 0.90000 -0.10000 1.10000 7.60000 0.90000 -0.10000 9.00000 7.60000 -4.50000 >>> Tabl( :, 2 ) = [ ] % Удалить из матрицы 2-й столбец Tabl = -1.20000 0.80000 0.90000 1.10000 7.60000 -0.10000 9.00000 -4.50000 >>> Tabl( 2, : ) = [ ] % Удалить из матрицы 2-ю строку Tabl = -1.20000 0.80000 7.60000 -0.10000 9.00000 -4.50000 >>> Matr % Представить матрицу в виде вектора–столбца Matr = 0.90000 -0.10000 7.60000 -4.50000 >>> Vector=Matr ( : ) Vector = 0.90000 7.60000 -0.10000 -4.50000 >>> V=Vector( 1 : 3 ) % Выделить из вектора элементы со 1-го по 3-й V = 0.90000 7.60000 -0.10000 >>> V( 2 ) = [ ] % Удалить из массива 2-й элемент V = 0.90000 -0.10000
Листинг 5.1. Пример использования знака двоеточия «:»
Дальше >>
< Лекция 12 || Лекция 5: 123456789
Векторы и координаты в пространстве. Профильный уровень 11 класс онлайн-подготовка на Ростелеком Лицей
Векторы и координаты в пространстве. Геометрический подход
Мы с вами уже знаем про такие математические инструменты, как векторы и координаты; подробно говорили о том, почему в них возникает необходимость и где мы их используем.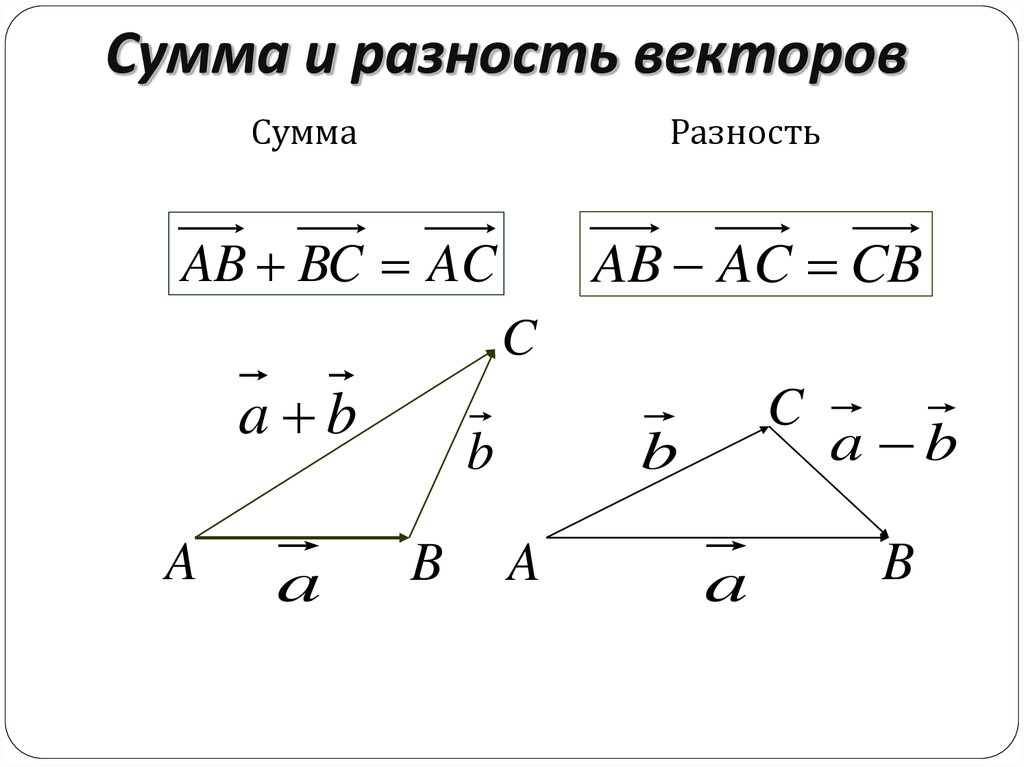
В планиметрии мы рассматривали векторные величины на плоскости (или, по-другому, в двумерном пространстве). Для того чтобы задать вектор, нам было достаточно двух координат. В стереометрии мы решаем задаче в привычном нам трехмерном пространстве, и теперь двух координат для задания вектора нам будет недостаточно.
Действительно, представьте себе лягушку, которая собирается поймать комара. Если она будет знать только то, что он в 3 см впереди и на 2 см правее ее, то шансы на удачную охоту будут невысокими. Другой пример: два самолета могут одновременно лететь 30 км южнее и 40 км восточнее Москвы, если будут находиться на разной высоте (на разных эшелонах).
Чтобы задать вектор в трехмерном пространстве, нам понадобятся три координаты. Повлияет ли это на уже полученные нами свойства векторов? Мы расширяем математические инструменты таким образом, чтобы все уже известные нам свойства и характеристики сохранялись. Такая же ситуация и с векторами и координатами в пространстве – принципиально нового будет немного.
Такая же ситуация и с векторами и координатами в пространстве – принципиально нового будет немного.
В планиметрии мы параллельно рассматривали два подхода к описанию вектора:
- Геометрический: вектор – направленный отрезок.
- Алгебраический: вектор – это упорядоченная пара чисел – координат вектора.
Используем их для определения вектора в пространстве.
C геометрической точки зрения вектором называется направленный отрезок, т. е. отрезок в пространстве, для которого указаны начало и конец (см. рис. 1).
Рис. 1. Вектор
Обозначается вектор двумя большими или одной малой буквами со стрелкой или черточкой наверху: . Направление вектора считается от начала вектора к концу. Длина отрезка называется длиной или модулем вектора: . Отдельную точку пространства можно считать вектором нулевой длины. Направление такого вектора не определено. Обозначается он как ноль со стрелочкой: .
Векторы могут образовывать разные углы, но есть особые случаи: векторы, которые действуют строго в одном направлении или в прямо противоположных.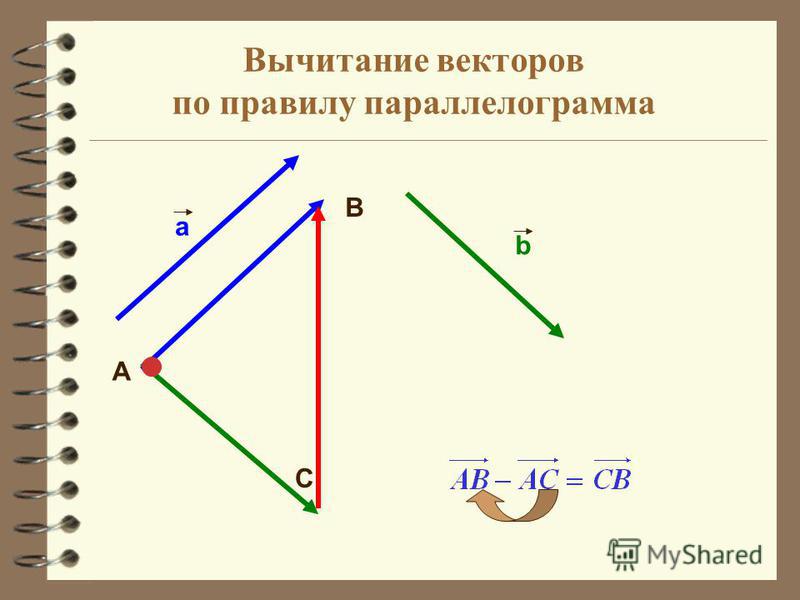 Например, во втором законе Ньютона результирующая внешних сил и ускорение – векторы, направленные в одну сторону, а в третьем законе Ньютона силы направлены в противоположных направлениях. Формальные понятия сонаправленности и противоположной направленности, а также их общего случая – коллинеарности в пространстве остаются без изменений.
Например, во втором законе Ньютона результирующая внешних сил и ускорение – векторы, направленные в одну сторону, а в третьем законе Ньютона силы направлены в противоположных направлениях. Формальные понятия сонаправленности и противоположной направленности, а также их общего случая – коллинеарности в пространстве остаются без изменений.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Проще говоря, параллельные векторы мы называем коллинеарными.
Рис. 2. Коллинеарные векторы
Два коллинеарных вектора, направленные в одну сторону, называются сонаправленными:
Если они направлены в разные стороны, то их называют противоположно направленными (см. рис. 3):
Рис. 3. Противоположно направленные векторы
Нулевой вектор считается сонаправленным с любым другим вектором. Для обозначения коллинеарности, сонаправленности и противоположно направленности мы используем знак параллельности, сонаправленные или противоположные стрелки.
В параллелепипеде (см. рис. 4):
и не являются коллинеарными.
Рис. 4. Рассматриваемый параллелепипед
Равными векторами, как и прежде, будем называть сонаправленные векторы равной длины. Т. к. векторы и сонаправлены и имеют равную длину, то:
и не являются коллинеарными, следовательно:
и сонаправлены, но имеют разную длину, следовательно:
и имеют равную длину, но противоположно направлены, следовательно:
Векторы и координаты в пространстве. Алгебраический подход
Рассмотрим теперь алгебраический подход к определению вектора. Для этого расширим понятие декартовой системы координат с плоской до пространственной.
Проведем три взаимно перпендикулярные прямые через одну точку. Выберем направление на каждой прямой и назовем их координатными осями. Общую точку назовем началом координат и обозначим буквой . Выберем масштаб, для этого на каждой оси отметим единицу (см. рис. 5).
рис. 5).
Рис. 5. Пространственная система координат
Стандартное обозначение для осей . Стандартное расположение осей – и в горизонтальной плоскости, направлена в нашу сторону, – вправо. Ось направлена вертикально вверх. Как и раньше, ось называется осью абсцисс, а – осью ординат. Ось называется осью аппликат.
Чтобы выяснить координаты произвольной точки, необходимо, как и в плоском случае, опустить перпендикуляры из точки на каждую координатную ось.
При изображении важным является то обстоятельство, что если изобразить оси и точку, то еще непонятно, где она находится. Кажется, что точки и находятся в одном и том же месте (см. рис. 6). На самом деле, мы этого еще не знаем. Для определения позиции точек обычно строят их проекции на плоскость .
Рис. 6. Расположение точек и
У точек и их проекций координаты и совпадают. Чтобы найти координату , проекцию точки соединяют с началом координат, а потом из точки проводят параллельный отрезок до пересечения с осью аппликат.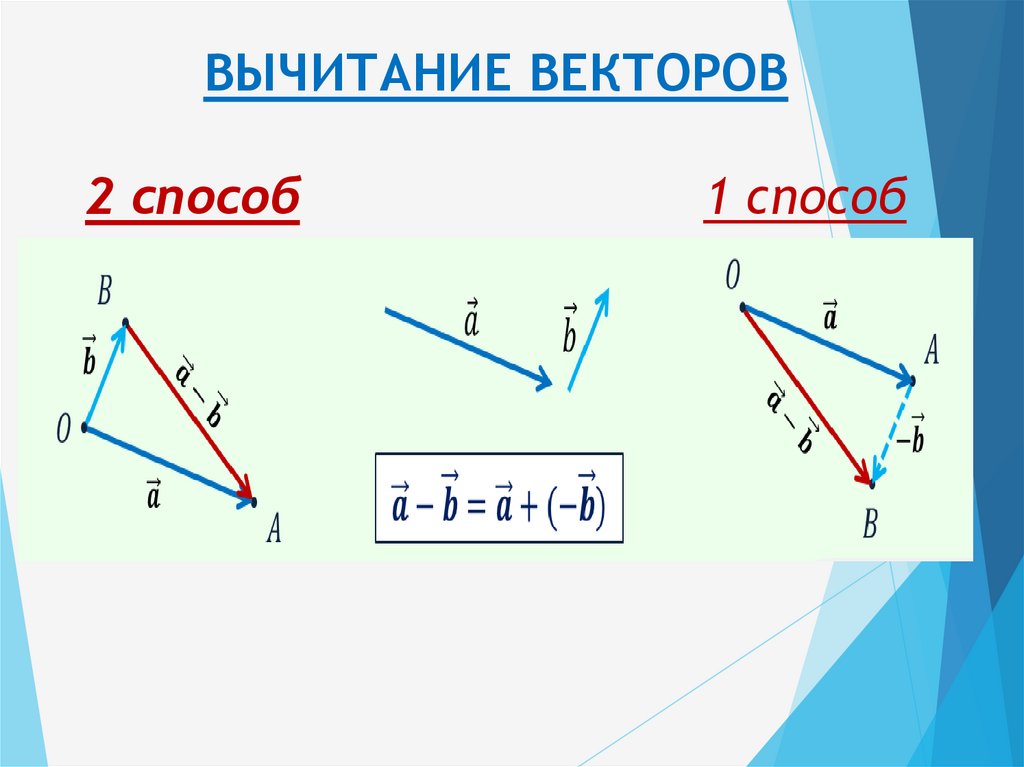 Полученные координаты называются, соответственно, абсциссой, ординатой и аппликатой точки (см. рис. 7). Записываются координаты точки в виде упорядоченной тройки чисел: абсцисса, ордината, аппликата.
Полученные координаты называются, соответственно, абсциссой, ординатой и аппликатой точки (см. рис. 7). Записываются координаты точки в виде упорядоченной тройки чисел: абсцисса, ордината, аппликата.
Рис. 7. Полученные координаты точек и
Теперь перейдем к векторам и их координатам. Вспомним, как на плоскости мы задавали координаты вектора. Если на векторе как на гипотенузе построить прямоугольный треугольник с катетами, параллельными осям, то длины катетов и принимаются за координаты вектора. При таком определении равные векторы получают равные координаты. Координаты вектора с началом в точке совпадают с координатами конца вектора (см. рис. 8).
Рис. 8. Векторы
При этом если вектор смотрит влево, т. е. его проекция на ось отрицательна, то координата вектора считается отрицательной. Аналогично для координаты . Если вектор смотрит вниз, то его координата у отрицательна.
Вектор смотрит вправо и вниз – у него положительная координата и отрицательная .
Вектор смотрит влево и вверх, координата отрицательная, положительная.
Вектор смотрит влево и вниз, обе координаты отрицательны (см. рис. 9).
Рис. 9. Векторы
Чтобы найти координаты, очевидно, нужно из координат конца вектора вычесть координаты начала. Длину вектора можно было выразить, используя теорему Пифагора:
Используем описанный для плоскости подход в пространстве. А именно – у равных векторов должны быть равные координаты (чтобы геометрический и алгебраический подход описывал один и тот же инструмент).
На векторе, как на диагонали, строим прямоугольный параллелепипед с ребрами, параллельными координатным осям.
Рис. 10. Построенный параллелепипед
Очевидно, на равных векторах будут построены равные параллелепипеды (см. рис. 11).
Рис. 11. На равных векторах построены равные параллелепипеды
Три измерения параллелепипеда назовем координатами вектора. У равных двух векторов на рисунке выше равны координаты: . Вычислить их можно как разности соответствующих координат конца и начала вектора:
Вычислить их можно как разности соответствующих координат конца и начала вектора:
При этом учитывается направление. Если вектор смотрит в отрицательную сторону вдоль какой-то из осей, то координата отрицательна.
Т. к. длина вектора – это длина диагонали параллелепипеда, то ее можно вычислить по теореме Пифагора:
Пример 1. Найти координаты и длину вектора с началом в точке и концом в точке (см. рис. 12).
Рис. 12. Иллюстрация к примеру 1
Решение
Найдем координаты вектора. Для этого вычтем из координат конца координаты начала:
Отрицательные первая и третья координаты означают тот факт, что вдоль осей и вектор смотрит в отрицательном направлении.
Вычислим его длину:
Ответ: ; .
С алгебраической точки зрения вектором называется любая упорядоченная тройка чисел. Равные тройки называются равными векторами. Небольшое противоречие состоит в том, что с геометрической точки зрения два несовпадающих, но равных направленных отрезка – это два вектора, равных друг другу.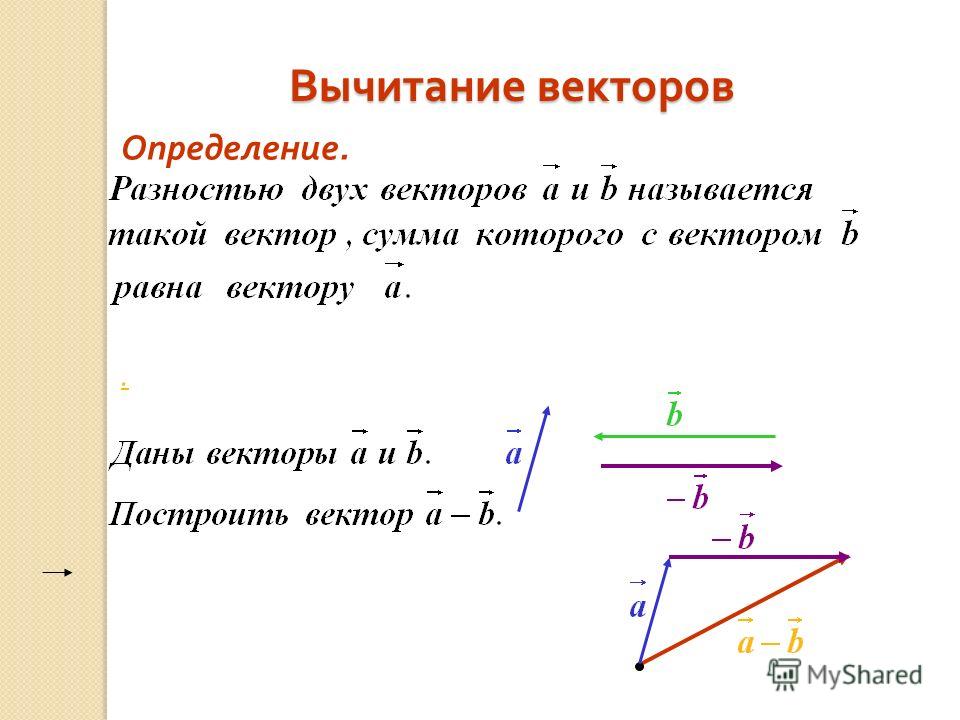 А с алгебраической, т. к. они имеют одинаковый набор координат – это просто один вектор.
А с алгебраической, т. к. они имеют одинаковый набор координат – это просто один вектор.
Разрешается это противоречие следующим образом. Все равные геометрические векторы считают одним вектором, а конкретные направленные отрезки – различными представлениями этого вектора. Так что в дальнейшем для нас не будет особой разницы сказать «векторы равны» или «это один и тот же вектор».
Рассмотрим коллинеарность векторов с алгебраической точки зрения. Мы знаем, что на плоскости коллинеарность векторов означает пропорциональность их координат. В самом деле, два коллинеарных вектора можно заменить на равные им радиус-векторы. Они будут лежать на одной прямой. Из подобия прямоугольных треугольников следует пропорциональность их координат (см. рис. 13). Во сколько раз длиннее вектор, во столько раз больше модули его координат.
Рис. 13. Коллинеарные векторы
Векторы и коллинеарны, и их координаты пропорциональны:
Абсолютно аналогичная ситуация в трехмерном случае.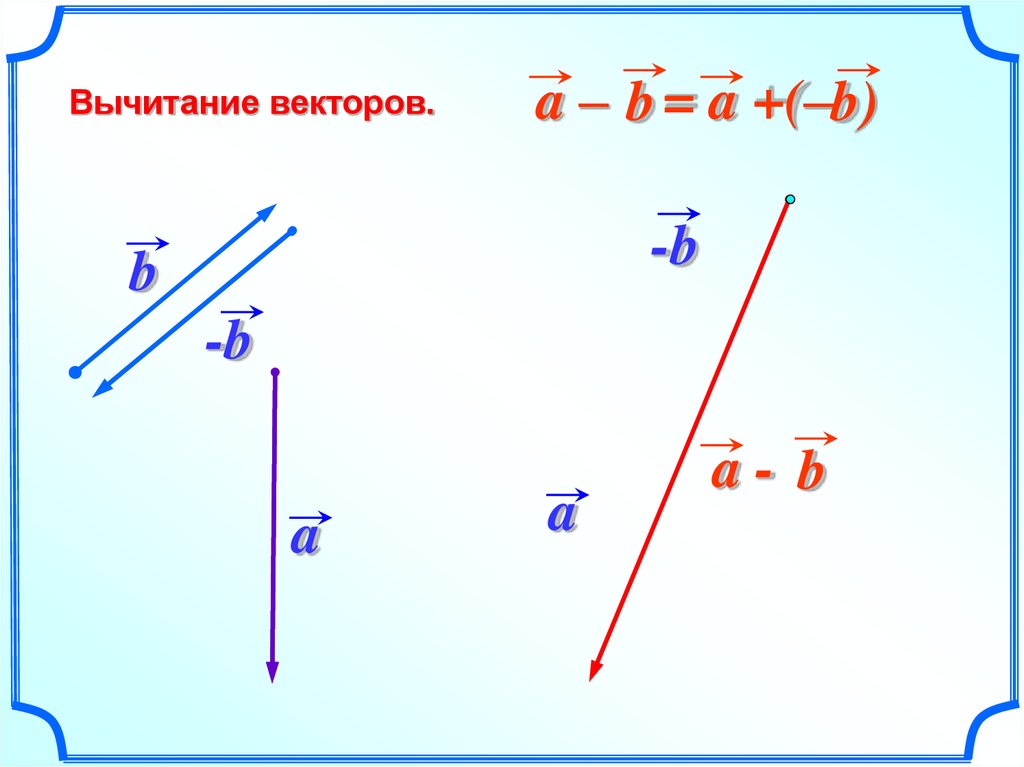 Пусть и – коллинеарные векторы. Соответствующие им радиус-векторы лежат на одной прямой. Тогда из подобия двух параллелепипедов следует пропорциональность их координат (см. рис. 14). Таким образом, чтобы выяснить коллинеарность двух векторов, нужно попарно поделить их координаты друг на друга.
Пусть и – коллинеарные векторы. Соответствующие им радиус-векторы лежат на одной прямой. Тогда из подобия двух параллелепипедов следует пропорциональность их координат (см. рис. 14). Таким образом, чтобы выяснить коллинеарность двух векторов, нужно попарно поделить их координаты друг на друга.
Рис. 14. Коллинеарные векторы
Пример 2. Выяснить, коллинеарны ли пары векторов:
1. и ;
2. и ;
3. и .
Решение
1. и :
Координаты пропорциональны, значит, векторы коллинеарны. Отношение координат – положительное число . Значит, вектор в раза длиннее и сонаправлен вектору .
2. и :
Координаты пропорциональны, значит, векторы коллинеарны. Отношение – отрицательное число . Значит, вектор в раза длиннее и противоположно направлен вектору .
3. и :
Координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: да, да, нет.
Сложение и вычитание векторов.
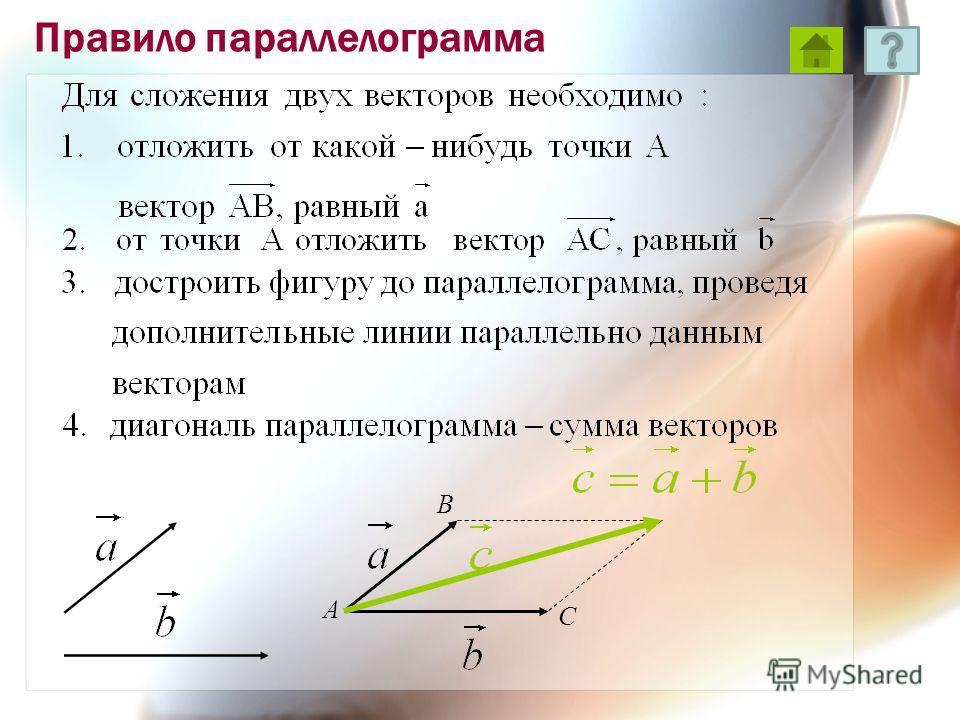 Умножение вектора на число
Умножение вектора на число
Рассмотрим два произвольных вектора в пространстве. Совместим конец вектора и начало вектора (см. рис. 15).
Рис. 15. Конец вектора совместили с началом вектора
Если у двух векторов есть общая точка, то они лежат в одной плоскости. Тогда, чтобы расширенная модель не противоречила исходной, для сложения векторов нужно использовать правило треугольника.
Суммой будет вектор , начало которого совпадает с началом вектора , а конец – с концом вектора (см. рис. 16):
Рис. 16. Вектор
Иллюстрирует это правило нагляднее всего перемещение: переместиться из точки на вектор в точку , а затем из точки на вектор в точку эквивалентно перемещению из точки в точку (см. рис. 17).
Рис. 17. Иллюстрация правила сложения векторов
Точно так же сохраняется и правило параллелограмма. Если совместить два вектора, и не последовательно, а так, чтобы совпали их начала, то одна диагональ построенного на них параллелограмма будет суммой, а вторая диагональ – разностью данных векторов (см.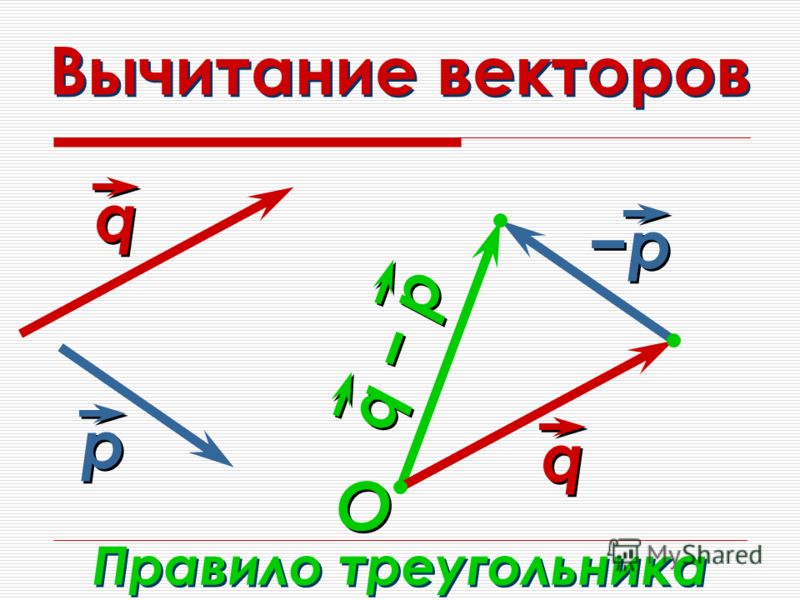 рис. 18):
рис. 18):
Рис. 18. Векторы и
Проверяем себя, куда направить векторы разности, как и раньше:
Два вектора называются противоположными, если они в сумме дают нулевой вектор.
Понятно, что это должны быть противоположно направленные равные по модулю векторы:
Как и в плоском случае, последовательное применение несколько раз правила треугольника для сложения нескольких векторов дает правило многоугольника. Единственная разница будет в том, что многоугольник уже может не быть плоским.
Чтобы сложить несколько векторов, нужно совместить последовательно их концы и начала, и результатом будет вектор, начало которого совпадает с началом первого, а конец – с концом второго:
Например, чтобы сложить векторы (см. рис. 19), рассмотрим сумму:
Рис. 19. Векторы
С алгебраической точки зрения тоже никаких изменений с определением сложения не произошло. Складывая два вектора и в декартовой системе координат, расположим начало вектора в начале координат, с его концом совместим начало вектора . По правилу треугольника построим их сумму (см. рис. 20).
По правилу треугольника построим их сумму (см. рис. 20).
Рис. 20. Вектор
Очевидно, как и в плоском случае, координаты суммы – это сумма координат исходных векторов:
Как обратную операцию получаем разность векторов. Чтобы найти разность векторов, нужно из координат первого вектора вычесть координаты второго вектора:
Противоположным данному называется вектор с противоположными координатами:
Умножение вектора на число также не претерпевает изменений по сравнению с плоским случаем. С геометрической точки зрения умножить вектор на положительное число означает изменить его длину в это количество раз, а направление оставить прежним, например (см. рис. 21):
Рис. 21. Векторы и
Если умножить на отрицательное число, то длина вектора меняется пропорционально модулю множителя, а направление меняется на противоположное, например (см. рис. 22):
Рис. 21. Векторы и
Т. е. умножение на число, по модулю большее единицы, удлиняет вектор, а на число, по модулю меньшее единицы, укорачивает.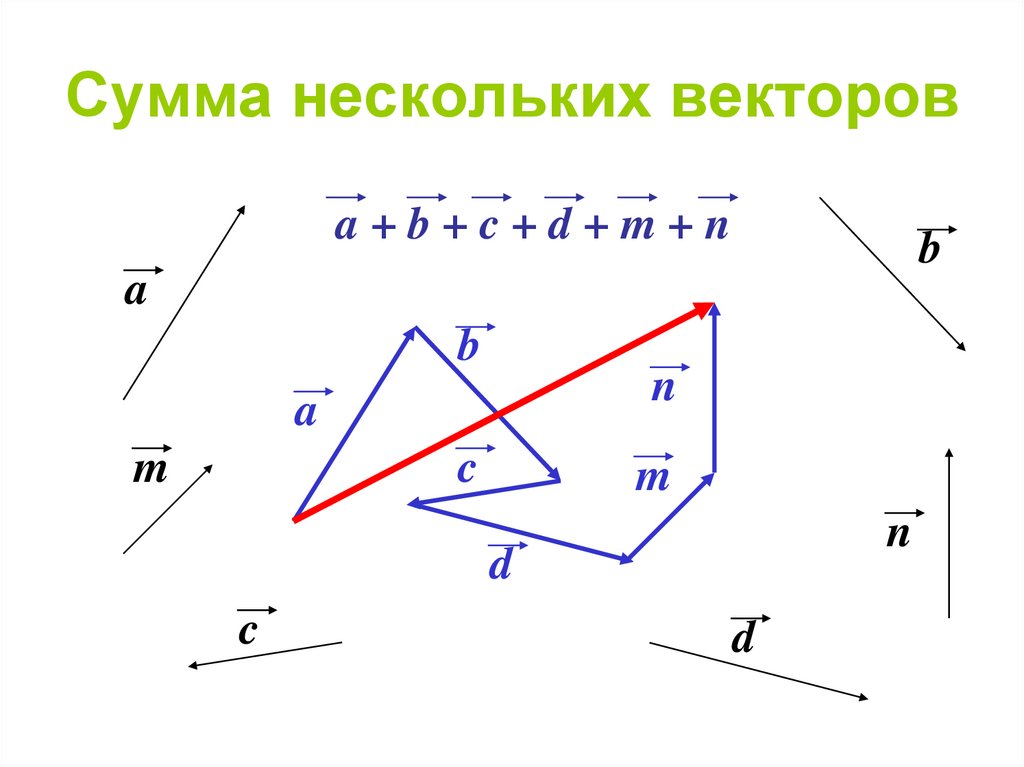
Важно понимать, что результатом умножения вектора на число всегда является вектор, поэтому при умножении вектора на ноль получаем нулевой вектор, а не число ноль.
Понятно, что, если умножить вектор на , получим вектор той же длины, но направленный в другую сторону – это соответствует нашему определению противоположного вектора:
Рассмотрим теперь вектор в декартовой системе координат. Построенный на нем как на диагонали прямоугольный параллелепипед задает координаты вектора. Умножим вектор на число в геометрическом смысле, т. е. удлиним его в раз. Новый параллелепипед будет подобен прежнему с коэффициентом подобия (см. рис. 22). Значит, его измерения будут отличаться в раз от исходных. Но его измерения и есть координаты нового вектора. Следовательно, изменение длины вектора в раз означает умножение его координат на . Изменение направления вектора означает изменение знака его координат на противоложный.
Рис. 22. Параллелепипеды подобны с коэффициентом
Таким образом, чтобы умножить вектор на число, надо умножить все его координаты на это число:
Абсолютно без изменения остаются основные свойства умножения вектора на число – сочетательный и два распределительных закона.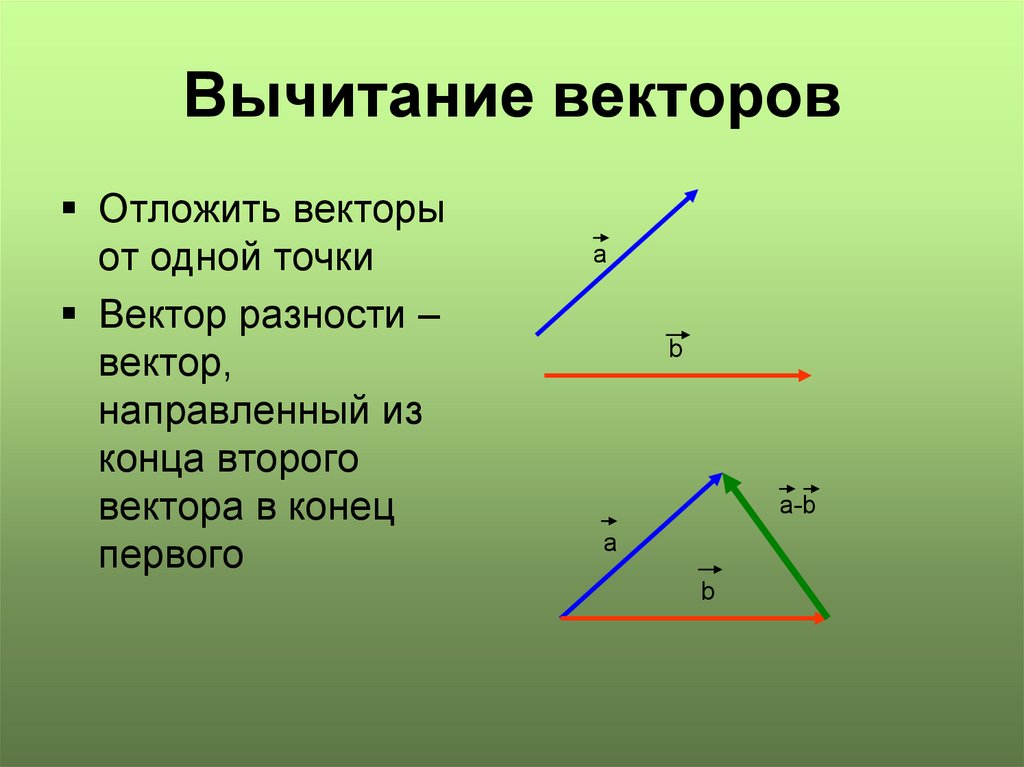 Сочетательный закон утверждает, что можно перемножить два числа, а потом умножить результат на вектор либо поочередно умножать вектор на эти числа. Результат будет одинаков:
Сочетательный закон утверждает, что можно перемножить два числа, а потом умножить результат на вектор либо поочередно умножать вектор на эти числа. Результат будет одинаков:
Распределительные законы утверждают, что можно раскрывать скобки при умножении суммы чисел на вектор и умножении числа на сумму векторов:
Убедиться в истинности этих законов не составит никакого труда, если использовать координатную форму записи векторов. Попробуйте сделать это самостоятельно.
Компланарные векторы
Пока ничего нового по сравнению с плоским случаем мы про векторы не рассказали.
Но вот следующее понятие имеет смысл только в трехмерном случае. Если несколько векторов имеют общее начало, то они могут лежать в одной плоскости или нет.
Если они лежат в одной плоскости, то их называют компланарными.
Векторы компланарны (см. рис. 23).
Рис. 23. Компланарные векторы
Мы не различаем равные векторы, поэтому в этом примере вектор можем заменить на равный ему вектор . Таким образом, векторы компланарны. Иными словами, векторы компланарны, если они все параллельны одной плоскости, в данном случае плоскости нижнего основания.
Таким образом, векторы компланарны. Иными словами, векторы компланарны, если они все параллельны одной плоскости, в данном случае плоскости нижнего основания.
Векторы некомпланарны (см. рис. 24).
Рис. 24. Некомпланарные векторы
Понятно, что два вектора всегда компланарны. Разберемся, каковы условия компланарности векторов. Вспомним из курса планиметрии еще одно понятие – разложение вектора. Если верно равенство , то говорят, что вектор разложен по векторам и .
Но из курса планиметрии мы также знаем, что такой вектор будет лежать в одной плоскости с векторами и . В самом деле, векторы лежат в плоскости одного и того же параллелограмма, как следует из правил умножения векторов на число и сложения векторов. Таким образом, если один из трех векторов раскладывается по двум другим, то такие три вектора компланарны.
Верно и обратное. Если три вектора компланарны, то любой из них можно разложить по двум оставшимся при условии, что эти два вектора не коллинеарны. Это легко доказать, перейдя в плоскость, в которой лежит эта тройка векторов, и воспользоваться соответствующим утверждением из планиметрии, а именно, что любой вектор можно разложить по двум неколлинеарным векторам.
Это легко доказать, перейдя в плоскость, в которой лежит эта тройка векторов, и воспользоваться соответствующим утверждением из планиметрии, а именно, что любой вектор можно разложить по двум неколлинеарным векторам.
Что касается алгебраического представления векторов, то здесь проверка компланарности трех векторов сводится к решению соответствующего уравнения c переменными и .
Пример 3. Проверить, являются векторы компланарными.
Решение
Запишем уравнение:
Умножим в правой части векторы на числа и сложим их:
Два вектора равны, если попарно равны все их координаты. Получаем систему трех простых уравнений:
Ее решение:
Таким образом:
Ответ: векторы компланарны.
Рассмотрим три некомпланарных вектора и найдем их сумму. В алгебраическом подходе нет никакой разницы, складывать ли компланарные или некомпланарные векторы – нужно сложить все соответствующие координаты.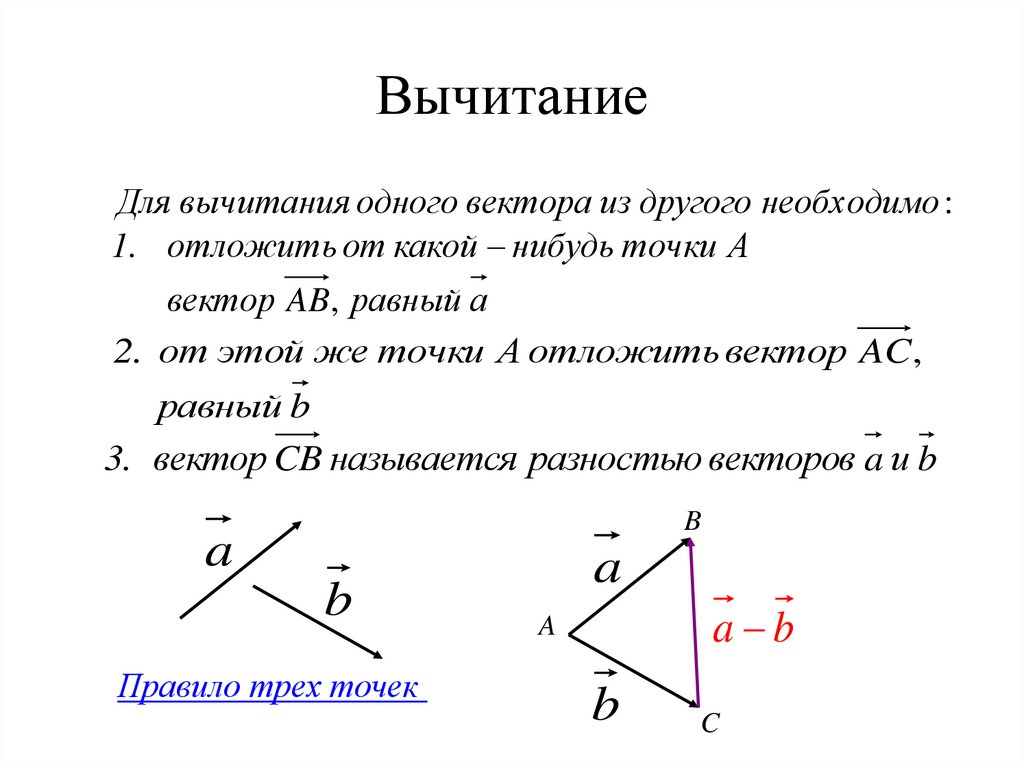
Для геометрического подхода можно сформулировать простое правило параллелепипеда.
Совместим три вектора в общее начало. Построим на них, как на ребрах, параллелепипед (см. рис. 25).
Рис. 25. Построенный параллелепипед
Сложим сначала векторы и :
Теперь сложим и вектор :
Таким образом, сумма трех некомпланарных векторов равна диагонали параллелепипеда, построенного на этих векторах.
Теорема о разложении вектора по трем некомпланарным
Мы уже знаем, что любой вектор на плоскости можно разложить по двум неколлинеарным векторам. Аналогичное утверждение сформулируем для векторов в пространстве.
Понятно, почему речь идет о некомпланарных векторах. Если мы возьмем компланарные векторы, будем их умножать на разные и числа и складывать друг с другом, мы не выйдем за пределы плоскости, в которой они лежат. Итак, докажем утверждение.
Итак, докажем утверждение.
Доказательство
Пусть – данные некомпланарные векторы (см. рис. 26).
Рис. 26. Иллюстрация к доказательству
Докажем для начала, что любой вектор можно разложить по этим трем векторам, а потом докажем единственность такого разложения.
Совместим все четыре вектора в общее начало . Обозначим концы векторов такими же буквами, как векторы, только заглавными (см. рис. 27).
Рис. 27. Иллюстрация к доказательству
Через точку проведем прямую, параллельную вектору . Она пересечет плоскость в некоторой точке . Через проведем прямую, параллельную . Она пересечет прямую в некой точке (см. рис. 28).
Рис. 28. Иллюстрация к доказательству
Легко увидеть, что:
Но каждый из векторов в правой части равенства коллинеарен одному из исходных трех векторов, т. е. получается из них умножением на некое число. Тогда:
Таким образом, мы разложили вектор по векторам .
Докажем единственность такого разложения.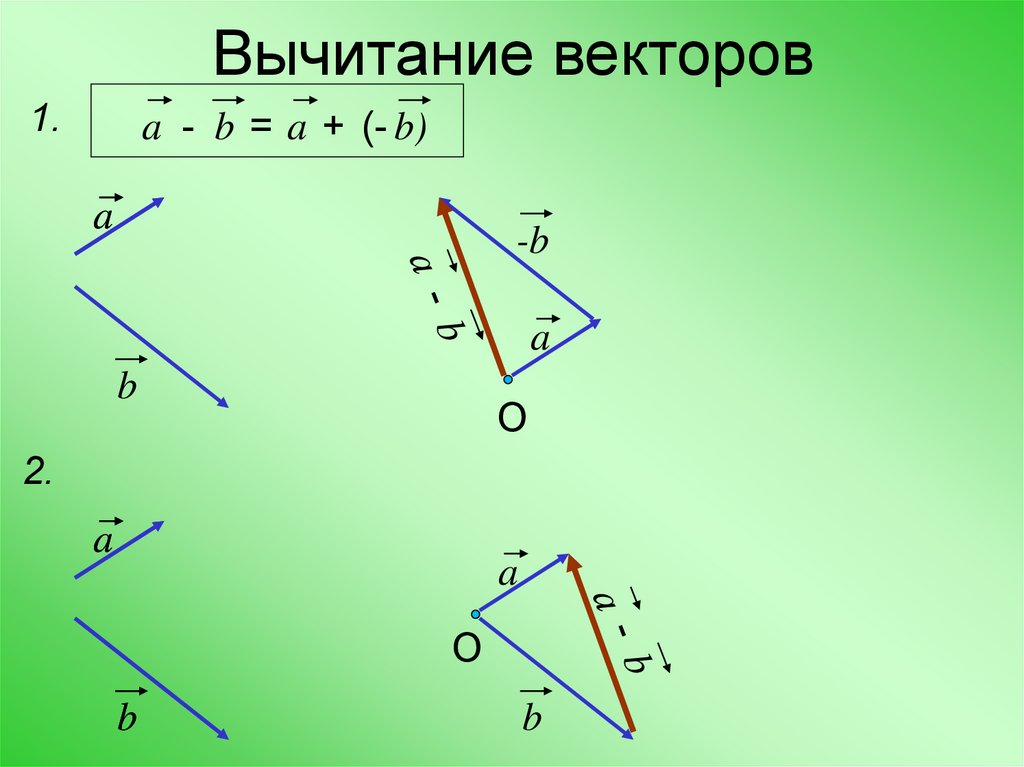 Предположим, что существует два разложения вектора :
Предположим, что существует два разложения вектора :
Вычтем из первого второе уравнение:
Т. к. ни один из векторов не является нулевым (ответьте, почему), то это означает, что все разности в скобках равны нулю. В самом деле, если, например, , то:
Но это означает, что векторы компланарны, что противоречит условию. А раз все разности в скобках равны нулю, то рассматриваемые разложения совпадают – получили противоречие. Значит, такое разложение будет единственным.
Доказано.
Рассмотрим три единичных вектора, т. е. три вектора с длиной , направленных вдоль осей координат. Стандартное обозначение для них (см. рис. 29). Т. к. эти векторы некомпланарны, то по ним можно разложить любой другой вектор.
Рис. 29. Векторы
Разложим вектор по этим трем векторам (см. рис. 30).
Рис. 30. Вектор
Для этого умножим вектор на число . Очевидно, получим вектор . Аналогично умножим вектор на , а вектор – на . Сумма полученных векторов по правилу параллелепипеда равна вектору (см. рис. 31).
Сумма полученных векторов по правилу параллелепипеда равна вектору (см. рис. 31).
Рис. 31. Построенный параллелепипед
Т. е., чтобы разложить вектор по этим трем, нужно в качестве коэффициентов использовать его координаты:
В связи с этим векторы называют координатными.
Правило разложения по координатным векторам можно увидеть и из других соображений.
Выпишем координаты самих координатных векторов:
Тогда, очевидно, разложение вектора имеет вид:
Таким образом, координаты вектора и коэффициенты при его разложении по координатным векторам – это одно и то же. Впрочем, мы уже сталкивались с идентичной ситуацией в планиметрии. Только координатных векторов было всего два.
Список литературы
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.
 Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА». - Погорелов А.В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал mathprofi.ru
- Интернет-портал ru.onlinemschool.com
Домашнее задание
- Найти координаты и длину вектора , если и .
- Даны векторы и . Найти координаты вектора .
- – тетраэдр, – середины его ребер . Компланарны ли векторы ?
Программирование
R для вычитания всех значений в векторе из всех значений в другом векторе.
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, мы можем использовать
sapply функция со знаком вычитания.
Например, если у нас есть два вектора, скажем, X и Y, и мы хотим вычесть все значения в Y из всех значений в X, мы можем использовать приведенную ниже команду —
sapply (X, «-», Y)
Пример 1
Следующий фрагмент создает образец фрейма данных —
x1<-1:10 у1<-10:1 sapply (x1, «-», y1)
Вывод
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] [2] [3] [4] [5 ] [6] [7] [8] [9] [10] [1,] -9 -8 -7 -6 -5 -4 -3 -2 -1 0 [2,] -8 -7 -6 -5 -4 -3 -2 -1 0 1 [3,] -7 -6 -5 -4 -3 -2 -1 0 1 2 [4,] -6 -5 -4 -3 -2 -1 0 1 2 3 [5,] -5 -4 -3 -2 -1 0 1 2 3 4 [6,] -4 -3 -2 -1 0 1 2 3 4 5 [7,] -3 -2 -1 0 1 2 3 4 5 6 [8,] -2 -1 0 1 2 3 4 5 6 7 [9,] -1 0 1 2 3 4 5 6 7 8 [10,] 0 1 2 3 4 5 6 7 8 9
Пример 2
Следующий фрагмент создает образец фрейма данных —
x2<-sample(0:9,10) x2
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] 2 3 0 8 5 6 9 4 1 7
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, добавьте следующее код к приведенному выше фрагменту —
x2 <-sample (0: 9,10) y2<-sample(0:9,20,replace=TRUE) y2
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] 9 9 6 9 7 1 8 3 6 4 8 5 2 0 0 9 9 3 2 2
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, добавьте следующее код к приведенному выше фрагменту —
x2 <-sample (0: 9,10) y2<-sample(0:9,20,replace=TRUE) sapply (x2, «-», y2)
Вывод
Если вы выполните все приведенные выше фрагменты как одну программу, она сгенерирует следующий вывод —
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [1,] -7 -6 -9 -1 -4 -3 0 0 -5 -8 -2 [2,] -7 -6 -9 -1 -4 -3 0 0 -5 -8 -2 [3,] -4 -3 -6 2 -1 0 3 -2 -5 1 [4,] -7 -6 -9 -1 -4 -3 0 -5 -8 -2 [5,] -5 -4 -7 1 -2 -1 2 -3 -6 0 [6,] 1 2 -1 7 4 5 8 3 0 6 [7,] -6 -5 -8 0 -3 -2 1 -4 -7 -1 [8,] -1 0 -3 5 2 3 6 1 -2 4 [9,] -4 -3 -6 2 -1 0 3 -2 -5 1 [10,] -2 -1 -4 4 1 2 5 0 -3 3 [11,] -6 -5 -8 0 0 -3 -2 1 1 -4 -7 -1 [12,] -3 -2 -5 3 0 1 4 -1 -4 2 [13,] 0 1 -2 6 3 4 7 2 -1 5 [14,] 2 3 0 8 5 6 9 4 1 7 [15,] 2 3 0 8 5 6 9 4 1 7 [16,] -7 -6 -9 -1 -4 -3 0 0 -5 -8 -2 [17,] -7 -6 -9 -1 -4 -3 0 0 -5 -8 -2 [18,] -1 0 -3 5 2 3 6 1 -2 4 [19,] 0 1 -2 6 3 4 7 2 -1 5 [20,] 0 1 -2 6 3 4 7 2 -1 5
Пример 3
Следующий фрагмент кода создает образец фрейма данных —
x3<-rpois(2,5) x3
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] 5 2
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, добавьте следующее код к приведенному выше фрагменту —
x3 <-rpois (2,5) y3<-rpois(20,1) у3
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] 0 1 1 0 0 0 1 1 1 0 0 0 2 1 0 1 2 0 1 1
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, добавьте следующее код к приведенному выше фрагменту —
x3 <-rpois (2,5) y3<-rpois(20,1) sapply (x3, «-», y3)
Вывод
Если вы выполните все приведенные выше фрагменты как одну программу, она сгенерирует следующий вывод —
[1] [2] [1,] 5 2 [2,] 4 1 [3,] 4 1 [4,] 5 2 [5,] 5 2 [6,] 5 2 [7,] 4 1 [8,] 4 1 [9,] 4 1 [10,] 5 2 [11,] 5 2 [12,] 5 2 [13,] 3 0 [14,] 4 1 [15,] 5 2 [16,] 4 1 [17,] 3 0 [18,] 5 2 [19,] 4 1 [20,] 4 1
Пример 4
Следующий фрагмент создает образец фрейма данных —
x4<-sample(1:20,5) x4
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] 15 4 9 8 3
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, добавьте следующее код к приведенному выше фрагменту —
x4<-sample(1:20,5) y4<-образец (1:20,15) y4
Если вы выполните приведенный выше фрагмент, он сгенерирует следующий вывод —
[1] 19 16 1 9 8 4 2 12 3 18 13 5 20 10 6
Чтобы вычесть все значения в векторе из всех значений в другом векторе в R, добавьте следующее код к приведенному выше фрагменту —
x4 <-sample (1: 20,5) y4<-образец (1:20,15) sapply (x4, «-», y4)
Вывод
Если вы выполните все приведенные выше фрагменты как одну программу, она сгенерирует следующий вывод —
[1] [2] [3] [4] [5] [1,]-4-15-10-11-16 [2,]-1-12-7-8-13 [3,] 14 3 8 7 2 [4,] 6 -5 0 -1 -6 [5,] 7 -4 1 0 -5 [6,] 11 0 5 4 -1 [7,] 13 2 7 6 1 [8,] 3-8-3-4-9 [9,] 12 1 6 5 0 [10,]-3-14-9-10-15 [11,] 2-9-4-5-10 [12,] 10 -1 4 3 -2 [13,]-5-16-11-12-17 [14,] 5-6-1-2-7 [15,] 9 -2 3 2 - 3
Объяснение урока: Вычитание векторов | Нагва
В этом объяснителе мы научимся вычитать один вектор из другого за два
размеры, используя как графические, так и алгебраические методы.
Рассмотрим векторы ⃑𝐴 и ⃑𝐵 показано на сетке ниже.
Напомним, что мы можем вычислить результат ⃑𝐴+⃑𝐵 графически путем перемещения вектора ⃑𝐵 так, чтобы «хвост» вектора ⃑𝐵 расположен на «кончике» вектора ⃑𝐴. Это показано на сетке ниже, и результатом сложения двух векторов является ⃑𝑉.
Но что получится, если из вычесть ? ⃑𝐵 из ⃑𝐴 быть? Каким будет результат ⃑𝐴−⃑𝐵?
Напомним, что отрицательное вектора — это вектор, который имеет то же самое магнитуда но противоположное направление . На приведенной ниже диаграмме показан вектор, ⃑𝐵, и его отрицательный, −⃑𝐵.
С обычными числами вычитание числа равносильно сложению отрицательного числа. этого числа. Так, например, 12−4 такой же как 12+(−4).
То же самое относится и к векторам: ⃑𝐴−⃑𝐵 такой же как ⃑𝐴+−⃑𝐵.
Итак, мы можем вычесть один вектор из другого, сначала найдя отрицательное значение
вектор, который мы хотим вычесть, а затем сложить два вектора.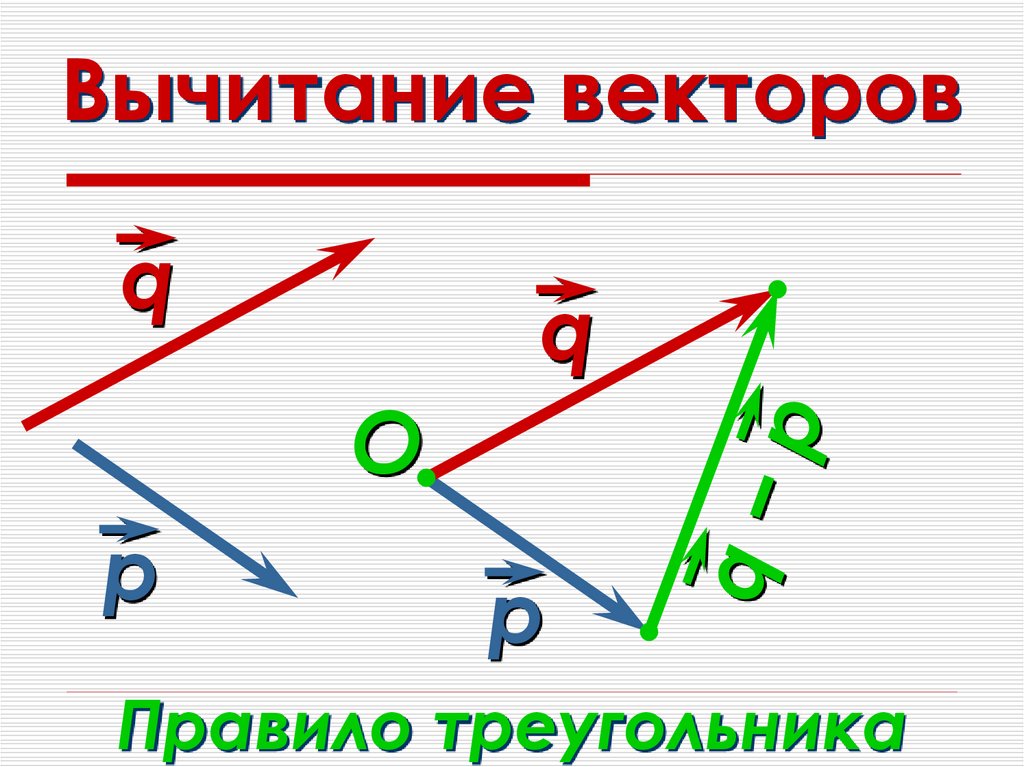
Возвращаясь к первой диаграмме, давайте изменим от ⃑𝐵 до −⃑𝐵.
Теперь мы можем просто сложить эти два вектора, поместив хвост −⃑𝐵 на кончике ⃑𝐴. Результат вектор ⃑𝑉 показано на сетке ниже.
Это один из способов графического вычитания векторов, но есть и другой способ, что обычно быстрее. Рассмотрим снова два вектора ⃑𝐴 и ⃑𝐵, показано на сетке ниже.
Результатом ⃑𝐴−⃑𝐵 является вектор, идущий от кончик второго вектора (в данном случае ⃑𝐵) к кончик первого вектора (в данном случае ⃑𝐴). Это вектор ⃑𝑉, показанный на сетке ниже.
Если мы подумаем о векторах ⃑𝐴 и ⃑𝐵 как векторы положения точек 𝐴 и 𝐵, то результат ⃑𝐴−⃑𝐵 может быть рассматривается как вектор, который идет « с 𝐵 по 𝐴», как показано ниже.
Обратите внимание, что из-за этого результат
⃑𝐴−⃑𝐵 равно , а не , что и результат
⃑𝐵−⃑𝐴. Результат
⃑𝐵−⃑𝐴 — вектор, идущий от
𝐴 до 𝐵, как показано ниже.
Как видно из диаграммы, изменение порядка двух векторов в вычитание дает отрицательный результат. Мы можем записать это алгебраически как ⃑𝐵−⃑𝐴=−⃑𝐴−⃑𝐵.
Пример 1: графическое вычитание векторов
На схеме показаны семь векторов: ⃑𝐴, ⃑𝐵, ⃑𝑃, ⃑𝑄, ⃑𝑅, ⃑𝑆 и ⃑𝑇.
- Какой из векторов равен ⃑𝐴−⃑𝐵?
- Какой из векторов равен ⃑𝐵−⃑𝐴?
Ответ
Часть 1
Напомним, что мы можем найти результат ⃑𝐴−⃑𝐵, нарисовав вектор, идущий от кончика второго вектора, ⃑𝐵, к кончику первого вектор, ⃑𝐴. Это показано на сетке ниже.
Сравнивая это с другими векторами, показанными на диаграмме в вопросе, мы видим что результат ⃑𝐴−⃑𝐵 соответствует вектору ⃑𝑄.
Часть 2
Напомним, что когда мы меняем порядок векторов в векторе
вычитание, мы получаем отрицательный результат. Выраженный алгебраически,
⃑𝐵−⃑𝐴=−⃑𝐴−⃑𝐵.
Выраженный алгебраически,
⃑𝐵−⃑𝐴=−⃑𝐴−⃑𝐵.
Итак, мы можем использовать наш ответ из части 1, чтобы быстро найти ответ на эту часть. Если ⃑𝐴−⃑𝐵=⃑𝑄, то ⃑𝐵−⃑𝐴=−(⃑𝑄)⃑𝐵−⃑𝐴=−⃑𝑄.
Возвращаясь к диаграмме в вопросе, мы видим, что вектор то есть отрицание вектора ⃑𝑄 является вектором ⃑𝑆.
Пример 2: графическое вычитание векторов
Какой из векторов, ⃑𝑃, ⃑𝑄, ⃑𝑅, ⃑𝑆 или ⃑𝑇, показанный на диаграмме, равен ⃑𝐴−⃑𝐵?
Ответ
Напомним, что мы можем найти результат ⃑𝐴−⃑𝐵 с помощью рисование вектора, идущего от вершины второго вектора, ⃑𝐵, к вершине первого вектора, ⃑𝐴. Это показано на сетке ниже.
Сравнивая это с другими векторами, показанными на диаграмме в вопросе, мы видим что результат ⃑𝐴−⃑𝐵 соответствует вектору ⃑𝑃.
До сих пор мы рассматривали, как графически вычитать векторы, но мы также можем
сделать это алгебраически.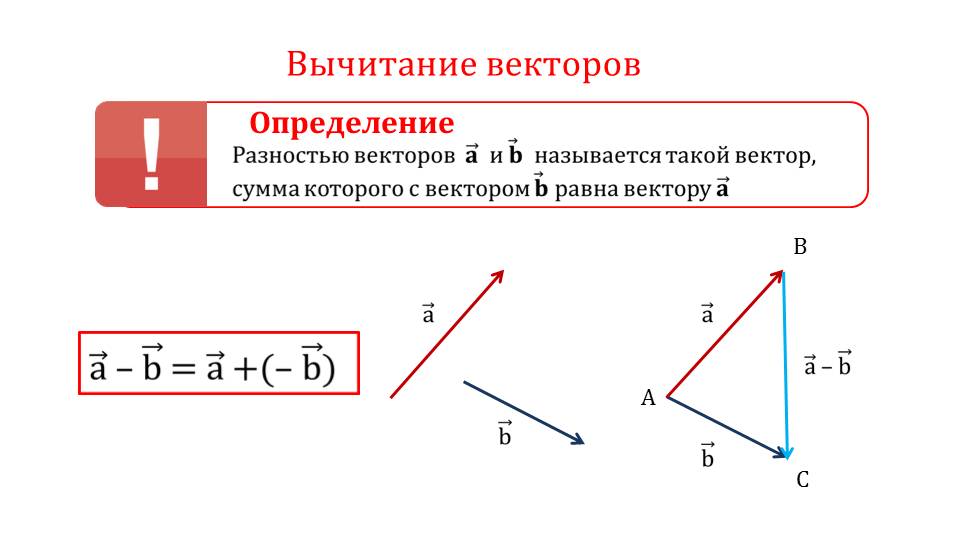
Напомним, что любой вектор ⃑𝐴 можно представить в виде сумма кратных единичных векторов вдоль осей 𝑥 и 𝑦. Если горизонтальная составляющая ⃑𝐴 равна 𝐴, вертикальная составляющая ⃑𝐴 равна 𝐴, ⃑𝑖 — единичный вектор вдоль 𝑥-ось, а ⃑𝑗 — единица вектор вдоль оси 𝑦, то ⃑𝐴=𝐴⃑𝑖+𝐴⃑𝑗.
Точно так же, если мы скажем, что ⃑𝐵=𝐵⃑𝑖+𝐵⃑𝑗, тогда ⃑𝐴−⃑𝐵=𝐴⃑𝑖+𝐴⃑𝑗−𝐵⃑𝑖+𝐵⃑𝑗.
Если раскрыть скобки, получим ⃑𝐴−⃑𝐵=𝐴⃑𝑖+𝐴⃑𝑗−𝐵⃑𝑖−𝐵⃑𝑗.
Затем мы можем собрать подобные термины, чтобы получить ⃑𝐴−⃑𝐵=(𝐴−𝐵)⃑𝑖+𝐴−𝐵⃑𝑗.
Итак, если мы знаем компоненты двух векторов, мы можем использовать эту формулу для вычесть один вектор из другого и получить компоненты полученного вектор.
Пример 3. Вычитание двух векторов по их компонентам
Рассмотрим два вектора ⃑𝐴 и ⃑𝐵, где ⃑𝐴=8⃑𝑖+10⃑𝑗 и ⃑𝐵=3⃑𝑖+2⃑𝑗. Вычислите ⃑𝐴−⃑𝐵.
Ответ
Мы можем использовать формулу
⃑𝐴−⃑𝐵=(𝐴−𝐵)⃑𝑖+𝐴−𝐵⃑𝑗
чтобы найти результат ⃑𝐴−⃑𝐵, где
𝐴 и 𝐵 — горизонтальные компоненты
два вектора и 𝐴 и
𝐵 являются
вертикальные компоненты двух векторов.
Подставляя значения, указанные в вопросе, получаем ⃑𝐴−⃑𝐵=(8−3)⃑𝑖+(10−2)⃑𝑗⃑𝐴−⃑𝐵=5⃑𝑖+8⃑𝑗.
Результатом ⃑𝐴−⃑𝐵 является 5⃑𝑖+8⃑𝑗.
Пример 4. Вычитание двух векторов по их компонентам
Рассмотрим два вектора ⃑𝐴 и ⃑𝐵. ⃑𝐴=4⃑𝑖−9⃑𝑗 и ⃑𝐵=1⃑𝑖−12⃑𝑗. Какой из пяти векторов, изображенных на диаграмме, равен ⃑𝐴−⃑𝐵?
Ответ
В этом вопросе мы должны вычислить результат векторного вычитания алгебраически, а затем определить полученный вектор на диаграмме.
Мы можем использовать формулу ⃑𝐴−⃑𝐵=(𝐴−𝐵)⃑𝑖+𝐴−𝐵⃑𝑗 чтобы найти результат ⃑𝐴−⃑𝐵, где 𝐴 и 𝐵 — горизонтальные компоненты два вектора и 𝐴 и 𝐵 являются вертикальными компоненты двух векторов.
Подставляя значения, указанные в вопросе, получаем ⃑𝐴−⃑𝐵=(4−1)⃑𝑖+((−9)−(−12))⃑𝑗⃑𝐴−⃑𝐵=(4−1)⃑𝑖+(−9+12)⃑𝑗⃑𝐴−⃑𝐵=3⃑𝑖+3⃑𝑗.
Результатом ⃑𝐴−⃑𝐵 является
3⃑𝑖+3⃑𝑗.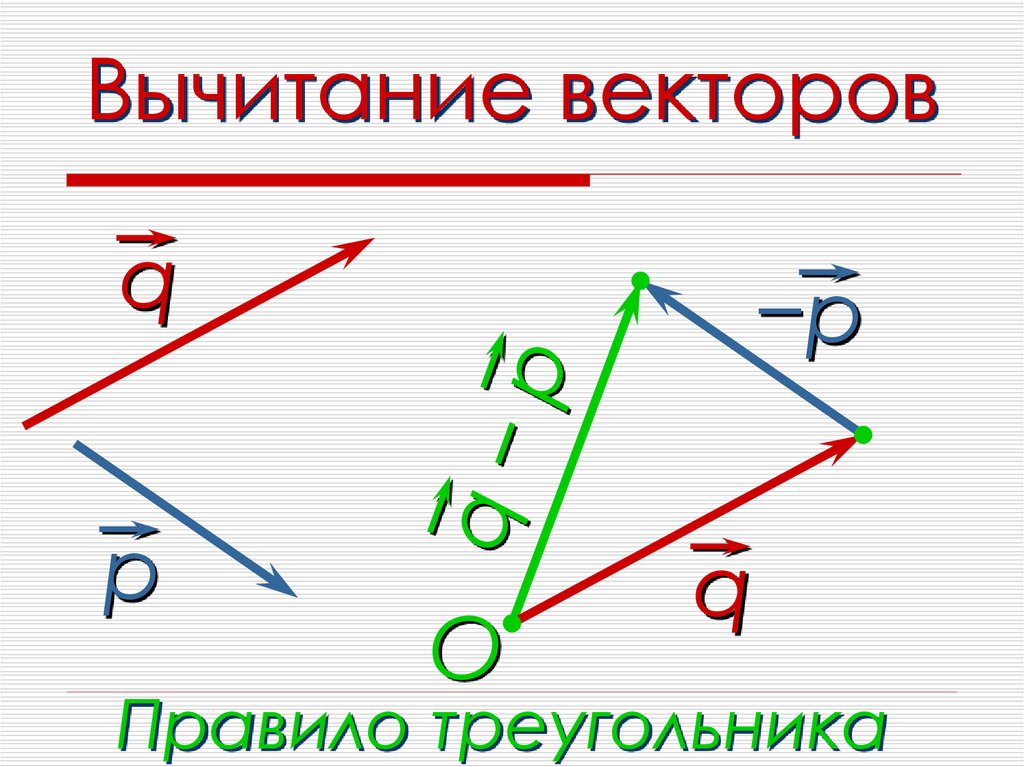


 1416
1416

 Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».