Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. 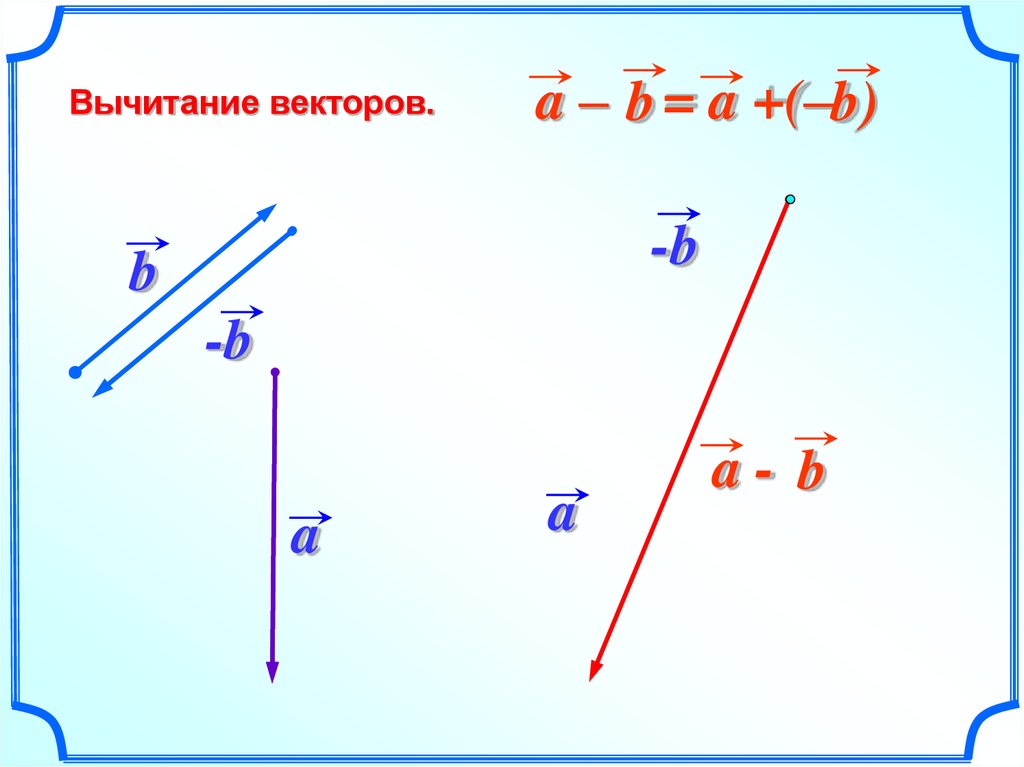 § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. 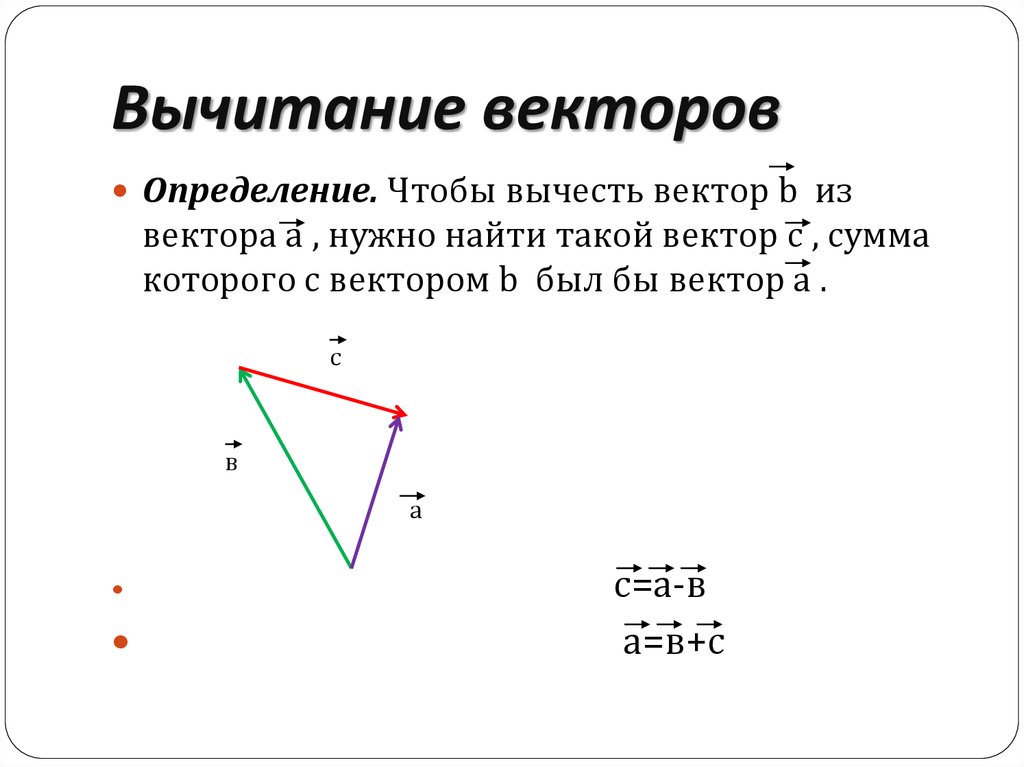 § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии.  Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. Упражнения ГЛАВА III. 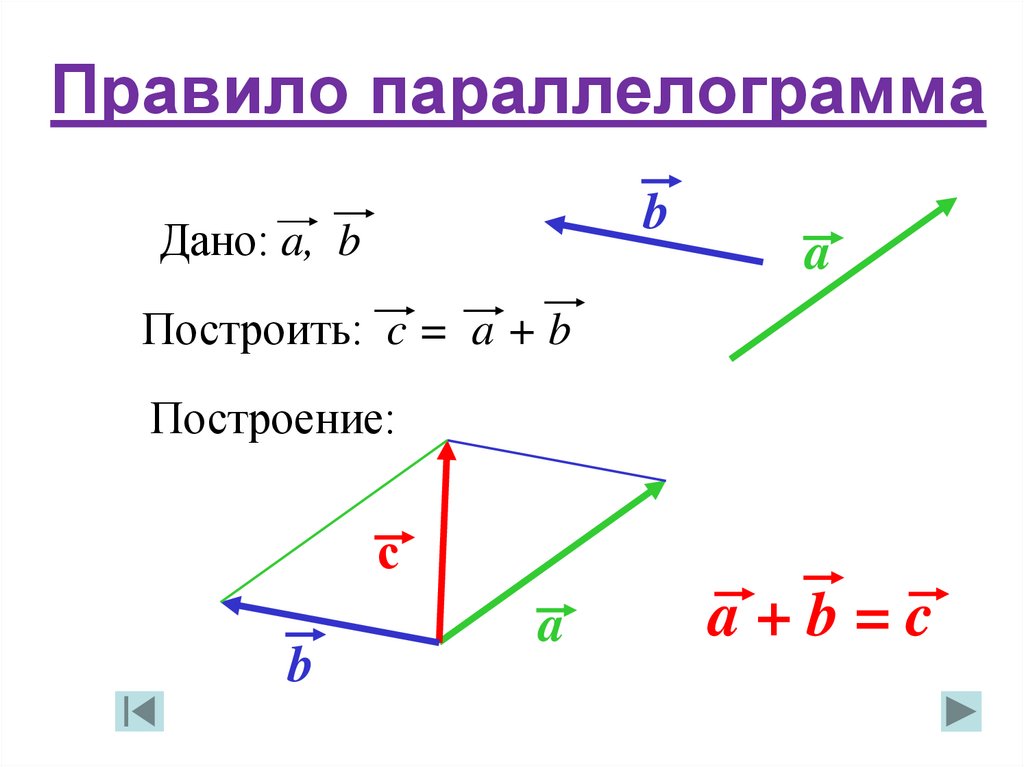 ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей.  Общие уравнения прямой. Общие уравнения прямой.§ 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. 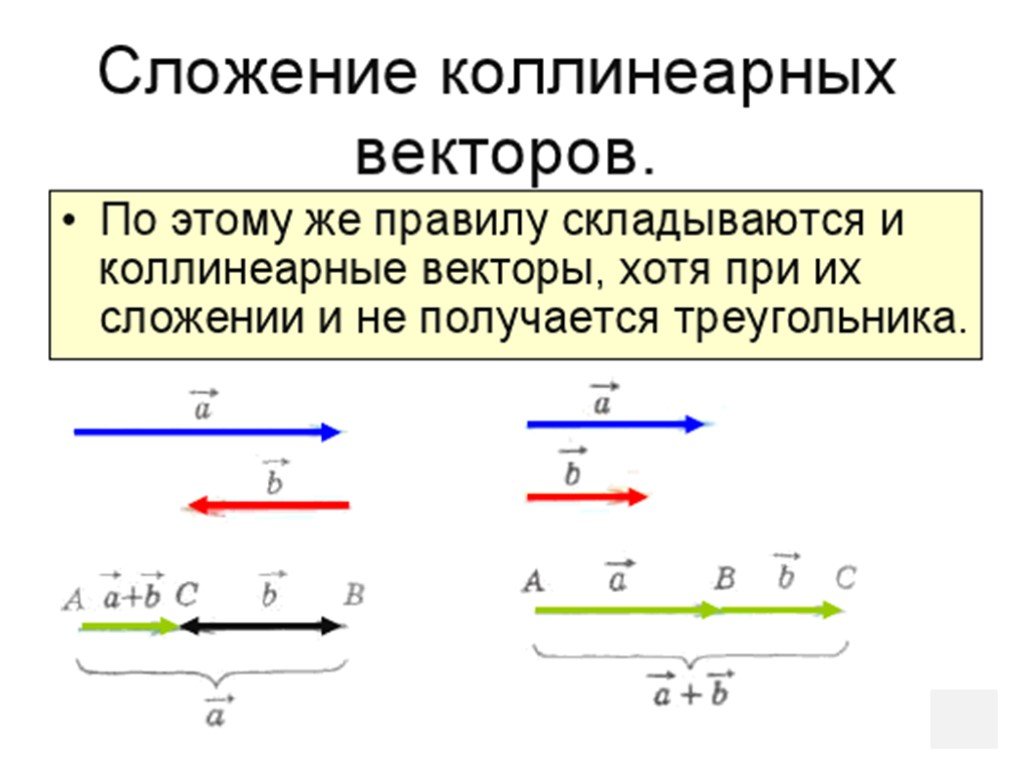 Конструкции В. Г. Шухова. Конструкции В. Г. Шухова.Упражнения Ответы |
Простейшие задачи Как найти вектор по двум точкам?
Если даны две точки плоскости и , то вектор имеет следующие координаты:
Если даны две точки пространства и , то вектор имеет следующие координаты:
То есть, из координат конца вектора
Пример
Даны две точки плоскости и . Найти координаты вектора
Решение: по соответствующей формуле:
Как вариант, можно было использовать следующую запись:
Можно и так:
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты
же вектора –
это его разложение по базису
,
в данном случае
.
Записи координат точек и координат векторов вроде бы схожи: , а смысл координат абсолютно разный, и следует хорошо понимать эту разницу.
Пример
Даны точки . Найти векторы .
Как найти длину отрезка?
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример
Даны
точки
и
.
Найти длину отрезка
.
Ответ:
Если дан вектор плоскости , то его длина вычисляется по формуле .
Если дан вектор пространства , то его длина вычисляется по формуле .
Пример
Даны точки и . Найти длину вектора .
Решение: Сначала найдём вектор :
По формуле вычислим длину вектора:
Ответ:
Пример
а) Даны точки и . Найти длину вектора . б) Даны векторы , , и . Найти их длины.
а) Решение: найдём вектор : Вычислим длину вектора: Ответ:
б) Решение: Вычислим длины векторов:
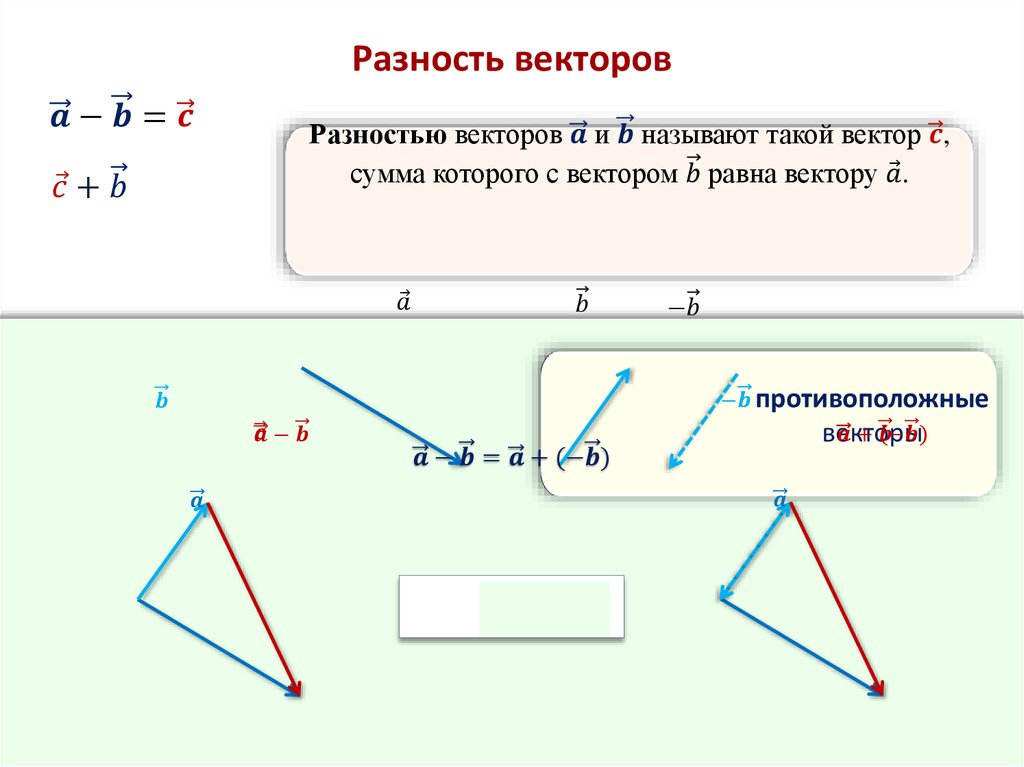
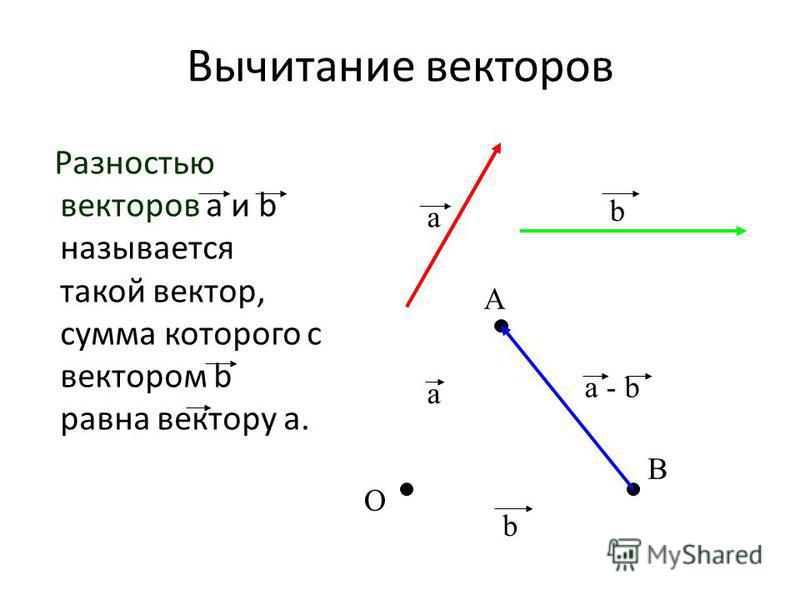
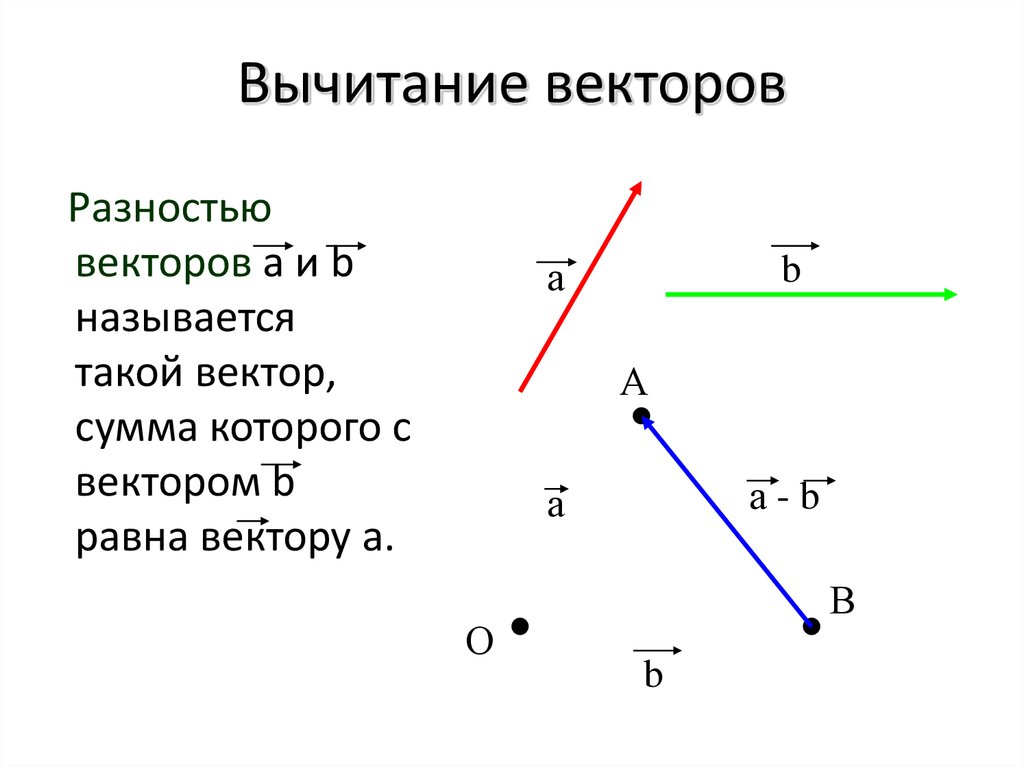
Действия с векторами в координатах
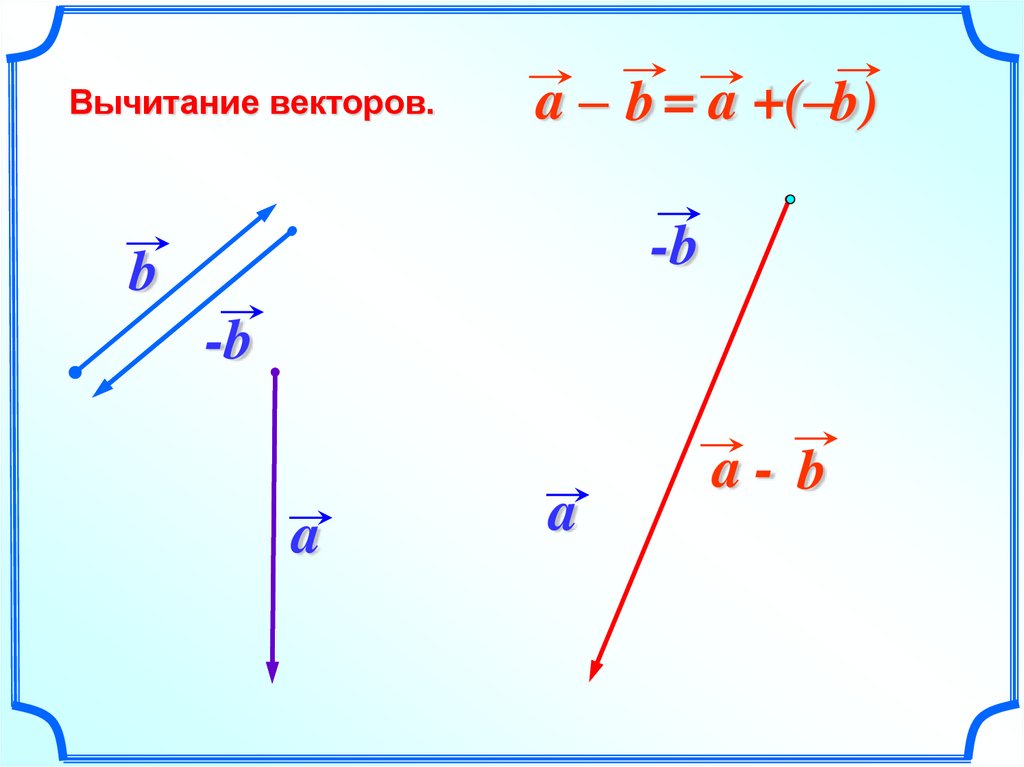
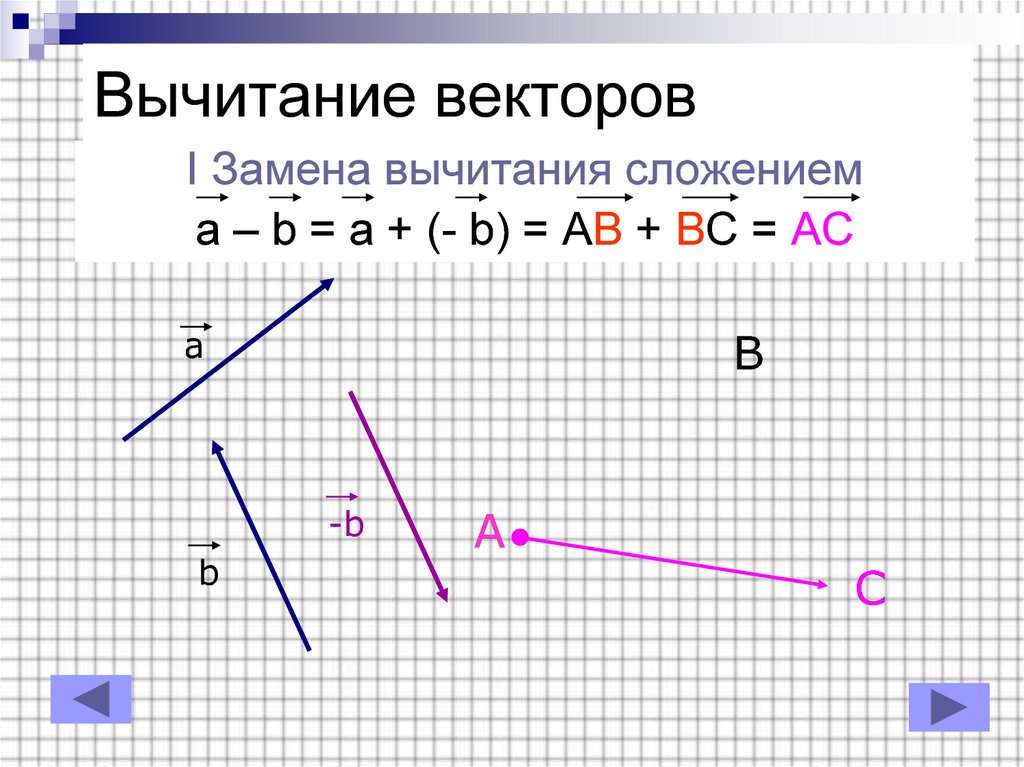
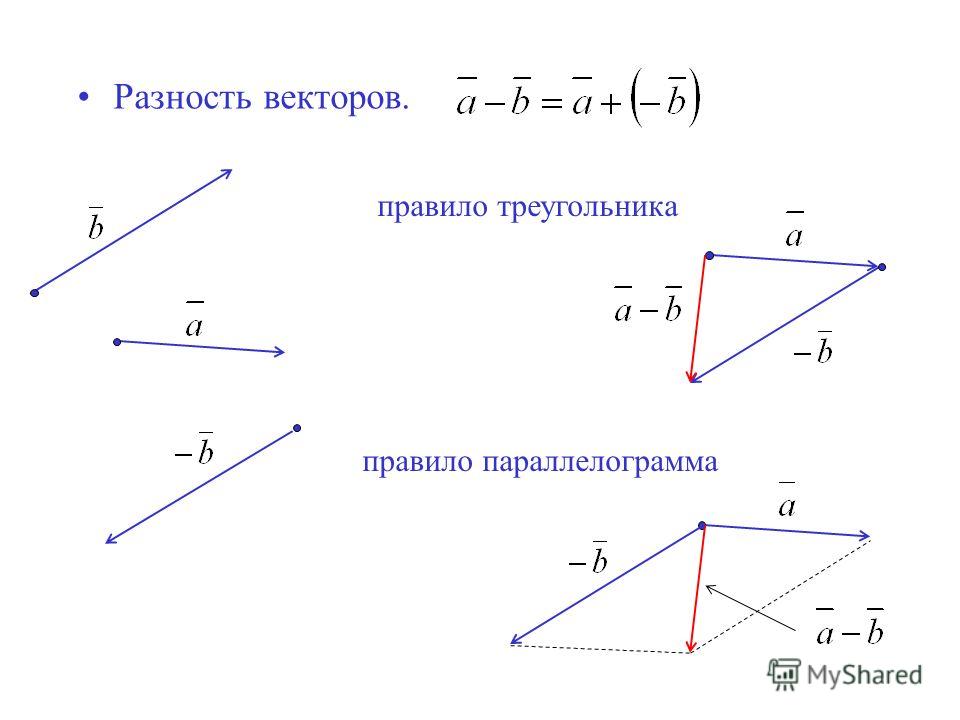
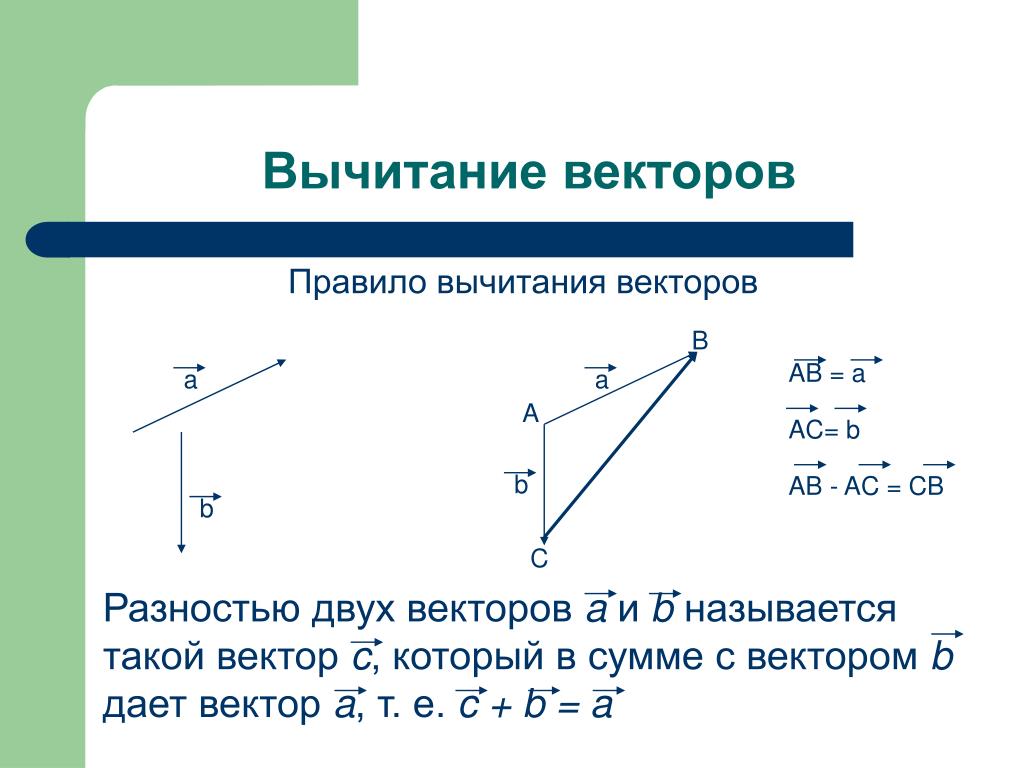
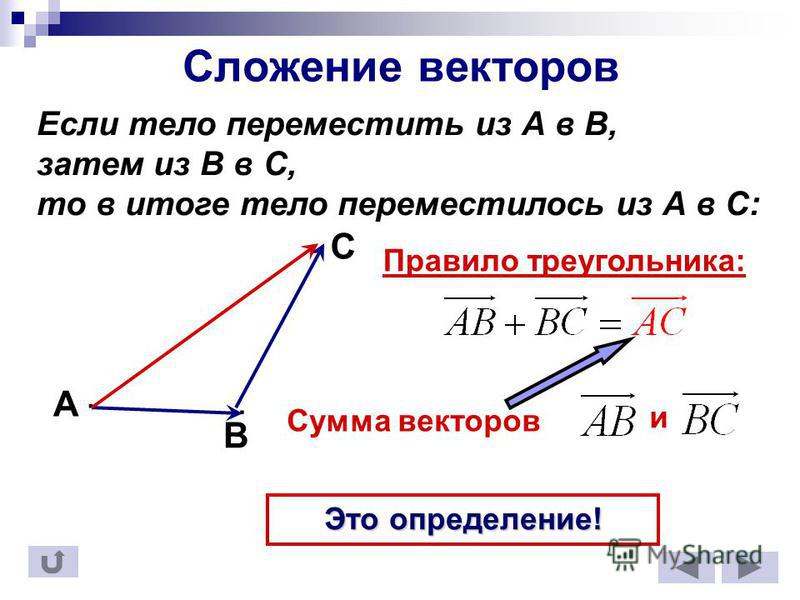
1) Правило сложения векторов. Рассмотрим два вектора плоскости и . Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты: .
Частный
случай – формула разности векторов:
.
Аналогичное правило справедливо для суммы любого количества векторов, например, найдём сумму трёх векторов:
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы , то их суммой является вектор .
2) Правило умножения вектора на число. Для того чтобы вектор умножить на число , необходимо каждую координату данного вектора умножить на число : .
Для пространственного вектора правило такое же:
Пример
Даны векторы и . Найти и
Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
Ответ:
векторных операций — предварительный расчет | Сократ
Каково определение сложения векторов?
Векторы можно добавлять, добавляя компоненты по отдельности, если они имеют одинаковые размеры.
 Добавление двух векторов просто дает результирующий вектор.
Добавление двух векторов просто дает результирующий вектор.То, что означает результирующий вектор, зависит от того, какую величину он представляет. Если вы добавляете скорость с изменением скорости, вы получите новую скорость. Если вы добавите 2 силы, то вы получите чистую силу.
Если вы складываете два вектора, имеющих одинаковую величину, но противоположные направления, ваш результирующий вектор будет равен нулю. Если вы добавляете два вектора, которые находятся в одном направлении, то результат будет в одном направлении с величиной, которая является суммой двух величин.
Как сделать векторное вычитание?
Для двух векторов #vecv# и #vecw# у вас есть:
#vecv-vecw=vecv+(-vecw)#Графически мы можем использовать закон параллелограмма:
Если у вас есть векторы в компонентной форме, вы снова используете :
#vecv-vecw=vecv+(-vecw)# работает с каждым набором соответствующих компонентов.
Например:
#vecv=4veci+2vecj-5veck# и:
#vecw=-2veci+4vecj+veck##vecv-vecw=vecv+(-vecw)=[4+(2)]veci+[ 2+(-4)]vecj+[-5+(-1)]vec=#
92)#
#=6veci-2vecj-6veck#Затем определите #theta#
Если вы нарисуете треугольник, где a — ось x, а b — ось y, вы получите прямоугольный треугольник. Угол #theta# имеет следующие измерения:
#tan(theta) = b/a#
#theta = artcan(b/a)#Наконец, у нас есть формула вертикальной составляющей:
#v_y = ||A || sin(θ)#Для помощи в калькуляторе используйте кнопку компонента здесь:
http://www.mathcelebrity.com/vector.php
Что понимают под компонентом вектора?
Рассмотрим вектор #vecv#, например, в пространстве:
Если вы хотите описать его, скажем, другу, вы можете сказать, что он имеет «модуль» (= длина) и направление (вы можете использовать, например, , север, юг, восток, запад. .. и т.д.).
.. и т.д.).Существует и другой способ описания этого вектора.
Вы должны ввести свой вектор в систему отсчета, чтобы с ним были связаны некоторые числа, а затем вы берете координаты кончика стрелки… ваши КОМПОНЕНТЫ !
Теперь вы можете записать свой вектор как: #vecv=(a,b)#
Например: #vecv=(6,4)#В трех измерениях вы просто добавляете третий компонент к #z# ось.
Например: #vecw=(3,5,4)#
Векторов. Векторы | by Gajendra
Векторы
V Векторы чаще всего используются во многих областях науки о данных, чтобы представляли функцию. Объединение нескольких функций, и мы получаем матрицу, наш набор данных.
Все, что имеет направление и величину . Величина, имеющая направление, а также величину, особенно определяющую положение одной точки в пространстве относительно другой.
Столбец Вектор
Все элементы векторов записываются вертикально в виде столбца.
Row Vector
Все элементы векторов записываются горизонтально в виде строки.
Row VectorОбъединение нескольких векторов Row или Column дает нам матрицу. 9 .
Единичные векторы являются строительными блоками для всех векторов. Это означает, что любой вектор можно разбить на эти единичные векторы. Давайте разберемся в этом на примерах.
Разбиение вектора на единичные векторыКак мы видим, вектор можно разбить на единичные векторы и построить из них.
Величина вектора равна длине вектора. Величина вектора a v обозначается как ∥v∥ .
2D3DОбычно вычисляется путем извлечения квадратного корня из суммы квадратов каждого элемента вектора.
GeneralizedМы узнаем об этом больше в следующих разделах этой статьи.
Транспонирование
При транспонировании вектора строк становятся столбцами, а столбцы — строками.
Исходный векторный транспонированный вектор
Добавление
Вектор к векторуМы можем добавить только два одинаковых и одинаковых типа векторов, т. е. мы можем добавить только векторы Строка к строке и Столбец к столбцу с одинаковыми размерами или элементами.
Векторы столбцов ДополнениеВизуализация: Мы можем визуализировать сложение двух векторов как следующую последовательность векторов, один вектор за другим, точка, в которой мы заканчиваем, дает нам выходной вектор.
Добавление вектораСледуйте за вектором v, затем за вектором w, и мы получим наш новый вектор v + w.
Обратите внимание, что изменение последовательности векторов, которым мы следуем, не меняет выходной или конечный вектор.
Вектор к нулевому векторуДобавление вектора к нулевому вектору и наоборот приводит к тому же вектору.
Добавление нулевого вектора Скаляр к векторуСкалярную величину нельзя добавить к векторной величине, поскольку они имеют разные размерности.
ПримечаниеПоследовательность, в которой добавляются векторы, не изменяет выходной вектор ни по величине, ни по направлению.
ПримечаниеВычитание
Вектор из вектораТочно так же, как сложение, мы можем вычесть только два одинаковых и одинаковых типа векторов, т.е. мы можем вычесть только строку из строки и столбец из вектора столбца с одинаковыми размерами или элементами.
Column VectorsSubtractionВизуализация: Точно так же, как и при добавлении, мы следуем здесь векторам, но меняем направление вычитаемого вектора.
ВычитаниеСледуйте за вектором v, затем следуйте в направлении, противоположном вектору w, и мы получим наш новый вектор v-w.
Нулевой вектор из вектораВычитание вектора из нулевого вектора, наоборот, дает аналогичный вектор (направление может измениться).
Вычитание нулевого вектора Скаляр из вектораСкалярную величину нельзя вычесть из векторной величины, поскольку они имеют разные размерности.
Примечание
Последовательность, в которой вычитаются векторы, изменяет только направление выходного вектора. Величина остается неизменной.
ПримечаниеУмножение или перекрестное произведение
Вектор и вектор
Мы можем умножать строку на столбец или столбец на вектор-строку только при условии, что векторы имеют одинаковое количество элементов. Результатом этой операции может быть вектор или матрица.
Умножение приведенных ниже векторов невозможно, так как они оба являются векторами-строками, хотя количество элементов равно.
Векторы-строкиНо мы можем умножить их, если сможем транспонировать один из векторов.
УмножениеИ
УмножениеВизуализация: Перекрестное произведение двух векторов в 2D дает нам площадь параллелограмма, а в 3D оно дает нам объем параллелограмма.
Cross ProductМы не можем визуализировать больше, чем 3D, но компьютер может выполнять эту операцию в еще более высоких измерениях.
Скаляр и вектор
Возможно умножение скаляра на вектор.
Скаляр и векторВизуализация : Мы можем визуализировать это как масштабирование, изменение размера вектора по определенному значению.
Vector ScalingScalingДеление
Деление между векторами запрещено. Однако, когда дело доходит до скаляра, мы всегда можем рассматривать делитель как дробь и использовать умножение.
Vector by ScalarТочечное или скалярное произведение
Точечное или скалярное произведение — это алгебраическая операция, которая берет две последовательности чисел одинаковой длины и возвращает одно число.
Скалярный продуктВ векторном произведении, как мы видели выше, выход представляет собой матрицу или вектор, однако выход скалярного произведения является скаляром.
Скалярный продукт может использоваться для расчета проекции одного вектора на другой, а также для определения подобия между векторами.
Существует 2 метода расчета скалярного произведения.
Метод 1
Использование угла между векторами.
VectorsDot ProductВизуализация
Dot ProductКосинусное сходствоСкалярный продукт — это один из распространенных методов, используемых во многих областях науки о данных для вычисления подобия косинусного сходства между векторами или признаками и, что более важно, является основой SVM (машины опорных векторов) .
В Скалярное произведение мы больше сосредоточены на вычислении произведения векторов , тогда как в Косинусное сходство мы фокусируемся на вычислении угла между векторами . Чем меньше угол, тем подобны векторы.
Для косинусного сходства мы можем вычислить скалярное произведение, используя метод, описанный ниже.
Метод 2
Использование элементов векторов.
Скалярное произведение векторов Визуализация Скалярное произведениеДлина вектора называется векторной нормой или величиной вектора. Длина вектора — это неотрицательное число, которое описывает размер вектора в пространстве и иногда называется величиной вектора или нормой.
Properties
Scalar Multiplication
Scalar Multiplication Inequality InequalityTypes or Norms
Euclidean Norm
Euclidean NormLp Norm
Its a generalized equation where p can take any nonnegative values .
Lp NormЗдесь следует отметить, что мы берем абсолютное значение |v| каждого элемента вектора.
Используя это уравнение, мы можем получить нормы L1 и L2.
L1 или манхэттенская норма
L1 или манхэттенская нормаL1 норма используется в двух важных методах науки о данных: регуляризации L1 и манхэттенском расстоянии.
L2 или евклидова норма
Мы получаем уравнение для евклидовой нормы, используя Lp Norm для p = 2.
L2 или евклидова норма используется в науке о данных, регуляризации L2 и евклидовом расстоянии.
L∞ Норма
L∞ НормаПример
L∞ НормаКак мы видим, в этой норме выход приблизительно равен максимальному значению элемента в векторе.
Позволяет понять, как различные наборы векторов ведут себя в данных обстоятельствах.
Для множества норм каково множество векторов с нормой вектора равной 1, ||v|| = 1.
L1 или Манхэттенская норма
В вышеописанных обстоятельствах уравнение нормы L1 может быть записано как
L1 при обстоятельствах. Используя это, мы можем вычислить v2 для любого значения v1 и нанести его на график.
L2 или Евклидова норма
В описанных выше обстоятельствах уравнение нормы L2 может быть записано как
L2 при обстоятельствахИспользуя это, мы можем вычислить v2 для любого значения v1 и изобразить его на графике.
График L1 и L2
После построения графика L1 и L2 для различных значений v1 и v2 мы получаем график, как показано ниже.
L1 и L2 NormМы увидим аналогичный график, когда узнаем о регуляризации L1 и L2.
Евклидово расстояние
Длина отрезка между двумя точками. Здесь мы используем евклидову геометрию, например, совершаем перелет из одного места в другое.
Евклидово расстояние Евклидово расстояниеМанхэттенское расстояние
Это сумма абсолютной разницы между измерениями всех измерений двух точек. Здесь мы используем геометрию такси, например, берем такси в центре города (Манхэттен), чтобы добраться из одного места в другое.
Манхэттенское расстояниеМанхэттенское расстояние1. Линейное преобразование
Все операции, которые мы обсуждали выше, такие как сложение, вычитание и умножение, представляют собой способ преобразования вектора в другой вектор. Вектор может быть линейно преобразован с использованием любой из упомянутых здесь операций, если он обладает свойством линейного преобразования.
Линейное преобразованиеСвойства
Чтобы конкретную функцию можно было назвать линейным преобразованием или линейной картой, она должна удовлетворять следующим свойствам
Свойства линейного преобразованияПример
Предположим, у нас есть функция.
ФункцияИ векторы,
ВекторыПервое свойство
Выход функции Первое свойствоВторое свойство
Скалярное произведение Второе свойство2. Вращение
Мы можем вращать вектор в любом направлении и вычислять результат вращения. Здесь мы рассмотрим простой пример вращения вектора 90 градусов против часовой стрелки.
Поворот против часовой стрелки на 90 градусовЧтобы выяснить, что произошло с вектором после поворота, мы можем использовать следующий метод.
Вывод — Поворот против часовой стрелки на 90 градусов3. Отклонение
Когда вектор подвергается сдвигу, его ось X остается на месте, но ось Y наклоняется на 45 градусов вправо.
SheerЧтобы выяснить, что произошло с вектором после поворота, мы можем использовать следующий метод.


 Добавление двух векторов просто дает результирующий вектор.
Добавление двух векторов просто дает результирующий вектор.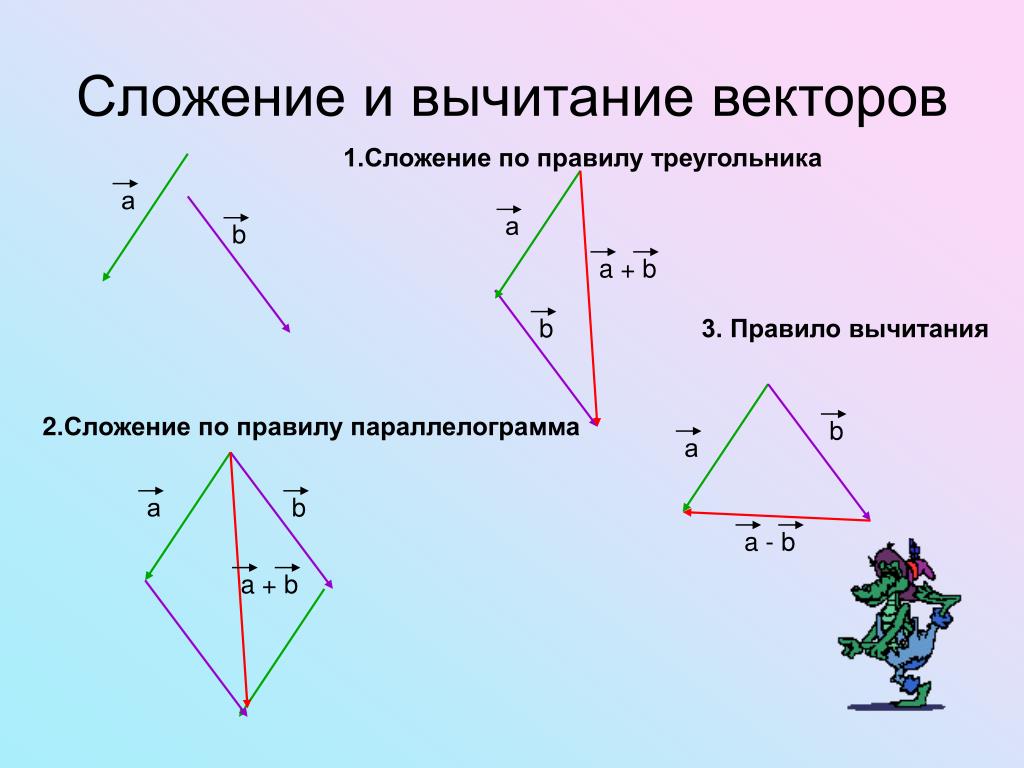
 .. и т.д.).
.. и т.д.).