Длина звуковой волны – формула
4.1
Средняя оценка: 4.1
Всего получено оценок: 149.
4.1
Средняя оценка: 4.1
Всего получено оценок: 149.
Звук – это механические волны, распространяющиеся в упругих средах, которые могут воспринимать слуховые анализаторы человека. Звук, как и любой другой волновой процесс, имеет ряд характеристик. Рассмотрим такую важную характеристику звука, как длина волны.
Звуковые волны в разных средах
В большинстве случаев мы воспринимаем звук, распространяющийся в воздухе. Воздушная звуковая волна – это ряд распространяющихся в воздухе колебаний плотности – сжатий и разрежений. То есть, звук представляет собой продольную механическую волну.
Рис. 1. Звук как ряд сжатий и разрежений.Для распространения механической волны необходимо наличие упругой среды, которой является не только воздух. А, значит, звук может распространяться и в других средах – в жидкостях и кристаллах. Однако, упругость жидкостей и кристаллов гораздо выше, чем упругость воздуха, поэтому колебания точек в таких средах среде происходит с гораздо большими внутренними напряжениями.
Длина звуковой волны
Если скорость распространения звука в различных средах различна, а его частота фиксирована, то расстояние между соседними сжатиями или разрежениями будет также различно.
Это расстояние и называется длиной звуковой волны. Поскольку частота и период связаны простой обратной зависимостью, формулу длины звуковой волны можно получить как на основе частоты колебаний, так и на основе периода:
$$\lambda = vT={v\over \nu},$$
где:
Из формулы можно видеть, что длина волны прямо пропорциональна скорости звука в среде. При одной и той же частоте длина волны будет наименьшей в газах при невысоких давлениях, будет больше в жидкостях, и самой большой будет в кристаллах. Например, для частоты 500гц:
Среда | v (м/с) | λ(м) |
Воздух | 330 | 0. |
Вода | 1500 | 3 |
Металл | 6000 | 12 |
Роль длины звуковой волны
Звуковые волны способны отражаться от границ сред. Это свойство используется в ряде случаев и человеком и Природой. Если в среде есть какие-то неоднородности – то звуковые волны отражаются от них, и по картине отражения можно делать выводы о расположении неоднородностей. Такой процесс называется эхолокацией. Природное использование эхолокации – поведение летучих мышей и дельфинов. Человек использует эхолокацию в целях дефектоскопии промышленных установок, а также в медицинской практике, для исследования внутренних органов.
Рис. 3. Эхолокация в природе и технике.Однако, для отражения волны граница между средами должна иметь размеры больше ее длины. Если длина волны будет больше, волна будет просто огибать неоднородность, не отражаясь.
Именно поэтому и человек и Природа для эхолокации использует ультразвук. Малая длина волны ультразвука способствует обнаружению самых мелких неоднородностей.
Что мы узнали?
Звук представляет собой распространяющиеся в среде сжатия и расширения. Длина звуковой волны – это расстояние между ближайшими сжатиями или расширениями. В разных средах длина волны различна, короткие ультразвуковые волны удобны для эхолокации.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.1
Средняя оценка: 4.1
Всего получено оценок: 149.
А какая ваша оценка?
Механические колебания и волны. Практика 9 класс онлайн-подготовка на Ростелеком Лицей
Введение
Сегодня мы потренируемся в решении задач по теме «Механические колебания и волны». Мы решим несколько задач, в которых описаны колебания, сохранение энергии при колебаниях, распространение волн в разных средах и применение их в эхолокации. При решении задач мы будем придерживаться нашей стандартной схемы решения, которую мы применяем к задачам курса физики:
Мы решим несколько задач, в которых описаны колебания, сохранение энергии при колебаниях, распространение волн в разных средах и применение их в эхолокации. При решении задач мы будем придерживаться нашей стандартной схемы решения, которую мы применяем к задачам курса физики:
- Проанализировать условие. Определить, какие процессы происходят.
- Определить закономерности, которым подчиняются происходящие процессы, записать эти закономерности в виде уравнений. Посмотреть на величины, входящие в эти формулы: определить, какие из них даны в условии, а какие нужно дополнительно выразить. При необходимости перевести величины в СИ.
- Математическая часть: решаем полученную систему уравнений. Получаем ответ, подставив численные значения переменных.
Задача 1.
Точка совершает колебания (см. рис. 1).
Рис. 1. График x(t)
Найти период, амплитуду, частоту колебаний, а также путь, который пройдет точка за 3/4 периода.
Анализ условия
В условии прямо сказано, какой процесс описан, есть график. График показывает, где в какой момент времени находится колеблющаяся точка, то есть по графику можно проследить, как она двигалась.
Физическая часть решения
Период колебаний – это, по определению, время, за которое точка совершает одно полное колебание. Смотрим: точка в начальный момент времени была в координате 0, затем двигалась вдоль оси х, пока не остановилась и не начала двигаться в обратном направлении, мимо положения равновесия и дальше, пока снова не остановилась (см. рис. 2).
Рис. 2. Движение точки
Затем она вернулась в точку , и дальше движение повторяется. Период по графику равен .
Частота связана с периодом простым соотношением:
Получим:
Вычисления простые, поэтому опустим математическую часть решения.
Амплитуда – это, по определению, максимальное расстояние, на которое точка отклоняется от положения равновесия. По рисунку 1 и 2 видно, что точки, наиболее отдаленные от , – это и . Обе они находятся на расстоянии 0,03 м (или 3 см) от положения равновесия, это и есть амплитуда.
По рисунку 1 и 2 видно, что точки, наиболее отдаленные от , – это и . Обе они находятся на расстоянии 0,03 м (или 3 см) от положения равновесия, это и есть амплитуда.
Определим путь, пройденный точкой за 3/4 периода. Период мы определили, 3/4 – это 6 секунд. За это время точка прошла из положения равновесия до крайнего положения и обратно (это дважды по 3 см) и до второго крайнего положения (это еще 3 см). Всего 9 см.
Задача 2
Гитарная струна колеблется с частотой 261,6 Гц (нота «до» первой октавы). Колебания на протяжении 2 с считайте незатухающими. За это время одна из точек струны прошла путь 75 см. Определите амплитуду колебаний.
Анализ условия
К описанному в задаче движению точки будем применять модель незатухающих колебаний. Сказано о пути, который прошла точка за некоторое время. Найдем путь за одно полное колебание (см. рис. 3).
Рис. 3. Пройденный путь за одно колебание
Путь за один период, пусть это будет , равен четырем амплитудам:
Физическая часть решения
По определению частота – это количество полных колебаний за единицу времени.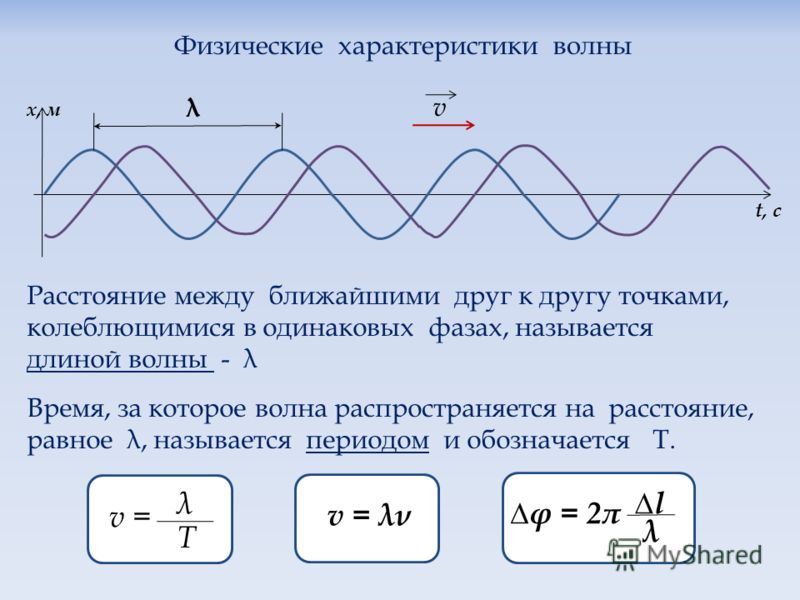 Запишем:
Запишем:
Точка за совершила колебаний. Если за одно колебание она проходит путь , его мы записали, то за 2 с путь равен:
Математическая часть решения
Подставим из первого уравнения в третье:
Выразим из второго уравнения и подставим сюда же:
Все члены уравнения известны, можем найти амплитуду:
Вычислим, переведя заданные значения в СИ:
или 0,36 мм
Амплитуда колебаний чуть больше трети миллиметра – вполне правдоподобно для гитарной струны.
Задача 3
Пружинный маятник вывели из состояния равновесия на 5 см и отпустили (см. рис. 4).
Рис. 4. Пружинный маятник
Он совершает свободные колебания, 5 колебаний за 10 секунд. Найдите потенциальную энергию пружины через 0,7 секунд после начала движения. Жесткость пружины равна 3 Н/м.
Проанализируем условие
В задаче описаны колебания пружинного маятника. Ничего не сказано о затухании на протяжении 10 секунд, за 0,7 секунд их тем более можно считать незатухающими.
Ничего не сказано о затухании на протяжении 10 секунд, за 0,7 секунд их тем более можно считать незатухающими.
Речь идет о потенциальной энергии сжатой пружины, она равна:
то есть определяется положением маятника.
Переходим к физической части решения.
Свободные гармонические колебания описываются уравнением:
Или
В нашем случае удобно описать движение функцией косинус. У нас отсчет времени ведется с того момента, как маятник отпустили из положения максимального отклонения, и график косинуса начинается в точке, соответствующей крайнему положению, так что начальная фаза равна нулю (см. рис. 5).
Рис. 5. График движения точки
Амплитуда задана в условии, 5 см, а циклическая частота равна:
Период, по определению, время одного полного колебания. Если за совершается колебаний, то время одного колебания равно:
обозначили так, потому что – это какой угодно момент времени, в который мы находим координату , а – конкретные 10 секунд, на протяжении которых мы наблюдаем за маятником.
Получили уравнения движения маятника, по которому можно найти его положение в интересующий нас момент времени . А по положению можно определить потенциальную энергию.
Проделаем всё это в математической части решения.
Подставим всё, что нам было неизвестно, в уравнение :
Подставив вместо интересующий нас момент времени , найдем координату в этот момент . В СИ:
Обратите внимание: значение фазы 2,198 получилось в радианах – мы подставляли один полный цикл в радианах. Обратите внимание, если считаете косинус на калькуляторе. Получается:
Знак минус означает, что отклонение составляет 3 см в направлении, противоположном начальному отклонению (рисунок): для расчета энергии это не важно, тем более там возводится в квадрат.
Задача решена.
Задача 4
Нитяной маятник с длиной нити 0,75 м совершает колебания. Найдите амплитуду угла отклонения, если максимальная скорость груза 1 м/с (см. рис. 6).
рис. 6).
Рис. 6. Задача 4
Проанализируем условие
Описаны колебания маятника, вероятнее всего, подразумеваются свободные колебания, другого не сказано. Какими закономерностями и уравнениями удобнее описать этот процесс? Мы мало можем сказать именно о протекании колебаний со временем, ничего не сказано о временных характеристиках. Зато четко видно два состояния маятника: когда его скорость максимальна – положение в центре и когда отклонение максимально. Переход из одного состояния в другое, когда нам не интересен сам процесс, удобно описать с помощью закона сохранения энергии – будем его применять.
Физическая часть решения
У нас свободные колебания, потерь энергии не подразумевается, поэтому применим закон сохранения полной механической энергии.
В первом положении кинетическая энергия грузика равна . Потенциальную энергию будем отсчитывать относительно нулевого уровня (см. рис. 7).
Рис. 7. Положения, в которых рассматривается энергия
Тогда
Во втором положении кинетическая энергия равна нулю, потому что в точке максимального отклонения груз останавливается.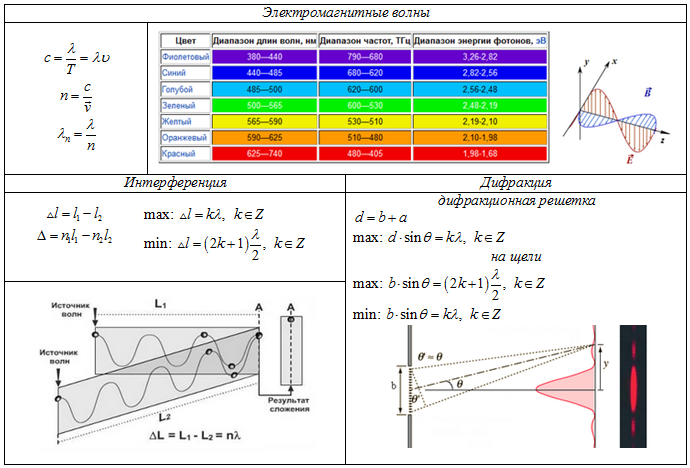 Потенциальная энергия груза на высоте над нулевым уровнем равна: .
Потенциальная энергия груза на высоте над нулевым уровнем равна: .
Запишем:
Мы связали максимальную скорость груза с его максимальной высотой, но нас интересует максимальный угол отклонения. Придется вспомнить геометрию, физика на этом закончилась.
Обратите внимание на прямоугольный треугольник (см. рис. 8).
Рис. 8. Математическая часть решения
В нем гипотенуза – это длина нити , а катет – длина нити минус высота . Свяжем их с углом через выражение для его косинуса – прилежащий катет, деленный на гипотенузу:
Математическая часть решения задачи 4
Выразим из первого уравнения высоту :
(масса груза у нас сократилась)
Подставим ее во второе уравнение:
Можем избавиться от двухэтажной дроби, выполнив деление всего числителя на
А зная косинус, можно найти и сам угол:
Подставим значения в СИ и вычислим:
Получили ответ 21 градус, задача решена.
Задача 5
Поплавок колеблется на волнах по закону .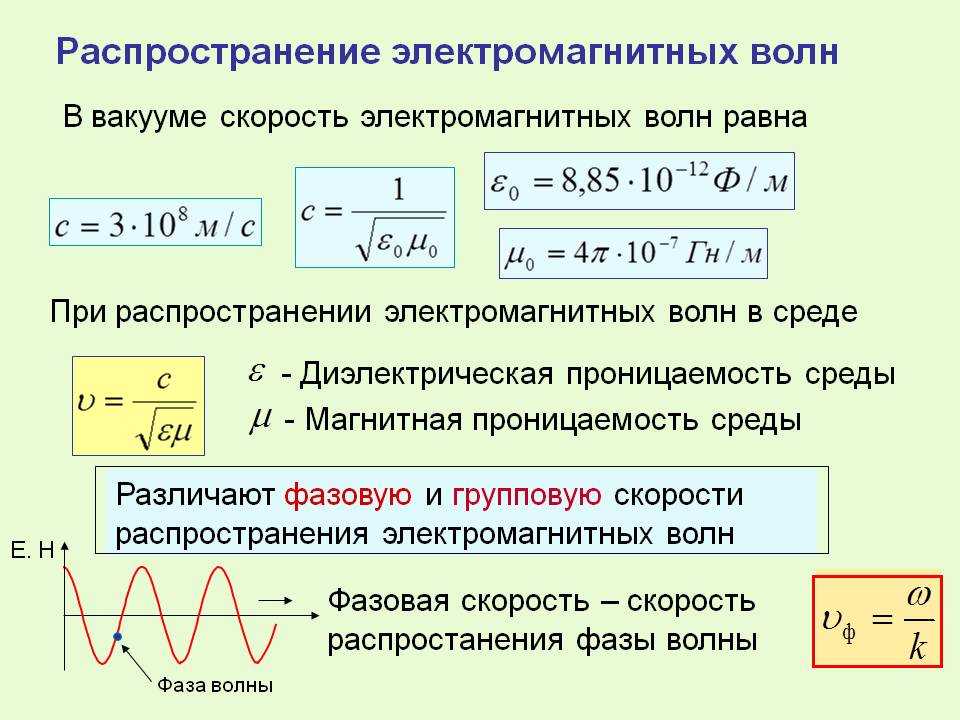 На рисунке изображена фотография волны. Найдите скорость волны (см. рис. 9).
На рисунке изображена фотография волны. Найдите скорость волны (см. рис. 9).
Рис. 9. Задача 5
Анализ условия
Выражение для скорости волны можно получить, проследив, что за время , равное периоду колебаний, волна проходит расстояние, равное длине волны:
Можно пользоваться этой формулой в готовом виде.Уравнение описывает колебания, в нем нет информации именно о распространении волны, но можно извлечь информацию о частоте.
То есть коэффициент при , для нашего поплавка это – это циклическая частота , которая равна :
По фотографии можно определить длину волны – это расстояние между соседними точками, которые колеблются в одинаковых фазах. Фазу точки, в которой находится поплавок, на глаз определить сложно, удобнее взять гребни волны, или точки, отмеченные красным (см. рис. 10).
Рис. 10. Фаза точки
Отсюда: 0,1 м и 1,3 м. Расстояние между ними 1,2 м, это и есть .
Пока мы анализировали условие, заодно нашли всё, что нам нужно, – проделали физическую часть решения задачи. Остались вычисления. Выразим частоту:
Остались вычисления. Выразим частоту:
Вычислим скорость волны:
Задача решена.
Задача 6
Два человека стоят возле стальных рельсов на некотором расстоянии . Один человек ударил молотком по рельсу, второй услышал звук удара два раза с интервалом 1 с. Найдите расстояние . Скорость звука в стали считайте равной 5100 м/с (см. рис. 11).
Рис. 11. Задача 6
У нас звук распространяется по воздуху, что естественно, и по рельсу – дана скорость звука в стали. Скорость звука в воздухе можем принять равной 340 м/с. Скорость звука в стали больше, чем в воздухе, поэтому по рельсу звук достигнет слушателя раньше – отсюда два удара. Считаем, что звук распространяется с постоянной скоростью, поэтому можно применять уравнения кинематики для равномерного прямолинейного движения.
Физическая часть решения
Скорость при равномерном прямолинейном движении, по определению, равна:
Звук в рельсе проходит путь между людьми за время со скоростью звука в стали , запишем:
Звук по воздуху со скоростью проходит этот же путь за время .
По рельсу звук достигает слушателя раньше, то есть на меньше, запишем это:
Решим полученную систему уравнений в ответвлении.
Математическая часть решения задачи 6
Выразим из первого и второго уравнений и :
Подставим их в третье уравнение:
Выразим отсюда .
Вычислим:
Задача решена.
Задача 7
Летучая мышь ориентируется в пространстве с помощью эхолокации – она испускает короткие ультразвуковые импульсы и обнаруживает препятствия по отраженной волне. Какой минимальный интервал должен быть между испусканием импульсов, чтобы максимальная дальность обнаружения была равна 20 м? Оцените минимальный размер препятствия, который может быть различим, если частота ультразвукового импульса равна 70 кГц? Предел разрешения считайте сопоставимым длиной волны.
Анализ условия
Принцип эхолокации состоит в том, что от мыши звуковая волна распространяется с известной скоростью (ультразвук распространяется со скоростью звука), отражается от препятствия и с той же скоростью снова проходит расстояние между стеной и мышью, только в обратном направлении (см.
Рис. 12. Эхолокация
Это занимает время между испусканием импульса и приемом отклика. За это время звук проходит путь . Запишем:
Это мы уже попутно занялись физической частью решения.
Следующий импульс нельзя посылать, не дождавшись отклика от самого дальнего препятствия. Поэтому вычислим, через какое время придет отклик от препятствия на расстоянии 20 м – это и будет минимально допустимым интервалом между импульсами.
Выразим :
Ответим на второй вопрос задачи, нам, по сути, нужно найти длину данной волны. Длина волны связана с частотой через скорость распространения волны (скорость звука), у нас есть для этого готовая формула:
Частота задана, найдем длину волны:
Минимальный различимый размер препятствия оказался равным нескольким миллиметрам. Это грубое приближение, но примерно понятно, что точность ультразвуковой эхолокации достаточно высока.
Список литературы
- Соколович Ю.
 А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е изд., передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е изд., передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с. - Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.ru» (Источник)
- Интернет-портал «class-fizika.ru» (Источник)
- Интернет-портал «class-fizika.ru» (Источник)
Домашнее задание
- Пружинный маятник совершил за 4 секунды 16 полных колебаний. Определите период и частоту колебаний этого маятника.
- Длина океанической волны составляет 270 метров, период составляет 13,5 секунды. Определите скорость распространения волн.
Какая связь между частотой и длиной волны электромагнитного излучения?
Ответ
Проверено
167,4 тыс. + просмотров
+ просмотров
Подсказка: Энергия, длина волны и частота могут использоваться для описания электромагнитного спектра. Каждый подход к представлению об электромагнитном спектре математически связан с другими. Соотношения между энергией, длиной волны и частотой можно сформулировать так: длина волны равна скорости света, деленной на частоту.
Полный ответ:
Длина волны и частота света неразрывно связаны. Чем короче длина волны, тем выше частота. Следовательно, частота и длина волны обратно пропорциональны друг другу. Поскольку все световые волны движутся в вакууме с одинаковой скоростью, количество волновых гребней, проходящих в данном месте за одну секунду, определяется длиной волны. Для коротковолновой волны это число, также известное как частота, будет выше, чем для длинноволновой волны.
Длина волны и частота электромагнитных волн связаны уравнением \[\lambda \nu = c\] , где \[\lambda \] — длина волны, \[\nu \] — частота, а \[c\ ] — скорость света.
Объяснение:
Длина волны и частота обратно пропорциональны.
$c = \nu \cdot \lambda $
(Скорость света прямо пропорциональна \[\nu \] и \[\lambda \] )
$\dfrac{c}{\nu } = \lambda $ (Скорость света прямо пропорциональна \[\nu \] , а \[\nu \] обратно пропорциональна \[\lambda \]
$\dfrac{c}{\lambda } = \nu $ (Скорость света прямо пропорциональна \[\lambda \] и \[\lambda \] обратно пропорциональна \[\nu \]
Примечание: Спектроскопия — это точное исследование цвета, расширенное от видимого света до всех диапазонов электромагнитного спектра; действительно, спектроскопия началась как исследование зависимости видимого света от длины волны, рассеянного призмой, при поглощении газофазными материалами. можно использовать почти все частоты и длины волн электромагнитного излучения.
Недавно обновленные страницы
Большинство эубактериальных антибиотиков получены из биологии ризобия класса 12 NEET_UG
Биоинсектициды саламин были извлечены из класса 12 Biology NEET_UG
Какое из следующих утверждений, касающихся Baculovirussess, Neet_ug
. Какое из следующих утверждений, касающихся Baculoviruses, Neet_ug
Какое из следующих утверждений, касающихся Baculoviruses, Neet_ug
. муниципальные канализационные трубы не должны быть непосредственно 12 класса биологии NEET_UG
Очистка сточных вод выполняется микробами A B Удобрения 12 класса биологии NEET_UG
Иммобилизация фермента – это конверсия активного фермента класса 12 биологии NEET_UG
Большинство эубактериальных антибиотиков получают из биологического класса Rhizobium 12 NEET_UG
Саламиновые биоинсектициды были извлечены из биологического класса А 12 NEET_UG
12 класс биологии NEET_UG
Канализационные или городские канализационные трубы не должны быть напрямую 12 класс биологии NEET_UG
Очистка сточных вод выполняется микробами A B Удобрения 12 класс биологии NEET_UG
Иммобилизация фермента — это преобразование активного фермента класса 12 в биологии NEET_UG
Тенденции сомнения
Длина волны, скорость и частота — Понимание звука
Бегущие волны
5Почему важна длина волны?
Рябь на озере Лох-Дуич перед замком Эйлин-Донан.
Когда вы создаете импульсы в среде, каждый импульс удаляется от источника с одной и той же постоянной скоростью. Если вы делаете импульсы через равные промежутки времени, результатом будет «последовательность» равномерно расположенных импульсов. С технической точки зрения периодическая вибрация создает волну. Расстояние между одним импульсом и следующим называется длиной волны.
Длина волны объясняет многое о том, как работает звук: почему тубы должны быть большими, почему низкочастотные звуки трудно сдержать, почему гидролокатор может обнаруживать определенные объекты (а не другие), как образуются мертвые зоны в аудиториях, почему инструменты производят обертоны… список можно продолжить. В этом разделе объясняется, как длина волны связана с частотой источника волны и свойствами среды, в которой распространяется волна.
Длина волны, скорость и частота
Когда источник с определенной частотой создает волны, каждый гребень проходит определенное расстояние, прежде чем сформируется следующий гребень.
Если частота звука низкая, между импульсами проходит много времени, и каждый импульс проходит большое расстояние, прежде чем будет создан следующий. Результатом являются импульсы, которые разнесены друг от друга на большую длину волны. Сократите временную задержку между импульсами, и длина волны станет короче. (Помните, что все волны в одной и той же среде распространяются с одинаковой скоростью). Суть в том, что низкочастотные источники создают длинноволновые волны, а высокочастотные источники создают короткие волны.
Длина волны также зависит от среды, поскольку волны распространяются с разной скоростью в разных средах. Если звук распространяется медленно в определенном материале, каждый гребень проходит лишь небольшое расстояние, прежде чем сформируется следующий гребень. Если источник той же частоты создает волны в среде, где звуки распространяются быстрее, каждый гребень распространяется дальше (за то же время), создавая гребни, которые находятся дальше друг от друга (более длинная длина волны).
Анимации особенно полезны для понимания понятий, изложенных в последних двух абзацах. Моделирование Desmos компании Abbott Pulse Train [1] показывает два источника, создающих волны в одной и той же среде. Несмотря на то, что источники имеют разные частоты, вы можете ясно видеть, что оба набора волн распространяются по экрану с одинаковой скоростью. Вы также можете видеть, что высокочастотный источник излучает короткие волны. Видео Майка Ричардсона на YouTube [2] (4:49) использует симуляцию PhET «Волна на струне», чтобы показать, что происходит, когда вы меняете частоту источника волны на струне. Если вы хотите попробовать некоторые вещи Ричардсон показывает в видео, что вы можете играть с симуляцией PhET [3] самостоятельно. Вам нужно будет установить флажок в левом верхнем углу моделирования, чтобы избавиться от зажима и заменить его открытым окном, иначе вы будете исследовать стоячие волны, а не бегущие волны.
Вот математическое уравнение, связывающее длину волны со скоростью волны и частотой источника:
[латекс]\лямбда = \dfrac{v} {f}[/латекс]
Скорость ([латекс]v[/латекс]) в уравнении — это скорость волны в среде. Частота ([латекс]f[/латекс]) — это основная частота источника волны, а [латекс]\лямбда[/латекс] — результирующая длина волны.
Частота ([латекс]f[/латекс]) — это основная частота источника волны, а [латекс]\лямбда[/латекс] — результирующая длина волны.
Откуда уравнение
Уравнение, приведенное выше, является прямым применением уравнения постоянной скорости к волне. Вот логика. Поскольку все гребни и впадины волны движутся с одной и той же постоянной скоростью, гребни и впадины (и все другие точки волны) движутся в соответствии с уравнением постоянной скорости:
[латекс]d = vt[/латекс]
Следующий шаг является ключевым: вы должны признать, что за время, необходимое источнику для завершения одного полного цикла, каждая рябь в волне проходит расстояние в одну длину волны. Поскольку каждый гребень (или впадина) перемещается ровно на одну длину волны за время, необходимое источнику для завершения одного полного цикла, вы можете заменить [latex]d[/latex] на [latex]\lambda[/latex], при условии, что вы также замените [латекс]т[/латекс] с [латекс]\тау[/латекс]. Результат
[латекс]\лямбда= v\тау[/латекс]
Проще говоря, длина волны равна расстоянию, которое гребень (или впадина) проходит за один период источника.
Несмотря на то, что это уравнение является верным и информативным, большинство людей говорят об источниках с точки зрения частоты, а не периода. Чтобы выразить это уравнение через частоту, замените [латекс]\тау[/латекс] на [латекс]1/f[/латекс]. Когда вы это сделаете, [латекс]\лямбда= v\тау[/латекс] станет
[латекс]\лямбда = \dfrac{v}{f}[/латекс]
Причина и следствие
Во многих учебниках приведенное выше уравнение выражается как [латекс]v=f\лямбда[/латекс]. Я думаю, что это заблуждение.
Вот почему: величины [латекс]\лямбда[/латекс], [латекс]в[/латекс] и [латекс]f[/латекс] не равноправны в уравнении. Причинами являются частота и скорость волны. Длина волны — это ответ. Частота полностью определяется источником — все остальное не имеет значения. Скорость волны полностью определяется свойствами среды — все остальное не имеет значения. Поместите источник, вибрирующий на определенной частоте, в определенную среду, и волна автоматически будет иметь определенную длину волны.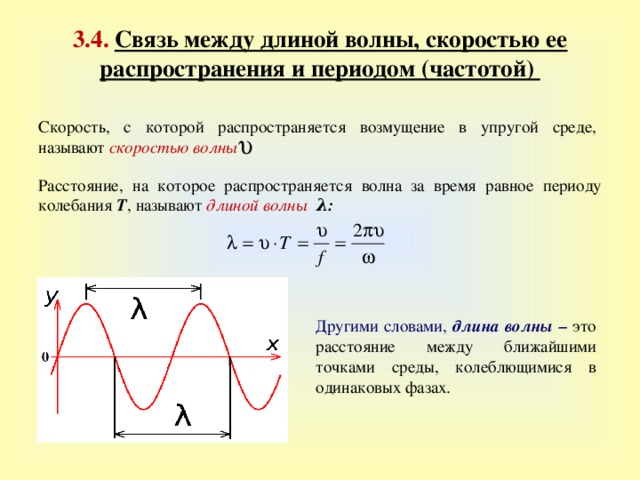
Уравнение как руководство для мышления
Если вы знаете, что делаете, уравнения могут стать мощным руководством для постановки вопросов «что, если»: что произойдет с длиной волны, если частота увеличится? Что происходит с длиной волны, когда звук переходит из воды в воздух?
Ключом к «чтению уравнений» является правильное определение того, какие величины изменяются, а какие нет. Бегло взглянув на уравнение [latex]v=f\lambda[/latex], можно предположить, что увеличение частоты источника увеличивает скорость волны. В конце концов, использование большего числа для звука [latex]f[/latex] приводит к большему числу для [latex]v[/latex]. Тем не менее, мы знаем, что вывод неверен — все звуки, распространяющиеся в одном и том же материале, распространяются с одинаковой скоростью. Что не так с математикой? Проблема в том, что мы предполагали, что [латекс]\лямбда[/латекс] не изменились. Реальность такова, что [латекс]v[/латекс] не может измениться (поскольку среда не изменилась), и [латекс]\лямбда[/латекс] должен измениться, чтобы компенсировать это. Если частота увеличивается, длина волны должна уменьшаться, чтобы скорость волны оставалась неизменной.
Если частота увеличивается, длина волны должна уменьшаться, чтобы скорость волны оставалась неизменной.
Что происходит с длиной волны звука, распространяющегося из воды в воздух? Ключом к чтению уравнения для ответа является определение того, какая величина меняется, а какая нет. При переходе звука из воды в воздух скорость уменьшается. (Вы можете посмотреть это; ключ в том, чтобы понять, что скорость волны должна меняться, потому что изменяется материал, в котором распространяется волна.) Это предполагает, что частота остается неизменной, и если вы подумаете под микроскопом, это имеет смысл — вибрации на дальней стороне границы должны совпадать с вибрациями их соседей на ближней стороне границы. Поскольку [латекс]f[/латекс] остается постоянным, а [латекс]v[/латекс] увеличивается, длина волны должна увеличиваться, чтобы уравнение работало.
Остановись, чтобы подумать
- Рябь, движущаяся по поверхности воды, создается путем покачивания длинной прямой палки вверх и вниз по поверхности воды.
 Рябь может быть изменена либо 1) изменением того, как часто вы качаете стик вверх и вниз, либо 2) изменением того, насколько далеко вверх и вниз перемещается стик в каждом цикле (без изменения того, как часто вы качаете стик вверх и вниз). Объясните, что вы можете сделать с источником для достижения каждой из следующих целей:
Рябь может быть изменена либо 1) изменением того, как часто вы качаете стик вверх и вниз, либо 2) изменением того, насколько далеко вверх и вниз перемещается стик в каждом цикле (без изменения того, как часто вы качаете стик вверх и вниз). Объясните, что вы можете сделать с источником для достижения каждой из следующих целей:- увеличить амплитуду волн
- сократить длину волны
- увеличить скорость создаваемых волн
- Один звук в воздухе имеет длину волны 10 см. Другой звук в воздухе имеет длину волны 20 см. Какой звук имеет более высокую частоту? Какой звук распространяется быстрее?
- Что происходит со скоростью волны при переходе из холодного воздуха в теплый? Что происходит с частотой? Что происходит с длиной волны звуковой волны?
Слышимые звуки в воздухе
Вы можете рассчитать длину волны слышимого звука в воздухе. Слышимые звуки в воздухе имеют частоту примерно от 20 Гц до 20 кГц. Неудивительно, что длины волн слышимых звуков также сильно различаются.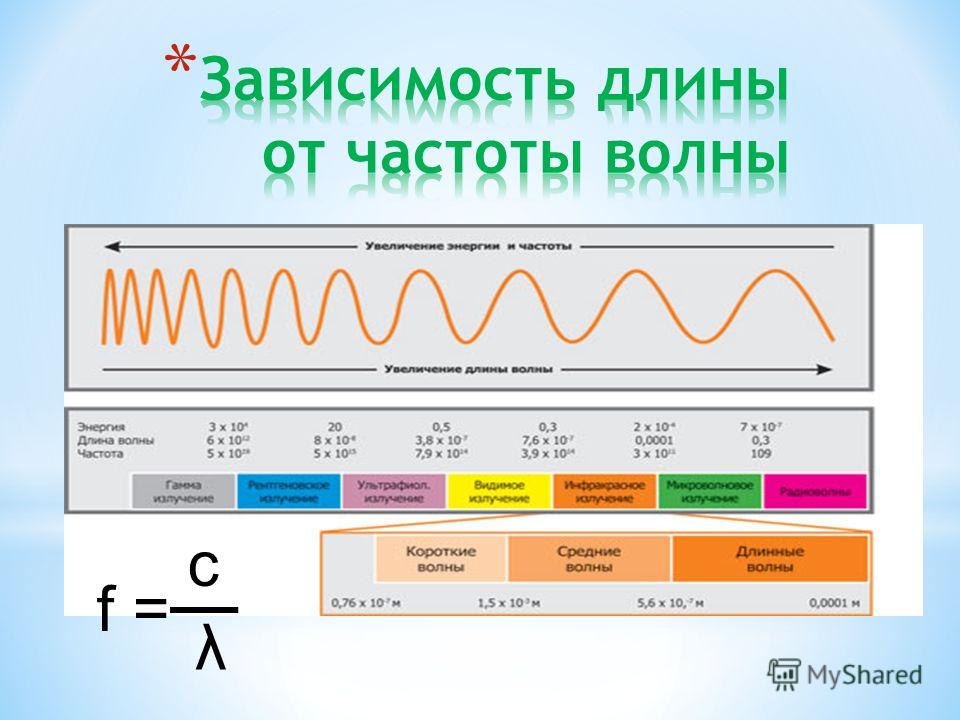 Предполагая скорость звука 340 м/с,
Предполагая скорость звука 340 м/с,
Для звука частотой 20 Гц в воздухе: [латекс]\лямбда = \dfrac{v}{f}= \dfrac{340 м/с}{20 Гц}=17 м[/латекс]
Для звука частотой 20 кГц в воздухе: [латекс]\лямбда = \dfrac{v}{f}= \dfrac{340 м/с}{20 000 Гц}=0,017 м=1,7 см[/латекс]
Этот расчет показывает, что длина звуковой волны в воздухе явно соответствует человеческому размеру. Длины волн варьируются от примерно диаметра десятицентовой монеты (для самых высоких частот) до примерно длины городского автобуса (для самых низких частот). Для сравнения, все длины волн видимого света намного меньше толщины одного человеческого волоса и имеют очень узкий диапазон (примерно от 400 до 700 нм).
Остановись, чтобы подумать ответы
- Чтобы увеличить амплитуду, увеличьте расстояние, которое проходит палочка за каждый цикл (т. е. увеличьте амплитуду источника). Чтобы сократить длину волны, увеличьте частоту взмахов палочкой (т. е. увеличьте частоту источника).
 Невозможно изменить скорость путей, изменив то, как вы двигаете палкой. Скорость волн определяется свойствами самой воды.
Невозможно изменить скорость путей, изменив то, как вы двигаете палкой. Скорость волн определяется свойствами самой воды. - Звук с более короткой длиной волны имеет более высокую частоту. Оба звука распространяются с одинаковой скоростью.
- Когда звук переходит от более холодного воздуха к более теплому, его скорость увеличивается (поскольку звук распространяется быстрее в более теплом воздухе). Частота не меняется (если не меняется источник). Поскольку скорость увеличивается, а частота остается неизменной, длина волны должна увеличиваться. (Увеличение числа для скорости волны в уравнении [латекс]\лямбда = v/f[/латекс] без изменения числа для частоты приведет к большему значению длины волны).
Интернет-ресурсы
Игра с PhET Симуляция звука (Java-апплет). [4] Отрегулируйте частоту и посмотрите, как изменится длина волны. Нажмите на вкладку «Измерение» вверху, чтобы добавить линейку и секундомер.
Игра с волнами PhET на струнной симуляции (HTML5).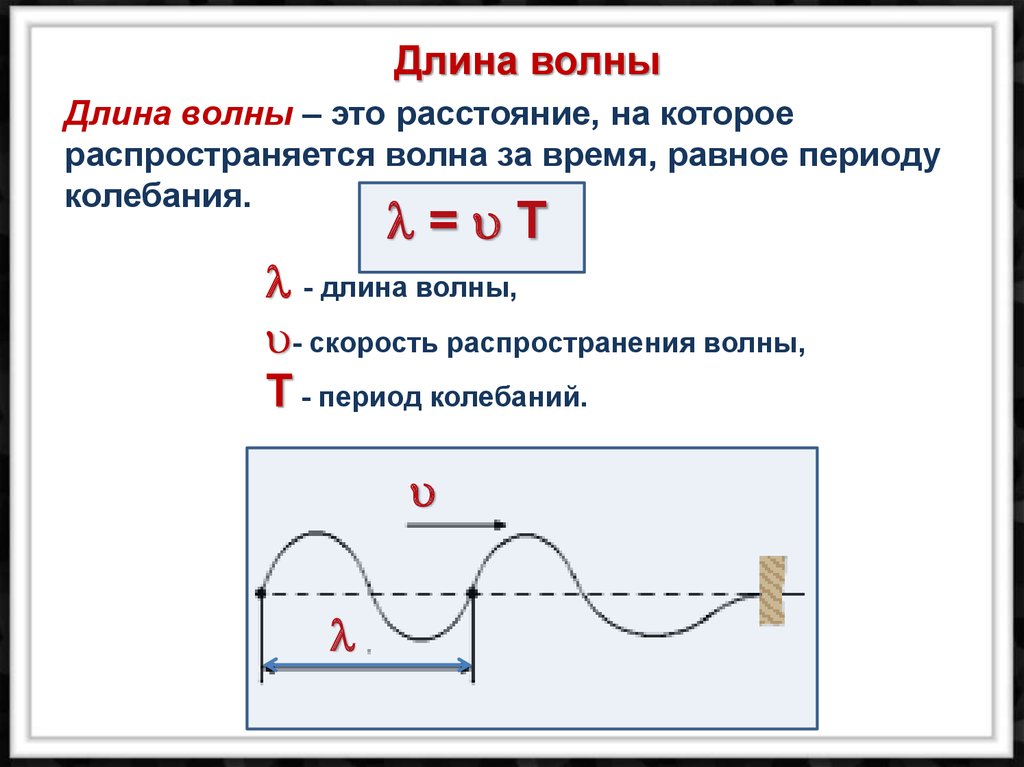


 66
66 А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е изд., передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е изд., передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с. Рябь может быть изменена либо 1) изменением того, как часто вы качаете стик вверх и вниз, либо 2) изменением того, насколько далеко вверх и вниз перемещается стик в каждом цикле (без изменения того, как часто вы качаете стик вверх и вниз). Объясните, что вы можете сделать с источником для достижения каждой из следующих целей:
Рябь может быть изменена либо 1) изменением того, как часто вы качаете стик вверх и вниз, либо 2) изменением того, насколько далеко вверх и вниз перемещается стик в каждом цикле (без изменения того, как часто вы качаете стик вверх и вниз). Объясните, что вы можете сделать с источником для достижения каждой из следующих целей: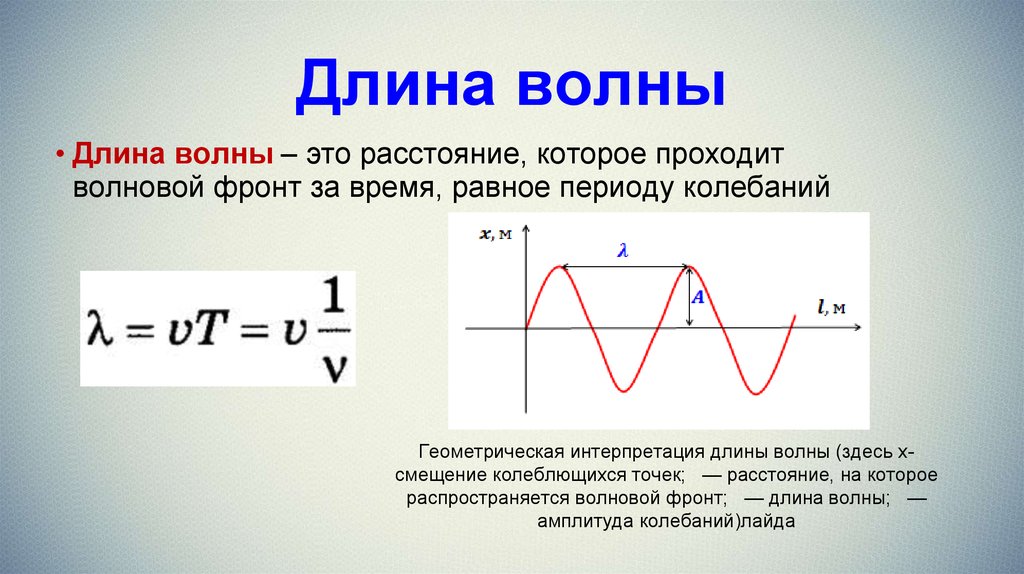 Невозможно изменить скорость путей, изменив то, как вы двигаете палкой. Скорость волн определяется свойствами самой воды.
Невозможно изменить скорость путей, изменив то, как вы двигаете палкой. Скорость волн определяется свойствами самой воды.