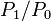Что значит децибел. Перевод из децибел в разы и обратно
Довольно часто в популярной радиотехнической литературе , в описании электронных схем употребляется единица измерения – децибел (дБ или dB).
При изучении электроники начинающий радиолюбитель привык к таким абсолютным единицам измерения как Ампер (сила тока), Вольт (напряжение и ЭДС), Ом (электрическое сопротивление) и многим другим, с помощью которых обозначают количественно тот или иной электрический параметр (ёмкость , индуктивность, частоту).
Начинающему радиолюбителю, как правило, не составляет особого труда разобраться, что такое ампер или вольт. Тут всё понятно, есть электрический параметр или величина, которую нужно измерить . Есть начальный уровень отсчёта, который принимается по умолчанию в формулировке данной единицы измерения. Есть условное обозначение этого параметра или величины (A, V). И вправду, как только мы читаем надпись 12 V, то мы понимаем, что речь идёт о напряжении, аналогичном, например, напряжению автомобильной аккумуляторной батареи .
Но как только встречается надпись, к примеру: напряжение повысилось на 3 дБ или мощность сигнала составляет 10 дБм (10 dBm), то у многих возникает недоумение. Как это? Почему упоминается напряжение или мощность, а значение указывается в каких-то децибелах?
Практика показывает, что не многие начинающие радиолюбители понимают, что же такое децибел. Попытаемся развеять непроглядный туман над такой таинственной единицей измерения как децибел.
Единицу измерения под названием Бел стали впервые применять инженеры телефонной лаборатории Белла. Децибел является десятой частью Бела (1 децибел = 0,1 Бел). На практике широко используется как раз децибел.
Как уже говорилось, децибел, это особенная единица измерения. Стоит отметить, что децибел не является частью официальной системы единиц СИ. Но, несмотря на это, децибел получил признание и занял прочное место наряду с другими единицами измерения.
Вспомните, когда мы хотим объяснить какое-либо изменение, мы говорим, что, например, стало ярче в 2 раза. Или, например, напряжение упало в 10 раз. При этом мы устанавливаем определённый порог отсчёта, относительно которого и произошло изменение в 10 или 2 раза. С помощью децибел также измеряют эти “разы”, только в логарифмическом масштабе .
Например, изменение на 1 дБ, соответствует изменению энергетической величины в 1,26 раза. Изменение на 3 дБ соответствует изменению энергетической величины в 2 раза.
Но зачем так заморачиваться с децибелами, если отношения можно измерять в разах? На этот вопрос нет однозначного ответа. Но уж, поскольку, децибелы активно применяются, то наверняка это оправдано.
Причины для использования децибел всё-таки есть. Перечислим их.
Частично ответ на этот вопрос кроется в так называемом законе Вебера-Фехнера . Это эмпирический психофизиологический закон, т.е основан он на результатах реальных, а не теоретических экспериментов. Суть его заключается в том, что любые изменения каких-либо величин (яркости, громкости, веса) ощущаются нами при условии, если эти изменения носят логарифмический характер.
График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера
Так, например, чувствительность человеческого уха уменьшается с ростом уровня громкости звукового сигнала. Именно поэтому, при выборе переменного резистора , который планируется применить в регуляторе громкости звукового усилителя стоит брать с показательной зависимостью сопротивления от угла поворота ручки регулятора. В этом случае, при повороте движка регулятора громкости звук в динамике будет нарастать плавно. Регулировка громкости будет линейной, так как показательная зависимость регулятора громкости компенсирует логарифмическую зависимость нашего слуха и в сумме станет линейной. При взгляде на рисунок это станет более понятно.
Зависимость сопротивления переменного резистора от угла поворота движка (А-линейная, Б-логарифмическая, В-показательная)
Здесь показаны графики зависимости сопротивления переменных резисторов разных типов: А – линейная, Б – логарифмическая, В – показательная. Как правило, на переменных резисторах отечественного производства указывается, какой зависимостью обладает переменный резистор. На тех же принципах основаны цифровые и электронные регуляторы громкости.
Также стоит отметить, что человеческое ухо воспринимает звуки, мощность которых различается на колоссальную величину в 10 000 000 000 000 раз! Таким образом, самый громкий звук отличается от самого тихого, который может уловить наш слух, на 130 дБ (10 000 000 000 000 раз).
Вторая причина широкого использования децибел является простота вычислений.
Согласитесь, что куда проще при вычислениях использовать небольшие числа вроде 10, 20, 60,80,100,130 (наиболее часто используемые числа при расчёте в децибелах) по сравнению с числами 100 (20 дБ), 1000 (30 дБ), 1000 000 (60 дБ),100 000 000 (80 дБ),10 000 000 000 (100 дБ), 10 000 000 000 000 (130 дБ). Ещё одним достоинством децибел является то, что их просто суммируют. Если проводить вычисления в разах, то числа необходимо умножать.
Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.
Также децибелы очень удобны при графическом построении различных зависимостей. Все графи
Перевод из дб в разы формула. Что такое децибел? Перевод из децибел в разы и обратно
Довольно часто в популярной радиотехнической литературе, в описании электронных схем употребляется единица измерения – децибел (дБ или dB).
При изучении электроники начинающий радиолюбитель привык к таким абсолютным единицам измерения как Ампер (сила тока), Вольт (напряжение и ЭДС), Ом (электрическое сопротивление) и многим другим, с помощью которых обозначают количественно тот или иной электрический параметр (емкость , индуктивность, частоту).
Начинающему радиолюбителю, как правило, не составляет особого труда разобраться, что такое ампер или вольт. Тут всё понятно, есть электрический параметр или величина, которую нужно измерить. Есть начальный уровень отсчёта, который принимается по умолчанию в формулировке данной единицы измерения. Есть условное обозначение этого параметра или величины (A, V). И вправду, как только мы читаем надпись 12 V, то мы понимаем, что речь идёт о напряжении, аналогичном, например, напряжению автомобильной аккумуляторной батареи.
Но как только встречается надпись, к примеру: напряжение повысилось на 3 дБ или мощность сигнала составляет 10 дБм (10 dBm), то у многих возникает недоумение. Как это? Почему упоминается напряжение или мощность, а значение указывается в каких-то децибелах?
Практика показывает, что не многие начинающие радиолюбители понимают, что же такое децибел. Попытаемся развеять непроглядный туман над такой таинственной единицей измерения как децибел.
Что такое децибел?
Единицу измерения под названием Бел стали впервые применять инженеры телефонной лаборатории Белла. Децибел является десятой частью Бела (1 децибел = 0,1 Бел). На практике широко используется как раз децибел.
Как уже говорилось, децибел, это особенная единица измерения. Стоит отметить, что децибел не является частью официальной системы единиц СИ. Но, несмотря на это, децибел получил признание и занял прочное место наряду с другими единицами измерения.
Вспомните, когда мы хотим объяснить какое-либо изменение, мы говорим, что, например, стало ярче в 2 раза. Или, например, напряжение упало в 10 раз. При этом мы устанавливаем определённый порог отсчёта, относительно которого и произошло изменение в 10 или 2 раза. С помощью децибел также измеряют эти “разы”, только в
Например, изменение на 1 дБ, соответствует изменению энергетической величины в 1,26 раза. Изменение на 3 дБ соответствует изменению энергетической величины в 2 раза.
Но зачем так заморачиваться с децибелами, если отношения можно измерять в разах? На этот вопрос нет однозначного ответа. Но уж, поскольку, децибелы активно применяются, то наверняка это оправдано.
Причины для использования децибел всё-таки есть. Перечислим их.
Частично ответ на этот вопрос кроется в так называемом
График зависимости ощущения громкости от силы (мощности) звука. Закон Вебера-Фехнера
Так, например, чувствительность человеческого уха уменьшается с ростом уровня громкости звукового сигнала. Именно поэтому, при выборе переменного резистора, который планируется применить в регуляторе громкости звукового усилителя стоит брать с показательной зависимостью сопротивления от угла поворота ручки регулятора. В этом случае, при повороте движка регулятора громкости звук в динамике будет нарастать плавно. Регулировка громкости будет линейной, так как показательная зависимость регулятора громкости компенсирует логарифмическую зависимость нашего слуха и в сумме станет линейной. При взгляде на рисунок это станет более понятно.
Зависимость сопротивления переменного резистора от угла поворота движка (А-линейная, Б-логарифмическая, В-показательная)
Здесь показаны графики зависимости сопротивления переменных резисторов разных типов: А – линейная, Б – логарифмическая, В – показательная. Как правило, на переменных резисторах отечественного производства указывается, какой зависимостью обладает переменный резистор. На тех же принципах основаны цифровые и электронные регуляторы громкости.
Также стоит отметить, что человеческое ухо воспринимает звуки, мощность которых различается на колоссальную величину в 10 000 000 000 000 раз! Таким образом, самый громкий звук отличается от самого тихого, который может уловить наш слух, на 130 дБ (10 000 000 000 000 раз).
Вторая причина широкого использования децибел является простота вычислений.
Согласитесь, что куда проще при вычислениях использовать небольшие числа вроде 10, 20, 60,80,100,130 (наиболее часто используемые числа при расчёте в децибелах) по сравнению с числами 100 (20 дБ), 1000 (30 дБ), 1000 000 (60 дБ),100 000 000 (80 дБ),10 000 000 000 (100 дБ), 10 000 000 000 000 (130 дБ). Ещё одним достоинством децибел является то, что их просто суммируют. Если проводить вычисления в разах, то числа необходимо умножать.
Например, 30 дБ + 30 дБ = 60 дБ (в разах: 1000 * 1000 = 1000 000). Думаю, с этим всё ясно.
Также децибелы очень удобны при графическом построении различных зависимостей. Все графики вроде диаграмм направленности антенн, амплитудно-частотных характеристик усилителей выполняют с применением деци
Некоторые думают, что децибелы придумали, чтобы свести их с ума. Но на самом деле децибелы придумали для удобства. Да, да, все эти логарифмы, производные и прочие интегралы всегда кем-то придумывались для удобства и облегчения жизни.
Итак, децибелы — это соотношение двух величин, выраженное в логарифмическом масштабе. При этом отношение тока и напряжения имеет коэффициент 20 а отношение мощности коэффициент 10. Если у нас есть напряжения 1В, 10В, 100В, 1000В, то каждое напряжение больше предыдущего на 20дБ. Переводить в уме разы в децибелы практически невозможно, но имеются два исключения. Увеличению в 2 раза и в 10 раз соответствуют круглые значения в децибелах, их легко запомнить, а промежуточные варианты прикидывать приблизительно. Кроме того, существуют таблицы. Таблица перевода из децибел в разы Источник |
Таблица перевода из децибел в разы
Некоторые думают, что децибелы придумали, чтобы свести их с ума. Но на самом деле децибелы придумали для удобства. Да, да, все эти логарифмы, производные и прочие интегралы всегда кем-то придумывались для удобства и облегчения жизни.
- Нам редко нужно знать какие-то конкретные величины. Кому интересен усилитель, способный усиливать с 4,9мВ до 490мВ? Зато нам очень часто надо знать отношение двух величин. И если мы напишем, что усилитель усиливает в 100 раз, то интерес к этому усилителю возрастёт.
- На практике используется чрезвычайно широкий диапазон разных величин. Он настолько широк, что пользоваться этими величинами неудобно. Человек способен слышать звуки, различающиеся по уровню в 100000 раз. Уложить этот диапазон на одном графике просто невозможно.
- К счастью, чувствительность слуха не линейна, а изменяется по логарифмическому закону. Допустим, на выходе усилителя имеется звуковой сигнал с напряжением 1В. Для увеличения громкости в 1,1 раза надо добавить напряжение всего 0,1В. Но если на выходе усилителя было 100В, то для увеличения громкости в 1,1 раза нужно добавить 10В. В обоих случаях человеку будет казаться, что приращение громкости было одинаковым. Этим можно воспользоваться, графики с логарифмической шкалой занимают гораздо меньше места, а информативность повышается.
- Выяснилось, что очень многое в природе удобнее отображать в логарифмическом масштабе. Похоже, бог любил логарифмы (либо логарифмы любит архитектор матрицы, кому что больше нравится).
Итак, децибелы — это соотношение двух величин, выраженное в логарифмическом масштабе. При этом отношение тока и напряжения имеет коэффициент 20


а отношение мощности коэффициент 10.
Если у нас есть напряжения 1В, 10В, 100В, 1000В, то каждое напряжение больше предыдущего на 20дБ.
Переводить в уме разы в децибелы практически невозможно, но имеются два исключения. Увеличению в 2 раза и в 10 раз соответствуют круглые значения в децибелах, их легко запомнить, а промежуточные варианты прикидывать приблизительно. Кроме того, существуют таблицы.
Таблица перевода из децибел в разы
Левая таблица для ослаблений сигнала, правая для усиления

Источник
Децибелы «по мощности», «по напряжению» и «по току»
Из правила (см. выше) следует, что дБ бывают только «по мощности». Тем не менее, в случае равенства R1 = R0 (в частности, если R1 и R0 — одно и то же сопротивление, или в случае, если соотношение сопротивлений R1 и R0 по той или иной причине не важно) говорят о дБ «по напряжению» и «по току», подразумевая при этом выражения:
дБ
по напряжению = 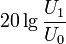 ;
;
дБ
по току = 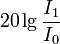 .
.
Для перехода от «дБ по напряжению» («дБ по току») к «дБ по мощности» следует чётко определить, на каких именно сопротивлениях (равных или не равных друг другу) регистрировались напряжение (ток). Если R1 не равно R0, следует пользоваться выражением для общего случая (см. выше).
Нетрудно подсчитать, что, в частности:
при регистрации мощности изменению на +1 дБ (+1 дБ «по мощности») соответствует приращение мощности в ≈1,259 раза, изменению на −3,01 дБ — снижение мощности в два раза, в то время как
при регистрации напряжения (силы тока) изменению на +1 дБ (+1 дБ «по напряжению», «по току») будет соответствовать приращение напряжения (силы тока) в ≈1,122 раза, при изменении на −3,01 дБ напряжение (сила тока) снизятся и составят
 ≈
0,707 от своего исходного значения.
≈
0,707 от своего исходного значения.
Примеры вычислений Переход к дБ
Пусть значение мощности P1 стало в 2 раза больше исходного значения мощности P0, тогда
10 lg(P1/P0) = 10 lg(2) ≈3,0103 дБ ≈ 3 дБ,
то есть рост мощности на 3 дБ означает её увеличение в 2 раза.
Пусть значение мощности P1 стало в 2 раза меньше исходного значения мощности P0, то есть P1 = 0,5 P0. Тогда
10 lg(P1/P0) = 10 lg(0,5) ≈ −3 дБ,
то есть снижение мощности на 3 дБ означает её снижение в 2 раза. По аналогии:
рост мощности в 10 раз: 10 lg(P1/P0) = 10 lg(10) = 10 дБ, снижение в 10 раз: 10 lg(P1/P0) = 10 lg(0,1)= −10 дБ;
рост в 1 млн раз: 10 lg(P1/P0) = 10 lg(1 000 000) = 60 дБ, снижение в 1 млн раз: 10 lg(P1/P0) = 10 lg(0,000001) = −60 дБ.
Переход от дБ к «разам»
Изменение «в разах» по известному изменению в дБ (условное обозначение «dB» в формулах ниже) вычисляется следующим образом:
для мощности:
 ;
таким образом, например, если изменение
мощности составило +20 децибел, это
значит, что «P1 больше
P0 на
два порядка» или «P1 больше
P0 в
100 раз»;
;
таким образом, например, если изменение
мощности составило +20 децибел, это
значит, что «P1 больше
P0 на
два порядка» или «P1 больше
P0 в
100 раз»;для напряжения (силы тока):
 ;
таким образом, например, если изменение
напряжения составило +20 децибел, это
значит, что «U1больше
U0 на
порядок» или «в 10 раз».
;
таким образом, например, если изменение
напряжения составило +20 децибел, это
значит, что «U1больше
U0 на
порядок» или «в 10 раз».
Перевод отношения мощностей в дБ: | |||||||||||||
| 10000 | 100 | 10 | ≈ 4 | ≈ 2 | ≈ 1.26 | 1 | ≈ 0.79 | ≈ 0.5 | ≈ 0.25 | 0.1 | 0.01 | 0.0001 |
| 40 дБ | 20 дБ | 10 дБ | 6 дБ | 3 дБ | 1 дБ | 0 дБ | −1 дБ | −3 дБ | −6 дБ | −10 дБ | −20 дБ | −40 дБ |
Переход от дБ к мощности
Для этого нужно знать значение опорного уровня мощности P0. Например, при P0 = 1 мВт и известном изменении на +20 дБ:
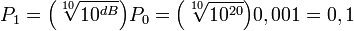 Вт.
Вт.
Переход от дБ к напряжению (току)
Для этого нужно знать значение опорного уровня напряжения U0 и определиться, регистрировалось ли напряжение на одинаковом сопротивлении, или же для решаемой задачи различие значений сопротивлений не важно. Например, при условии R0 = R1, заданном U0 = 2 В и приросте напряжения на 6 дБ:
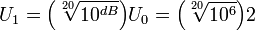 ≈
4 В.
≈
4 В.
Как перевести децибелы в разы ?
В разы не децибелы переводят, а герцы ( частоту, а не уровень звука) . Например, 50герц- это 50 раз в минуту. Децибел (от деци.. . и бел) , дольная единица от бела — единицы логарифмической относительной величины (десятичного логарифма отношения двух одноимённых физических величин — энергий, мощностей, звуковых давлений и др.) ; равна 0,1 бел. Обозначения: русское дб, международное dB.
По-моему с помощью десятичных логарифмов.
Куркулятор тебе! Еще ведь нужно знать, что ты в этих децибеллах измерять собираешься. В зависимости от этого, одному и тому же числу децибел будут соответствовать разы, отличающиеся в 2 раза. Миль пардон, за тавтологию.
Изменение на 6 дециБел = изменение в 2 раза. Соответственно увеличение в 4 раза = 2*2 = 6дБ + 6дБ = 12 дБ. И еще значение — 20 дециБел = в 10 раз.
по напряжени 6 дб в 2 раза. по мощности 3 дб в 2 раза


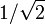 ≈
0,707 от своего исходного значения.
≈
0,707 от своего исходного значения.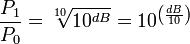 ;
таким образом, например, если изменение
мощности составило +20 децибел, это
значит, что «P1 больше
P0 на
два порядка» или «P1 больше
P0 в
100 раз»;
;
таким образом, например, если изменение
мощности составило +20 децибел, это
значит, что «P1 больше
P0 на
два порядка» или «P1 больше
P0 в
100 раз»;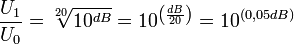 ;
таким образом, например, если изменение
напряжения составило +20 децибел, это
значит, что «U1больше
U0 на
порядок» или «в 10 раз».
;
таким образом, например, если изменение
напряжения составило +20 децибел, это
значит, что «U1больше
U0 на
порядок» или «в 10 раз».