Classmill — 10 класс
Delete Drag
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
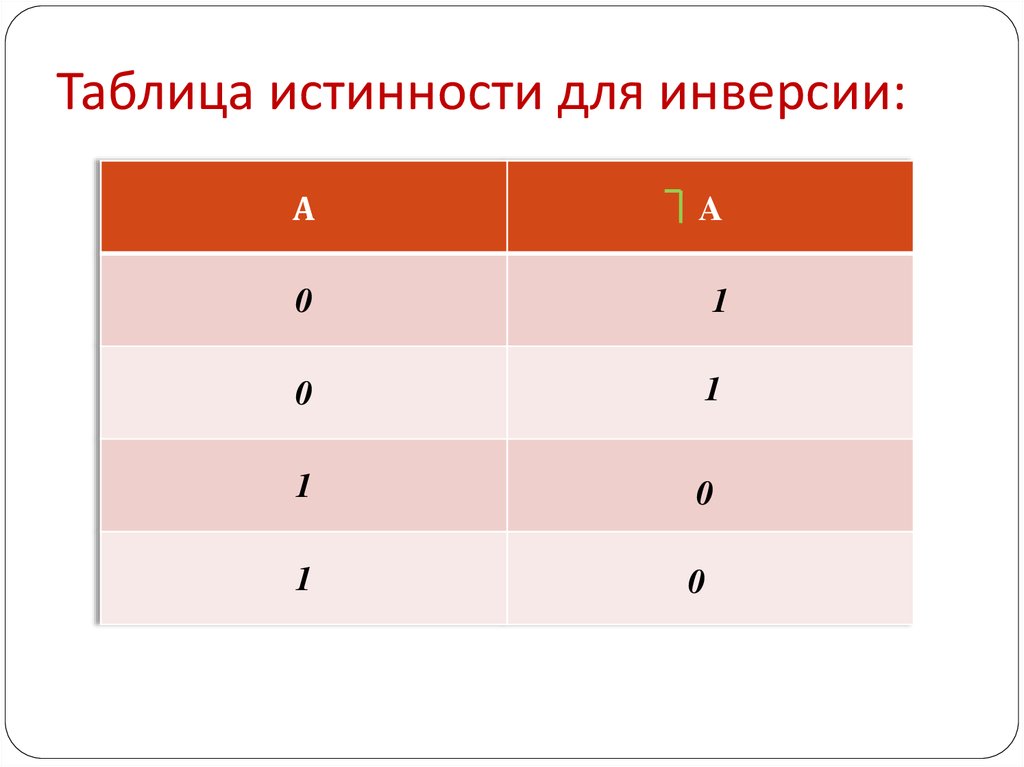
Таблица истинности для инверсии
| A | неА |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1.
Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Логические операции и таблицы истинности 1) Логическое умножение или конъюнкция:…
Delete Drag
Информатика. Алгебра логики: Таблицы истинности. Центр онлайн-обучения «Фоксфорд»
Информатика. Алгебра логики: Таблицы истинности. Центр онлайн-обучения «Фоксфорд»
Video
Title
Description
Duration (m)
-+
Delete Drag
Delete Drag
Таблицы истинности — Луч
Administrator
189 Hits
Таблица истинности — таблица, описывающая логическую функцию.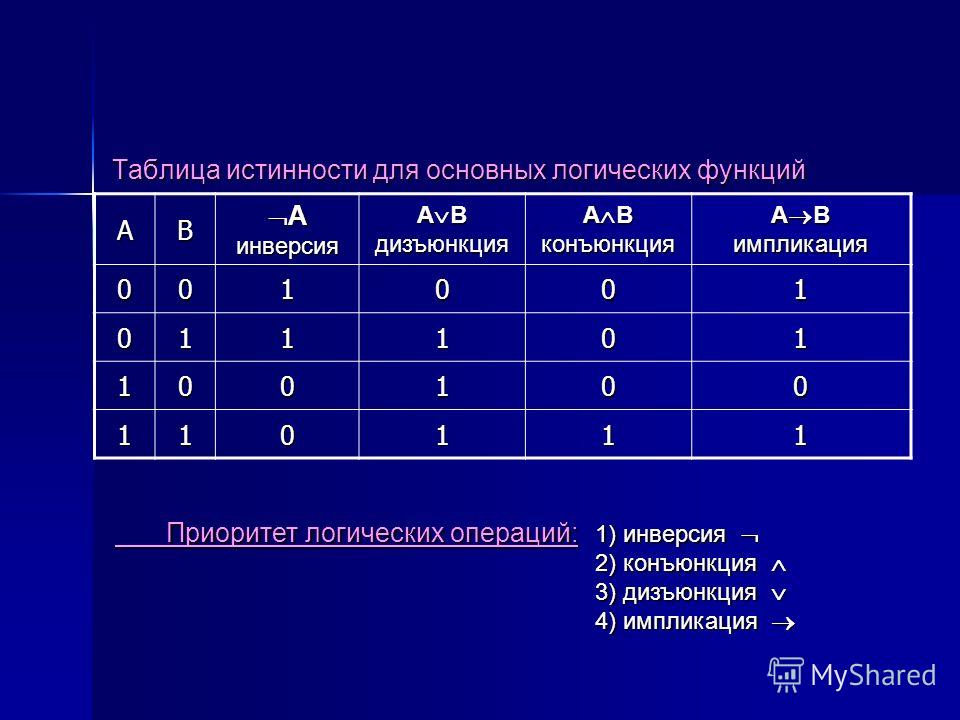
1. Операция НЕ — логическое отрицание (
- если исходное выражение истинно, то результат его отрицания будет ложным;
- если исходное выражение ложно, то результат его отрицания будет истинным.
Обозначения:
не А, Ā, not A, ¬А, !A
Результат: Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.
| A | не А |
| 0 | 1 |
| 1 | 0 |
2.
Операция ИЛИ — логическое сложение (дизъюнкция, объединение). Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Результат:
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.
| A | B | А или B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Результат: Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.
| A | B | А и B |
| 0 | 0 | 0 |
| 0 | 0 | |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
4. Операция «ЕСЛИ-ТО» — логическое следование (импликация). Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.
| A | B | А → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Обозначения: А ↔ В, А ~ В.
Результат: Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.
| A | B | А ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Работа цифрового буфера, определение, таблица истинности, двойная инверсия, разветвление
Буферный каскад, по сути, является усиленным промежуточным каскадом, который позволяет входному току достигать выходного, не подвергаясь влиянию выходной нагрузки.
В этом посте мы попытаемся понять, что такое цифровые буферы, и мы рассмотрим их определение, символ, таблицу истинности, двойную инверсию с использованием логического вентиля «НЕ», разветвление цифрового буфера, разветвление входа, три состояния буфер, эквивалент буфера с тремя состояниями, активный «ВЫСОКИЙ» буфер с тремя состояниями, активный «ВЫСОКИЙ» инвертирующий буфер с тремя состояниями, активный «НИЗКИЙ» буфер с тремя состояниями, активный «НИЗКИЙ» инвертирующий буфер с тремя состояниями, три состояния управление буфером, управление шиной данных буфера с тремя состояниями и, наконец, мы рассмотрим общедоступные микросхемы цифрового буфера и буфера с тремя состояниями.
В одном из предыдущих постов мы узнали о логическом элементе «НЕ», который также называют цифровым инвертором. В вентиле НЕ выход всегда дополняет вход.
Таким образом, если вход «ВЫСОКИЙ», выход становится «НИЗКИМ», если вход «НИЗКИЙ», выход становится «ВЫСОКИМ», поэтому это называется инвертором.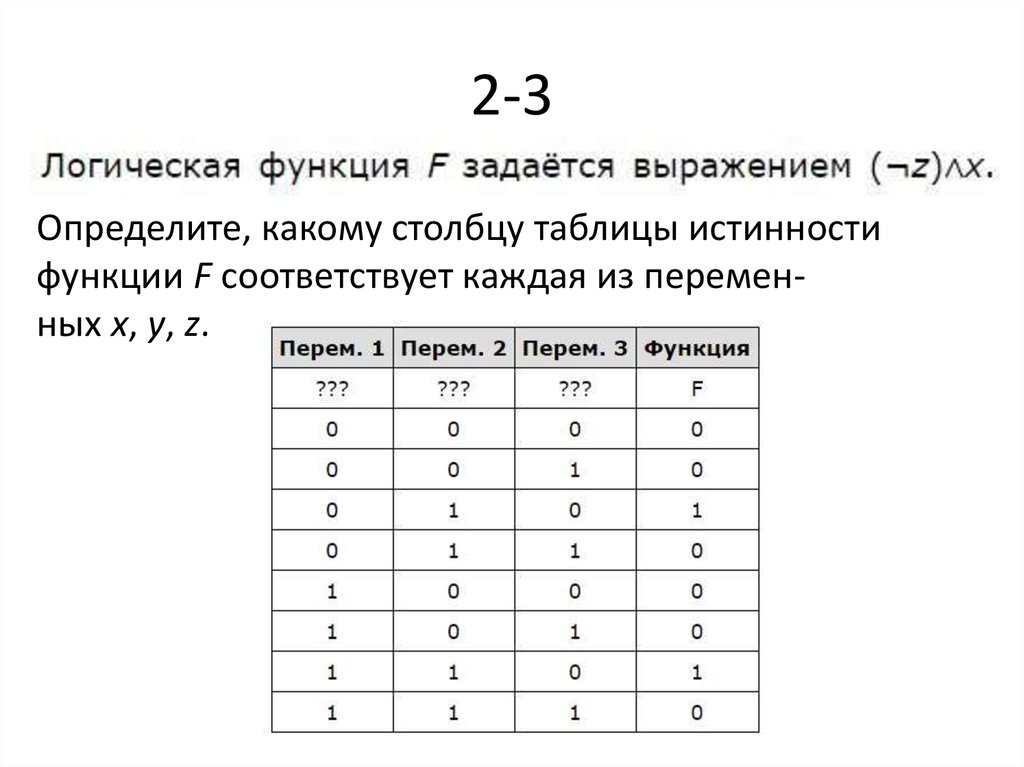
Может возникнуть ситуация, когда выход необходимо отделить или изолировать от входа, или в случаях, когда вход может быть довольно слабым и должен управлять нагрузками, требующими более высокого тока, без инвертирования полярности сигнала с помощью реле или транзистора. и т. д. В таких ситуациях становятся полезными цифровые буферы, которые эффективно применяются в качестве буферов между источником сигнала и каскадом фактического драйвера нагрузки.
Такие логические элементы, которые могут выдавать выходной сигнал так же, как и входной, и действовать как промежуточный буферный каскад, называются цифровыми буферами.
Цифровой буфер не производит никакой инверсии подаваемого сигнала и не является «принимающим решение» устройством, подобно логическому элементу «НЕ», а выдает тот же выход, что и вход.
Иллюстрация цифрового буфера:
Вышеприведенный символ подобен логическому элементу «НЕ» без буквы «о» на вершине треугольника, что означает, что он не выполняет инверсию.
Логическое уравнение для цифрового буфера: Y = A.
«Y» — это вход, а «A» — выход.
Таблица истинности:
Двойная инверсия с использованием логических элементов «НЕ»:
Цифровой буфер может быть построен с использованием двух логических элементов «НЕ» следующим образом:
Входной сигнал сначала инвертируется первым Логический элемент НЕ с левой стороны, а инвертированный сигнал затем инвертируется следующим логическим элементом НЕ с правой стороны, что делает выход таким же, как и входной.
Для чего используются цифровые буферы
Теперь вы, возможно, ломаете голову, зачем вообще существует цифровой буфер, он не выполняет никаких операций, как другие логические элементы, мы могли бы просто выбросить цифровой буфер из схемы и подключить кусок провод…….правильно? Ну не совсем.
Вот ответ : Логический вентиль не требует большого тока для выполнения каких-либо операций. Просто требуется уровень напряжения (5В или 0В) при малом токе достаточно.
Все типы логических элементов в первую очередь поддерживают встроенный усилитель, поэтому выходной сигнал не зависит от входных сигналов. Если мы последовательно подключим два логических элемента «НЕ», мы получим сигнал той же полярности, что и на входе на выходном контакте, но с относительно более высоким током. Другими словами, цифровой буфер работает как цифровой усилитель.
Цифровой буфер может использоваться в качестве изолирующего каскада между каскадами генератора сигналов и каскадами драйвера; также это помогает предотвратить влияние импеданса одной цепи на другую.
Цифровой буфер может обеспечить более высокий ток, который можно использовать для более эффективного управления переключающими транзисторами.
Цифровой буфер обеспечивает более высокое усиление, которое также называется возможностью «разветвления».
Возможность разветвления цифрового буфера:
Разветвление : разветвление может быть определено как количество логических вентилей или цифровых ИС, которые могут параллельно управляться цифровым буфером (или любыми цифровыми ИС).
Типичный цифровой буфер имеет разветвление 10, что означает, что цифровой буфер может параллельно управлять 10 цифровыми ИС.
FAN-IN : Fan-in — это количество цифровых входов, которое может принимать цифровой логический элемент или цифровая ИС.
На приведенной выше схеме цифровой буфер имеет разветвление 1, что означает один вход. Логический вентиль «И» с двумя входами имеет два входа и так далее.
На приведенной выше схеме буфер подключен к 3 входам трех разных логических элементов.
Если мы просто подключим кусок провода вместо буфера в приведенной выше схеме, входной сигнал может быть недостаточно точным, что приведет к падению напряжения на затворах и может даже не распознать сигнал.
Таким образом, цифровой буфер используется для усиления цифрового сигнала с более высоким выходным током.
Буфер с тремя состояниями
Теперь мы знаем, что делает цифровой буфер и почему он существует в электронных схемах.
Эти буферы имеют два состояния «HIGH» и «LOW». Существует еще один тип буфера, который называется «буфер с тремя состояниями».
В этом буфере есть дополнительный контакт, который называется «Включить контакт». Используя контакт включения, мы можем подключить или отключить выход от входа в электронном виде.
Подобно обычному буферу, он работает как цифровой усилитель и выдает выходной сигнал, такой же, как и входной сигнал, с той лишь разницей, что выход может подключаться и отключаться электронным способом с помощью контакта включения.
Таким образом, вводится третье состояние, в котором выход не является ни «ВЫСОКИМ», ни «НИЗКИМ», а является состоянием разомкнутой цепи или высоким импедансом на выходе и не будет реагировать на входные сигналы. Это состояние обозначается как «HIGH-Z» или «HI-Z».
Выше приведена эквивалентная схема буфера с тремя состояниями. Контакт включения может подключать или отключать выход от входа.
Существует четыре типа буфера с тремя состояниями:
• Активный «ВЫСОКИЙ» буфер с тремя состояниями
• Активный «НИЗКИЙ» буфер с тремя состояниями
• Активный «ВЫСОКИЙ» инвертирующий буфер с тремя состояниями
• Активный «НИЗКИЙ» инвертирующий буфер Буфер с тремя состояниями
Рассмотрим последовательно каждое из них.
Активный «ВЫСОКИЙ» буфер с тремя состояниями
В активном буфере с тремя состояниями «ВЫСОКИЙ» (например: 74LS241) выходной контакт подключается к входному контакту, когда мы применяем «ВЫСОКИЙ» или «1» или положительный сигнал в штифт включения.
Если мы подадим «LOW» или «0» или отрицательный сигнал на контакт включения, выход отключится от входа и перейдет в состояние «HI-Z», где выход не будет реагировать на вход, а выход будет в разомкнутой цепи. государство.
Активный «НИЗКИЙ» буфер с тремя состояниями
Здесь выход будет подключен к входу, когда мы подадим «НИЗКИЙ» или «0» или отрицательный сигнал на вывод включения.
Если мы применяем «HIGH» или «1» или положительный сигнал для включения вывода, выход отключается от входа, а выход переходит в состояние «HI-Z» / состояние разомкнутой цепи.
Таблица истинности:
Активный «ВЫСОКИЙ» инвертирующий буфер с тремя состояниями
включить пин.
Если мы подаем «ВЫСОКИЙ» или «1» или положительный сигнал на разрешающий вход, вентиль активируется и действует как обычный логический вентиль «НЕ», где его выход инвертирует/дополняет вход.
Если мы подадим «LOW» или «0» или отрицательный сигнал на контакт включения, выход будет в «HI-Z» или в состоянии разомкнутой цепи.
Таблица истинности:
Активный «НИЗКИЙ» инвертирующий буфер с тремя состояниями:
В активном «НИЗКИЙ» инвертирующий буфер с тремя состояниями логический элемент действует как логический элемент «НЕ», но с разрешающим контактом.
Если мы применяем «НИЗКИЙ» или «0» или отрицательный сигнал для включения вывода, вентиль активируется и работает как обычный логический вентиль «НЕ».
Если мы применяем «HIGH» или «1» или положительный сигнал для включения контакта, выходной контакт будет в состоянии «HI-Z» / в состоянии разомкнутой цепи.
Таблица истинности:
Управление буфером с тремя состояниями:
Из вышеизложенного мы видели, что буфер может обеспечивать цифровое усиление, а буферы с тремя состояниями могут полностью отсоединять свой выход от входа и давать состояние разомкнутой цепи.
В этом разделе мы узнаем о применении буфера с тремя состояниями и о том, как он используется в цифровых схемах для эффективного управления передачей данных.
В цифровых схемах мы можем найти шину данных / провода, передающие данные, они передают все виды данных по одной шине, чтобы уменьшить перегрузку проводки / уменьшить следы на печатной плате, а также снизить производственные затраты.
На каждом конце шины подключены несколько логических устройств, микропроцессоров и микроконтроллеров, которые пытаются взаимодействовать друг с другом одновременно, что создает так называемую конкуренцию.
Конфликт возникает в цепи, когда некоторые устройства на шине одновременно подают сигнал «ВЫСОКИЙ», а некоторые устройства — «НИЗКИЙ», что вызывает короткое замыкание и повреждение цепи.
Буфер с тремя состояниями позволяет избежать конфликтов и правильно отправлять и получать данные по шине.
Буфер с тремя состояниями используется для изоляции логических устройств, микропроцессоров и микроконтроллеров друг от друга на шине данных.
Декодер позволяет передавать данные через шину только одному набору буферов с тремя состояниями.
Допустим, набор данных «A» подключен к микроконтроллеру, набор данных «B» — к микропроцессору, а набор данных «C» — к некоторым логическим схемам.
На приведенной выше схеме все буферы являются активными буферами высокого уровня с тремя состояниями.
Когда декодер устанавливает ENA на «HIGH», активируется набор данных «A», теперь микроконтроллер может отправлять данные по шине.
Остальные два набора данных «B» и «C» находятся в состоянии «HI-Z» или в состоянии очень высокого импеданса, которое электрически изолирует микропроцессор и логические схемы от шины, которая в настоящее время используется микроконтроллером.
Когда декодер устанавливает ENB на «HIGH», набор данных «B» может отправлять данные по шине, а остальные наборы данных «A» и «C» изолированы от шины в состоянии «HI-Z». Аналогично, когда набор данных «C» включен.
Шина данных используется любым из наборов данных «A», «B» или «C» в данный момент времени для предотвращения конфликтов.
Мы также можем установить дуплексную (двунаправленную) связь, соединив два буфера с тремя состояниями параллельно и в противоположном направлении. Разрешающие контакты могут использоваться для управления направлением. Для таких приложений можно использовать IC 74245.
Вот общедоступный список цифровых буферов и буферов с тремя состояниями:
• 74LS07 Hex Non-Inverting Buffer
• 74LS17 Hex Buffer/Driver
• 74LS244 Octal Buffer/Line Driver
• 74LS245 Octal Bidirectional Buffer
• CD4050 Шестнадцатеричный неинвертирующий буфер
• CD4503 Шестнадцатеричный буфер с тремя состояниями
• HEF40244 Восьмеричный буфер с тремя состояниями
На этом мы завершаем обсуждение того, как работают цифровые буферы и их различные цифровые конфигурации. Надеюсь, это помогло вам понять детали. хорошо. Если у вас есть какие-либо дополнительные вопросы или предложения, пожалуйста, выскажите свои вопросы в разделе комментариев, вы можете получить быстрый ответ.
цифровая логика — таблица истинности вентиля XOR с 3 входами
спросил
Изменено 1 год, 6 месяцев назад
Просмотрено 15 тысяч раз
\$\начало группы\$
Учитывая таблицу истинности для XOR с 3 входами, почему выход равен 1, когда все входы равны 1? Это логически не распространяется на XOR с двумя входами, где выход равен 0, когда все входы равны 1. Есть ли способ понять это интуитивно, или нам нужны kmaps и т. д.?
(источник: electronicshub.org)
- цифровая логика
- логические вентили
\$\конечная группа\$
4
\$\начало группы\$
Это может помочь разбить его: сначала выполните \$ A \oplus B = 1 \oplus 1 = 0 \$.
Тогда имеем \$ 0 \oplus C = 0 \oplus 1 = 1 \$.
\$\конечная группа\$
1
\$\начало группы\$
Если вы обрабатываете входные данные как знак числа, где ввод «0» соответствует положительному знаку, а «1» соответствует отрицательному знаку, то функция XOR работает как множитель .
И если вы измените логическое назначение (логический «0» соответствует знаку -ve, а логическая «1» соответствует знаку +ve), это тоже сработает.
Но два входа — это XNOR, три входа XOR, 4 входа XNOR… Я использовал два входа XOR как смеситель-умножитель на два входа прямоугольных импульсов разной частоты. Выходные данные содержат спектральные компоненты, аналогичные аналоговому умножающему микшеру: Мне кажется странным, что общепринятый символ XOR, по-видимому, включает сложение, тогда как его более фундаментальной операцией является умножение в моем извращенном уме.
