Основы автоматики и технической кибернетики
Основы автоматики и технической кибернетики
ОглавлениеПРЕДИСЛОВИЕГЛАВА ПЕРВАЯ. ВВОДНАЯ 1-1. О КЛАССИФИКАЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 1-2. ОБЫКНОВЕННЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 1-3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 1-4. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 1-5. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПО ДРУГИМ ПРИЗНАКАМ ГЛАВА ВТОРАЯ. ОБЩИЕ ПЕРЕДАТОЧНЫЕ СВОЙСТВА ЭЛЕМЕНТОВ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 2-1. УРАВНЕНИЯ ЭЛЕМЕНТОВ. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ СВОЙСТВА ЭЛЕМЕНТОВ б) Центробежный измеритель скорости вращения в) Электромагнитный измеритель напряжения 2-3. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ 2-4. ТИПОВЫЕ ВХОДНЫЕ СИГНАЛЫ. ВОЗМУЩАЮЩИЕ ФУНКЦИИ 2-5. ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ 2-6. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ 2-7. РЕАКЦИЯ ЗВЕНЬЕВ НА ПРОИЗВОЛЬНЫЕ ИЗВЕСТНЫЕ ФУНКЦИИ ВРЕМЕНИ 2-8.  ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИб) Частотные характеристики элементарных звеньев в) Логарифмические характеристики элементарных звеньев 2-9. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЯХ 2-10. СОЕДИНЕНИЯ ЗВЕНЬЕВ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СОЕДИНЕНИИ 2-11. ЭЛЕМЕНТЫ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КАК ЧЕТЫРЕХПОЛЮСНИКИ. ПЕРЕДАТОЧНЫЕ УРАВНЕНИЯ 3-1. ОБЩИЕ СВОЙСТВА ДАТЧИКОВ 3-2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ДАТЧИКИ б) Выходная мощность потенциометрических датчиков и условия согласования в) Динамические свойства г) Ошибка ступенчатости. Параметры потенциометрических датчиков 3-3. ИНДУКТИВНЫЕ ДАТЧИКИ б) Двухтактные индуктивные датчики в) Характеристики двухтактных индуктивных датчиков г) Трансформаторные индуктивные датчики д) Динамические свойства индуктивных датчиков е) Шумы индуктивных датчиков ж) Общие свойства индуктивных датчиков 3-4. СЕЛЬСИНЫ В ТРАНСФОРМАТОРНОМ РЕЖИМЕ б) Характеристики сельсинного датчика г) Шумы и ошибки датчика д) Устанавливающий момент е) Дифференциальные сельсины ж) Сельсины точного и грубого каналов ГЛАВА ЧЕТВЕРТАЯ.  УСИЛИТЕЛИ СИГНАЛОВ4-2. МАГНИТНЫЕ УСИЛИТЕЛИ а) Рабочий процесс и статическая характеристика магнитного усилителя с прямоугольной кривой намагничивания сердечников б) Двухтактные магнитные усилители с выходом на переменном токе в) Магнитные усилители с обратной связью г) Динамические свойства магнитных усилителей 4-3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ б) Однокаскадный электромашицный усилитель как четырехполюсник в) Двухкаскадный электромашинный усилитель с поперечным полем г) Шумы электромашинных усилителей 4-4. РЕЛЕ б) Поляризованные реле в) Магнитоэлектрическое реле 4-5. РЕЛЕЙНЫЕ УСИЛИТЕЛИ б) Вибрационная линеаризация релейных усилителей в) Релейный усилитель как четырехполюсник 4-6. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ б) Фазочувствительные усилители и синхронные детекторы в) Электронные усилители постоянного тока г) Шумы электронных усилителей 4-7.  ГЛАВА ПЯТАЯ. ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 5-2. СЕРВОДВИГАТЕЛИ ПОЧТОЯННОГО ТОКА 5-3. СЕРВОДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА 5-4. СЕРВОДВИГАТЕЛИ С ЭЛЕКТРОМАГНИТНЫМИ И ПОРОШКОВЫМИ МУФТАМИ б) Характеристики серводвигателей с электромагнитными муфтами в) Порошковые муфты г) Характеристики серводвигателей с порошковыми муфтами 5-5. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ б) Обратные связи в гидравлических серводвигателях в) Свойства гидравлических серводвигателей г) Электрогидравлические серводвигатели д) Пневматические серводвигатели ГЛАВА ШЕСТАЯ. СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ б) Интегрирующие и интегродифференцирующие цепи 6-2. АКТИВНЫЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА СИСТЕМ ПОСТОЯННОГО ТОКА 6-3. КОРРЕКТИРУЮЩИЕ ЦЕПИ СИСТЕМ ПЕРЕМЕННОГО ТОКА 6-4. ФИЛЬТРЫ В ЦЕПЯХ ОБРАТНЫХ СВЯЗЕЙ. 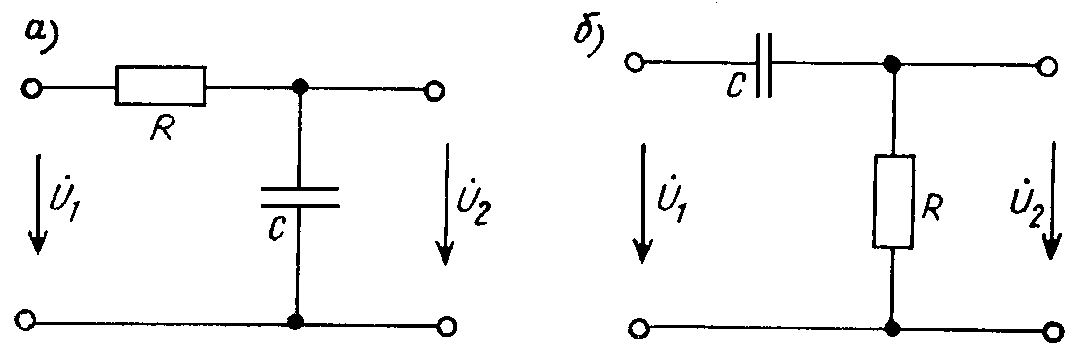 МЕХАНИЧЕСКИЕ СТАБИЛИЗИРУЮЩИЕ УСТРОЙСТВАГЛАВА СЕДЬМАЯ. СТРУКТУРНЫЕ СХЕМЫ И ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 7-1. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 7-2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВХОДНОЙ ВЕЛИЧИНЫ 7-3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ДЛЯ ВОЗМУЩЕНИЯ б) Стабилизация напряжения самолетных генераторов в) Следящая система копировально-фрезерного станка г) Следящая система автосопровождения д) Автоматическое управление углом тангажа самолета 7-5. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 7-6. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ б) Частотные характеристики замкнутой системы в) Связь частотных характеристик замкнутой и разомкнутой систем ГЛАВА ВОСЬМАЯ. ЭНЕРГЕТИЧЕСКИЙ РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СОГЛАСОВАНИЕ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ 8-1. ВЫБОР МОЩНОСТИ ИСПОЛНИТЕЛЬНЫХ УСТРОЙСТВ И УСЛОВИЯ СОГЛАСОВАНИЯ С НАГРУЗКОЙ б) Мгновенная мощность при гармонических колебаниях в) Необходимая мощность при случайных колебаниях регулирующего органа г) Выбор мощности сервомотора д) Условия согласования с нагрузкой сервомотора без обратной связи е) Согласование с нагрузкой сервомотора с жесткой обратной связью 8-2.  СОГЛАСОВАНИЕ ДАТЧИКОВ, УСИЛИТЕЛЬНЫХ И КОРРЕКТИРУЮЩИХ УСТРОЙСТВ. РАСПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯб) Передаточные функции последовательных соединений элементов г) Распределение коэффициентов усиления ГЛАВА ДЕВЯТАЯ. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 9-2. КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА—ГУРВИЦА 9-3. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА 9-4. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА б) Использование логарифмических характеристик системы для исследования устойчивости. Понятие о запасе устойчивости 9-5. КОЭФФИЦИЕНТ УСИЛЕНИЯ И УСТОЙЧИВОСТЬ. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА УСТОЙЧИВОСТЬ 9-6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ В ПРОСТРАНСТВЕ ПАРАМЕТРОВ СИСТЕМЫ ДИАГРАММЫ ВЫШНЕГРАДСКОГО б) Общий метод D-разбиения в плоскости двух параметров. Линейная задача г) Выделение области устойчивости в плоскости одного комплексного параметра ГЛАВА ДЕСЯТАЯ.  КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ10-1. КРИТЕРИИ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ 10-2. ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В УСТАНОВИВШИХСЯ РЕЖИМАХ. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ б) Точность при медленно меняющихся воздействиях. Коэффициенты ошибок. Астатические системы высших порядков в) Общие условия неискаженного воспроизведения входных сигналов в вынужденном режиме г) Повышение точности системы коррекцией входного сигнала д) Повышение точности системы путем компенсации возмущения F(t) б) Некоторые особенности вычисления переходных функций 10-4. РАСПРЕДЕЛЕНИЕ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ И ПЕРЕХОДНЫЕ ПРОЦЕССЫ б) Оценки распределения корней. Степень устойчивости. Коэффициент затухания колебаний в) Влияние параметров на распределение корней. Метод Эванса г) Оценка переходных функций по распределению полюсов передаточной функции или корней характеристического уравнения д) Влияние нулей на характер переходной функции е) Определение коэффициентов уравнений по заданному распределению корней. Стандартные коэффициенты характеристических уравненийб) Приближенное вычисление переходных функций и переходных процессов в) Оценка качества процесса регулирования по характеристикам замкнутой системы Ф(w) и ф(w) и характеристике разомкнутой системы W(jw) г) Оценка качества по амплитудным логарифмическим характеристикам. Минимально-фазовые системы д) Связь между логарифмическими амплитудными характеристиками разомкнутой системы и полюсами передаточной функции замкнутой системы 10-6. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ г) Приближение кривых x(t) к эталонной кривой хэ(t) по критерию … ГЛАВА ОДИННАДЦАТАЯ. НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 11-1. ОБЩИЕ СВЕДЕНИЯ О НЕСТАЦИОНАРНЫХ СИСТЕМАХ 11-2. ПРИМЕРЫ СУЩЕСТВЕННО НЕСТАЦИОНАРНЫХ СИСТЕМ 11-3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕСТАЦИОНАРНЫХ СИСТЕМ АВТОМАТИЧ ЕСКОГО РЕГУЛИРОВАНИЯ 11-4. ОСОБЕННОСТИ СОСТАВЛЕНИЯ УРАВНЕНИЙ И СТРУКТУРНЫХ СХЕМ НЕСТАЦИОНАРНЫХ СИСТЕМ 11-5. МЕТОДЫ ОПРЕДЕЛЕНИЯ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ И ИМПУЛЬСНОЙ РЕАКЦИИ НЕСТАЦИОНАРНЫХ СИСТЕМГЛАВА ДВЕНАДЦАТАЯ. СТАТИСТИЧЕСКАЯ ДИНАМИКА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 12-1. СТАЦИОНАРНЫЕ И НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ б) Стационарные и нестационарные случайные функций в) Свойства корреляционной функции г) Свойство эргодичности д) Гауссовы случайные процессы 12-2. ПРЕОБРАЗОВАНИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ФУНКЦИЙ СТАЦИОНАРНЫМИ ЛИНЕЙНЫМИ СИСТЕМАМИ б) Преобразование корреляционных функций при прохождении случайного сигнала через линейную систему в) Интегральная квадратичная оценка импульсной переходной функции и дисперсия реакции системы на белый шум г) Преобразование спектральных плотностей при прохождении случайного сигнала через линейную систему 12-3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ б) Условия оптимальности при свободном выборе передаточной функции ГЛАВА ТРИНАДЦАТАЯ. О СИНТЕЗЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 13-2. МЕТОД ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИКб) Синтез корректирующих цепей в) О синтезе на основе требований к реакции системы на возмущение F(t) 13-3. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ АНАЛИЗА РАСПРЕДЕЛЕНИЯ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ 13-4. ВЫБОР ПАРАМЕТРОВ НА ОСНОВЕ ИНТЕГРАЛЬНЫХ КВАДРАТИЧНЫХ ОЦЕНОК 13-5. СПЕЦИАЛЬНЫЕ ПРИЕМЫ УЛУЧШЕНИЯ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ б) Подавление помех во входном сигнале при инерционном объекте управления в) Использование двух источников информации для выделения истинного сигнала г) Компенсация влияния запаздывания измерителей на динамические свойства системы д) Исключение перерегулирования в системах, передаточные функции которых имеют только вещественные полюсы ГЛАВА ЧЕТЫРНАДЦАТАЯ. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 14-2. ИМПУЛЬСЫ И ИМПУЛЬСНЫЕ ЭЛЕМЕНТЫ б) Формирующие цепи и импульсные элементы 14-3. ДИСКРЕТНЫЕ ФУНКЦИИ И ПОСЛЕДОВАТЕЛЬНОСТИ. ИХ РАЗНОСТИ И СУММЫ 14-4. РЕАКЦИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ НА ПОСЛЕДОВАТЕЛЬНОСТИ ИЛИ ДЕЛЬТА-ИМПУЛЬСОВ б) Свертка двух дискретных функций в) Уравнения в конечных разностях непрерывных звеньев первого и второго порядков г) Символические изображения дискретных функций и их использование для решения уравнений в конечных разностях 14-5. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА ИЛИ z-ПРЕОБРАЗОВАНИЕ. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА14-6. ДИНАМИКА РАЗОМКНУТЫХ ИМПУЛЬСНЫХ СИСТЕМ б) Значение выходной величины непрерывной системы внутри интервалов повторения в) Передаточные функции, систем с запаздыванием г) Свободные и вынужденные движения д) Полюсы. Устойчивость разомкнутых систем е) Переходные функции ж) Частотные характеристики 14-7. СВЯЗЬ МЕЖДУ ЧАСТОТНЫМИ И ПЕРЕХОДНЫМИ ФУНКЦИЯМИ. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ 14-8. ИНТЕГРАЛЬНАЯ КВАДРАТИЧНАЯ ОЦЕНКА 14-9. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ (СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ) ГЛАВА ПЯТНАДЦАТАЯ. ДИНАМИКА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 15-1. УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ С ОДНИМ ИМПУЛЬСНЫМ ЭЛЕМЕНТОМ 15-2. УСТОЙЧИВОСТЬ ЗАМКНУТЫХ СИСТЕМ 15-3. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ 15-4. ПРИМЕРЫ ИМПУЛЬСНЫХ СИСТЕМ 15-5. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДИСКРЕТНЫМИ КОРРЕКТИРУЮЩИМИ ЦЕПЯМИ ГЛАВА ШЕСТНАДЦАТАЯ. СТРУКТУРНЫЕ СХЕМЫ, ХАРАКТЕРИСТИКИ И УРАВНЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯб) Уравнения продольного движения самолета в) Уравнения продольного движения ракеты 16-2. НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ б) Структурные схемы с нелинейными элементами в) Релейные системы. Релейные элементы 16-3. НЕЛИНЕЙНЫЙ ОБЪЕКТ РЕГУЛИРОВАНИЯ И НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛА ОШИБКИ ГЛАВА СЕМНАДЦАТАЯ. СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ И (МЕТОДЫ ИССЛЕДОВАНИЯ б) Суждение об устойчивости по уравнениям первого приближения. Теоремы Ляпунова в) Суждение о качестве процессов регулирования по уравнениям первого приближения г) Прямой метод Ляпунова д) Техническая устойчивость 17-2. АВТОКОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ б) Автоколебания релейных систем в) Метод точечных преобразований г) Описание процесса в релейной системе разностным уравнением. Устойчивость автоколебаний д) Примера исследования автоколебаний релейных систем второго порядка 17-3. ВЛИЯНИЕ КОРРЕКТИРУЮЩИХ ЦЕПЕЙ НА АВТОКОЛЕБАНИЯ И НА ПЕРЕХОДНЫЕ ПРОЦЕССЫ НЕЛИНЕЙНЫХ СИСТЕМб) Влияние корректирующих цепей на переходные процессы. Скользящие режимы. Оптимальные переходные процессы 17-4. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ б) Исследование автоколебаний при помощи гармонической линеаризации в) Гармоническая линеаризация и критерии устойчивости линейных систем 17-5. ТЕОРИЯ РЕЛЕЙНЫХ СИСТЕМ в) Частотные характеристики релейных систем г) Оценка устойчивости релейных систем д) Вынужденные колебания релейных систем. Захватывание (синхронизация или подавление) автоколебаний е) Вибрационная линеаризация релейных систем, Реакция релейных систем на медленно меняющиеся возмущения 17-6. ОПТИМАЛЬНЫЕ ПРОЦЕССЫ РЕГУЛИРОВАНИЯ б) Системы, оптимальные по быстродействию. Принцип максимума в) Системы, близкие к оптимальным по быстродействию ГЛАВА ВОСЕМНАДЦАТАЯ. ЭНТРОПИЯ, ИНФОРМАЦИЯ, АЛГОРИТМ В СИСТЕМАХ АВТОМАТИЧЕОКОГО УПРАВЛЕНИЯ 18-1. ЭНТРОПИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ УПРАВЛЯЕМОГО ПРОЦЕССА18-2. КОЛИЧЕСТВО ИНФОРМАЦИИ В ПРОЦЕССАХ УПРАВЛЕНИЯ 18-3. ЭНТРОПИЯ И ИНФОРМАЦИЯ В ЗАМКНУТЫХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 18-4. АЛГОРИТМЫ ПРОЦЕССОВ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ГЛАВА ДЕВЯТНАДЦАТАЯ. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ 19-1. ПРИМЕРЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ 19-2. СПОСОБЫ ПОИСКА ЭКСТРЕМУМА б) Методы организации процесса поиска 19-3. СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ 19-4. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ б) Динамика квазистационарного режима систем экстремального регулирования, основанных на методе градиента 19-5. ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ СИГНАЛАХ ПОИСКА б) Уравнения замкнутой системы экстремального регулирования в) Точность экстремального регулирования 19-6. ФОРСИРОВАННЫЕ ПРОЦЕССЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ ОДНОМЕРНОГО БЕЗЫНЕРЦИОННОГО ОБЪЕКТА ГЛАВА ДВАДЦАТАЯ. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С САМОНАСТРАИВАЮЩИМИСЯ КОРРЕКТИРУЮЩИМИ УСТРОЙСТВАМИ20-1. СИСТЕМЫ С РАЗОМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ 20-2. СИСТЕМЫ С ЗАМКНУТЫМИ ЦЕПЯМИ НАСТРОЙКИ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ 20-3. СИСТЕМЫ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ 20-4. СТАТИСТИЧЕСКАЯ ДИНАМИКА НЕПРЕРЫВНЫХ СИСТЕМ С ЭКСТРЕМАЛЬНОЙ НАСТРОЙКОЙ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ б) Уравнения замкнутой самонастраивающейся системы в) Случай сильной фильтрации. Квазистационарный режим г) Общий случай квазистационарного режима ГЛАВА ДВАДЦАТЬ ПЕРВАЯ. ИГРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 21-1. НАЗНАЧЕНИЕ И ПРИНЦИПЫ ДЕЙСТВИЯ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 21-2. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ИГР 21-3. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 21-4. ОБ АЛГОРИТМАХ ИГРОВЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПРИЛОЖЕНИЯ |
мир электроники — Интегрирующие и дифференцирующие цепи
материалы в категории
На логических элементах собираются всякие формирователи, генераторы импульсов, устройства задержки. Для этого используют различные сочетания логических элементов с конденсаторами и резисторами. Наиболее употребительными являются RC-цепи, изображенные ниже.
Вот такое соединение резистора и конденсатора называется дифференцирующей цепью или укорачивающей цепью. На графиках показаны эпюры напряжения на входе и выходе этой цепи. Допустим кондер разряжен. При подаче на вход RC-цепи импульса напряжения кондер сразу же начнет заряжаться током, проходящим через него самого и резик. Сначала ток будет максимальным, затем по мере увеличения заряда конденсатора постепенно уменьшится до нуля по экспоненте. Когда через резик проходит ток, на нем образуется падение напряжения, которое определяется, как U=i R, где i-ток заряда кондера. Поскольку ток изменяется экспоненциально, то и напряжение будет изменяться также — экспоненциально от максимума до нуля. Падение напряжения на резике как раз таки и является выходным. Его величину можно определить по формуле Uвых = U0e-t/τ. Величина τ называется постоянной времени цепи и соответствует изменению выходного напряжения на 63% от исходного (e-1 = 0.37). Очевидно, что время изменения выходного напряжения зависит от сопротивления резистора и емкости конденсатора и, соответственно, постоянная времени цепи пропорциональна этим значениям, т. е. τ = RC. Если емкость в Фарадах, сопротивление в Омах, то τ в секундах.
Если поменять местами резистор и конденсатор, как показано на рисунке 2, то получим интегрирующую цепь или удлиняющую цепь.
Выходным напряжением в интегрирующей цепи является напряжение на кондере. Естественно, если кондер разряжен, оно равно нулю. При подаче импульса напряжения на вход цепи кондер начнет накапливать заряд, и накопление будет происходить по экспоненциальному закону, соответственно, и напряжение на нем будет нарастать по экспоненте от нуля до своего максимального значения. Его значение можно определить по формуле Uвых = U0(1 — e-t/τ). Постоянная времени цепи определяется по такой же формуле, как и для дифференцирующей цепи и имеет тот же смысл.
Для обеих цепей резик ограничивает ток заряда кондера, поэтому чем больше его сопротивление, тем больше время заряда конденсатора. Также и для кондера, чем больше емкость, тем большее время он заряжается.
Если после дифференцирующей цепи влепить инвертор, то наблюдается следующая картина. В исходном состоянии на входе инвертора лог. 0 (резик сидит на корпусе). На его выходе лог. 1. При подаче скачка напряжения в течении некоторого времени на входе инвертора будет присутствовать логическая единица, затем спустя какое-то время напряжение на входе уменьшится до значения, меньше порогового (т. е. до лог. 0), в результате чего на выходе инвертора сначала напряжение упадет до лог. 0, затем опять поднимется до лог. 1, т. е. будет сформирован импульс. Дифференцирующие и интегрирующие цепи не раз будут встречаться в дальнейшем.
Примечание: подсмотрено на сайте naf-st. ru
об. III — Полупроводники — Практические аналоговые полупроводниковые схемы
Глава 9: ПРАКТИЧЕСКИЕ АНАЛОГОВЫЕ ПОЛУПРОВОДНИКОВЫЕ СХЕМЫ
Когда кто-то упоминает слово «компьютер», речь идет о цифровом устройстве. обычно приходит на ум. Цифровые схемы представляют числовые величины в двоичном формате : шаблоны из 1 и 0, представленные множество транзисторных схем, работающих в режиме насыщения или отсечки состояния. Однако аналоговая схема также может использоваться для представления числовые величины и выполнять математические расчеты, используя сигналы переменного напряжения вместо дискретных состояний включения/выключения.
Вот простой пример двоичного (цифрового) представления по сравнению с аналоговым представлением числа «двадцать пять»:
Цифровые схемы сильно отличаются от схем, построенных на аналоговых
принципы. Цифровые вычислительные схемы могут быть невероятно сложными,
и расчеты часто должны выполняться последовательными «шагами», чтобы получить
окончательный ответ, так же, как человек выполняет арифметические
расчеты в шагах с карандашом и бумагой. Аналоговый вычислительный
схемы, с другой стороны, довольно просты по сравнению с ними и выполняют
свои расчеты в непрерывном режиме в режиме реального времени. Eсть
однако недостаток использования аналоговой схемы для представления чисел:
неточность. Цифровая схема, показанная выше, представляет число
двадцать пять, точно. Аналоговая схема, показанная выше, может или не может
быть точно откалиброван на 25 000 вольт, но подвержен «дрейфу» и
ошибка.
В приложениях, где точность не критична, аналоговые вычислительные схемы очень практичны и элегантны. Здесь показаны несколько операционных усилителей. схемы для выполнения аналоговых вычислений:
Каждая из этих схем может быть использована по модульному принципу для создания схема, способная к множественным вычислениям. Например, предположим, что мы необходимо вычесть определенную долю одной переменной из другой переменная. Комбинируя схему деления на константу с вычитателем схемы, мы могли бы получить требуемую функцию:
Устройства, называемые аналоговыми компьютерами , раньше были обычным явлением в университетах. и инженерные мастерские, где можно было найти десятки схем операционных усилителей.
«залатаны» вместе со съемными перемычками для математического моделирования
заявления, обычно с целью моделирования какого-либо физического процесса
основные уравнения которых были известны. Цифровые компьютеры сделали
аналоговые компьютеры почти устарели, но аналоговые вычислительные схемы
не может быть побежден цифровым с точки зрения чистой элегантности и экономии
необходимые компоненты.
Аналоговая вычислительная схема отлично справляется с выполнением вычислительных операций интегрирования и дифференцирования по времени с помощью конденсаторов в цепи обратной связи операционного усилителя.
Однако, чтобы полностью понять работу и применение этих схем,
мы должны сначала понять смысл этих основных концепций исчисления.
К счастью, применение схем на операционных усилителях для решения реальных задач
с участием исчисления служит отличным средством для обучения основам исчисления. По словам Джона И. Смита, взятым из его выдающегося учебника, Современная операционная схема :
«Некоторым читателям предлагается поощрительная записка: интегральная исчисление — одна из математических дисциплин, которая оперирует Схема [усилителя] использует и в процессе скорее разрушает, чем барьер для понимания.» (стр. 4)
Мнение г-на Смита о педагогической ценности аналоговых схем как средство обучения математике не является уникальным. Учитывайте мнение о инженер Джордж Фокс Ланг в статье, которую он написал для журнала за август 2000 г. номер журнала Звук и вибрация под названием «Аналоговый был , а не товарным знаком компьютера!»:
«Создание реального физического объекта (цепи), управляемого определенным набор уравнений и взаимодействие с ним обеспечивает уникальное понимание эти математические утверждения. Нет лучшего способа развить «внутреннюю чувствовать» взаимодействие между физикой и математикой, чем испытывать такое взаимодействие.
Аналоговый компьютер был мощным междисциплинарный инструмент обучения; его устаревание оплакивают многие педагогов по разным специальностям» (стр. 23)
Дифференциация — это первая операция, которую обычно изучают, начиная студенты расчеты. Проще говоря, дифференциация определяет мгновенная скорость изменения одной переменной по отношению к другой. В схемах аналогового дифференциатора независимой переменной является время, и поэтому скорость изменения, с которой мы имеем дело, — это скорость изменения для электронный сигнал (напряжение или ток) во времени.
Предположим, нам нужно измерить положение автомобиля, движущегося по прямому путь (без поворотов) от начальной точки. Назовем это измерение, х . Если автомобиль движется с такой скоростью, что его расстояние от «начало» неуклонно увеличивается с течением времени, его положение будет отображаться на графике как линейная функция (прямая):
Если бы мы вычислили производную положения автомобиля с
относительно времени (то есть определить скорость изменения автомобиля
положение по времени), мы пришли бы к величине
представляющая скорость автомобиля. Функция дифференцирования
представлена дробной записью d/d , поэтому при дифференцировании положения ( x ) по времени ( t ) мы обозначаем результат (производную) как dx/dt :
Для линейного графика x с течением времени производная от положения ( dx/dt ), иначе и более известная как скорость , будет плоской линией, неизменной по значению. Производная математической функции может быть графически понята как ее наклон при построении на графике, и здесь мы можем видеть, что положение ( x ) график имеет постоянный наклон, что означает, что его производная ( dx/dt ) должна быть постоянной во времени.
Теперь предположим, что расстояние, пройденное автомобилем, увеличилось экспоненциально. со временем: то есть он начал свое путешествие медленными движениями, но покрыл больше дополнительного расстояния с каждым проходящим периодом времени. Мы будем затем видим, что производная положения ( dx/dt ), также известная как скорость ( v ), не будет постоянной во времени, а будет увеличиваться:
Высота точек на графике скоростей соответствует скорости изменения или наклона точек в соответствующие моменты времени на график положения:
Какое это имеет отношение к аналоговым электронным схемам? Хорошо, если мы должны были иметь аналоговый сигнал напряжения, представляющий положение автомобиля (подумайте об огромном потенциометре, стеклоочиститель которого был прикреплен к машине, генерируя напряжение, пропорциональное положению автомобиля), мы могли бы подключите схему дифференциатора к этому сигналу и получите схему непрерывно вычислить скорость автомобиля, отображая результат с помощью вольтметра, подключенного к выходу схемы дифференциатора:
Напомним из предыдущей главы, что схема дифференциатора выдает напряжение, пропорциональное скорости изменения входного напряжения за время ( d/dt ). Таким образом, если входное напряжение изменяется во времени с постоянной скоростью ,
выходное напряжение будет постоянным. Если машина движется в
таким образом, чтобы его пройденное расстояние с течением времени увеличивалось с постоянной
скорости, то это означает, что автомобиль движется с постоянной скоростью, и
схема дифференциатора будет выводить постоянное напряжение, пропорциональное
к этой скорости. Если пробег автомобиля с течением времени изменяется в
нестационарным образом, выход схемы дифференциатора также будет
непостоянный, но всегда на уровне репрезентативной входной
скорость изменения во времени.
Обратите внимание, что вольтметр, регистрирующий скорость (на выходе
цепь дифференциатора) подключается в «обратной» полярности к выходу
операционного усилителя. Это связано с тем, что показанная схема дифференциатора инвертирует :
вывод отрицательного напряжения для положительного входного напряжения
скорость изменения. Если мы хотим, чтобы вольтметр регистрировал положительный
значения скорости, он должен быть подключен к операционному усилителю, как показано на рисунке. Каким бы непрактичным ни было подключение гигантского потенциометра к
движущегося объекта, такого как автомобиль, концепция должна быть ясной:
электронно выполняя исчисление функции дифференцирования на
сигнал, представляющий положение, мы получаем сигнал, представляющий скорость.
Начинающие студенты изучают символические методы для дифференциация. Однако для этого необходимо, чтобы уравнение, описывающее исходный график известен. Например, студенты, изучающие математику, узнают, как взять такую функцию, как y = 3x , и найти ее производную относительно x ( d/dx ), 3 , просто манипулируя уравнением. Мы можем проверить точность эту манипуляцию путем сравнения графиков двух функций:
Нелинейные функции, такие как y = 3x 2 , также можно дифференцировать с помощью символьных средств. В этом случае производная y = 3x 2 по отношению к x равна 6x :
Однако в реальной жизни мы часто не можем описать поведение какого-либо физического события простым уравнением вроде y = 3x ,
и поэтому символическая дифференциация типа, изученного исчислением
студентов может быть невозможно применить к физическому измерению. Если
кто-то хотел определить производную от нашего гипотетического автомобиля
позиция ( dx/dt = скорость) символическими средствами они сначала
необходимо получить уравнение, описывающее положение автомобиля во времени,
на основе измерений положения, взятых из реального эксперимента — почти
невыполнимая задача, если автомобиль не эксплуатируется под тщательным контролем
условия, приводящие к очень простому графу позиций. Тем не менее, аналог
схема дифференциатора, используя поведение конденсатора с
по напряжению, току и времени i = C(dv/dt) , естественно
дифференцирует любой реальный сигнал по времени и может
выдать сигнал, соответствующий мгновенной скорости ( дх/дт )
в любой момент. Регистрируя сигнал положения автомобиля вместе с
выходной сигнал дифференциатора с использованием самописца или других данных
устройства сбора данных, оба графика естественным образом представлялись бы для
осмотр и анализ.
Мы можем продвинуть принцип дифференцирования еще на один шаг,
применяя его к сигналу скорости, используя другую схему дифференциатора. Другими словами, используйте его для расчета скорости изменения скорости,
то, что мы знаем, является скоростью изменения положения. Какая практическая мера
к чему бы мы пришли, если бы сделали это? Подумайте об этом с точки зрения единиц
мы используем для измерения положения и скорости. Если бы мы измеряли
положение автомобиля от начальной точки в милях, то мы, вероятно,
выразите его скорость в милях в час ( dx/dt ).
Если бы мы должны были дифференцировать скорость (измеряемую в милях в час)
по отношению ко времени мы получили бы единицу миль в час в час . На вводных занятиях по физике учащиеся изучают поведение падающих объектов, измеряя положение в метров , скорость в метров в секунду и изменение скорости во времени в метров в секунду, в секунду. Эта последняя мера называется ускорением : скорость изменения скорости во времени:
Выражение d 2 x/dt 2 называется секундной производной положения ( x ) по времени ( t ). Если бы мы подключили вторую схему дифференциатора к выходу
первый, последний вольтметр регистрировал ускорение:
Выводя скорость из положения и ускорение из скорости, мы видим очень ясно показан принцип дифференциации. Это не единственные физические измерения, связанные друг с другом таким образом, но они, пожалуй, самые распространенные. Другой пример исчисления в действие есть отношение между расходом жидкости ( q ) и объем жидкости ( v ), накопленный в сосуде с течением времени:
Устройство «Уровнемер», установленное на резервуаре для хранения воды, обеспечивает
сигнал прямо пропорционален уровню воды в баке, который — если
цистерна имеет постоянное поперечное сечение по всей высоте —
напрямую соответствует хранящемуся объему воды. Если бы мы взяли этот том
сигнала и продифференцируем его по времени ( dv/dt ), мы получим сигнал, пропорциональный воде расход по трубе, подающей воду в бак. Цепь дифференциатора
подключен таким образом, чтобы прием этого сигнала громкости производил
выходной сигнал, пропорциональный потоку, возможно, заменяющий
расходомер («Расходомер»), установленный в трубе.
Возвращаясь к эксперименту с автомобилем, предположим, что наш гипотетический автомобиль был оснащен тахогенератором на одном из колес, вырабатывающим напряжение сигнал прямо пропорционален скорости. Мы могли бы дифференцировать сигнал для получения ускорения с одной схемой, например:
По самой своей природе тахогенератор дифференцирует положение автомобиля
относительно времени, генерируя напряжение, пропорциональное тому, как быстро
угловое положение колеса со временем меняется. Это дает нам
необработанный сигнал, уже представляющий скорость, всего с одним шагом
дифференцирования, необходимого для получения сигнала ускорения. А
тахогенератор, измеряющий скорость, конечно, гораздо практичнее
пример автомобильных приборов, чем гигантский потенциометр
измеряя его физическое положение, но то, что мы получаем на практике, мы
потерять в измерении положения. Сколько бы раз мы
дифференцировать, мы никогда не сможем определить положение автомобиля по скорости
сигнал. Если бы процесс дифференциации привел нас от положения к
скорости в ускорение, то как-то надо выполнить «обратное»
процесс дифференциации перехода от скорости к положению. Такой
математический процесс существует, и он называется интеграция . Схема «интегратор» может использоваться для выполнения этой функции интегрирования по времени:
Вспомним из предыдущей главы, что схема интегратора выдает
напряжение, скорость изменения которого во времени пропорциональна входному
величина напряжения. Таким образом, при постоянном входном напряжении выход
напряжение будет изменять с постоянной скоростью . Если машина
движется с постоянной скоростью (постоянное напряжение на входе интегратора
цепи от тахогенератора), то его пройденный путь будет
неуклонно увеличивается с течением времени, и интегратор будет выводить
стабильно изменяющееся напряжение, пропорциональное этому расстоянию. Если машина
скорость непостоянна, то и скорость изменения во времени не будет
на выходе схемы интегратора, но выходное напряжение будет точно представлять расстояние, пройденное автомобилем в любой момент времени.
Символ интегрирования выглядит как очень узкая буква «S» (∫), написанная курсивом. Уравнение, использующее этот символ (∫ v dt = x ), говорит нам, что мы интегрируем скорость ( v ) по времени ( dt ) и в результате получаем положение ( x ).
Таким образом, мы можем выразить три меры движения автомобиля (положение, скорость и ускорение) через скорость ( v ) так же легко, как мы могли бы с точки зрения положения ( x ):
Если бы к машине был прикреплен акселерометр, генерирующий сигнал пропорционально скорости ускорения или замедления, мы могли бы (гипотетически) получить сигнал скорости с одним шагом интегрирования, и сигнал положения со вторым шагом интегрирования:
Таким образом, все три меры движения автомобиля (положение, скорость и ускорение) могут быть выражены через ускорение:
Как вы могли догадаться, процесс интеграции может быть
проиллюстрировано и применено к другим физическим системам. Брать
например, резервуар для хранения воды и пример потока, показанный ранее. Если
скорость потока — это производная объема резервуара по времени ( q = dv/dt ), тогда мы могли бы также сказать, что объем — это интеграл скорости потока по времени:
Если бы мы использовали устройство «датчик потока» для измерения расхода воды, тогда путем интегрирования по времени мы могли бы вычислить объем воды накапливается в баке со временем. Хотя это теоретически можно использовать схему интегратора емкостного операционного усилителя для получения сигнал объема от сигнала расхода, механический и цифровой электронный Устройства «интегратор» больше подходят для интеграции в течение длительного времени. времени и находят частое применение в очистке и распределении воды отрасли.
Точно так же, как существуют символические техники дифференциации, существуют
также символические методы интеграции, хотя они, как правило, более
сложный и разнообразный. Применение символической интеграции к реальному миру
Однако такая проблема, как ускорение автомобиля, по-прежнему зависит от
наличие уравнения, точно описывающего измеряемый сигнал
— часто трудно или невозможно получить из измеренных данных. Однако схемы электронных интеграторов выполняют эту математическую функцию.
работать непрерывно, в режиме реального времени и в течение любой профиль входного сигнала , что обеспечивает мощный инструмент для ученых и инженеров.
Сказав это, есть предостережения относительно использования методов исчисления для вывести один тип измерения из другого. Дифференциация имеет нежелательная тенденция усиления «шума», обнаруженная в измеренных переменной, так как шум обычно проявляется в виде частот, сильно выше измеряемой переменной, а высокие частоты по самой своей природа обладает высокой скоростью изменения во времени.
Чтобы проиллюстрировать эту проблему, предположим, что мы получили измерение
ускорение автомобиля по сигналу скорости, полученному от тахогенератора
с изношенными щетками или коллекторными стержнями. Точки плохого контакта между
щетка и коллектор вызовут кратковременные «провалы» в
выходное напряжение тахогенератора и цепь дифференциатора
связанные с ним, будут интерпретировать эти провалы как очень быстрые изменения в
скорость. Для автомобиля, движущегося с постоянной скоростью, ни ускорение
ни замедления — сигнал ускорения должен быть 0 вольт, но
«шум» в сигнале скорости, вызванный неисправным тахогенератором, будет
привести к тому, что дифференцированный сигнал (ускорения) будет содержать «всплески»,
ложное указание на короткие периоды сильного ускорения и замедления:
Шумовое напряжение, присутствующее в различимом сигнале, не обязательно должно быть значительной амплитуды, чтобы вызвать проблемы: все, что требуется, это чтобы профиль шума имеет быстрое время нарастания или спада. Другими словами, любой электрический шум с высокой составляющей dv/dt будет проблематичным при дифференциации, даже если он имеет низкую амплитуду.
Следует отметить, что эта проблема не является артефактом (а
идиосинкразическая погрешность измерительного/вычислительного прибора) аналога
схема; скорее, это присуще процессу дифференциации.
Как бы мы ни производили дифференцирование, «шум» в
сигнал скорости неизменно искажает выходной сигнал. Конечно,
если бы мы дважды дифференцировали сигнал, как мы делали, чтобы получить оба
скорость и ускорение от сигнала положения, усиленный шум
выходной сигнал первой схемы дифференциатора будет усилен
снова следующим дифференциатором, что усугубляет проблему:
Интеграция не страдает от этой проблемы, потому что интеграторы действуют как фильтры нижних частот, ослабляющие высокочастотные входные сигналы. В эффект, все высокие и низкие пики, возникающие из-за шума в сигнале усредняются вместе с течением времени, что приводит к уменьшению чистого результата. Один можно предположить, что мы могли бы избежать всех неприятностей, измеряя прямое ускорение и интегрирование этого сигнала для получения скорости; в эффект, вычисляемый «в обратном порядке» от способа, показанного ранее:
К сожалению, следование этой методологии может привести нас к другим
трудности, одна из которых является обычным артефактом схем аналоговых интеграторов.
известный как дрейф . Все операционные усилители имеют некоторое смещение на входе.
ток, и этот ток будет вызывать накопление заряда на
конденсатор в дополнение к тому заряду, который накапливается в результате
сигнал входного напряжения. Другими словами, все аналоговые интеграторы
схемы страдают от тенденции к дрейфу выходного напряжения.
или «ползти» даже при абсолютном отсутствии входного напряжения, накапливая
ошибка со временем в результате. Кроме того, несовершенные конденсаторы будут иметь тенденцию к
теряют накопленный заряд с течением времени из-за внутреннего сопротивления, в результате чего
в «дрейфе» к нулевому выходному напряжению. Эти проблемы — это артефактов аналоговой схемы, и их можно устранить с помощью цифровых вычислений.
Несмотря на артефакты схемы, возможные ошибки могут быть результатом
интегрирование одного измерения (например, ускорения) для получения другого
(например, скорость) просто из-за того, как работает интеграция. Если
«нулевая» точка калибровки датчика необработанного сигнала не идеальна, она
будет выводить небольшой положительный или отрицательный сигнал даже в условиях, когда
он не должен ничего выводить. Рассмотрим автомобиль с неидеальным
калиброванный акселерометр или тот, на который влияет гравитация для обнаружения
небольшое ускорение, не связанное с движением автомобиля. Даже при идеальном
интегратора, эта ошибка датчика приведет к тому, что интегратор
накапливать ошибку, что приводит к выходному сигналу, указывающему на изменение
скорость, когда автомобиль не ускоряется и не тормозит.
Как и в случае дифференцирования, эта ошибка также усугубится, если интегрированный сигнал передается на другую схему интегратора, так как «дрейфующий» результат первого интегратора очень скоро представит значимый положительный или отрицательный сигнал для следующего интегратора интегрировать. Поэтому следует соблюдать осторожность при интеграции датчика сигналов: если «нулевая» настройка датчика не соответствует идеальному , результат интегрирования будет дрейфовать, даже если сама схема интегратора идеальна.
До сих пор единственные обсуждаемые ошибки интегрирования были искусственными в
природа: возникающие из-за несовершенства схемы и датчиков. Существует также источник ошибок, присущий процессу
сама интеграция, и это проблема неизвестной константы .
Начинающие студенты математики узнают, что всякий раз, когда функция
интегрированы, существует неизвестная константа (обычно представляемая как
переменная C ) добавляется к результату. Эту неопределенность легче всего
понять, сравнивая производные нескольких функций, различающихся
только путем добавления постоянного значения:
Обратите внимание, как каждая из параболических кривых ( y = 3x 2 + C )
имеют точно такую же форму, отличаясь друг от друга в отношении их
вертикальное смещение. Однако все они имеют одну и ту же производную
функция: y’ = (d/dx)( 3x 2 + C) = 6x , потому что все они имеют одинаковые скорости изменения (наклоны) в соответствующих точках вдоль x ось. Хотя это кажется вполне естественным и ожидаемым с точки зрения
дифференцирования (разные уравнения имеют общую производную),
это обычно кажется начинающим студентам странным с точки зрения
интегрирование, потому что есть несколько правильных ответов для интеграла
функции. При переходе от уравнения к его производной существует только
один ответ, но переходя от этого производного к исходному
уравнение приводит нас к ряду правильных решений. В честь этого
неопределенности, символическая функция интегрирования называется неопределенный интеграл .
Когда интегратор выполняет интеграцию живого сигнала относительно
время, выход представляет собой сумму интегрированного входного сигнала за время и начальное значение произвольной величины, представляющее интегратор
ранее существовавшие выходные данные на момент начала интеграции. Например, если я
интегрировать скорость автомобиля, движущегося прямолинейно от
город, рассчитывая, что постоянная скорость 50 миль в час в течение
время 2 часа даст расстояние (∫ в дт ) 100 миль,
это не обязательно означает, что автомобиль будет в 100 милях от
город через 2 часа. Все, что это говорит нам, это то, что машина будет 100 миль дальше от города после 2 часов езды. Фактическое расстояние от
город после 2-х часов езды зависит от того, на каком расстоянии находилась машина
город, когда началась интеграция. Если мы не знаем это начальное значение
для расстояния мы не можем определить точное расстояние автомобиля от города
через 2 часа езды.
Та же проблема возникает, когда мы интегрируем ускорение по времени для получения скорости:
В этой системе интегратора расчетная скорость автомобиля будет действительна только в том случае, если схема интегратора инициализирована до нулевого выходного значения, когда автомобиль неподвижен ( v = 0). В противном случае интегратор вполне мог бы выводить ненулевой сигнал скорости ( v 0 ). когда машина стоит, акселерометр не может определить разница между стационарным состоянием (0 миль в час) и состоянием постоянная скорость (скажем, 60 миль в час, неизменная). Этот неопределенность на выходе интегратора присуща процессу интеграция, а не артефакт схемы или датчика.
Таким образом, если для любого физического измерения требуется максимальная точность,
лучше всего измерять эту переменную напрямую, а не вычислять ее
от других измерений. Это не означает, что вычисления
бесполезный. Наоборот, часто это единственное практическое средство.
получения желаемого измерения. Однако пределы вычислений
должны быть поняты и соблюдены для того, чтобы точные измерения были
полученный.
— Учебные пособия по электронике
Опубликовано
Вы когда-нибудь задумывались, как создать дифференциатор операционного усилителя? Изучая исчисление, вы узнаете о дифференцировании или производных, которые математически описывают скорость изменения функции. Для электроники мы получаем скорость изменения входного напряжения в цепи через дифференциатор операционного усилителя. В этом уроке мы узнаем о принципиальной схеме дифференциатора операционного усилителя, мы попытаемся концептуально понять, как работает дифференциатор операционного усилителя, затем мы рассмотрим, как мы приходим к стандартному уравнению, которое описывает поведение схемы операционного усилителя.
Начнем со стандартной схемы схемы дифференциатора операционного усилителя.
Стандартное уравнение, описывающее эту схему:
Обладая этой информацией, вы должны быть в состоянии собрать и начать тестирование операционного усилителя самостоятельно, но было бы полезно получить более подробные сведения о том, как именно работает схема дифференциатора. и почему он ведет себя именно так.
Как работает дифференциатор операционных усилителей
Как вы, возможно, помните (если нет, у нас есть туториал по конденсаторам), конденсаторы блокируют сигналы постоянного тока, но пропускают сигналы переменного тока. И их импеданс зависит от частоты этого сигнала переменного тока — чем выше частота, тем ниже импеданс и тем легче ток проходит через конденсатор. Теперь, помня об этом, давайте снова посмотрим на схему.
Если на вход подается сигнал постоянного тока, конденсатор полностью блокирует его, и V out не нужно ничего делать, чтобы инвертирующий вход был равен неинвертирующему входу. Таким образом, любой входной сигнал постоянного тока не окажет никакого влияния на V out . Это интересно, но бесполезно! Давай продолжим.
Магия схемы проявляется, когда меняется V в . Во временной области мы моделируем ток через конденсатор с помощью уравнения:
При изменении напряжения V в мы получаем ток через конденсатор и этот ток начинает изменять напряжение на инвертирующем входе. Когда напряжение на инвертирующем входе начинает изменяться, выход операционного усилителя немедленно изменяется, чтобы как дать току куда-то течь, так и поддерживать инвертирующий вход на уровне 0 В. В частности, по мере увеличения входного напряжения выходное напряжение уменьшается, так что ток может течь от 0 В на инвертирующем входе до отрицательного напряжения на выходе. И наоборот, по мере уменьшения входного напряжения выходное увеличивается, так что ток, который теперь течет в обратном направлении, может течь от выхода к инвертирующему входному узлу на вход.
Как это создает эффект дифференциации, так это то, что эта реакция *только* происходит при изменении входного напряжения — как только входное напряжение достигает устойчивого состояния и ток больше не протекает через конденсатор, выходное напряжение снова падает до 0.
Вывод уравнения, описывающего поведение дифференциатора операционного усилителя
Если вы спешите, вы можете просто использовать стандартное уравнение для моделирования поведения схемы дифференциатора операционного усилителя, но всегда полезно знать, как прийти к уравнению самостоятельно. Я настоятельно рекомендую попробовать самостоятельно составить это стандартное уравнение, а затем вернуться к нему, чтобы либо проверить ответ, либо найти другой способ получения того же ответа, либо дать себе подсказку, если вы боретесь.
Вот шаги, которые мы выполняем, чтобы вывести это уравнение. Если вы хотя бы поверхностно знакомы с KCL, к этому уравнению легко прийти, если вспомнить несколько важных моментов. Во-первых, ток через конденсатор не подчиняется закону Ома, а описывается как:
Во-вторых, ток не течет через входы и выходы операционного усилителя.
В-третьих, выход операционного усилителя будет управлять входами, чтобы они имели одинаковое напряжение.
С этими напоминаниями давайте приступим к решению этого уравнения.
При осмотре видно, что можно использовать узел на инвертирующем входе с KCL. Ток, втекающий и выходящий из узла, будет только с двух направлений. Во-первых, ток через конденсатор идет в одну сторону, а во-вторых, выходит через резистор в другую и мы знаем, что они будут равны между собой. Мы также знаем, что напряжение в этом узле равно 0, потому что оно находится на виртуальной земле из-за того, что неинвертирующий вход подключен непосредственно к земле. Опишем это математически.
и
Или, с точки зрения напряжения:
И заменив V — на 0, мы получим:
И самое сложное сделано, теперь это простая алгебра, которая сложна только если вы склонны делать простые ошибки, как я. Давайте сначала избавимся от этих 0.
Обратите внимание, что у нас все еще есть отрицательный знак на V из . Я не знаю, сколько раз я видел, как студенты опускали отрицательный знак, избавляясь от 0 перед чем-то. В основном, этими учениками был я. Не будь мной. Теперь мы можем изменить это, чтобы получить окончательный ответ.
Вуаля! Как только исходное уравнение KCL настроено, это очень просто. И теперь у вас должно быть хорошее математическое понимание того, как выход будет инвертированным входом, но масштабированным с помощью RC.
Примеры входных и выходных данных дифференциатора
Для упрощения понимания приведем несколько входных и выходных данных, которые можно ожидать от вашего дифференциатора. Однако здесь следует отметить две вещи. Во-первых, выходные данные инвертируются по сравнению с простым выводом, потому что, опять же, выходные данные масштабируются по RC и инвертируются. Во-вторых, хотя эти примеры являются непрерывными, вы можете рассматривать их части как отдельные события, и соответствующие выходные данные все равно будут точными.
Практические соображения при работе со схемами дифференциатора
В отличие от схемы интегратора, схема дифференциатора не накапливает ошибки с течением времени, что очень удобно. Однако, как и у схемы интегратора или любой схемы на операционном усилителе, существует только ограниченная полоса пропускания, в пределах которой схема имеет линейный отклик. Когда частота увеличивается слишком высоко, операционный усилитель не будет таким отзывчивым, и выходной сигнал будет ослаблен.
Еще одно соображение из реальной жизни заключается в том, что иногда реакция не такая быстрая или линейная, как можно было бы ожидать математически. В частности, при входе прямоугольной волны вы ожидаете очень короткие и крутые всплески на выходе. На самом деле шипы длятся дольше и не такие высокие, как вы, вероятно, интуитивно ожидаете. Изменение размеров резистора и конденсатора повлияет на эту чувствительность, и вы можете получить то, что оптимизировано для вашего требуемого приложения.
Резюме
В этом обзоре мы рассмотрели дифференциаторы операционных усилителей, как их сделать, как они работают концептуально, как их производительность рассчитывается математически, а также показаны некоторые типичные входы и выходы, используемые в цепь дифференциатора. Наконец, мы кратко обсудили несколько неидеальных соображений, которые следует учитывать при работе с ними в лаборатории или в реальных приложениях. После этого вы сможете уверенно начать работу с дифференцирующими схемами операционных усилителей. Если вы все еще в замешательстве или у вас есть дополнительные вопросы, вы можете посмотреть видеоурок, просмотреть его еще раз (в этом нет ничего постыдного!), задать вопрос в комментариях ниже или перейти и задать вопрос на нашем канале Discord.
- Операционный усилитель (11)
- Усилитель (6)
Автор:
Джош Бишоп
Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе.
