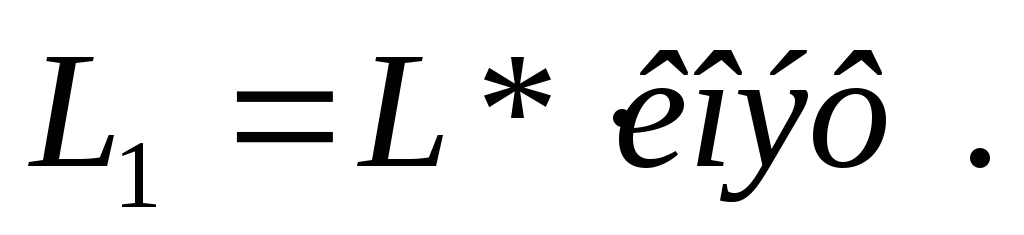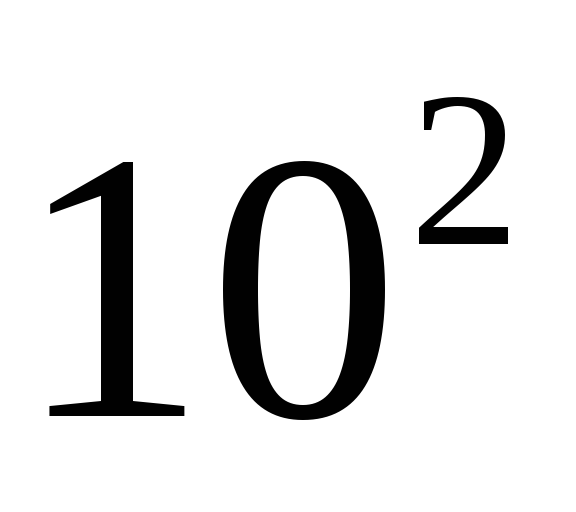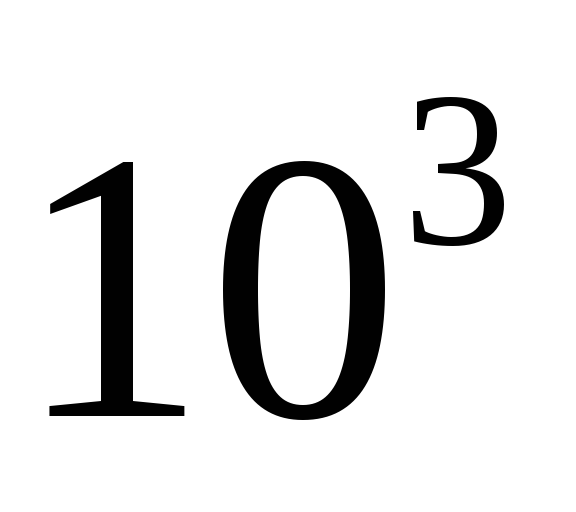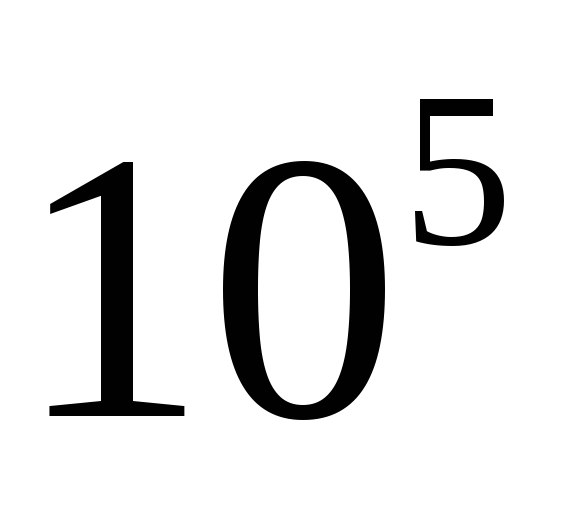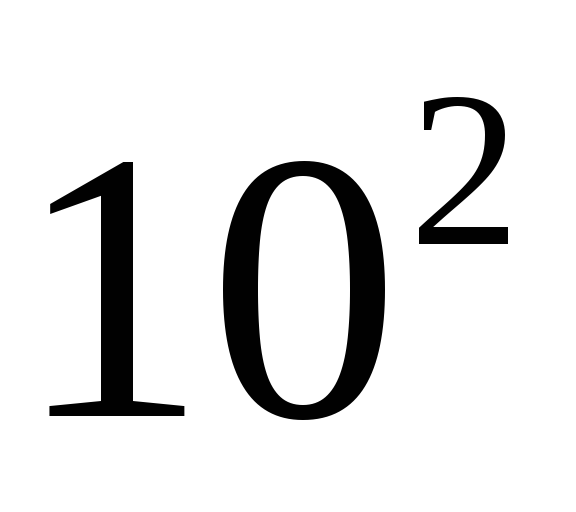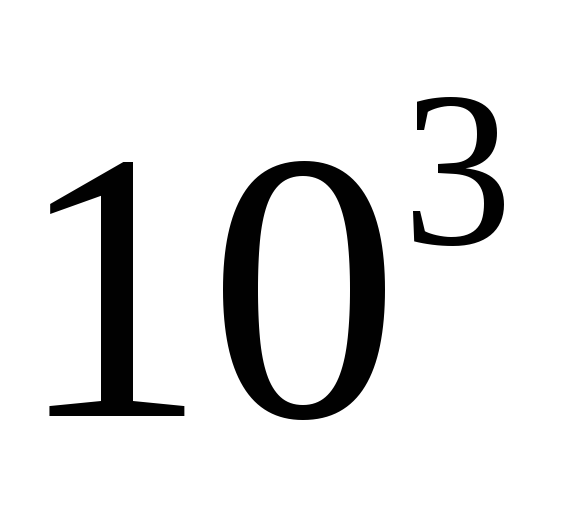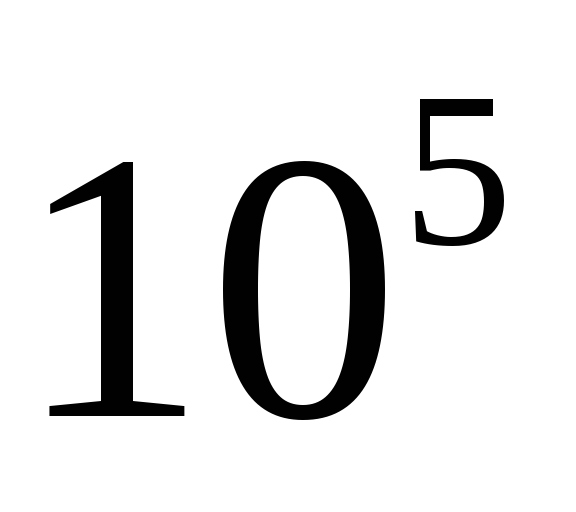Интегрирующая rl-цепь
Такая цель показана на рис 13-37, выходное напряжение (сигнал) снимается с индуктивности L.
Все рассуждения и выводы об интегрирующих RC– цепях можно сделать и дляRL- цепей. ИнтегрирующиеRL- цепи конструктивно сложнееRC- цепей.
Отметим, что для дифференцирование и интегрирование с помощью RC– иRL- цепей можно осуществлять и в случаях, когда сигнал имеет не прямоугольную, а другую форму, например, трапециидальную.
Так как
интегрирующая электрическая цепь
является четырехполюсником, то все
расчеты ФНЧ аналогичны расчетам ФВЧ.
Следует добавить, что на практике, кроме
уровня 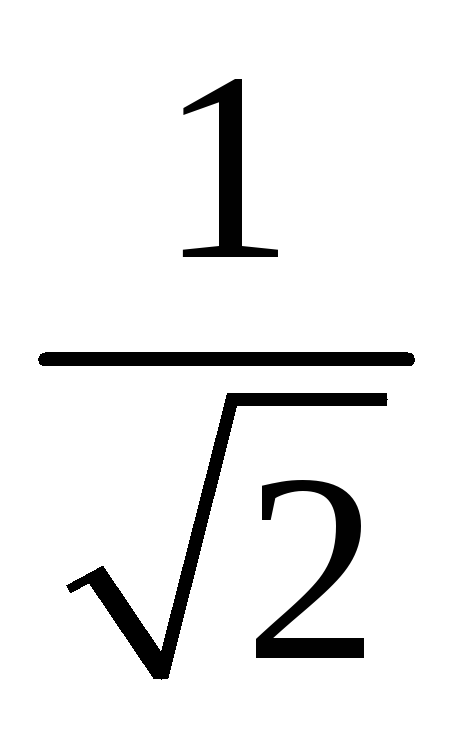 используются
дополнительные частоты
используются
дополнительные частоты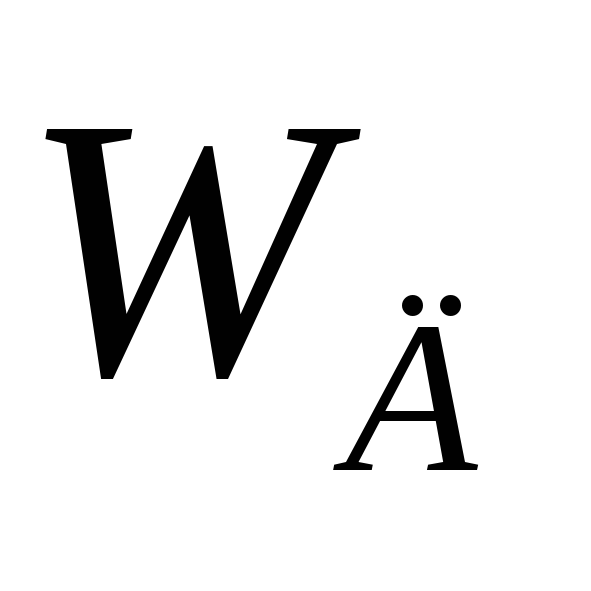 ,
которые показывают границу полосы
подавления частоты фильтром. АЧХ
интегрирующей цепи показаны на рисунке
13-40.
,
которые показывают границу полосы
подавления частоты фильтром. АЧХ
интегрирующей цепи показаны на рисунке
13-40.
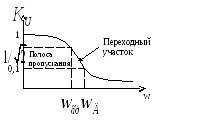
Рис.13-40. Амплитудно-частотная характеристика ФНЧ.
Активные фильтры.
В области частот порядка 100кГц необходимы электрические фильтры, требующие значительные электроемкости и индуктивности катушек. В связи с этим при построении электрических фильтров в качестве базовых элементов используют операционные усилители, тогда электрические фильтры называют активными. Следует добавить, что в его схеме присутствуют RC-цепи и операционные усилители. На рис. 13-41 приведена схема активного фильтра ФНЧ (фильтр низких частот).
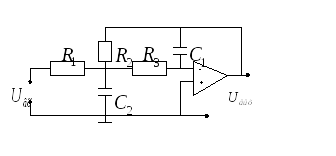
Рис.13-41. Схема активного фильтра ФНЧ.
Коэффициент передачи активного фильтра с ФНЧ имеет вид:
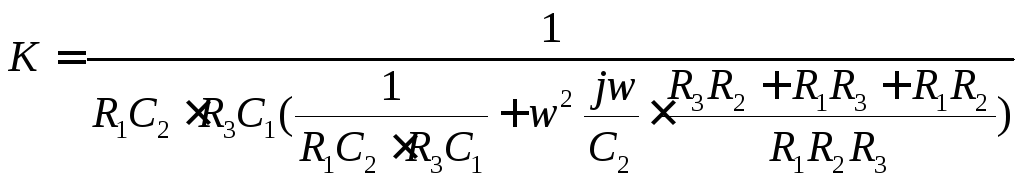 (13.30)
(13.30)
В уравнении (13.30) подбором величин R,Cможно получить желаемый вид АЧХ.
Если в фильтрах нижних частот заменить сопротивления и конденсаторы, то можно получить схему активного фильтра высоких частот. Следует заметить, что если параметры схемы остаются прежними, то коэффициенты передачи и граничные частоты уже становятся нижними границами, а крутизна спада АЧХ остается прежней.
Интегральные микросхемы
Рассмотренные выше усилители нашли применение в интегральных аналоговых микросхемах (ИС), но отличаются тем, что дискретное исполнение элементов и функциональных узлов выполнено другими методами изготовления – методами интегральных схематичных микросхем (ИС). ИС – это микроэлектронное изделие (высокая степень миниатюризации ), которая выполняет выбранную функцию обработки электрического сигнала. Такие схемы имеют очень высокую степень упаковки соединений элементов и кристаллов. Интегральные схемы по технологиям изготовления разделяются на гибридные, полупроводниковые, пленочные.
Гибридные ИС содержат компоненты и отдельные кристаллы полупроводника. Полупроводниковая ИС- все элементы и их соединения выполнены в объеме или на поверхности полупроводника.
Пленочные ИС – все элементы и их соединения выполнены на поверхности диэлектрика.
Интегральные микросхемы имеют степени интеграции, показанные в таблице 13.1.
Таблица 13.1.
Название схем | ИС (простые интег- ральные схемы) | СИС (средние интег- ральные схемы) | БИС (большие интег- ральные схемы) | СБИС (сверхбольшие интегральные схемы) |
Отдельные компоненты | 10 |
|
|
|
При изготовлении интегральных микросхем используется способ обогащения отдельных участков полупроводниковой пластины донорными и акцепторными примесями с использованием высоких технологий.
В интегральных схемах для получения
конденсаторов используют электроемкость
p-nпереходов
или наносят на поверхность металла слой
диэлектрика, а затем наносят проводящий
слой. Сопротивления могут быть получены
в видеp-nпереходов, включаются в обратной
полярности, а также в виде полупроводника,
который находится между двумя
полупроводниками с другой проводимостью.
Индуктивность в схемах получают созданием
эффекта отставания тока от напряжения
(этот эффект наблюдается в реальной
индуктивности), что может быть получено
путем замедления движения носителей
заряда в полупроводнике. Биполярные
транзисторы (напримерn-p-nтипа) для интегральных микросхем
создаются в основном следующим способом:
на пластину полупроводника кремния при
сложном техническом процессе (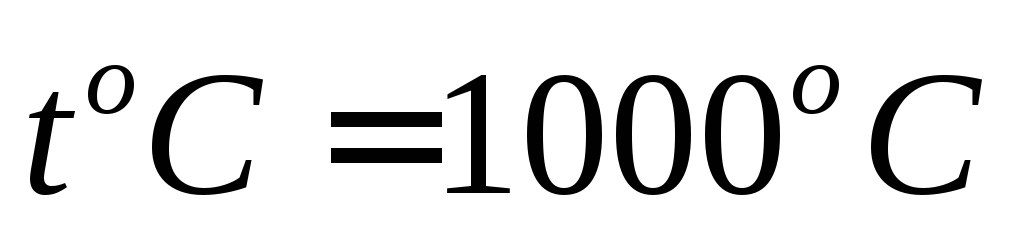
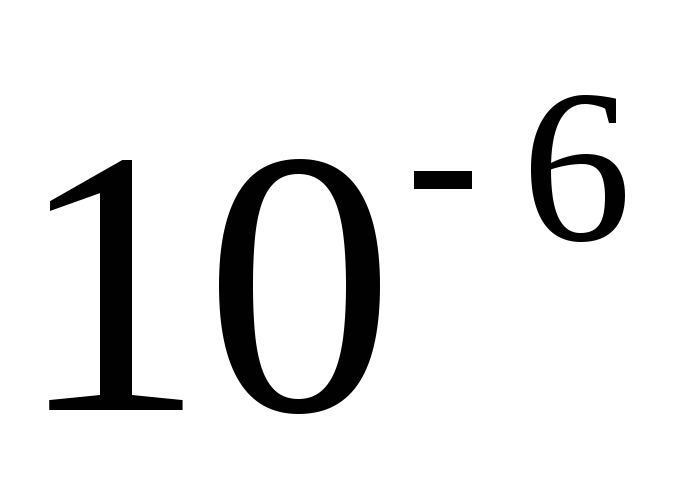 м,
а затем почти при такой же температуре
вводят бор(p-проводимость)
и создается база транзистора, а затем
вводят фосфор-эмиттер(n-проводимость),
затем создаются контакты напряжениям
алюминия в области базы и эмиттера,
осаждают слой на область коллектора и
присоединяют контакты, выполненные и
проволоки. Чтобы оценить степень
миниатюризации приведем пример: на
кремниевой пластине можно выполнить
около 50,000 транзисторов, а современные
технологии повышают это число во много
раз.
м,
а затем почти при такой же температуре
вводят бор(p-проводимость)
и создается база транзистора, а затем
вводят фосфор-эмиттер(n-проводимость),
затем создаются контакты напряжениям
алюминия в области базы и эмиттера,
осаждают слой на область коллектора и
присоединяют контакты, выполненные и
проволоки. Чтобы оценить степень
миниатюризации приведем пример: на
кремниевой пластине можно выполнить
около 50,000 транзисторов, а современные
технологии повышают это число во много
раз.Приведем интегральную схему усилительного каскада(рис 13-43) и аналогичную этой схеме – принципиальную схему(рис 13-42).
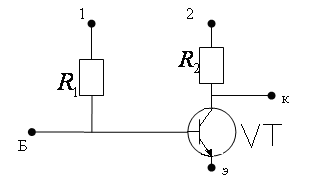
Рис 13-42. Принципиальная схема усилительного каскада.

Рис 13-43. Интегральная схема усилительного каскада.
На
схеме транзистор состоит из трех слоев,
Э (эмиттер)- 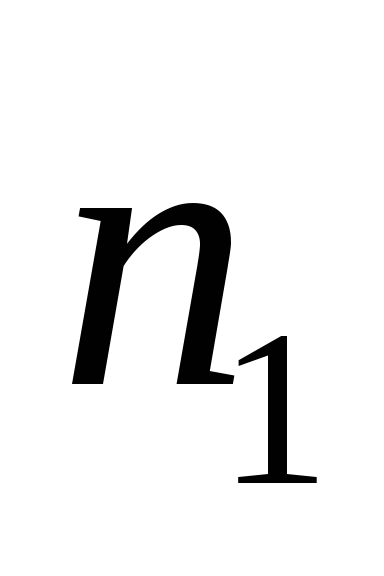
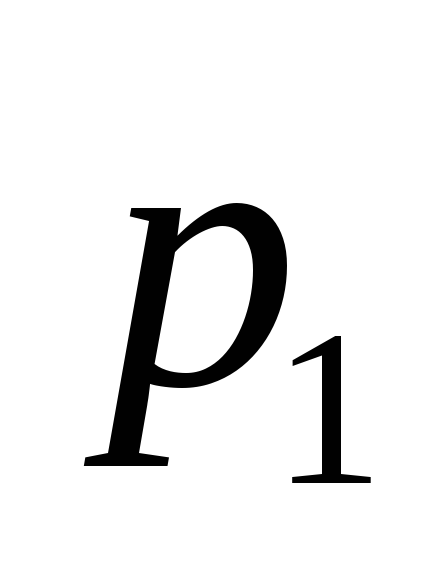 ,
К (коллектор) —
,
К (коллектор) —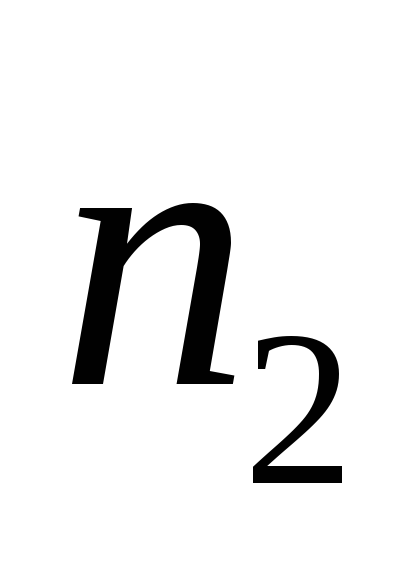 ,
сопротивление
,
сопротивление и
и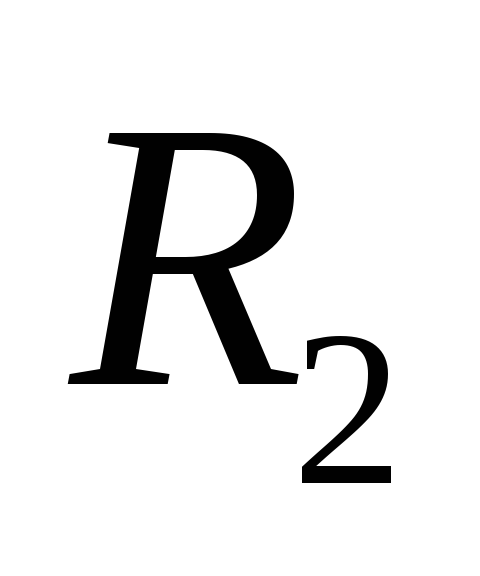 созданы слоями
созданы слоями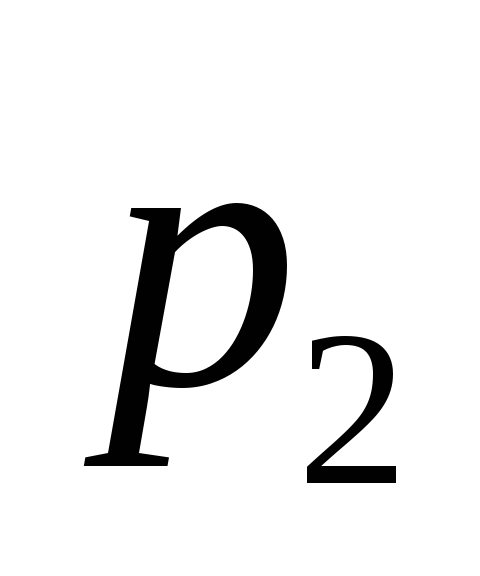 и
и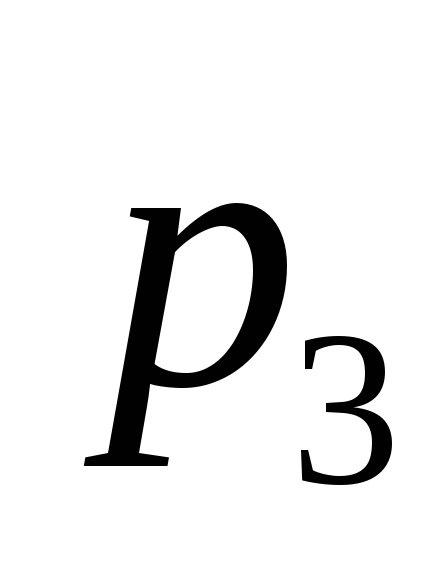 ,
слои
,
слои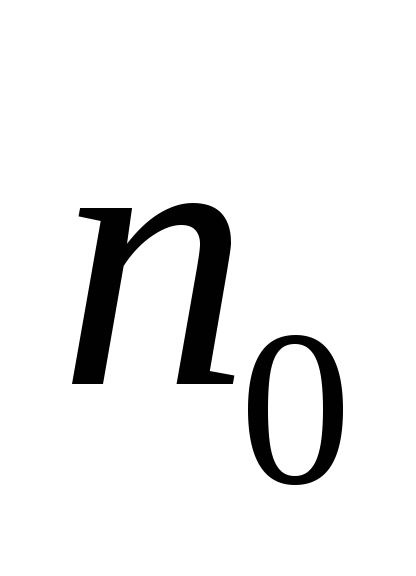
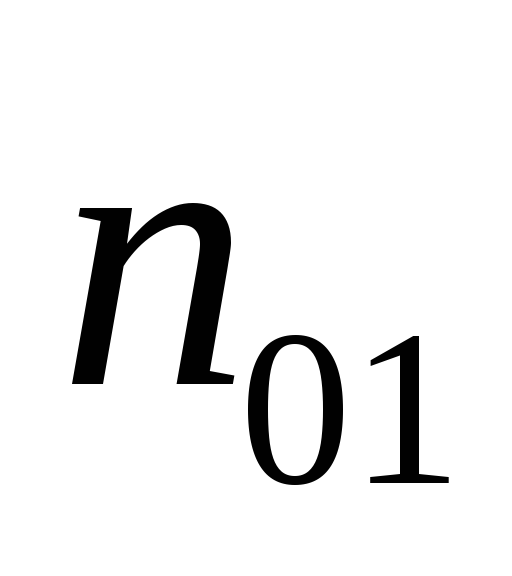 — изолируют резисторы от транзистора
при запертыхp-nпереходах, слои
— изолируют резисторы от транзистора
при запертыхp-nпереходах, слои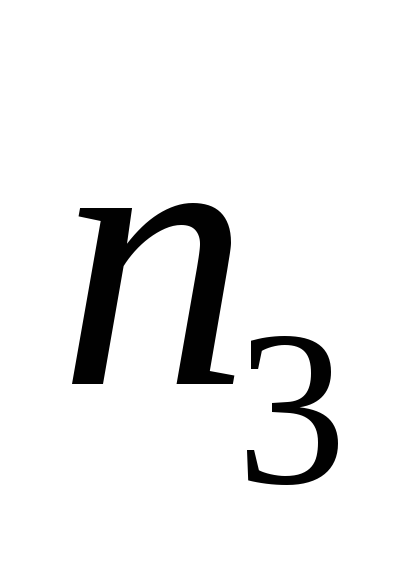 и
и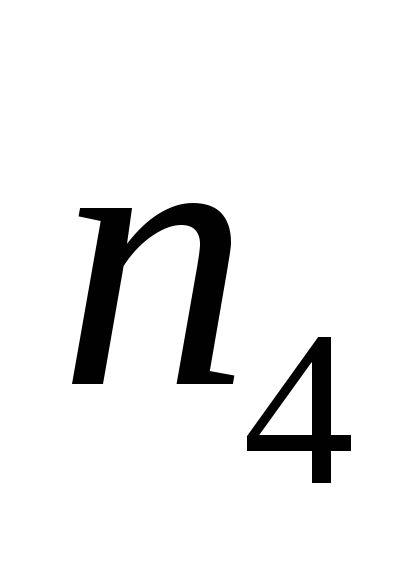 определяют толщину слоев
определяют толщину слоев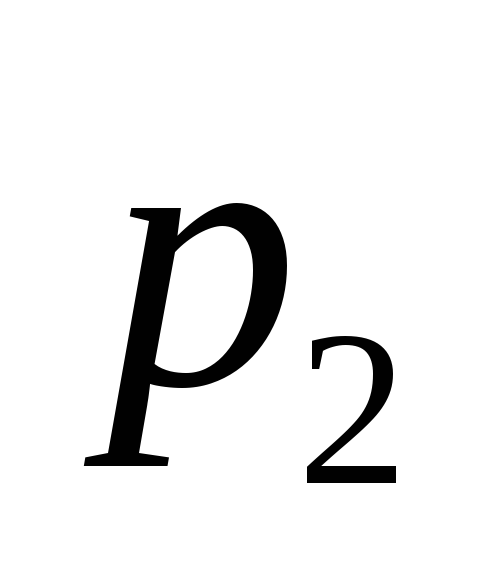 и
и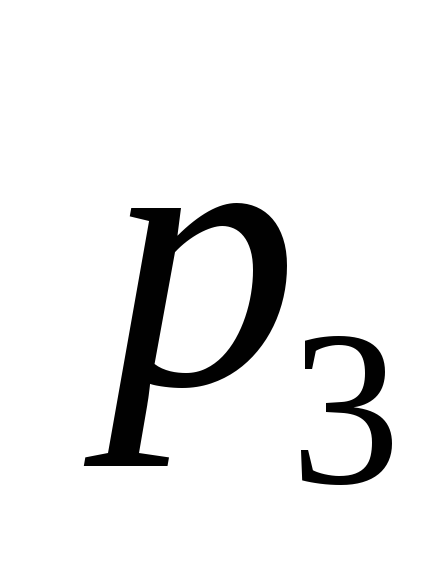 ,
и , соответственно, величину
,
и , соответственно, величину и
и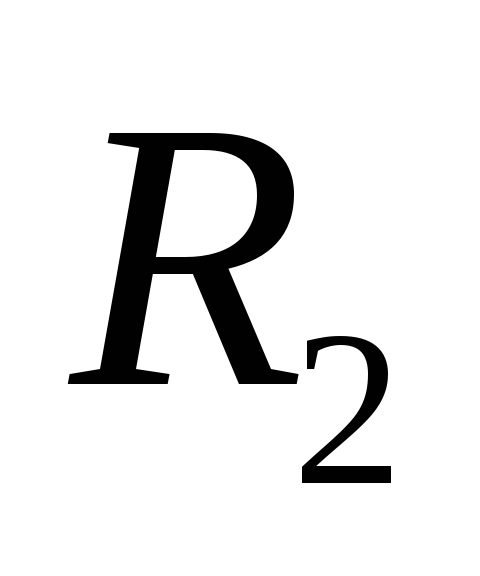
Интегрирующая rl-цепь
Такая цель показана на рис 13-37, выходное напряжение (сигнал) снимается с индуктивности L.
Все рассуждения и выводы об интегрирующих RC– цепях можно сделать и дляRL- цепей. ИнтегрирующиеRL- цепи конструктивно сложнееRC- цепей.
Отметим, что для дифференцирование и интегрирование с помощью RC– иRL- цепей можно осуществлять и в случаях, когда сигнал имеет не прямоугольную, а другую форму, например, трапециидальную.
Так как
интегрирующая электрическая цепь
является четырехполюсником, то все
расчеты ФНЧ аналогичны расчетам ФВЧ.
Следует добавить, что на практике, кроме
уровня 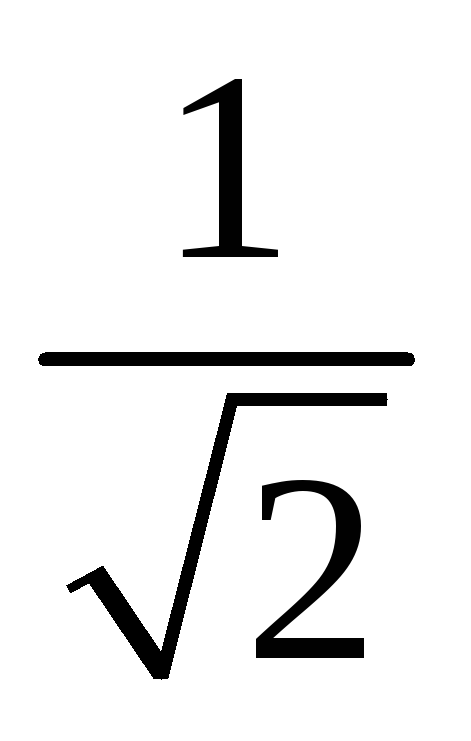 используются
дополнительные частоты
используются
дополнительные частоты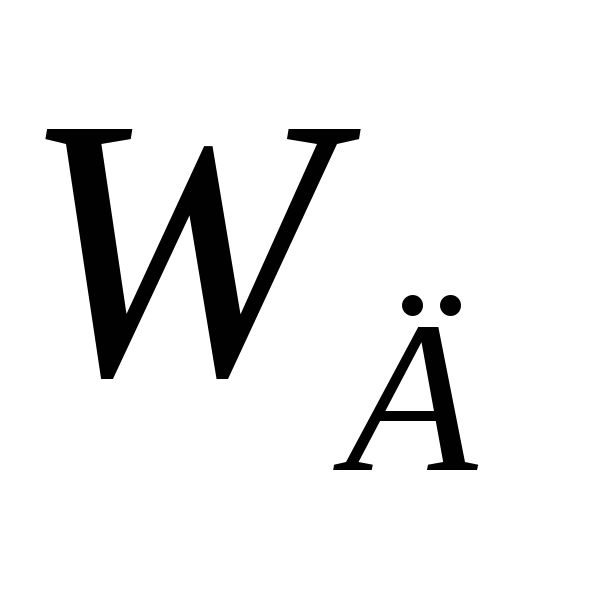 ,
которые показывают границу полосы
подавления частоты фильтром. АЧХ
интегрирующей цепи показаны на рисунке
13-40.
,
которые показывают границу полосы
подавления частоты фильтром. АЧХ
интегрирующей цепи показаны на рисунке
13-40.
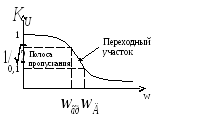
Рис.13-40. Амплитудно-частотная характеристика ФНЧ.
Активные фильтры.
В области частот порядка 100кГц необходимы электрические фильтры, требующие значительные электроемкости и индуктивности катушек. В связи с этим при построении электрических фильтров в качестве базовых элементов используют операционные усилители, тогда электрические фильтры называют активными. Следует добавить, что в его схеме присутствуют RC-цепи и операционные усилители. На рис. 13-41 приведена схема активного фильтра ФНЧ (фильтр низких частот).
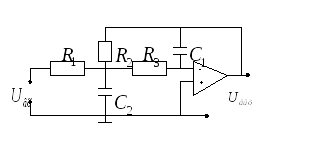
Рис.13-41. Схема активного фильтра ФНЧ.
Коэффициент передачи активного фильтра с ФНЧ имеет вид:
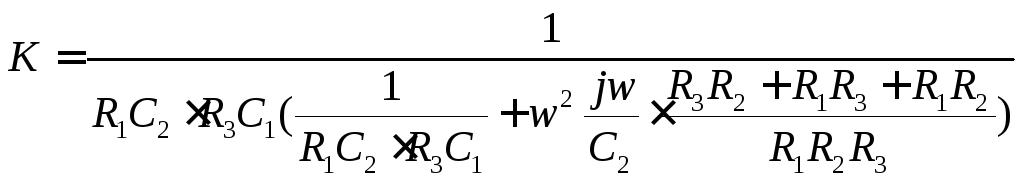 (13.30)
(13.30)
В уравнении (13.30) подбором величин R,Cможно получить желаемый вид АЧХ.
Если в фильтрах нижних частот заменить сопротивления и конденсаторы, то можно получить схему активного фильтра высоких частот. Следует заметить, что если параметры схемы остаются прежними, то коэффициенты передачи и граничные частоты уже становятся нижними границами, а крутизна спада АЧХ остается прежней.
Интегральные микросхемы
Рассмотренные выше усилители нашли применение в интегральных аналоговых микросхемах (ИС), но отличаются тем, что дискретное исполнение элементов и функциональных узлов выполнено другими методами изготовления – методами интегральных схематичных микросхем (ИС). ИС – это микроэлектронное изделие (высокая степень миниатюризации ), которая выполняет выбранную функцию обработки электрического сигнала. Такие схемы имеют очень высокую степень упаковки соединений элементов и кристаллов. Интегральные схемы по технологиям изготовления разделяются на гибридные, полупроводниковые, пленочные.
Гибридные ИС содержат компоненты и отдельные кристаллы полупроводника. Полупроводниковая ИС- все элементы и их соединения выполнены в объеме или на поверхности полупроводника.
Пленочные ИС – все элементы и их соединения выполнены на поверхности диэлектрика.
Интегральные микросхемы имеют степени интеграции, показанные в таблице 13.1.
Таблица 13.1.
Название схем | ИС (простые интег- ральные схемы) | СИС (средние интег- ральные схемы) | БИС (большие интег- ральные схемы) | СБИС (сверхбольшие интегральные схемы) |
Отдельные компоненты | 10 |
|
|
|
При изготовлении интегральных микросхем используется способ обогащения отдельных участков полупроводниковой пластины донорными и акцепторными примесями с использованием высоких технологий.
В интегральных схемах для получения
конденсаторов используют электроемкость
p-nпереходов
или наносят на поверхность металла слой
диэлектрика, а затем наносят проводящий
слой. Сопротивления могут быть получены
в видеp-nпереходов, включаются в обратной
полярности, а также в виде полупроводника,
который находится между двумя
полупроводниками с другой проводимостью.
Индуктивность в схемах получают созданием
эффекта отставания тока от напряжения
(этот эффект наблюдается в реальной
индуктивности), что может быть получено
путем замедления движения носителей
заряда в полупроводнике. Биполярные
транзисторы (напримерn-p-nтипа) для интегральных микросхем
создаются в основном следующим способом:
на пластину полупроводника кремния при
сложном техническом процессе (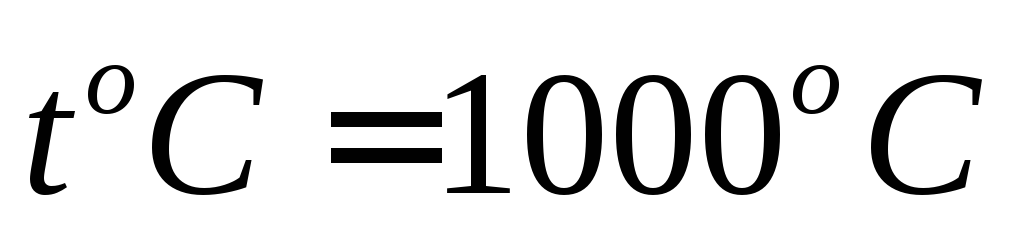 )
наносят диоксид кремния толщиной
)
наносят диоксид кремния толщиной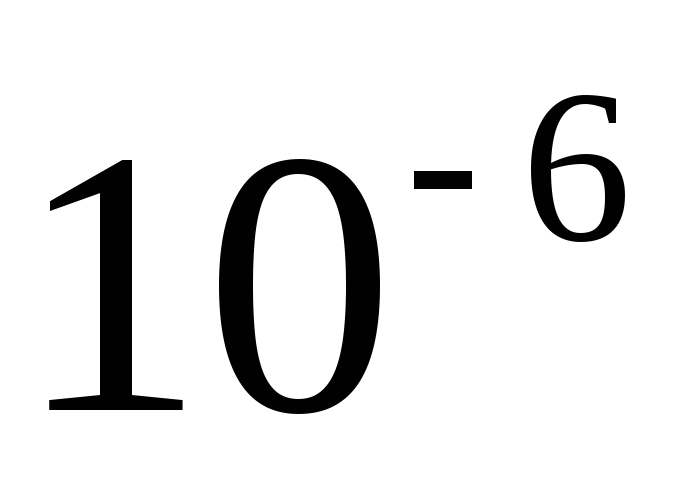 м,
а затем почти при такой же температуре
вводят бор(p-проводимость)
и создается база транзистора, а затем
вводят фосфор-эмиттер(n-проводимость),
затем создаются контакты напряжениям
алюминия в области базы и эмиттера,
осаждают слой на область коллектора и
присоединяют контакты, выполненные и
проволоки. Чтобы оценить степень
миниатюризации приведем пример: на
кремниевой пластине можно выполнить
около 50,000 транзисторов, а современные
технологии повышают это число во много
раз.
м,
а затем почти при такой же температуре
вводят бор(p-проводимость)
и создается база транзистора, а затем
вводят фосфор-эмиттер(n-проводимость),
затем создаются контакты напряжениям
алюминия в области базы и эмиттера,
осаждают слой на область коллектора и
присоединяют контакты, выполненные и
проволоки. Чтобы оценить степень
миниатюризации приведем пример: на
кремниевой пластине можно выполнить
около 50,000 транзисторов, а современные
технологии повышают это число во много
раз.
Приведем интегральную схему усилительного каскада(рис 13-43) и аналогичную этой схеме – принципиальную схему(рис 13-42).
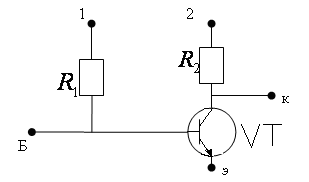
Рис 13-42. Принципиальная схема усилительного каскада.

Рис 13-43. Интегральная схема усилительного каскада.
На
схеме транзистор состоит из трех слоев,
Э (эмиттер)- 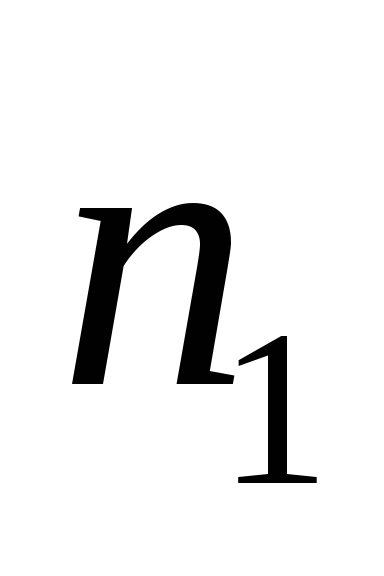 ,
Б (база)-
,
Б (база)-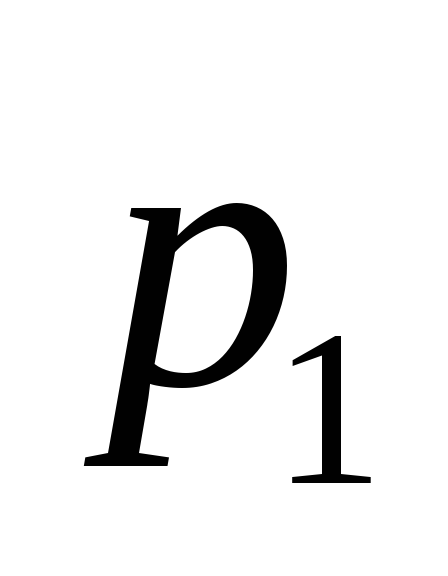 ,
К (коллектор) —
,
К (коллектор) —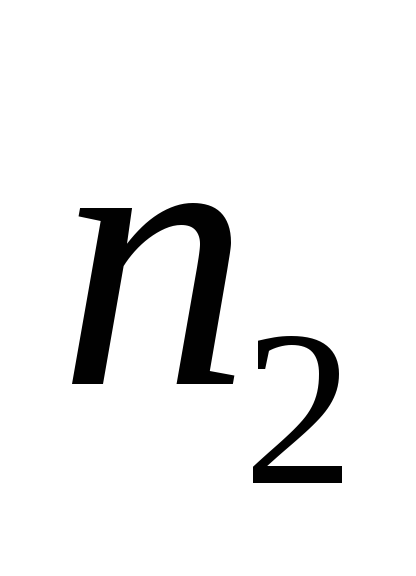 ,
сопротивление
,
сопротивление и
и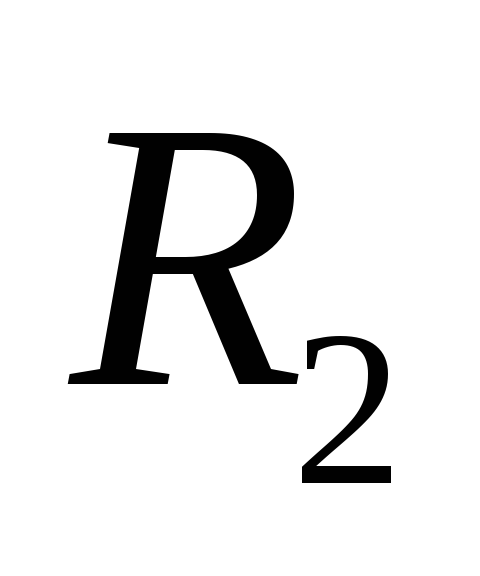 созданы слоями
созданы слоями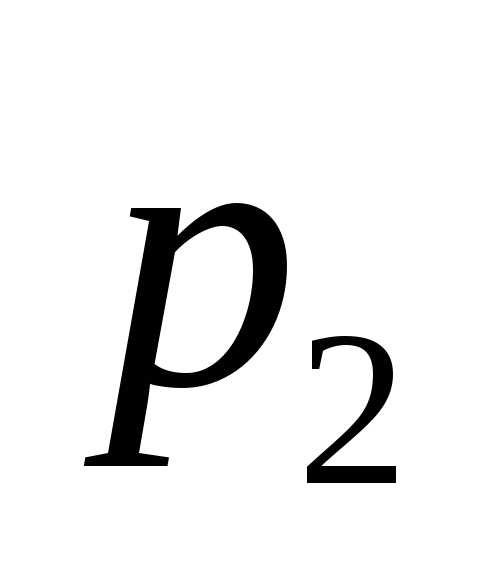 и
и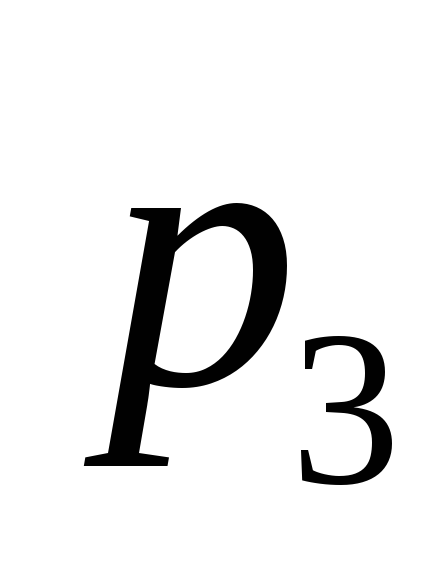 ,
слои
,
слои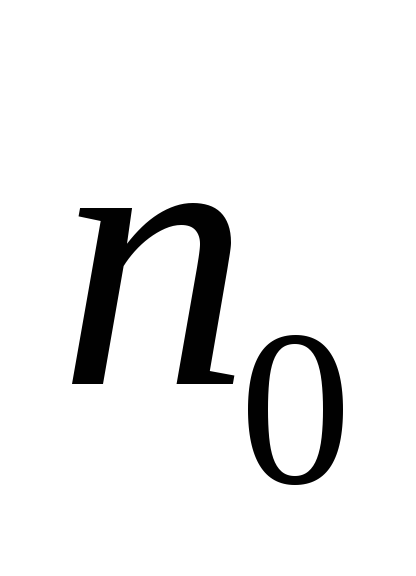 и
и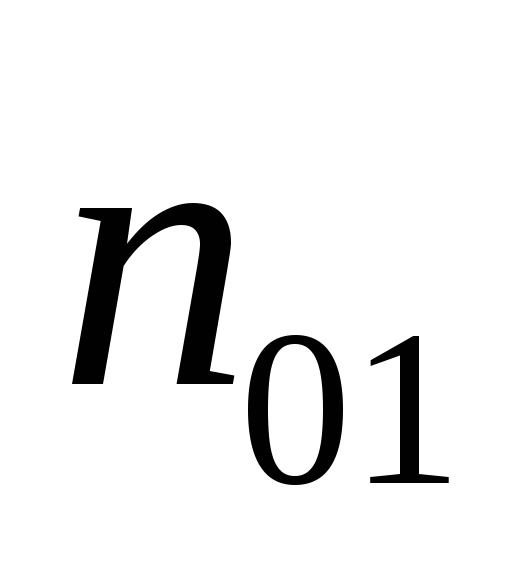 — изолируют резисторы от транзистора
при запертыхp-nпереходах, слои
— изолируют резисторы от транзистора
при запертыхp-nпереходах, слои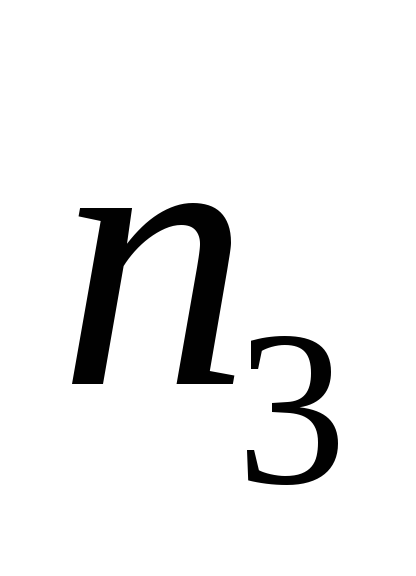 и
и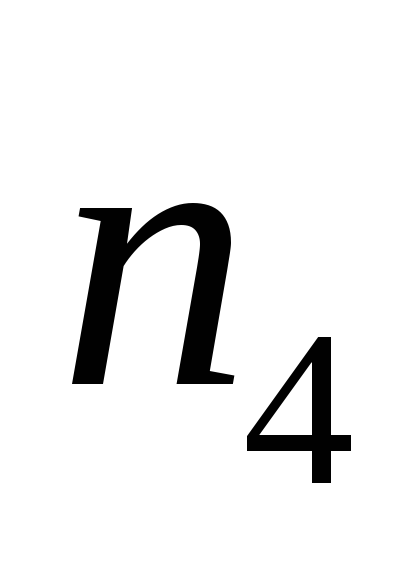 определяют толщину слоев
определяют толщину слоев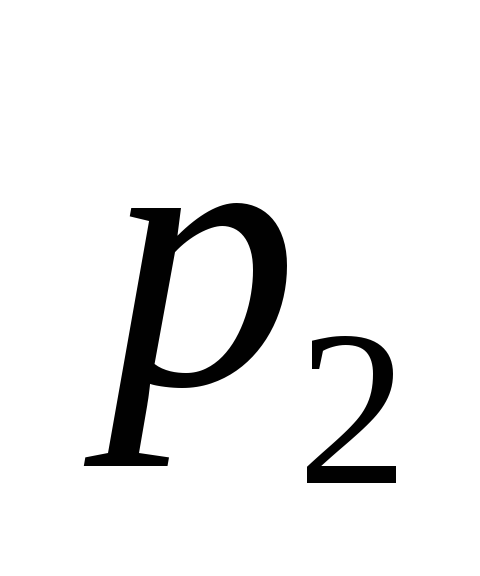 и
и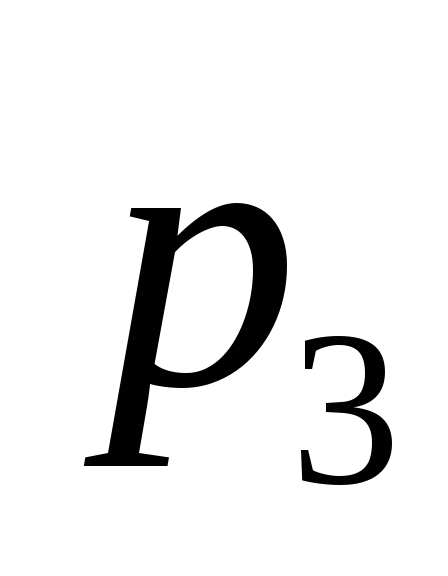 ,
и , соответственно, величину
,
и , соответственно, величину и
и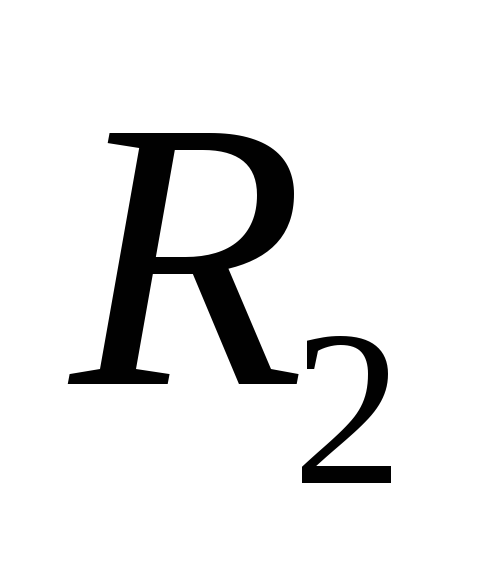 .
Включение усилительного каскада в
электрическую цепь осуществляется с
помощью контактов 1,2,Э,Б,К.
.
Включение усилительного каскада в
электрическую цепь осуществляется с
помощью контактов 1,2,Э,Б,К.
Дифференцирующая rl-цепь
Дифференцирующая RL-цепь показана на рис 2-33 б, выходное напряжение снимается с индуктивностьюL. В этом случае при рассмотрении процессов в цепи при дифференцировании прямоугольного импульса следует воспользоваться первым законом коммутации. Все рассуждения аналогичны тем, какие были при рассмотренииRC- цепей.
Следует отметить, что RL-цепи используются режеRC-цепей, так как конструктивно сложнее.
В связи с тем, что электрический фильтр
является четырехполюсником, то для
описания его используют коэффициент
передачи(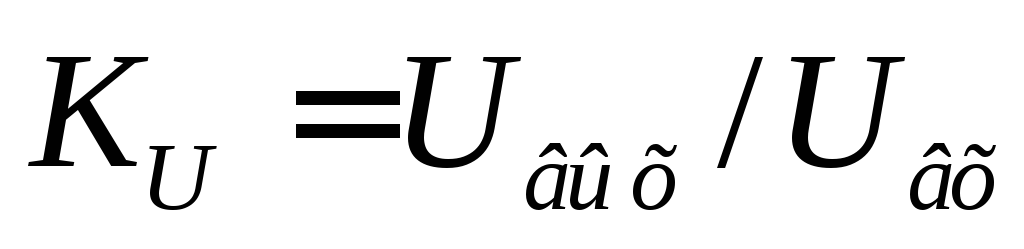 ),
с помощью которого можно определять
диапазон пропускных частот. (рис 13-36).В
том случае, если
),
с помощью которого можно определять
диапазон пропускных частот. (рис 13-36).В
том случае, если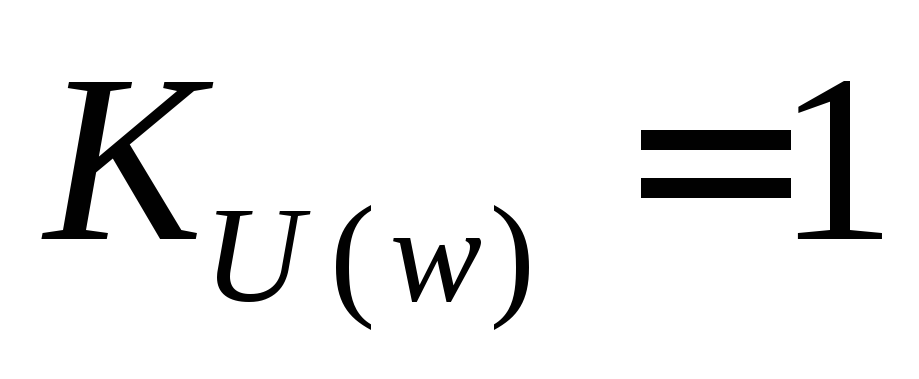 ,
то электрический импульс с высокой
частотой будет пропускаться электрическим
фильтром. Если
,
то электрический импульс с высокой
частотой будет пропускаться электрическим
фильтром. Если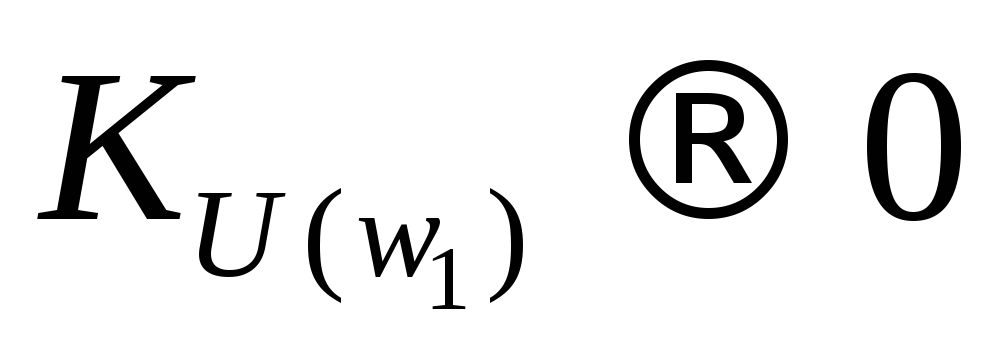 , то электрический сигнал с низкой
частотой будет подавляться.
, то электрический сигнал с низкой
частотой будет подавляться.

Рис 13-36. Амплитудно-частотная характеристика ФВЧ.
Рассмотрим АЧХ интегрирующей RCцепи, изображённом на рис. 2-39а
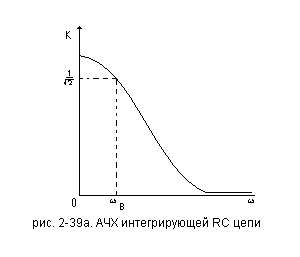
Частный
коэффициент передачи интегрирующей
цепи равен 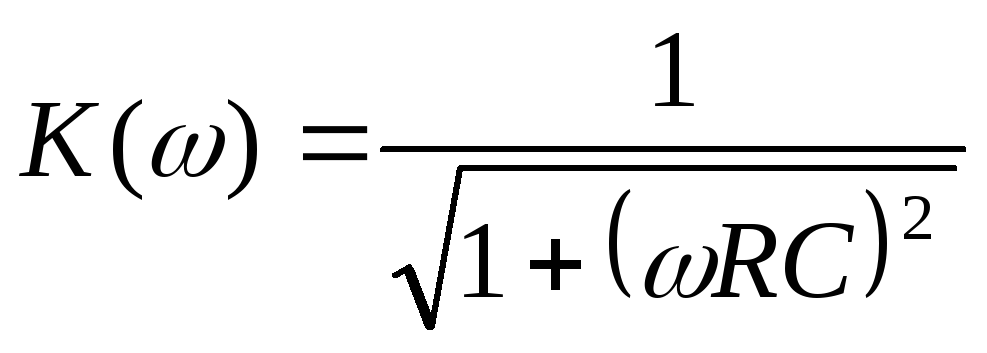
Если приравнять 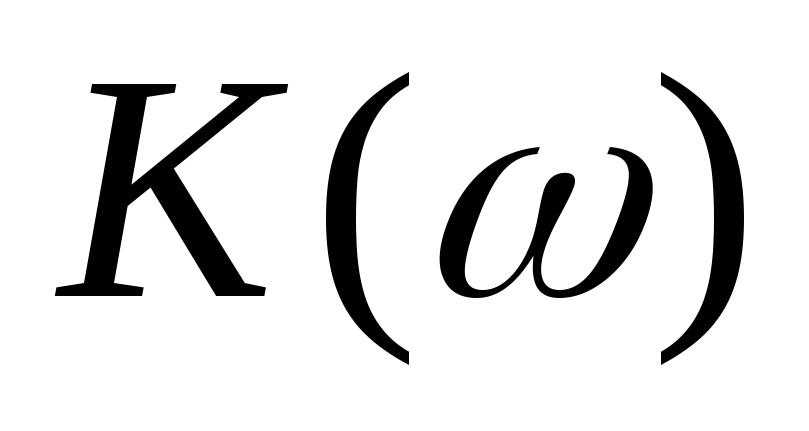 к 1/
к 1/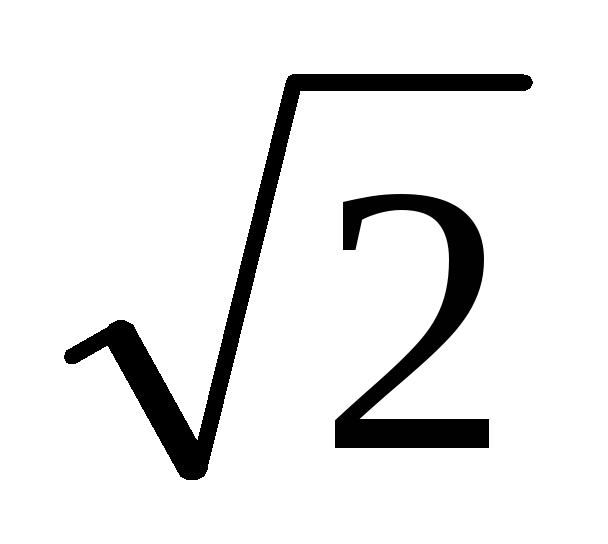 ,
то получают нижнюю границу полосы
пропускания интегрирующейRC-цепи
,
то получают нижнюю границу полосы
пропускания интегрирующейRC-цепи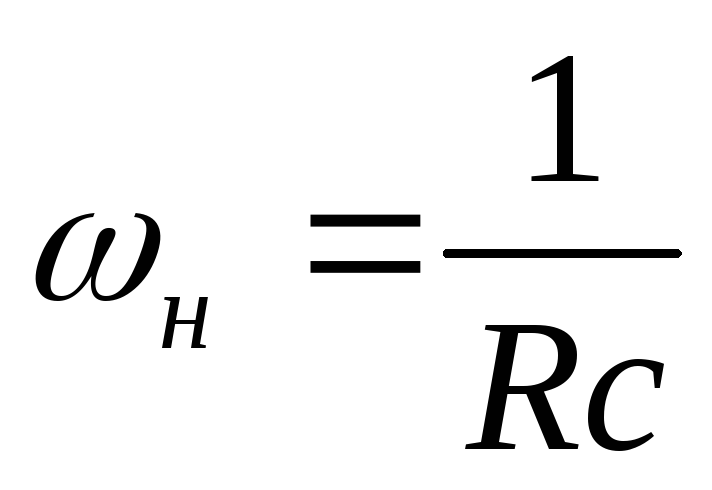 ,
,
и это объясняет, что интегрирующая RCцепь не пропускает высокочастотных составляющих спектров входных сигналов. Также фильтры ещё называют сглаживающими или низкочастотными фильтрами
Интегрирующие цепи(фнч) (фильтр высоких частот)
Сигнал
на выходе интегрирующей цепи пропорционален
интегралу входного сигнала 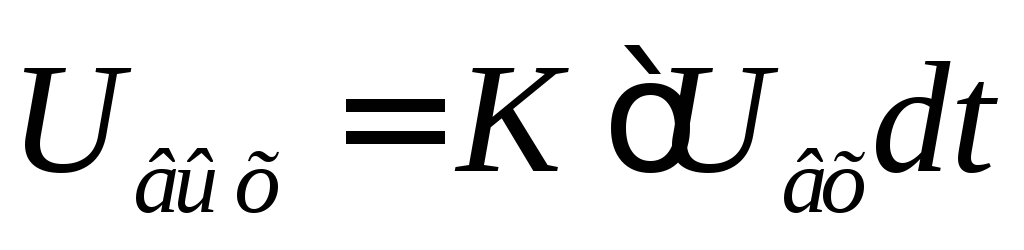 .
.
Схемы
реальных интегрирующих цепей показаны
на рис 13-37 а и 13-37 б. Коэффициент
пропорциональности К в уравнении 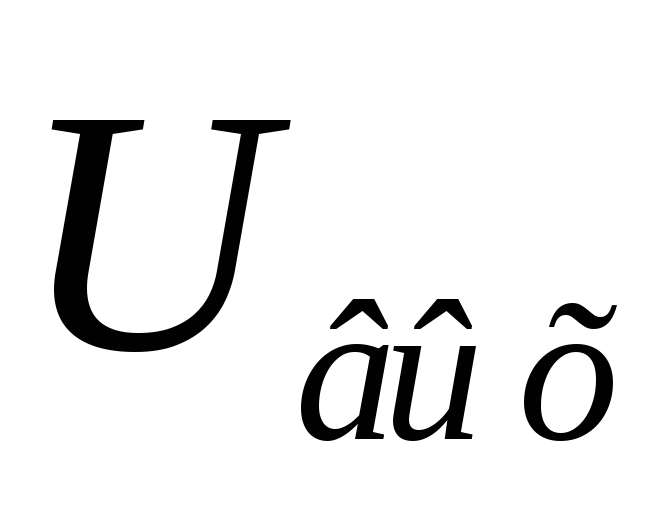 есть величина, обратная времени цепи
есть величина, обратная времени цепи (
(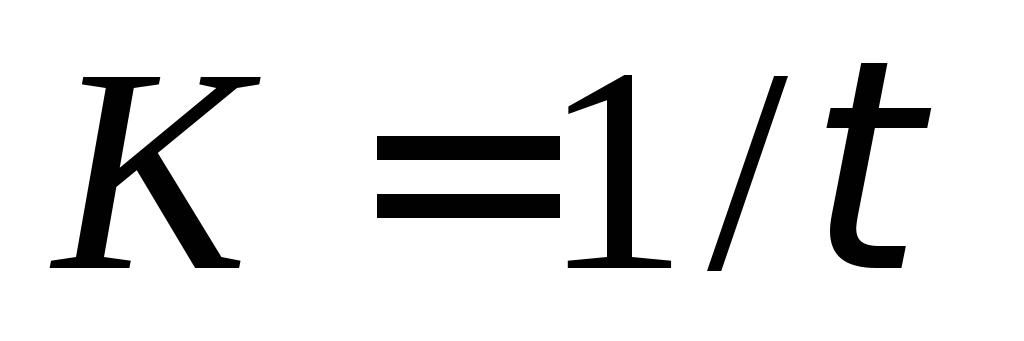 ).
Для цепиRC
).
Для цепиRC =RC,
для цепиRL
=RC,
для цепиRL =L/R.
=L/R.
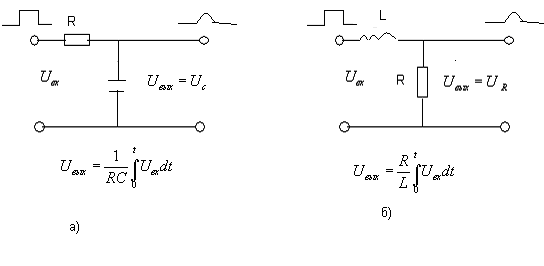
Рис 13-37. Схемы интегрирующих цепей.
Интегрирующая rc-цепь.
Эта цепь является также четырехполюсником.
В
интегрирующий RC-цепи
выходной сигнал (импульс напряжения)
снимается с конденсатораC,
то есть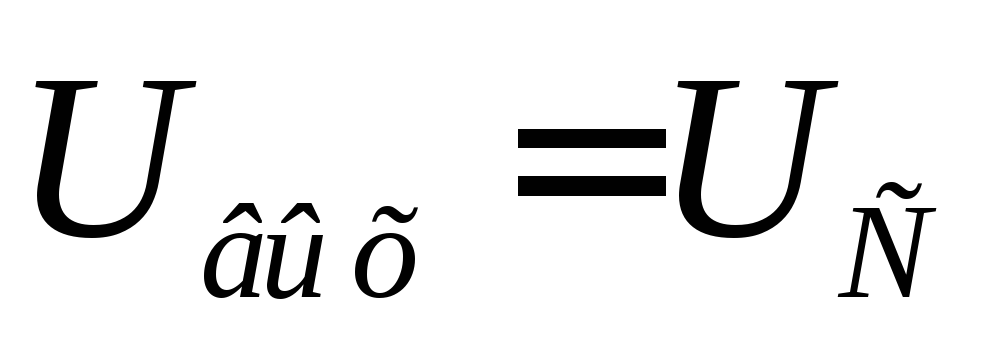 (смотри
рис 13-37 а).
(смотри
рис 13-37 а).
Рассмотрим,
какую форму будет иметь сигнал на выходе,
если интегрируемый сигнал (входной
импульс) будет прямоугольной формы. При
этом сначала, положим, что длительность
входного импульса 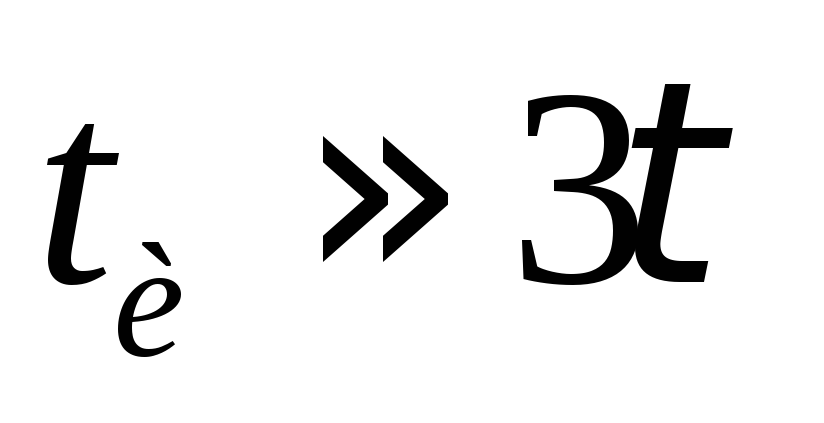 (смотри
рис 13-38).
(смотри
рис 13-38).
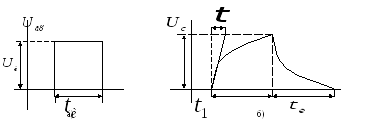
Рис
13-38. Интегрируемый сигнал (а) и сигнал
на выходе интегрирующей RC-цепи
(б),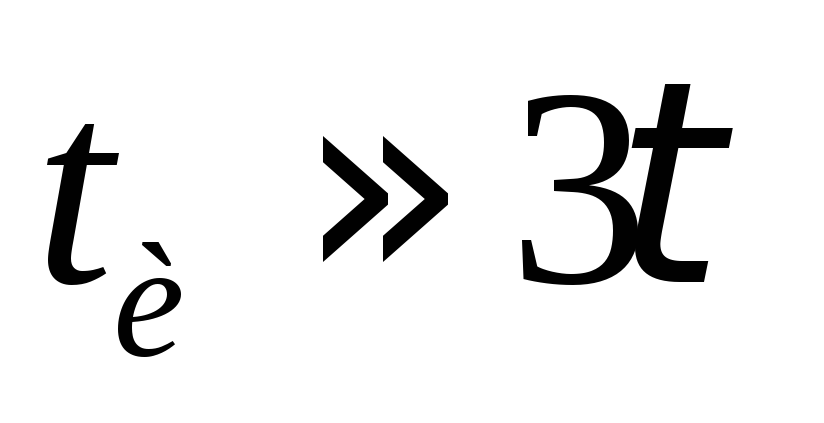 .
.
В момент
включения цепи (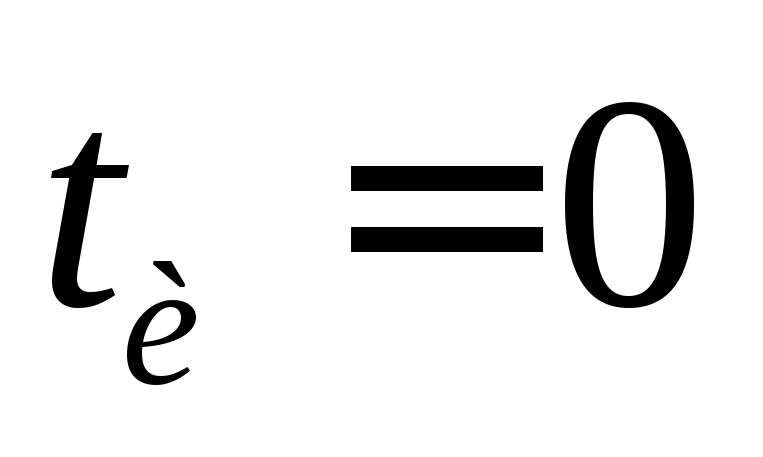 )
напряжение на выходе в силу второго
закона коммутации будет равно 0, а затем
конденсатор будет заряжаться и напряжение
на нем будет возрастать по экспоненциальному
закону
)
напряжение на выходе в силу второго
закона коммутации будет равно 0, а затем
конденсатор будет заряжаться и напряжение
на нем будет возрастать по экспоненциальному
закону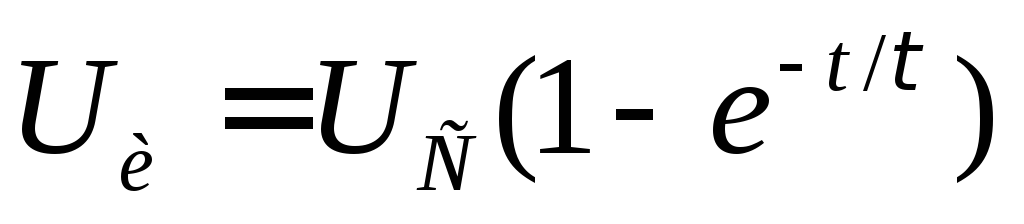 .
.
По
истечению времени действия импульсов  конденсатор полностью зарядится и в
момент времени
конденсатор полностью зарядится и в
момент времени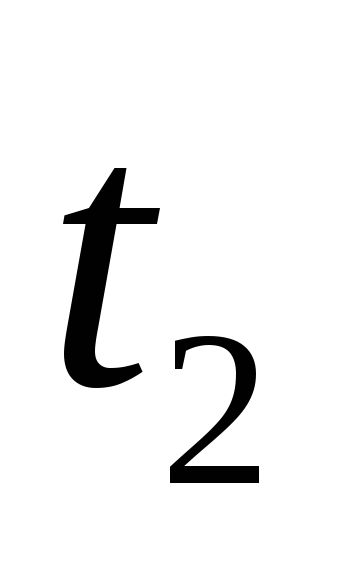 напряжение на нем достигнет
напряжение на нем достигнет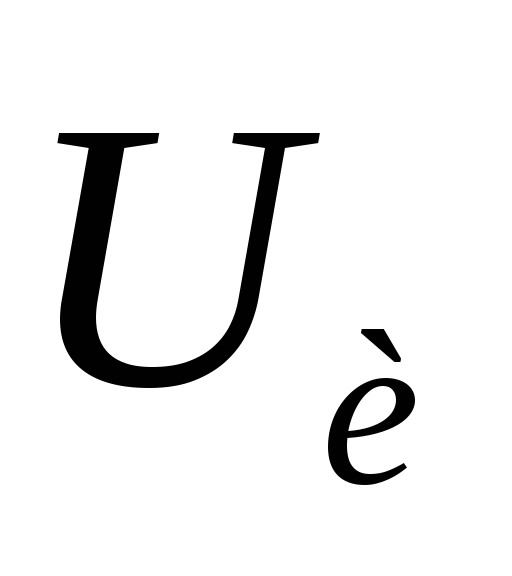 .
С этого момента действие импульса на
цель прекращается, конденсатор начинает
разряжаться по экспоненциальному закону
.
С этого момента действие импульса на
цель прекращается, конденсатор начинает
разряжаться по экспоненциальному закону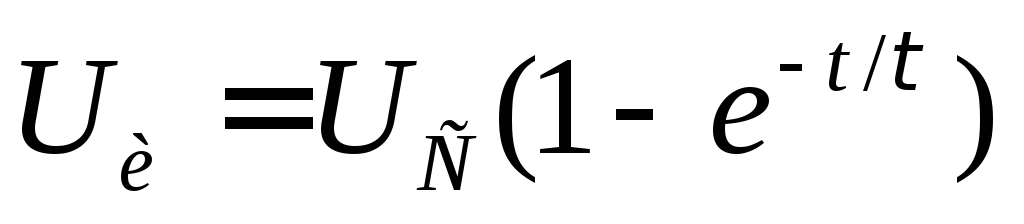 и через время, равное
и через время, равное ,
напряжение на нем спадет до 0.
,
напряжение на нем спадет до 0.
Если 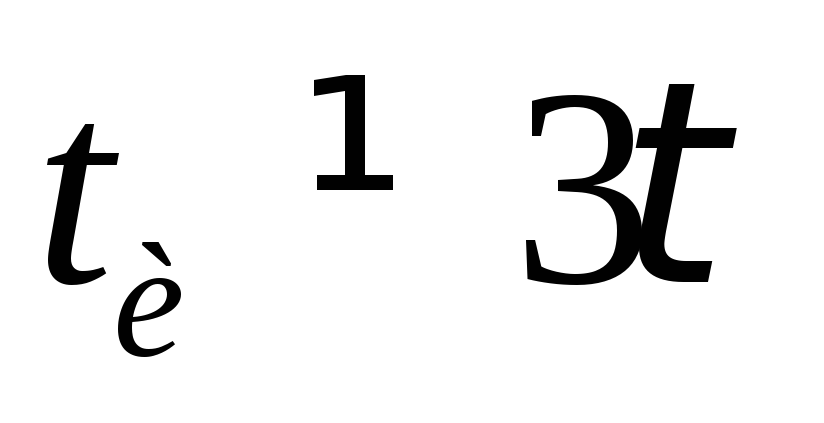 ,
амплитуда и форма импульсов на выходе
будут другими. Такие импульсы
,
амплитуда и форма импульсов на выходе
будут другими. Такие импульсы
Показаны
на рис 2-39 б для случая, когда 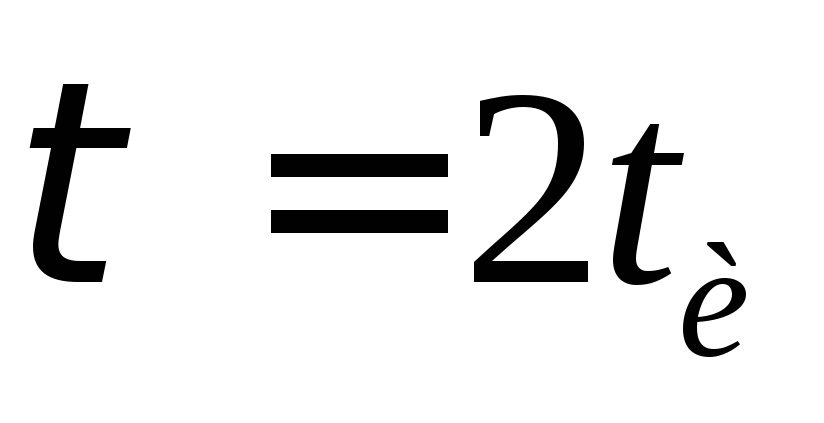 ,на
рис 13-39 в для случая когда
,на
рис 13-39 в для случая когда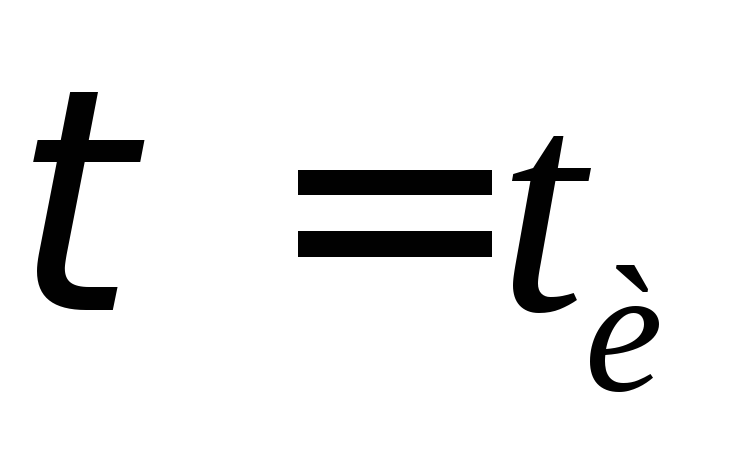 и нас рис13-39 г
и нас рис13-39 г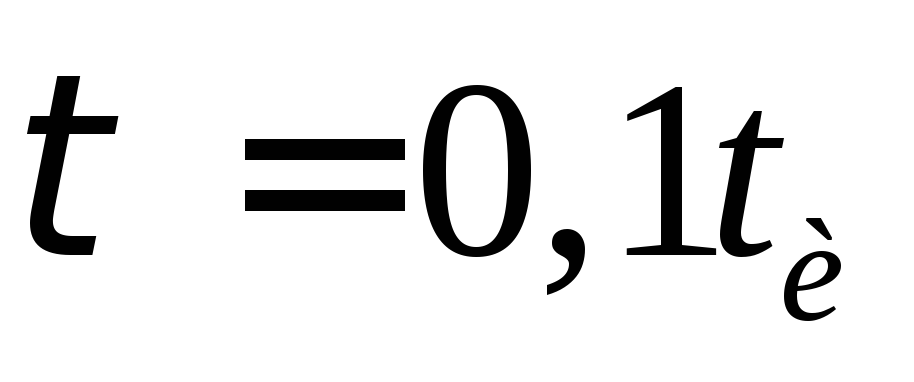 .
.

Рис
13-39. Изменение формы импульса на выходе
интегрирующей цепи в зависимости от
соотношения между  и
и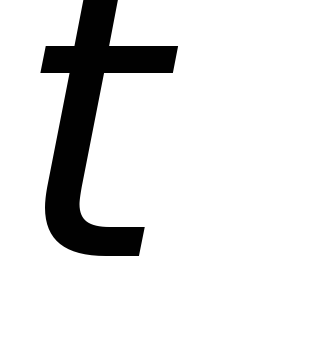 .
.
Из
формул и рис 13-39 следует, что в случае,
если постоянная времени цепи  ,
амплитуда выходного сигнала (импульса)
будет меньше амплитуды входного сигнала.
И она будет тем меньше, чем больше
,
амплитуда выходного сигнала (импульса)
будет меньше амплитуды входного сигнала.
И она будет тем меньше, чем больше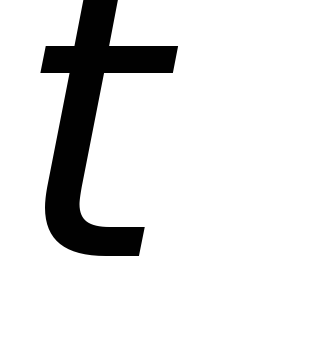 .
.
Для
обеспечения более точного интегрирования
постоянная времени цепи 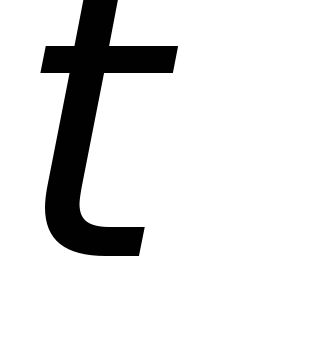 выбирается такой величины, чтобы она
была значительно больше длительности
интегрируемого импульса
выбирается такой величины, чтобы она
была значительно больше длительности
интегрируемого импульса .
При этом учитывается уменьшение
амплитуды. Наиболее точное интегрирование,
как и дифференцирование, можно осуществить
с помощью операционных усилителей.
.
При этом учитывается уменьшение
амплитуды. Наиболее точное интегрирование,
как и дифференцирование, можно осуществить
с помощью операционных усилителей.
Интегрирующая и дифференцирующая цепи RC
Интегрирующая цепь RC
Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C, представленную на рисунке.
Элементы R и C соединены последовательно,
значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R.
Напряжение на выводах резистора обозначим UR.
Тогда будет иметь место равенство:
Проинтегрируем последнее выражение . Интеграл левой части уравнения будет равен Uout + Const .
Перенесём постоянную составляющую Const в правую часть с тем же знаком.
В правой части постоянную времени RC вынесем за знак интеграла:
В итоге получилось, что выходное напряжение Uout прямо-пропорционально интегралу напряжения на выводах резистора,
следовательно, и входному току Iin.
Постоянная составляющая Const не зависит от номиналов элементов цепи.
Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения Uout от интеграла входного Uin, необходима пропорциональность входного напряжения от входного тока.
Нелинейное соотношение Uin/Iin во входной цепи вызвано тем,
что заряд и разряд конденсатора происходит по экспоненте e-t/τ, которая наиболее нелинейна при t/τ ≥ 1,
то есть, когда значение t соизмеримо или больше τ.
Здесь t — время заряда или разряда конденсатора в пределах периода.
τ = RC — постоянная времени — произведение величин R и C.
Если взять номиналы RC цепи, когда τ будет значительно больше t,
тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным,
что обеспечит необходимую пропорциональность между входным напряжением и током.
Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала,
тогда основная и значительная часть входного напряжения будет падать на выводах резистора, обеспечивая в достаточной степени линейную зависимость Uin/Iin ≈ R.
В таком случае выходное напряжение Uout будет с допустимой погрешностью пропорционально интегралу входного Uin.
Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.
В большинстве случаев, переменная составляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const, тогда номиналы RC можно выбирать по возможности большими, но с учётом входного сопротивления следующего каскада.
В качестве примера, сигнал с генератора — положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:
R = 10 kOhm, С = 1 uF. Тогда τ = RC = 10 mS.
В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно.
График показывает, что выходное напряжение на уровне постоянной составляющей 0.5в будет треугольной формы, потому как участки,
не меняющиеся во времени, для интеграла будут константой (обозначим её a), а интеграл константы будет линейной функцией. ∫adx = ax + Const. Величина константы a определит тангенса угла наклона линейной функции.
Проинтегрируем синусоиду, получим косинус с обратным знаком ∫sinxdx = -cosx + Const.
В данном случае постоянная составляющая Const = 0.
Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение.
Интеграл линейного участка функции — парабола. В простейшем варианте ∫xdx = x2/2 + Const.
Знак множителя определит направление параболы.
Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.
Рассмотрим в качестве интегратора Операционный Усилитель (ОУ) по схеме, показанной на рисунке.
С учётом бесконечно большого сопротивления ОУ и правила Кирхгофа здесь будет справедливо равенство:
Iin = IR = Uin/R = — IC.
Напряжение на входах идеального ОУ здесь равно нулю, тогда на выводах конденсатора UC = Uout = — Uin .
Следовательно, Uout определится, исходя из тока общей цепи.
При номиналах элементов RC, когда τ = 1 Sec,
выходное переменное напряжение будет равно по значению интегралу входного. Но, противоположно по знаку.
Идеальный интегратор-инвертор при идеальных элементах схемы.
Дифференцирующая цепь RC
Рассмотрим дифференциатор с применением Операционного Усилителя.
Идеальный ОУ здесь обеспечит равенство токов IR = — IC по правилу Кирхгофа.
Напряжение на входах ОУ равно нулю, следовательно, выходное напряжение Uout = UR = — Uin = — UC .
Исходя из производной заряда конденсатора, закона Ома и равенства значений токов в конденсаторе и резисторе, запишем выражение:
Uout = RIR = — RIC = — RC(dUC /dt) = — RC(dUin /dt)
Отсюда видим, что выходное напряжение Uout пропорционально производной заряда конденсатора dUin /dt , как скорости изменения входного напряжения.
При величине постоянной времени RC, равной единице, выходное напряжение будет равно по значению производной входного напряжения, но противоположно по знаку. Следовательно, рассмотренная схема дифференцирует и инвертирует входной сигнал.
Производная константы равна нулю, поэтому постоянная составляющая при дифференцировании на выходе будет отсутствовать.
В качестве примера, подадим на вход дифференциатора сигнал треугольной формы.
На выходе получим прямоугольный сигнал.
Производная линейного участка функции будет константой, знак и величина которой определится наклоном линейной функции.
Для простейшей дифференцирующей цепочки RC из двух элементов используем пропорциональную зависимость выходного напряжения от производной напряжения на выводах конденсатора.
Uout = RIR = RIC = RC(dUC /dt)
Если взять номиналы элементов RC, чтобы постоянная времени была на 1-2 порядка меньше длины периода, тогда отношение приращения входного напряжения к приращению времени в пределах периода может определять скорость изменения входного напряжения в определённой степени точно. В идеале это приращение должно стремиться к нулю. В таком случае основная часть входного напряжения будет падать на выводах конденсатора, а выходное будет составлять незначительную часть от входного, поэтому для вычислений производной такие схемы практически не используются.
Наиболее часто дифференцирующие и интегрирующие цепи RC применяют для изменения длины импульса в логических и цифровых устройствах.
В таких случаях номиналы RC рассчитывают по экспоненте e-t/RC исходя из длины импульса в периоде и требуемых изменений.
Например, ниже на рисунке показано, что длина импульса Ti на выходе интегрирующей цепочки
увеличится на время 3τ. Это время разряда конденсатора до 5% амплитудного значения.
На выходе дифференцирующей цепи амплитудное напряжение после подачи импульса появляется мгновенно,
так как на выводах разряженного конденсатора оно равно нулю.
Далее следует процесс заряда и напряжение на выводах резистора убывает. За время 3τ оно уменьшится до 5% амплитудного значения.
Здесь 5% — величина показательная. В практических расчётах этот порог определится входными параметрами применяемых логических элементов.
Замечания и предложения принимаются и приветствуются!
Дифференцирующая rl-цепь
Дифференцирующая RL-цепь показана на рис 2-33 б, выходное напряжение снимается с индуктивностьюL. В этом случае при рассмотрении процессов в цепи при дифференцировании прямоугольного импульса следует воспользоваться первым законом коммутации. Все рассуждения аналогичны тем, какие были при рассмотренииRC- цепей.
Следует отметить, что RL-цепи используются режеRC-цепей, так как конструктивно сложнее.
В связи с тем, что электрический фильтр
является четырехполюсником, то для
описания его используют коэффициент
передачи(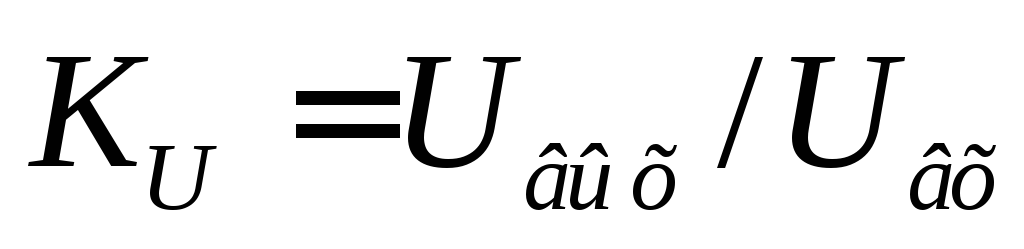 ),
с помощью которого можно определять
диапазон пропускных частот. (рис 13-36).В
том случае, если
),
с помощью которого можно определять
диапазон пропускных частот. (рис 13-36).В
том случае, если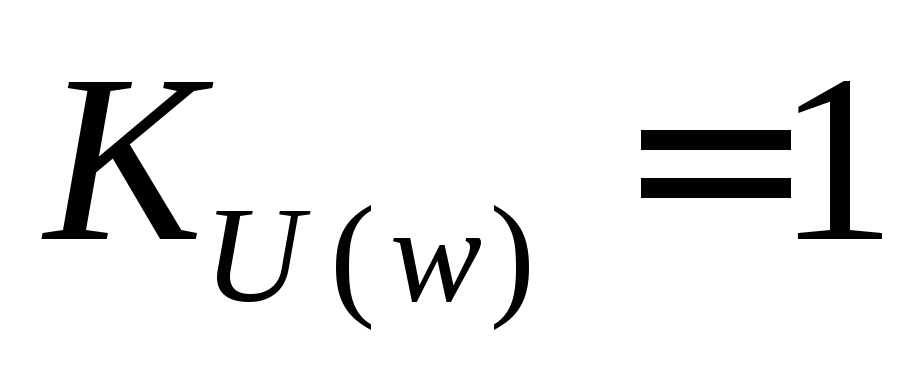 ,
то электрический импульс с высокой
частотой будет пропускаться электрическим
фильтром. Если
,
то электрический импульс с высокой
частотой будет пропускаться электрическим
фильтром. Если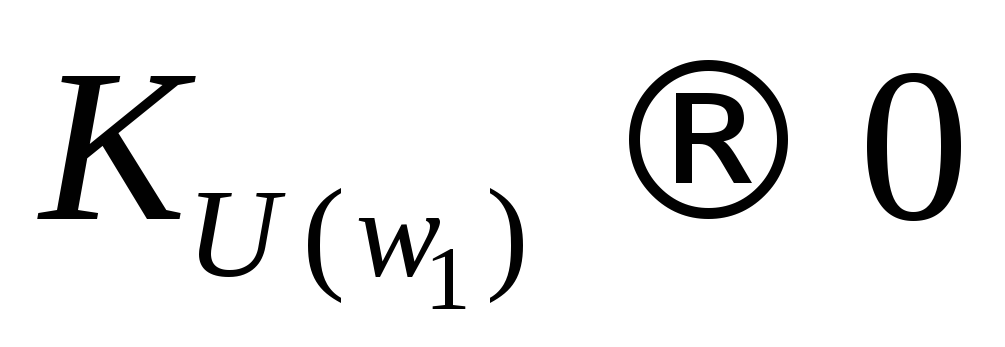 , то электрический сигнал с низкой
частотой будет подавляться.
, то электрический сигнал с низкой
частотой будет подавляться.

Рис 13-36. Амплитудно-частотная характеристика ФВЧ.
Рассмотрим АЧХ интегрирующей RCцепи, изображённом на рис. 2-39а
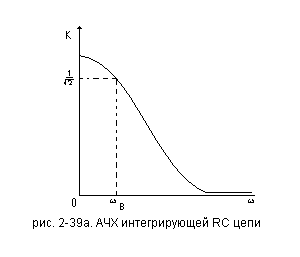
Частный
коэффициент передачи интегрирующей
цепи равен 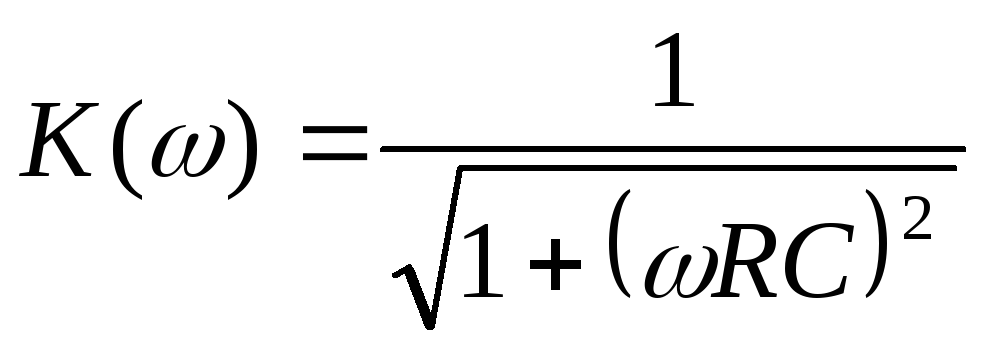
Если приравнять 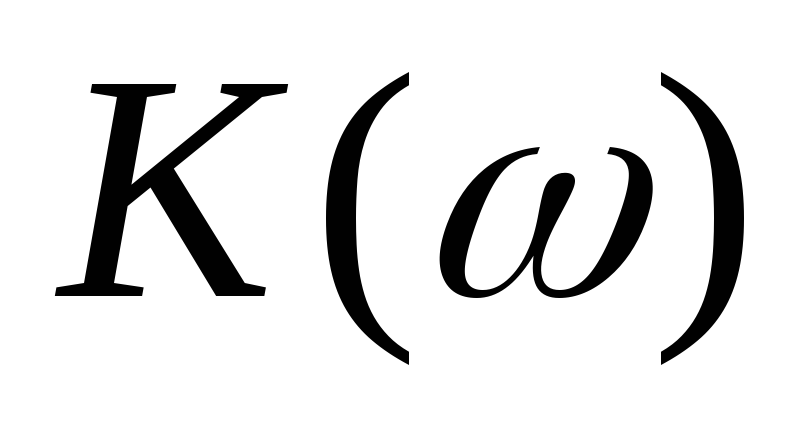 к 1/
к 1/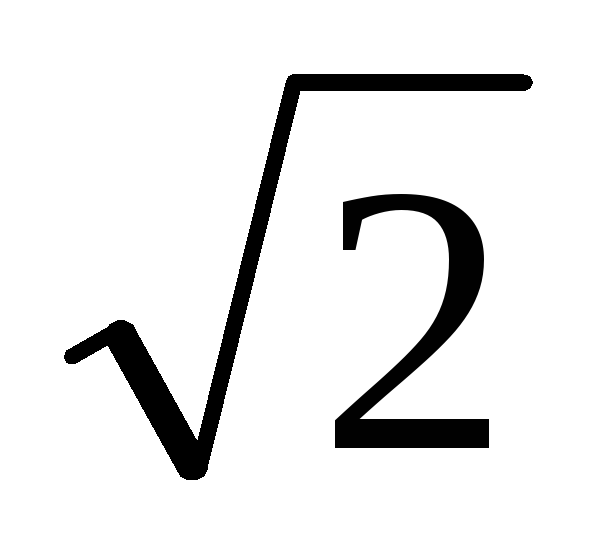 ,
то получают нижнюю границу полосы
пропускания интегрирующейRC-цепи
,
то получают нижнюю границу полосы
пропускания интегрирующейRC-цепи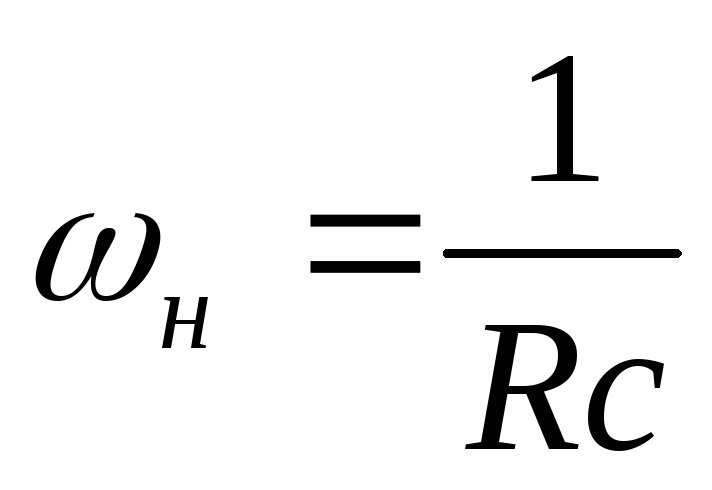 ,
,
и это объясняет, что интегрирующая RCцепь не пропускает высокочастотных составляющих спектров входных сигналов. Также фильтры ещё называют сглаживающими или низкочастотными фильтрами
Интегрирующие цепи(фнч) (фильтр высоких частот)
Сигнал на выходе интегрирующей цепи пропорционален интегралу входного сигнала .
Схемы
реальных интегрирующих цепей показаны
на рис 13-37 а и 13-37 б. Коэффициент
пропорциональности К в уравнении 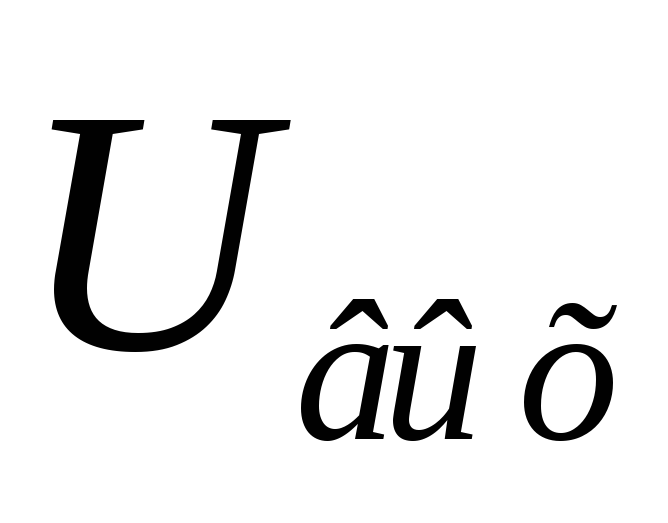 есть величина, обратная времени цепи
есть величина, обратная времени цепи (
(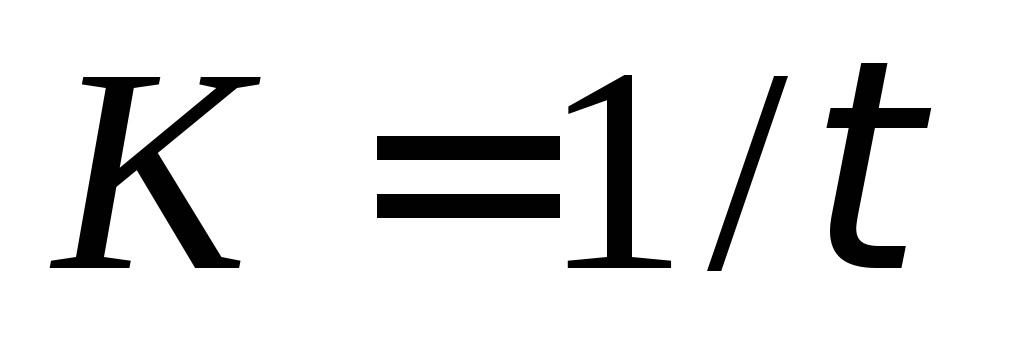 ).
Для цепиRC
).
Для цепиRC =RC,
для цепиRL
=RC,
для цепиRL =L/R.
=L/R.
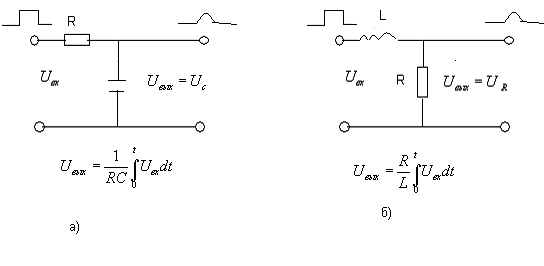
Рис 13-37. Схемы интегрирующих цепей.
Интегрирующая rc-цепь.
Эта цепь является также четырехполюсником.
В
интегрирующий RC-цепи
выходной сигнал (импульс напряжения)
снимается с конденсатораC,
то есть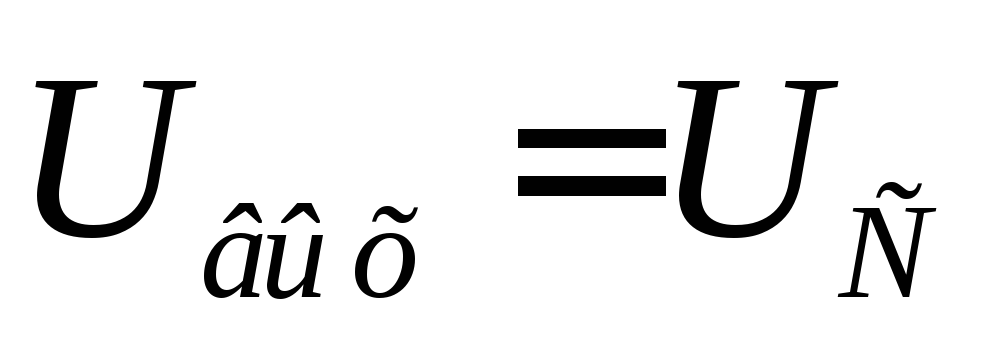 (смотри
рис 13-37 а).
(смотри
рис 13-37 а).
Рассмотрим,
какую форму будет иметь сигнал на выходе,
если интегрируемый сигнал (входной
импульс) будет прямоугольной формы. При
этом сначала, положим, что длительность
входного импульса 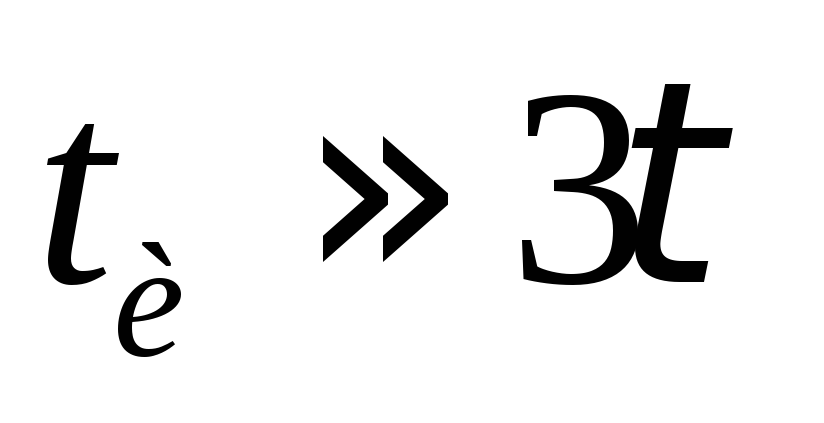 (смотри
рис 13-38).
(смотри
рис 13-38).
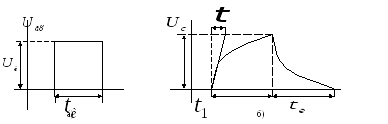
Рис
13-38. Интегрируемый сигнал (а) и сигнал
на выходе интегрирующей RC-цепи
(б),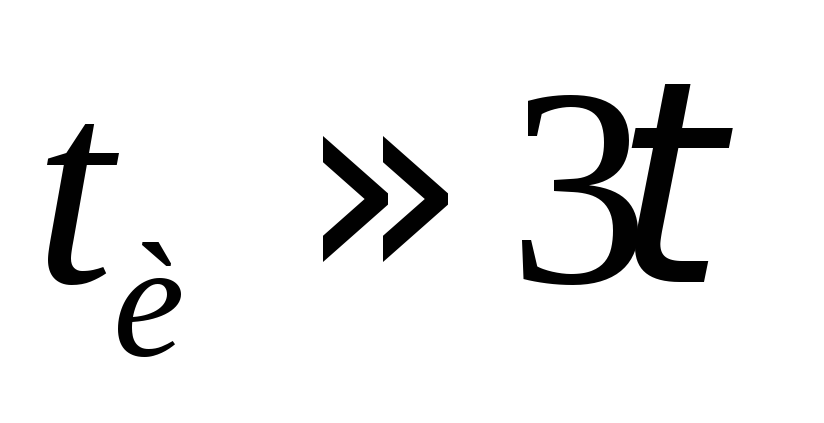 .
.
В момент
включения цепи (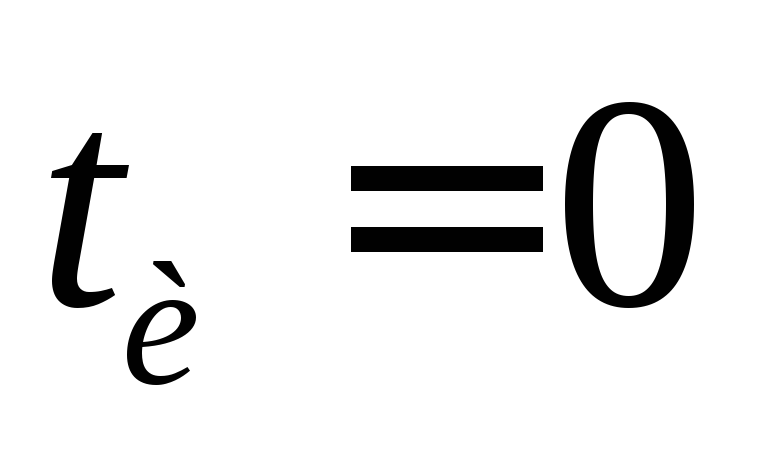 )
напряжение на выходе в силу второго
закона коммутации будет равно 0, а затем
конденсатор будет заряжаться и напряжение
на нем будет возрастать по экспоненциальному
закону
)
напряжение на выходе в силу второго
закона коммутации будет равно 0, а затем
конденсатор будет заряжаться и напряжение
на нем будет возрастать по экспоненциальному
закону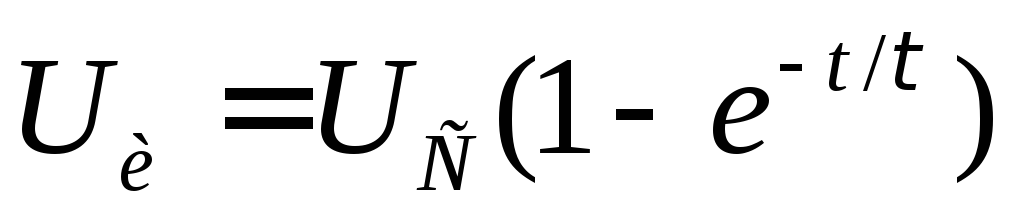 .
.
По
истечению времени действия импульсов  конденсатор полностью зарядится и в
момент времени
конденсатор полностью зарядится и в
момент времени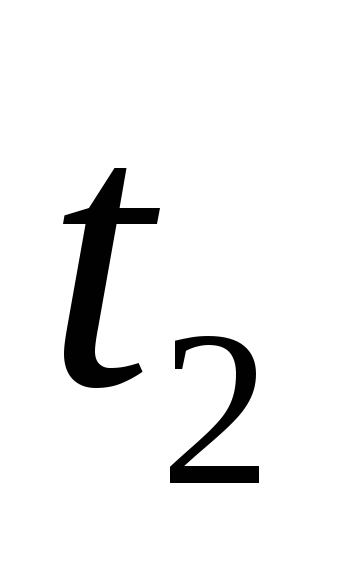 напряжение на нем достигнет
напряжение на нем достигнет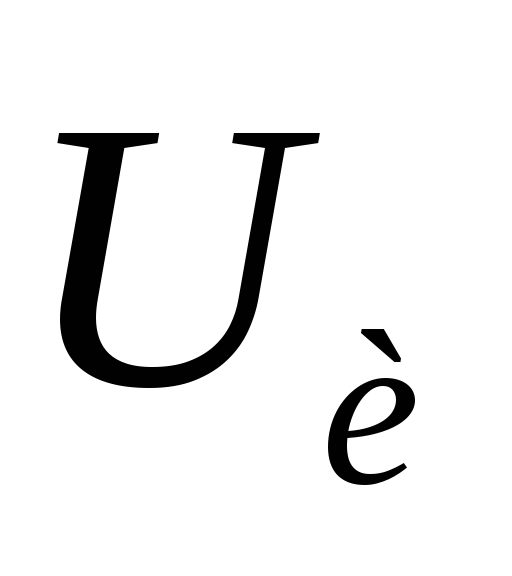 .
С этого момента действие импульса на
цель прекращается, конденсатор начинает
разряжаться по экспоненциальному закону
.
С этого момента действие импульса на
цель прекращается, конденсатор начинает
разряжаться по экспоненциальному закону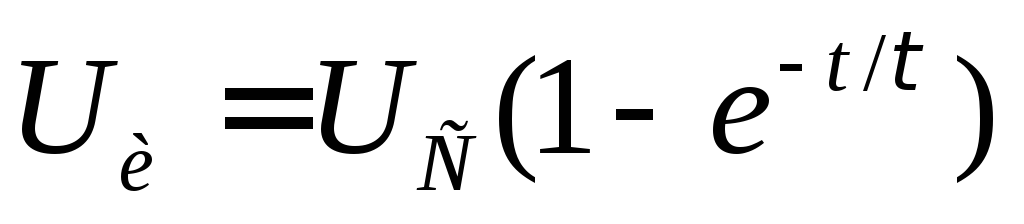 и через время, равное
и через время, равное ,
напряжение на нем спадет до 0.
,
напряжение на нем спадет до 0.
Если 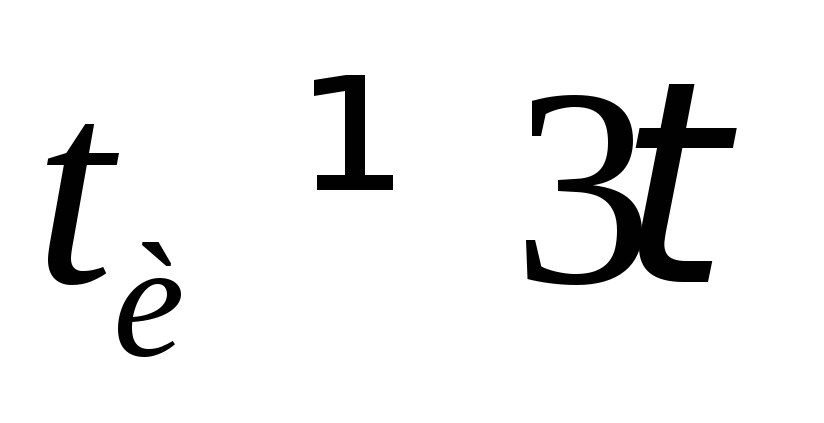 ,
амплитуда и форма импульсов на выходе
будут другими. Такие импульсы
,
амплитуда и форма импульсов на выходе
будут другими. Такие импульсы
Показаны
на рис 2-39 б для случая, когда 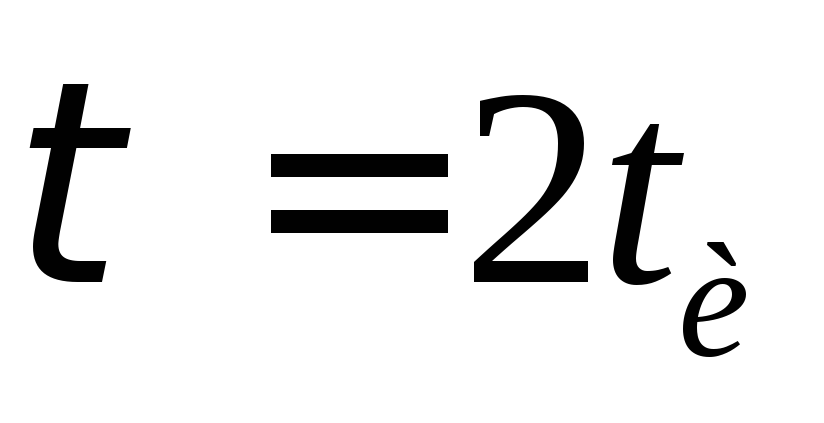 ,на
рис 13-39 в для случая когда
,на
рис 13-39 в для случая когда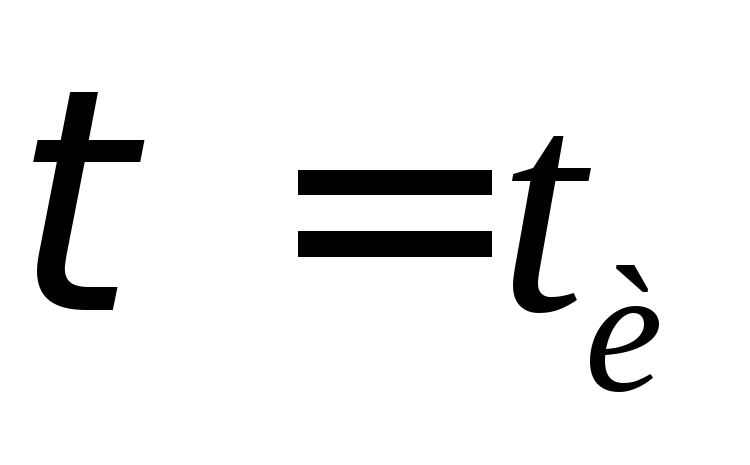 и нас рис13-39 г
и нас рис13-39 г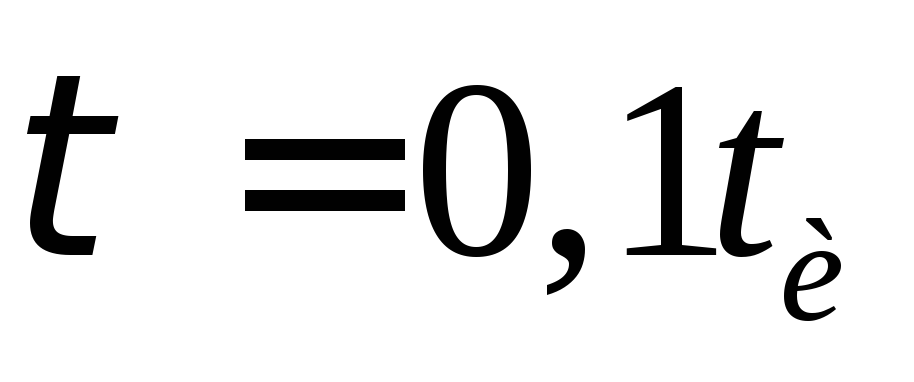 .
.

Рис
13-39. Изменение формы импульса на выходе
интегрирующей цепи в зависимости от
соотношения между  и
и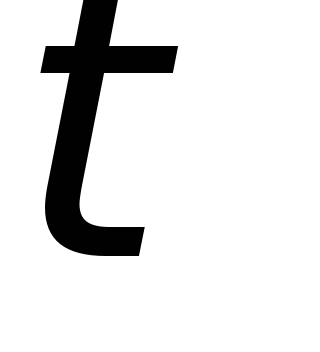 .
.
Из
формул и рис 13-39 следует, что в случае,
если постоянная времени цепи  ,
амплитуда выходного сигнала (импульса)
будет меньше амплитуды входного сигнала.
И она будет тем меньше, чем больше
,
амплитуда выходного сигнала (импульса)
будет меньше амплитуды входного сигнала.
И она будет тем меньше, чем больше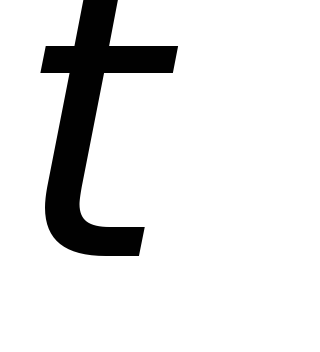 .
.
Для
обеспечения более точного интегрирования
постоянная времени цепи 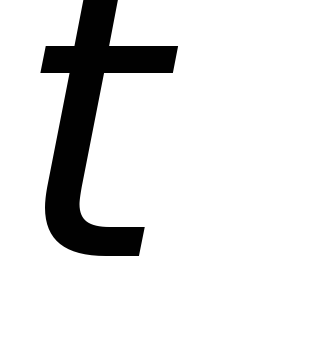 выбирается такой величины, чтобы она
была значительно больше длительности
интегрируемого импульса
выбирается такой величины, чтобы она
была значительно больше длительности
интегрируемого импульса .
При этом учитывается уменьшение
амплитуды. Наиболее точное интегрирование,
как и дифференцирование, можно осуществить
с помощью операционных усилителей.
.
При этом учитывается уменьшение
амплитуды. Наиболее точное интегрирование,
как и дифференцирование, можно осуществить
с помощью операционных усилителей.
Интегрирующие и дифференцирующие цепи
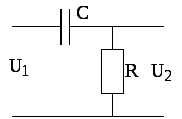
Рисунок 8.1 ‑ДифференцирующаяRC—цепь
Напряжение на резисторе R (рис.8.1)
UR=U2=IR,
где 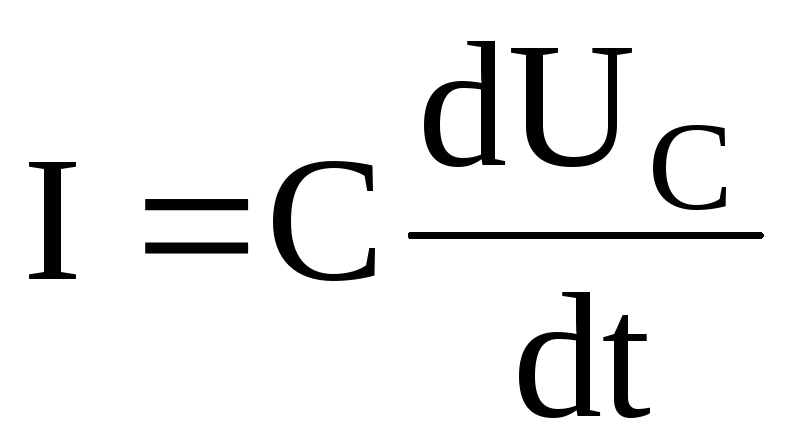 ,
,
тогда 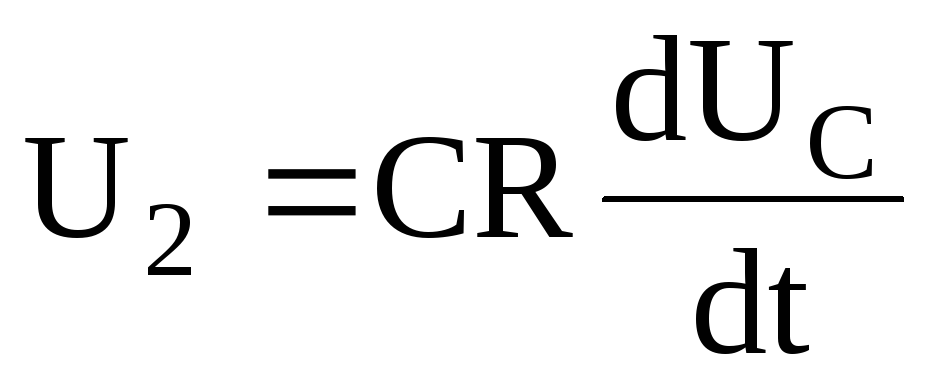 .
.
Зная, что UC = U1 – U2,
получим
для 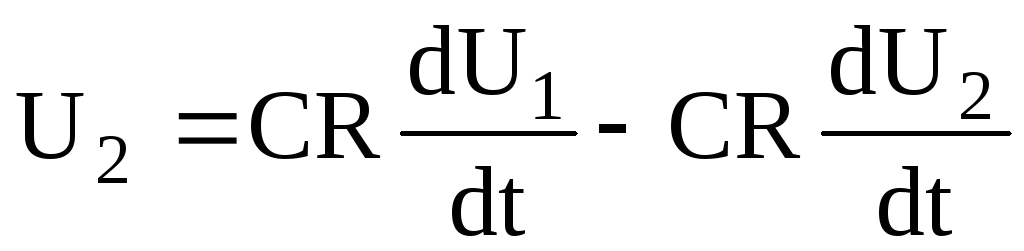 .
.
При малых частотах и постоянных токах UR – величина малая, тогда
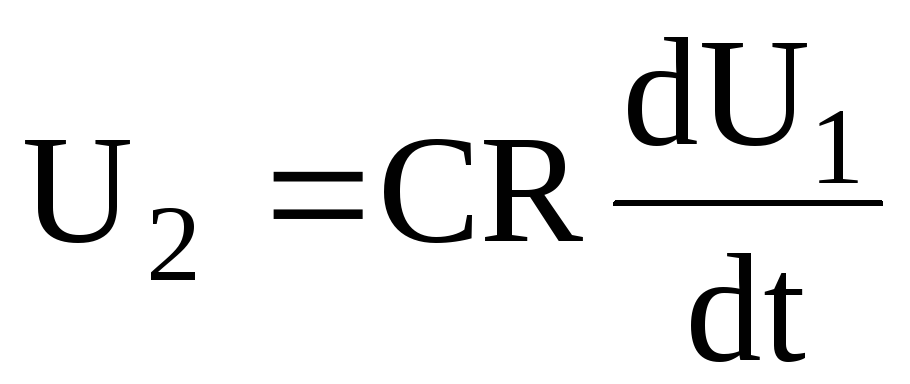 ,
,
т.е. напряжение на выходе цепи пропорционально дифференциалу U1, поэтому ее называют дифференцирующей (рис.8.1).
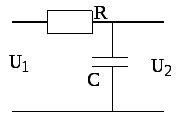
Рисунок 8.2 – Интегрирующая RC—цепь
Ток в цепи конденсатора (рис.8.2)
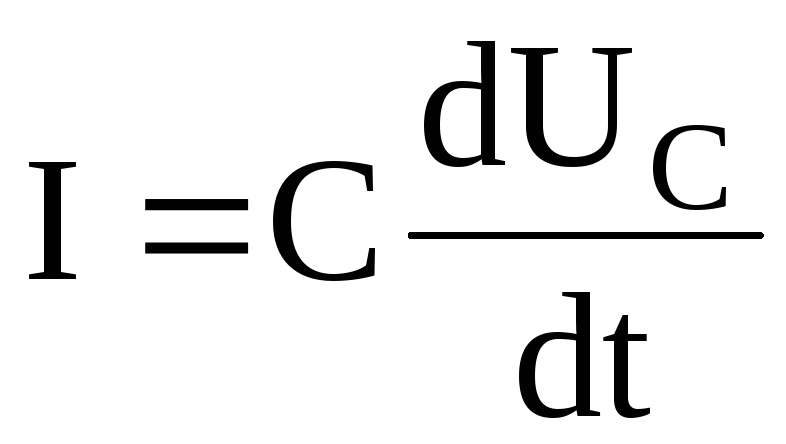 ,
,
а
напряжение 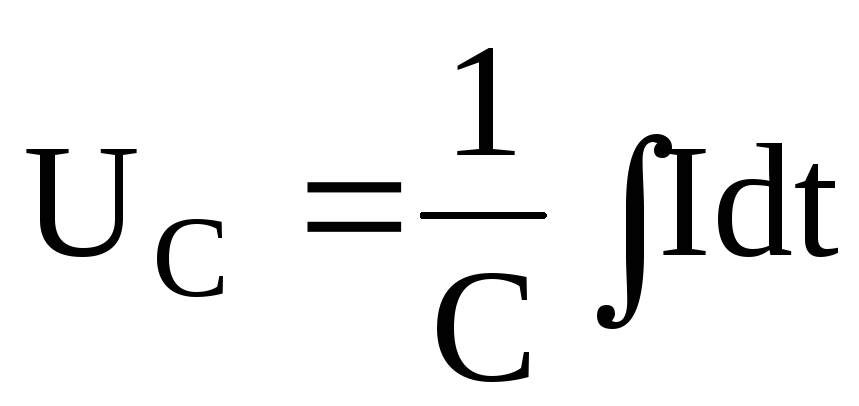 ,
,
где 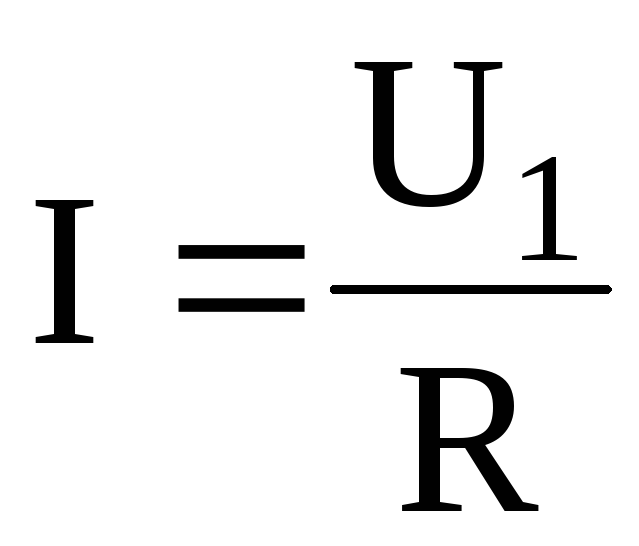 ,
,
тогда 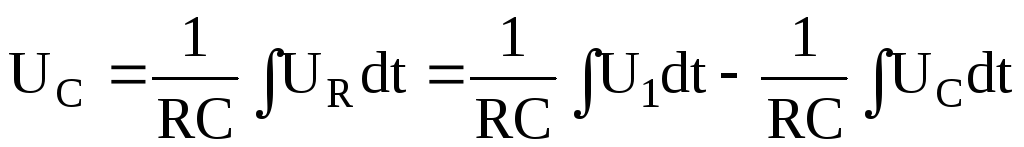 .
.
При 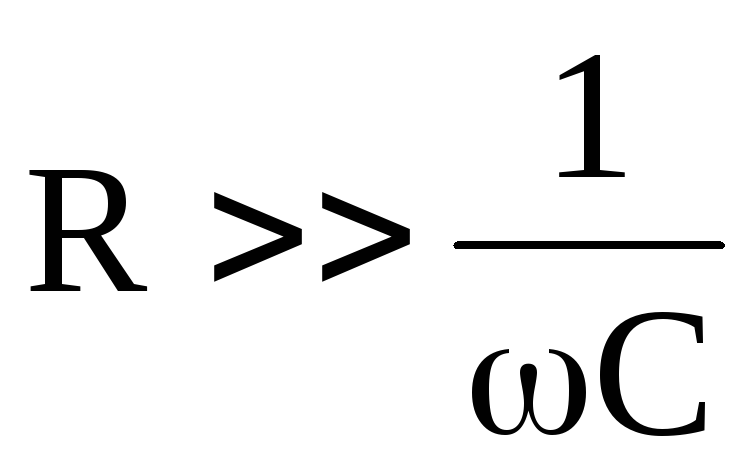 ,
,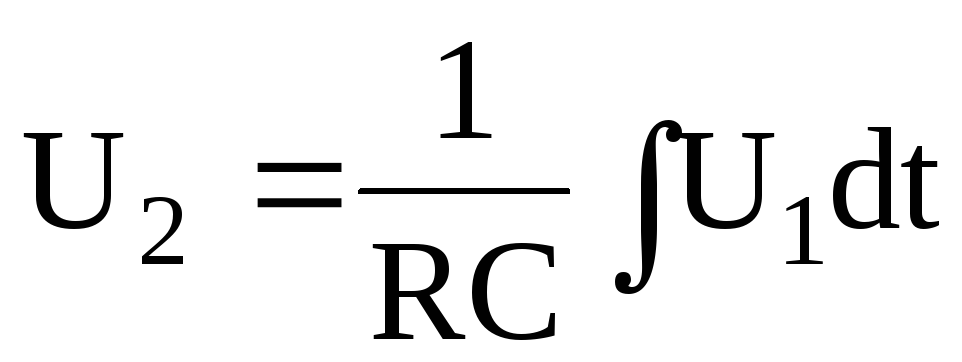 ,
,
т.е. напряжение на выходе RC – цепи пропорционально интегралу от входного напряжения. Такая RC – цепь именуется интегрирующей.
Постоянная времени
Произведение τ = RC называют постоянной времени цепи.
Если R измерять в Омах, а С – в Фарадах, то произведение RC будет измеряться в секундах. Для конденсатора емкостью 1 мкФ, подключенного к резистору сопротивлением 1 кОм, постоянная времени составляет 1 мс, если конденсатор был предварительно заряжен и напряжение на нём составляет 1 В, то при подключении резистора в цепи появится ток, равный 1 мА.
При условии t >> RC, напряжение на выходе интегрирующей цепочки практически равно выходному напряжению. Следует запомнить правило пяти RC (или пяти τ): за время равное пяти постоянным времени, конденсатор заряжается или разряжается на 99%.
Интегрирующая (иногда её называют сглаживающая) цепочка при определенных условиях может выполнять функцию интегрирующего звена.
Дифференцирующая цепочка в зависимости от своих параметров может выполнять функции разделительного звена, укорачивающей или дифференцирующей цепочки.
Эффективность рассматриваемых цепочек зависит от соотношения между постоянной времени τ = RC и периодом входного сигнала T, поступающего на цепочку.
Например, функция интегрирования выполняется тем лучше, чем сильнее выражено неравенство τ >T. При этом автоматически выполняется неравенство U2 < U1.
Функция
дифференцирования цепочкой, выполняется
тем лучше, чем сильнее выражено неравенство 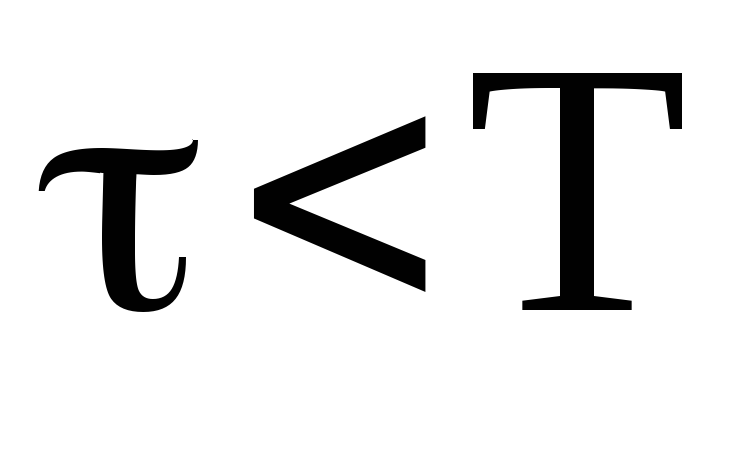 .
При этом, опять-таки, U2 <U1.
В этом заключается существенный
недостаток рассматриваемых цепочек,
они делят (уменьшают) амплитуду выходного
сигнала по сравнению с входным
.
При этом, опять-таки, U2 <U1.
В этом заключается существенный
недостаток рассматриваемых цепочек,
они делят (уменьшают) амплитуду выходного
сигнала по сравнению с входным
Эксперимент 1: Исследование дифференцрующей цепи
Соберите схему дифференциальной цепочки и подключите к её входу генератор прямоугольных импульсов как показано на рис. 8.3.
Амплитуда прямоугольных импульсов 5 В, скважность 2.
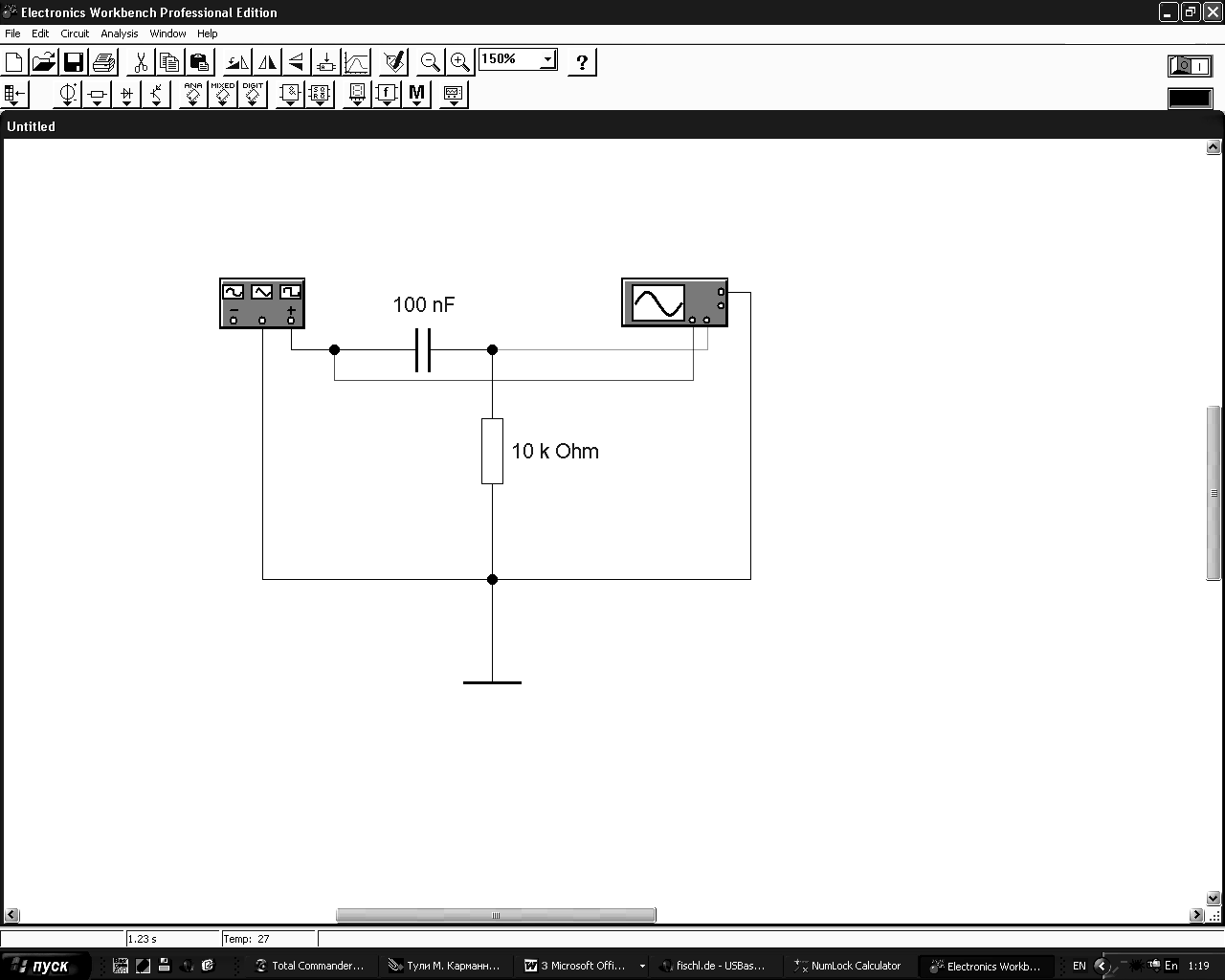
Рисунок 8.3 – Схема к эксперименту 1
В соответствии с номером варианта по табл.8.1 определите период следования импульсов, и для заданного значения емкости выберите три различных значения сопротивлений для того чтобы выполнялись условия Т = RC; Т = 0,1 RC; Т = 10 RC.
Таблица 8.1 ‑ Характеристика входного сигнала и емкость конденсатора
№ варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
f, Гц | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 850 | 900 | 950 |
C, нФ | 100 | 50 | 10 | 20 | 100 | 50 | 10 | 20 | 100 | 50 |
Получите и сохраните осциллограммы входного и выходных сигналов для различных значений выбранных сопротивлений, по осциллограмме определите период входного сигнала, длительность входного положительного импульса и длительность выходного положительного импульса, амплитуду входного и выходного положительных импульсов. Получите АЧХ дифференциальной цепочки.
Расчеты представьте в таблице 8.2.
Таблица 8.2 Результаты эксперимента 1
R, Ом | f, Гц | C, нФ | Tвх, c | tвх, c | tвых, c | Uвх | Uвых |
37. Интегрирующие цепи. Область применения. Принципиальные электрические схемы. Анализ работы цепи при воздействии сигналов различной формы. Активные интегрирующие цепи
Цепь называется интегрирующей, если напряжение на выходе пропорционально интегралу от напряжения на входе.

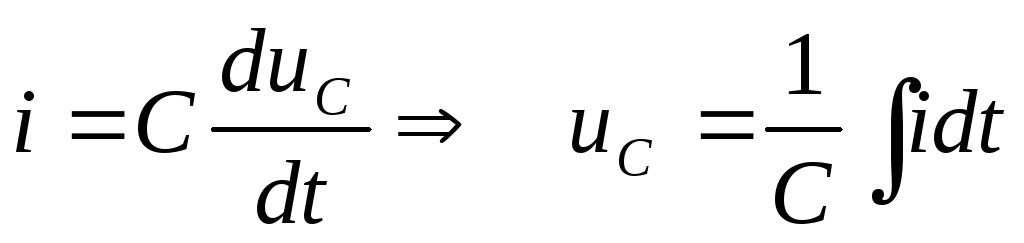
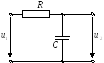
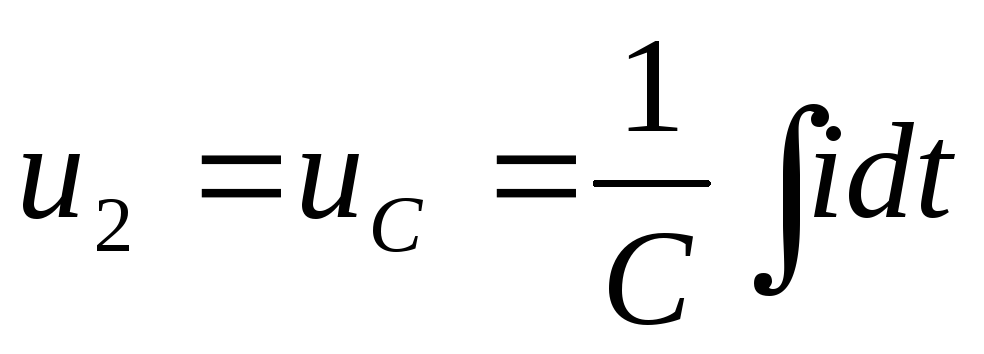
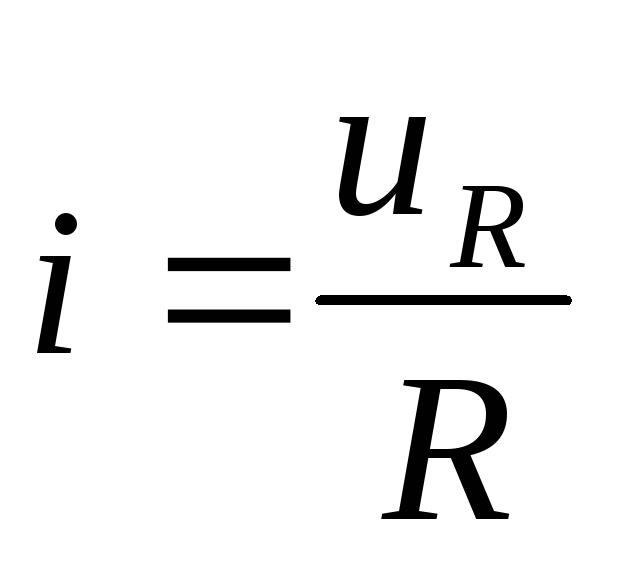
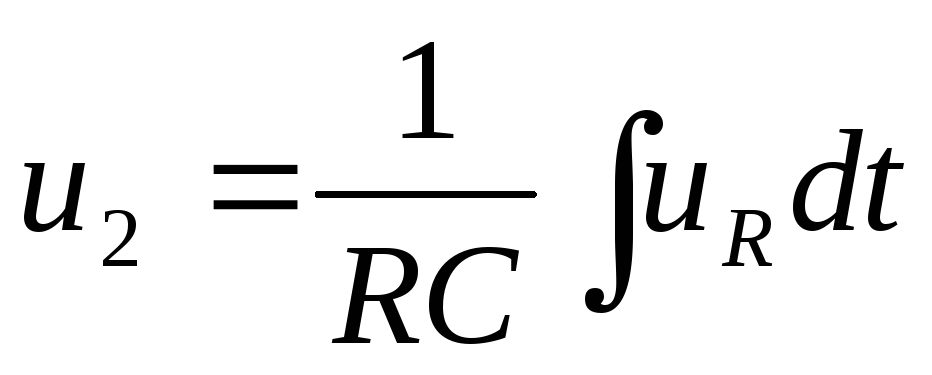
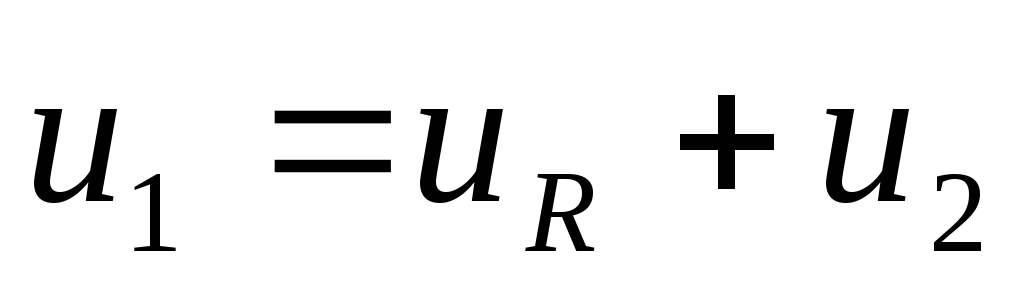
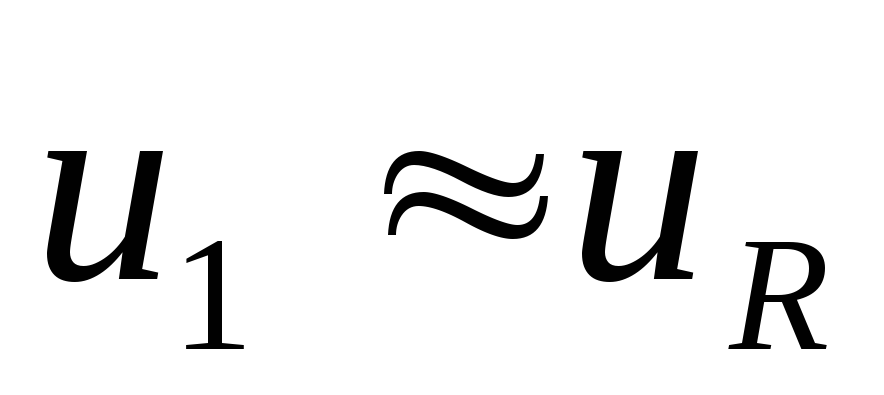 ,
если
,
если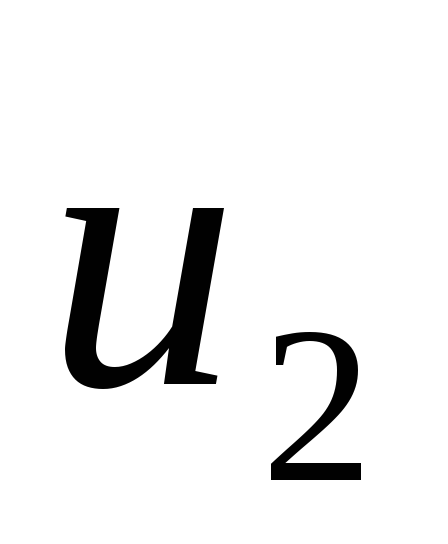 — мало.
— мало.
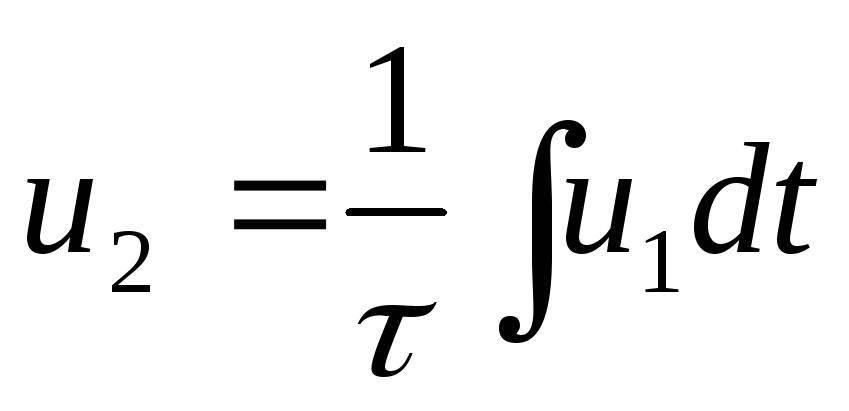
Выводы:цепь RC интегрирует при условии:
1. 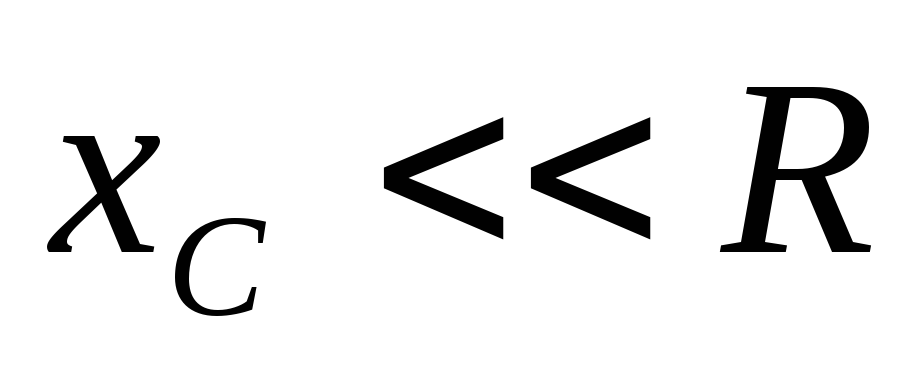
На практике 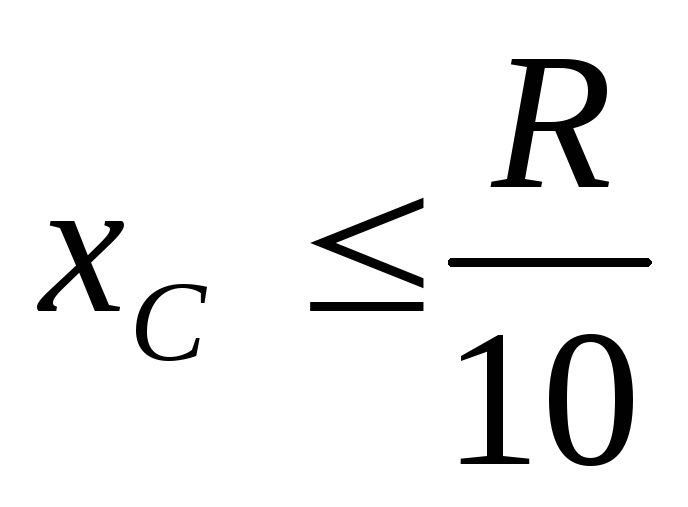
2. 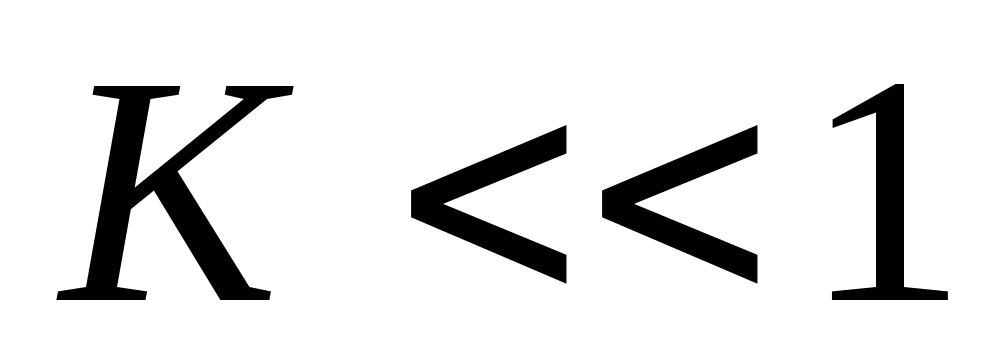
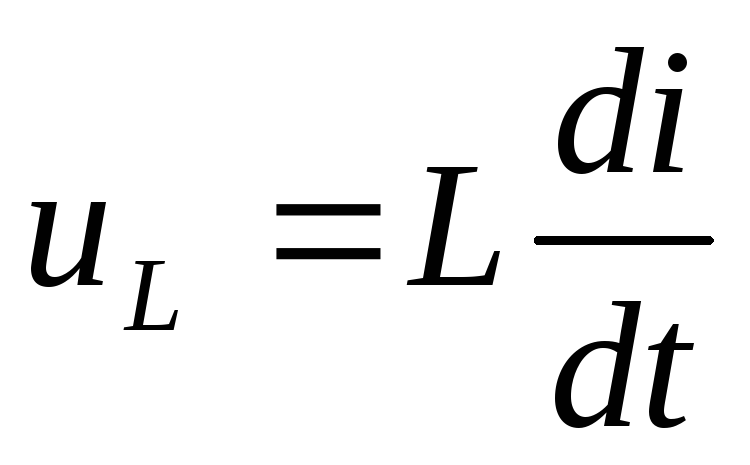

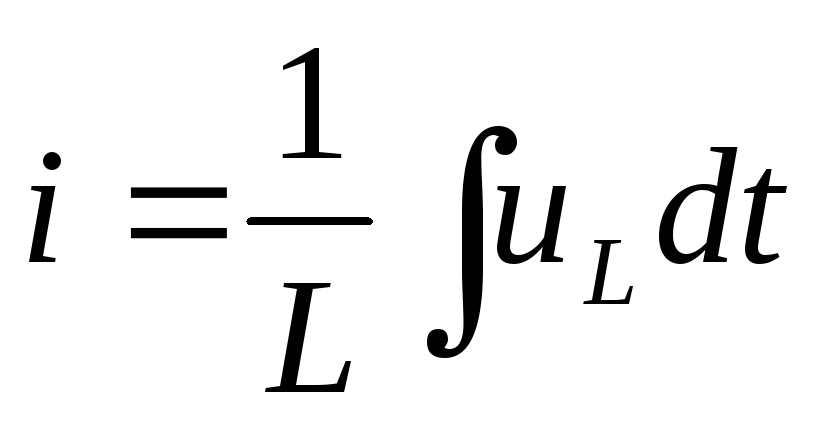
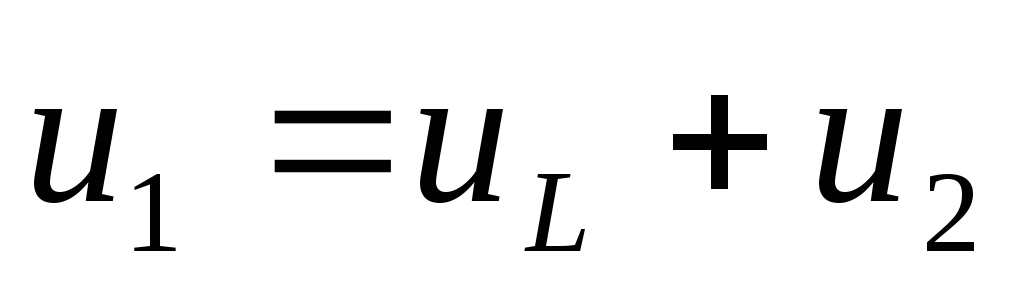
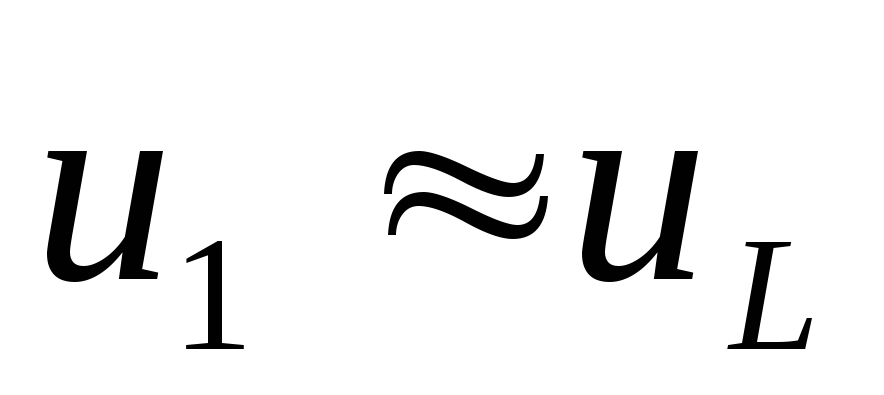 ,
если
,
если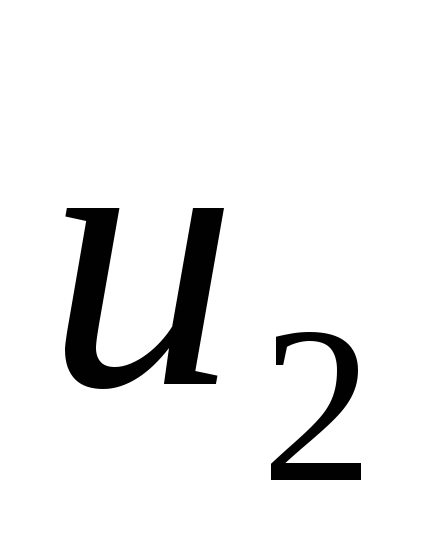 — мало.
— мало.
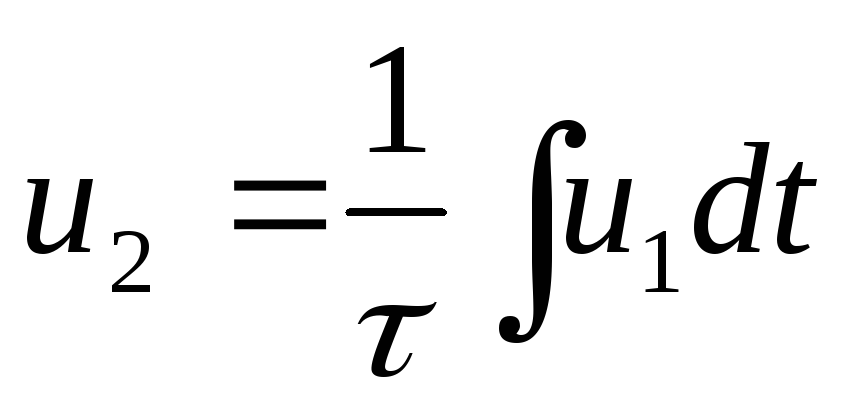
Вывод:цепь RL дифференцирует, если:
1. 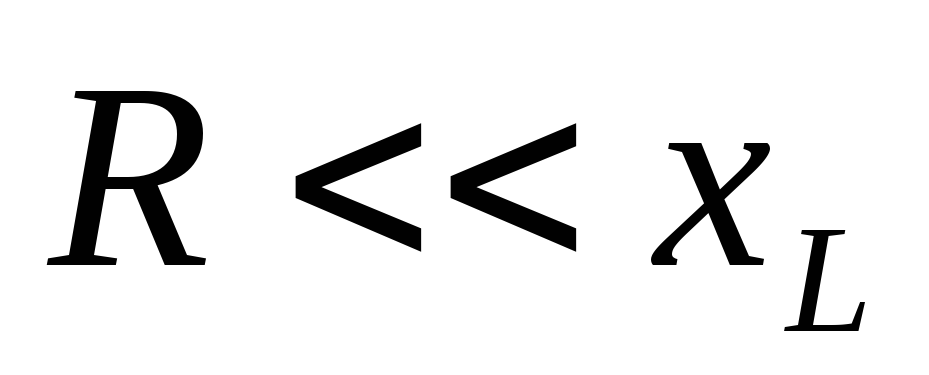
На практике 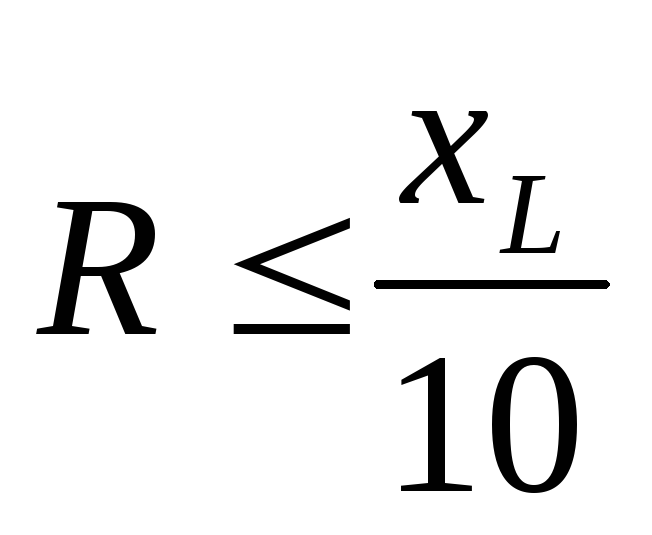
2. 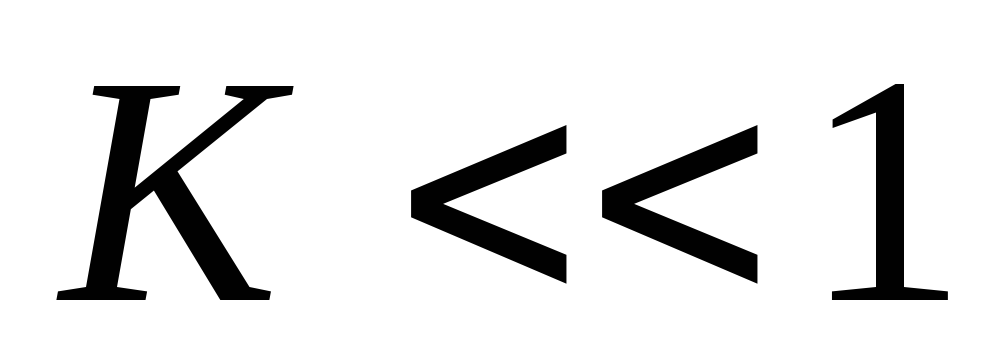
Форма некоторых сигналов после интегрирования
После интегрирования сигнала sin получается сигнал, который изменяется по закону –cos.
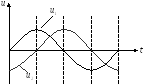

После интегрирования сигнала треугольной формы сигнал изменяется по кривой, близкой к синусоиде.
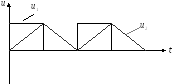
После интегрирования сигнала прямоугольной формы получается сигнал треугольной формы.
Вывод:интегрирующую цепь называют ещёудлиняющей цепью, т. к. после интегрирования прямоугольного импульса длительность сигнала увеличивается.
Коэффициент передачи интегрирующей цепи
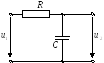
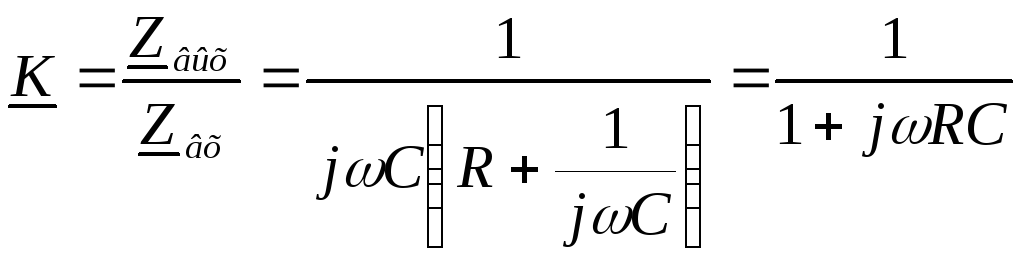
Вывод:цепь интегрирует, если её
коэффициент передачи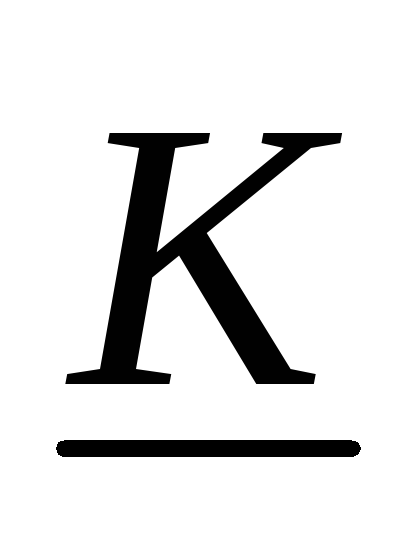 обратно пропорционален частоте.
обратно пропорционален частоте.
Чтобы увеличить коэффициент передачи, используют активные интегрирующие цепи, построенные на основе ОУ.
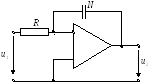
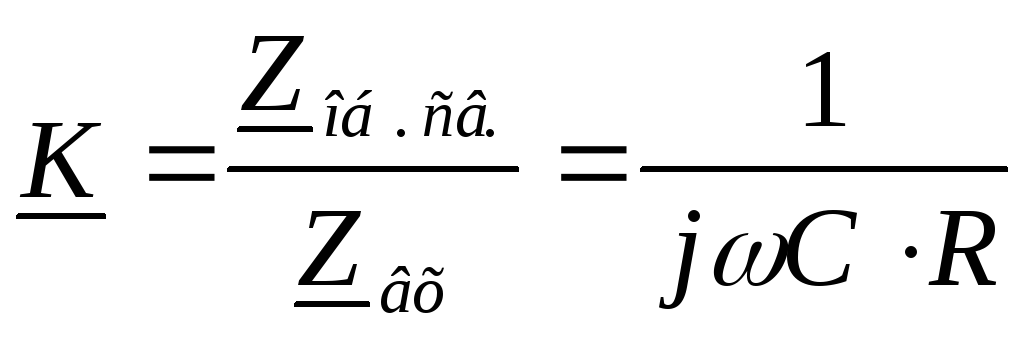
Вывод:эта цепь интегрирует, т. к. её коэффициент передачи обратно пропорционален частоте.
Интегрирующую цепь используют для преобразования сигналов разных по длительностив сигналыразные по амплитуде.

Вывод:при воздействии короткого
импульса конденсатор не успевает
зарядиться до конца, длительного —
успевает. Получается разница в величине
выходного напряжения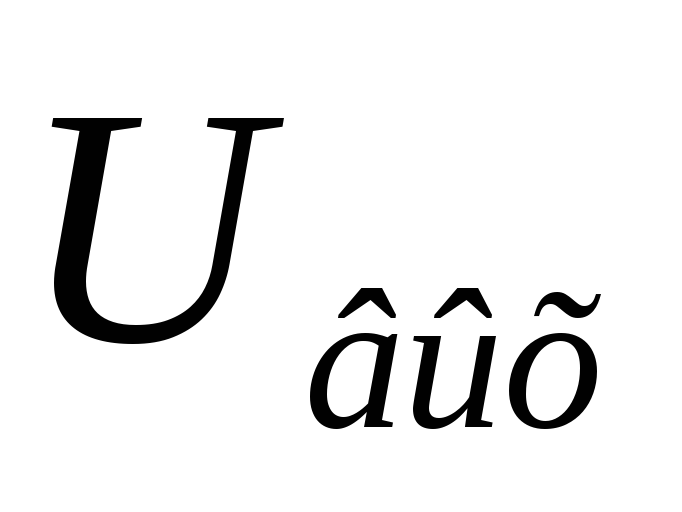 .
.
38. Понятие об электрических фильтрах, их классификация. Определения полосы пропускания и полосы задерживания фильтров
Электрический фильтр— четырёхполюсник, который токи одних частот пропускает хорошо с малым затуханием ~ 3 дБ, а токи других частот пропускает плохо с большим затуханием ~ 30 дБ.
Основными характеристиками фильтра является зависимость его рабочего затухания от частоты.
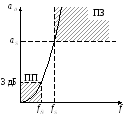
Частота среза 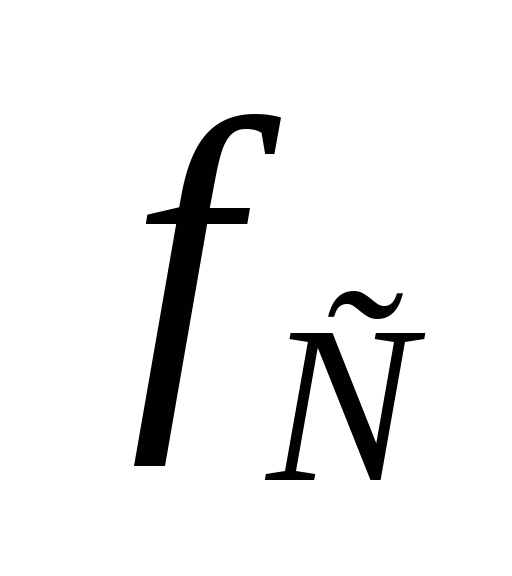 —
частота, на которой рабочее затухание
равно 3 дБ.
—
частота, на которой рабочее затухание
равно 3 дБ.
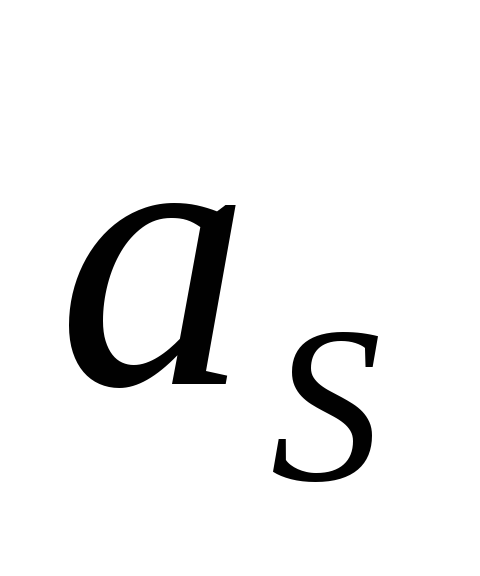 — допустимое затухание, задаётся
техническими условиями.
— допустимое затухание, задаётся
техническими условиями.
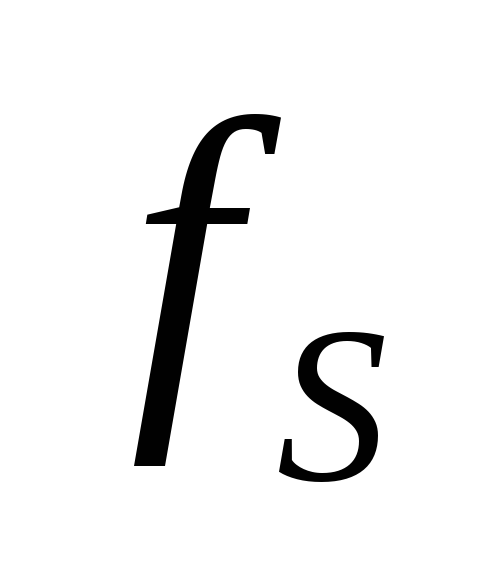 — соответствует допустимому затуханию
(допустимая частота)
— соответствует допустимому затуханию
(допустимая частота)
ПП (полоса пропускания) — область частот, где рабочее затухание меньше 3 дБ.
ПЗ (полоса задерживания) — область частот, где рабочее затухание выше допустимого.
Между ПП и ПЗ лежит промежуточная полоса.
Классификация электрических фильтров:
по расположению ПП:
по элементной базе:
– пьезоэлектрический фильтр;
– магнитострикционный фильтр;
– электромеханический фильтр.
по математическому обеспечению:
фильтры Баттерворта
фильтры Чебышева
фильтры Золотарёва
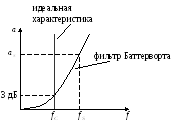
Фильтр Баттервортаимеет самую плоскую характеристику в ПП, однако в ПЗ характеристика идёт не круто, и это его недостаток.
Чтобы получить более крутую характеристику, применяют фильтр Чебышева, но у него появляется волнистость в ПП, это его недостаток.
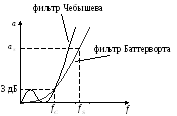
Чтобы получить ещё более крутую характеристику, используют фильтр Золотарёва, но у него кроме волнистости в ПП появляется ещё провал характеристики в ПЗ, и это его недостаток.
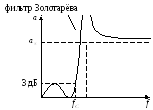
39. Фильтры нижних частот Баттерворта. Электрическая схема фильтра, прохождение токов различных частот, характеристика рабочего затухания. Порядок расчета фильтра
ФНЧ Баттерворта должен пропускать в нагрузку токи нижних частот.

Баттерворт предложил следующую формулу рабочего затухания:
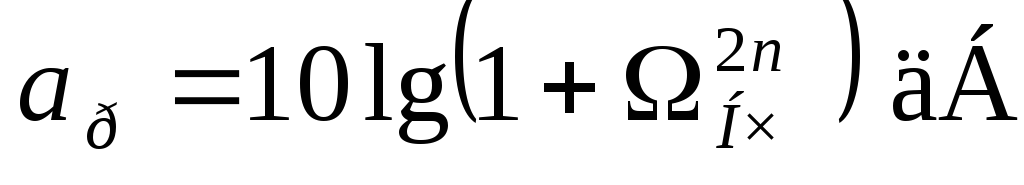 ,
где
,
где
n — порядок фильтра
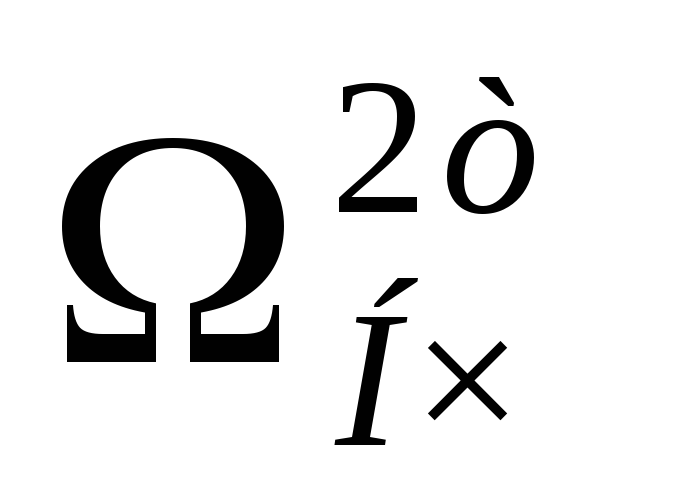 — нормированная частота:
— нормированная частота:
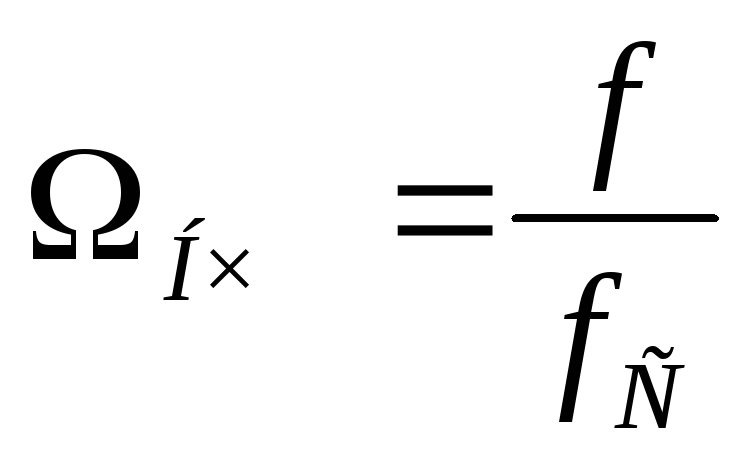
Реализовать такую характеристику можно с помощью элементов L и C. Сколько в схеме таких элементов, таков порядок фильтра.
ФНЧ 1-го порядка
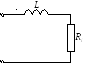
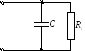
Катушку ставят последовательно с
нагрузкой, потому что её сопротивление 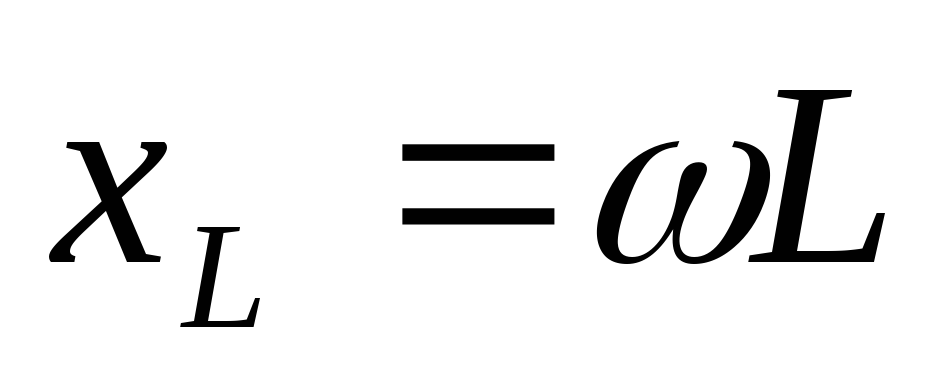 с ростом частоты увеличивается, значит
токи НЧ легко пройдут в нагрузку, а токи
ВЧ задержатся.
с ростом частоты увеличивается, значит
токи НЧ легко пройдут в нагрузку, а токи
ВЧ задержатся.
Конденсатор ставят параллельно с
нагрузкой, потому что его сопротивление 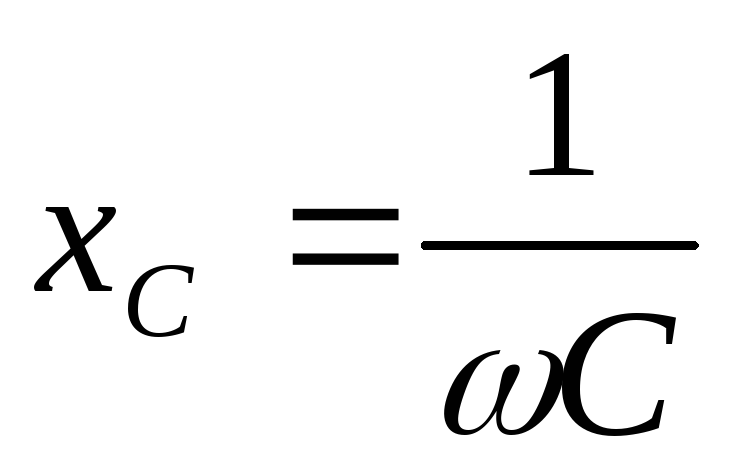 с ростом частоты уменьшается, значит
токи ВЧ замкнутся через конденсатор, а
токи НЧ пойдут в нагрузку.
с ростом частоты уменьшается, значит
токи ВЧ замкнутся через конденсатор, а
токи НЧ пойдут в нагрузку.
Чтобы получить схему более высокого порядка, элементы соединяют по лестничной схеме.
ФНЧ Баттерворта 5-го порядка
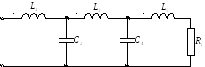
Более экономичной является схема, где больше конденсаторов.
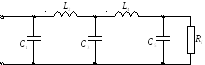
Расчёт ФНЧ Баттерворта
Определяем порядок фильтра
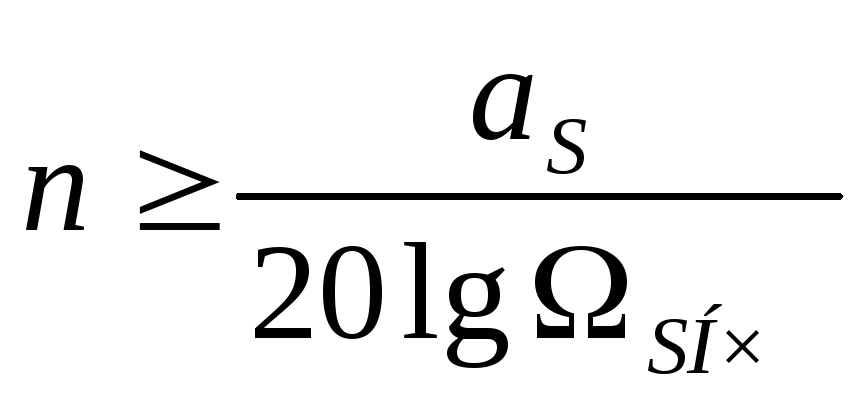
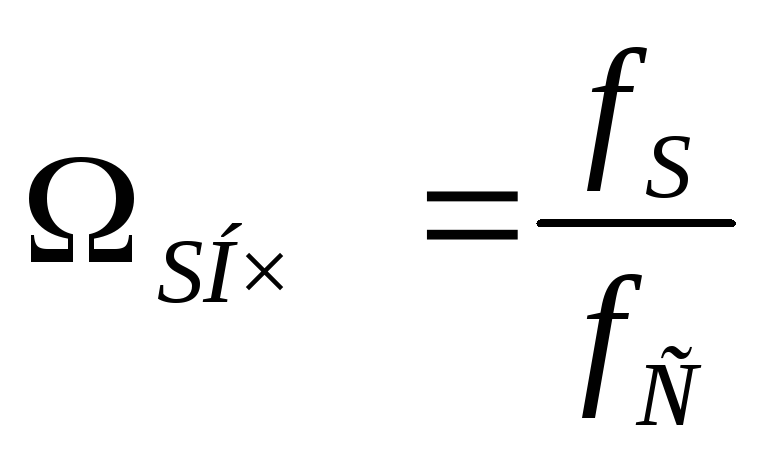
Чертим схему полученного порядка
Определяем постоянные преобразования фильтра
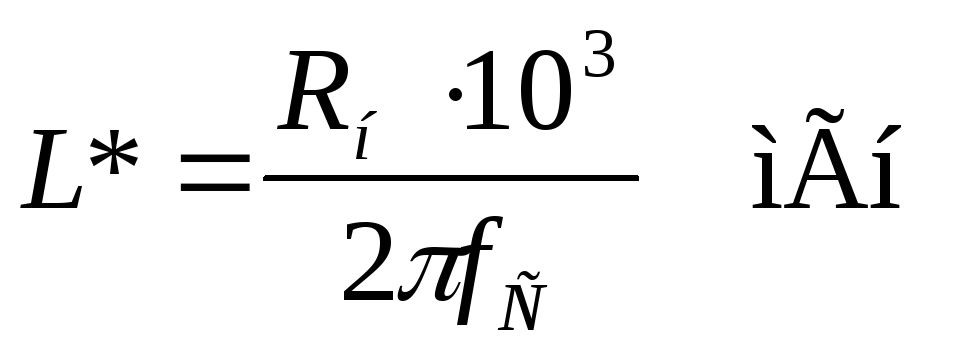
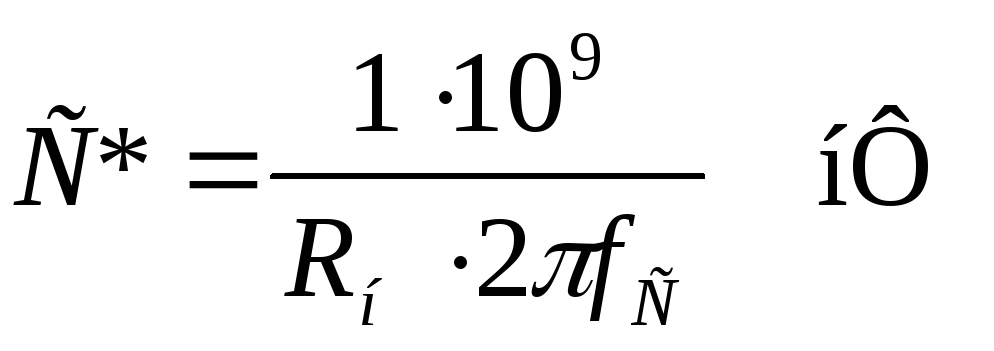
Для идеального фильтра:
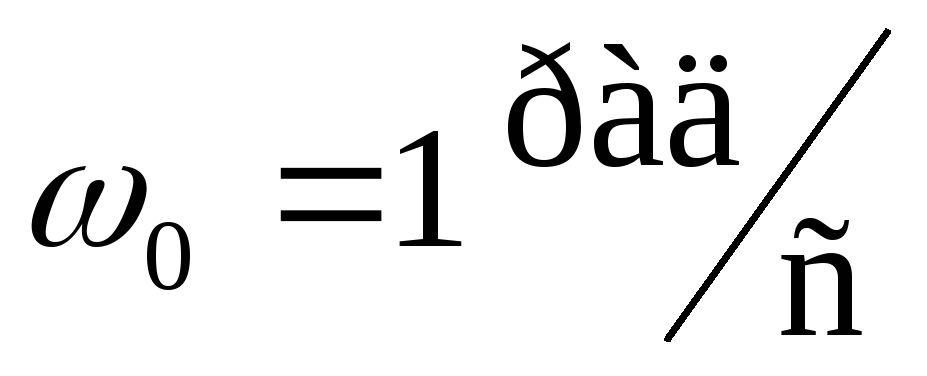
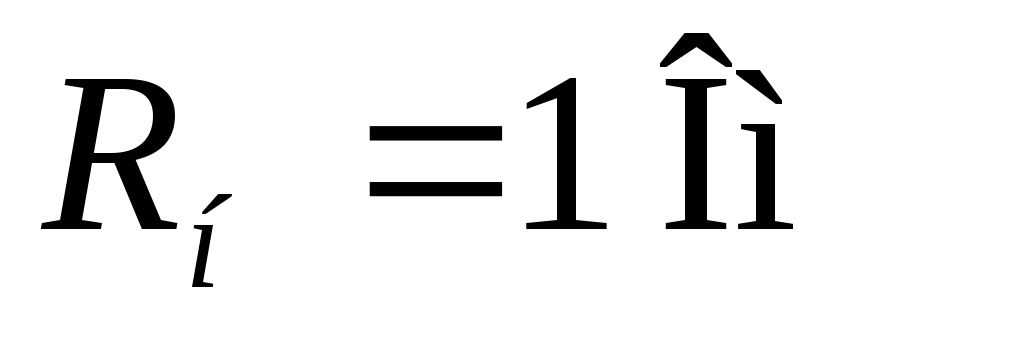
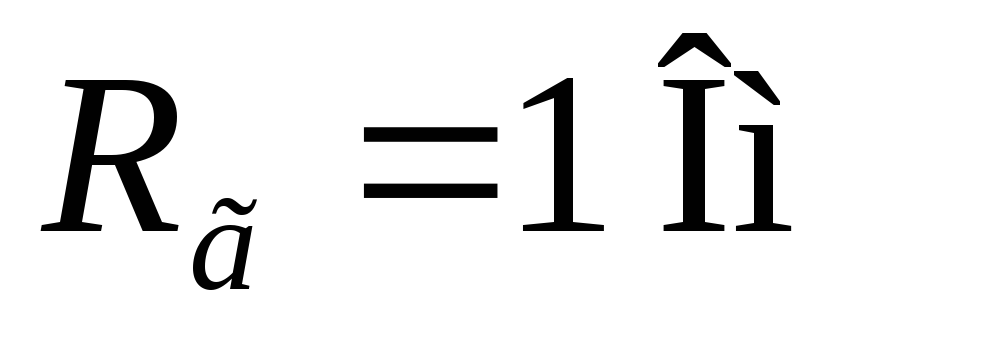
Получена специальная таблица нормированных коэффициентов фильтров Баттерворта.
Чтобы найти элементы ФНЧ, надо постоянные преобразования умножитьна коэффициенты из таблицы: