Электронный справочник по ИНФОРМАТИКЕ (Автор Панов В.А.)

История логики Логические задачи Высказывания Логические функции … Таблицы истинности Запись выражений на языке алгебры логики Законы логики Решение задач

Логические функции Логическая функция — это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием которое называется значением функции. Это определение почти не отличается от определения числовой функции. Разница лишь та, что аргументом и значением числовой функции являются числа, а аргументом логической функции — высказывания. Как можно составить логическую функцию? Очень просто. Приведем пример: Пусть дано высказывание А. Оно может быть либо истинно, либо ложно. Определим высказывание В следующим образом: пусть В истинно, когда А ложно, и ложно когда А истинно. Мы только что установили соответствие между высказыванием А и высказыванием В. Другими словами мы составили логическую функцию, аргументом которой является высказывание А и результатом высказывание В. 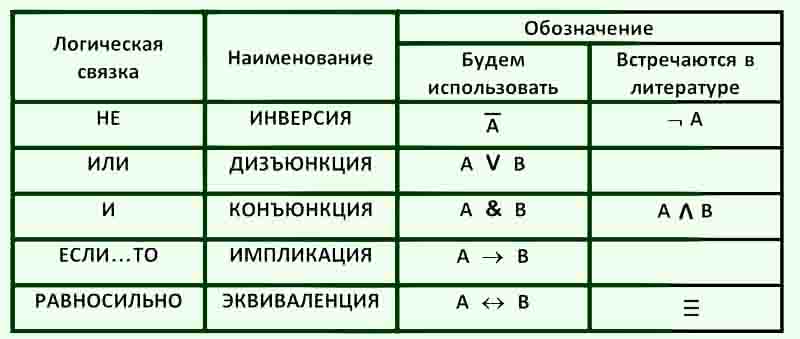Функция, определённая таким образом, называется отрицанием и записывается так: Читается так: “не А”   Определим логические функции: 1) Инверсия (отрицание) — это логическое не. Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А» Для обозначения отрицания суждения употребляется символ ¬ или – над переменной. Запись ¬А читается как «не А». 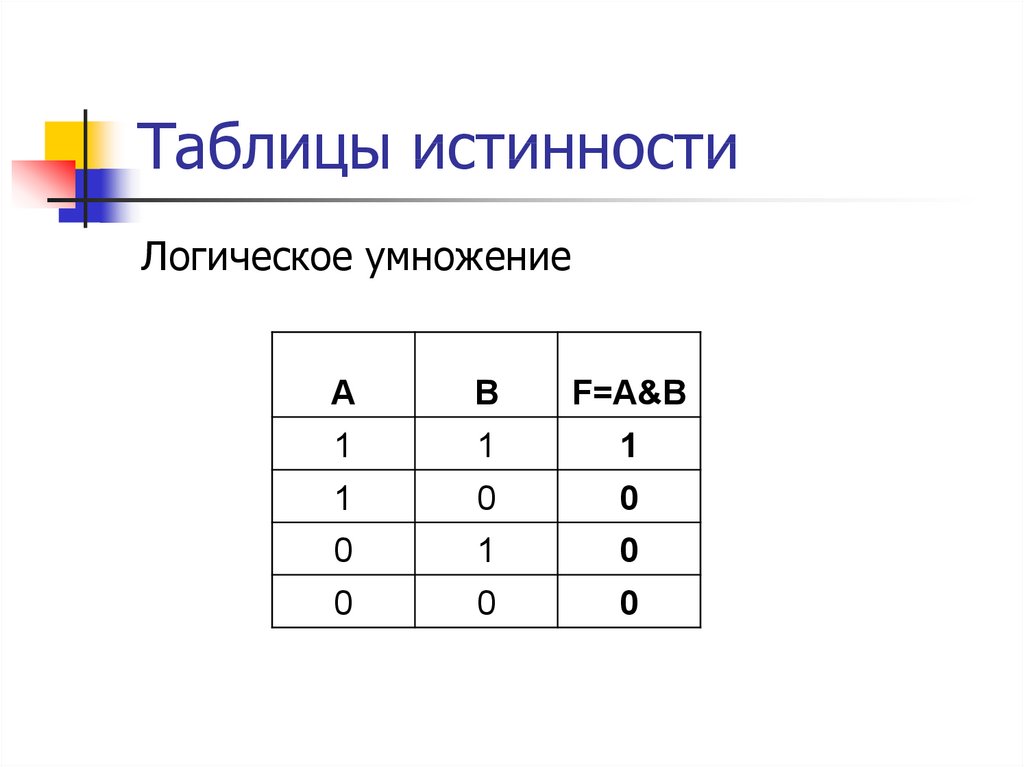А ¬А 1 1 1 1   2) Коньюкция — это логическое умножение. Обозначение: А & В ( АВ, А /\ В ) . Читается так “ А и В “. А В А & В 1 1 1 1 1   3) Дизьюкция — это логическое сложение. Обозначение: А V В , ( А + В ). Читается так: “ А или В ”. А В А V В 1 1 1 1 1 1 1   4) Эквиваленция — это функция тождества. Она обозначается символами = , ~ , или <=>. Выбираем обозначение А = В. («тогда и только тогда»). Запись А = В читается как «А эквивалентно В». А В А = В 1 1 1 1 1 1   5) Импликация — это логическое следование. Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО». Она обозначается символом -> Читается как «из А следует В» Обозначение: А В 1 1 1 1 1 1 1   Импликация устроена немного сложнее других функций. В импликации существенное значение имеет порядок аргументов. Первый называется посылкой, а второй следствием. Можно сказать, что первое высказывание является как бы причиной второго, а второе как бы вытекает из первого.

что такое, способы представления, значение / Справочник :: Бингоскул

Логическая функция: что такое, способы представления, значение

добавить в закладки удалить из закладок

Содержание:

Логическая функция — это такая функция, которая может принимать только одно из 2-х значений: 0 («ложь», «false») или 1 («истина», «true»). Логическую функцию можно обозначить как F (A), где А — это логический аргумент, чье количество в функции никак не ограничено.

Любая современная компьютерная система состоит из множества логических схем, где присутствуют логические функции и логические переменные. Для того чтобы описать эти взаимоотношения, есть таблицы истинности, в которых расписаны значения логической функции для разных наборов аргументов функции.

Логическая функция, что это

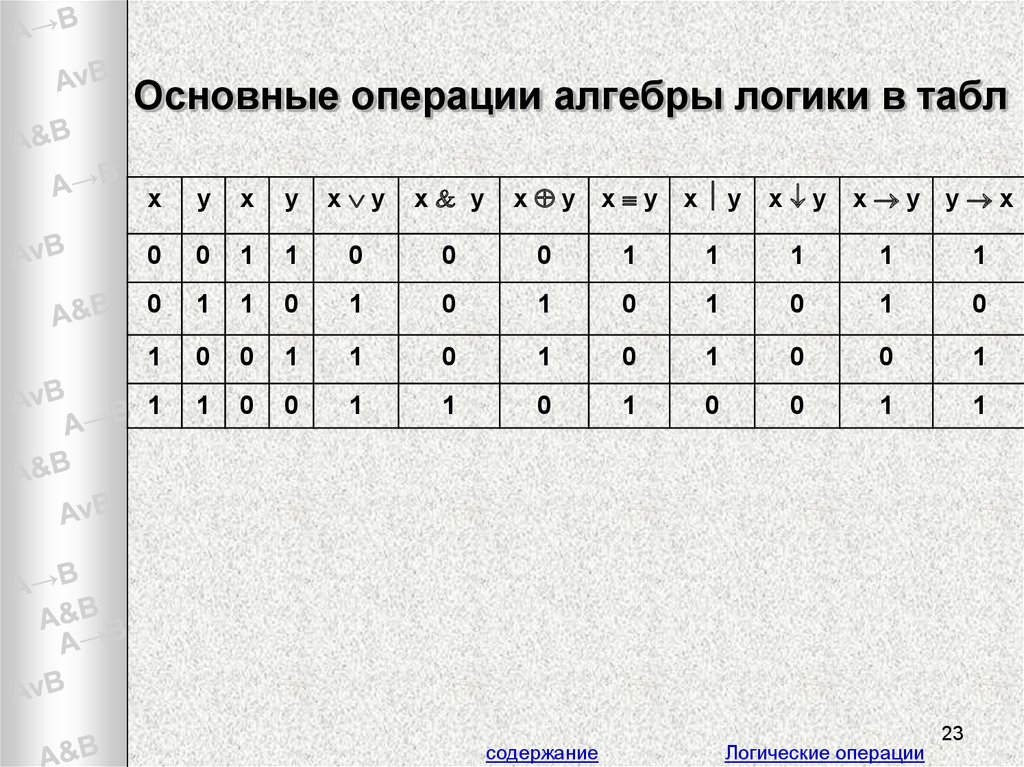
Над аргументами логической функции можно выполнить различные операции. В зависимости от операций можно выделить основные логические функции:

• отрицание;
• конъюнкция;
• дизъюнкция;
• импликация;
• эквиваленция.

Логическая функция: отрицание

Под отрицанием понимается логическая функция с аргументом «не А» (обозначается в виде «¬ А»), которая в конечном счете является истинной, если аргумент будет «false» и ложной, если аргумент будет «true»:

• если А будет 1, то ¬ А будет  0;


• если А будет 0, то ¬ А будет  1.

Логическая функция: конъюнкция

Логическая функция «конъюнкция» всегда представлена несколькими аргументами. Она будет являться «true» только в том случае, если все аргументы внутри нее будут тоже «true». Например, у нас есть два аргумента «А и В». Если рассматривать их  точки зрения истинности конъюнкции, тогда мы получаем следующее:

• если А будет 1 и В будет 1, тогда А˄В будет тоже 1;


• если А будет 1, а В будет 0, тогда А˄В будет 0;


• если А будет 0, а В будет 1, тогда А˄В будет 0;


• если А будет 0 и В будет 0, тогда А˄В будет тоже 0.

Логическая функция: дизъюнкция

Эта логическая функция, как и предыдущая, должна быть представлена несколькими аргументами. Ее значение буде «false» только в том случае, когда значения всех аргументов будет «false», во всех остальных случаях она будет «true».

Например нам даны два аргумента «А и В», тогда их таблица дизъюнкции будет выглядеть следующим образом:

• если А будет 1 и В будет 1, тогда и А˅В будет 1;


• если А будет 1, а В будет 0, тогда  А˅В все равно будет 1;


• если А будет 0, а В будет 1,  А˅В также будет 1;


• если А будет 0 и В будет 0, только тогда  А˅В будет 0.

Логическая функция: импликация

Логическая функция «импликация» — это такое выражение, которое показывает зависимость одного аргумента от другого. Его еще можно «прочитать» как «если А, то В». Обозначается как «А→В» и оно будет считаться «false» только тогда, когда А будет «true», а «В» будет «false».

Например:

• если А будет 1 и В будет 1, тогда  А→В будет тоже 1;


• если А будет 1, а В будет 0, только тогда  А→В будет тоже 0;


• если А будет 0, а В будет 1, то  А→В будет 1;


• если А будет 0 и В будет 0, тогда  А→В также будет 0.

Логическая функция: эквиваленция

Логическая функция «эквиваленция» простыми словами может читаться как «для А нужно и достаточно В». Его значение будет «true», только тогда, когда А и В вместе, либо «false», либо «true». Такая функция обозначается как «А↔В».

Вот как выглядит таблица истинности эквиваленции:

• если А будет 1 и В будет 1, тогда  А↔В тоже будет 1;


• если А будет 1, а В будет 0, тогда  А↔В будет 0;


• если А будет 0, а В будет 1, тогда  А↔В будет 0;


• если А будет 0 и В будет 0, тогда  А↔В будет 1.

Заключение

Логическая функция — это основа вычислений любого компьютера. Компьютеру постоянно приходится обрабатывать какую-то информацию, причем ему нужно приводить ее к логической последовательности нулей и единиц. Любые операции в компьютере с нулями и единицами происходят по условиям математической логики. А это означает, что для более глубокого понимания вычислительной мощности компьютерного устройства знать, что такое логическая функция очень важно.

Поделитесь в социальных сетях:

9 сентября 2021, 17:46

Информатика

Could not load xLike class!

404: Страница не найдена

Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.

Что я могу сделать сейчас?

Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся.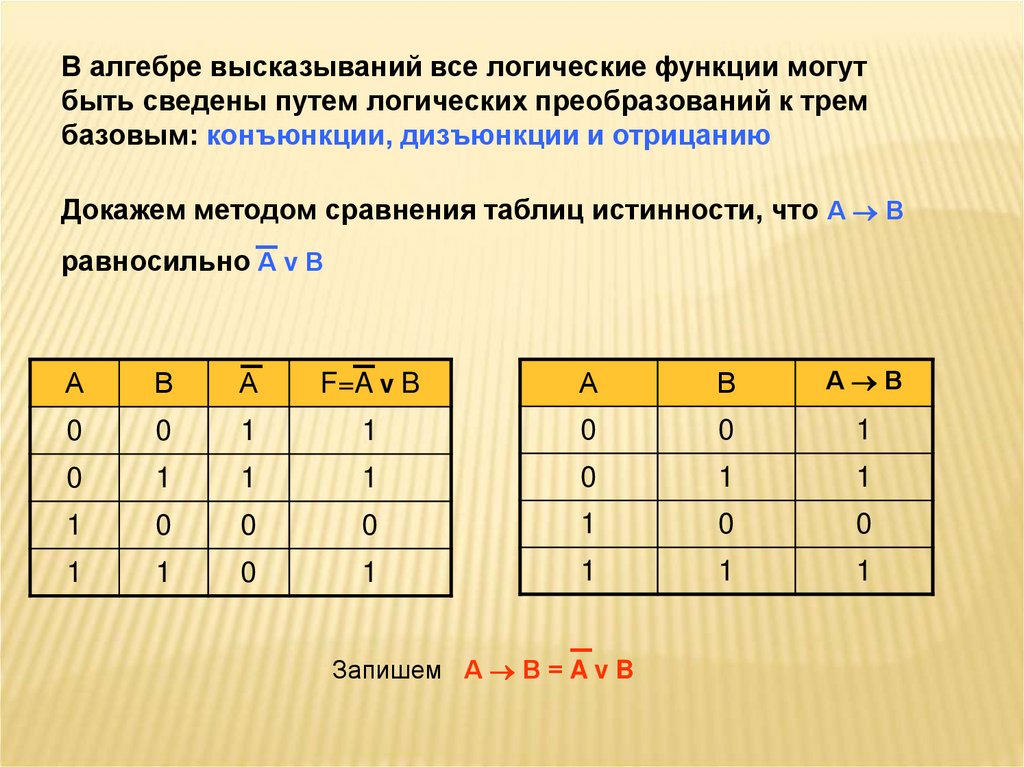 Вот куда вы можете пойти отсюда:

Поиск

• Пожалуйста, свяжитесь с нами, чтобы сообщить, что эта страница отсутствует, или используйте поле выше, чтобы продолжить поиск
• Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, WhatIs.com.
• Посетите нашу домашнюю страницу и просмотрите наши технические темы

Просмотр по категории

Сеть

• поставщик сетевых услуг (NSP)

  Поставщик сетевых услуг (NSP) — это компания, которая владеет, управляет и продает доступ к магистральной инфраструктуре Интернета и …

• неэкранированная витая пара (UTP)

  Неэкранированная витая пара (UTP) — это повсеместно распространенный тип медных кабелей, используемых в телефонной проводке и локальных сетях (LAN).

• Многопротокольная коммутация по меткам (MPLS)

  Многопротокольная коммутация по меткам (MPLS) — это механизм коммутации, используемый в глобальных сетях (WAN).

Безопасность

• Требования PCI DSS 12

  Требования PCI DSS 12 представляют собой набор мер безопасности, которые предприятия должны внедрить для защиты данных кредитных карт и соблюдения …

• данные держателя карты (CD)

  Данные держателя карты (CD) — это любая личная информация (PII), связанная с лицом, у которого есть кредитная или дебетовая карта.

• Уровни продавца PCI DSS

  Стандарт безопасности данных индустрии платежных карт (PCI DSS) ранжирует продавцов по количеству транзакций за …

ИТ-директор

• системное мышление

  Системное мышление — это целостный подход к анализу, который фокусируется на том, как взаимодействуют составные части системы и как…

• краудсорсинг

  Краудсорсинг — это практика обращения к группе людей для получения необходимых знаний, товаров или услуг.

• синтетические данные

  Синтетические данные — это информация, созданная искусственно, а не в результате событий реального мира.

HRSoftware

• вовлечения сотрудников

  Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.

• кадровый резерв

  Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.

• разнообразие, равенство и инклюзивность (DEI)

  Разнообразие, равенство и инклюзивность — термин, используемый для описания политики и программ, которые способствуют представительству и …

Обслуживание клиентов

• требующий оценки

  Оценка потребностей — это систематический процесс, в ходе которого изучается, какие критерии должны быть соблюдены для достижения желаемого результата.

• точка взаимодействия с клиентом

  Точка соприкосновения с покупателем — это любой прямой или косвенный контакт покупателя с брендом.

• устав обслуживания клиентов

  Устав обслуживания клиентов — это документ, в котором описывается, как организация обещает работать со своими клиентами наряду с …

Полное руководство по булевой логике

Ключевые моменты:

• Булева логика строго фокусируется на двоичных переменных, которые обычно представляют собой 1 и 0, которые представляют «истина» или «ложь».
• В то время как стандартная алгебра оперирует числами с помощью сложения, вычитания, умножения, деления и т. д., булева алгебра использует логические функции, такие как отрицание, конъюнкция и дизъюнкция.
• Простейший вентиль, который только можно себе представить, называется вентилем НЕ или инвертором. Он просто переворачивает любой ввод, который вы ему даете, чтобы получить противоположный результат.

Что такое булева логика? – Complete Explanation

Булева логика — это подраздел алгебры, описывающий набор простых правил и вентилей, помогающих сравнивать логические операторы и манипулировать ими. Что отличает булеву логику от других логических систем, так это то, что она фокусируется строго на двоичных переменных, которые обычно имеют форму 1 и 0, представляющих истину и ложь.

В то время как обычная алгебра охватывает числовые операции, булева алгебра занимается логическими операциями. Обычная алгебра оперирует числами, используя сложение, вычитание, умножение, деление и другие математические функции. Булева алгебра маневрирует своими предметами, используя логические функции, такие как отрицание, конъюнкция и дизъюнкция. В обеих системах используются те же операторы отношения, что и в обычной математике, включая символы «равно» (=), «больше» (>) и «меньше».

Обычная алгебра и булева логика подчиняются многим из одних и тех же основных правил. К ним относятся:

• Коммутативные законы, которые позволяют вам менять местами ваши переменные при сложении и умножении
• Ассоциативные законы, которые позволяют вам менять порядок операций при сложении и умножении
• Распределительные законы, которые позволяют вам распределить операции умножения над операциями сложения

Эти и еще несколько простых правил и вентилей для логических манипуляций позволяют нам отображать удивительное количество идей и утверждений непосредственно в цифровые биты и байты. Булева логика сегодня является основой большинства языков программирования. В мире финансов он используется инвесторами для оценки вариантов и рисков. Он также обеспечивает простой способ точной настройки поиска в больших базах данных.

Булева логика: точное определение

Булева логика — это система, используемая для анализа истинности любого двоичного утверждения, а также отношений между наборами двоичных утверждений с использованием алгебраических правил в сочетании с логическими вентилями для выполнения логических операций.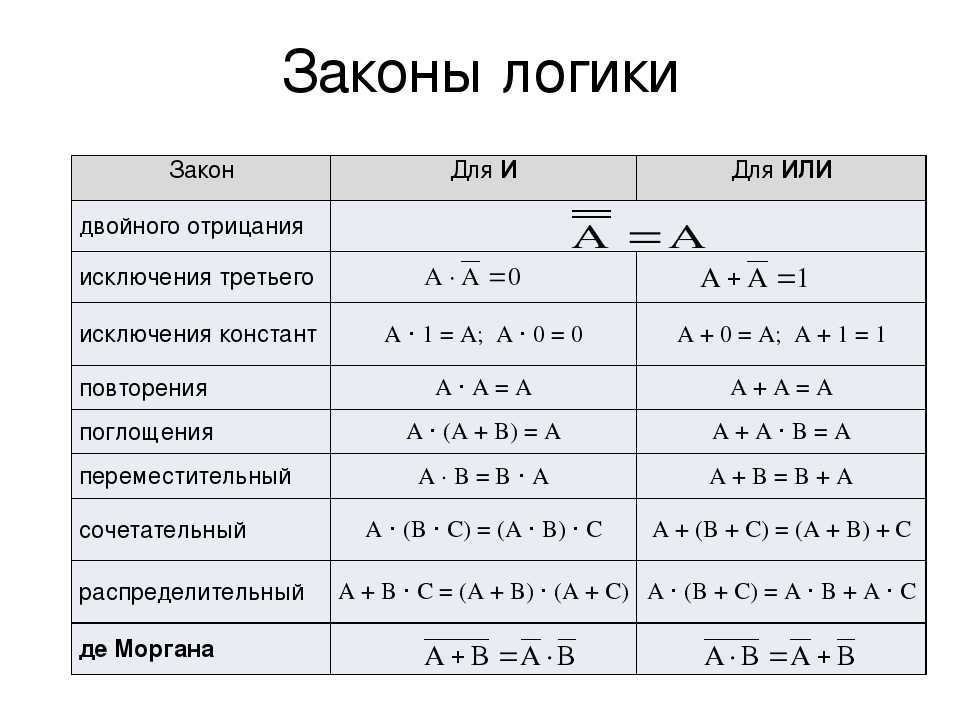

Как работает логическая логика?

Булева логика начинается с типичных математических функций и добавляет несколько собственных. Основные идеи булевой логики вращаются вокруг трех простых логических элементов, а также нескольких более сложных элементов. Вы можете комбинировать эти вентили со стандартными математическими операторами отношения и базовыми алгебраическими правилами для построения ветвящихся деревьев идей, которые можно реализовать в любой бинарной цифровой системе.

К трем простейшим логическим элементам относятся:

• НЕ
• И
• ИЛИ

НЕ

Самый простой из возможных логических элементов называется вентилем НЕ или инвертором. Все, что он делает, — это переворачивает любой ввод, который вы ему даете, чтобы получить противоположный результат. В цифровой системе, основанной на двоичных переменных, состоящих из 1 и 0, ввод 1 в логический элемент НЕ приведет к выводу 0 и наоборот.

Мы называем эту логическую функцию вентилем НЕ, потому что состояние ввода не совпадает с состоянием вывода. Для обозначения этой операции инверсии в большинстве определений булевой логики используется верхняя черта, которая представляет собой простую черту над заданным входным символом (¯). Например, если мы используем X для обозначения того, что переключатель замкнут, то «НЕ X» или X с надчеркнутой линией над ним означает, что переключатель разомкнут.

В булевой логике вентиль НЕ имеет только один вход и один выход. Два вентиля НЕ, соединенные друг с другом, производят двойную инверсию, которая возвращает исходное значение вашей переменной.

И

Логический элемент И будет производить выходное действие только в том случае, если все операторы или связанные с ним переменные присутствуют одновременно. Выход вентиля И будет истинным только тогда, когда все переменные, объединенные вентилем И, истинны. Если одно из них ложно, вывод будет ложным.

Логический элемент И подобен сложению в том, что он следует простым правилам коммутации, позволяя любой переменной, которую он соединяет, менять положение.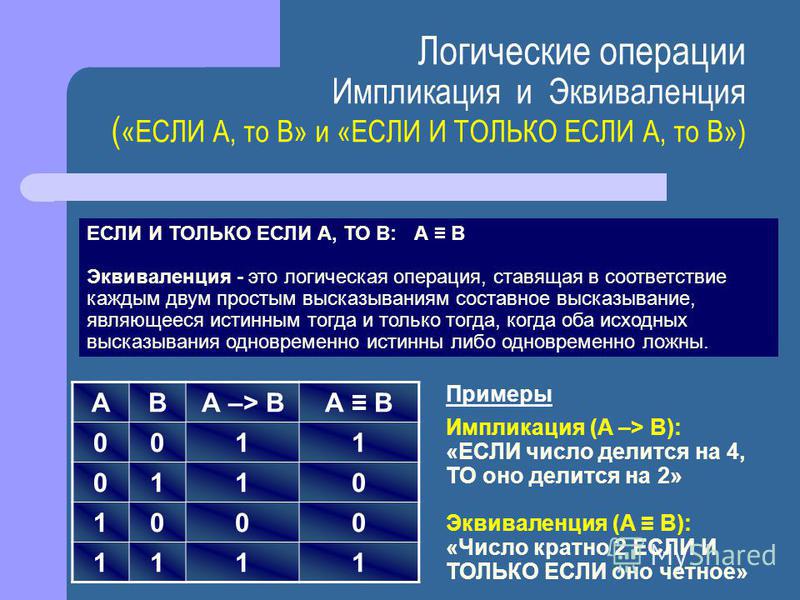 Один из самых простых примеров: «X AND Y = Y AND X». Порядок переменных не влияет на конечный результат, поэтому считается неважным.

Мы обычно обозначаем логический элемент И точкой или символом точки (.). Логический элемент И с двумя входами X и Y преобразуется в логическое выражение «X.Y», которое многие языки программирования упрощают до «XY».

ИЛИ

Булев логический элемент ИЛИ выдает результат, если присутствует какая-либо из связанных им переменных. Выходное действие этого типа ворот будет иметь значение true, если один или несколько его входов истинны. В мире электроники вентиль ИЛИ известен как параллельная схема.

Как и вентиль И, вентиль ИЛИ обладает коммутативными свойствами, позволяя любой из своих входных переменных изменять порядок, не влияя на выход. Полное название вентиля ИЛИ на самом деле «включающее ИЛИ», что контрастирует с более сложным логическим логическим вентилем «исключающее ИЛИ» (XOR). Вентиль XOR выполняет противоположную функцию, исключая все свои входы и создавая выход только в том случае, если ни один из них не присутствует.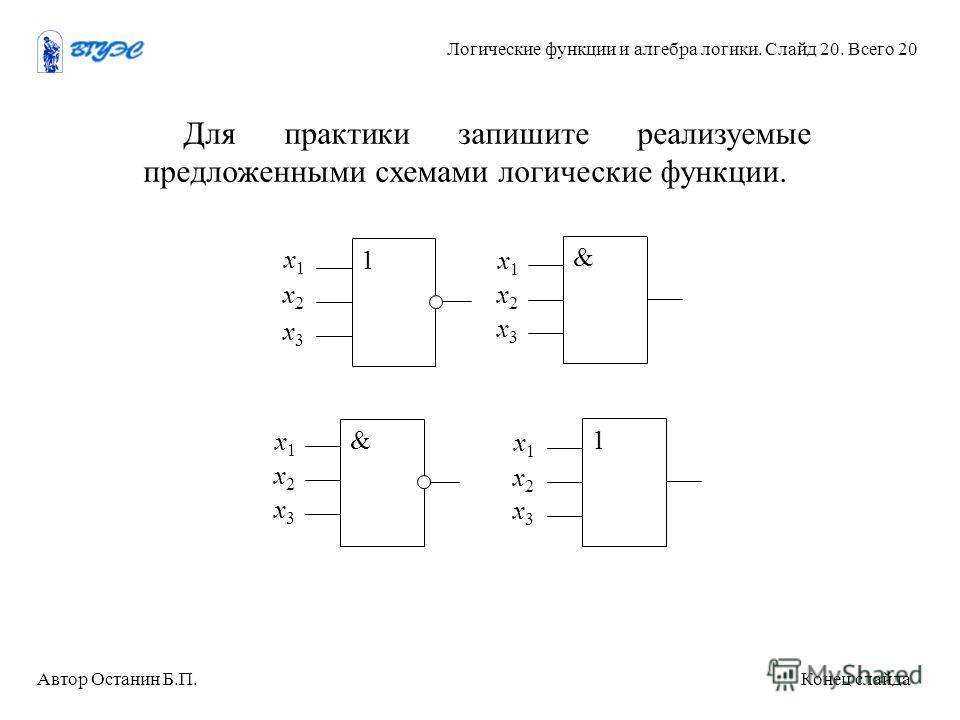

Парадоксально, но символ, который мы используем для вентиля ИЛИ, — это знак плюса (+). Вентиль ИЛИ с двумя входами X и Y может быть представлен булевым выражением «X+Y».

Учебный стенд с датчиками, переключателями и схемой логических элементов, используемых при обучении студентов для иллюстрации булевой логики. Булева логика — это подраздел алгебры, описывающий набор простых правил и вентилей, помогающих сравнивать логические операторы и манипулировать ими.

Дополнительные логические элементы

Если мы углубимся на один уровень в нашу систему булевой логики, мы получим более совершенные логические элементы. Это в основном просто комбинации трех простейших ворот. Вот пара наиболее важных из них.

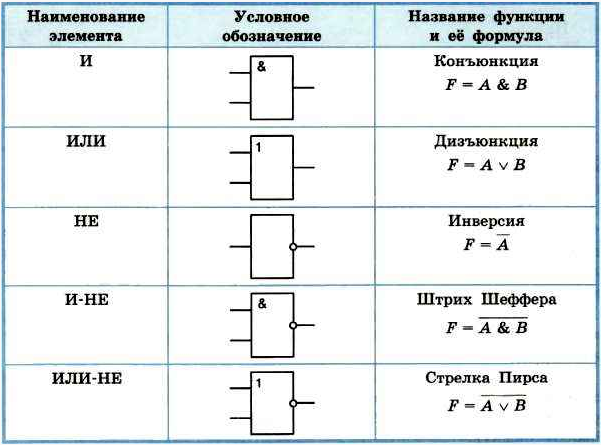
НЕ-И

Элемент НЕ-И объединяет два простых логических элемента, вентиль НЕ и вентиль И, образуя функцию НЕ-И. И-НЕ является дополнением к И, как вы могли догадаться, выполняя точную инверсию правил вентиля И. Выход вентиля И-НЕ будет ложным только в том случае, если все входы, которые к нему подключаются, истинны.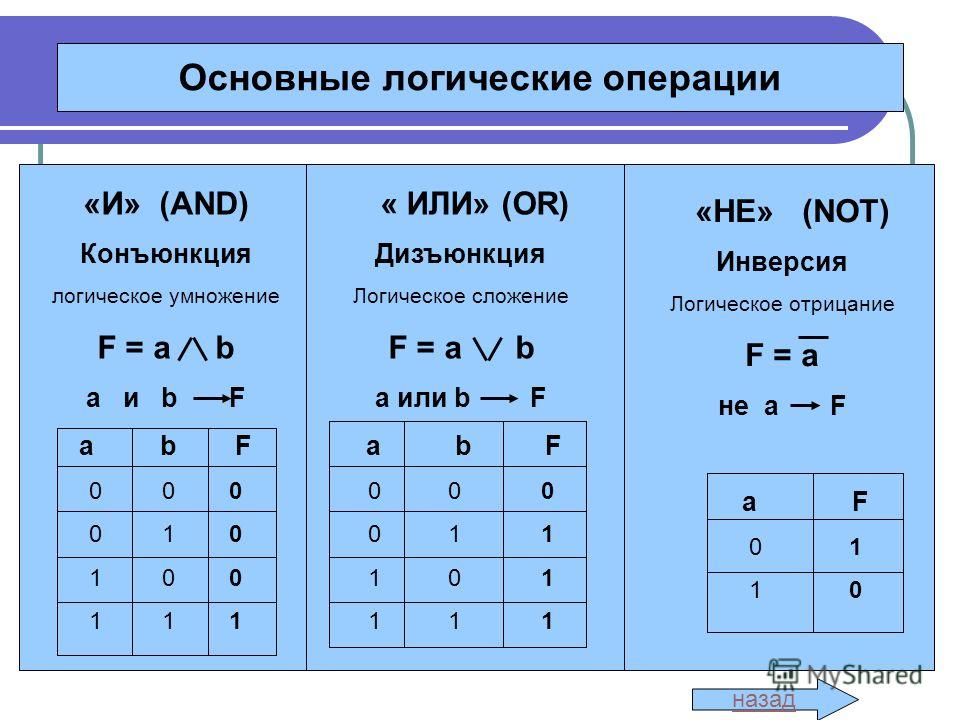 Если один или несколько его входов ложны, выход будет истинным.

Символ, который мы используем для обозначения И-НЕ, иногда называют штрихом Шеффера. Он выглядит как стрелка, указывающая вверх (↑), но иногда его упрощают до вертикальной линии (|). Примеры логических выражений, включающих логические элементы И-НЕ для объединения переменных X и Y, включают «X↑Y» и «X|Y».

ИЛИ-НЕ

Элемент ИЛИ-НЕ соединяет два простых логических элемента, НЕ и ИЛИ, для создания функции НЕ-ИЛИ. Это действует точно так же, как простой вентиль ИЛИ с инвертированным выходом. Вентиль ИЛИ-ИЛИ даст вам результат только тогда, когда ни одна из его переменных не присутствует. Выходная переменная будет иметь истинное значение, только если все ее входные переменные ложны.

Есть два символа, которые мы можем использовать для вентиля НЕ-ИЛИ. Первый сочетает в себе символы для вентилей НЕ и ИЛИ. Используя переменные X и Y, это будет выглядеть как «X + Y» с верхней чертой. Второй — более упрощенный символ, известный как стрелка Пирса, который выглядит как направленная вниз стрелка (↓). При объединении двух наших любимых переменных это выглядит как «X↓Y».

Как создать логическое выражение?

Логические выражения — это то, как языки программирования, такие как Java, C и Python, реализуют логическую логику. По определению логическое выражение должно быть простым логическим утверждением, которое может быть представлено либо как истинное, либо как ложное.

Вы можете использовать эти выражения для сравнения любых типов данных, если вы вводите один и тот же тип данных во всех частях всех выражений. Они могут действовать как своего рода логический калькулятор для проверки утверждений и других входных данных и проверки, равны ли они, меньше или больше, чем другие утверждения или данные.

Простые логические выражения должны состоять как минимум из трех частей: первого элемента, который вы хотите сравнить, вентиля или оператора сравнения, который вы хотите выполнить, и второго элемента для сравнения. Вы также можете создавать более запутанные логические выражения, соединяя любое простое выражение с любым другим, используя НЕ, ИЛИ, И, НЕ-И, ИЛИ или другие логические элементы.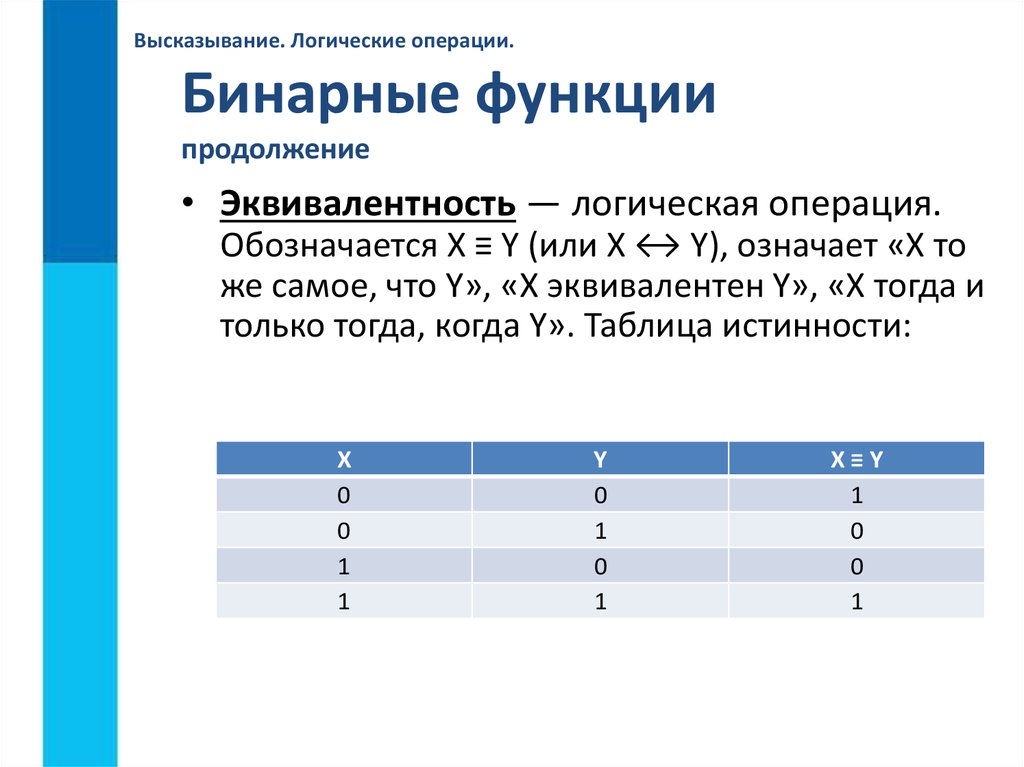

Убедитесь, что любое подключаемое выражение само по себе является полным логическим выражением. Это может означать, что вам нужно указать одну и ту же переменную в нескольких местах.

Откуда взялась булева логика?

Бюст Джорджа Буля в Университете Корк-Колледжа Буль был профессором математики в UCC. Его булева алгебра стала основой современной информатики.

Истоки булевой логики можно проследить до книги, опубликованной в 1854 году Джорджем Булем, математиком и философом. Буль был тихим молодым англичанином с родителями из рабочего класса. Его знания математики были в основном самоучкой. В возрасте 34 лет он стал первым профессором математики в Ирландии в первом светском колледже страны, Королевском колледже.

Буль представил свои логические концепции в своей первой книге «Математический анализ логики» и продолжил их дальнейшее исследование в более поздней публикации «Исследование законов мышления». Эти книги были одними из первых, в которых серьезно исследовалась идея логики и ее связь с математикой. В них он утверждал, что вместо философии логика может быть классифицирована как математическая дисциплина, которая может давать результаты для логических задач так же точно, как калькулятор решает математические задачи.

Он заметил много общего между алгебраическими символами и правилами и силлогизмами и логическими формами, которые мы используем в своих рассуждениях. Он начал амбициозное путешествие, пытаясь разработать логическую систему, основанную на алгебре, которая моделировала бы наше мышление. Буль потратил годы на разработку своих идей о том, как закодировать логические аргументы, естественно вырабатываемые человеческим мозгом, в математический язык. Булева логика — это лингвистическая алгебра, которую он придумал.

Джордж Буль был первым профессором математики в Королевском колледже Корка в Ирландии.

В 1864 году Буль умер в возрасте всего 49 лет. Его работа в течение многих лет оставалась без особого практического применения, пока американский инженер-электрик и математик по имени Клод Шеннон не вдохнул в нее жизнь через 70 лет после смерти Буля. Шеннон понял, что символическую логику Буля можно использовать в схемах электромеханических реле, чтобы сформировать основу реальных механизмов решения задач, или, как мы их сегодня называем, компьютеров.

Оглядываясь назад, многие историки считают Джорджа Буля одним из основоположников информатики. Его вклад в концептуальные структуры современных цифровых схем и языков программирования снискал ему заслуженное признание как одного из самых важных основоположников информационной эпохи.

Каковы приложения булевой логики?

В основе всех современных цифровых компьютеров лежит основная идея о том, что бинарные электрические переключатели могут использоваться для обработки логики. То, что начиналось как проблеск в глазах Джорджа Буля, превратилось в конкретную основу дизайна всех цифровых схем и концептуального заземляющего провода компьютерной эры.

Ранний механический калькулятор. Это было одно из первых применений булевой логики.

Калькуляторы для процессоров

Если мы используем различные уровни напряжения для обозначения двоичных битов, мы можем превратить чрезвычайно простые логические элементы в компоненты, необходимые для создания простых механических калькуляторов, включая счетчики, сумматоры и другие математические инструменты. Оттуда остается всего лишь небольшой шаг до разработки схем, использующих булеву логику для вычитания, умножения, деления и многого другого. Поскольку не так давно Homo sapiens были единственными машинами, способными к концептуальной математике, это само по себе уже большое дело.

После того, как мы использовали эти схемы и их логические концепции для создания карманного калькулятора, полноценный ЦП уже не за горами.

Оперативная память

Еще одна полезная вещь, которую вы можете создать с помощью булевых логических вентилей, — это идея памяти. Концепция памяти основана на обратной связи.

Когда выход гейта возвращается на его вход, вы получаете память. Все, что вам нужно сделать, чтобы булевы логические элементы запомнили входное значение, — это правильно их организовать. Эта до неприличия простая концепция дает нам оперативную память (ОЗУ) в наших компьютерах.

Примеры булевой логики в реальном мире

В вашей голове

Ваш мозг использует булеву логику каждый день. Мы называем булевы концепции в наших головах «условными». Идея ветвящихся деревьев решений, которые зависят от определенных условий, является важным инструментом, который мы используем, чтобы мыслить ясно.

Вот несколько примеров булевой логики, которые могут возникнуть у вас в голове:

• Если я чихаю и нахожусь в пыльной комнате, со мной все в порядке. Если я чихаю или кашляю и у меня жар, идите к врачу.
• Если я хочу пить, выпейте что-нибудь. Если я хочу пить и голоден, закажи напитки и еду. Если я не хочу пить и не голоден, ложись спать.

В поиске и в исследованиях

Вы можете использовать логические термины в исследованиях. Они могут помочь вам сузить или расширить область поиска при просмотре баз данных или библиотечных каталогов. Булева логика также может помочь вам лучше искать в Интернете.

Логический термин И позволяет нацелить поиск на поиск более конкретных результатов. И сузит область поиска.

Логический термин ИЛИ позволяет включать связанные понятия. Вы можете использовать его, чтобы указать вашей поисковой системе найти любой из различных синонимов. ИЛИ расширит область поиска.

Логический термин НЕ позволяет исключить несвязанные результаты. Например, если вы ищете информацию о налогах в Америке, но продолжаете получать результаты для Латинской Америки, вы можете отточить правильные результаты, используя логическое поисковое выражение «налоги И Америка, а не Латинская Америка». Если вы пользуетесь Google, НЕ обозначается знаком минус.

Далее…

• Какой IQ у Илона Маска, действительно ли он самый умный человек на Земле? Учитывая его решение о поглощении Twitter, делает ли Илон Маск один только IQ самым умным человеком на свете?
• Познакомьтесь с этими 6 известными женщинами в области технологий и информатики Узнайте о 6 женщинах, которые внесли большой вклад в области технологий и информатики.
• История Apache HBase: полное руководство Все, что вам нужно знать об истории Apache HBase, включено в наше руководство.

Полное руководство по булевой логике Часто задаваемые вопросы (часто задаваемые вопросы) 

В чем разница между булевой логикой и нечеткой логикой?

Каждое утверждение, описанное в булевой логике, должно быть двоичным, со значением либо true, либо false. Булева логика налагает строгие абсолютные значения на переменные, которыми она может манипулировать.

Нечеткая логика работает намного лучше с неоднозначностью, необходимой для размышлений о континуумах. Это позволяет его переменным быть частичными членами нескольких наборов по скользящей шкале в серой области между истинным и ложным.

В то время как логическая логика требует, чтобы ее переменные были фиксированными и дискретными, нечеткая логика позволяет вам работать с идеями в спектре. Булева логика уходит своими корнями в теорию вероятностей, а нечеткая логика представляет собой теорию возможностей.

Как вы объясните булеву логику?

Булева логика — это вид логической математики, используемый для определения истинности утверждения или комбинации утверждений таким же образом, как математика используется для определения достоверности числовых уравнений. Там, где математика использует сложение, вычитание, умножение и деление в качестве основных операторов, логическая логика и цифровые схемы, которые она позволяет использовать, используют НЕ, И и ИЛИ в качестве основных строительных блоков.

Что является примером булевой логики?

Булева логика — важная концепция в исследованиях Google и других поисковых систем. Вот несколько примеров:

• Если вы получаете слишком много совпадений по данному ключевому слову, вы можете добавить И плюс соответствующий поисковый запрос, чтобы сузить результаты.
• Если у вас слишком мало совпадений, вы можете добавить ИЛИ и соответствующий термин, чтобы получить больше совпадений.
• Если вы получаете смешанные результаты с большим количеством нерелевантных веб-сайтов, вы можете использовать NOT, чтобы исключить обращения не по теме.

Как вы используете булеву логику?

Начните с утверждения, которое можно определить как истинное или ложное, и используйте основные операторы булевой логики НЕ, И и ИЛИ, чтобы сравнить его или объединить с другими бинарными утверждениями для создания более сложных наборов, которые также можно классифицировать.