Учебный курс «Информатика»

Алгебра логики

Логические элементы

Построение комбинационных схем

Арифметико-логическое устройство

Моделирование памяти. Триггер

Вопросы и упражнения

     Современный этап промышленного развития характеризуется тем, что разработчики систем автоматики и вычислительной техники стремятся использовать функциональные модули, выполняющие определённые схемные задачи: логические преобразования, хранение информации и т.д. Конкретный вид электрической схемы, использованной для реализации заданной логической функции, как правило, не имеет существенного значения. Техническое устройство, реализующее логическую функцию, может рассматриваться просто как логический элемент, внутренняя структура которого не конкретизируется.     На принципиальных и функциональных схемах логический элемент

ИЛИ изображается прямоугольником с единицей в левом верхнем углу.

    Логический элемент ИЛИ предназначен для “вычисления” значения логического сложения. Работа этого логического элемента эквивалентна проверке составного условия со служебным словом “или”. Алгоритм работы логического элемента “или” записывается следующим образом: “Если А=1 или В=1, то f(А,В)=1, иначе f(А,В)=0”.     Логический элемент И предназначен для “вычисления” значения логического умножения. Работа этого логического элемента эквивалентна проверке составного условия со служебным словом “и”. Алгоритм работы логического элемента “и” записывается следующим образом: “Если А=1 и В=1, то f(А,В)=1, иначе f(А,В)=0”.     Изображение логических элементов

И на функциональных и принципиальных схемах выглядит так:

    Логические элементы НЕ изображаются с кружком, который называется индикатором уровня сигнала.

    Итак, нам известны три основных логических элемента И, ИЛИ, НЕ. Сигналы, вырабатываемые одним логическим элементом, можно подавать на вход другого элемента — это даёт возможность образовывать цепочки из отдельных логических элементов.
    Например:

    Каждую такую цепочку называют логическим устройством, а соответствующую схему — функциональной схемой. Функциональную схему, которую полностью можно описать таблицей истинности, называют комбинационной схемой.      Комбинационная схема — это схема, в которой значения входных переменных в текущий момент времени полностью определяют значения выходных переменных.     Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, и более сложных элементов И-НЕ, ИЛИ-НЕ и др., соединяя их так, как это следует из логической функции. Рассмотрим элементы И-НЕ

и ИЛИ-НЕ:

    Логическая функция И-НЕ, которая представляет собой отрицание логического умножения, называется операцией Шеффера и кратко может быть записана в следующем виде:

    Логическая функция ИЛИ-НЕ, т.е. отрицание логического сложения, носит название «стрелка Пирса» и обозначается так:

    Связь операций И-НЕ и ИЛИ-НЕ с основными операциями алгебры логики устанавливается законами, открытыми английским математиком Августусом де Морганом (1806-1871) и поэтому носящими его имя. Первый из них устанавливает, что

отрицание логического умножения равносильно сумме отрицаний сомножителей:

    Второй закон показывает, что отрицание логического сложения равносильно произведению отрицаний слагаемых:

    Законы де Моргана сведены в таблицу законов алгебры логики.

Логические элементы

Мы с вами знаем следующие логические операции: конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и инверсия (отрицание). Все эти операции используются в алгебре логики.

Сегодня на уроке мы с вами узнаем, что такое логический элемент, познакомимся с такими логическими элементами, как конъюнктор, дизъюнктор и инвертор. А также научимся находить выходные данные исходя из предоставленной электронной схемы.

Алгебра логики является незаменимым элементом в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.

Мы с вами уже знаем, что любую информацию можно представить в дискретной форме. Дискретная форма

– это форма представления, при которой информация преподнесена в виде фиксированного набора отдельных значений. То есть, например, последовательностью нулей и единиц. В свою очередь, дискретные устройства – это устройства, которые обрабатывают дискретные значения (сигналы).

В свою очередь, логический элемент – это дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций.

Перед вами представлены условные обозначения (схемы) логических элементов, с помощью которых реализуется логическое умножение, логическое сложение и отрицание. Давайте разберёмся с каждой схемой отдельно.

Итак, первый логический элемент И (конъюнктор). С его помощью реализуется операция логического умножения. Рассмотрим его.

А – это входные данные первого элемента, B – второго, F – выходные данные. Вспомним таблицу истинности для конъюнкции.

Всевозможные входные данные А и B нам даны в первых двух столбцах. В третьем нам дан результат при выполнении конъюнкции – выходные данные. То есть значение F. Таким образом, можно сказать, что единица на выходе получится тогда и только тогда, когда на всех входах будут единицы. Или же, другими словами, в результате мы можем получить для F единицу тогда и только тогда, когда А и B равны единице.

Следующий логический элемент – ИЛИ (дизъюнктор).

Как вы уже, наверное, догадались, с его помощью реализуется операция логического сложения. И снова обратимся к таблице истинности для дизъюнкции.

В первых двух столбцах даны всевозможные входные данные для А и B. В третьем выходные данные, которые будут равны F. Исходя из этой таблицы можно сказать, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. То есть, если А или B будет равно единице, то F также будет равно единице.

И последний логический элемент – НЕ (инвертор).

С его помощью реализуется операция отрицания.

Здесь всё просто. Снова нам понадобится таблица истинности для инверсии. Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. То есть, если А = 0, то F будет равно 1. И, если А = 1, то F = 0.

Также необходимо знать, что все компьютерные устройства, которые производят операции над двоичными числами, и ячейки, в которых хранятся данные, представляют собой электронные схемы. Они же в свою очередь состоят из отдельных логических операций.

А сейчас давайте попробуем проанализировать несколько электронных схем и узнать, какой сигнал получится на выходе.

Смотрим на первую схему.

В ней используется только один элемент А. Снова будем использовать таблицу истинности. В первый столбец внесём входные данные ноль и один. Во второй столбец будем вносить данные, которые получаются при конъюнкции, в третьей – при инверсии. Он же будет являться столбцом, который будет обозначать выходные данные.

Мы видим, что от А идут две прямые. Это говорит о том, что одни и те же данные будут идти в двух направлениях. Первая операция – конъюнкция. При конъюнкции получим те же данные, что и в самом начале.

Далее идёт операция отрицания. При исходных данных, равных нулю получаем единицу, и наоборот, при исходных данных, равных единице получаем ноль.

Таким образом в итоге мы получили Ā. То есть можно сказать, что F = Ā.

Рассмотрим ещё одну схему.

Она немного сложнее первой. Снова будем использовать таблицу истинности. Она будет состоять из 8 столбцов. В первых двух будут находится входные данные А и B. В третьем конъюнкция А, в четвёртом – конъюнкция B. В пятые и шестые столбцы запишем отрицания конъюнкций А и B соответственно. Для упрощения отрицания конъюнкций А и B запишем как Ā и . В седьмом будет находится конъюнкция Ā и . И в последнем отрицание конъюнкции Ā и .

Таким образом мы с вами переписали все операции со схемы в таблицу истинности. Нам осталось только заполнить таблицу соответствующими данными. Итак, при конъюнкции двух А мы получим такие же данные как и в первом столбце. Перепишем их.

Аналогично поступим и с конъюнкцией двух B. Только данные будем брать со второго столбца.

Пятый столбец – Ā. Преобразуем данные, находящиеся в третьем столбце. Необходимо помнить, что при исходных данных, равных нулю, мы получим единицу. А при исходных данных, равных единице, получим ноль.

Аналогично и с шестым столбцом, а данные будем брать с четвёртого.

Седьмой столбец – это конъюнкция Ā и . Данные будем брать из пятого и шестого столбцов. Мы с вами помним, что на выходе получим единицу тогда и только тогда, когда на всех входах будут единицы. Заполним таблицу.

И последняя операция – отрицание конъюнкции Ā и . Исходные данные будем брать из седьмого столбца. И снова нужно знать, что если исходные данные равны нулю, то на выходе мы получим один, и наоборот, если исходные данные равны единице, то на выходе получим ноль.

Таким образом мы с вами узнали, какие получатся выходные данные в нашей схеме. То есть данные из восьмого и есть наша F.

Если мы построим выражение исходя из таблицы истинности, то получим следующее:

И снова рассмотрим схему, но более простую.

Для начала составим логическое выражение. Будем идти справа налево. Последний логических элемент, который к нас изображён – это инвертор. В него поступают сигналы от дизъюнктора. В свою очередь в дизъюнктор поступают данные от входа А и входа Бэ. В результате мы получим следующее:

А сейчас давайте на основании этого логического выражения составим таблицу истинности и узнаем, какие данные получатся на выходе.

Таблица будет состоять из 4 столбцов. В первые два вносим исходные данные А и B соответственно. Далее мы будем выполнять дизъюнкцию, а затем инверсию. Это и будет являться заголовками наших столбцов.

Итак, первая операция – дизъюнкция. Мы с вами знаем, что на выходе мы получим единицу тогда, когда хотя бы на одном входе будет единица. Данные будем брать из первого и второго столбцов. Заполним третий столбец.

Для того, чтобы внести данные в четвёртый столбец, нам нужно брать входные данные из третьего. Если у нас входные данные равны нулю, то на выходе мы получим единицу, а если входные данные равны единицы, то на выходе будет ноль. Снова заполним таблицу.

В четвёртом столбце находятся выходные данные для нашего выражения F.

А сейчас давайте рассмотрим пример, в котором мы сами научимся строить электронную схему исходя из логического выражения. А также найдём выходные данные с помощью таблицы истинности.

Итак, наше выражение выглядит следующим образом:

Сначала будет выполняться конъюнкция А и B. Изобразим А и B.

От них проведём две прямых и нарисуем прямоугольник, который будет обозначать конъюнктор. Поставим внутри соответствующий знак.

Далее у нас идёт дизъюнкция конъюнкции А и B с C. Изобразим C.

Затем проведём от неё ломанную. От конъюнктора также проведём прямую. И снова нарисуем прямоугольник, который будет изображать дизъюнктор. Снова поставим внутри соответствующий знак.

Нам осталось изобразить инвертор. Проведём от правой стороны дизъюнктора прямую и на пересечении дизъюнктора и прямой нарисуем незакрашенный кружок. Над выходной прямой напишем букву F.

Мы построили электронную схему. Теперь осталось построить таблицу истинности и найти выходные данные.

Таблица будет состоять из 6 столбцов. В первых трёх запишем всевозможные входные данные для А, B и C.

Четвёртый столбец – конъюнкция А и B, пятый дизъюнкция конъюнкции А и B и переменной C. Шестой инверсия всего выражения.

Теперь осталось заполнить таблицу данными.

При конъюнкции на выходе единица будет тогда и только тогда, когда на всех входах будут единицы. Для заполнения четвёртого столбца будем брать данные из первого и второго. Внесём данные в соответствии с данными.

Пятый столбец – дизъюнкция. Данные будем брать из третьего и четвёртого столбцов. Заполним столбец в соответствии с правилом: на выходе будет единица тогда, когда хотя бы на одном входе будет единица.

И последний, шестой столбец – инверсия. Данные будем брать из пятого столбца. Если на входе у нас элемент ноль, то на выходе будет единица, и наоборот. Заполним столбец.

Данные этого столбца являются выходными данными построенной нами электронной схемы.

А теперь давайте исходя из таблицы истинности составим выражение, а исходя из выражения – построим электронную схему.

Нам дана таблица истинности, в которой записаны входные данные и операции, которые необходимо выполнить. Все операции указаны в порядке выполнения их в выражении. Для начала давайте заполним таблицу и найдём выходные данные.

Первая операция – дизъюнкция А и B. На выходе будет единица тогда, когда хотя бы на одном входе будет единица. Заполним четвёртый столбец исходя из данных первого и второго столбцов.

Вторая операция – инверсия C. Заполним пятый столбец исходя из данных третьего столбца. Необходимо помнить, что если входные данные равны нулю, то на выходе мы получим единицу. А если входные данные равны единице, то на выходе мы получим ноль. Внесём данные.

И последний столбец – конъюнкция дизъюнкции А или B и инверсии C. При выполнении конъюнкции мы с вами знаем, что на выходе единица будет тогда и только тогда, когда все входные данные равны единице. Заполним шестой столбец исходя из данных третьего и четвёртого столбцов.

Можно заметить, что всё наше выражение записано в шапке последнего шестого столбца. То есть, мы получим следующее:

Нам осталось построить электронную схему.

Запишем А и B и проведём от них прямые к прямоугольнику, который будет обозначать дизъюнктор. Обозначим это соответствующим символом.

Теперь нам нужно изобразить инвертор. Для этого от C идут ломанные к конъюнктору. А на пересечение прямой, которая выходит из конъюнктора изобразим кружок, который и будет изображать отрицание.

Теперь проводим кривые от дизъюнктора и конъюнктора к новому прямоугольнику. Он будет изображать конъюнктор. Обозначим его соответствующим знаком.

Проводим прямую из правой стороны крайнего конъюнктора, которая будет обозначать выходные данные. Обозначим её буквой F.

Мы выполнили с вами задание, в котором записали выражение исходя из таблицы истинности и построили электронную схему.

А сейчас пришла пора подвести итоги урока.

Сегодня мы с вами познакомились с такими логическими элементами, как конъюнктор, дизъюнктор и инвертор.

Научились исходя из схемы при помощи таблицы истинности определять, какие данные должны получиться на выходе, а также научились строить электронные схемы по данному выражению и таблице истинности.

Предикаты и кванторы. Логические элементы компьютера. Логические задачи

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, полный углубленный курс, 4 часа в неделю) | Логические элементы компьютера

Содержание урока

§23. Предикаты и кванторы

§24. Логические элементы компьютера

Простейшие элементы

Триггер

Сумматор

Вопросы и задания

Задачи

§25. Логические задачи

§24. Логические элементы компьютера

Простейшие элементы

В компьютерах все вычисления производятся с помощью логических элементов — электронных схем, выполняющих логические операции. Обозначения простейших элементов приводятся в таблице на рис. 3.21 (ГОСТ 2.743-91). Заметьте, что небольшой кружок на выходе (или на входе) обозначает операцию «НЕ» (отрицание, инверсию).

Рис. 3.21

Может показаться, что для реализации сложных логических функций нужно много разных видов логических элементов. Однако, как мы видели в § 22, любую логическую функцию можно представить с помощью операций «НЕ», «И» и «ИЛИ» (такой набор элементов называется полным). Именно эта классическая «тройка» используется в книгах по логике, а также во всех языках программирования. Тем не менее инженеры часто предпочитают строить логические схемы на основе элементов «ИЛИ-НЕ». Как показано в § 19, эта функция (штрих Шеффера) позволяет реализовать операции «НЕ», «И» и «ИЛИ», а значит, и любую другую операцию.

Если нужно составить схему по известному логическому выражению, её начинают строить с конца. Находят операцию, которая будет выполняться последней, и ставят на выходе соответствующий логический элемент. Затем повторяют то же самое для сигналов, поступающих на вход этого элемента. В конце концов должны остаться только исходные сигналы — переменные в логическом выражении.

Составим схему, соответствующую выражению

Х = А • В + А • В • С.

Последняя операция — это логическое сложение, поэтому на выходе схемы будет стоять элемент «ИЛИ» (рис. 3.22).

Рис. 3.22

Для того чтобы получить на первом входе А • В, нужно умножить А на В, поэтому добавляем элемент «И» (рис. 3.23).

Рис. 3.23

Чтобы получить А, ставим элемент «НЕ» (рис. 3.24).

Рис. 3.24

Аналогично разбираем вторую ветку, которая поступает на второй вход элемента «ИЛИ» (рис. 3.25).

Рис. 3.25

Схема составлена, её входами являются исходные сигналы А, В и С, а выходом — X.

Следующая страница Триггер

Cкачать материалы урока

Базовые логические элементы компьютера — Информатика, информационные технологии

При построении функциональных узлов компьютерных систем используются элементы, которые реализуют базовую систему логических функций. Одним из таких базовых наборов является набор из трех функций: дизъюнкции (логическое ИЛИ), конъюнкции (логическое И) и отрицание (логическое НЕ). На рисунке 2.4 показаны условные обозначения и значения выходного сигнала в зависимости от входных сигналов. Ноль изображается на диаграммах низким значением сигнала, а единица – высоким. Используя эти базовые элементы, строятся все функциональные узлы цифровых вычислительных систем.

Рисунок 2.4. Базовая система логических элементов цифровых устройств

Рассмотрим некоторые функциональные узлы КС, построенные на логических элементах.

Элемент памяти

Основой любого компьютера является ячейка памяти, которая может хранить данные или команды. Основой любой ячейки памяти является функциональное устройство, которое может по команде принять или выдать один двоичный бит и сохранять его сколь угодно долго. Такое устройство называется триггер, или защелка. Оно строится на основе базового набора логических схем. На рисунке 2.5 показана схема триггера.

Рисунок 2.5. Схема триггера в состоянии хранения бита информации

Он собран па четырех логических элементах: два элемента «логическое НЕ» (схемы 1 и 2) и два элемента «логическое И-НЕ» (схемы 3 и 4). Два последних элемента представляют собой комбинацию логических элементов «логическое И» и «логическое НЕ». Такой элемент на входе выполняет операцию логического умножения, результат которой инвертируется на выходе логическим отрицанием. Триггер имеет два выхода Q и . Сигнал на выходе Q соответствует значению, хранящемуся в триггере. Выход используется при необходимости получить инверсное значение сигнала. Входы S и R предназначены для записи в триггер одного бита со значением ноль или единица.

Рассмотрим состояние триггера во время хранения бита. Пусть в триггер записан ноль (на выходе Q низкий уровень сигнала). Единица на выходе схемы 4 и единица на выходе схемы 1 поддерживают состояние выхода схемы 3 в состоянии нуля ( ). В свою очередь, ноль на выходе схемы 3 поддерживает единицу на выходе схемы 4 ( ). Такое состояние может поддерживаться триггером бесконечно долго.

Для записи в триггер единицы на вход S подается единица (рисунок 2.6).

Рисунок 2.6. Запись в триггер единицы

На выходе схемы 1 получится ноль, который обеспечит на выходе схемы 3 единицу. С выхода схемы 3 единица поступит на вход схемы 4, па выходе которой значение изменится на ноль ( ). Этот ноль на входе схемы 3 будет поддерживать сигнал на се выходе в состоянии единицы. Теперь можно снять единичный сигнал на входе S, на выходе схемы 3 все равно будет высокий уровень. Т.е. триггер сохраняет записанную в него единицу. Единичный сигнал на входе S необходимо удерживать некоторое время, пока на выходе схемы 4 не появится нулевой сигнал. Затем вновь на входе S устанавливается нулевой сигнал, но триггер поддерживает единичный сигнал на выходе Q, т.е. сохраняет записанную в него единицу. Точно так же, подав единичный сигнал на вход R, можно записать в триггер ноль.

Условное обозначение триггера показано на рисунке 2.7.

Рисунок 2.7. Условное обозначение триггера

Триггер служит основой для построения функциональных узлов, способных хранить двоичные числа, осуществлять их синхронную параллельную передачу и запись, а также выполнять с ними некоторые специальные операции. Такие функциональные узлы называются регистрами.

Регистр представляет собой набор триггеров, число которых определяет разрядность регистра. Разрядность регистра кратна восьми битам: 8-, 16-, 32-, 64-разрядные регистры. Кроме этого в состав регистра входят схемы управления его работой.

Устройства обработки информации

Для обработки информации компьютер должен иметь устройство, выполняющее основные арифметические и логические операции над числовыми данными. Такие устройства называются арифметико-логическими устройствами (АЛУ). В основе АЛУ лежит устройство, реализующее арифметическую операцию сложения двух целых чисел. Остальные арифметические операции реализуются с помощью представления чисел в дополнительном коде.

Сумматор АЛУ представляет собой многоразрядное устройство, каждый разряд которого представляет собой схему на логических элементах, выполняющих суммирование двух одноразрядных двоичных чисел с учетом переноса из предыдущего младшего разряда. Результатом является сумма входных величин и перенос в следующий старший разряд. Такое функциональное устройство называется одноразрядным, полным сумматором. Его условное обозначение показано на рисунке 2.8.

Рисунок 2.8. Условное обозначение полного одноразрядного сумматора

Рассмотренные выше функциональные элементы являются основными при построении схем компьютерных систем.

Операционные системы

Как уже говорилось выше, в состав вычислительной системы входят как аппаратные, так и программные средства, которые для вычислительной техники принято рассматривать отдельно. Отдельно рассматривают аппаратную конфигурацию вычислительных систем и их программную конфигурацию. Такой принцип разделения имеет для информатики особое значение, поскольку очень часто решение одних и тех же задач может обеспечиваться как аппаратными, так и программными средствами. От верного выбора программного решения конфигурации зависят производительность и эффективность всей вычислительной системы в целом.

Статьи к прочтению:

Логические элементы И, ИЛИ, НЕ

Похожие статьи:

Логические элементы

1. 1. Общие сведения о логических элементах

В любой цифровой системе присутствуют логические элементы и память.

Логическими элементами (ЛЭ) называют устройства, преобразующие входную информацию в выходную по определенным правилам.

В цифровой технике входная и выходная информация является бинарной (все переменные принимают только два значения: 1 или 0). Будем обозначать сигналы входной информации переменными Х₁, Х₂,…, Х_n, а сигнал выходной информациипеременнымиF, Y₁,Y₂ и т.д..

Основные логические операции:

Логическое сложение(дизъюнкция) реализуется логическим элементом ИЛИ. Элемент, выполняющий функцию ИЛИ, имеет несколько входов и один выход. Сигнал логической единицы появляется на выходе такого устройства, если хотя бы на один из входов подана логическая единица. Функцию логического сложения математически записывают в виде

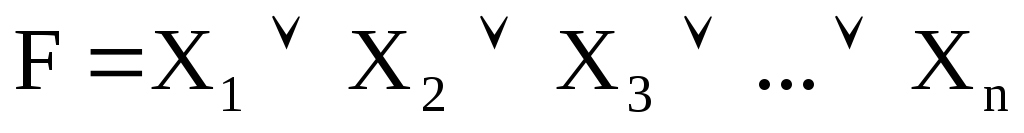. (1.1)

Схему ИЛИ обозначают как на рис. 1.1.

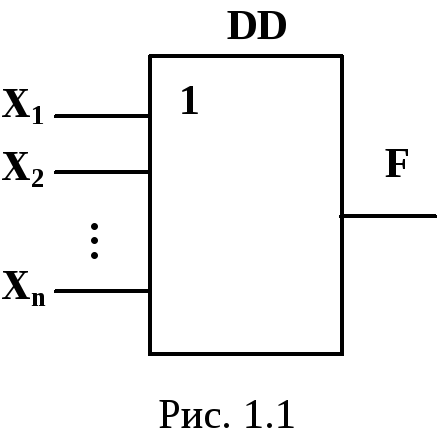
Логическое умножение (конъюнкция) реализуется логическим элементом И. Сигнал логической единицы появляется на выходе такого устройства, если на все входы подана логическая единица. Функцию логического умножения математически записывают в виде

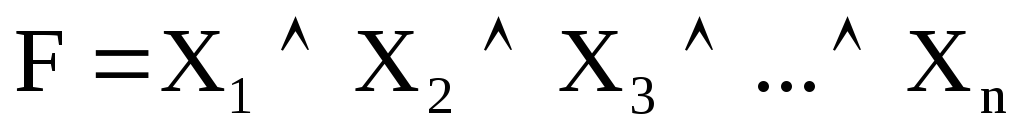. (1.2)

Схему И (схему совпадения) обозначают как на рис. 1.2.

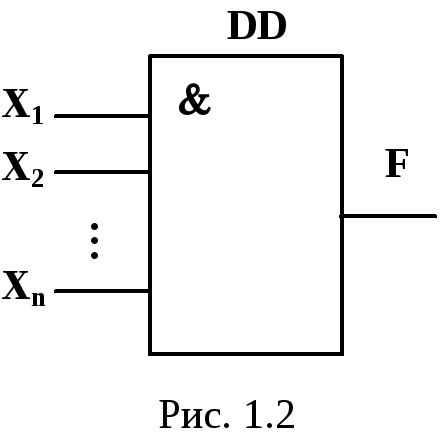
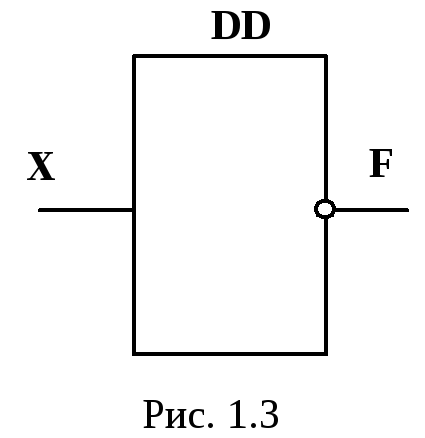
Логическое отрицание (инверсия) реализуется логическим элементом НЕ, который называют инвертором. Сигнал логической единицы появляется на выходе такого устройства, если на вход подан логический ноль. Функцию логического отрицания математически записывают в виде

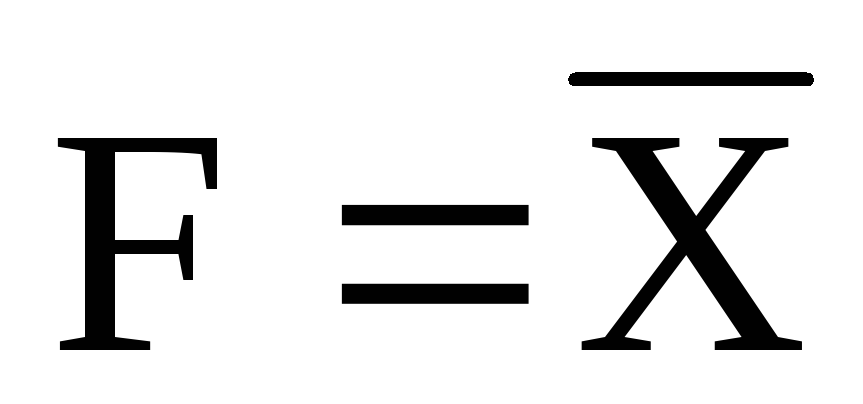. (1.3)

Инверсия по выходу (входу) обозначается кружком в контуре прямоугольника, изображающем схему (рис. 1.3).

1. Основные характеристики и параметры логических элементов

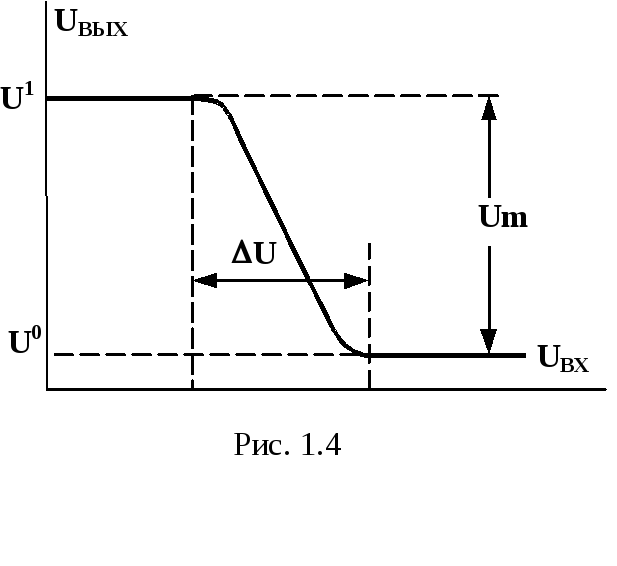
1. Характеристика передачи U_ВЫХ(U_ВХ). На рис. 1.4 представлена характеристика передачи инвертора, на которой обозначены напряженияU¹ иU⁰  напряжения высокого и низкого уровней, соответствующие логической единице и логическому нулю,Uширина активной зоны,Umлогический перепад.

2. Коэффициент объединения по входу nопределяет число входов логического элемента. Обычноn  8.

3. Коэффициент разветвления по выходу mопределяет возможное число одновременно подключаемых логических элементов к данному логическому элементу. Обычноm ограничивают на уровнеn, но оно может доходить и до 100, и в общем случаеmот структуры логического элемента.

Параметры m иn определяютфункциональную возможностьлогического элемента.

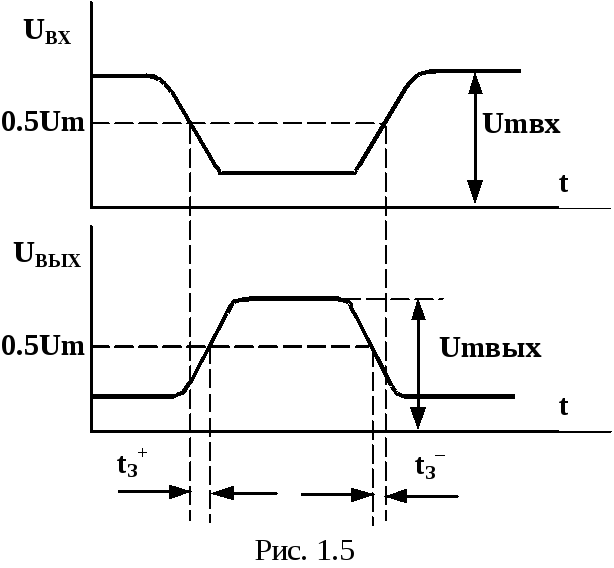
4. Быстродействие характеризуется временем задержки распространения сигналов. Обычно различают (рис. 1.5) время задержки распространения сигнала при включении логического элементаt_З⁺, время задержки распространения сигнала при выключении логического элементаt^– и среднее время задержки распространения

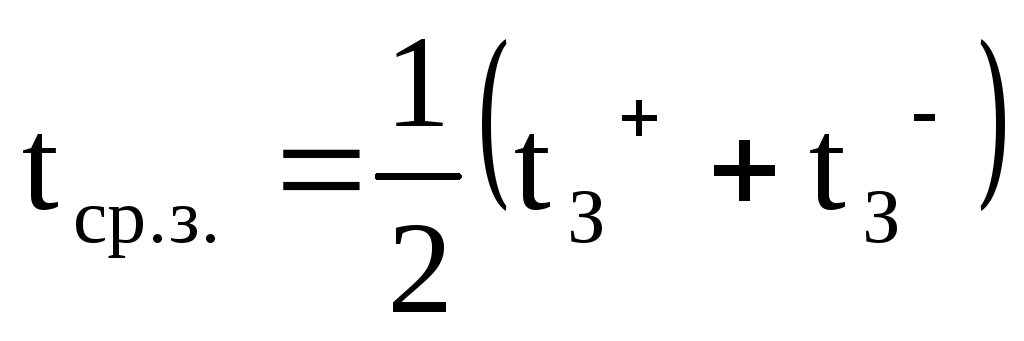. (1.4)

В зависимости отсреднего времени задержки распространения логические элементы подразделяют на:

• сверхбыстродействующие элементы (t_ср.з. 5 нс)

• быстродействующие элементы (5 нс  t_ср.з. 10нс)

• элементы со среднимбыстродействием (10 нс  t_ср.з. 50нс)

• медленнодействующие элементы (t_ср.з. 50нс)

5. Помехоустойчивость логического элемента определяется максимальной величиной помехи на входе, которая не переключает логический элемент из одного состояния в другое. В зависимости от величины помехи логические элементы подразделяют на:

6. Экономичность определяется мощностью, потребляемой от источника питания.

«Логические элементы и основные логические устройства компьютера» (8 класс)

Урок №

Класс _____. Дата «____» __________ 200__ г.

Класс _____. Дата «____» __________ 200__ г.

Класс _____. Дата «____» __________ 200__ г.

Тема: Логические элементы и основные логические устройства компьютера

Цель урока:

• Дать учащимся представление о том, как в компьютере при помощи логических элементов выполняются арифметические и логические операции..

Опорные понятия:

Новые понятия:

Задачи учителя:

• На аналогиях из повседневной жизни показать, что логика хорошо реализуется при помощи электронных схем;

• Познакомить учащихся с логическими элементами;

• Познакомить учащихся с некоторыми логическими устройствами компьютера;

• Дать представление учащимся о последовательности создания логического устройства.

План урока

1. Организационный момент;

1. Повторение пройденного материала

• сложные логические выражения;

• порядок выполнения операций в сложном логическом выражении;

• правила составления таблиц истинности;

• дополнительный материал.

2. Логические элементы и основные логические устройства компьютера:

   • реализация логики при помощи электронных схем;

   • логические элементы;

   • некоторые логические устройства компьютера;

   • последовательность создания логического устройства (полусумматор, сумматор).

3. Подведение итогов за урок

Домашнее задание – конспект.

Читать тема 24.4 стр. 319-321

Устно: стр. 321, вопросы 6–8.

Вопросы:

1. Какие логические элементы вам известны?

2. Что такое регистр?

3. В чем состоит принцип работы сумматора?

4. Составить таблицу истинности, а по ней – схему умножения двух двоичных разрядов числа. С чем совпадает такая схема?

Методика проведения урока:

Реализация логики при помощи электронных схем

Историческая справка

С 1867 года американский логик Чарльз Сандерс Пирс (в его честь названа одна из логических операций – «стрелка Пирса») работает над модификацией и расширением булевой алгебры. Пирс первым осознал, что бинарная логика имеет сходство с работой электрических переключательных схем. Электрический переключатель либо пропускает ток (что соответствует значению Истина), либо не пропускает (что соответствует значению Ложь). Позже Пирс даже придумал простую электрическую логическую схему, но так и не собрал ее.

В настоящее время существуют электронные схемы, реализующие все логические операции.

Логические элементы

Как при строительстве дома применяют различного рода типовые блоки – кирпичи, рамы, двери и т. п., так и при разработке компьютера используют типовые электронные схемы. Каждая схема состоит из определенного набора типовых электронных элементов.

Электронным элементом называется соединение различных деталей, в первую очередь – диодов и транзисторов, а также резисторов и конденсаторов в виде электрической схемы, выполняющей некоторую простейшую функцию.

Электронный элемент, реализующий логическую функцию, называется логическим элементом.

Любая информация при обработке на компьютере представляется в двоичной форме, то есть кодируется некоторой последовательностью 0 и 1. Такую обработку в любом компьютере выполняют так называемые логические элементы, из которых составляются логические схемы, выполняющие различные логические операции. Реализация любых логических операций над двоичными сигналами основана на использовании логических элементов трех типов: И, ИЛИ, НЕ.

Логический элемент – это электронное устройство, реализующее одну из логических функций. Рассмотрим указанные три простейших логических элемента. В зависимости от типа элемента на его вход подается один или несколько входных сигналов, а на выходе – снимается один выходной сигнал. Названия и условные обозначения этих логических элементов являются стандартными и используются при составлении и описании логических схем компьютеров.

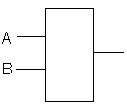
Логический элемент И (конъюктор)

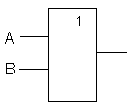
Логический элемент ИЛИ (дизъюнктор)

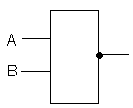
Логический элемент НЕ (инвертор)

Результат (0 или 1) на выходе каждого из указанных логических элементов определяется согласно таблицам истинности для той логической операции, которую реализует данный логический элемент.

Физически каждый логический элемент представляет собой электронную схему, в которой на вход подаются некоторые сигналы, кодирующие 0 или 1, а с выхода снимается также сигнал, соответствующий0 или 1 в зависимости от типа логического элемента.

Решение задач «Базовые логические элементы»

Цели урока:

1. Образовательные:

• отработать навыки построения функциональных схем, записи логических функций
• сформировать навыки построения однотактных автоматов,
• научиться синтезировать логические схемы

2. Воспитательные:

• воспитание познавательного интереса учащихся, умения слушать, аккуратности в работе, трудолюбия, умения работать в группах.
• формирование интеллектуальной и эмоциональной активности учащихся.

3. Развивающие:

• становление и развитие логического мышления:
• развитие познавательного интереса:
• формирование информационной культуры и потребности приобретения знаний.
• развитие конструкторских умений,
• формирование элементов графической культуры;
• восприятие компьютера, как инструмента, работающего по законам логики

Ход урока

Поминутный план урока: см. Приложение 1 (“План урока.doc”)

Ход всего урока сопровождается показом презентации “Логические основы компьютера.ppt” (см. Приложение 2)

Перед началом урока на компьютерах учащихся должен быть размещен необходимый материал для работы: папки “Задание для работы в группах ,,Алмазы,, и “Дополнительное задание для самостоятельной работы”; файл “Задания для самостоятельной работы.doc” (см. Приложение 3).

I. Организационный момент. Постановка целей урока

– На предыдущем уроке мы с вами познакомились с основами базовых логических элементов, с построением логических схем и даже пытались решать простейшие задания, основанные на построении логических схем по заданной формуле.

Цели нашего сегодняшнего урока:

• закрепить навыки построения функциональных схем и записи логических функций;
• а так же научиться синтезировать логические схемы, т.е. попытаемся научиться применять полученные знания для построения более сложных схем и решения практических задач.

– Но, прежде, чем мы приступим к основной работе, давайте повторим основный теоретические момент, изученные на предыдущем уроке.

II. Проверка домашнего задания

– При ответе на вопросы вам надо будет либо записать на листке пропущенное слово (или несколько слов), либо указать через запятую номера правильных, как вы считаете, ответов. В некоторых вопросах правильный ответ – единственно верный, а в некоторых – их несколько. Время на выполнение ограничено. Подпишите, пожалуйста, листочки … и приступим….

Задания теста на слайдах презентации к уроку. По окончании тестирования, собрать листочки.

III. Разделение на группы и объяснение задачи.

– Вы прекрасно понимаете, что строя электрические цепи можно обмотать весь дом проводами и не добиться нужного эффекта, а можно, используя минимальное число элементов и соединений добиться задуманного. Стоит только задуматься и выбрать правильное решение.

“Всё наше достоинство заключено в мысли
Не пространство, не время, которые мы не можем заполнить,
возвышает нас, а именно она, наша мысль.
Будем же учиться хорошо мыслить.”
Французский математик и философ XVII века Б.Паскаль

Правила игры.

Задача заключается в том, чтобы последовательно передавать алмаз с верхней площадки на нижнюю. Подавая ток на вход механизмов в правой части схемы, можно выдвигать площадки на пути алмаза. Если на входе механизма нет тока, площадка убирается.

• Для управления механизмами используют выключатели в левой части поля. Их состояние изменяется щелчком мыши. Если выключатель включен, по цепи идет ток и поступает на логические схемы, включенные в эту цепь (средняя часть поля). Логические схемы различны: инвертор, конъюнктор и т.д.

Алмаз нельзя передавать сразу через несколько «пролетов» – в этом случае он разбивается и приходится начинать уровень заново. Кроме того, у вас есть только 5 алмазов на всю игру, если вы разобьете их все, задание считается невыполненным. Придется начинать с самого начала – с первого уровня.

Игра состоит из 10 уровней. На все отводится 4 минуты. Ваша задача – пройти на более высокий уровень. Я призываю вас не жать на выключатели бездумно, а, действительно, пытаться “хорошо мыслить”. Начинаем.

IV. Работа в группах (алмаз).

Задание: см. Приложение 4 (папка “Задание для работы в группах ,,Алмазы,,).

Выполнение задания на компьютерах (работа в парах). На работу 4 минуты.

– Поднимите руки те команды, которые смогли подняться выше 6-го уровня. (Выставление оценок.)

V. Работа в группах (задания по схемам).

Задание: см. Приложение 5 (“Задания для команд.doc”).

Класс разбивается на группы по 4 человека для работы в группах по схемам.

Цель работы: при выполнении заданий продумать и сформулировать алгоритм для решения задач подобного типа.

– По окончании работы представитель группы будет защищать решение перед классом. На всю работу 6 минут.

Через 5 минут после начала работы зазвучит музыка. Предупредить учащихся, что время для выполнения работы подходит к концу и пора заканчивать. Через 1,5 минуты все учащиеся рассаживаются на места.

VI. Физкультминутка (1 минута (до окончания музыки)).

VII. “Выступление” представителей групп.

Решение заданий для групп: см. Приложение 6 (“Решение заданий для групп.doc”).

1-я группа: объясняет решение задания № 1.
2-я группа: объясняет алгоритм решения задач, подобных заданию № 1.
3-я группа: объясняет решение задания № 2.
4-я группа: объясняет алгоритм решения задач, подобных заданию № 2.

На защиту решений каждой группе дается 1, 5 минуты.

VIII. Решение задачи “Синтез автоматов”.

Объяснение нового материала учителем: совместная работа учащихся и учителя.

Синтез однотактных автоматов.

Конструирование (синтез) автоматов – одна из основных задач кибернетики.

(Кибернетика – наука о процессах управления в сложных динамических системах, основывающаяся на теоретическом фундаменте математики и логики, а также применении ВТ.)

Автомат – агрегат, представляющий собой систему механизмов и устройств, в которой полностью механизированы, т.е. выполняются без непосредственного участия человека, процессы получения, преобразования, передачи и использования энергии, вещества или информации.

Алгоритм синтеза автоматов

Рис. 1

Задача 1. Для оповещения зрителей, наблюдающих за ходом состязаний по тяжелой атлетике, изготовлен светящийся транспарант: “Вес взят правильно”. Подсвечивание транспаранта осуществляется по команде, выдаваемой автоматом. Этот автомат обрабатывает сигналы, поступающие от трех судей А, В, С. Судья А – старший. Сигнал на подсвечивание транспаранта автомат выдаст тогда, когда нажмут кнопки все трое судей или двое, один из которых – старший. Сконструировать автомат.

Решение.

1-й шаг. Описание задачи, которую должен решать автомат принято называть словесной формой задания автомата. Автомат предстает при этом как некий “черный ящик”: еще неизвестно как будет устроен внутри, но уже ясно, что ему предстоит делать, известно как он связан с внешней средой. В данном случае будущий автомат имеет три входа – это линии, по которым поступают сигналы от судей А, В и С и один выход Х (сигнал для подсвечивания транспаранта “вес взят правильно”).

2-й  шаг.

Рис. 2

3-й шаг. Теперь можно составить таблицу работы автомата.

Рис. 3

4-й шаг.

Рис.4

5-й шаг.

Рис. 5

IX. Разбор домашнего задания (на следующий урок):

Уровень знания:

Выучить новые понятия конспекту урока в тетради

№ 1. Постройте схему для логической функции F (a, b, c) = (￢a & ￢b) & (c v ￢a) & c.

№ 2. Дана логическая схема:

Рис. 6

 

Составьте логическую функцию, которая ей соответствует. Найдите значения выходного сигнала.

Уровень понимания:

+ Сформулировать алгоритм построения структурных формул и функциональных схем при решении задач о синтезе однотактных автоматов.

Уровень применения:

+ № 3. Три цеха – А, В и С – обеспечивает электроэнергией небольшая электростанция, на которой установлены два генератора – Х и Y. Если в энергии нуждается один из трех цехов, то достаточно включить генератор Y. Если же в энергии нуждаются два цеха одновременно – достаточно генератора Х. Снабжение всех трех цехов одновременно обеспечивается совместной работой генераторов X и Y. Необходимо построить такой автомат, который получая заявки от цехов А, В и С на снабжение энергией, может разумно перераспределять нагрузку между генераторами.

X. Самостоятельная работа: решение в тетрадях задачи № 1 и № 2. На решение отводится 7 минут.

Прежде чем решать задачу, подумай, что делать с ее решением!
Д.Пойа

№ 1. Постройте логическую схему выражения f = не (а или b) и (с или b).

Определите значение логического выражения, если а = истина, b = ложь, с = истина.

№ 2. Сконструировать автомат для подсчета голосов при тайном голосовании. Голосуют три человека. Автомат выдаст сигнал “избран”, если число голосов “за” не менее двух.

Дополнительное задание: № 3.

Рис. 7

Дополнительное задание: № 4 (см. Приложение 7 (“Дополнительное задание для самостоятельной работы”)).

XI. Подведение итогов урока:

– Выставление оценок, выборочный сбор тетрадей (“у менее активных учеников”; цель: выяснить, как и они, в том числе, усвоили материал урока.).

1. Оценить работу класса и назовите учащихся, отличившихся на уроке.

2. Выборочный сбор тетрадей (“у менее активных учеников”; цель: выяснить, как и они, в том числе, усвоили материал урока.).

– Нами были рассмотрены различные задачи, основанные на построении логических схем. Приемы для их решения различны. Мы, конечно, рассмотрели далеко не все возможные способы решения подобных задач. Возможно, вы найдете более простой и более интересный по сравнению с рассмотренными. Из этого можно сделать вывод, что, решая, какую-либо задачу не надо останавливаться на каком-то одном приеме, ведь вероятнее всего эту же задачу можно решить и другим методом, который будет и легче и проще для данной задачи. Я еще раз призываю вас “учиться думать красиво”.

– Работая в группах, вы выделили в каждой группе одного самого активного. Я согласна с вашей оценкой их работы и тоже оцениваю их работу сегодня, на «отлично». Но мне хотелось бы убедиться, что и все остальные поняли эту тему не хуже. Поэтому по окончании урока попрошу некоторых из вас сдать тетрадь с самостоятельной работой на проверку.

– Надеюсь, что все, что мы сегодня с вами делали на уроке, было и понятно, и интересно. По крайней мере, мне с вами работать было приятно. Спасибо всем за урок!